
第四章傅里叶变换在系统分析中的应用 4.1学习要求 通过本章的学习,学生应重点掌握系统函数H(⊙)的意义及其在系统分析中的作用: 无失真传输条件和理想低通滤波器的概念及其物理不可实现性:希尔伯特变换及系统函数的 约束特性:与傅里叶变换相关的基本通信原理和技术。 4.2内容概述 4.2.1线性时不变系统的频率响应H(o) 如果LT系统的单位冲激响应为h(t),激励为f(t),其零状态响应y(t)=f(t)*h(t), 根据傅里叶变换的卷积特性有Y(Ujo)=F(jo)H(jo)。 定义描述LTI系统的频率响应H(jo)为 H(j0)=Y(jo)=FTTK(t) (4-1) F(jo) 系统的频率响应(简称频响),是系统输出与输入的傅里叶变换之比,也就是系统冲激响 应的傅里叶变换,H(jo)与h(t)构成一对傅里叶变换对。实际上,频率响应H(jo)反映了 LTI系统对不同频率的信号所起的作用。 4.2.2系统的无失真传输 (一)无失真传输条件 设激励为f(t),响应为y(t),则按照定义,无失真传输的条件是 y(t)=Kf(t-to) (4-2) 式中K为常数,1。为滞后时间。满足上式的系统,其输出信号的幅度是输入信号的K 倍,并延时1。出现,但波形不变。 满足无失真传输系统的频响应为
1 第四章 傅里叶变换在系统分析中的应用 4.1 学习要求 通过本章的学习,学生应重点掌握系统函数 H j ( ) 的意义及其在系统分析中的作用; 无失真传输条件和理想低通滤波器的概念及其物理不可实现性;希尔伯特变换及系统函数的 约束特性;与傅里叶变换相关的基本通信原理和技术。 4.2 内容概述 4.2.1 线性时不变系统的频率响应H j ( ) 如果 LTI 系统的单位冲激响应为h(t) ,激励为 f (t),其零状态响应 y(t) f (t) h(t), 根据傅里叶变换的卷积特性有Y( j) F( j)H( j) 。 定义描述 LTI 系统的频率响应 H( j)为 [ ( )] ( ) ( ) ( ) FT h t F j Y j H j (4-1) 系统的频率响应(简称频响),是系统输出与输入的傅里叶变换之比,也就是系统冲激响 应的傅里叶变换,H( j)与h(t)构成一对傅里叶变换对。实际上,频率响应 H( j)反映了 LTI 系统对不同频率的信号所起的作用。 4.2.2 系统的无失真传输 (一)无失真传输条件 设激励为 f (t),响应为 y(t) ,则按照定义,无失真传输的条件是 ( ) ( ) 0 y t Kf t t (4-2) 式中 K 为常数, 0 t 为滞后时间。满足上式的系统,其输出信号的幅度是输入信号的 K 倍,并延时 0 t 出现,但波形不变。 满足无失真传输系统的频响应为

H(j)=Ke-jo=H(jo)e) H(j@)=K (4-3) p(0)=-010 可见,要使信号通过线性系统时不产生失真,则要求在信号的全部频带内,系统频响的 幅频特性为一常数,相频特性是一过原点的直线。 (二)线性系统引起的信号失真 不满足无失真传输条件的系统,将引起输入信号的传输失真,分为两种: ()幅度失真:系统对信号不同频率分量产生不等的幅度衰减,使响应中各频率分量的 幅度相对于激励发生变化。 (2)相位失真,即系统对信号不同频率分量产生的相移与频率不成正比,使响应的各频 率分量在时间轴出现的位置不同。 系统的幅度失真和相位失真可能同时存在。信号通过线性系统产生的幅度失真和相位失 真均不会产生新的频率分量,属于线性失真。 4.2.3理想低通滤波器 (一)理想低通滤波器 1.理想低通滤波器 理想滤波器通带内的幅频特性均满足无失真传输特性,而且其通带和阻带之间具有明显 的界线,但这种滤波器实际上是不可实现的。 理想低通滤波器的频率响应定义为 H(jo)=H(jo)ei) (44) 其中 1 I H(j@)F0 |o长o。 o>0。 p(o)=-00 2.理想低通滤波器的冲激响应 h)=o-Sal[o.(t-】 (4-5) n 是一个延时采样函数。 3.理想低通滤波器的阶跃响应 )=sinxdx 2π0 (4-6) 式中的积分称为“正弦积分”用S)表示为:S列=“本。阶跃 应上升时间与系统的带宽(截止频率)成反比。 2
2 ( ) ( ) ( ) 0 j t j H j Ke H j e 0 ( ) | ( ) | t H j K (4-3) 可见,要使信号通过线性系统时不产生失真,则要求在信号的全部频带内,系统频响的 幅频特性为一常数,相频特性是一过原点的直线。 (二)线性系统引起的信号失真 不满足无失真传输条件的系统,将引起输入信号的传输失真,分为两种: (1) 幅度失真:系统对信号不同频率分量产生不等的幅度衰减,使响应中各频率分量的 幅度相对于激励发生变化。 (2) 相位失真,即系统对信号不同频率分量产生的相移与频率不成正比,使响应的各频 率分量在时间轴出现的位置不同。 系统的幅度失真和相位失真可能同时存在。信号通过线性系统产生的幅度失真和相位失 真均不会产生新的频率分量,属于线性失真。 4.2.3 理想低通滤波器 (一)理想低通滤波器 1.理想低通滤波器 理想滤波器通带内的幅频特性均满足无失真传输特性,而且其通带和阻带之间具有明显 的界线,但这种滤波器实际上是不可实现的。 理想低通滤波器的频率响应定义为 ( ) ( ) ( ) j H j H j e (4-4) 其中 0 1 | | | ( ) | 0 | | ( ) c c H j t 2.理想低通滤波器的冲激响应 0 ( ) [ ( )] c c h t Sa t t (4-5) 是一个延时采样函数。 3.理想低通滤波器的阶跃响应 ( ) 0 1 0 sin 2 1 ( ) t t c dx x x y t (4-6) 上式中 x sin x 的积分称为“正弦积分”,用Si( y) 表示为: dx x x Si y y 0 sin ( ) 。阶跃响 应上升时间与系统的带宽(截止频率)成反比

(二)物理可实现滤波器频率响应的约束条件 1.佩利一维纳准则 如果一个因果系统的幅频特性平方可积,即 H(j)do0时存在,因此可以写为 h(t)=h(t)u(t) (4-8) 设系统的频响H(jo)用实部和虚部表示为 H(jo)=FT[h(t)]=R(jo)+ix(jo) (4-9) 其中, R(j0)=X(2)dz π-0- (4-10) X(j0)=-- R(A)di 式(4-10)称为希尔伯特变换对。它表明因果系统频响的实部R(jo)被已知的虚部 X(0)完全确定,而虚部也被已知的实部完全确定。从这一关系可知,物理可实现系统频 响的实部和虚部具有满足希尔波特变换对的相互依赖关系。在设计一个实际滤波器时,若给 定了实部,而虚部任意给定,则设计的滤波系统可能就是非因果的。 3
3 (二)物理可实现滤波器频率响应的约束条件 1.佩利-维纳准则 如果一个因果系统的幅频特性平方可积,即 H j d 2 ( ) 则对于幅频特性,物理可实现系统的必要条件是 d H j 2 1 ln ( ) (4-7) 上式称为佩利-维纳(Paley-Wiener)准则。 佩利-维纳准则要求物理可实现的幅频响应的衰减不能太快。 佩利-维纳准则只对幅频特性提出要求,对相频特性没有限制,实际上物理可实现系 统的幅频特性和相频特性之间是存在相互制约关系的,因而该准则仅为必要条件而不是充分 条件。对于物理可实现系统,允许 H j ( ) 在某些不连续的频率点上为零,但不允许在一个 有限频带内为零。 2.希尔伯特变换 因果系统的冲激响应h(t) 在t 0 时为零,仅在t 0时存在,因此可以写为 h(t) h(t)u(t) (4-8) 设系统的频响 H( j)用实部和虚部表示为 H( j) FT[h(t)] R( j) jX ( j) (4-9) 其中, d R X j d X R j 1 ( ) ( ) 1 ( ) ( ) (4-10) 式(4-10)称为希尔伯特变换对。它表明因果系统频响的实部 R( j) 被已知的虚部 X ( j) 完全确定,而虚部也被已知的实部完全确定。从这一关系可知,物理可实现系统频 响的实部和虚部具有满足希尔波特变换对的相互依赖关系。在设计一个实际滤波器时,若给 定了实部,而虚部任意给定,则设计的滤波系统可能就是非因果的

4.2.4调制与解调 (一)调制的物理意义 调制是指用一个信号去改变或控制另一个信号的某一参量(幅度、频率或相位)的过程, 分别为调幅、调频和调相。其中控制信号称为调制信号,而被控制信号称为载波,调制后的 信号称为已调信号。 解调是从已调信号中恢复调制信号的过程,分别有检波、鉴频和鉴相。 1.双边带幅度调制(DSB)与解调 f(t)为调制信号,载波为正弦信号c(t)=coso,1,其中o。为载波角频率,则已调信号 ∫(1)是调制信号与载波的乘积 f(1)=f(t)c(t)=f(t)cos@t 取傅里叶变换得 FTL.(O=E(@)= F(o)*[δ(0+0)+δ(0-o)] 2元 (411) =2F(@+o,)+Fo-a,】 1 其中F(o)为f()的傅里叶变换,设其频谱占据-⊙m到om的有限频带,则已调信号 的频谱F(o)是原信号频谱幅度减半,并分别向左、右各平移oo。在F(o)的频谱中,从 ⊙,到⊙0+⊙m及其关于纵轴对称部分的频谱称为上边带信号,而⊙0一⊙m到@,及其对称部 分频谱称为下边带信号,所以称为双边带调制。 解调是从已调信号∫(t)中恢复f(t)的过程。若传输信道理想,则已调信号f(t)在传 输过程中无失真,在接收端f(t)作为解调器的输入。同步解调的原理是在接收端用与发射 端同频同相的载波cos@,1去乘以接收到的已调信号∫(t),再通过一理想低通滤波器,从 而恢复出原始调制信号f(t)。 2.幅度调制(A)与解调 AM调制是在发射信号中加入一定强度的载波信号A,Cos⊙,1,则已调信号变为 f(t)=[4+f(t)]cosoot (4-12)
4 4.2.4 调制与解调 (一)调制的物理意义 调制是指用一个信号去改变或控制另一个信号的某一参量(幅度、频率或相位)的过程, 分别为调幅、调频和调相。其中控制信号称为调制信号,而被控制信号称为载波,调制后的 信号称为已调信号。 解调是从已调信号中恢复调制信号的过程,分别有检波、鉴频和鉴相。 1.双边带幅度调制(DSB)与解调 f (t)为调制信号,载波为正弦信号 0 c t t ( ) cos ,其中0 为载波角频率,则已调信号 ( ) c f t 是调制信号与载波的乘积 0 ( ) ( ) ( ) ( )cos c f t f t c t f t t 取傅里叶变换得 0 0 0 0 1 [ ( )] ( ) ( ) [ ( ) ( )] 2 1 [ ( ) ( )] 2 FT f t F F c c F F (4-11) 其中 F()为 f (t)的傅里叶变换,设其频谱占据 m 到 m 的有限频带,则已调信号 的频谱 ( ) Fc 是原信号频谱幅度减半,并分别向左、右各平移0 。在 () Fc 的频谱中,从 0 到0 m 及其关于纵轴对称部分的频谱称为上边带信号,而0 m 到0 及其对称部 分频谱称为下边带信号,所以称为双边带调制。 解调是从已调信号 ( ) c f t 中恢复 f (t)的过程。若传输信道理想,则已调信号 ( ) c f t 在传 输过程中无失真,在接收端 ( ) c f t 作为解调器的输入。同步解调的原理是在接收端用与发射 端同频同相的载波 t 0 cos 去乘以接收到的已调信号 ( ) c f t ,再通过一理想低通滤波器,从 而恢复出原始调制信号 f (t)。 2.幅度调制(AM)与解调 AM 调制是在发射信号中加入一定强度的载波信号 0 0 A t cos ,则已调信号变为 0 0 ( ) [ ( )]cos c f t A f t t (4-12)

其频谱 F(@)=Aπ[6(0+o)+δ(0-o)】+[F(o+0)+F(o-o)】 设K为f()的最大幅度值,为满足A+f(t)总为正,要求A>K。一般定义调幅指 数m为 (4-13) Ao 如果调幅指数m>1,则已调波的包络不再与调制信号形状相同,也就不能用包络检波 器解调出调制信号。当m<1,且调制信号f(t)的频率比载波频率o。小很多时,就可以利 用包络检波器恢复出调制信号f(t)。 3.单边带调制(SSB)和残留边带调制(VSB) 单边带(single side-band调制,就是只产生一个边带,而抑制另一个边带的调制方式。 使已调信号通过一带通滤波器,就可以得到单边带调制信号,但单边带调制信号的滤波器实 现较困难。 残留边带(vestigial side-band信号不是将一个边带完全抑制,而是部分抑制,使其残留 一小部分信号的调制方式,其滤波器的设计可以简化,使得下边带大部分通过,而使上边带 小部分残留。当然,也可以用带通(或高通)滤波器使上边带大部分通过,而下边带小部分残 留。 4.2.5频分多路复用和时分多路复用 (一)频分多路复用(FDM) 在发送端将各路信号的频谱搬移到各不相同的频段范围,使得他们互不重叠,这样就可 复用同一信道传输。在接收端再利用若干带通滤波器将各路信号分离,并用解调技术将各路 信号被搬移过的频谱再搬回到他们各自原来的频段上,这样各路原始信号就被还原了。 (二)时分多路复用(TDM) 时分复用的理论依据是抽样定理,连续信号被抽样后,它的传送可通过抽样值的传送来 代替。抽样间隔最大可达1/2∫,。在传送抽样值时,信道仅在抽样瞬间被占用,而在其余 的空闲时间内可传送第二路、第三路..等其他各路信号的抽样值。将各路信号的抽样值有 序的排列起来,就可实现时分复用。在接收端,这些抽样值由适当的同步检测器分离。 4.3本章知识点 5
5 其频谱 0 0 0 0 0 1 ( ) [ ( ) ( )] [ ( ) ( )] 2 F A F F c 设 K 为 f (t)的最大幅度值,为满足 0 A f t ( ) 总为正,要求 A K 0 。一般定义调幅指 数 m 为 0 K m A (4-13) 如果调幅指数m 1,则已调波的包络不再与调制信号形状相同,也就不能用包络检波 器解调出调制信号。当m 1,且调制信号 f (t)的频率比载波频率0 小很多时,就可以利 用包络检波器恢复出调制信号 f (t)。 3.单边带调制(SSB)和残留边带调制(VSB) 单边带(single side-band)调制,就是只产生一个边带,而抑制另一个边带的调制方式。 使已调信号通过一带通滤波器,就可以得到单边带调制信号,但单边带调制信号的滤波器实 现较困难。 残留边带(vestigial side-band)信号不是将一个边带完全抑制,而是部分抑制,使其残留 一小部分信号的调制方式,其滤波器的设计可以简化,使得下边带大部分通过,而使上边带 小部分残留。当然,也可以用带通(或高通)滤波器使上边带大部分通过,而下边带小部分残 留。 4.2.5 频分多路复用和时分多路复用 (一) 频分多路复用(FDM) 在发送端将各路信号的频谱搬移到各不相同的频段范围,使得他们互不重叠,这样就可 复用同一信道传输。在接收端再利用若干带通滤波器将各路信号分离,并用解调技术将各路 信号被搬移过的频谱再搬回到他们各自原来的频段上,这样各路原始信号就被还原了。 (二)时分多路复用(TDM) 时分复用的理论依据是抽样定理,连续信号被抽样后,它的传送可通过抽样值的传送来 代替。抽样间隔最大可达 。在传送抽样值时,信道仅在抽样瞬间被占用,而在其余 的空闲时间内可传送第二路、第三路……等其他各路信号的抽样值。将各路信号的抽样值有 序的排列起来,就可实现时分复用。在接收端,这些抽样值由适当的同步检测器分离。 4.3 本章知识点 1/ 2 m f

(1)系统的频率响应 (2)无失真传输 (3)理想低通滤波器 (4)调制与解调 (5)多路复用 4.4例题 例4-1:一线性系统频率特性曲线如下图所示,求下列信号通过此系统是否发生线性失真。 H(j) ◆p(0) 500 1000 -45 5001000 例4-1图 1)e(t)=cos(400t)+3cos(600t) 2)e(t)=3cos(100t)cos(300t) 解: 1)e(t)=cos(400t)+3cos(600t) 频率在400到600之间,不同频率放大不同:相位与频率不成正比,所以失真。 2)e(t)=3cos(100t)cos(300t) =2cos(200叶cos(4001 频率在200到400之间,不同频率放大相同:相位是过原点的一条直线,所以不失真。 例42:高斯幅频特性是否物理可实现? 解:根据Paley-.Wiener准则:物理可实现的必须满足 In H(jo) d@<oo 1+02 而高斯幅频特性 1+o -L1+oitiHo-jml-o =m28-g8=▣8-到
6 (1)系统的频率响应 (2)无失真传输 (3)理想低通滤波器 (4)调制与解调 (5)多路复用 4.4 例题 例 4-1:一线性系统频率特性曲线如下图所示,求下列信号通过此系统是否发生线性失真。 例 4 -1 图 2) ( ) 3 cos( 100 ) cos( 300 ) 1) ( ) cos( 400 ) 3 cos( 600 ) e t t t e t t t 解: 1)e(t) cos(400t) 3cos(600t) 频率在 400 到 600 之间,不同频率放大不同; 相位与频率不成正比,所以失真。 2)e(t) 3cos(100t)cos(300t) [cos(200t) cos(400t)] 2 3 = + 频率在 200 到 400 之间,不同频率放大相同;相位是过原点的一条直线,所以不失真。 例 4-2: 高斯幅频特性是否物理可实现? 解:根据 Paley-Wiener 准则:物理可实现的必须满足 d H j 2 1 ln ( ) 而高斯幅频特性 2 lim 2( 2 lim lim 1 1 1 1 1 ln( ) 1 ln ( ) 1 1 2 2 2 2 2 2 B tg B B d tg d d e d H j B B B B B

从上可以看出具有高斯幅频特性不满足Paley-Wiener准则,是发散的,所以物理不可实 现。 例43:一线性系统频响曲线如下图所示,设激励信号为(t)=2+2cos1+2cos21, 求零状态输出响应。 数) Hgjo) 例4-2图 解(1)求输入激励的频谱。 由周期信号的频谱密度函数可得 E(Ujo)=4πδ(o)+2π6(o+1)+6(0-1)]+2π6(o+2)+6(0-2)】 (2)求系统函数H(jo)。 由给出的频响曲线可以写出 H(j0)= -ole l@2 (3)求响应的频谱。 R(Ujo)=E(jo)·H(jo) =8xio)+2ei6o+l)+2e'片60-) (4)由输出响应的频谱经傅里叶反变换求取时域响应。 r(t)=F-R(jo) =4+e )+e =4+2o-引 =4+2sin t 可见输入信号中的二次谐波被滤除,只留有直流与基波分量。输入输出频谱结构如下图所示。 青测 (匹) 4g》 2x)e) m agi 2元) -2-101 2 -0☑ 风 >
7 从上可以看出具有高斯幅频特性不满足 Paley-Wiener 准则,是发散的,所以物理不可实 现。 例 4-3:一线性系统频响曲线如下图所示,设激励信号为e t t t ( ) 2 2cos 2cos 2 , 求零状态输出响应。 例 4 -2 图 解 (1)求输入激励的频谱。 由周期信号的频谱密度函数可得 E( j) = 4 () + 2 ( 1) ( 1) + 2 ( 2) ( 2) (2)求系统函数 H j ( ) 。 由给出的频响曲线可以写出 2 2 2 ( ) 0 2 j e H j (3)求响应的频谱。 8 ( ) 2 ( 1) 2 ( 1) ( ) ( ) ( ) 2 2 j j e e R j E j H j (4)由输出响应的频谱经傅里叶反变换求取时域响应。 t t e e r t F R j j t j t 4 2sin 2 4 2cos 4 ( ) ( ) 2 2 1 可见输入信号中的二次谐波被滤除,只留有直流与基波分量。输入输出频谱结构如下图所示

4.5习题 1.设某系统的频率响应为 1 H(jo)= j0+5 试求当输入信号为x()=e4'u(t)时的零状态响应。 2.系统如题2图所示,求系统的频响H(jo),若f(t)=e2'u(t),求零状态响应y(t)。 f(t) y(t) 4 题2图 3.一个LTI系统的冲激响应为h(0)=-s血41,试求当输入f0)=cos2πt+sin6x1 πt 时系统的输出y(t)。 4.题4图是理想高通滤波器的幅频和相频特性,求该滤波器的冲激响应。 41H(Uo)川 .1 0 p(@))】 题4图 5.已知一带通滤波系统,带通滤波器频响如题5图,试求激励为f(t)=Sa(o1)cos1 时的输出信号∫(t),并判断f(t)经传输后是否失真。 8
8 4.5 习题 1.设某系统的频率响应为 1 ( ) 5 H j j 试求当输入信号为 4 ( ) ( ) t x t e u t 时的零状态响应。 2. 系统如题 2 图所示,求系统的频响 H j ( ) ,若 2 ( ) ( ) t f t e u t ,求零状态响应 y t( ) 。 题2图 3. 一个LTI系统的冲激响应为 t t h t sin 4 ( ) ,试求当输入 f t t t ( ) cos 2 sin 6 时系统的输出 y (t) 。 4. 题4图是理想高通滤波器的幅频和相频特性,求该滤波器的冲激响应。 0 | | H j 1 c c 0 ( ) 0 t 题 4 图 5. 已知一带通滤波系统,带通滤波器频响如题 5 图,试求激励为 0 ( ) ( ) cos c f t Sa t t 时的输出信号 ( ) 1 f t ,并判断 f (t)经传输后是否失真
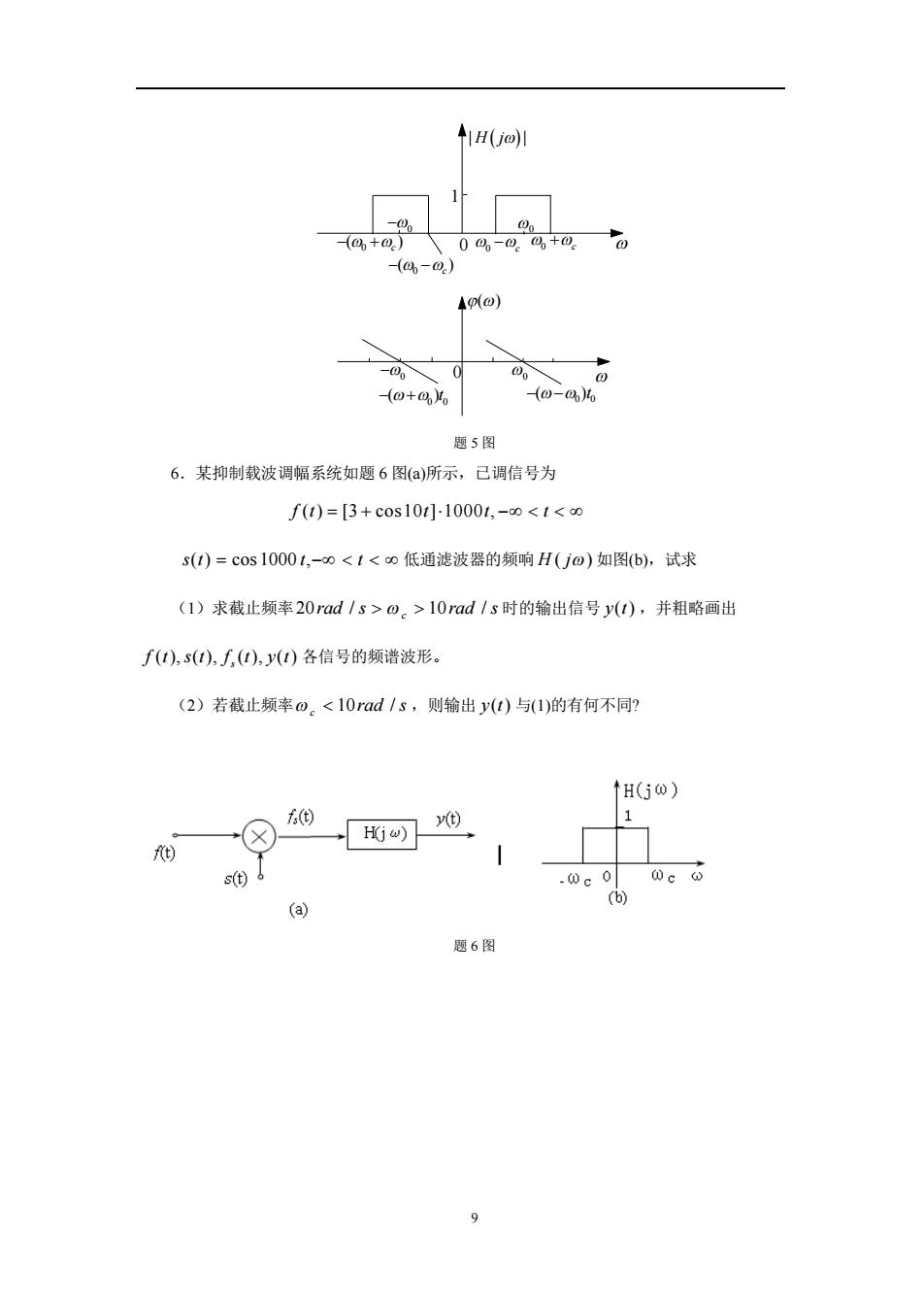
AH(j)I -0 00 -(4+0)00-0。%+0. (0-o) 4p(o) 00 (0+4 (0-)i% 题5图 6.某抑制载波调幅系统如题6图(a)所示,已调信号为 f(t)=[3+cos10t]10001,-oo。>10rad/s时的输出信号y(t),并粗略画出 ∫(t),s(t),∫,(t),y(t)各信号的频谱波形。 (2)若截止频率o。<10rad/s,则输出y(t)与(1)的有何不同? ↑H(0) ft ① 1 Hjω) ft) s(t) -0c0 0c⊙ ) (a) 题6图 9
9 1 0 | | H j 0 ( ) c 0 c 0 ( ) c 0 c 0 0 0 ( ) 0 0 0 0 ( ) t 0 0 ( ) t 题 5 图 6.某抑制载波调幅系统如题 6 图(a)所示,已调信号为 f t t t t ( ) [3 cos10 ] 1000 , s(t) cos 1000 t, t 低通滤波器的频响 H j ( ) 如图(b),试求 (1)求截止频率 rad s rad s c 20 / 10 / 时的输出信号 y(t) ,并粗略画出 ( ), ( ), ( ), ( ) s f t s t f t y t 各信号的频谱波形。 (2)若截止频率 rad s c 10 / ,则输出 y(t) 与(1)的有何不同? 题 6 图