
傅立叶变换公式 傅立叶正变换公式 F(o)=FT[f(】=∫f(t)eod 傅立叶反变换公式 f0=FTF-2z∫F(w)edw F(ω)称为f(t)的频谱 f(t)称为F(o)的原函数
傅立叶变换公式 傅立叶正变换公式 傅立叶反变换公式 ( ) ( ) ( ) ( ) F f t f t F 称为 的频谱, 称为 的原函数。 1 1 ( ) [ ( )] ( ) 2 j t f t FT F F e d F FT f t f t e dt j t ( ) [ ( )] ( )

§3.4常用非周期信号的频谱 1。矩形脉冲信号 己知矩形脉冲信号g(),其表示式为 0 t<t/2 t 712 其中,E为脉冲幅度,τ为脉冲宽度。 t/2 Am-∫ei=nE边
§3.4常用非周期信号的频谱 1。矩形脉冲信号 已知矩形脉冲信号g(t),其表示式为 其中,E为脉冲幅度,τ为脉冲宽度。 g(t) E t / 2 0 t / 2 /2 /2 ( ) ( ) j t j t F g t e dt Ee dt
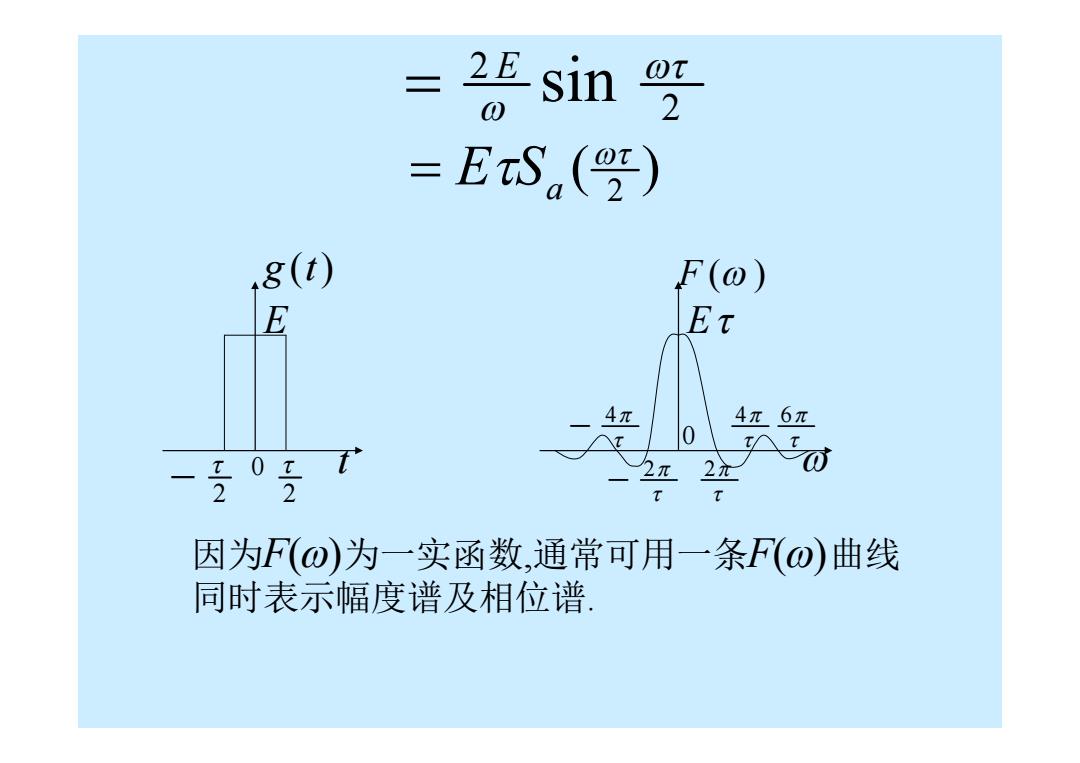
三 sin =EtS() 8(t) F(0) E Et 4元 4π6π 0 -号0号 2元 因为F(o)为一实函数,通常可用一条F(⊙)曲线 同时表示幅度谱及相位谱
2 2 sin E 0 E g (t) t 2 2 2 2 E F ( ) 0 4 4 6 因为 为一实函数,通常可用一条 曲线 同时表示幅度谱及相位谱. F() F() ( ) 2 E Sa

其幅度谱和相位谱分别为 F(ω=EtS(竖 0 p(ao)={a <<22mD 22a<k22 n= 0,1,2,…
其幅度谱和相位谱分别为 ( ) ( ) 2 F E Sa () 4 2(2 1) 0 n n 2(2 1) 2(2 2) n n n 0 ,1, 2 ,

2.单边指数信号 。设单边指数函数表示式为 f(t)= t>0,0>0 t≤0 ·或写作 f(t)=e-atu (t) ¥> 0
2.单边指数信号 • 设单边指数函数表示式为 • 或写作 f ( t ) 0, 0 e t t 0 t 0 ( ) ( ) 0 f t e u t t
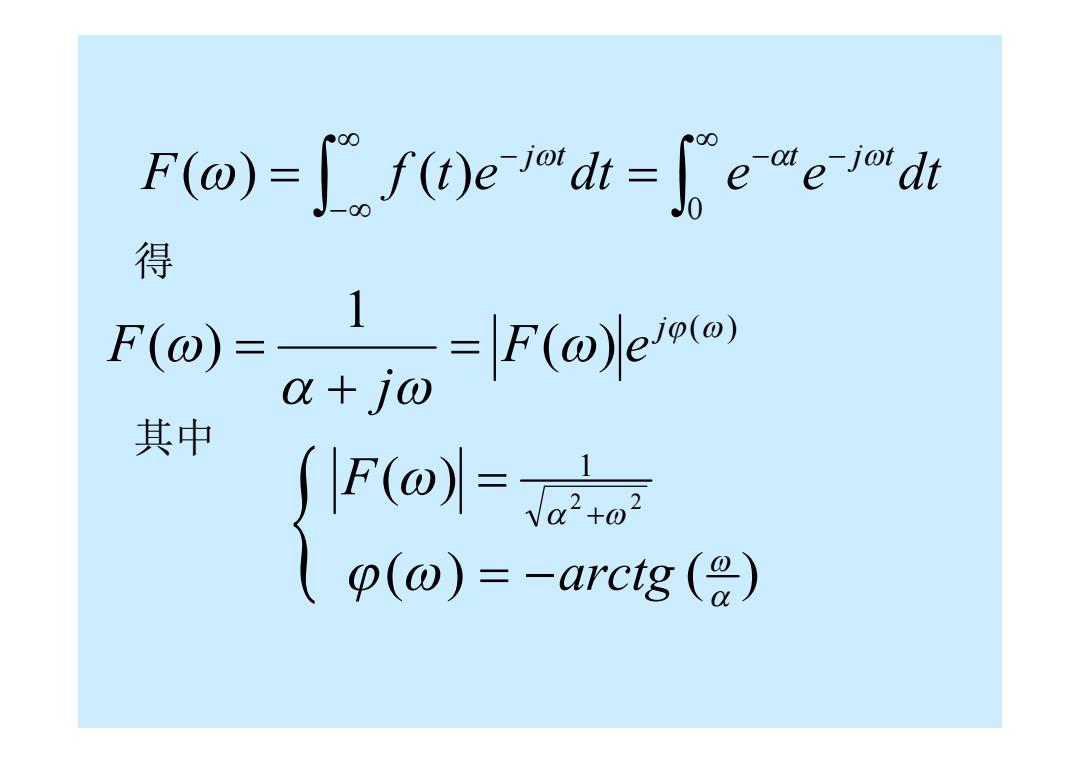
Fo)=∫f)edh=e“e"dh 得 l=a石ogn 其中 (F()- p(@)=-arctg (
F f t e dt e e dt j t t j t 0 ( ) ( ) 得 其中 ( ) ( ) 1 ( ) j F e j F ( ) ( ) arctg 2 2 1 ( ) F
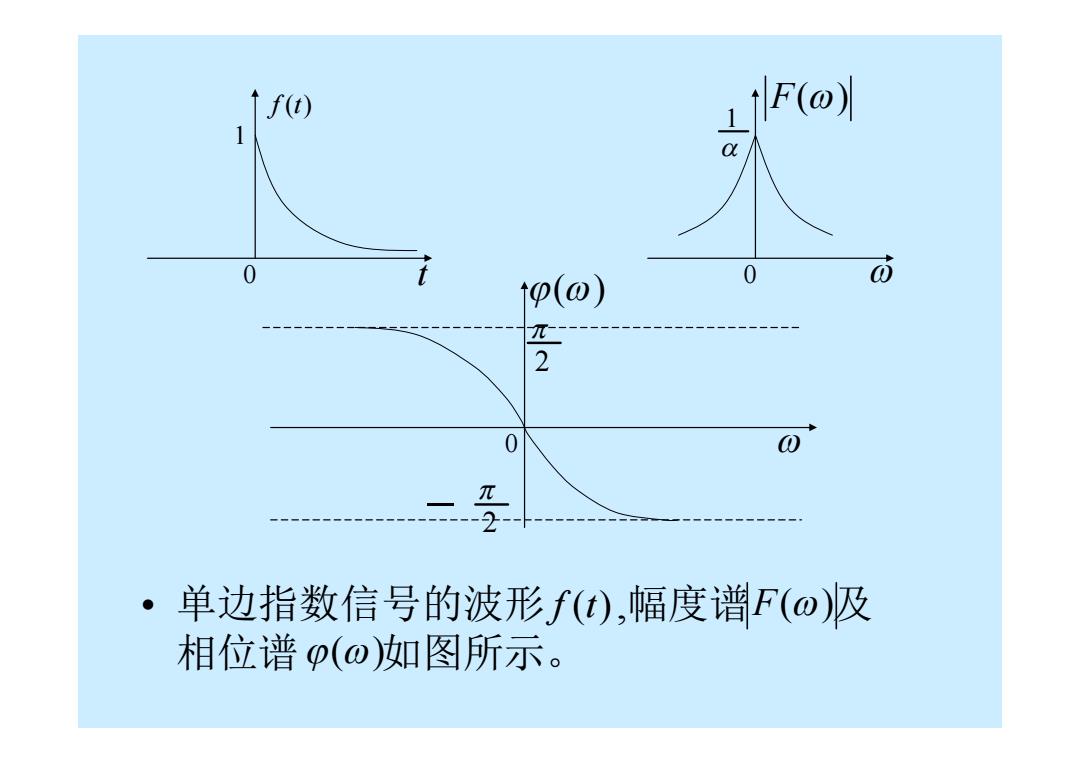
f(t) 1 F(@) 1 0 p(o) 2 0 0 单边指数信号的波形f(t),幅度谱F(o)及 相位谱p(ω)如图所示
0 1 f (t) t 0 F() 1 0 () 2 2 • 单边指数信号的波形 ,幅度谱 及 相位谱 如图所示。 f (t) F() ()

3.双边奇指数信号 ·已知双边奇指数信号表示式为 1 t0,频谱函数为 F()=f(t)e 'dt -e eaedt
3.双边奇指数信号 • 已知双边奇指数信号表示式为 • 其中 ,频谱函数为 f (t) 0 t e t 0 e t t 0 F f t e dt j t () ( ) e e dt e e dt t j t t j t 0 0

F(@)=-ao+a =-j30 a2+02 ·其幅度谱及相位谱为 F()= 2@ 2+o2 ≤0 ⊙<0
• 其幅度谱及相位谱为 F j j 1 1 ( ) 2 2 2 ( ) F () 0 2 0 2 2 2 2 j

4@ +1 -0t e 2 0 -0 0 2 -1 上图为双边奇指数信号的幅度谱及相位谱
上图为双边奇指数信号的幅度谱及相位谱 0 () 2 2 0 1 1 f(t) t t e t e 0 F() 1