华东理工大学：《信号与系统》课程教学资源（学习指导书）第三章 傅里叶变换（连续时间信号的傅里叶分析）

第三章连续时间信号的傅里叶分析 3.1学习要求 通过本章的学习，学生应理解信号分解为正交函数的意义。掌握信号的频域分析方法一 傅里叶级数和傅里叶变换。理解周期信号与非周期信号频谱的特点、区别和联系，周期信号 傅里叶变换的特点，信号时域特性与频域特性之间的关系，抽样信号频谱的特点与抽样定理。 掌握典型信号的傅里叶变换，并能灵活运用傅里叶变换的性质对信号进行正反变换。掌握周 期序列的离散傅里叶级数表示，非周期序列的离散时间傅里叶变换及其性质。 3.2内容概述 3.2.1周期信号的傅里叶级数表示 (一)三角形式的傅里叶级数表示 设满足狄里赫利条件的周期信号f(),周期为T,角频率为o1= 2元 ,分解为三角函 T 数形式的傅里叶级数为 f()=d+acosn0t+b,sin no) (3-1) 其中an,bn为傅里叶系数。式(3-28)中直流分量、余弦分量和正弦分量傅里叶系数分别 为 a0= T。 (3-2) an -If f()cosnontdt (3-3) f(t)sin no tdt (3-4) (二)指数形式的傅里叶级数 ()->F.emm (3-5) 其中F,为复指数形式傅里叶级数的复系数

1 第三章 连续时间信号的傅里叶分析 3.1学习要求 通过本章的学习，学生应理解信号分解为正交函数的意义。掌握信号的频域分析方法— 傅里叶级数和傅里叶变换。理解周期信号与非周期信号频谱的特点、区别和联系，周期信号 傅里叶变换的特点，信号时域特性与频域特性之间的关系，抽样信号频谱的特点与抽样定理。 掌握典型信号的傅里叶变换，并能灵活运用傅里叶变换的性质对信号进行正反变换。掌握周 期序列的离散傅里叶级数表示，非周期序列的离散时间傅里叶变换及其性质。 3.2内容概述 3.2.1 周期信号的傅里叶级数表示 （一）三角形式的傅里叶级数表示 设满足狄里赫利条件的周期信号 f (t)，周期为T1，角频率为 1 1 2 T    ，分解为三角函 数形式的傅里叶级数为 ( ) ( cos sin ) 1 1 1 0 f t a a n t b n t n n n        (3-1) 其中 n n a ,b 为傅里叶系数。式(3-28)中直流分量、余弦分量和正弦分量傅里叶系数分别 为    0 1 0 ( ) 1 1 0 t T t f t dt T a (3-2)    0 1 0 1 1 ( )cos 2 t T t n f t n tdt T a  (3-3) f t n tdt T b t T t n    0 1 0 1 1 ( )sin 2  (3-4) （二）指数形式的傅里叶级数 jn t n n f t F e 1 ( )      (3-5) 其中 Fn 为复指数形式傅里叶级数的复系数

Fn= f(1e-movdt n=0,±1，±2， (3-6) (三)周期信号的对称性与傅里叶系数的关系 1.偶对称信号 偶对称信号是指信号f()是时间的偶函数，即f(t)=f(-),其波形相对于纵轴对称。 Fn=En= 2 n=0 (3-7) Cn=a =2F 实偶信号的傅里叶系数是实函数，且是的偶函数，实偶信号的傅里叶级数中不包含正 弦项，只可能含有直流项和余弦项。 2.奇对称信号 奇对称信号是指信号f()是时间的奇函数，即f(t)=一f(-),其波形相对于原点对称。 1 F=-F=- π Pn=- 2 (3-8) Cn =b =2jF 实奇信号的傅里叶系数F,是虚函数，且是的奇函数，实奇信号的傅里叶级数中不包含 余弦项，只可能含有正弦项。 3.奇谐信号 如果信号∫()的前半周期波形沿时间轴平移半个周期T/2后，与后半周期波形相对于 横轴对称，即满足f0)=一士马），这样的函数称为半波对称函数或称为奇谐函数。 其傅里叶级数展开式中将只含有基波和奇次谐波的正、余弦项，不含有偶次谐波项，即 a0=a2=a4=…=b2=b4=b6=…=0。 3.2.2非周期信号的傅里叶变换 (一)非周期信号的傅里叶变换 傅里叶正变换 F(o)=FT[f】=fu)edi (3-9) 傅里叶反变换

2 ( ) 0, 1, 2, 1 2 1 2 1 1 1       f t e dt n T F T T jn t n  (3-6) （三）周期信号的对称性与傅里叶系数的关系 1. 偶对称信号 偶对称信号是指信号 f (t)是时间的偶函数，即 f (t)  f (t) ，其波形相对于纵轴对称。 2 0 2 n n n n n n n a F F c a F               (3-7) 实偶信号的傅里叶系数是实函数，且是n的偶函数，实偶信号的傅里叶级数中不包含正 弦项，只可能含有直流项和余弦项。 2．奇对称信号 奇对称信号是指信号 f (t)是时间的奇函数，即 f (t)   f (t) ，其波形相对于原点对称。 1 2 2 2 n n n n n n n F F jb c b jF                     (3-8) 实奇信号的傅里叶系数 Fn 是虚函数，且是n的奇函数，实奇信号的傅里叶级数中不包含 余弦项，只可能含有正弦项。 3．奇谐信号 如果信号 f (t)的前半周期波形沿时间轴平移半个周期 / 2 T1 后，与后半周期波形相对于 横轴对称，即满足 ) 2 ( ) ( T1 f t   f t  ，这样的函数称为半波对称函数或称为奇谐函数。 其傅里叶级数展开式中将只含有基波和奇次谐波的正、余弦项，不含有偶次谐波项，即 0 a0  a2  a4  b2  b4  b6  。 3.2.2 非周期信号的傅里叶变换 （一）非周期信号的傅里叶变换 傅里叶正变换     F  FT f t  f t e dt jt () [ ( )] ( ) (3-9) 傅里叶反变换

0=TroI=2 F(o)eido (3-10) F(o)称为f(t)的频谱密度函数，频谱密度函数F(o)一般为复函数，可表示为 F(@)=F(@)ei()=R(@)+jX(@). (二)求频谱密度函数F(oO)的方法 (1)由定义求F(o)。 (2)根据傅里叶变换的性质求F(o)。 (3)利用周期信号傅里叶级数与傅里叶变换的关系求F(⊙)。 (三)非周期信号频谱的特点 (1)连续谱。非周期信号的频谱包含0~0的所有频率分量： (2)收敛性。信号的能量大部分集中在低频段，F(o)随回增大，总趋势减小。 3.2.3常见非周期信号的傅里叶变换 (一)典型非周期信号的傅里叶变换 1.矩形脉冲信号 1 G()= (3-11) 其频谱为 Fo)-Gaeh=emh-子sng受 n号 (3-12) =T a 其幅度谱及相位谱分别为 Fo=a受 (3-13) 2(2n+10z p(o)= (3-14) π 22n+D 2.单边指数信号 3

3            f t FT F F e d j t ( ) 2 1 ( ) [ ( )] 1 (3-10) F() 称为 f (t) 的频谱密度函数，频谱密度函数 F() 一般为复函数，可表示为 ( ) ( ) ( ) ( ) ( )       F F e R jX j    。 （二）求频谱密度函数 F()的方法 （1）由定义求 F()。 （2）根据傅里叶变换的性质求 F()。 （3）利用周期信号傅里叶级数与傅里叶变换的关系求 F()。 （三）非周期信号频谱的特点 （1）连续谱。非周期信号的频谱包含0~的所有频率分量； （2）收敛性。信号的能量大部分集中在低频段， F()随  增大，总趋势减小。 3.2.3 常见非周期信号的傅里叶变换 （一）典型非周期信号的傅里叶变换 1. 矩形脉冲信号 1 2 ( ) 0 2 t G t t            (3-11) 其频谱为 / 2 / 2 2 ( ) ( ) sin( ) 2 sin( ) 2 ( ) 2 2 j t j t F G t e dt e dt Sa                                    (3-12) 其幅度谱及相位谱分别为 ( ) ( ) 2 F Sa     (3-13) 4 2(2 1) 0 [ ] ( ) 2(2 1) 4( 1) [ ] n n n n                           (3-14) 2. 单边指数信号

设单边指数信号表达式为 e-ar f0=0 (1≥0) a>0 (t0)(3-15) a+j@ 幅度谱和相位谱分别为 Fo以2a2+o 1 p(a)=-arcg(巴) C 3.双边奇指数信号 双边奇指数信号表达式为 (1>0) f()= a>0 (t0 p(o)= 2 2 00 其频谱为 2a F(0)= 2+02 幅度谱和相位谱分别为 IF(@)-- 2a a2+02 p(o)=0 5.钟形脉冲信号 4

4 设单边指数信号表达式为 0 0 ( 0) ( 0) ( )           t e t f t t 其频谱为 ( 0) 1 ( ) ( ) 0                     j F f t e dt e e dt j t t j t (3-15) 幅度谱和相位谱分别为 2 2 1 ( )     F  ( ) ( )      arctg 3. 双边奇指数信号 双边奇指数信号表达式为 0 ( 0) ( 0) ( )             e t e t f t t t 其频谱为 ( ) ( ) j t F f t e dt         2 2 1 1 2 j j j              幅度谱和相位谱分别为              0 2 0 2 ( ) 2 | | ( ) 2 2          F  4．双边偶指数信号 双边偶指数信号表达式为 ( ) , 0 | |           f t e t t 其频谱为 2 2 2 ( )      F  幅度谱和相位谱分别为 ( ) 0 2 ( ) 2 2         F  5．钟形脉冲信号

钟形脉冲信号表达式为 f(t)=Ee -00<t<00 其频谱为 F(0)=f()emldi=EedEe (二)奇异信号的傅里叶变换 1.单位冲激函数 F)F))=1 7-0T 2.单位直流信号 幅度为1的单位直流信号，其FT1]=2πδ(o) 3.符号函数 符号函数不满足绝对可积条件，但其傅里叶变换是存在的，为 F()=FT[sgn(t)]=lim- -2j02 a0a2+02j0 4.阶跃信号 阶跃信号不满足绝对可积条件，但其傅里叶变换存在，为 -FrFTern-sa) 5.单位冲激偶 FT[δ'(]=δ()e'dh=-(-jo)=jo 3.2.4傅里叶变换的性质 1.线性 若FT[Uf)]-F(o) i=2a.n则m[0-o5oa为常数， n为正整数。 2.奇偶虚实性 无论f(t)为实函数或虚函数，都有如下性质 (1) FTLf(-t)]=F(-@) FTLf"(t)]=F"(-@) FTLf(-1)]=F(@) (2)实偶函数f(t)的频谱是o的实偶函数。 5

5 钟形脉冲信号表达式为        f t Ee t t 2 ( ) ( )  其频谱为 2 2 ( ) ( ) 2 ( ) ( ) t j t j t F f t e dt E e e dt E e                         （二） 奇异信号的傅里叶变换 1. 单位冲激函数 ) 1 2 ( 1 ( ) [ ( )] lim 0            F FT t Sa 2．单位直流信号 幅度为1的单位直流信号，其 FT[1]  2 () 3．符号函数 符 号 函 数 不 满 足 绝 对 可 积 条 件 ， 但 其 傅 里 叶 变 换 是 存 在 的 ， 为       j j F FT t 2 2 ( ) [sgn( )] lim 2 2 0       4．阶跃信号 阶跃信号不满足绝对可积条件，但其傅里叶变换存在，为        j FT u t FT FT t 1 sgn( ) ( ) 2 1 2 1 ( )           5. 单位冲激偶      FT t t e dt j j j t          [ ( )] ( ) ( ) ' ' 3.2.4 傅里叶变换的性质 1. 线性 若 FTf t  F i n i i ( )  () 1,2,3,, ，则           n i i i n i FT ai f i t a F 1 1 ( ) () ，其中a 为常数， n 为正整数。 2．奇偶虚实性 无论 f (t)为实函数或虚函数，都有如下性质 （1） * * * * [ ( )] ( ) [ ( )] ( ) [ ( )] ( ) FT f t F FT f t F FT f t F                （2）实偶函数 f (t)的频谱是 的实偶函数

(3)实奇函数f(t)的频谱是o的虚奇函数。 3.对称性 若F(o)=FT[f(O],则 FT[F()]=2πf(-o) 4.尺度变换特性 设FTLf(t)]=F(o),当f(t)经压缩或扩展为f(at)(a为非零实常数)时，其傅里叶变换 为 5.时移特性 设FTL()]=F(o),则 FTLf(t±t)】=eoF(o) 6.时域微分和积分特性 设FT[f(t)]=F(o),则 时域微分特性为： FTI(D]=joF() dt 时域积分特性为：FTnf(r)dr]=πF(0)δ(o)+】F(o) 7.频域微分和积分特性 设FT[f(t)】=F(o),，则 频域微分特性为： T221=0 频域积分特性为： F(d--) it 8.卷积定理 (1)时域卷积定理 设两函数∫(t)和，(t)的傅里叶变换分别为F(o)和F(⊙)，则两函数卷积的傅 里叶变换为： FT[f(t)*f2()]=F()F2(@) 6

6 （3）实奇函数 f (t)的频谱是 的虚奇函数。 3．对称性 若 F()  FT f (t)，则 FTF(t)  2 f () 4．尺度变换特性 设 FT[ f (t)]  F() ,当 f (t)经压缩或扩展为 f (at) (a为非零实常数)时，其傅里叶变换 为        a F a FT f at 1  [ ( )] 5．时移特性 设FT[ f (t)]  F() ，则 FT[ ( )] ( ) 0 0   f t t e F  j t   6．时域微分和积分特性 设 FT [ f (t)]  F ( ) ，则 时域微分特性为： ] ( ) ( ) [ jF  dt df t FT  时域积分特性为： ( ) 1 [ ( ) ] (0 ) ( )        F j FT f d F t     7．频域微分和积分特性 设 FT [ f (t)]  F ( ) ，则 频域微分特性为： ] ( ) ( ) ( ) [ 1 jt f t d dF FT      频域积分特性为： 1 ( ) [ ( ) ] (0) ( ) f t FT F u du f t jt          8．卷积定理 （1）时域卷积定理 设两函数 ( ) 1 f t 和 ( ) 2 f t 的傅里叶变换分别为 ( ) F1  和 ( ) F2  ，则两函数卷积的傅 里叶变换为： [ ( ) ( )] ( ) ( ) FT f 1 t  f 2 t  F1  F2 

(2)频域卷积定理 设两信号f()和∫(t)的傅里叶变换分别为F(O)和F(O),则 FT()F() 9.能量谱和功率谱 (1)能量谱 如果信号f()是实信号，则信号总能量可表示为 E=.f产h=2aF(ofdn 该式称为帕斯瓦尔方程。它表示时域内信号的能量等于频域内信号的能量，即信号经过 傅里叶变换，其总能量不变，符合能量守恒定律。 2.功率谱 在时间区间-o<1<o内信号f(t)的平均功率表示为 p=2/u 其功率谱P(o) P()-imF T 功率谱是0的偶函数，只决定于信号的幅度谱，与相位谱无关，其单位是WHz。 3.2.5周期信号的傅里叶变换 周期信号的傅里叶变换即频谱密度函数是由无穷多个冲激函数所组成。这些冲激函数位 于信号的各谐波频幸0=n@(n=0,士1，+2，)处，其强度等于傅里叶复系数的2r倍。即 Pml=2π2F.o-na,） 中。三（⊙，该式表明，周期信号傅里叶级数的复系数下，等于其 的单脉冲信号的傅里叶变换F。(o)在o=no,处的值乘以1/T。这样就可以利用单脉冲的 傅里叶变换方便地求得周期信号的傅里叶复系数F。。 3.2.6抽样信号的傅里叶变换 (一)时域抽样信号及其频谱 1.矩形脉冲抽样 矩形脉冲抽样信号的频谱为 7

7 （2）频域卷积定理 设两信号 ( ) 1 f t 和 ( ) 2 f t 的傅里叶变换分别为 ( ) F1  和 ( ) F2  ，则 ( ) ( ) 2 1 [ ( ) ( )] 1 2 1  2   FT f t  f t  F  F 9．能量谱和功率谱 （1）能量谱 如果信号 f (t)是实信号，则信号总能量可表示为    E f t dt F d         2 2 ( ) 2 1 ( ) 该式称为帕斯瓦尔方程。它表示时域内信号的能量等于频域内信号的能量，即信号经过 傅里叶变换，其总能量不变，符合能量守恒定律。 2．功率谱 在时间区间   t   内信号 f (t) 的平均功率表示为 f t dt T P Lim T T T 2 ( ) 2 1      其功率谱 P( )  T F P T 2 ( ) ( ) lim      功率谱是 的偶函数，只决定于信号的幅度谱，与相位谱无关，其单位是W/Hz。 3.2.5 周期信号的傅里叶变换 周期信号的傅里叶变换即频谱密度函数是由无穷多个冲激函数所组成。这些冲激函数位 于信号的各谐波频率 ( 0, 1, 2, )   n1 n     处，其强度等于傅里叶复系数的2π倍。即 [ ( )] 2 ( )  F   n1 FT f t n n      其中 1 ( ) 1 0 1 F   n T Fn   ，该式表明，周期信号傅里叶级数的复系数 Fn 等于其对应 的单脉冲信号的傅里叶变换 ( ) F0  在 1    n 处的值乘以1 T1 。这样就可以利用单脉冲的 傅里叶变换方便地求得周期信号的傅里叶复系数 Fn 。 3.2.6 抽样信号的傅里叶变换 （一）时域抽样信号及其频谱 1. 矩形脉冲抽样 矩形脉冲抽样信号的频谱为

F(o)=】 无a受Po- 。T 2 上式表明，用矩形脉冲抽样时，F(⊙)是以⊙、为间隔周期地重复出现，且幅度以 S-二Sa(0马)的规律变化. T. 2 2.冲激抽样 冲激抽样信号的频谱为 F(o)=】 LF(@-n@.) =- 上式表明，冲激抽样信号的频谱由原信号频谱F(⊙)的无限个频移项组成，其频移的角 颜率分别为0.n=0,±，其幅值为原频谱的工宁 3.2.7抽样定理 (一)时域抽样定理 设有一频带受限信号f(),其频谱函数只在有限区间（一0m,⊙m)内为有限值，在此区 2元供中人。=0./2x时，信号f0 域外频谱值为零。那么，只有当抽样间隔T,不大 可以用等间隔的抽样值f(nT,)唯一地确定。这就是时域抽样定理，也称为奈奎斯特Nyquist) 定理。 （二)频域抽样定理 若f(t)是时间有限信号（或称时限信号），即它只作用于（一tm,tm)时间域内，如果在频 1 域中以不大于 的频半何弱斤（卿斤2附f0的须裤F@述行抽样，则拍样后的 频谱F(@)可以唯一地表示原信号。 3.3本章知识点 (1)周期信号的傅里叶级数表示 (2)傅里叶变换及其性质 (3)周期信号的傅里叶变换 (4)抽样信号的傅里叶变换 (5)抽样定理

8 ( ) ( ) ( ) 2 s s s n s n F Sa F n T            上式表明，用矩形脉冲抽样时， F () 是以s 为间隔周期地重复出现，且幅度以 ( ) 2 s n s n S Sa T     的规律变化。 2．冲激抽样 冲激抽样信号的频谱为 1 ( ) ( ) s s n s F F n T         上式表明，冲激抽样信号的频谱由原信号频谱 F()的无限个频移项组成，其频移的角 频率分别为 s n ( 0, 1,...) n   ，其幅值为原频谱的 1 Ts 。 3.2.7 抽样定理 （一）时域抽样定理 设有一频带受限信号 f (t)，其频谱函数只在有限区间(  m  m  , )内为有限值，在此区 域外频谱值为零。那么，只有当抽样间隔Ts 不大于 m 2 f 1 (其中 fm  m / 2 )时，信号 f (t) 可以用等间隔的抽样值 ( ) s f nT 唯一地确定。这就是时域抽样定理，也称为奈奎斯特(Nyquist) 定理。 （二）频域抽样定理 若 f (t)是时间有限信号(或称时限信号)，即它只作用于( m m  t ,t )时间域内，如果在频 域中以不大于 m 2t 1 的频率间隔 1 f (即 1 f < m 2t 1 )对 f (t)的频谱F ()进行抽样，则抽样后的 频谱 ( ) F1  可以唯一地表示原信号。 3.3 本章知识点 （1）周期信号的傅里叶级数表示 （2）傅里叶变换及其性质 （3）周期信号的傅里叶变换 （4）抽样信号的傅里叶变换 （5）抽样定理

3.4例题 例31：选择题：如图所示的信号中，含有谐波分量为 4 例3-1图 A直流、正弦及余弦项 B 只有直流、正弦项 C只有直流、余弦项 D 只有直流、奇次余弦项 E 只有直流、奇次正弦项 分析：将上图变成一直流分量和下图所示信号和即可判断。 解：只有直流和正弦项，选B。 例3-2：求下面非周期信号的傅立叶变换 例3-2图 分析：我们既可以根据傅立叶变换的数学定义直接求得：也可以根据周期信号傅立叶级 数来求。 解： F)-f(dr=-A_E=ArSa(o/2) -10 例3-3：利用对称性求下列函数的傅立叶变换 2a f0=a+0<1<0 解： ea 2a 由于 a2+w2 9

9 3.4 例题 例3-1 ：选择题：如图所示的信号中，含有谐波分量为 -3 -1 1 1 t 2 3 … … -3 -1 1 5 1 t 2 3 … … 5 例3-1图 A 直流、正弦及余弦项 B 只有直流、正弦项 C 只有直流、 余弦项 D 只有直流、奇次余弦项 E 只有直流、奇次正弦项 分析：将上图变成一直流分量和下图所示信号和即可判断。 -3 1 -1 1 t … 3 … -3 1 5 -1 1 t … 3 … 5 解：只有直流和正弦项，选B。 例3-2：求下面非周期信号的傅立叶变换 x y  2  A x y  2  A 例3-2图 分析：我们既可以根据傅立叶变换的数学定义直接求得；也可以根据周期信号傅立叶级 数来求。 解： / 2 / 2 ( ) ( ) | ( / 2) j t A F f t e dt A Sa j                 例3-3：利用对称性求下列函数的傅立叶变换       t a t a f t , 2 ( ) 2 2 解： 由于 2 2 2 a w a e a t   

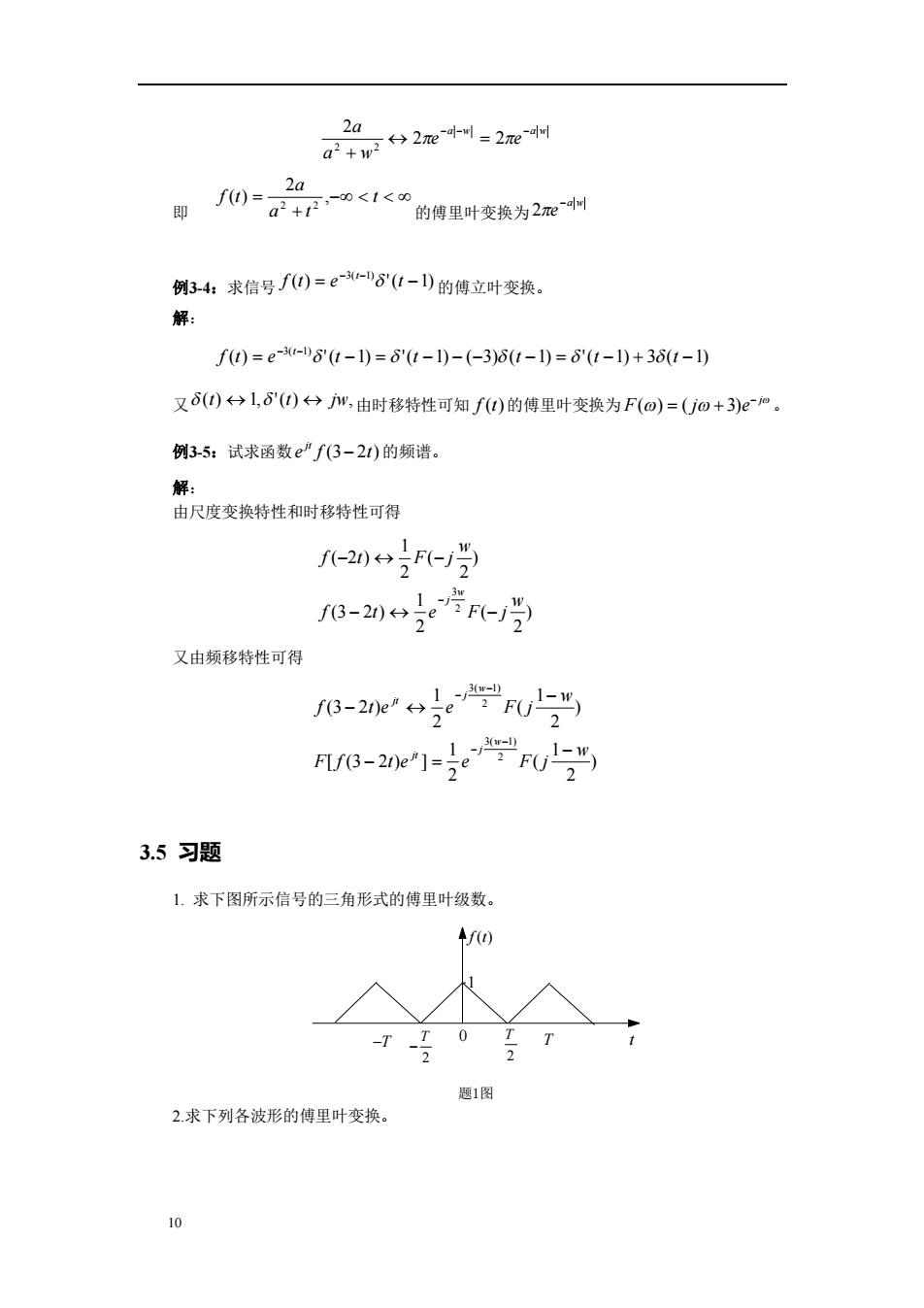
a2+n92ne=2e时 2a 2a f()= 即 a2+12,0<1<o 的傅里叶变换为2ea 例3-4：求信号f)=e--6'(1-l)的傅立叶变换。 解： f)=e-3-8'(1-1)=8'(t-1)-(-3)t-1)=8'(t-1)+36t-1) 又δ()→l,'()→m,由时移特性可知f)的傅里叶变换为F(o)=(o+3)em。 例3-5：试求函数e”f(3-2t)的频谱。 解： 由尺度变换特性和时移特性可得 f-20F-党 2 8-204号e(-5 又由频移特性可得 fB-2e”eg -e 号rU2 /8-2e1-=e 3.5习题 1.求下图所示信号的三角形式的傅里叶级数。 个f) 0 题1图 2.求下列各波形的傅里叶变换。 10

10 a w a w e e a w a       2 2 2 2 2 即       t a t a f t , 2 ( ) 2 2 的傅里叶变换为 a w e  2 例3-4：求信号 ( ) '( 1) 3( 1)     f t e t t  的傅立叶变换。 解： ( ) '( 1) '( 1) ( 3) ( 1) '( 1) 3 ( 1) 3( 1)              f t e t t t t t t      又 (t) 1, '(t)  jw,由时移特性可知 f t( )的傅里叶变换为 ( ) ( 3) j F j e       。 例3-5：试求函数 (3 2 ) jt e f t  的频谱。 解： 由尺度变换特性和时移特性可得 ) 2 ( 2 1 (3 2 ) ) 2 ( 2 1 ( 2 ) 2 3 w f t e F j w f t F j w j        又由频移特性可得 ) 2 1 ( 2 1 [ (3 2 ) ] ) 2 1 ( 2 1 (3 2 ) 2 3( 1) 2 3( 1) w F f t e e F j w f t e e F j w j jt w j jt           3.5 习题 1. 求下图所示信号的三角形式的傅里叶级数。 T T 2 T  2 0 T t f t( ) 1 题1图 2.求下列各波形的傅里叶变换