华东理工大学：《信号与系统》课程教学资源（课件讲稿）第三章 傅里叶变换 §3.2 非周期信号的傅立叶变换

§3.2非周期信号的傅立叶变换 则指数形式 00 付氏级数： f(1)=∑Fnem' n=-00 傅立叶级数 1 cto +71 f(t)e-modi 的复系数Fn r.=k.e=2a,6) b g 傅立叶级数的复系数F与频率的关系称为周期 信号的复数频谱（频谱特性）

§3.2 非周期信号的傅立叶变换 jn t n n f t F e 1 ( )           0 1 0 1 ( ) 1 1 t T t jn t n f t e dt T F  则指数形式 付氏级数 : 傅立叶级数 的复系数Fn ( ) 2 1 n n j n n F F e a jb n     n n n a b tg    傅立叶级数的复系数Fn与频率的关系称为周期 信号的 复数频谱（频谱特性）

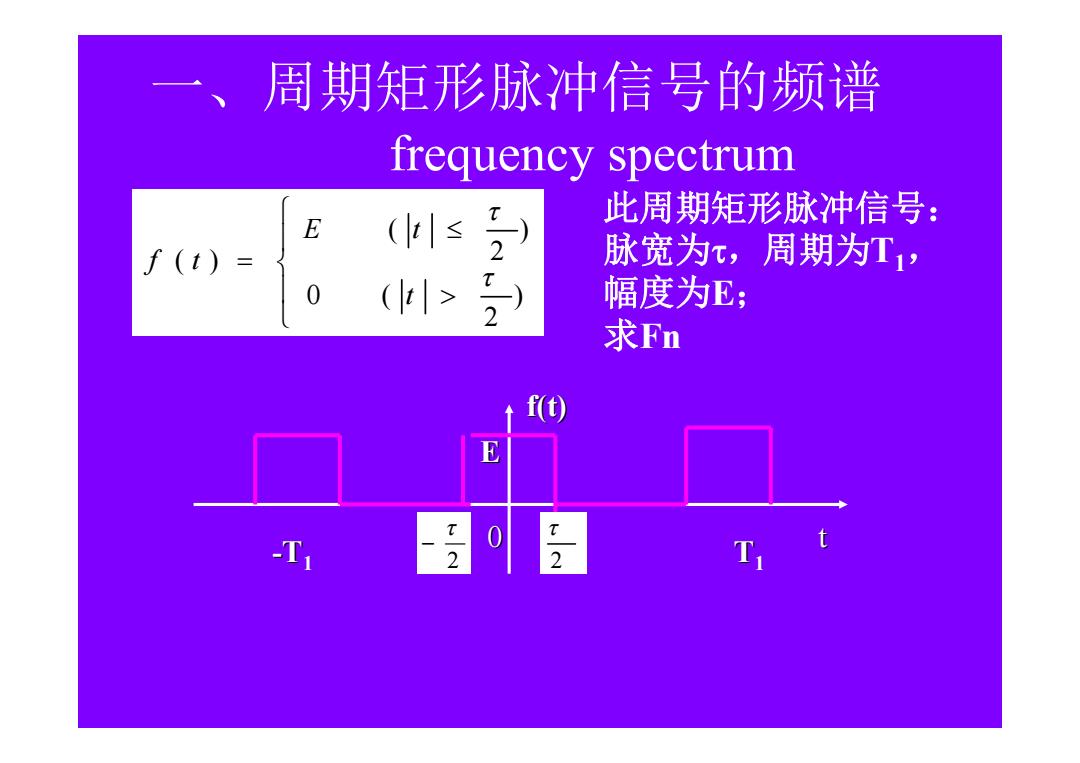
一、 周期矩形脉冲信号的频谱 frequency spectrum (≤ 此周期矩形脉冲信号： E (t) 2 脉宽为，周期为T1, 0(> 2) 幅度为E； 求Fn f(t) E T 2 T

一 、周期矩形脉冲信号的频谱 frequency spectrum         ) 2 0 ( ) 2 ( ( )   t E t f t f(t) 0 t E 2  2   -T1 T1 此周期矩形脉冲信号： 脉宽为，周期为T1， 幅度为E； 求Fn

Fn= f(t)e-mowdi n= Ee-dt 一2 T((emo12 E einot12) Et 2 T T 2

               2 ) 2 sin( ( ) ( ) 1 1 1 1 / 2 / 2 1 1 2 1 2 1 1 1              n n T E e e T jn E Ee dt T F jn jn jn t n 1 1 ( ) 2 E n Sa T        / 2 / 2 1 1 1 1 ( ) 1 T T jn t n f t e dt T F 

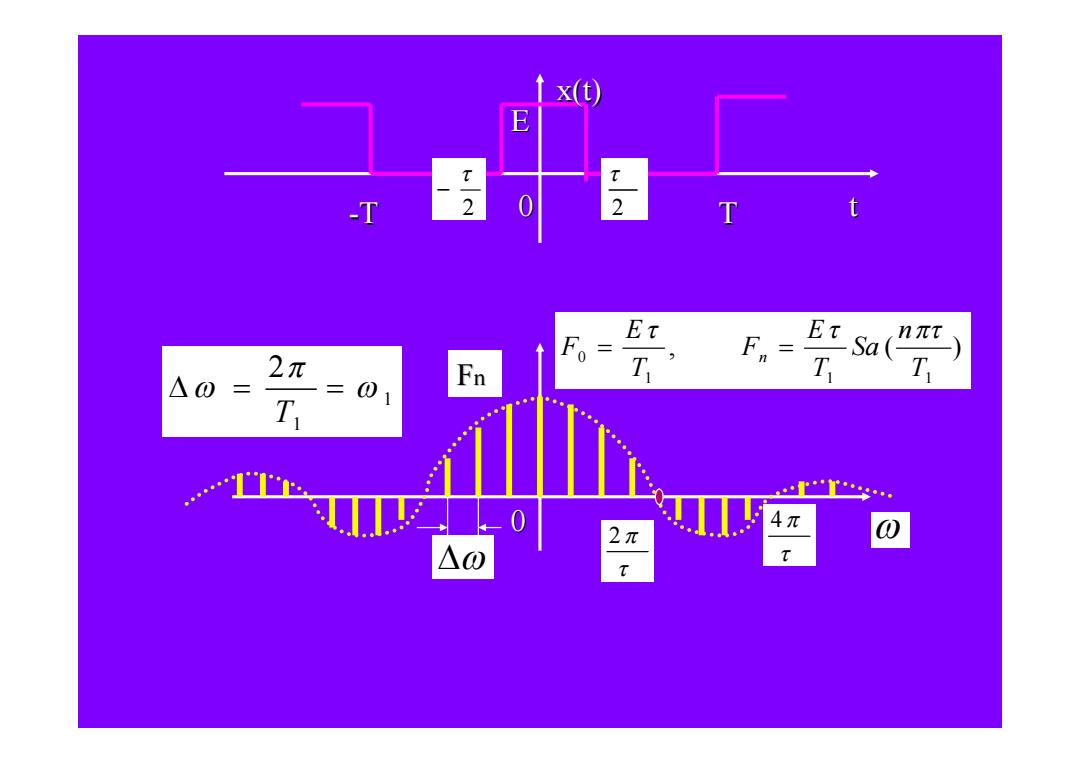
↑x) E T -T 2 0 2 T F Et E F. Sa nπt 2π T △0 01 Fn T 4π 2π △0 T

x(t) Fn t  0 0  2  4 E 2  2   -T T  1 1 2      T , ( ) 1 1 1 0 T n Sa T E F T E F n     

周期矩形的频谱变化规律： If T is constant,change t If t is constant,change T

周期矩形的频谱变化规律：  If T is constant, change τ  If τ is constant, change T T 

频谱分析表明 离散频谱，谱线间隔为基波频率，脉冲 周期越大，谱线越密 ●各分量的大小与脉幅成正比，与脉宽成 正比，与周期成反比。 ●各谱线的幅度按 n@T 包络线变化。过 Sa( 2 2mn 零点为 T ·主要能量在第一过零点内。带宽 2π B T

频谱分析表明  离散频谱，谱线间隔为基波频率，脉冲 周期越大，谱线越密。  各分量的大小与脉幅成正比，与脉宽成 正比，与周期成反比。  各谱线的幅度按 包络线变化。过 零点为  主要能量在第一过零点内。带宽 1 ( ) 2 n Sa      2m     2 B 

。由以上分析可知，若脉冲宽度为τ，幅 度E=1,周期为T则其傅立叶系数为 n sin( T 三 0 na 1

 由以上分析可知，若脉冲宽度为 ，幅 度E=1，周期为 则其傅立叶系数为  T1 1 1 1 1 1 ) 2 ( 2 ) 2 sin(          Sa n T n n T F n         

当脉宽τ保持不变，T,增大时，相应的频谱图 上的谱线间隔变小，相应的频谱包络线2sinoπ/2 的幅度变小。 T T,→时，周期矩形波变成了非周期的矩形 脉冲，相应的F,→0。因此，无法再用傅立 叶级数描述非周期信号的频域特性。 ◆用I乘上Fn,得TFn=S,(ot/2)a=m 式中T,Fn为一有限值

 当脉宽 τ 保持不变， 增大时，相应的频谱图 上的谱线间隔变小，相应的频谱包络线 的幅度变小。  时，周期矩形波变成了非周期的矩形 脉冲，相应的 。因此，无法再用傅立 叶级数描述非周期信号的频域特性。  用 乘上 ，得 ， 式中 为一有限值。 T1  2 sin / 2 T1 T1   Fn  0 T1 Fn 1 ( / 2) 1     T Fn  Sa  n T1Fn

=2 F TE, T 资5T 2π L22 0 I=4 F T 2元 0 T 互-8 TF 2π 2 V2π 0 T T T

2  2 4 1  T T1 t  2   2 T1 Fn  Fn   2   2 2 1  T 2  2 T1 t T1 Fn  2    2   2   2 Fn 2    2 8 1  T T1 t Fn  2   2  T1 Fn  2   2

非周期信号的频谱分析 Frequency spectrum analysis of aperiodic signals 当周期信号的周期T无限大时，就演变成了 非周期信号的单脉冲信号 00 频率也变成连续变量 2元 →0→d0 T no1-→o

非周期信号的频谱分析 Frequency spectrum analysis of aperiodic signals 当周期信号的周期T1无限大时,就演变成了 非周期信号的单脉冲信号 T1      d T  0 2 1 1 n1  频率也变成连续变量