
第二章连续时间系统的时域分析方法 本章主要内容: 1求微分(差分)方程的解 求时域响应 齐次解+特解 经典解法 全解 零输入响应+零状态响应 2单位冲激响应h(t),单位样值响应h(n) 3激励与冲激响应的卷积积分(卷积和)及其应用
第二章 连续时间系统的时域分析方法 本章主要内容: 1 求微分(差分)方程的解——求时域响应 全解 齐次解 + 特解 经典解法 零输入响应 +零状态响应 2 单位冲激响应h(t),单位样值响应h(n) 3 激励与冲激响应的卷积积分(卷积和)及其应用

§2-1连续系统的时域分析 §2-1-1系统微分方程及其经典解 任何LT连续时间系统,阶一元常系数微分方程一般式为: d"r dr" de be 经典法求解该方程: 全解=齐次解+特解 ↓ r(t)=r,(t)+r,(t) 齐次解)是齐次方程的通解: ag+aw-0 d" 通解一般式为:ce 特征方程为:a”+an-”-+…+a,Q+a,=0
b e dt de b dt d e b dt d e a r b dt dr a dt d r a dt d r m m m m m n m n n n n 1 1 0 1 1 1 0 1 1 1 §2-1 连续系统的时域分析 §2-1-1 系统微分方程及其经典解 任何LTI连续时间系统,n阶一元常系数微分方程一般式为: 全解=齐次解 + 特解 r(t) r (t) r (t) n f 1 0 0 1 1 1 a r dt dr a dt d r a dt d r n n n n n 通解一般式为: t ce 1 0 0 1 1 a a a n n n 特征方程为: 经典法求解该方程: 齐次解rn (t)是齐次方程的通解:
该一元n次方程的n个特征根为: 自然频率 固有频率 01,02…0n, (i=1,2…n) 讨论通解的形式: 1o为互异实根: r,(t)=>c,ee. 2a有k重根:n()=∑c,e1-1+c,e i=1 i=k+1 其中为k重根,o;为单根 特解的形式:根据激励查表得r() 求系数C,C 全解的形式:r(t)=rn(t)+rr(t)
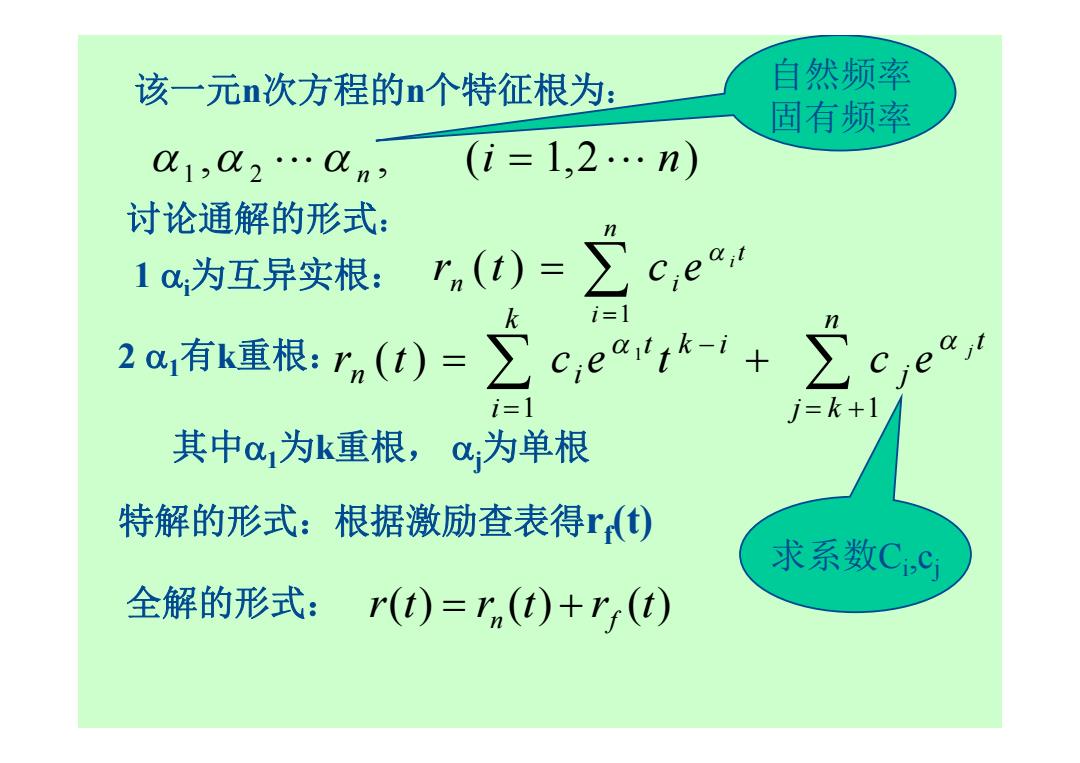
该一元n次方程的n个特征根为: , , ( 1,2 ) 1 2 i n n 自然频率 固有频率 讨论通解的形式: 1 i为互异实根: n i t n i i r t c e 1 ( ) 2 1有k重根: n j k t j k i k i t n i j r t c e t c e 1 1 1 ( ) 其中1为k重根, j为单根 特解的形式:根据激励查表得rf (t) 全解的形式: r(t) r (t) r (t) n f 求系数Ci ,cj

例1:求齐次解:r(t)+5r(t)+6r(t)=e(t) 解:该微分方程的特征方程为:02+50+6=0 解得特征根: 01=-2,02=-3 齐次解为: I(t)=ce2+cze 例3:求齐次解:r(t)+4r'(t)+4r(t)=e(t) 解:a2+4a+4=0→a12=-2二重根 rn(t)=cite+cze 2
例1:求齐次解: ( ) 5 ( ) 6 ( ) ( ) " ' r t r t r t e t 解:该微分方程的特征方程为: 5 6 0 2 解得特征根: 2, 3 1 2 t t n r t c e c e 3 2 2 1 ( ) 齐次解为: 例3:求齐次解: ( ) 4 ( ) 4 ( ) ( ) " ' r t r t r t e t 解: 4 4 0 2 1,2 2 二重根 t t n r t c te c e 2 2 2 1 ( )

例4:方程为:r(t)+3r(t)+2r(t)=e(t)+2(t) 若激励为:e(t)=t2求其特解r). 查表23-1得对应的特征解为:r(t)=A,t+At+A) (),(),r()e(t),e(t)代入原微分方程得: 24+324,t+4)+2(4t2+4t+A)=2t+22 241+(64,+2A)t+(24,+34t+2A)=2t+22 等式两边同次幂系数相等:2A,=2 A=2 6A+2A=2 →A=-2 24,+3A+2A=0 A,=1 rr(t)=t2-2t+2 t≥0
例4:方程为: ( ) 3 ( ) 2 ( ) ( ) 2 ( ) " ' ' r t r t r t e t e t 若激励为: 2 e(t) t 求其特解 rf (t). 查表2-3-1得对应的特征解为: 1 0 2 2 rf (t) A t At A ( ), ( ), ( ) " ' r t r t r t f f f ( ), ( ) ' e t e t 代入原微分方程得: 2 1 0 2 2 2 1 2 2A 3(2At A)2(At At A ) 2t 2t 2 2 1 2 1 0 2 2 2At (6A 2A)t (2A 3At 2A ) 2t 2t 等式两边同次幂系数相等: 1 2 2 2 3 2 0 6 2 2 2 2 2 1 0 2 1 0 2 1 2 A A A A A A A A A ( ) 2 2 2 rf t t t t 0

例5:方程为: r(t)+3r(t)+2r(t)=e(t)+2(t) 求:当 e(t)=t2,r(0)=1,r(0)=1时的全解 解: 特征方程为 02+30+2=0→1=-1,x2=-2 所以齐次解为: m(t)=ce +cze2 与例4相同: rr(t)=t2-2t+2 所以全解r()=ce+c2e21+12-2t+2 其-阶导为:r()=-℃e1-2c,e21+2t-2 =0时初值代入: 8=2e; 全解:r(t)=et-2e21+t2-2t+2 t≥0
例5:方程为: ( ) 3 ( ) 2 ( ) ( ) 2 ( ) " ' ' r t r t r t e t e t 求: 当 ( ) , (0) 1, (0) 1 2 ' e t t r r 时的全解 解: 特征方程为 3 2 0 1, 2 1 2 2 所以齐次解为: t t n r t c e c e 2 1 2 ( ) 与例4相同: ( ) 2 2 2 rf t t t 所以全解 ( ) 2 2 2 2 1 2 r t c e c e t t t t 其一阶导为: ( ) 2 2 2 2 1 2 ' r t c e c e t t t t=0时 初值代入: r(0) c1 c2 2 1 (0) 1 2 2 2 1 ' r c c c1 1, c2 2 ( ) 2 2 2 0 2 2 r t e e t t t 全解 t t :

解题思路: 1齐次解:其形式与激励e)无关,仅依赖于系统 本身特征 -一>自由响应或固有响应,系数c,C 与激励有关. 2特解的形式:由激励信号决定一一>强迫响应
1 齐次解:其形式与激励e(t)无关,仅依赖于系统 本身特征――>自由响应或固有响应,系数ci,cj 与激励有关. 2 特解的形式:由激励信号决定――>强迫响应. 解题思路:

§2-1-2零输入响应与零状态响应 全解可分解为: r(t)=rz(t) zs (t) 零输入响应 零状态响应 没有外加激励信号的作用,仅有系统的初始储能 引起的响应。解的形式是齐次解的形式。 r(t)= e C心;单根 初始状态决定的待定系数 x(t): 是零初始条件下的非齐次微分方程的全解 r(t)=∑cae+r() i=1 系数 的确定与前述方法相同。只是在系统初始 zsi 状态为0时的解
§2-1-2 零输入响应与零状态响应 r(t) r (t) r (t) Zi ZS 零输入响应 零状态响应 r (t): Zi 没有外加激励信号的作用,仅有系统的初始储能 引起的响应。解的形式是齐次解的形式。 初始状态决定的待定系数 全解可分解为: rzs (t) : 是零初始条件下的非齐次微分方程的全解 ( ) ( ) 1 r t c e r t f n i t zs zsi i 的确定与前述方法相同。只是在系统初始 状态为0时的解。 zsi 系数 c n i t zi zii i r t c e 1 ( ) 单根, i zii c

全响应的两种分解方式: r(t)=∑c,e&‘+r(t) i=1 自由响应 强迫响应 =2ce1+2ce+r,) i=1 i=1 零输入响应 零状态响应 所以有: C-Czi+cusi
( ) ( ) 1 r t c e r t f n i t i i 自由响应 强迫响应 n i t zii i c e 1 零输入响应 零状态响应 所以有: i zii zsi C c c 全响应的两种分解方式: ( ) 1 c e r t f n i t zsi i

例5:例4方程r(t)+3r(t)+2r(t)=e(t)+2(t) 求:当e(t)=t2,r(0)=1,r(0)=1时的零输入响应与 解:特征根为0%1=-1,02=-2 零输入状态响应 零输入响应:z()=Ce1+Cz2e21 r(0)=1,r(0)=1代入原方程 。ea 零输入响应为 rz(t)=3e-1-2e-21 t≥ 求零状态响应:根据上例结果有: 's(0=Cs1e+C2s2e21+t2-21+2 有零初始条件得:r公(0)=Cs1+Cs2+2=0 rs(0)=-Cs1-2Czs2-2=0 - 2s(t)=-2ef+t2-2t+2 t≥0
解:特征根为 1, 2 1 2 t Zi t Zi Zi r t C e C e 2 1 2 ( ) (0) 1, 0 1 ' r r 代入原方程 2 3 (0) 2 1 (0) 1 2 1 1 2 ' 1 2 Zi Zi Zi Zi Zi Zi Zi Zi C C r C C r C C 零输入响应为 ( ) 3 2 0 2 r t e e t t t Zi 求零状态响应:根据上例结果有: ( ) 2 2 2 2 1 2 r t C e C e t t t ZS t ZS ZS 有零初始条件得: 0 2 (0) 2 2 0 (0) 2 0 2 1 1 2 ' 1 2 ZS ZS ZS ZS ZS ZS ZS ZS C C r C C r C C ( ) 2 2 2 0 2 r t e t t t t ZS 例5:例4方程 ( ) 3 ( ) 2 ( ) ( ) 2 ( ) " ' ' r t r t r t e t e t 求: 当 ( ) , (0) 1, (0) 1 2 ' e t t r r 时的零输入响应与 零输入状态响应 零输入响应: