华东理工大学：《信号与系统》课程教学资源（课件讲稿）第三章 傅里叶变换 3.1 Frequency analysis of periodic signals（FS）

第三章傅里叶变换 Fourier Transform.FT 本章主要内容 •周期信号的傅里叶级数(Ch1) (Fourier Series,FS) •非周期信号的傅里叶变换 •傅里叶变换的性质 卷积和卷积定理 •周期信号傅立叶变换 抽样信号的傅里叶变换和抽样定理 模拟滤波器(ch7

1 第三章 傅里叶变换 本章主要内容 •周期信号的傅里叶级数（Ch1) (Fourier Series,FS) •非周期信号的傅里叶变换 •傅里叶变换的性质 •卷积和卷积定理 •周期信号傅立叶变换 •抽样信号的傅里叶变换和抽样定理 •模拟滤波器(ch7) Fourier Transform,FT

The introduction of Fourier 1768年生于法国 1807年提出“任何周期信号 都可用正弦函数级数表示” 拉格朗日Lagrange反对发表 1822年首次发表在“热的分 析理论”一书中 1829年狄里赫利Dirichlet) 第一个给出收敛条件

2 The introduction of Fourier • 1768年生于法国 • 1807年提出“任何周期信号 都可用正弦函数级数表示” • 拉格朗日Lagrange反对发表 • 1822年首次发表在“热的分 析理论” 一书中 • 1829年狄里赫利(Dirichlet) 第一个给出收敛条件

傅立叶的两个最主要的贡献 “周期信号都可表示为谐波关系的 正弦信号的加权和” 傅里叶的 第一个主要论点 “非周期信号都可用正弦信号的加 权积分表示 ” 傅里叶的第二个主要论点

3 傅立叶的两个最主要的贡献—— • “周期信号都可表示为谐波关系的 正弦信号的加权和”——傅里叶的 第一个主要论点 • “非周期信号都可用正弦信号的加 权积分表示” ——傅里叶的第二个主要论点

frequency-domain analysis: 一一Fourier transform,自变量为jo complex frequency analysis 一一Laplace transform,自变量为S=o+jo ·Z-domain analysis:一--Z变换，自变量为z 2=est =elo+jo)r

4 • frequency-domain analysis： －－ Fourier transform ，自变量为 j  • complex frequency analysis ： －－ Laplace transform, 自变量为 S =  +j  • Z-domain analysis ：－－－Z 变换，自变量为 z sT j T z e e (  )  

3.1 Frequency analysis of periodic signals--FS 满足狄利赫利条件的周期信号可展开成 正交函数线性组合的无穷级数： 三角函数式的傅立里叶级数{cosn@,t sinno t Trigonometric series .复指数函数式的傅里叶级数{ejno} complex exponential function

5 3.1 Frequency analysis of periodic signals --FS • 满足狄利赫利条件的周期信号可展开成 正交函数线性组合的无穷级数： . 三角函数式的 傅立里叶级数 {cosn1 t, sinn1 t} . 复指数函数式的傅里叶级数 { e j n  1 t } Trigonometric series complex exponential function

三角函数是正交函数 Trigonometric founctions are Orthogonal cosno t.sin mo t.dt =0 (所有m,n) na- (m=n） (m≠m) 0+ cosa0tcosmmd- ( m=n) 0(m≠n)

6 三角函数是正交函数 Trigonometric founctions are Orthogonal cos .sin . 0 ( , ) 1 1 0 1 0 n t m t dt m n t T t   所有    ( ) ( ) 0 sin sin 0 0 1 2 1 1 m n m n n t m tdt t T t T           ( ) ( ) 0 cos cos 0 0 1 2 1 1 m n m n n t m tdt t T t T          

狄利赫利条件： ()在一个周期内函数绝对可积，即 o(lt≤o (2)在一个周期内有有限个极值点： 3)在一个周期内，只有有限个间断点； 且在这些间断点上函数是有限值 ·一般周期信号都满足这些条件

7 狄利赫利条件： (1)在一个周期内函数绝对可积，即 (2)在一个周期内有有限个极值点； (3)在一个周期内,只有有限个间断点； 且在这些间断点上函数是有限值 • 一般周期信号都满足这些条件

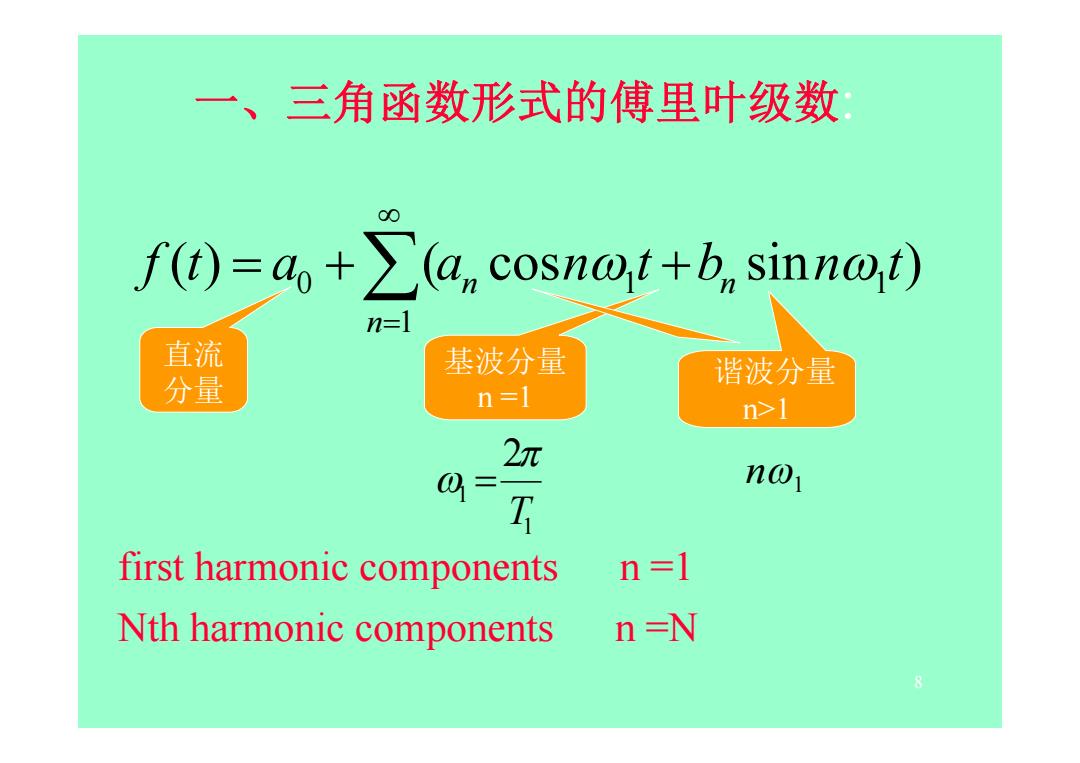
一、三角函数形式的傅里叶级数 f)=4+∑(a,cosn@t+-b,sinno,t)） n=] 直流 基波分量 分量 谐波分量 n=1 n>1 2π 0=1 n01 T first harmonic components n =1 Nth harmonic components n=N

8 一 、三角函数形式的傅里叶级数: 1 1 2 T    ( ) ( cos sin ) 1 1 1 0 f t a a n t b n t n n n        直流 分量 基波分量 n =1 谐波分量 n>1 n1 first harmonic components n =1 Nth harmonic components n =N

直流 系数 余弦分登a,= roowe 系数 正弦分量 f(t).sin notdi 系数

9    0 1 0 ( ). 1 1 0 t T t f t dt T a    0 1 0 ( ).cos . 2 1 1 t T t n f t n t dt T a  f t n t dt T b t T t n ( ).sin . 2 0 1 0 1 1     直流 系数 余弦分量 系数 正弦分量 系数

二、余弦形式的傅立叶级数 f (t)=ao+(a,cos not+b sin nat) n= f(t)=C。+∑C,CoS(not+φn) n=1 比较几种系数的关系 a0= Cm=V√a7+b7 u"=C"c02" ”=-C“W

10 二、 余弦形式的傅立叶级数 ( ) ( ) 1 1 0 n n n f t  C   C COS n  t     ( ) ( cos sin ) 1 1 1 0 f t a a n t b n t n n n         比较几种系数的关系 0 C 0 a  2 2 C n  a n  b n n n n a b tg   