
3.8 Fourier transform of sampling signals 时域抽样Time-domain sampling 一矩形脉冲抽样 冲激抽样Impulse-train 频域抽样 Frequency-domain sampling Q1:时域抽样,抽样后信号的F,(o)与原信号频 谱F(o)有何关系? Q2:频域抽样,频域抽样后原函数f)与原始 信号f(t)有何关系? Q3:何种情况下,可以从抽样信号中恢复原始 信号?
1 §3.8 Fourier transform of sampling signals • 时域抽样Time-domain sampling – 矩形脉冲抽样 – 冲激抽样 Impulse-train • 频域抽样 Frequency-domain sampling Q1:时域抽样,抽样后信号的 与原信号频 谱 有何关系? Q2:频域抽样,频域抽样后原函数 与原始 信号 有何关系? Q3:何种情况下,可以从抽样信号中恢复原始 信号? () Fs F() ( ) 1 f t f (t)
时域抽样 设有一连续信号t),对其进行抽样的过程可 以看成是由原信号t)与一抽样脉冲序列s() 相乘的结果。 s(t f方可 s( i/() 0 1 如果s()为周期信号,即各脉冲间隔T,相同, 称为均匀抽样。f=1/T称为抽样频率,Q,=2π/T称 为抽样角频率。 2
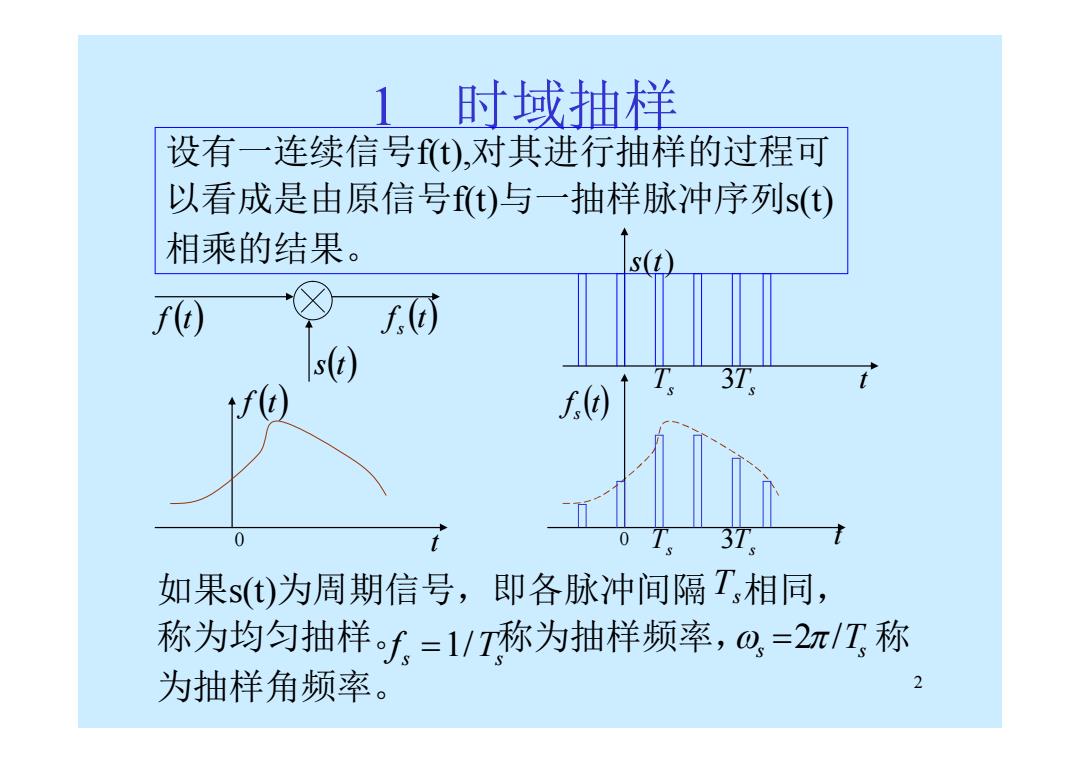
2 1 时域抽样 设有一连续信号f(t),对其进行抽样的过程可 以看成是由原信号f(t)与一抽样脉冲序列s(t) 相乘的结果。 f t st f t s f t s 0 t Ts 3Ts f t 0 t Ts 3Ts s(t) t 如果s(t)为周期信号,即各脉冲间隔 相同, 称为均匀抽样。 称为抽样频率, 称 为抽样角频率。 Ts s Ts f 1/ s Ts 2/
矩形脉冲抽样信号的傅立叶变换 f、(t) × 0 0 2T:-Ts 0 T 2Ts o -2T、-T0Tg2T t So R回 米 30 -3 3 3
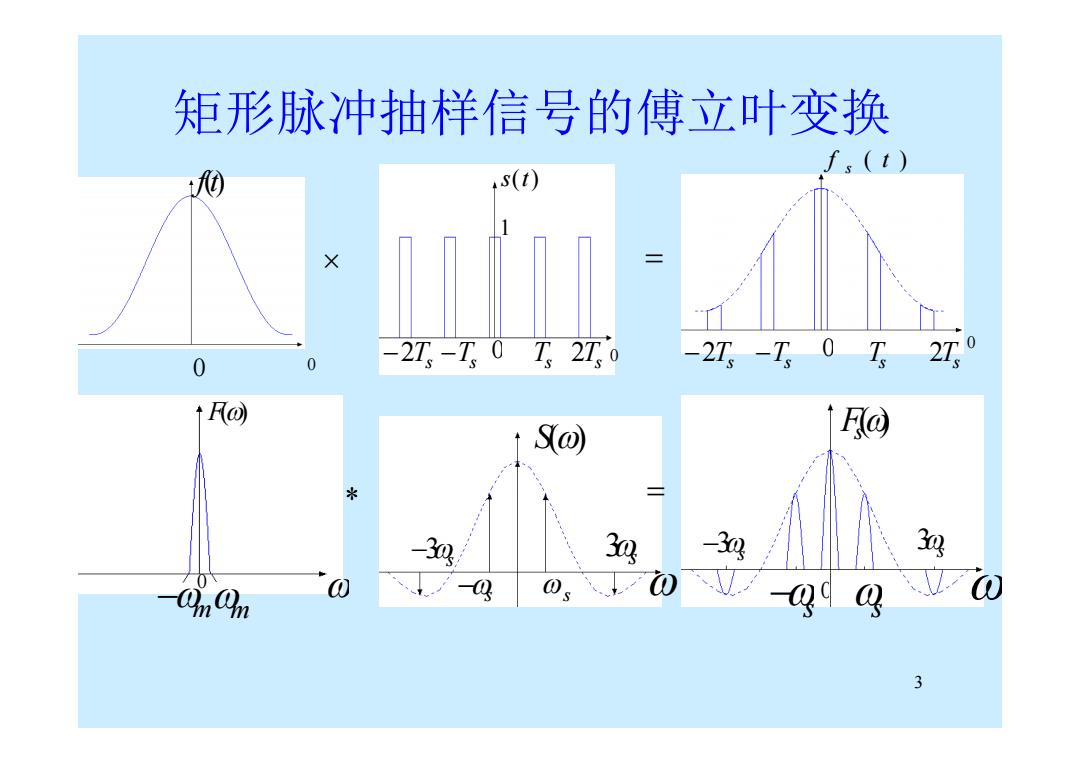
3 f(t) 0 0 0 0 s(t) 1 Ts Ts 2 Ts 2 Ts f ( t ) s 0 Ts Ts 2 Ts 2 Ts 0 m F() 0 m s 3s 3s S() s () Fs s s 0 s 3 s 3 * 矩形脉冲抽样信号的傅立叶变换
时域冲激抽样抽样的傅立叶变换 f(t) ↑s(t) ∫,(t) 0 0 F(@) S(@) F,(0) (0) 米 444 -0m0-t4 0 -20g -00 0,200 0 4
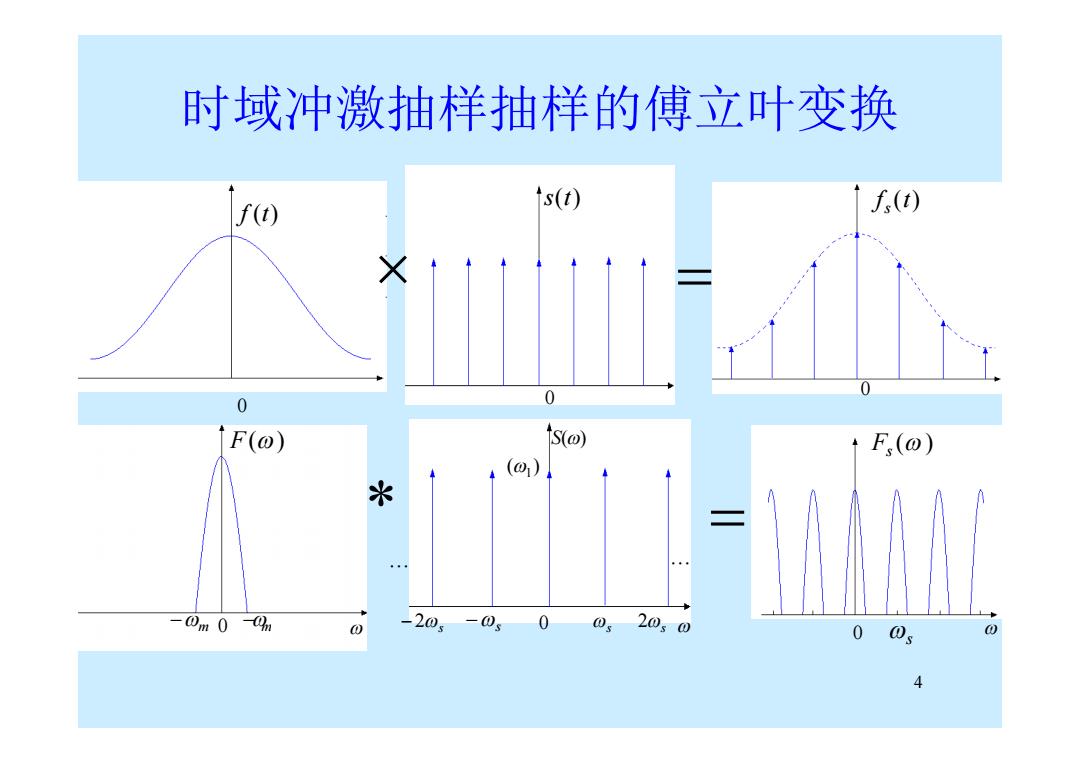
4 时域冲激抽样抽样的傅立叶变换 ( ) 1 S() ... ... 2s 0 s 2s f (t) s(t) f (t) s () Fs F() 0 0 0 0 0 m m s s

原信号的频谱Fo与抽样信号频谱(⊙之间 的关系 在Fo冲完整的保留了F@这就是F(耐 =0(即图形最中间)的部分 ·风o与@在幅度上相差一个常数 当取矩形脉冲抽样时,系数为鸣) 当取冲激脉冲抽样时,系数为
5 原信号的频谱 与抽样信号频谱 之间 的关系 F() () Fs Ts 1 当取冲激脉冲抽样时,系数为 2 s s n Sa T E 当取矩形脉冲抽样时,系数为 •F()与Fs () 在幅度上相差一个常数 • 在 中完整的保留了 ,这就是 中 n=0(即图形最中间)的部分 () Fs () Fs F()
2、频域抽样 F(o) 6(0 (@) 0 -00⊙ -01001 6
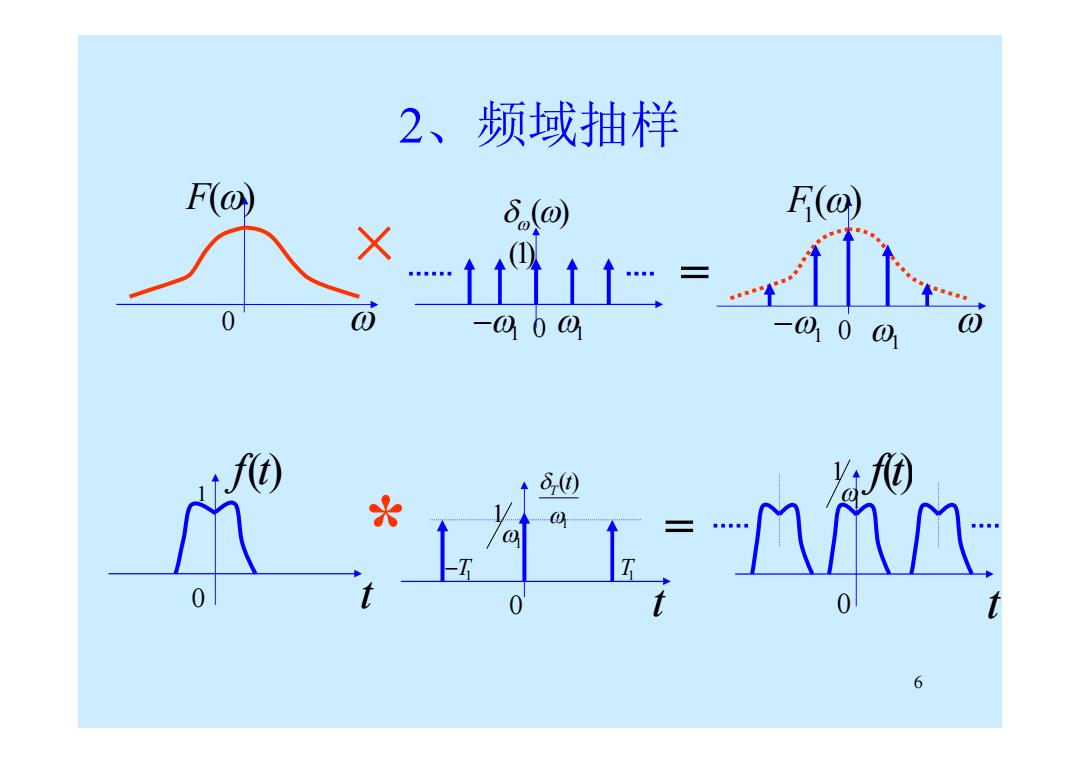
6 2、频域抽样 F() 0 f(t) 0 t 1 1 f(t) 0 t 1 1 ( ) t T 1 1 T1 T1 0 t ( ) F1 0 1 0 1 () (1) 1 1 = = × *

§3.9抽样定理sampling theorem (一)时域抽样定理 奈奎斯特定理(Nyquist) 一个频率有限信号f(t)如果频谱只占据-0m→+0m 的范围,则信号∫(t)可以用等间隔的抽样值来唯一地表 示。而抽样间隔T,不大于 2fm 或者说最低抽样频率 为2fm· 奈奎斯特频率: fs=2fm 或 0=20 其中 m =2πfm 奈奎斯特周期: 2 7
7 §3.9 抽样定理sampling theorem • (一)时域抽样定理——奈奎斯特定理(Nyquist) 一个频率有限信号 如果频谱只占据 的范围,则信号 可以用等间隔的抽样值来唯一地表 示。而抽样间隔 不大于 ,或者说最低抽样频率 为 。 奈奎斯特频率: 或 其中 奈奎斯特周期: f (t) m m f (t) m 2 f 1 m m 2 f m 2 f s m f 2 f Ts m s f T 2 1 s 2 m
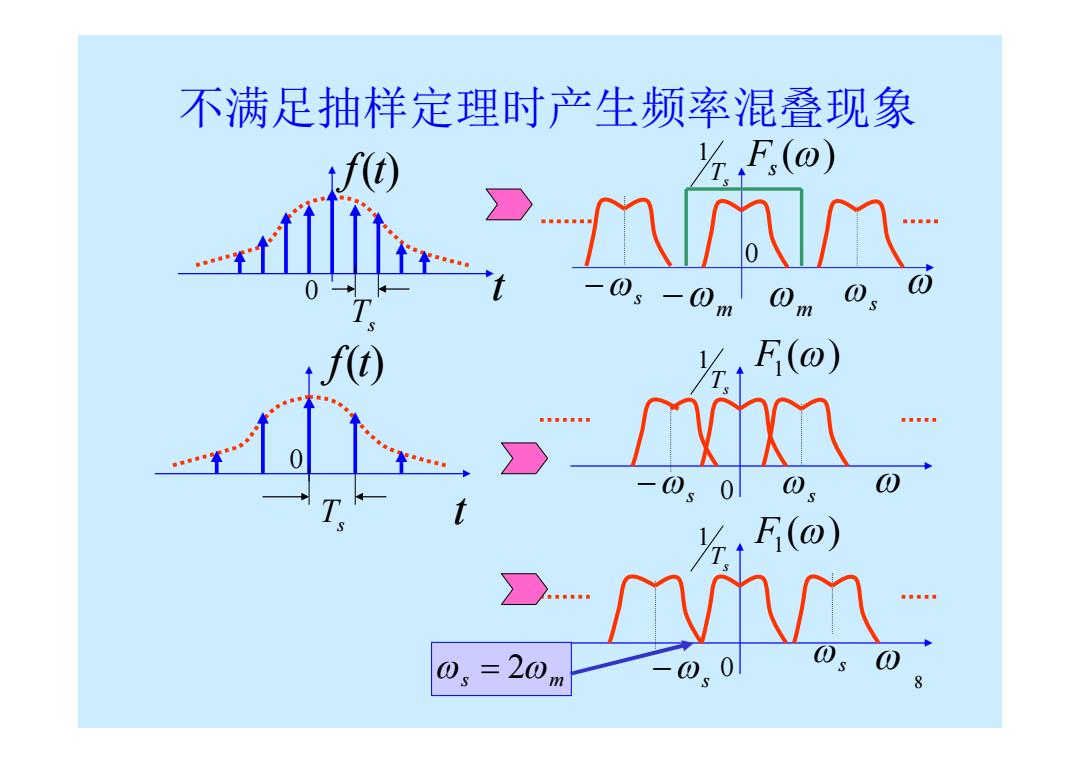
不满足抽样定理时产生频率混叠现象 六F,(⊙) F(@) O F(O) 0,=20 0 m
8 不满足抽样定理时产生频率混叠现象 0 t f(t) Ts ( ) F1 s 0 s Ts 1 () Fs 0 f(t) 0 t Ts 1 s Ts s m m ( ) F1 0 s s Ts 1 s 2 m

能从抽样信号无失真恢复原信号的两 个条件 信号t)因该是频带受限的,其频谱函数 在0>0,时为零 抽样频率不能过低,应有o,>20,或抽 样间隔不能太大,要求T,<12fm)。 9
9 能从抽样信号无失真恢复原信号的两 个条件 • 信号f(t)因该是频带受限的,其频谱函数 在 时为零。 • 抽样频率不能过低,应有 ,或抽 样间隔不能太大,要求 。 m s 2m 1/(2 ) s m T f
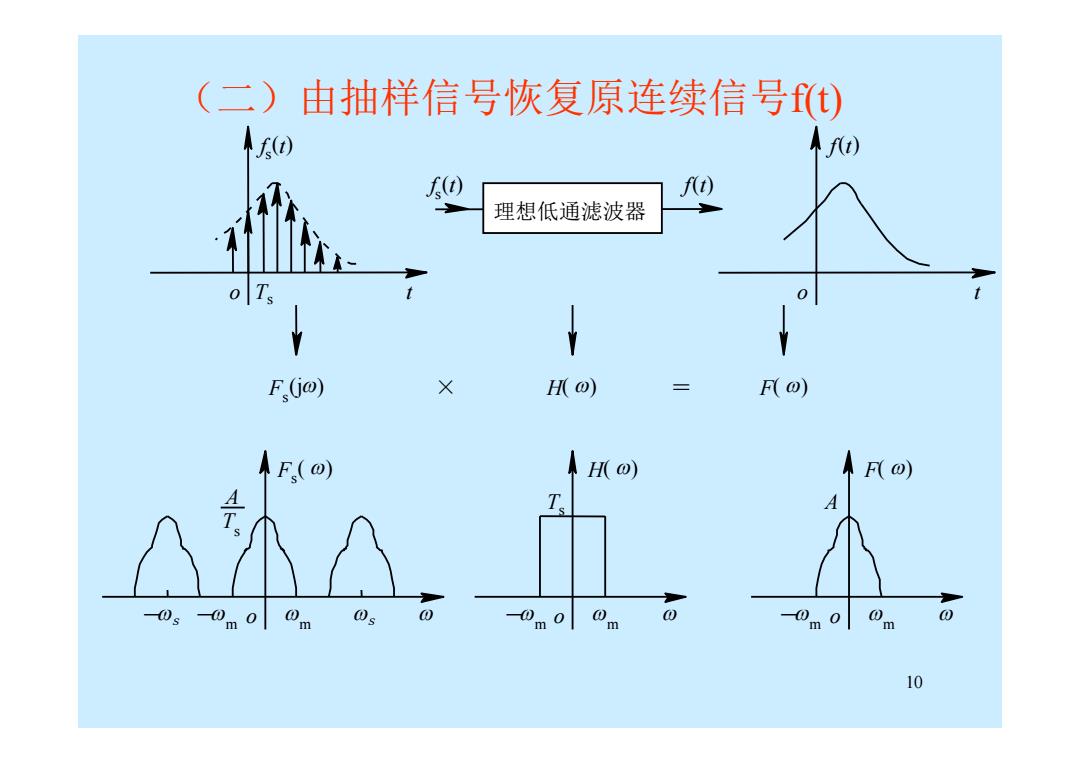
(二)由抽样信号恢复原连续信号t) ) Afi) f(t) 理想低通滤波器 F(j@) H F(O) F() H(⊙) F(O) T A m0 0 0 0 m m m 10
10 o t o t f s (t) Ts 理想低通滤波器 f s (t) F × H( ) = F( ) s (j) - m o m -s s Fs ( ) T s A - m o m H( ) Ts - m o m F( ) A f(t) f(t) (二)由抽样信号恢复原连续信号f(t)