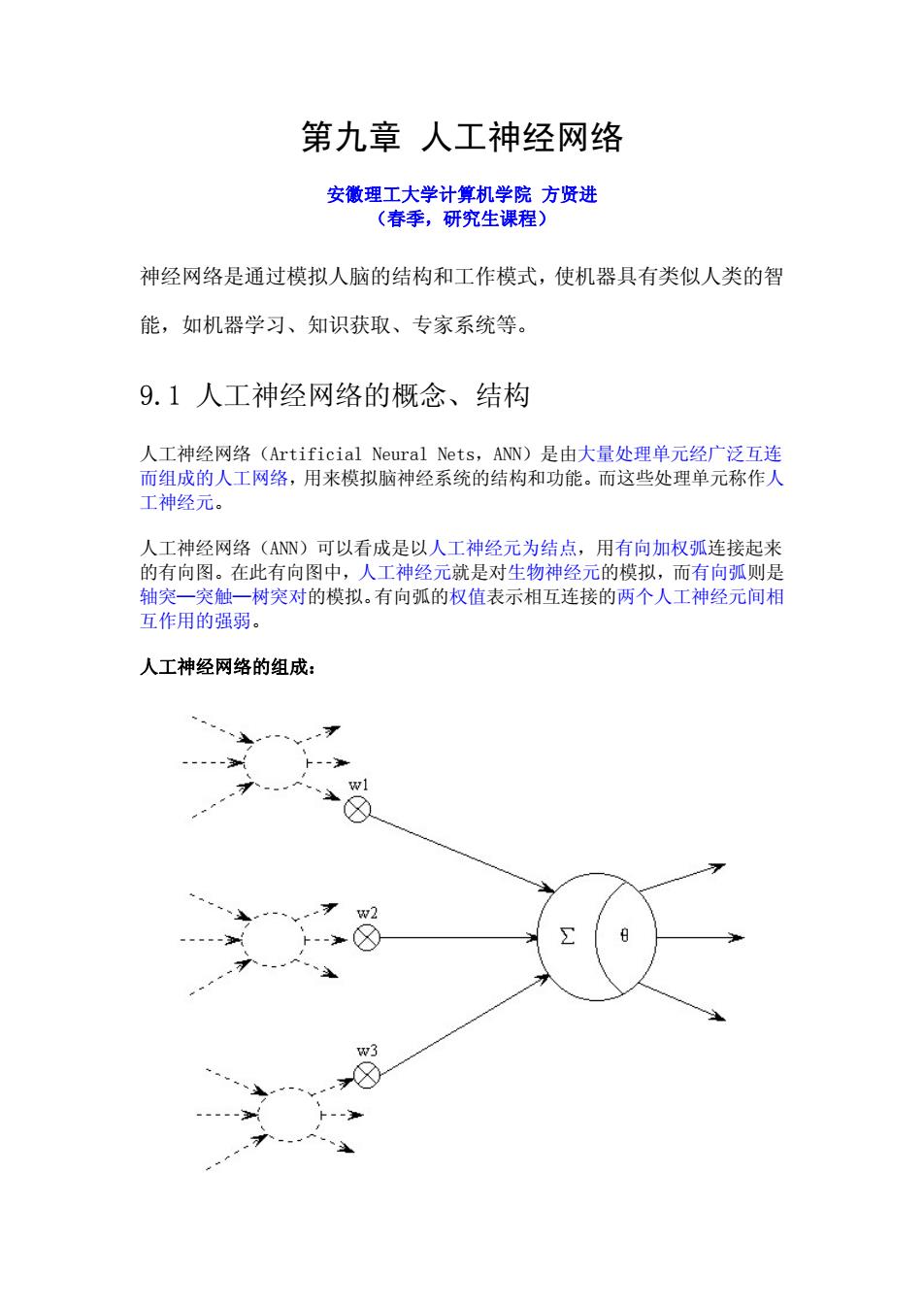
第九章人工神经网络 安徽理工大学计算机学院方贤进 (春季,研究生课程) 神经网络是通过模拟人脑的结构和工作模式,使机器具有类似人类的智 能,如机器学习、知识获取、专家系统等。 9.1人工神经网络的概念、结构 人工神经网络(Artificial Neural Nets,ANN)是由大量处理单元经广泛互连 而组成的人工网络,用来模拟脑神经系统的结构和功能。而这些处理单元称作人 工神经元。 人工神经网络(AN)可以看成是以人工神经元为结点,用有向加权弧连接起来 的有向图。在此有向图中,人工神经元就是对生物神经元的模拟,而有向弧则是 轴突一突触一树突对的模拟。有向弧的权值表示相互连接的两个人工神经元间相 互作用的强弱。 人工神经网络的组成: w2 8 w3
第九章 人工神经网络 安徽理工大学计算机学院 方贤进 (春季,研究生课程) 神经网络是通过模拟人脑的结构和工作模式,使机器具有类似人类的智 能,如机器学习、知识获取、专家系统等。 9.1 人工神经网络的概念、结构 人工神经网络(Artificial Neural Nets,ANN)是由大量处理单元经广泛互连 而组成的人工网络,用来模拟脑神经系统的结构和功能。而这些处理单元称作人 工神经元。 人工神经网络(ANN)可以看成是以人工神经元为结点,用有向加权弧连接起来 的有向图。在此有向图中,人工神经元就是对生物神经元的模拟,而有向弧则是 轴突—突触—树突对的模拟。有向弧的权值表示相互连接的两个人工神经元间相 互作用的强弱。 人工神经网络的组成:
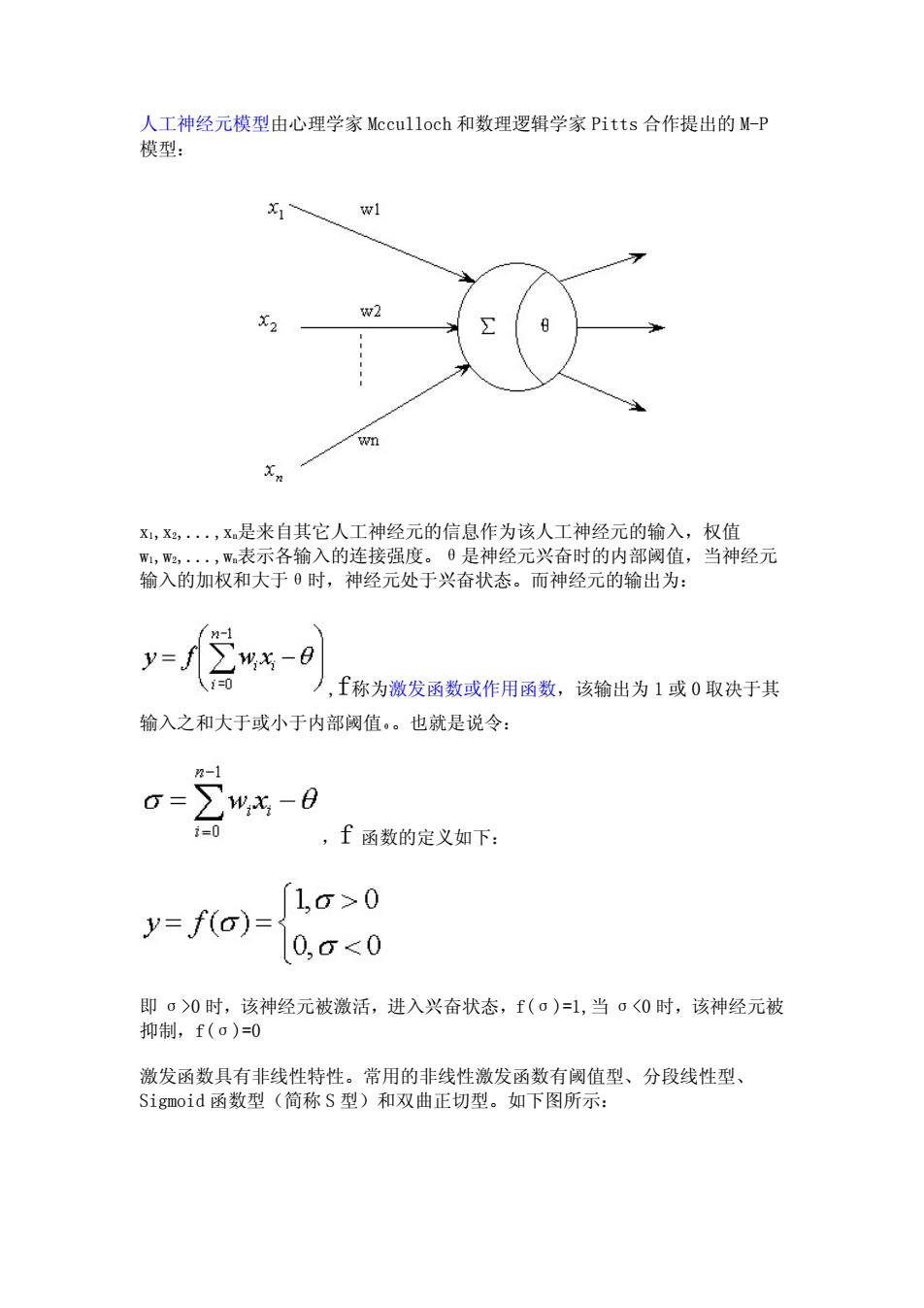
人工神经元模型由心理学家Mcculloch和数理逻辑学家Pitts合作提出的M-P 模型: w1 下2 w2 8 wn x,x2,··,X是来自其它人工神经元的信息作为该人工神经元的输入,权值 W,W2,.,W表示各输入的连接强度。0是神经元兴奋时的内部阈值,当神经元 输入的加权和大于0时,神经元处于兴奋状态。而神经元的输出为: y=J f称为激发函数或作用函数,该输出为1或0取决于其 输入之和大于或小于内部阈值。也就是说令: 2 ∑- i=0 ,f函数的定义如下 1,6>0 y=f(o)= 0,60时,该神经元被激活,进入兴奋状态,f(o)=1,当o<0时,该神经元被 抑制,f(o)=0 激发函数具有非线性特性。常用的非线性激发函数有阈值型、分段线性型、 Sigmoid函数型(简称S型)和双曲正切型。如下图所示:
人工神经元模型由心理学家 Mcculloch 和数理逻辑学家 Pitts 合作提出的 M-P 模型: x1,x2,...,xn是来自其它人工神经元的信息作为该人工神经元的输入,权值 w1,w2,...,wn表示各输入的连接强度。θ是神经元兴奋时的内部阈值,当神经元 输入的加权和大于θ时,神经元处于兴奋状态。而神经元的输出为: ,f称为激发函数或作用函数,该输出为1或0 取决于其 输入之和大于或小于内部阈值θ。也就是说令: ,f 函数的定义如下: 即 σ>0 时,该神经元被激活,进入兴奋状态,f(σ)=1,当 σ<0 时,该神经元被 抑制,f(σ)=0 激发函数具有非线性特性。常用的非线性激发函数有阈值型、分段线性型、 Sigmoid 函数型(简称 S 型)和双曲正切型。如下图所示:

io) f(o 阈值型 分段线性 f(o) f(o) .1 Sigmoid函数型 双曲正切型 9.2单层感知器(Perceptron)模型及其学习算法 9.2.1感知器训练法则 1957年美国学者Rosenblatt提出了一类具有自学习能力的感知器模型,它是一 个具有单层计算单元的前向神经网络,其神经元为线性阈值单元,称为单层感知 器。它和M-P模型相似,当输入信息的加权和大于或等于阈值时,输出为1,否 则输出为0或-1。与M-P模型不同之处是神经元之间的连接权值W是可变的,这 种可变性就保证了感知器具有学习能力。 Rosenblatt提出的单层感知器由输入部分和输出层构成,输出层即为它的计算 层。在该感知器模型中,输入部分和输出层都可由多个神经元(处理单元)构成, 输入部分的神经元与输出层的各种神经元间均有连接。当输入部分将输入数据传 送给连接的处理单元时,输出层就会对所有输入数据进行加权求和,经阈值型作 用函数产生一组输出数据
9.2 单层感知器(Perceptron)模型及其学习算法 9.2.1 感知器训练法则 1957 年美国学者Rosenblatt提出了一类具有自学习能力的感知器模型,它是一 个具有单层计算单元的前向神经网络,其神经元为线性阈值单元,称为单层感知 器。它和M-P模型相似,当输入信息的加权和大于或等于阈值时,输出为 1,否 则输出为 0 或-1。与M-P模型不同之处是神经元之间的连接权值wi是可变的,这 种可变性就保证了感知器具有学习能力。 Rosenblatt 提出的单层感知器由输入部分和输出层构成,输出层即为它的计算 层。在该感知器模型中,输入部分和输出层都可由多个神经元(处理单元)构成, 输入部分的神经元与输出层的各种神经元间均有连接。当输入部分将输入数据传 送给连接的处理单元时,输出层就会对所有输入数据进行加权求和,经阈值型作 用函数产生一组输出数据

81 W 1 x2 ym 输入部分一 输出层 1, 若∑%,-日,20 到 y=1 0, 若∑州-日,<0 Jj=1,2,,m 1959年Rosenblatt提出了感知器模型中连接权值参数的学习算法。算法的思想 是首先把连接权值和阈值初始化为较小的非零随机数,然后把有个连接权值的 输入送入网络,经加权运算处理,得到的输出如果与所期望的输出有较大的差别, 就对连接权值参数按照某种算法进行自动调整,经过多次反复,直到所得到 的输出与所期望的输出间的差别满足要求为止。 感知器信息处理的规则为: 其中y(t)为t时刻输出,xi为输入向量的一个分量,Wi(t)为t时刻第i个输入 的加权,0为阈值,f0为阶跃函数。 感知器的学习规则如下: W(1+1)=W(t)+nd-xt)k 其中n为学习率(0<n<1),d为期望输出,y(t)为实际输出
1959 年 Rosenblatt 提出了感知器模型中连接权值参数的学习算法。算法的思想 是首先把连接权值和阈值初始化为较小的非零随机数,然后把有 n 个连接权值的 输入送入网络,经加权运算处理,得到的输出如果与所期望的输出有较大的差别, 就对连接权值参数按照某种算法进行自动调整,经过多次反复,直到所得到 的输出与所期望的输出间的差别满足要求为止。 感知器信息处理的规则为: , 其中 y(t)为 t 时刻输出,xi 为输入向量的一个分量,Wi(t)为 t 时刻第 i 个输入 的加权,θ 为阈值,f()为阶跃函数。 感知器的学习规则如下: 其中 η 为学习率(0<η<1),d 为期望输出,y(t)为实际输出

单层感知器学习算法(learning algorithm for single layer perceptron): stepl:initialize connection weight and threshold.set a smaller nonzero random value for wi(i=1,...,n)and 0 as their initial value.wi(0)represents connection weight of i-th input at the moment of t; step2:input a training parameter =(x1(t),x2(t),...,xn(tand the expectation output d(t); step3:compute the actual output of ANN: 0=f(②0,0x,(0-6.1=1,2,为 step4:compute the difference value between actual output and expectation output: DEL=d(t)-y(t) if DEL<e (e is a very small positive number),then training of ANN is over,otherwise goto step 5; step5:regulate the connection weight according to the following fomular: m,t+1)=m,⑤+p(d(⑤-⑤)x,,1=1-n where 0<n<=1 is an incremental factor,it is used to control regulation speed,and called learning rate.Usualy,the value of n can't be too large or small.if its value is too large,then n will impact the convergence of wi(t),otherwise make the convergence speed of wi(t)slower: step 6:goto step 2;
单层感知器学习算法(learning algorithm for single layer perceptron): step1:initialize connection weight and threshold. set a smaller nonzero random value for wi(i=1,...,n) and θ as their initial value. wi(0) represents connection weight of i-th input at the moment of t; step2:input a training parameter X=(x1(t),x2(t),...,xn(t))and the expectation output d(t); step3:compute the actual output of ANN: step4:compute the difference value between actual output and expectation output: DEL=d(t)-y(t) if DEL<ε(ε is a very small positive number), then training of ANN is over, otherwise goto step 5; step5: regulate the connection weight according to the following fomular: where 0<η<=1 is an incremental factor, it is used to control regulation speed, and called learning rate. Usualy, the value of η can't be too large or small. if its value is too large, then η will impact the convergence of wi(t),otherwise make the convergence speed of wi(t) slower; step 6: goto step 2;

9.2.2线性不可分问题 1962年Rosenblatt宣布人工神经网络可以学会它能表示的任何东西。但是 l969 Minsky发表了一书《perceptron》,书中指出单层感知器不能解决许多最 基本的问题,如异或问题(XO),这类问题统称为线性不可分问题,即输入的 训练样本集是否是线性可分的,如果是线性可分的,则训练算法收敛,否则不收 敛。 异或问题的定义如下: 0,fx1=x2 y(x1,x2)= (9.1) 1,其它 相应的真值表如下: 点 输入x1 输入x2 输出y A1 0 0 0 B1 1 0 1 A2 1 1 0 B2 0 如果用单层感知器的话,其输出为 y(xI,x2)=f(ol*x1+02*x2-0) (9.2) 如果用单层感知器解决异或问题的话,根据异或问题的定义以及真值表可知,日 o1,o1的取值必须满足下面方程组: 0+0-0<0 o1-020 (9.3) ol+o2-0<0 02-0≥0 该方程组是无解的。所以单层感知器是无法解决异或问题的。 该问题的几何意义如图所示,感知器的输出为1用空心圆表示,输出为0用实心 圆表示,可以看出满足x1XORx2=1的点集(输入集)为B={B1,B2},满足x1XOR x2=0的点集(输入集)为A={A1,A2}。显然无论如何选择0,o1,o1的取值
9.2.2 线性不可分问题 1962 年 Rosenblatt 宣布人工 神经网络可以学会它能表示的任何东西。但是 1969Minsky 发表了一书《perceptron》,书中指出单层感知器不能解决许多最 基本的问题,如异或问题(XOR),这类问题统称为线性不可分问题,即输入的 训练样本集是否是线性可分的,如果是线性可分的,则训练算法收敛,否则不收 敛。 异或问题的定义如下: (9.1) ⎩ ⎨ ⎧ = = ,1 其它 21 ,0 ),( 21 xxif xxy 相应的真值表如下: 点 输入 x1 输入 x2 输出 y A1 0 0 0 B1 1 0 1 A2 1 1 0 B2 0 1 1 如果用单层感知器的话,其输出为 = ω ∗ ω ∗+ xxfxxy −θ )2211()2,1( (9.2) 如果用单层感知器解决异或问题的话,根据异或问题的定义以及真值表可知,θ ω1,ω1 的取值必须满足下面方程组: ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ≥− <−+ ≥− <−+ 02 021 01 000 θω θωω θω θ (9.3) 该方程组是无解的。所以单层感知器是无法解决异或问题的。 该问题的几何意义如图所示,感知器的输出为 1 用空心圆表示,输出为 0 用实心 圆表示,可以看出满足 x1 XOR x2=1 的点集(输入集)为 B={B1,B2},满足 x1 XOR x2=0 的点集(输入集)为 A={A1,A2}。显然无论如何选择θ,ω1,ω1 的取值

都无法找到一条直线在该平面上将A、B两类输入集分开,即使其它的激发函数 也很难做到。这种单层感知器所不能表达的问题称为线性不可分问题。 事实上很多问题都不能用单层感知器表达,这也是单层感知器的缺陷。 x2 B2(0.1 A21.1) ● xl ○ A1(0,0) B1(1,0) 9.2.3梯度下降和Delta法则 尽管训练样本线性可分时,感知器法则可以成功地找到一个权向量,但如果样本 不是线性可分的它将不能收敛。因此人们设计了另一个训练法则来克服这个不 足,称为Delta法则(delta rule)。如果训练样本不是线性可分的,那么delta 法则会收敛到目标概念的最佳近似。 Delta法则的关键思想是使用梯度下降(gradient descent)来搜索可能的权向 量的假设空间,以找到最佳拟合训练样本的权向量。 可以把Delta训练法则理解为训练一个无阈值的感知器,也就是一个线性单元 (Linear unit),它的输出o如下: 0(x)=0●x (9.4) 为了推导线性单元的权值学习法则,先指定一个度量标准来衡量假设的权向量相 对于训练样本的训练误差(training error): E=∑-o)尸 (9.5) 2 deD 其中D是训练样本集合,t,是训练样本d的目标输出,o。是线性单元对训练样 本d的输出。在这里把E定义为o的函数,是因为线性单元的输出o依赖于这个
都无法找到一条直线在该平面上将 A、B 两类输入集分开,即使其它的激发函数 也很难做到。这种单层感知器所不能表达的问题称为线性不可分问题。 事实上很多问题都不能用单层感知器表达,这也是单层感知器的缺陷。 x2 B2(0,1) A1(0,0) B1(1,0) A2(1,1) x1 9.2.3 梯度下降和 Delta 法则 尽管训练样本线性可分时,感知器法则可以成功地找到一个权向量,但如果样本 不是线性可分的它将不能收敛。因此人们设计了另一个训练法则来克服这个不 足,称为 Delta 法则(delta rule)。如果训练样本不是线性可分的,那么 delta 法则会收敛到目标概念的最佳近似。 Delta 法则的关键思想是使用梯度下降(gradient descent)来搜索可能的权向 量的假设空间,以找到最佳拟合训练样本的权向量。 可以把 Delta 训练法则理解为训练一个无阈值的感知器,也就是一个线性单元 (Linear unit),它的输出 o 如下: )( ω •= xxo (9.4) 为了推导线性单元的权值学习法则,先指定一个度量标准来衡量假设的权向量相 对于训练样本的训练误差(training error): ∑∈ −≡ Dd E ot dd 2 )( 2 1 ω)( (9.5) 其中 D 是训练样本集合, 是训练样本 d 的目标输出, 是线性单元对训练样 本 d 的输出。在这里把 E 定义为 dt od ω 的函数,是因为线性单元的输出 o 依赖于这个

权值,当然E也依赖于特定的训练样本集合,但一般在训练期间训练样本集合是 固定的,所以没有把E也定义成训练样本的函数。 1.可视化假设空间 为了理解梯度下降算法,可视化地表示包含所有可能的权向量和相关联的E值的 整个假设空间。如图所示。这里坐标,o,表示一个简单的线性单元中两个权可 能的取值,纵轴表示相对于某固定训练样本的误差E。因此图中的误差曲面概括 了假设空间中每一个权向量的期望度(desirability)(期望得到一个具有最小 误差的假设)。如果定义E的方法已知,那么对于线性单元,这个误差曲面必然 是具有单一全局最小值的抛物面。当然抛物面的形状依赖于具体的训练样本集。 25 20 15 10 wO w1 为了确定一个E最小化的权向量,梯度下降搜索从一个任意的初始权向量开始, 然后以很小的步伐反复修改这个向量。每一步都沿误差曲面产生最陡峭下降的方 面修改权向量,继续这个过程直到得到全局最小误差点。 2.梯度下降法则的推导 如何计算出沿误差曲面最陡峭下降的方向?可通过计算E相对于向量。的每个 分量的偏导数来得到这个方向。这个向量导数被称为E对于0的梯度,记作 VE(@)
权值,当然 E 也依赖于特定的训练样本集合,但一般在训练期间训练样本集合是 固定的,所以没有把 E 也定义成训练样本的函数。 1.可视化假设空间 为了理解梯度下降算法,可视化地表示包含所有可能的权向量和相关联的 E 值的 整个假设空间。如图所示。这里坐标 10 ω ,ω 表示一个简单的线性单元中两个权可 能的取值,纵轴表示相对于某固定训练样本的误差 E。因此图中的误差曲面概括 了假设空间中每一个权向量的期望度(desirability)(期望得到一个具有最小 误差的假设)。如果定义 E 的方法已知,那么对于线性单元,这个误差曲面必然 是具有单一全局最小值的抛物面。当然抛物面的形状依赖于具体的训练样本集。 为了确定一个 E 最小化的权向量,梯度下降搜索从一个任意的初始权向量开始, 然后以很小的步伐反复修改这个向量。每一步都沿误差曲面产生最陡峭下降的方 面修改权向量,继续这个过程直到得到全局最小误差点。 2. 梯度下降法则的推导 如何计算出沿误差曲面最陡峭下降的方向?可通过计算 E 相对于向量ω 的每个 分量的偏导数来得到这个方向。这个向量导数被称为 E 对于ω 的梯度,记作 ∇E ω)(

OE OE VE(0)≡ (9.6) 00,d0 do 当梯度被解释为权空间的一个向量时,它确定了使E最陡峭上升的方向,那么其 反方向就是最陡峭下降方向。上图中的箭头显示了o0,①1平面的一个特定点的 负梯度-VE(@)。那么梯度下降的训练法则是: 0←0+△0,其中△0=-77E(0) (9.7) n称为learning rate,它决定梯度下降搜索中的步长。公式中的负号是因为我 们想让权向量向E下降的方向移动。这个训练法则可以写成它的分量形式: a←间,+△@,其中△0,=-”a0 (9.8) 根据9.5和9.8可以计算权值迭代更新的算法,以下是推导过程。 6正0.50,-o0,-o2-000=o 0,a0,2D 2a0 2 deD =∑4-oa) (ta-0a) deD 00 =∑4-o4) (ta-o●xa) deD 00 OE -=∑4-oa-xa) (9.9) 0 deD 其中-xa表示训练样本d的一个输入分量x 将9.9代入9.8得到梯度下降权值更新法则 △o,=n∑(ta-oa)xa (9.10) deD 以下是训练线性单元的梯度下降算法: Gradient-Descent(training_examples,n)
⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ ∂ ∂ ∂ ≡∇ n EEE E ωωω ω ,,,)( 10 " (9.6) 当梯度被解释为权空间的一个向量时,它确定了使 E 最陡峭上升的方向,那么其 反方向就是最陡峭下降方向。上图中的箭头显示了ω0,ω1 平面的一个特定点的 负梯度-∇E ω)( 。那么梯度下降的训练法则是: Δ+← ωωω ,其中 ∇−=Δ E ωηω )( (9.7) η称为 learning rate,它决定梯度下降搜索中的步长。公式中的负号是因为我 们想让权向量向 E 下降的方向移动。这个训练法则可以写成它的分量形式: Δ+← ωωω iii ,其中 i i E ω ηω ∂ ∂ −=Δ (9.8) 根据 9.5 和 9.8 可以计算权值迭代更新的算法,以下是推导过程。 )()( )()( )()(2 2 1 )( 2 1 )( 2 1 2 2 d d i dd Dd dd i dd Dd dd i dd Dd dd Dd Dd i dd ii xtot otot ot ot otot E •− ∂ ∂ −= − ∂ ∂ −= − ∂ ∂ =− − ∂ ∂ =−• ∂ ∂ = ∂ ∂ ∑ ∑ ∑ ∑ ∑ ∈ ∈ ∈ ∈ ∈ ω ω ω ωω ω ω )()( id Dd dd i xot E −−= ∂ ∂ ∑ ω ∈ (9.9) 其中 表示训练样本 − xid d 的一个输入分量 i x 将 9.9 代入 9.8 得到梯度下降权值更新法则: ∑∈ −=Δ Dd i iddd ηω )( xot (9.10) 以下是训练线性单元的梯度下降算法: Gradient-Descent(training_examples, η)

//training examples中每个训练样本形式为序偶,其中x是输入值向量, t是目标输出值,n是学习速率 Stepl:初始化每个wi为某个小的随机值: Step2:遇到终止条件之前,做以下操作 Step2.1初始化每个△w,=0 Step2.2对训练样本training_examples中的每个,做 Step2.2.1把样本实例x输入到此单元,计算输出o: Step2.2.2对于线性单元的每个权wi,做 △w,=△w:+7(t-0)x,: (9.11) Step2.3对于线性单元的每个权wi,做 w:=w,+△w: (9.12) 3.梯度下降的随机近似 应用梯度下降的主要实践问题是:(1)有时收敛过程可能非常慢(需要数千步): (2)如果在误差曲面上有多个局部极小值,那么不能保证会找到全局最小值。 解决这个问题的办法是一种改进,即增量梯度下降(incremental gradient descent)或随机梯度下降(stochastic gradient descent)。公式9.l0给出 的梯度下降法则在对D中所有训练样本求和后计算权值更新,随机梯度下降的思 想是根据每个单独样本的误差增量计算权值更新,得到近似的梯度下降搜索。将 公式9.10改成: △w,=7(t-0)x (9.13) 对应地,将梯度下降算法修改只要删除其中的公式9.12,另外再将9.11替换成 公式9.14即可
//training_examples 中每个训练样本形式为序偶 ,tx >< ,做 Step2.2.1 把样本实例 x 输入到此单元,计算输出 o; Step2.2.2 对于线性单元的每个权 wi,做 ii i Δ +Δ= η − )( xotww ; (9.11) Step2.3 对于线性单元的每个权 wi,做 Δ+= www iii (9.12) 3. 梯度下降的随机近似 应用梯度下降的主要实践问题是:(1)有时收敛过程可能非常慢(需要数千步); (2)如果在误差曲面上有多个局部极小值,那么不能保证会找到全局最小值。 解决这个问题的办法是一种改进,即增量梯度下降(incremental gradient descent)或随机梯度下降(stochastic gradient descent)。公式 9.10 给出 的梯度下降法则在对 D 中所有训练样本求和后计算权值更新,随机梯度下降的思 想是根据每个单独样本的误差增量计算权值更新,得到近似的梯度下降搜索。将 公式 9.10 改成: i i η −=Δ )( xotw (9.13) 对应地,将梯度下降算法修改只要删除其中的公式 9.12,另外再将 9.11 替换成 公式 9.14 即可