
第三章 控制网平差 完成控制网测量的外业工作后要进行 内业计算,内业计算分为概算、平差计 算和编制控制点成果表。本章重点介绍 独立三角网的条件平差方法。 ·第一节测量平差的数学模型 ·第二节条件平差原理 ·第三节独立三角网条件平差

第一节测量平差的数学模型、必要观测与多余观测在测量工作中,最常见的问题是要确定某些几何量的大小。由各种几何量构成的模型(测量中就是各种控制网)就是几何模型。为了确定一个几何模型,并不需要知道该模型中所有元素的大小,而只需要知道其中部分元素,其它元素可以通过已知的元素确定。能够唯一地确定一个几何模型所必要的元素,称必要元素;确定必要元素的观测称为必要观测。必要元素的个数用t表示

为了确定一个几何模型就必须进行观测。如果观测个数 n 少于必要元素的个数,即 nt,即必须进行多余观测。多余观测的个数在测量中又称“自由度"。令r=n-t显然,r就是多余观测数
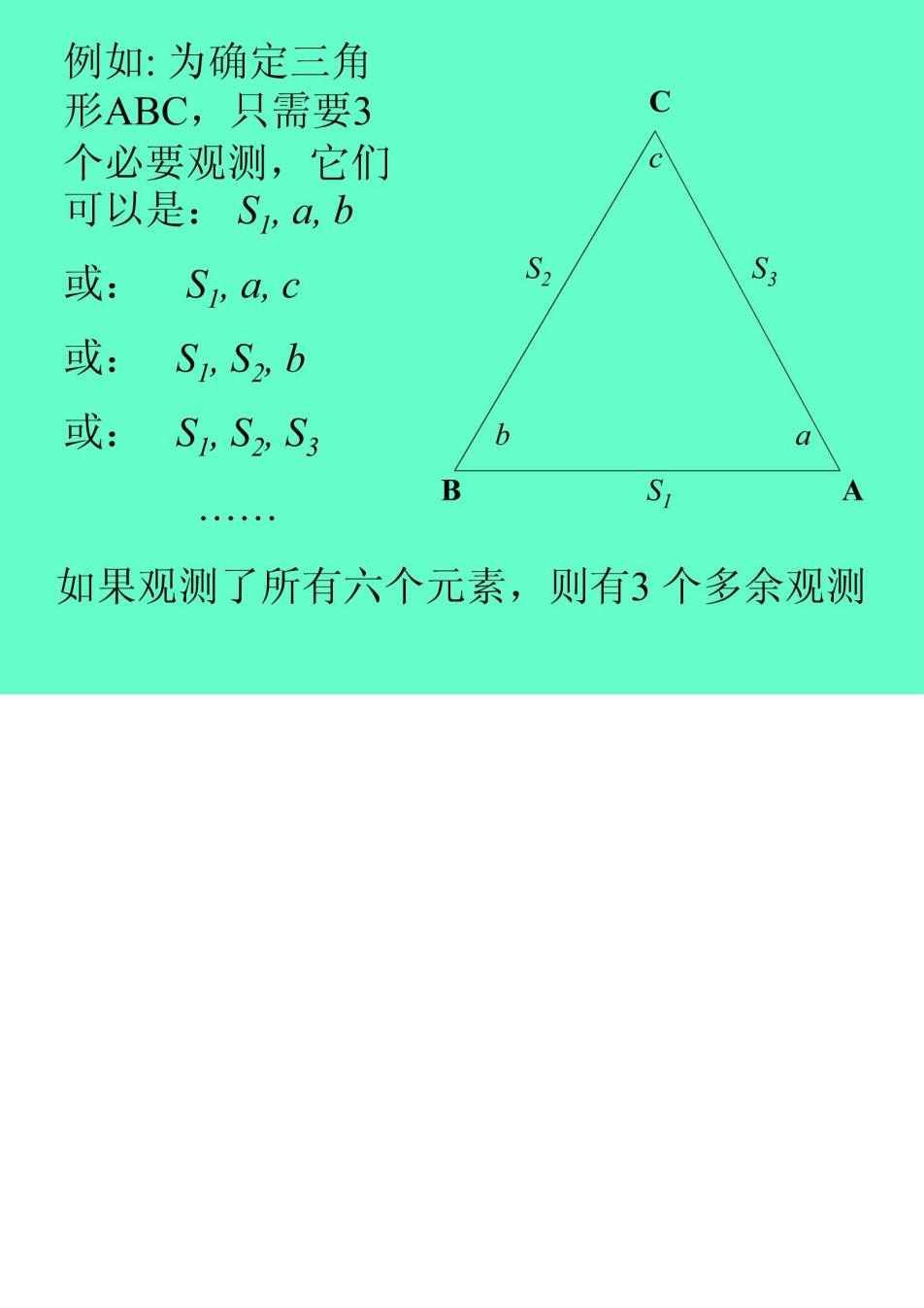
例如:为确定三角C形ABC,只需要3个必要观测,它们C可以是:S,a, bS,S或:S,a,c或:Si, S2, b或:Si, S2, S3baBS,A......如果观测了所有六个元素,则有3个多余观测

二、平差的数学模型·测量中是通过观测来确定控制网中的某些几何量,因而考虑的模型总是数学模型。因为观测量是一种随机变量,所以平差的数学模型应同时包含函数模型和随机模型。函数模型和随机模型总称为数学模型。函数模型是由描述观测量和待求量间的函数关系的模型,随机模型是描述观测量及其相互间统计相关性质的模型。建立这两种模型是测量平差中最基本而首先考虑的问题

·测量平差通常是基于线性函数模型的当函数模型为非线性形式时,是将其用泰勒公式展开,并取其一次项化为线性形式。·对于一个实际平差问题,可建立不同形式的函数模型,相应地就有不同的平差方法。测量中常见的控制网平差方法有条件平差和间接平差两种
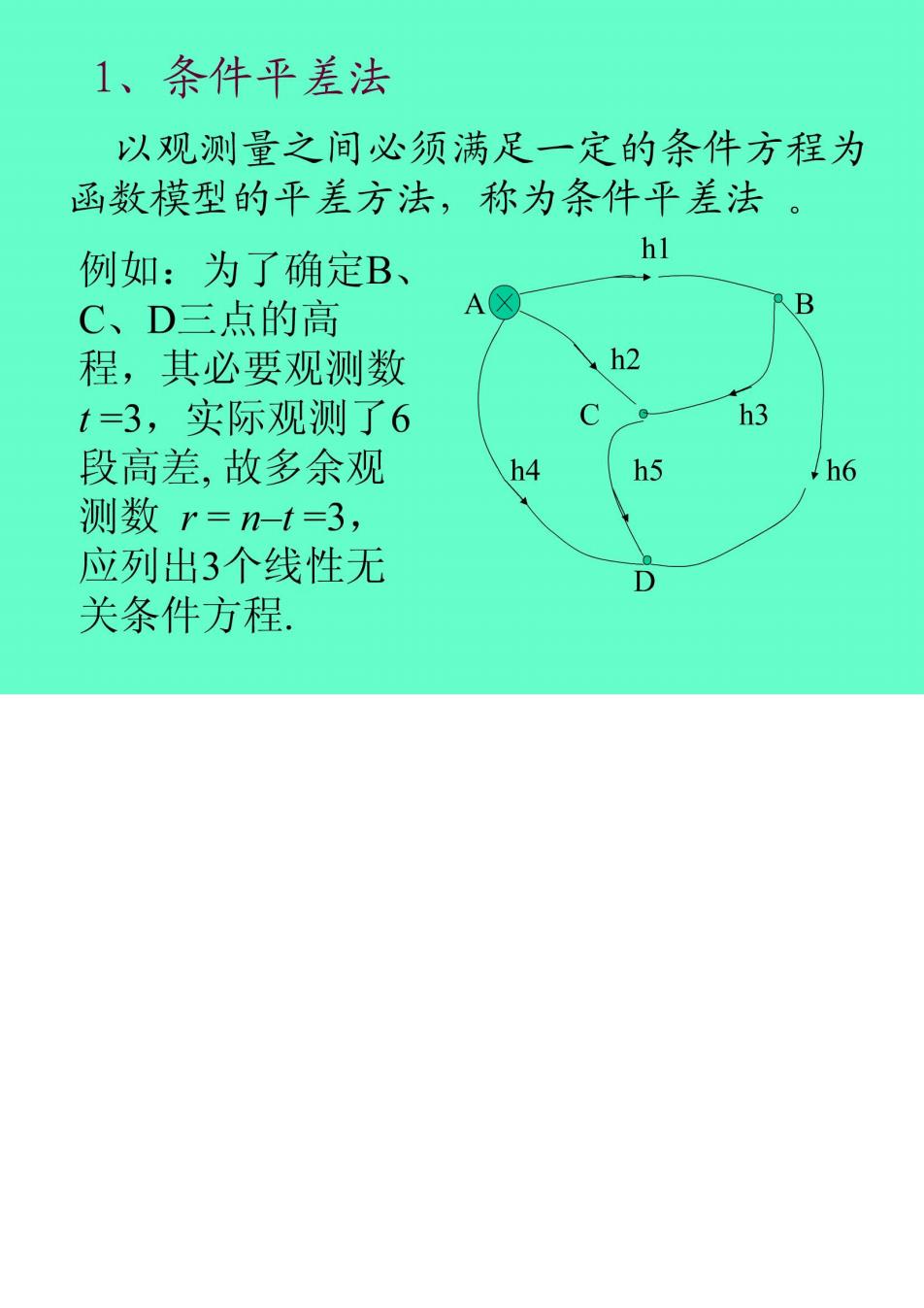
1、条件平差法以观测量之间必须满足一定的条件方程为函数模型的平差方法,称为条件平差法hl例如:为了确定B、AXBC、D三点的高h2程,其必要观测数t=3,实际观测了6h3段高差,故多余观T h6h4h5测数 r=n-t=3,应列出3个线性无D关条件方程

这个水准网可以列出7个条件方程,其中只有3个是相互独立的,我们取:h + h - h2 = 0hi + h- h = 0(a)h, +hs-h4 = Oh,表示观测量 h;的平差值。式中:这就是用平差值表达的条件方程
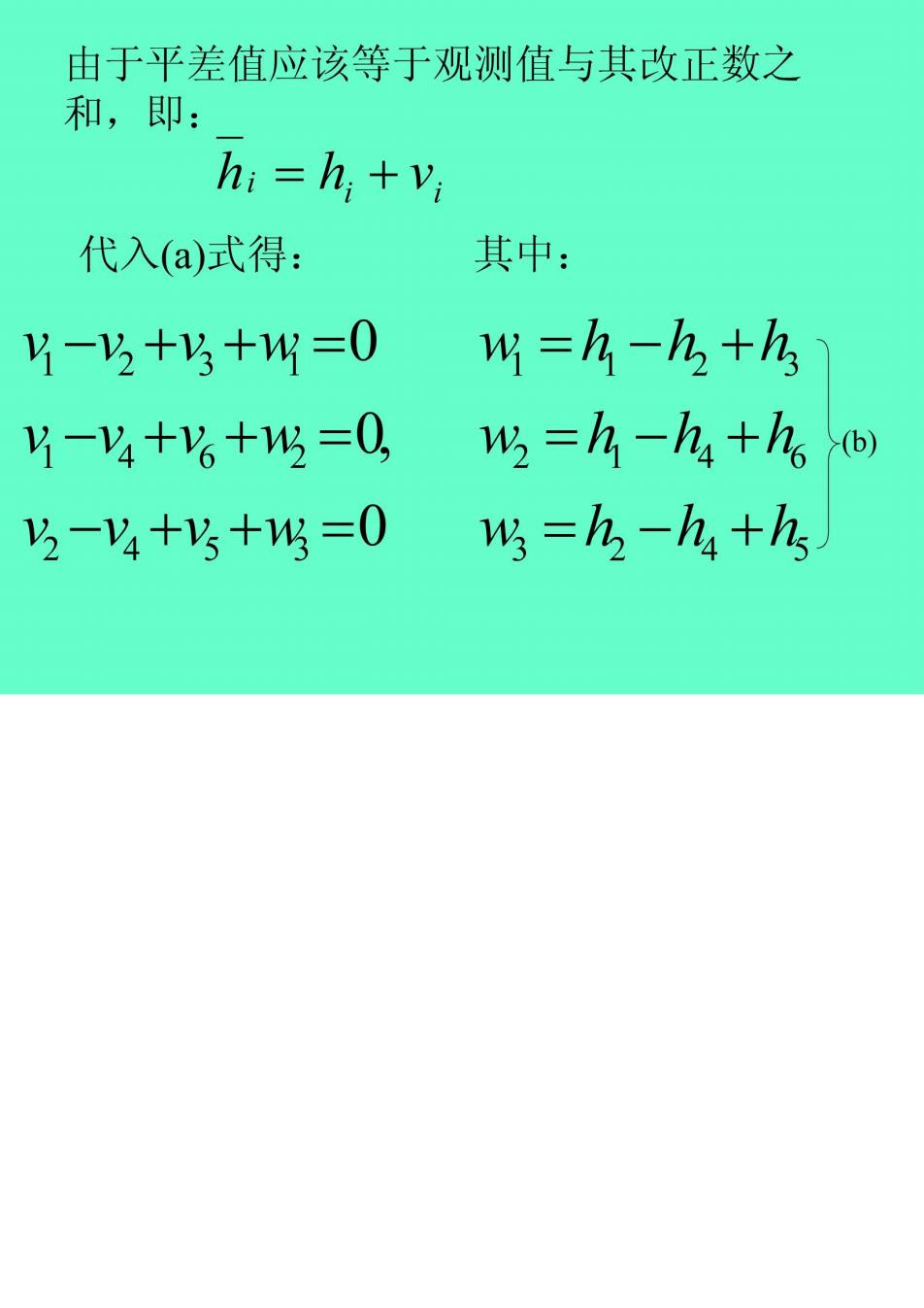
由于平差值应该等于观测值与其改正数之和,即:hi = h, +V;其中:代入(a)式得:Y-++w =0W =h -h+hY-V4+V+W =0,W =h -ha +he5(b)2-V4 +V+W =0W =h -h +hs

今OWV= (ViV2V3V4 Vsv6)T则条件方程可表达为以下矩阵形式:AV +W=0(c)这就是条件平差函数模型的一般形式