《经济数学基础》课程PPT教学课件（线性代数）第四章 线性方程组

第四章 线性方程组 一.高斯消元法 二.齐次线性方程组 三.非齐次线性方程组

1 第四章 线性方程组 一. 高斯消元法 二. 齐次线性方程组 三. 非齐次线性方程组

一.高斯消元法 设一般线性方程组为 411X1 L12X2 十 + = b L21X1 + 422X2 十. S : : : (1) amx1 + 0m2t2 三 02 则称矩阵A= 21 为方程组()的系数矩阵。 m2 mn 2

2 一. 高斯消元法 设一般线性方程组为 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 (1) n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b  + + + =   + + + =     + + + = 则称矩阵 11 12 1 21 22 2 1 2 n n m m mn a a a a a a A a a a     =         为方程组(1)的系数矩阵

1 12 ain 称矩阵B=(A,b)= a2i a22 a2n : Am2 Amn 为方程组()的增广矩阵。 当b=0(i=1,2,.,m)时，齐次线性方程组 411x1+012X2 十 ainXn 0 421x1 L22X2 。 + 0 (2) : am2X2 3 0 称为方程组（1)的导出组， 或称为（1)对应的齐次线性方程组。 3

3 称矩阵 11 12 1 1 21 22 2 2 1 2 ( , ) n n m m mn m a a a b a a a b B A b a a a a     = =         为方程组(1)的增广矩阵。 称为方程组（1）的导出组， 或称为（1）对应的齐次线性方程组。 当 0 ( 1,2, , ) i b i m = = 时,齐次线性方程组 11 1 12 2 1 21 1 22 2 2 1 1 2 2 0 0 (2) 0 n n n n m m mn n a x a x a x a x a x a x a x a x a x  + + + =   + + + =     + + + =

定义：线性方程组的初等变换 (1)用一非零的数乘某一方程 (2)把一个方程的倍数加到另一个方程 (3)互换两个方程的位置 可以证明一个线性方程组经过若干次初等变换， 所得到的新的线性方程组与原方程组同解 对一个方程组进行初等变换，实际上就是对它的增广矩阵 做初等行变换 初等行变换 B=(A,b) 4

4 定义：线性方程组的初等变换 （1） 用一非零的数乘某一方程 （2） 把一个方程的倍数加到另一个方程 （3） 互换两个方程的位置 可以证明一个线性方程组经过若干次初等变换， 所得到的新的线性方程组与原方程组同解 对一个方程组进行初等变换，实际上就是对它的增广矩阵 做初等行变换 B A b = ⎯⎯→ ( , ) 初等行变换

S11 S12 Sir S1,+1 Sin t 0 S22. Sir S2,+1. S20 : : 化为行阶 梯形矩阵 0 0. S」 t 入 S,r+1. rn 0 0. 0 0 0 r+ 0 0. 0 0 0 0 : : 0 0. 0 0 0 5

5 11 12 1 1, 1 1 1 22 1 2, 1 2 2 , 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 r r n r r n rr r r rn rr s s s s s t s s s s t s s s tt +++ +     ⎯⎯→   化为行阶 梯形矩阵

1 0.0 Cin d 0 1. 0 C2,+1 d2 ● : : 化为行最 简形矩阵 0 0. Crr+1' d (3) 0 0 0 0 0 0. 0 0 0 U 0. 0 0 U 则以矩阵（3)为增广矩阵的方程组与方程组(1)同解

6 则以矩阵（3）为增广矩阵的方程组与方程组（1）同解。 1, 1 1 1 2, 1 2 2 , 1 1 1 0 0 0 1 0 0 0 1 (3) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 r n r n r r rn r r c c d c c d c c d d + + + +     ⎯⎯→   化为行最 简形矩阵

由矩阵（3)可讨论方程组（1)的解的情况 1)若d,+1≠0，则方程组无解。 2)若dt1=0,则方程组有解， 当 r=n有唯一解。 r<n 有无穷多解。 3)特别地，方程组(1)的导出组， 即对应的齐次线性方程组 一定有解。 r=n 当 有唯一的零解。 r<n有无穷多解，即有非零解。 7

7 由矩阵（3）可讨论方程组（1）的解的情况 1) 若 dr+1  0 ，则方程组无解。 2) 若 1 0, r d + = 则方程组有解， 当 r n r n  =    有唯一解。 有无穷多解。 3) 特别地，方程组(1)的导出组，即对应的齐次线性方程组 一定有解。 当 r n r n  =    有唯一的零解。 有无穷多解，即有非零解

举例说明消元法具体步骤： 例1：书P108例4.1.1 2X1 一 X2 + 3X3 1 例2：解线性方程组 4X1 一 2x2 + 5x3 4 2x1 4x3 0 2 -1 3 1 2 解：(A,b)= 4 -2 5 4 00 3 -1 、2 -1 4 0 2 1 -1 2 -1 3 1 0 0 -1 2 最后一行有0x3=1, 0 0 0 可知方程组无解

8 举例说明消元法具体步骤： 例1：书P108 例4.1.1 例2：解线性方程组 1 2 3 1 2 3 1 2 3 2 3 1 4 2 5 4 2 4 0 x x x x x x x x x  − + =   − + =  − + =  解：           − − → 0 0 0 1 0 0 1 2 2 1 3 1 2 1 3 1 0 0 1 2 0 0 1 1   − → −         − 最后一行有 3 0 1, x = 可知方程组无解。 2 1 3 1 ( , ) 4 2 5 4 2 1 4 0 A b   −   = −       −

x1-2x2+3x3-4x4=1 x2-3+ x4=0 例3：解线性方程组 + 3X2 3x4=1 1X2 +3x3+x4=0 -2 3 -41 0 解： 1 -1 1 0 (A,b)= 1 3 0 -3 1 0 -7 3 10 -2 3 一4 1 -2 3 -4 1 0 1 -1 0 0 1 0 0 0 2 0 -2 0 0 -4 8 0 0 0 0 0 0 9

9 例3：解线性方程组 1 2 3 4 2 3 4 1 2 4 2 3 4 2 3 4 1 0 3 3 1 7 3 0 x x x x xxx x x x xxx  − + − =   − + =  + − =   − + + =  解： (A,b) = 1 2 3 4 1 0 1 1 1 0 0 0 2 4 0 0 0 4 8 0   − −   − →     −     −               − − − − → 0 0 0 0 0 0 0 1 2 0 0 1 1 1 0 1 2 3 4 1 1 2 3 4 1 0 1 1 1 0 1 3 0 3 1 0 7 3 1 0   − −   −     −     −

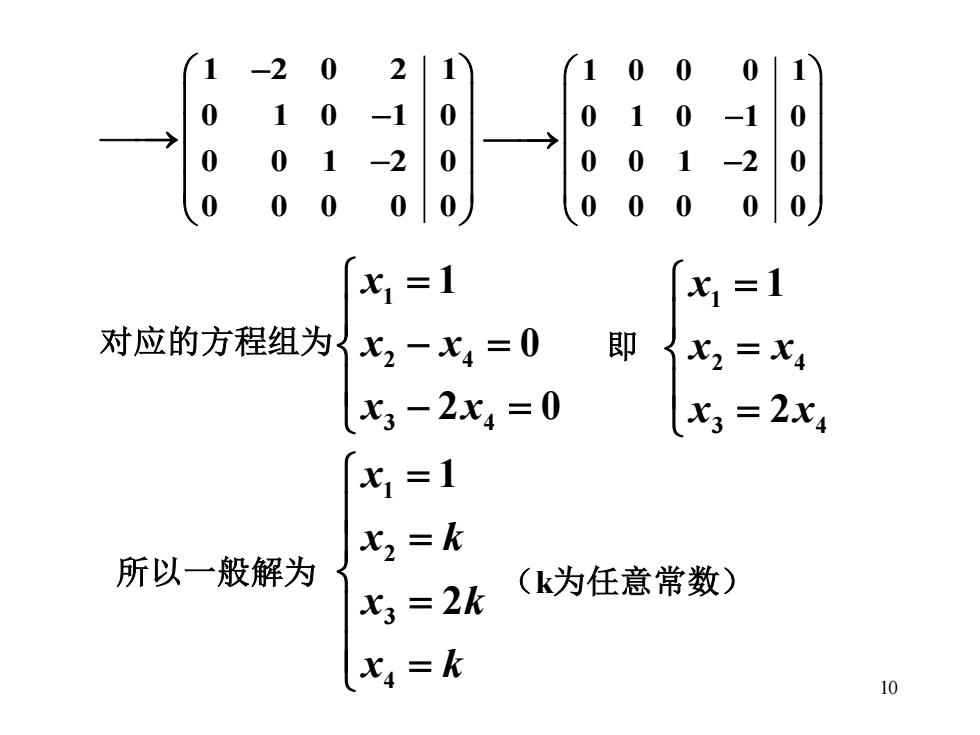
-2 0 2 1 1 0 0 01 0 1 0 -1 0 0 1 0 -1 0 0 0 1 -2 0 0 1 -2 0 0 0 0 0 0 .0 00 00 火1=1 x1=1 对应的方程组为X2一x4=0 即 X2=X4 3-2x4=0 3=2x4 七1=1 七2=k 所以一般解为 x3=2k (k为任意常数) 七4=k 10

10 1 2 0 2 1 0 1 0 1 0 0 0 1 2 0 0 0 0 0 0   −   − ⎯⎯→    −     1 0 0 0 1 0 1 0 1 0 0 0 1 2 0 0 0 0 0 0     − ⎯⎯→    −     对应的方程组为 1 2 4 3 4 1 0 2 0 x x x x x  =   − =  − =  1 2 4 3 4 1 2 x x x x x  =   =  =  即 所以一般解为 1 2 3 4 1 2 x x k x k x k  =   =  =    = （k为任意常数）