
通信原理 第3章随机过程
1 通信原理 第3章 随机过程

第3章随机过程 ● 3.1随机过程的基本概念 ■什么是随机过程? ◆随机过程是一类随时间作随机变化的过程,它不能 用确切的时间函数描述。可从两种不同角度看: ◆角度1:对应不同随机试验结果的时间过程的集合。 2
2 第3章 随机过程 ⚫ 3.1 随机过程的基本概念 ◼ 什么是随机过程? ◆ 随机过程是一类随时间作随机变化的过程,它不能 用确切的时间函数描述。可从两种不同角度看: ◆ 角度1:对应不同随机试验结果的时间过程的集合
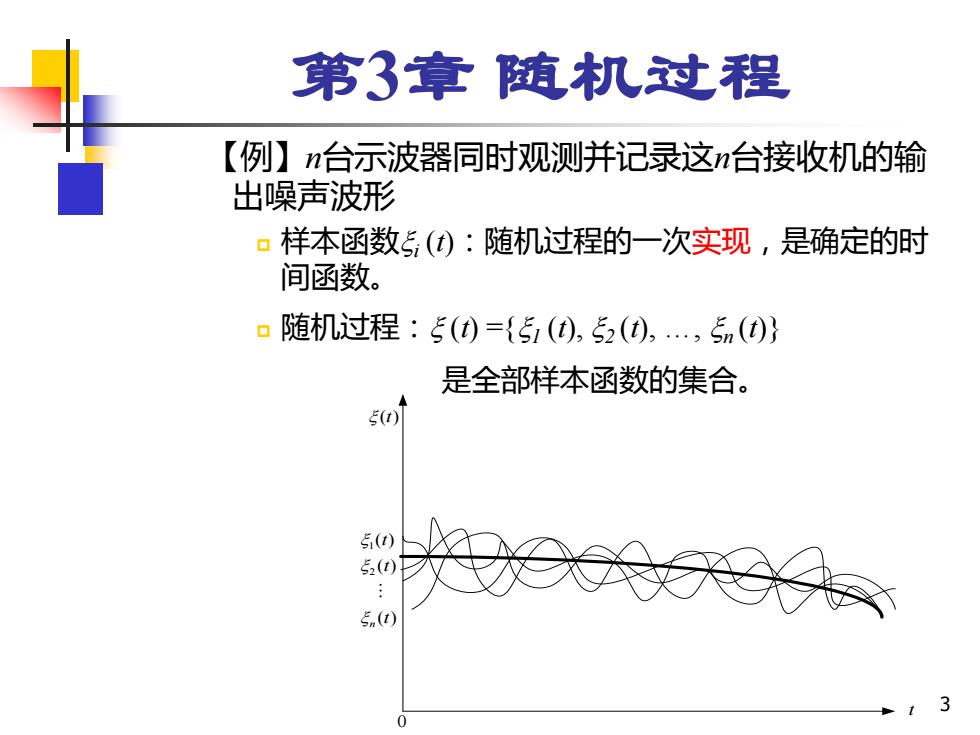
第3章随机过程 【例】n台示波器同时观测并记录这n台接收机的输 出噪声波形 ▣样本函数5():随机过程的一次实现,是确定的时 间函数。 口随机过程:5(t)={51(),52(t),.,5n()} 是全部样本函数的集合。 5u) 5() 52(t)) 5n(0
3 第3章 随机过程 【例】n台示波器同时观测并记录这n台接收机的输 出噪声波形 样本函数i (t):随机过程的一次实现,是确定的时 间函数。 随机过程: (t) ={1 (t), 2 (t), ., n (t)} 是全部样本函数的集合。 ()t t 0 1 2 ( ) ( ) ( ) n t t t

第3章随机过程 角度2:随机过程是随机变量概念的延伸 ▣在任一给定时刻1上,每一个样本函数5(都是一个确定的 数值,(t),但是每个5(t)都是不可预知的。 ▣在一个固定时刻t上,不同样本的取值{(t),i=1,2,.,n} 是一个随机变量,记为5(t)。 口换句话说,随机过程在任意时刻的值是一个随机变量。 ▣因此,我们又可以把随机过程看作是在时间进程中处于不同 时刻的随机变量的集合。 ▣这个角度更适合对随机过程理论进行精确的数学描述。 A
4 第3章 随机过程 ◆ 角度2:随机过程是随机变量概念的延伸。 在任一给定时刻t1上,每一个样本函数i (t)都是一个确定的 数值i (t1 ),但是每个i (t1 )都是不可预知的。 在一个固定时刻t1上,不同样本的取值{i (t1 ), i = 1, 2, ., n} 是一个随机变量,记为 (t1 )。 换句话说,随机过程在任意时刻的值是一个随机变量。 因此,我们又可以把随机过程看作是在时间进程中处于不同 时刻的随机变量的集合。 这个角度更适合对随机过程理论进行精确的数学描述

第3章随机过程 ● 3.1.1随机过程的分布函数 ◆设ξ(t)表示一个随机过程,则它在任意时刻t的值(t) 是一个随机变量,其统计特性可以用分布函数或概率密 度函数来描述。 ◆随机过程ξ()的一维分布函数: F(x1,t1)=P[5(t1)≤x] ◆随机过程5()的一维概率密度函数: (x,41)= F (x,4) Ox1 若上式中的偏导存在的话。 5
5 第3章 随机过程 ◼ 3.1.1随机过程的分布函数 ◆ 设 (t)表示一个随机过程,则它在任意时刻t1的值 (t1 ) 是一个随机变量,其统计特性可以用分布函数或概率密 度函数来描述。 ◆ 随机过程 (t)的一维分布函数: ◆ 随机过程 (t)的一维概率密度函数: 若上式中的偏导存在的话。 ( , ) [ ( ) ] 1 1 1 1 1 F x t = P t x 1 1 1 1 1 1 1 ( , ) ( , ) x F x t f x t =

第3章随机过程 ◆随机过程影(①)的二维分布函数: F(x1,x2;,t2,)=P{5t)≤x,5t2)≤x2} ◆随机过程影()的二维概率密度函数: 5(x,x241,42)= a2F2(x,x24,2) Ox1·dx2 若上式中的偏导存在的话。 ◆随机过程5(0)的n维分布函数: En(1x2.xt12.In) =P{5(t1)≤x1,5(t2)≤x2,.,5(tn)≤xn} ◆随机过程5(t)的n维概率密度函数: fn(xpx2y.yxn;tt2.,tn)= a™Fn(x,x2,.,Xn;t,t2.,tn) 0x1ax2.dX。 6
6 第3章 随机过程 ◆ 随机过程 (t) 的二维分布函数: ◆ 随机过程 (t)的二维概率密度函数: 若上式中的偏导存在的话。 ◆ 随机过程 (t) 的n维分布函数: ◆ 随机过程 (t) 的n维概率密度函数: F2 (x1 , x2 ;t 1 ,t 2 ,) = P(t 1 ) x1 ,(t 2 ) x2 1 2 2 1 2 1 2 2 2 1 2 1 2 ( , ; , ) ( , ; , ) x x F x x t t f x x t t = n n n n n P t x t x t x F x x x t t t = ( ) , ( ) , , ( ) ( , , , ; , , ) 1 1 2 2 1 2 1 2 1 2 n n 1 2 n 1 2 n n n 1 2 n 1 2 n x ( x t ) ( x t ) = x x F x x t t f x x t t , , , ; , , , , , , ; , ,

第3章随机过程 ·3.1.2随机过程的数字特征 ◆均值(数学期望): 在任意给定时刻的取值ξ(t1)是一个随机变量,其均值 E56,】=xf(x,)dk 式中f(x,t)·5(t1)的概率密度函数 由于t是任取的,所以可以把t直接写为t,x改为x, 这样上式就变为 E[5(t)]=xf(x,) 7
7 第3章 随机过程 ◼ 3.1.2 随机过程的数字特征 ◆ 均值(数学期望): 在任意给定时刻t1的取值 (t1 )是一个随机变量,其均值 式中 f (x1 , t1 ) - (t1 )的概率密度函数 由于t1是任取的,所以可以把 t1 直接写为t, x1改为x, 这样上式就变为 − E (t) = xf1 (x,t)dx − 1 = 1 1 1 1 1 E (t ) x f (x ,t )dx
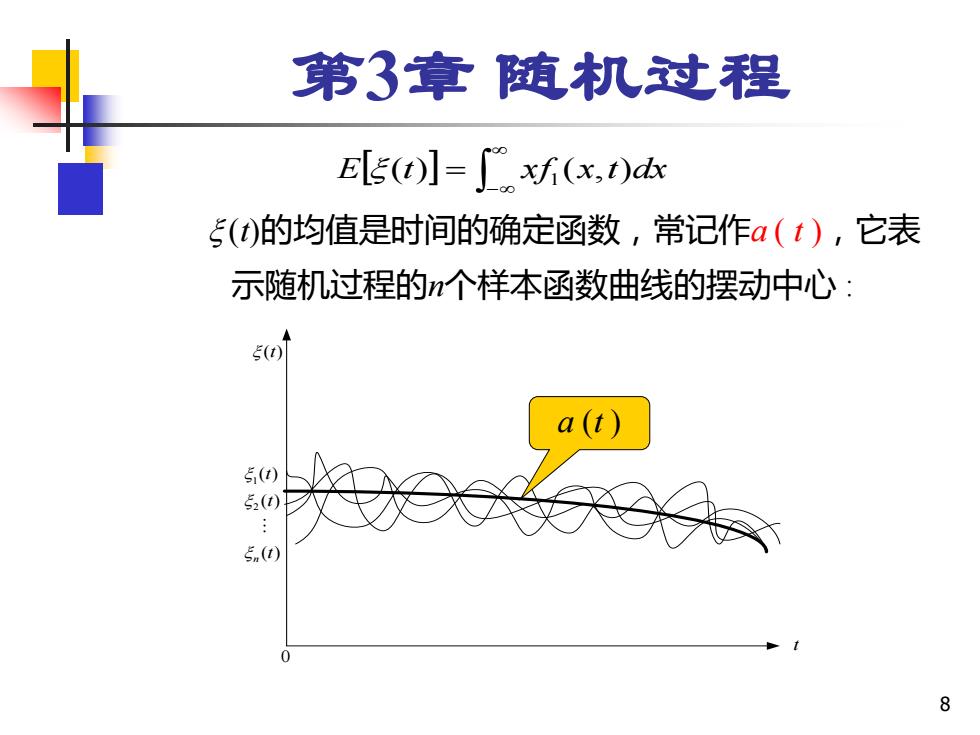
第3章随机过程 E[5(】=xf(x,) 5()的均值是时间的确定函数,常记作a(t),它表 示随机过程的n个样本函数曲线的摆动中心: a(t) 5(t) 52() 5n(t) 8
8 第3章 随机过程 (t)的均值是时间的确定函数,常记作a ( t ),它表 示随机过程的n个样本函数曲线的摆动中心 : − E (t) = xf1 (x,t)dx ()t t 0 1 2 ( ) ( ) ( ) n t t t a (t )

第3章随机过程 ◆方差 D[5t]=E[5(t)-a(t]} 方差常记为σ2(t)。这里也把任意时刻1直接写成了t。 因为 D[Et】=E52(t)-2a(t)(t)+a2t)】 =E[2(t】-2at)E[5(t】+a2(t) =E[52(t)]-a2(t) =Lxf(x.t)dx-Ia( 均方值] 均值平方 所以,方差等于均方值与均值平方之差,它表示随 机过程在时刻t对于均值a(t)的偏离程度。 9
9 第3章 随机过程 ◆ 方差 方差常记为 2 ( t )。这里也把任意时刻t1直接写成了t 。 因为 所以,方差等于均方值与均值平方之差,它表示随 机过程在时刻 t 对于均值a ( t )的偏离程度。 2 D[(t)] = E [(t) − a(t)] ( ) ( ) ( ) ( ) ( ) ( ) ( ) [ ( )] ( ) [ ( )] 2 ( ) 2 2 2 2 2 2 2 E ξ t a t E ξ t a t E ξ t a t D ξ t E ξ t a t ξ t a t = − = − + = − + 2 1 2 = x f (x,t)dx −[a(t)] − 均方值 均值平方

第3章随机过程 ◆相关函数 R(t1,t2)=E[5(t)5(t2)] =)d da 式中,5(t1)和5(2)分别是在1和2时刻观测得到的随机变 量。可以看出,R(t1,t2)是两个变量,和的确定函数。 ◆协方差函数 B(t,t2)=E5(41)-a(6[5(t2)-a(t2} =[x-a4Jx,-a,f(x,x24,4)kk, 式中a(t1)a(2)-在和时刻得到的(t)的均值 方(x1,x2;t1,2)-5()的二维概率密度函数。 10
10 第3章 随机过程 ◆ 相关函数 式中, (t1 )和 (t2 )分别是在t1和t2时刻观测得到的随机变 量。可以看出,R(t1 , t2 )是两个变量t1和t2的确定函数。 ◆ 协方差函数 式中 a ( t1 ) a ( t2 ) - 在t1和t2时刻得到的 (t)的均值 f2 (x1 , x2 ; t1 , t2 ) - (t)的二维概率密度函数。 1 2 2 1 2 1 2 1 2 1 2 1 2 ( , ; , ) ( , ) [ ( ) ( )] x x f x x t t dx dx R t t E t t − − = = 1 1 2 2 2 1 2 1 2 1 2 1 2 1 1 2 2 [ ( )][ ( )] ( , ; , ) ( , ) [ ( ) ( )][ ( ) ( )] x a t x a t f x x t t dx dx B t t E t a t t a t = − − = − − − −