
通信原理 第2章随机信号分析 主要内容及要求(以复习方式学习): 1、掌握随机过程及数学特征的定义, 2、熟练掌握平稳随机过程定义、特点; 3、掌握高斯过程的定义、性质, 4、熟悉窄带随机过程的表达式及统计特性 5、熟悉白噪声和带限白噪声的特点; 6、掌握平稳随机过程通过线性系统后特点
通信原理 第2章 随机信号分析 主要内容及要求(以复习方式学习): 1、掌握随机过程及数学特征的定义; 2、熟练掌握平稳随机过程定义、特点; 3、掌握高斯过程的定义、性质; 4、熟悉窄带随机过程的表达式及统计特性 5、熟悉白噪声和带限白噪声的特点; 6、掌握平稳随机过程通过线性系统后特点

通信原理 2.几种常见的概率密度函数 (1)均匀分布 概率密度函数为(x)= b-a a≤x≤b 0 x<0 概率分布函数为F(x)= x-a a≤x≤b b-a x≥a E(x) f(x) 1 b-a x 0 6 (a) (b) 概率分布函数 概率密度函数
通信原理 2.几种常见的概率密度函数 (1)均匀分布 x F(x) 0 a b 0 a b x f (x) 1 b − a 1 (a) (b) 概率分布函数 概率密度函数 a x b b a f x − = 1 概率密度函数为 ( ) − − = x a a x b b a x a x F x 1 0 0 概率分布函数为 ( )
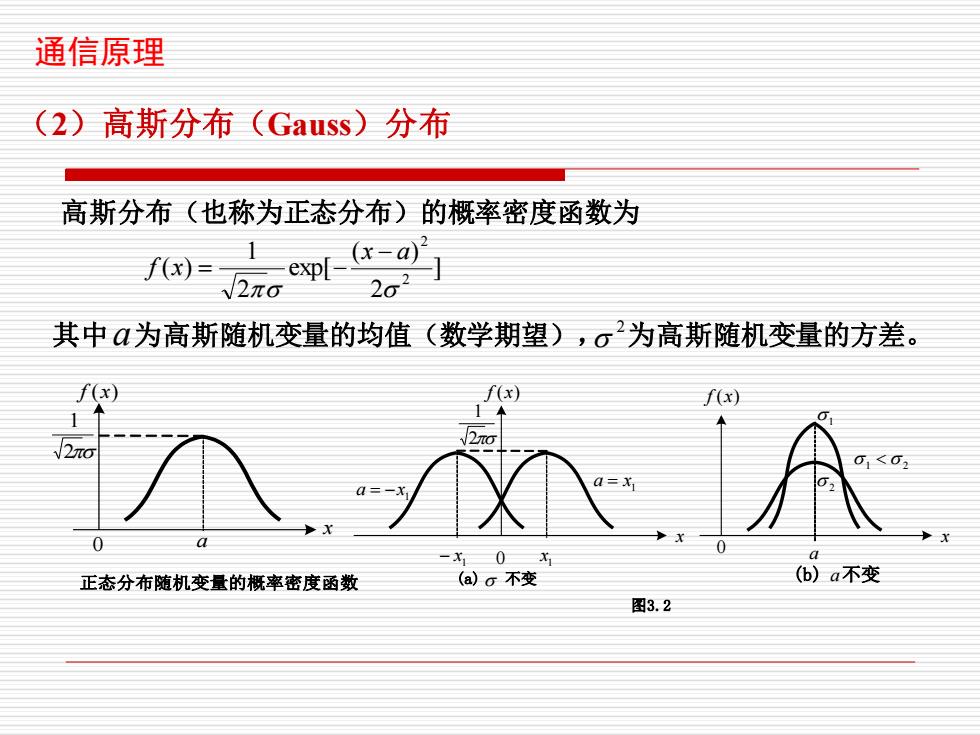
通信原理 (2)高斯分布(Gauss)分布 高斯分布(也称为正态分布)的概率密度函数为 p-a) 2o2 其中a为高斯随机变量的均值(数学期望),6为高斯随机变量的方差。 f(x) f(x) f(x) 1 1◆ N2πo √2πo 01<02 Q=-x a=x 0 a 1 0 -x10X1 正态分布随机变量的概率密度函数 (a)o不变 (b)a不变 图3.2
通信原理 (2)高斯分布(Gauss)分布 高斯分布(也称为正态分布)的概率密度函数为 ] 2 ( ) exp[ 2 1 ( ) 2 2 x a f x − = − 其中 a 为高斯随机变量的均值(数学期望), 2 为高斯随机变量的方差。 x f (x) 0 a 2 1 正态分布随机变量的概率密度函数 x f (x) 0 0 1 a = −x a x f (x) 2 1 (a) 不变 (b) 不变 图3.2 1 − x 1 a = x 1 x 1 2 1 2 a

通信原理 2o2 b-a 其中 eyw 为误差补函数
) 2 ( 2 1 exp( ) 2 . 2 1 ] 2 ( ) exp[ 2 1 ( ) 2 2 2 2 b a z dz erfc dx x a P X b b a b − = − = − = − − 通信原理 erfc x y dy x exp( ) 2 ( ) 2 = − 其中 为误差补函数
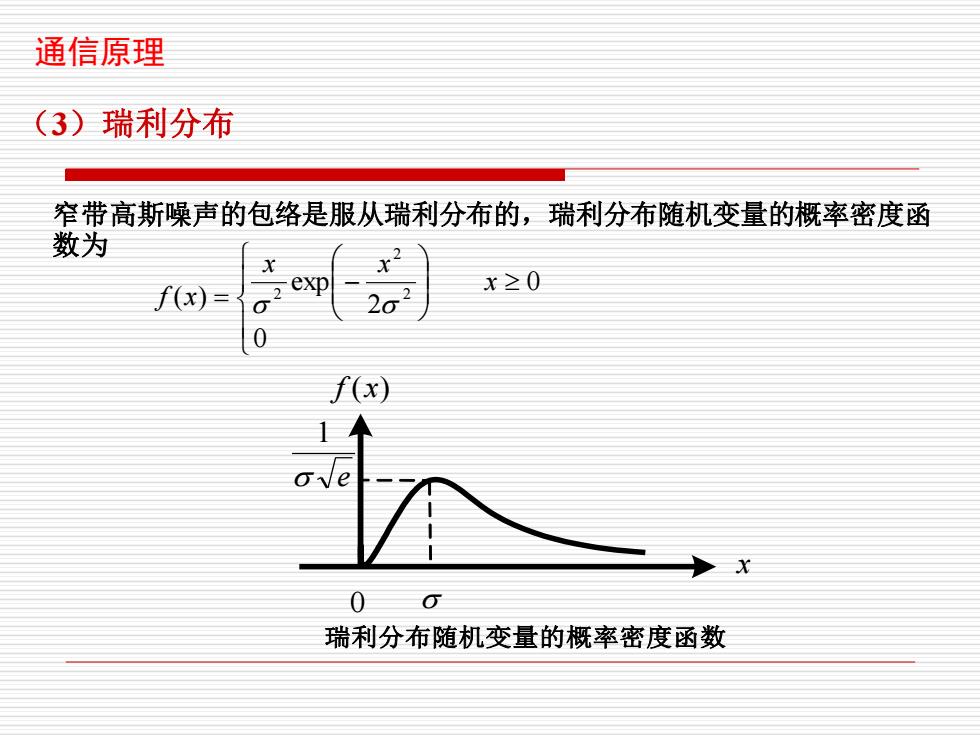
通信原理 (3)瑞利分布 窄带高斯噪声的包络是服从瑞利分布的,瑞利分布随机变量的概率密度函 数为 f(x)= 2exp 202 x≥0 0 f(x) 14 ove 0 瑞利分布随机变量的概率密度函数
通信原理 (3)瑞利分布 窄带高斯噪声的包络是服从瑞利分布的,瑞利分布随机变量的概率密度函 数为 − = 0 0 2 exp ( ) 2 2 2 x x x f x x f (x) 0 e 1 瑞利分布随机变量的概率密度函数

通信原理 (4)莱斯分布 正弦(或余弦)信号加上窄带高斯噪声的包络瞬时值服从莱斯分布。莱斯 分布随机变量的概率密度函数为 f(x)= x≥0 0 X<0 式中(x)为零阶贝塞尔函数,A为正弦波的振幅。当A=0时,莱斯分布 退化为瑞利分布
通信原理 (4)莱斯分布 正弦(或余弦)信号加上窄带高斯噪声的包络瞬时值服从莱斯分布。莱斯 分布随机变量的概率密度函数为 + − = x x σ Ax I x A x f x 0 0 ] 0 2 ( ) exp[ ( ) 2 0 2 2 2 2 式中 为零阶贝塞尔函数, 为正弦波的振幅。当 时,莱斯分布 退化为瑞利分布。 ( ) 0 I x A A = 0

通信原理 §2.3随机过程的基本概念 主要内容: 一、随机过程的定义 二、随机过程的概率密度函数 三、随机过程的数字特征
§2.3 随机过程的基本概念 主要内容: 一、随机过程的定义 二、随机过程的概率密度函数 三、随机过程的数字特征 通信原理

通信原理 一、随机过程的定义 X(=Acos(27+0) 当相位为随机变量时: X()=4cos(27+0) 机过 程 X2(=4cos(2+03) X()=A4 cos(27i+03) 随机过程定义为全体样本函数的集合
一、随机过程的定义 X (t) = A cos(2f t + ) = + = + = + . ( ) cos(2 ) ( ) cos(2 ) ( ) cos(2 ) 3 3 2 2 1 1 X t A f t X t A f t X t A f t 当相位为随机变量时: 随机过 程 随机过程定义为全体样本函数的集合。 通信原理

通信原理 X(t1)=Acos(2g可t1+B) 随机过程的一个重要特点: 任一时刻的取值是一个随机变量
( ) cos(2 ) X t 1 = A f t 1 + 随机过程的一个重要特点: 任一时刻的取值是一个随机变量。 通信原理

通信原理 二、随机过程概率密度函数 设5(t)表示一个随机过程,5()是任一时刻的取值 它是一个随机变量,此随机变量的概率密度函数定义 为随机过程(t的一维概率密度函数,记为(x)。 随机过程X(t任意两个不同时刻t,、2的取值X)、X(t2是两个不同的随 机变量,这两个随机变量之间的联合概率密度函数相应地定义为随机过程) 的二维概率密度函数,二维概率密度函数记为f(x,x2;,2)。几维概率 密度函数的定义与此类似,记为 (x,x2.xntt.tn)
二、随机过程概率密度函数 通信原理 设 (t ) 表示一个随机过程, ( ) 1 t 是任一时刻的取值 它是一个随机变量,此随机变量的概率密度函数定义 为随机过程 (t ) 的一维概率密度函数,记为 f 1 (x1 ;t 1 ) 。 随机过程 任意两个不同时刻 、 的取值 、 是两个不同的随 机变量,这两个随机变量之间的联合概率密度函数相应地定义为随机过程 的二维概率密度函数,二维概率密度函数记为 。 维概率 密度函数的定义与此类似,记为 X (t) 1 t 2 t ( ) 1 X t ( ) 2 X t X (t) ( , ; , ) 2 1 2 1 2 f x x t t n ( , ,. ; , ,. ) n 1 2 n 1 2 n f x x x t t t