
通信原理 第12章正交编码与伪随机序列 1
1 通信原理 第12章 正交编码与伪随机序列

第12章正交编码与伪随机序列 引言 正交编码与伪随机序列在数字通信技术中都 是十分重要的。正交编码不仅可以用作纠错 编码,还可以用来实现码分多址通信,目前 已经广泛用于蜂窝网中。伪随机序列在误码 率测量、时延测量、扩谱通信、密码及分离 多径等方面都有着十分广泛的应用。因此 本章将在简要讨论正交编码概念之后,着重 讨论伪随机序列及其应用。 2
2 第12章 正交编码与伪随机序列 ⚫ 引言 正交编码与伪随机序列在数字通信技术中都 是十分重要的。正交编码不仅可以用作纠错 编码,还可以用来实现码分多址通信,目前 已经广泛用于蜂窝网中。伪随机序列在误码 率测量、时延测量、扩谱通信、密码及分离 多径等方面都有着十分广泛的应用。因此, 本章将在简要讨论正交编码概念之后,着重 讨论伪随机序列及其应用

第12章正交编码与伪随机序列 12.2正交编码 "12.2.1正交编码的基本概念 ◆正交性 口若两个周期为T的模拟信号s1()和s2()互相正交,则有 s,0s,0h=0 同理,若M个周期为的模拟信号s1(),S2(),., 5()构成一个正交信号集合,则有 s()s.(d=0 i≠ji,j=1,2,.,M ◆互相关系数 ·对于二进制数字信号,用一数字序列表示码组。这里 我们只讨论二进制且码长相同的编码。这时,两个码 组的正交性可用如下形式的互相关系数来表述
3 第12章 正交编码与伪随机序列 ⚫ 12.2 正交编码 ◼ 12.2.1 正交编码的基本概念 ◆ 正交性 若两个周期为T的模拟信号s1 (t)和s2 (t)互相正交,则有 同理,若M个周期为T的模拟信号s1 (t),s2 (t),., sM(t)构成一个正交信号集合,则有 ◆ 互相关系数 对于二进制数字信号,用一数字序列表示码组。这里, 我们只讨论二进制且码长相同的编码。这时,两个码 组的正交性可用如下形式的互相关系数来表述。 = T s t s t dt 0 1 ( ) 2 ( ) 0 = T s t s t dt 0 1 ( ) 2 ( ) 0 i j;i, j=1, 2, ., M

第12章正交编码与伪随机序列 设长为的编码中码元只取值+1和-1,以及x和y是其中两个码 组: X=(X1,X2,x3,.,xn) y=(y1,y2,y3,.,yn) 其中 x,y∈(+1,-1)。 i=1,2,.,n 则x和y间的互相关系数定义为 p(.)= n i=l 若码组x和正交,则必有p(x,y)=0
4 第12章 正交编码与伪随机序列 设长为n的编码中码元只取值+1和-1,以及x和y是其中两个码 组: 其中 则x和y间的互相关系数定义为 若码组x和y正交,则必有(x, y) = 0。 ( , , , , ) 1 2 3 n x = x x x x ( , , , , ) 1 2 3 n y = y y y y xi , yi (+1,−1), i =1,2, ,n = = n i i i x y n x y 1 1 ( , )
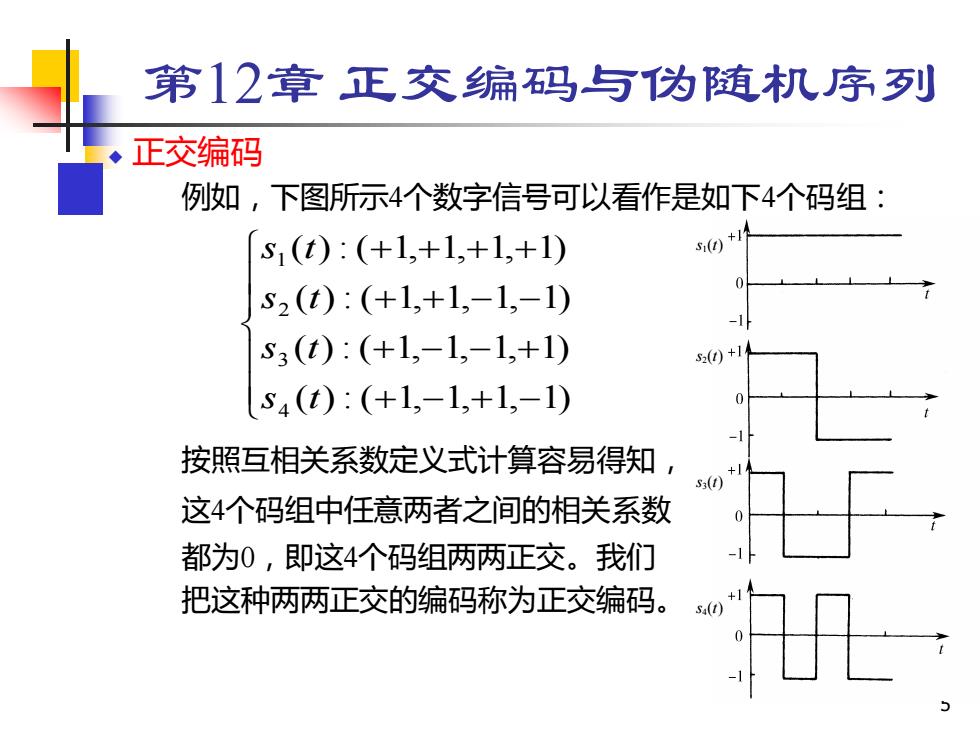
第12章正交编码与伪随机序列 正交编码 例如,下图所示4个数字信号可以看作是如下4个码组: S1(t):(+1,+1,+1,+1) S2(t):(+1,+1,-1,-1) -1 S3(t):(+1,-1,-1,+1) 0+1 S4(t):(+1,-1,+1,-1) 按照互相关系数定义式计算容易得知 S3(t) 这4个码组中任意两者之间的相关系数 都为0,即这4个码组两两正交。我们 把这种两两正交的编码称为正交编码。 s4()
5 第12章 正交编码与伪随机序列 ◆ 正交编码 例如,下图所示4个数字信号可以看作是如下4个码组: 按照互相关系数定义式计算容易得知, 这4个码组中任意两者之间的相关系数 都为0,即这4个码组两两正交。我们 把这种两两正交的编码称为正交编码。 s1(t) s2(t) s3(t) s4(t) + − + − + − − + + + − − + + + + ( ) : ( 1, 1, 1, 1) ( ) : ( 1, 1, 1, 1) ( ) : ( 1, 1, 1, 1) ( ) : ( 1, 1, 1, 1) 4 3 2 1 s t s t s t s t

第12章正交编码与伪随机序列 自相关系数: 类似上述互相关系数的定义,可以对于一个长为的码组x 定义其自相关系数为 j=0,1,.,(n-1) ni= 式中,x的下标按模n运算,即有xn+k三xk。例如,设 x=(x1,x2,x3,x4)=(+1,-1,-1,+1) 如索二2 P0)= x2=1 xX=x4,+33 1 P(0= 6+xx+x)=4-1+1-1+1=0 P(2)= X,X+2=(xX3+x2x4+X31+x4x2)=-1 4 p(3) XX+3=4x++2+x)=0 6
6 第12章 正交编码与伪随机序列 ◆ 自相关系数: 类似上述互相关系数的定义,可以对于一个长为n的码组x 定义其自相关系数为 式中,x的下标按模n运算,即有xn+k xk 。例如,设 则有 = = + = − n i x xi xi j j n n j 1 , 0,1, ,( 1) 1 ( ) ( , , , ) ( 1, 1, 1, 1) x = x1 x2 x3 x4 = + − − + ( ) 0 4 1 4 1 (3) ( ) 1 4 1 4 1 (2) ( 1 1 1 1) 0 4 1 ( ) 4 1 4 1 (1) 1 4 1 (0) 1 4 2 1 3 2 4 3 4 1 3 1 3 2 4 3 1 4 2 4 1 2 1 2 2 3 3 4 4 1 4 1 1 4 1 2 = = + + + = = = + + + = − = = + + + = − + − + = = = = + = + = + = x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x i x i i i x i i i x i i i x i

第12章正交编码与伪随机序列 ◆用二进制数字表示互相关系数 ▣在二进制编码理论中,常采用二进制数字"0和“1表示 码元的可能取值。这时,若规定用二进制数字“0代替上 述码组中的”+1”,用二进制数字“1”代替”-1”,则上 述互相关系数定义式将变为 P(x,y)= A-D A+D 式中,A一x和中对应码元相同的个数; D一x和y中对应码元不同的个数。 口例如,按照上式规定,上面例子可以改写成 S1():(0,0,0,0) S2(t):(0,0,1,1 S3(t):(0,1,1,0) S4(t):(0,1,0,1)
7 第12章 正交编码与伪随机序列 ◆ 用二进制数字表示互相关系数 在二进制编码理论中,常采用二进制数字“0”和“1”表示 码元的可能取值。这时,若规定用二进制数字“0”代替上 述码组中的“+1”,用二进制数字“1”代替“-1”,则上 述互相关系数定义式将变为 式中,A — x和y中对应码元相同的个数; D — x和y中对应码元不同的个数。 例如,按照上式规定,上面例子可以改写成 A D A D x y + − ( , ) = ( ) : (0,1,0,1) ( ) : (0,1,1,0) ( ) : (0,0,1,1) ( ) : (0,0,0,0) 4 3 2 1 s t s t s t s t

第12章正交编码与伪随机序列 ◆用二进制数字表示自相关系数 ▣上式中,若用的次循环移位代替y,就得到x的自相关系 数p,()。具体地讲,令 X=(X12X2,.,Xn) y=(x1+j3X2+j3.,Xn,x1,X2,.Xj) 代入定义式 p(x,y)= A-D 4+D 就得到自相关系数p()。 P
8 第12章 正交编码与伪随机序列 ◆ 用二进制数字表示自相关系数 上式中,若用x的j次循环移位代替y,就得到x的自相关系 数x (j)。具体地讲,令 代入定义式 就得到自相关系数x (j)。 ( , , , , , , ) ( , , , ) 1 2 1 2 1 2 j j n j n y x x x x x x x x x x = + + = A D A D x y + − ( , ) =

第12章正交编码与伪随机序列 ◆超正交码和双正交码 ▣超正交码:相关系数p的取值范围在±1之间,即有-1≤p ≤+1。若两个码组间的相关系数p<0,则称这两个码组 互相超正交。如果一种编码中任两码组间均超正交,则 称这种编码为超正交码。 ~例如,在上例中,若仅取后3个码组,并且删去其第 一位,构成如下新的编码: s1'(t):(0,1,1) S2'(t):(1,1,0) s3'(t):(1,0,1) 则不难验证,由这3个码组所构成的编码是超正交码。 9
9 第12章 正交编码与伪随机序列 ◆ 超正交码和双正交码 超正交码:相关系数 的取值范围在1之间,即有-1 +1。若两个码组间的相关系数 < 0,则称这两个码组 互相超正交。如果一种编码中任两码组间均超正交,则 称这种编码为超正交码。 ➢ 例如,在上例中,若仅取后3个码组,并且删去其第 一位,构成如下新的编码: 则不难验证,由这3个码组所构成的编码是超正交码。 '( ) : (1,0,1) '( ) : (1,1,0) '( ) : (0,1,1) 3 2 1 s t s t s t

第12章正交编码与伪随机序列 。双正交编码 ,由正交编码和其反码便可以构成双正交编码。 ,例:上例中正交码为 S1(t):(0,0,0,0) s2(t):(0,0,1,1) s3(t):(0,1,1,0) (11,1,1) s4(t):(0,1,0,1) 其反码为 (11,0,0) (1,0,0,1) (1,01,0) 上两者的总体即构成如下双正交码: (0,0,0,0) (1,1,1,1)(0,0,1,1)(1,1,0,0) (0,1,1,0)(1,0,0,1)(0,1,0,1)(1,0,1,0) 此码共有8种码组,码长为4,任两码组间的相关系数为0 或-1。 10
10 第12章 正交编码与伪随机序列 双正交编码 ➢ 由正交编码和其反码便可以构成双正交编码。 ➢ 例: 上例中正交码为 其反码为 上两者的总体即构成如下双正交码: (0,0,0,0) (1,1,1,1) (0,0,1,1) (1,1,0,0) (0,1,1,0) (1,0,0,1) (0,1,0,1) (1,0,1,0) 此码共有8种码组,码长为4,任两码组间的相关系数为0 或-1。 ( ) :(0,1,0,1) ( ) :(0,1,1,0) ( ) :(0,0,1,1) ( ) :(0,0,0,0) 4 3 2 1 s t s t s t s t (1,0,1,0) (1,0,0,1) (1,1,0,0) (1,1,1,1)