
通信原理 第2章确知信号
通信原理 第2章 确知信号

第2章确知信号 2.1确知信号的类型 ·按照周期性区分: ◆周期信号:s)=st+To), -000 ◆非周期信号 ·按照能量区分: ◆能量信号:能量有限,0<E=广s2()dt<0 ◆功率信号: 口归一化功率:P=V2/R=I2R=V2=I2 a平均功率P为有限正值:P=典7%20h ·能量信号的功率趋于0,功率信号的能量趋于0
第2章 确知信号 ⚫ 2.1 确知信号的类型 ◼ 按照周期性区分: ◆ 周期信号: T0-信号的周期, T0 > 0 ◆ 非周期信号 ◼ 按照能量区分: ◆ 能量信号:能量有限, ◆ 功率信号: 归一化功率: 平均功率P为有限正值: ◼ 能量信号的功率趋于0,功率信号的能量趋于 s(t) = s(t +T0 ), − t + = − 0 E s (t)dt 2 → − = / 2 / 2 2 ( ) 1 lim T T T s t dt T P 2 2 2 2 P = V / R = I R = V = I

第2章确知信号 ● 2.2确知信号的频域性质 ·2.2.1功率信号的频谱 ◆周期性功率信号频谱(函数)的定义 C.cd T%/2 (2.2-1) 式中,6=1/To,n为整数,-o<n<+oo。 s(t)=∑Cne2mm (2.2-2) (t)dt (2.2-3) Cn=Cneo.-双边谱,复振幅 (2.2-4) Cml-振幅,O,-相位
第2章 确知信号 ⚫ 2.2 确知信号的频域性质 ◼ 2.2.1 功率信号的频谱 ◆ 周期性功率信号频谱(函数)的定义 式中,f0 = 1/T0,n为整数,- < n < +。 -双边谱,复振幅 (2.2 - 4) |Cn | -振幅, n-相位( ) (2.2 1) 1 ( ) / 2 / 2 2 0 0 0 0 0 = = − − − T T j n f t n s t e dt T C C nf ( ) (2.2 2) 0 2 / = − n=− j n t T s t Cn e ( ) (2.2 3) 1 / 2 / 2 0 0 0 0 = − − T T s t dt T C n j Cn Cn e =
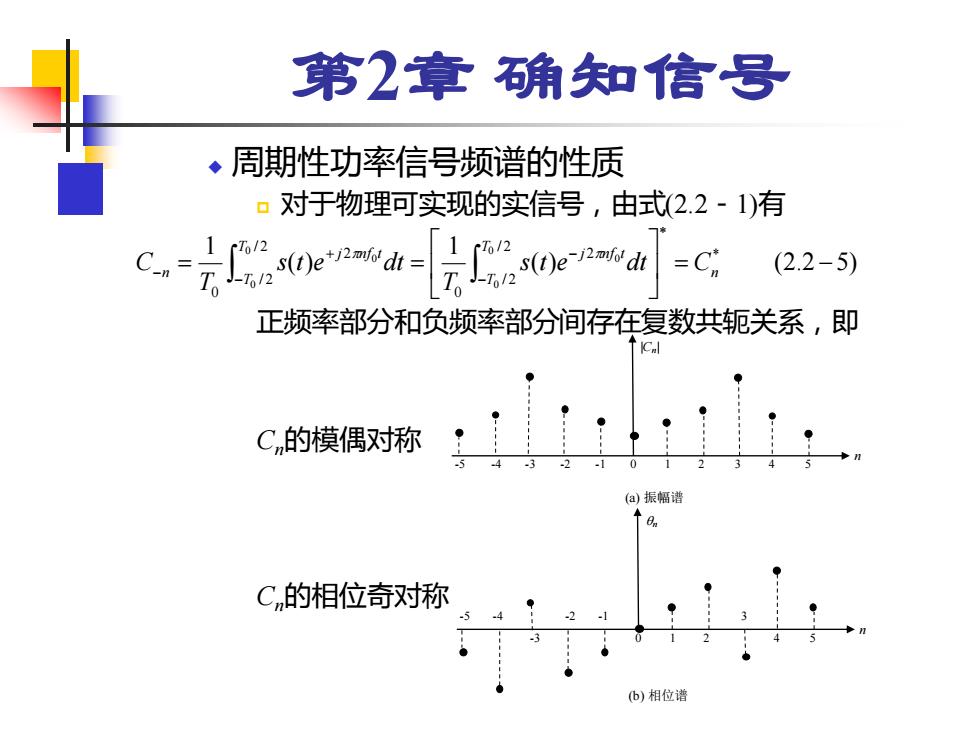
第2章确知信号 ◆周期性功率信号频谱的性质 。对于物理可实现的实信号,由式2.2-1)有 C-n 6/2 T0/2 =Ci (2.2-5) 正频率部分和负频率部分间存在复数共轭关系,即 C的模偶对称 (a)振幅谱 0 C的相位奇对称 b)相位谱
第2章 确知信号 ◆ 周期性功率信号频谱的性质 对于物理可实现的实信号,由式(2.2-1)有 正频率部分和负频率部分间存在复数共轭关系,即 Cn的模偶对称 Cn的相位奇对称 ( ) (2.2 5) 1 ( ) 1 * / 2 / 2 2 0 / 2 / 2 2 0 0 0 0 0 0 0 = − = = − − − + − n T T j n f t T T j n f t n s t e dt C T s t e dt T C n -5 -4 -3 -2 -1 0 1 2 3 4 5 |Cn| (a) 振幅谱 0 1 2 3 4 5 -2 -1 -3 -5 -4 n n (b) 相位谱

第2章确知信号 将式(2.2-5)代入式2.2-2),得到 s0)=∑C,e2m=C。+∑[a.cos(2m/T)+b.sin(2m1/T,】 -C++cos(2t/T+0) (2.2-8) 式中0=tan'6,1a,)lC.=)va+b 式(2.2-8)表明: 1.实信号可以表示成包含直流分量C、基波(n=1时)和各次谐 波(n=1,2,3,.)。 2.实信号s()的各次谐波的振幅等于Va+b 称为单边谱。 3.实信号s(t)的各次谐波的相位等于0 4.频谱函数Cn又称为双边谱,|C的值是单边谱的振幅之半
第2章 确知信号 将式(2.2-5)代入式(2.2-2),得到 式中 式(2.2-8)表明: 1. 实信号可以表示成包含直流分量C0、基波(n = 1时)和各次谐 波(n = 1, 2, 3, .)。 2. 实信号s(t)的各次谐波的振幅等于 3. 实信号s(t)的各次谐波的相位等于 4. 频谱函数Cn又称为双边谱,|Cn |的值是单边谱的振幅之半。 ( ) ( ) cos(2 / ) (2.2 8) ( ) cos 2 / sin 2 / 1 0 2 2 0 1 0 0 0 2 / 0 = + + + − = = + + = = =− n n n n n n n j n t T n C a b nt T s t C e C a nt T b nt T ( ) n n tan b / a −1 = 2 2 an + bn 2 2 2 1 n n n C = a + b 称为单边谱

第2章确知信号 口若s()是实偶信号,则Cn为实函数。因为 n= U)co) 12 (eod2m.y-(si2mfrd Re(C)-j(C 而 w2s0sn2a听0dt=0 所以C为实函数
第2章 确知信号 若s(t)是实偶信号,则Cn为实函数。因为 而 所以Cn为实函数。 ( )sin( 2 ) Re( ) Im( ) 1 ( ) cos(2 ) 1 ( )[cos(2 ) sin( 2 )] 1 ( ) 1 / 2 / 2 0 / 2 / 2 0 / 2 / 2 0 0 / 2 / 2 2 0 0 0 0 0 0 0 0 0 0 n n T T T T T T T T j n f t n s t nf t dt C j C T s t nf t dt j T s t nf t j nf t dt T s t e dt T C = − = − = = − − − − − − ( )sin( 2 ) 0 / 2 / 2 0 0 0 = − T T s t nf t dt
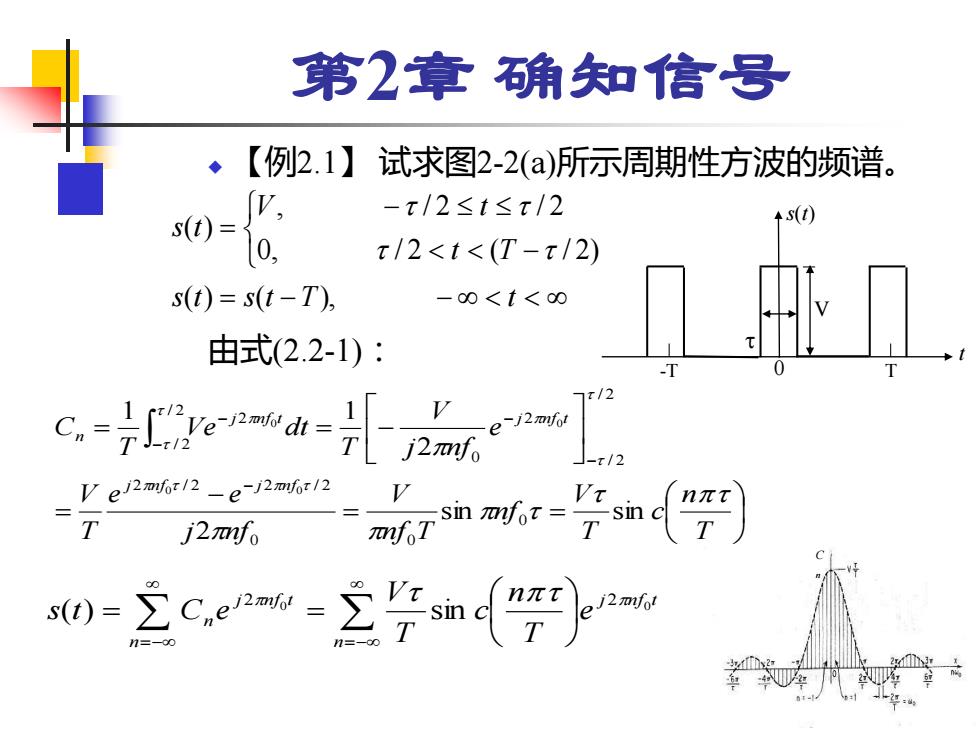
第2章确知信号 ◆ 【例2.1】 试求图2-2(a)所示周期性方波的频谱。 s(t)= v, -x/2≤t≤x/2 0, π/2<t<(T-t/2) s(t)=s(t-T), -0<t<00 由式(2.2-1): C. y e2mhr12e-j2mfor12 T j2anfo 0-ce-2号snn
第2章 确知信号 ◆ 【例2.1】 试求图2-2(a)所示周期性方波的频谱。 由式(2.2-1): -T 0 T t V s(t) = − − − − = s t s t T t t T V t s t ( ) ( ), 0, / 2 ( / 2) , / 2 / 2 ( ) = = − = = = − − − − − − T n c T V nf nf T V j nf e e T V e j nf V T Ve dt T C j n f j n f j n f t j n f t n sin sin 2 2 1 1 0 0 0 2 / 2 2 / 2 / 2 / 2 2 0 / 2 / 2 2 0 0 0 0 =− =− = = n n j n f t j n f t n e T n c T V s t C e 2 0 2 0 ( ) sin C n

第2章确知信号 ◆【例2.2】试求图2-3所示周期性方波的频谱。 V, 0≤t≤x s(t)= 0, t<t<T s(t)=s(t-T), -0<t<0 由式(2.2-1): C.d 2V1-e26=V_ (-eJ2mx1T) 、j2m 因为此信号不是偶函数,其频谱C是复函数
第2章 确知信号 ◆ 【例2.2】试求图2-3所示周期性方波的频谱。 由式(2.2-1) : 因为此信号不是偶函数,其频谱Cn是复函数。 -T T t 0 V s(t) = − − = s t s t T t t T V t s t ( ) ( ), 0, , 0 ( ) ( ) j n T j n f j n f t j n f t n e j n V j nf e T V e j nf V T Ve dt T C 2 / 0 2 0 2 0 0 2 1 2 2 1 2 1 1 0 0 0 − − − − = − − = = = −
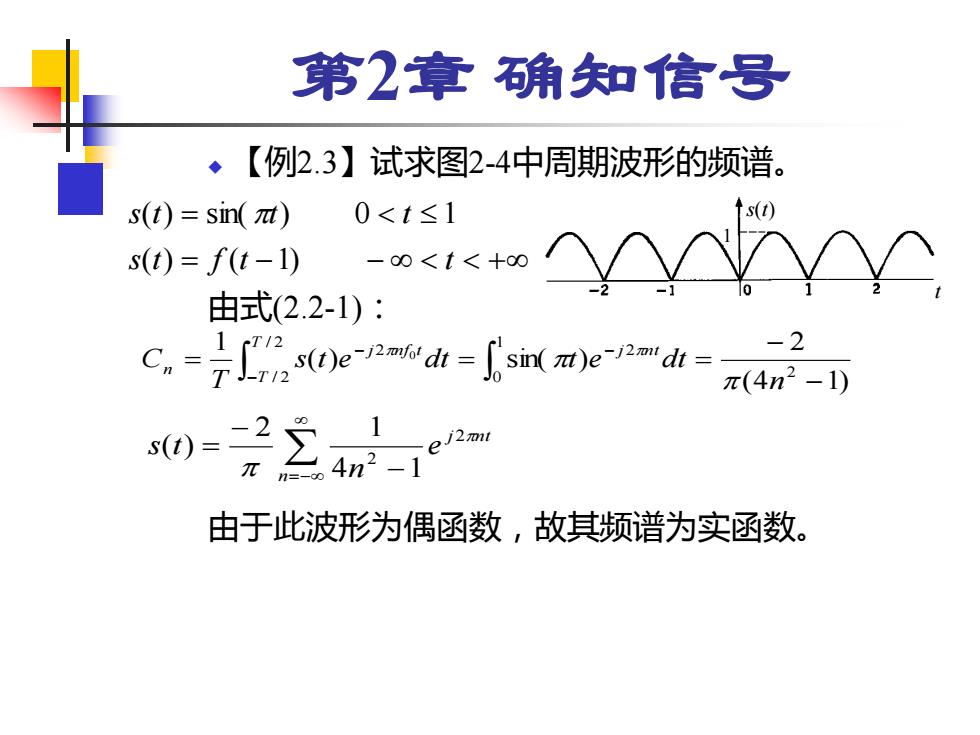
第2章确知信号 ◆【例2.3】试求图2-4中周期波形的频谱。 s(t)=sin(nt) 0<t≤1 s(I) s(t)=f(t-1) -0<t<+00 由式(2.2-1): C.)e-f sin )ed -2 π(4n2-1) 41 由于此波形为偶函数,故其频谱为实函数
第2章 确知信号 ◆ 【例2.3】试求图2-4中周期波形的频谱。 由式(2.2-1): 由于此波形为偶函数,故其频谱为实函数。 t 1 s(t) = − − + = s t f t t s t t t ( ) ( 1) ( ) sin( ) 0 1 − − = = = − − − 1 0 2 2 / 2 / 2 2 (4 1) 2 ( ) sin( ) 1 0 n s t e dt t e dt T C j n t T T j n f t n =− − − = n j nt e n s t 2 2 4 1 2 1 ( )

第2章确知信号 ·2.2.2能量信号的频谱密度 ◆频谱密度的定义: 能量信号s(0的傅里叶变换:S(f)=s()e2dt ◆S的逆傅里叶变换为原信号:s()=S(f)e2d山 ◆Sf和Cn的主要区别: 口S)是连续谱,Cn是离散谱; aS)的单位是V/Hz,而C的单位是V。 ◆注意:在针对能量信号讨论问题时,也常把频谱密 度简称为频谱。 ◆实能量信号:负频谱和正频谱的模偶对称,相位奇 对称,即复数共轭,因 广so0erdi=soeh Sf)=[S(-f)
第2章 确知信号 ◼ 2.2.2 能量信号的频谱密度 ◆ 频谱密度的定义: 能量信号s(t) 的傅里叶变换: ◆ S(f)的逆傅里叶变换为原信号: ◆ S(f)和Cn的主要区别: S(f)是连续谱,Cn是离散谱; S(f)的单位是V/Hz,而Cn的单位是V。 ◆ 注意:在针对能量信号讨论问题时,也常把频谱密 度简称为频谱。 ◆ 实能量信号:负频谱和正频谱的模偶对称,相位奇 对称,即复数共轭,因 − − S f = s t e dt j2ft ( ) ( ) − s t = S f e df j2ft ( ) ( ) − − − + = − = ( ) ( ) , ( ) ( ) 2 2 s t e dt s t e dt S f S f j f t j f t