
通信原理 第10章数字信号最佳接收 1
1 通信原理 第10章 数字信号最佳接收

第10章数字信号最佳接收 。10.1数字信号的统计特性 ·以二进制为例研究接收电压的统计特性。 ·假设:通信系统中的噪声是均值为0的带限高斯白噪声,其 单边功率谱密度为,;其发送概率分别为P(O)和P(1),则有 P(0)+P(1)=1 ·若此通信系统的基带截止频率小于H,则根据低通信号抽样 定理,接收噪声电压可以用其抽样值表示,抽样速率要求 不小于其奈奎斯特速率2f。 ·设在一个码元持续时间Ts内以2f的速率抽样,共得到k个抽 样值:,则有k=2fTs。 2
2 第10章 数字信号最佳接收 ⚫ 10.1数字信号的统计特性 ◼ 以二进制为例研究接收电压的统计特性。 ◼ 假设:通信系统中的噪声是均值为0的带限高斯白噪声,其 单边功率谱密度为n0;其发送概率分别为P(0)和P(1),则有 P(0) + P(1) = 1 ◼ 若此通信系统的基带截止频率小于fH,则根据低通信号抽样 定理,接收噪声电压可以用其抽样值表示,抽样速率要求 不小于其奈奎斯特速率2fH。 ◼ 设在一个码元持续时间Ts内以2fH的速率抽样,共得到k个抽 样值:,则有k = 2fHTs

第10章数字信号最佳接收 由于每个噪声电压抽样值都是正态分布的随机变量,故其一维 概率密度可以写为 f(n)= exp √2π0m 2o2 式中,σ,-噪声的标准偏差; σ2~噪声的方差,即噪声平均功率; i=1,2,.,k。 ·设接收噪声电压(t)的个抽样值的维联合概率密度函数为 fk(n1,n2,.,nk) 3
3 第10章 数字信号最佳接收 ◼ 由于每个噪声电压抽样值都是正态分布的随机变量,故其一维 概率密度可以写为 式中,n - 噪声的标准偏差; n 2 - 噪声的方差,即噪声平均功率; i =1,2,.,k。 ◼ 设接收噪声电压n(t)的k个抽样值的k维联合概率密度函数为 = − 2 2 2 exp 2 1 ( ) n i n i n f n ( , , , ) k n1 n2 nk f

第10章数字信号最佳接收 由于高斯噪声的概率分布通过带限线性系统后仍为高斯分布 所以其k维联合概率密度函数可以表示为 fk(n,n2,.,nk)=f(n)f(n2).f(nk)= i ·当k很大时,在一个码元持续时间T内接收的噪声平均功率可 表示为: 或者将上式左端的求和式写成积分式,则上式变成
4 第10章 数字信号最佳接收 ◼ 由于高斯噪声的概率分布通过带限线性系统后仍为高斯分布, 所以其k 维联合概率密度函数可以表示为 ◼ 当k 很大时,在一个码元持续时间Ts内接收的噪声平均功率可 表示为: 或者将上式左端的求和式写成积分式,则上式变成 ( ) = = − = k i i n k n f k n n nk f n f n f nk n 1 2 1 2 1 2 2 2 1 exp 2 1 ( , , , ) ( ) ( ) ( ) = = = k i i H s k i i n f T n k 1 2 1 2 2 1 1 = = k i i H s T s n f T n t dt T s 1 2 0 2 2 1 ( ) 1

第10章数字信号最佳接收 由于 则: fu-w 式中 f(m)=f(n,h,.,nx)=f(n)f(n).f(nk) n=(n1,n2,n)-k维矢量,表示一个码元内噪声的k个 抽样 ·注意,n)不是时间函数,虽然式中有时间函数(t),但是后者 在定积分内,积分后已经与时间变量无关。是一个维矢量, 它可以看作是k维空间中的一个点。 5
5 第10章 数字信号最佳接收 ◼ 由于 则: 式中 n = (n1 , n2 , ., nk ) - k 维矢量,表示一个码元内噪声的k个 抽样值。 ◼ 注意,f(n)不是时间函数,虽然式中有时间函数n(t),但是后者 在定积分内,积分后已经与时间变量t无关。n是一个k维矢量, 它可以看作是k 维空间中的一个点。 n H n f 0 2 = ( ) = − Ts k n n t dt n f 0 2 0 ( ) 1 exp 2 1 ( ) n ( ) ( , , , ) ( ) ( ) ( ) k 1 2 k 1 2 nk f n = f n n n = f n f n f

第10章数字信号最佳接收 在码元持续时间T、噪声单边功率谱密度和抽样数k(它和 系统带宽有关)给定后,)仅决定于该码元期间内噪声的能 量: n2(t)dr ■由于噪声的随机性,每个码元持续时间内噪声的波形和能量 都是不同的,这就使被传输的码元中有一些会发生错误,而 另一些侧无错。 6
6 第10章 数字信号最佳接收 ◼ 在码元持续时间Ts、噪声单边功率谱密度n0和抽样数k(它和 系统带宽有关)给定后,f(n)仅决定于该码元期间内噪声的能 量: ◼ 由于噪声的随机性,每个码元持续时间内噪声的波形和能量 都是不同的,这就使被传输的码元中有一些会发生错误,而 另一些则无错。 Ts n t dt 0 2 ( )

第10章数字信号最佳接收 设接收电压(t)为信号电压s(t)和噪声电压n(t)之和: (t)=s(t)+n(t) 则在发送码元确定之后,接收电压)的随机性将完全由噪声 决定,故它仍服从高斯分布,其方差仍为σ2,但是均值变为 s(①)。所以,当发送码元"0的信号波形为s(t)时,接收电压 (t)的维联合概率密度函数为 f(r)= 不-aojo 式中r=s+一k维矢量,表示一个码元内接收电压的k个抽 样值; 5-k维矢量,表示一个码元内信号电压的k个抽样值
7 第10章 数字信号最佳接收 ◼ 设接收电压r(t)为信号电压s(t)和噪声电压n(t)之和: r(t) = s(t) + n(t) 则在发送码元确定之后,接收电压r(t)的随机性将完全由噪声 决定,故它仍服从高斯分布,其方差仍为n 2,但是均值变为 s(t)。所以,当发送码元“0”的信号波形为s0 (t)时,接收电压 r(t)的k维联合概率密度函数为 式中 r = s + n — k 维矢量,表示一个码元内接收电压的k个抽 样值; s - k 维矢量,表示一个码元内信号电压的k个抽样值。 ( ) = − − r t s t dt n f Ts k n 2 0 0 0 0 ( ) ( ) 1 exp 2 1 ( ) r

第10章数字信号最佳接收 同理,当发送码元“1的信号波形为s()时,接收电压(t)的k 维联合概率密度函数为 f(r)= 若通信系统传输的是M进制码元,即可能发送s1,S2, SM之一,当发送码元是s,时,接收电压的k维联合概 率密度函数为 f() aiarnwsoliw 注意:以上三式中的k维联合概率密度函数不是时间的函数, 并且是一个标量,而仍是维空间中的一个点,是一个矢量。 8
8 第10章 数字信号最佳接收 ◼ 同理,当发送码元“1“的信号波形为s1 (t)时,接收电压r(t)的k 维联合概率密度函数为 ◼ 若通信系统传输的是M 进制码元,即可能发送s1,s2,., si,.,sM 之一,当发送码元是si时,接收电压的k 维联合概 率密度函数为 注意:以上三式中的k 维联合概率密度函数不是时间t的函数, 并且是一个标量,而r 仍是k维空间中的一个点,是一个矢量。 ( ) = − − r t s t dt n f Ts k n 2 0 1 0 1 ( ) ( ) 1 exp 2 1 ( ) r ( ) = − − r t s t dt n f Ts k i n i 2 0 0 ( ) ( ) 1 exp 2 1 ( ) r

第10章数字信号最佳接收 10.2数字信号的最佳接收 ·“最佳”的准测:错误概率最小 ·产生错误的原因:暂不考虑失真的影响,主要讨论二 进制数字通信系统中如何使噪声引起的错误慨率最小。 ·判决规则 设在一个二进制通信系统中发送码元“1的概率为P(1), 发送码元“0的慨率为P(0),则总误码率P等于 P。=P(I)P1+PO)Po 式中 Pe1=P0/1)-发送“1时,收到"0的条件概率; P0=P(1/0)·发送"0时,收到“1的条件概率; 上面这两个条件概率称为错误转移概率。 9
9 第10章 数字信号最佳接收 ⚫ 10.2 数字信号的最佳接收 ◼ “最佳”的准则:错误概率最小 ◼ 产生错误的原因:暂不考虑失真的影响,主要讨论二 进制数字通信系统中如何使噪声引起的错误概率最小。 ◼ 判决规则 设在一个二进制通信系统中发送码元“1”的概率为P(1), 发送码元“0”的概率为P(0),则总误码率Pe等于 式中 Pe1 = P(0/1) - 发送“1”时,收到“0”的条件概率; Pe0 = P(1/0) - 发送“0”时,收到“1”的条件概率; 上面这两个条件概率称为错误转移概率。 1 0 (1) (0) Pe = P Pe + P Pe
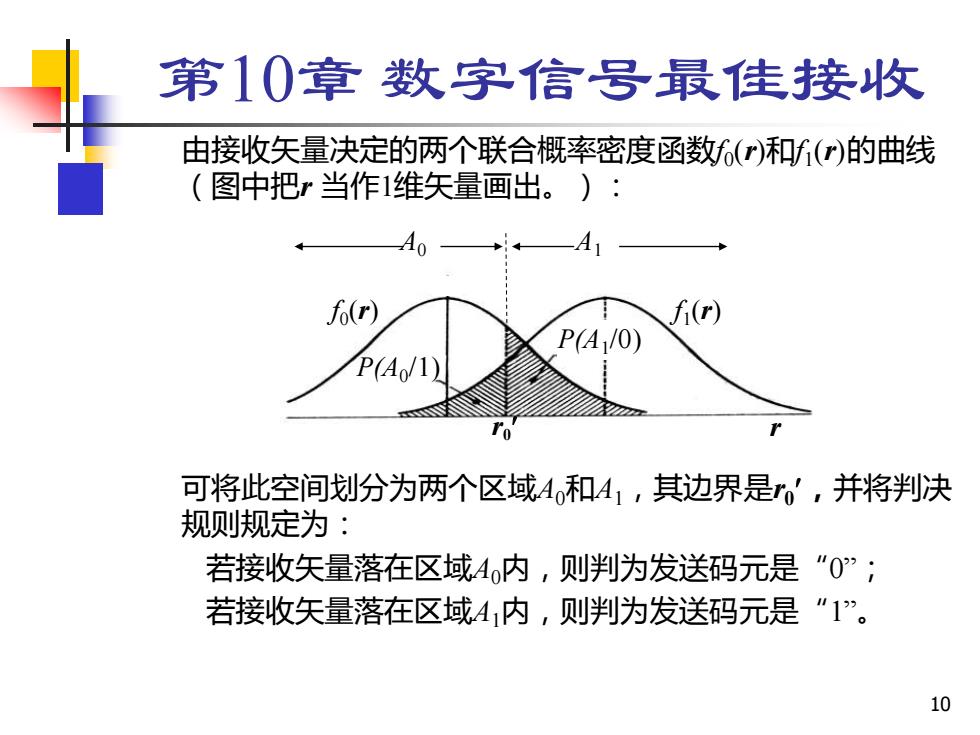
第10章数字信号最佳接收 由接收矢量决定的两个联合概率密度函数f()和f()的曲线 (图中把r当作1维矢量画出。): fo(r) f(r) PA1/0) PA/1) 可将此空间划分为两个区域4和A1,其边界是r。',并将判决 规则规定为: 若接收矢量落在区域A内,则判为发送码元是“0”; 若接收矢量落在区域41内,则判为发送码元是“1”。 10
10 第10章 数字信号最佳接收 由接收矢量决定的两个联合概率密度函数f0 (r)和f1 (r)的曲线 (图中把r 当作1维矢量画出。): 可将此空间划分为两个区域A0和A1,其边界是r0 ,并将判决 规则规定为: 若接收矢量落在区域A0内,则判为发送码元是“0”; 若接收矢量落在区域A1内,则判为发送码元是“1”。 A0 A1 r f0 (r) f1 (r) r0 P(A0 /1) P(A1 /0)