
第3章信源编码 ▣3.1信源编码的基本概念 ▣3.2脉冲编码调制 ▣3.3差分脉冲编码调制 ▣3.4增量调制
2 第3章 信源编码 3.1 信源编码的基本概念 3.2 脉冲编码调制 3.3 差分脉冲编码调制 3.4 增量调制
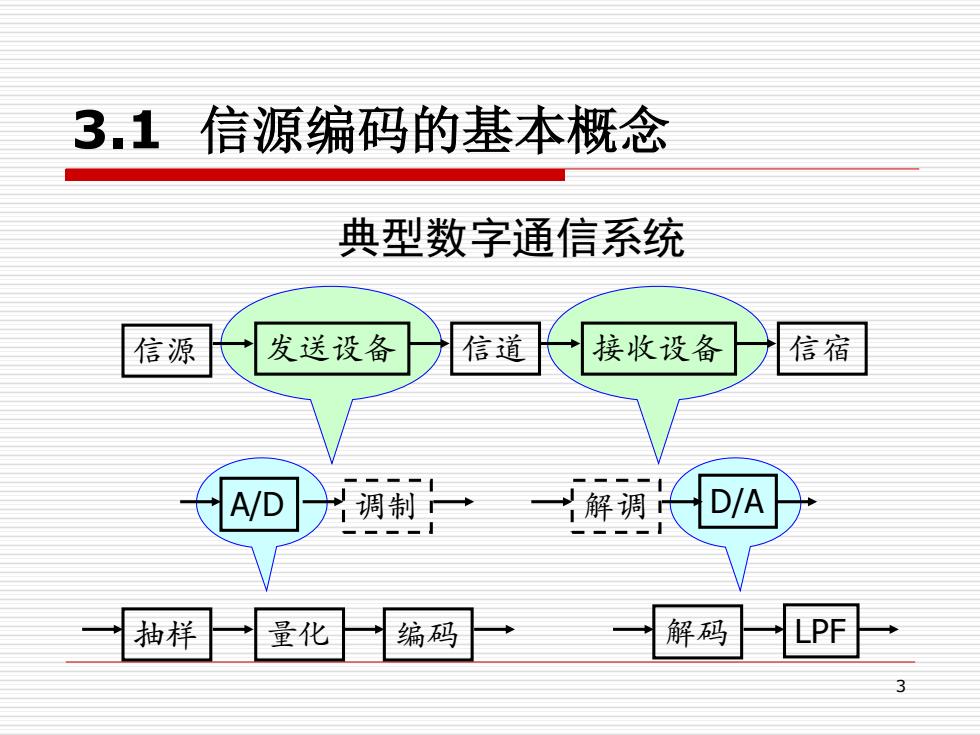
3.1信源编码的基本概念 典型数字通信系统 信源 发送设备 信道 接收设备 信宿 A/D 调制 解调长D/A 抽样 量化 编码 解码 LPF
3 抽样 量化 编码 解码 LPF A/D 调制 解调 D/A 3.1 信源编码的基本概念 典型数字通信系统 信源 发送设备 信道 接收设备 信宿
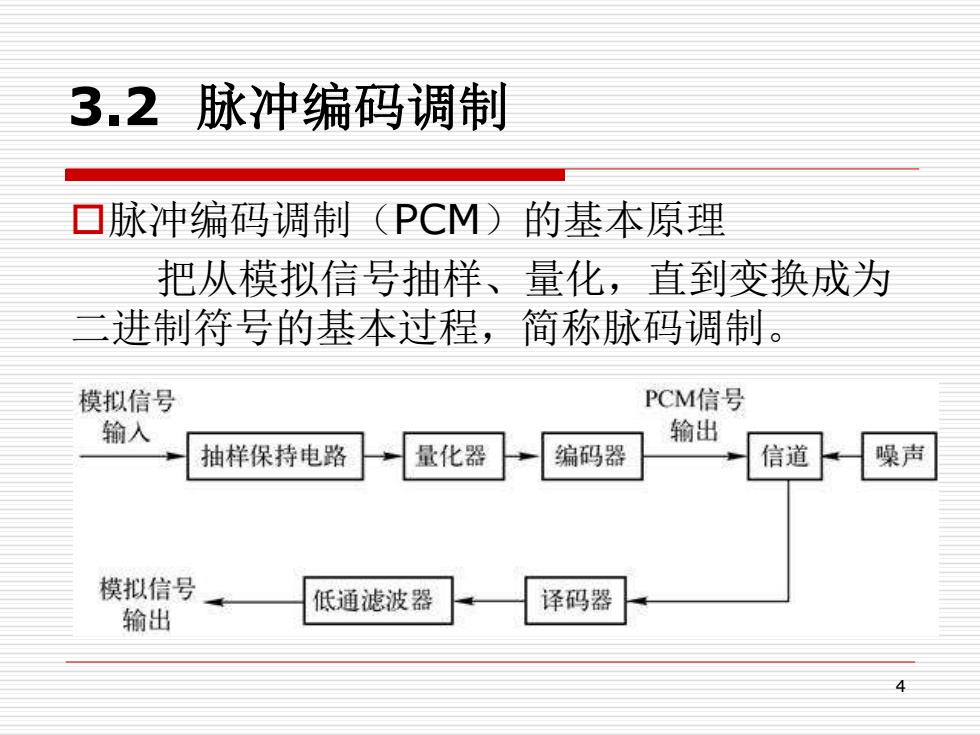
3.2脉冲编码调制 ▣脉冲编码调制(PCM)的基本原理 把从模拟信号抽样、量化,直到变换成为 进制符号的基本过程,简称脉码调制。 模拟信号 PCM信号 输入 输出 抽样保持电路 量化器 编码器 信道 噪声 模拟信号 低通滤波器 译码器 输出
4 3.2 脉冲编码调制 脉冲编码调制(PCM)的基本原理 把从模拟信号抽样、量化,直到变换成为 二进制符号的基本过程,简称脉码调制

3.2.1抽样与抽样定理 低通信号抽样定理 一个频带限制在0到财以内的低通信号x(), 如果以∫≥f的抽样速率进行均匀抽样, 则x()可以有抽样后的信号完全确定。 最小抽样速率∫=2f称为奈奎斯特速率, 最大抽样时间间隔1/2f称为奈奎斯特间隔。 5
5 低通信号抽样定理 3.2.1 抽样与抽样定理 一个频带限制在0到fH以内的低通信号x(t) , 如果以 fs 2fH 的抽样速率进行均匀抽样, 则x(t)可以有抽样后的信号完全确定。 最小抽样速率 f s =2fH 称为奈奎斯特速率, 最大抽样时间间隔 1/2fH 称为奈奎斯特间隔

理想抽样与信号的恢复 m() X m,() m,() 低通 m() 浅波器 G() (b) (a)· 6
6 理想抽样与信号的恢复
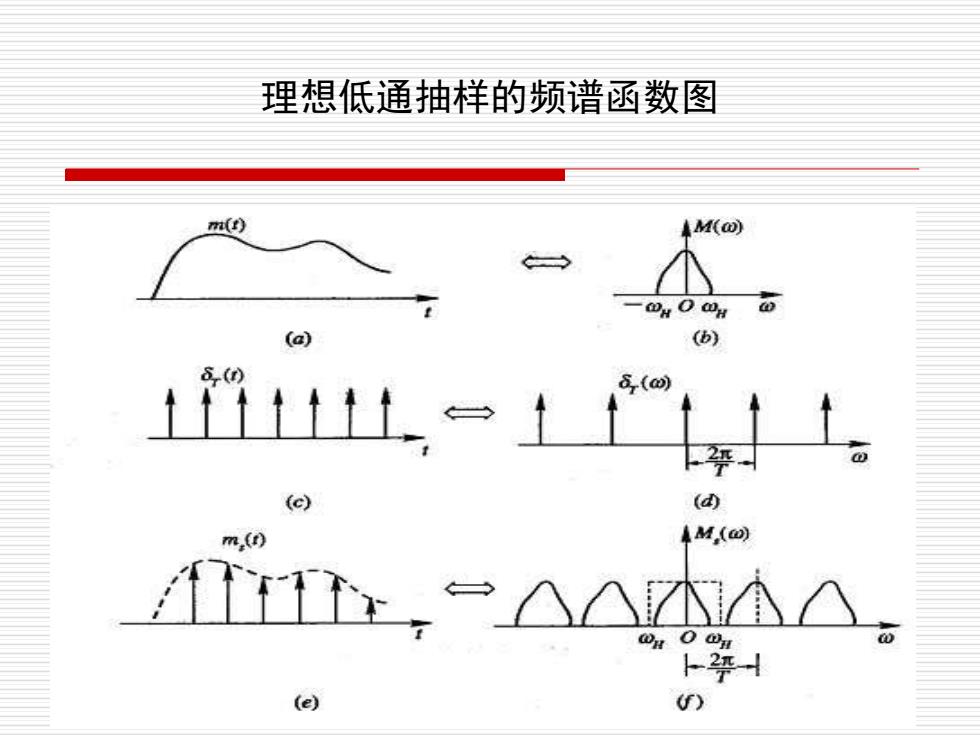
理想低通抽样的频谱函数图 () M(@) -OH O 0H (a) (b) 6() 6(a (c) (d) m,(n) 4M,(®) T (e) )
7 理想低通抽样的频谱函数图

理想低通抽样的证明 0=工1-n1)do280-a n=-00 cn=-00 m,0=m06,0=∑mnI,)8t-nI,) n=-00 Moj=u@)*ò(o Moao@ M(0-no,)
8 ( ) ( ) T s n t t nT =− = − =− = − n s s T n T ( ) 2 ( ) =− = = − n s T s nTs m (t) m(t) (t) m(nT ) (t ) ( )* ( ) 1 () T s s M T M = 理想低通抽样的证明 = − N=− s s M n T ( )* ( ) 1 = − N=− s s M n T ( ) 1
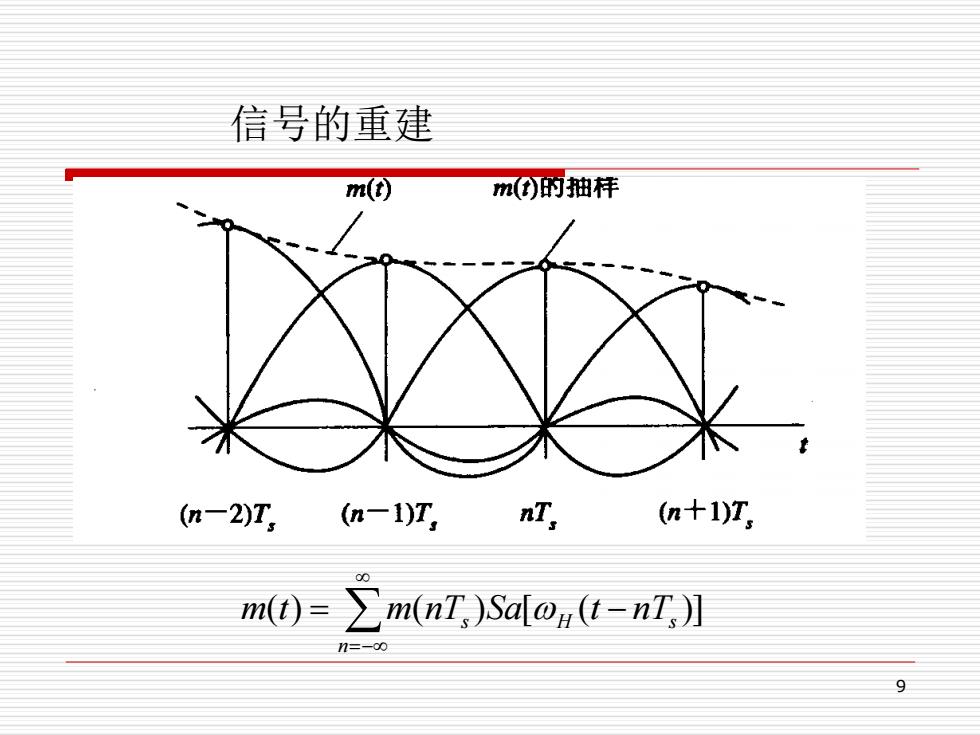
信号的重建 m(t) m)的抽样 (n-2)T, (n-1)T, nT, n十1)T, mt)=∑mnI,)Sao,t-nT,】 9
9 信号的重建 =− = − n s H nTs m(t) m(nT )Sa[ (t )]

带通信号抽样定理 一个带通信号m), 其频率限制在f与之间, 带宽为B= 如果抽样速率f2f/m, m是一个不超过f,/B的最大整数, 那么m()可完全由其抽样值确定。 10
10 带通信号抽样定理 一个带通信号m(t), 其频率限制在fL与fH之间, 带宽为 B=fH −fL, 如果抽样速率 f s=2fH /m, m是一个不超过 fH /B 的最大整数, 那么m(t)可完全由其抽样值确定

带通采样定理的两种情况 1、若最高频率为带宽的整数倍,即 fa=nB,则太=2B 2、若最高频率f=(nk)B不为B的整数倍 f,=(2fm1m)=2n+)Bn=2B1+ n 如对高频信号,>>k,则直接取两倍带宽 11
11 带通采样定理的两种情况 1、若最高频率fH为带宽的整数倍,即 fH =nB ,则 fS = 2B 2、若最高频率fH =(n +k)B不为B的整数倍 如对高频信号,n>>k,则直接取两倍带宽 (2 / ) 2( ) / 2 (1 ) n k f s = f H m = n + k B n = B +