
第6章正弦载波数字调制系统 6.1典型例题 【例6-1】设发送数字信息为011011100010,信息速率为103bit/s,载波频率为1.5 kHz: (1)分别画出2ASK、2PSK及2DPSK信号的波形: (2②)分别求2ASK、2PSK及2DPSK信号的谱零点带宽 思路因载频为信息速率的1.5倍,故一个码元间隔内有1.5个载波周期。信息代码与 2PSK及2DSK信号波形之间的关系分别是“异变同不变”及“1变0不变”。这三个信号的 谱零点带宽都等于信总速率的2倍。 解(1)2ASK、2PSK、2DPSK信号的波形如图6-30所示。 信息代 2sx形NMAAAAAAIAMAAA 2DPsx形AAAV 图6-30例6-1图 (2)2ASK、2PSK、2DPSK信号的谱零点带宽都为2000z。 【例6-2】设某2SX调制系统的码元传输速率为1000Bd,己调信号的载频为1000Hz 或2000Hz: (1)若发送数字信息为011010.试画出相应2SK信号波形: (2)若发送数字信息是等可能的,试画出它的功率谱密度草图 (3)试讨论这时的2FSx信号应选择怎样的解调器解调, 解(1)2SK信号波形如图6-31所示。 息代码,0 1 MMAMA 图6-31例6-2图1 (2)2FSK信号的功率谱密度草图如图6-32所示。 0102o000fH 图6-32例6-2图2 (3)不能采用非相干解调器解调此2℉SK信号。因为-f=1000z,与信息速率相等 两个2ASK信号的频谱(如图6-32虚线所示)重选。2FSK非相干解调器上、下两个支路的带 通滤波器不可能将两个2ASK信号分开。 可以用相干解调器解调此2S冰信号。因为此解调器上、下两个支路中的低通滤波器的 带宽可以小于码速率 差频f-可被低通滤波器滤掉,对抽样判决无影响。 也可以采用过零检测解调器解调此2SK信号。 还可以采用最佳接收机解调此2SK信号,因为频率为1000Hz和2000Hz的两个正弦 信号是正交的
1 第 6 章 正弦载波数字调制系统 6.1 典 型 例 题 【例 6-1】 设发送数字信息为 011011100010,信息速率为 103 bit/s,载波频率为 1.5 kHz: (1) 分别画出 2ASK、2PSK 及 2DPSK 信号的波形; (2) 分别求 2ASK、2PSK 及 2DPSK 信号的谱零点带宽。 思路 因载频为信息速率的 1.5 倍,故一个码元间隔内有 1.5 个载波周期。信息代码与 2PSK 及 2DPSK 信号波形之间的关系分别是“异变同不变”及“1 变 0 不变”。这三个信号的 谱零点带宽都等于信息速率的 2 倍。 解 (1) 2ASK、2PSK、2DPSK 信号的波形如图 6-30 所示。 图 6-30 例 6-1 图 (2) 2ASK、2PSK、2DPSK 信号的谱零点带宽都为 2000 Hz。 【例 6-2】 设某 2FSK 调制系统的码元传输速率为 1000 Bd,已调信号的载频为 1000 Hz 或 2000 Hz: (1) 若发送数字信息为 011010,试画出相应 2FSK 信号波形; (2) 若发送数字信息是等可能的,试画出它的功率谱密度草图; (3) 试讨论这时的 2FSK 信号应选择怎样的解调器解调。 解 (1) 2FSK 信号波形如图 6-31 所示。 图 6-31 例 6-2 图 1 (2) 2FSK 信号的功率谱密度草图如图 6-32 所示。 图 6-32 例 6-2 图 2 (3) 不能采用非相干解调器解调此 2FSK 信号。因为 f2-f1=1000 Hz,与信息速率相等, 两个 2ASK 信号的频谱(如图 6-32 虚线所示)重迭。2FSK 非相干解调器上、下两个支路的带 通滤波器不可能将两个 2ASK 信号分开。 可以用相干解调器解调此 2FSK 信号。因为此解调器上、下两个支路中的低通滤波器的 带宽可以小于码速率,差频 f2-f1 可被低通滤波器滤掉,对抽样判决无影响。 也可以采用过零检测解调器解调此 2FSK 信号。 还可以采用最佳接收机解调此 2FSK 信号,因为频率为 1000 Hz 和 2000 Hz 的两个正弦 信号是正交的

【例6-3】设发送数字信息序列为01011000110100,分别画出相应的4PSK及4DPSK 信号的所有可能波形 思路图6-17表示的双比特码元与相位中:的关系为B方式,还有一种A方式,如表 6-5所示。通常用A方式画4PSK的波形图,并且不考虑式(6-7)中Φ:前的负号,而表6-2 则是画4DSK信号波形的依据。本题没给出载波频率及信息速率,画波形时可设在一个双比 特码元内有一个载被周期。 表6-5双比特码元与4PS邻信号相位关系 双比特码元 4PSK信号相位中: a b A方式 B方式 0 0 0* 225° 0 90 315 1 1 180° 45° 0 1 270° 135° 解4PSR信号及4DPSK信号的所有可能波形如图6-33所示 信息代码 4PSK波形 4DPSK波形 NAUAAAN 图6-33例6-3图 【例6-4】设发送数字信息序列为1000001,试画出MSX信号的相位路径图。若码元 速率为1000Bd,载频为3000z,试画出MSX信号的波形。 解 1.=3000Hz f=f.+R=3250形 f=f。-R=2750z 可见,传1码时,一个码元内有3个载波周期:传0码时,一个码元内有2个载波周期。 MS的相位路径图及波形图分别如图6-34(a)、()所示
2 【例 6-3】 设发送数字信息序列为 01011000110100,分别画出相应的 4PSK 及 4DPSK 信号的所有可能波形。 思路 图 6-17 表示的双比特码元与相位φk 的关系为 B 方式,还有一种 A 方式,如表 6-5 所示。通常用 A 方式画 4PSK 的波形图,并且不考虑式(6-7)中φk 前的负号,而表 6-2 则是画 4DPSK 信号波形的依据。本题没给出载波频率及信息速率,画波形时可设在一个双比 特码元内有一个载波周期。 表 6-5 双比特码元与 4PSK 信号相位关系 双比特码元 4PSK 信号相位ψk a b A 方式 B 方式 0 0 0° 225° 1 0 90° 315° 1 1 180° 45° 0 1 270° 135° 解 4PSK 信号及 4DPSK 信号的所有可能波形如图 6-33 所示。 图 6-33 例 6-3 图 【例 6-4】 设发送数字信息序列为 1000001,试画出 MSK 信号的相位路径图。若码元 速率为 1000 Bd,载频为 3000 Hz,试画出 MSK 信号的波形。 解 fc=3000 Hz f1=fc+ 4 1 Rb=3250 Hz f2=fc-Rb=2750 Hz 可见,传 1 码时,一个码元内有 3 4 1 个载波周期;传 0 码时,一个码元内有 2 4 3 个载波周期。 MSK 的相位路径图及波形图分别如图 6-34(a)、(b)所示

z 图6-34例6-4图 【例6-5】假设在2DPSK系统中,载波频率为2400Hz,码元速率为1200Bd,己知相 对码序列为1100010111: (1)试画出2DPSK信号波形: (2)若采用茅分相干解调法接收该信号,试画出解调系统方框图及各点波形: )若采用相干解调法接收该信号,试画出解调系统方框图及各点波形: (④若发送信息符号0和1的概率分别为0.6和0.4,试式球2DPSK信号的功率谱密度 思路此题给的是相对码序列。对于绝对码是2DPSK的信号,对于相对码则是2PSX信 号。因此就相对码序列1100010111画出2PSK波形即是题目要求的2DPSK信号波形。 在画解调婴带通滤波器输出波形时不考虑调制信道的影响,否测无法画波形。 (④)中发送信息符号应理解为相对码符号。若为绝对码符号则还应由绝对码符号0码和 1码的概率求出相对码符号0码和1码的概率,这种转换关系目前在有关资料中还未见到 解(1)2DPSK信号波形如图6-35所示。 相对玛 Drx毛WAW 图6-35例6-5图1 (2)差分相干解调接收机原理方框图及各点波形如图6-36所示
3 图 6-34 例 6-4 图 【例 6-5】 假设在 2DPSK 系统中,载波频率为 2400 Hz,码元速率为 1200 Bd,已知相 对码序列为 1100010111: (1) 试画出 2DPSK 信号波形; (2) 若采用差分相干解调法接收该信号,试画出解调系统方框图及各点波形; (3) 若采用相干解调法接收该信号,试画出解调系统方框图及各点波形; (4) 若发送信息符号 0 和 1 的概率分别为 0.6 和 0.4,试求 2DPSK 信号的功率谱密度。 思路 此题给的是相对码序列。对于绝对码是 2DPSK 的信号,对于相对码则是 2PSK 信 号。因此就相对码序列 1100010111 画出 2PSK 波形即是题目要求的 2DPSK 信号波形。 在画解调器带通滤波器输出波形时不考虑调制信道的影响,否则无法画波形。 (4)中发送信息符号应理解为相对码符号。若为绝对码符号则还应由绝对码符号 0 码和 1 码的概率求出相对码符号 0 码和 1 码的概率,这种转换关系目前在有关资料中还未见到。 解 (1) 2DPSK 信号波形如图 6-35 所示。 图 6-35 例 6-5 图 1 (2) 差分相干解调接收机原理方框图及各点波形如图 6-36 所示
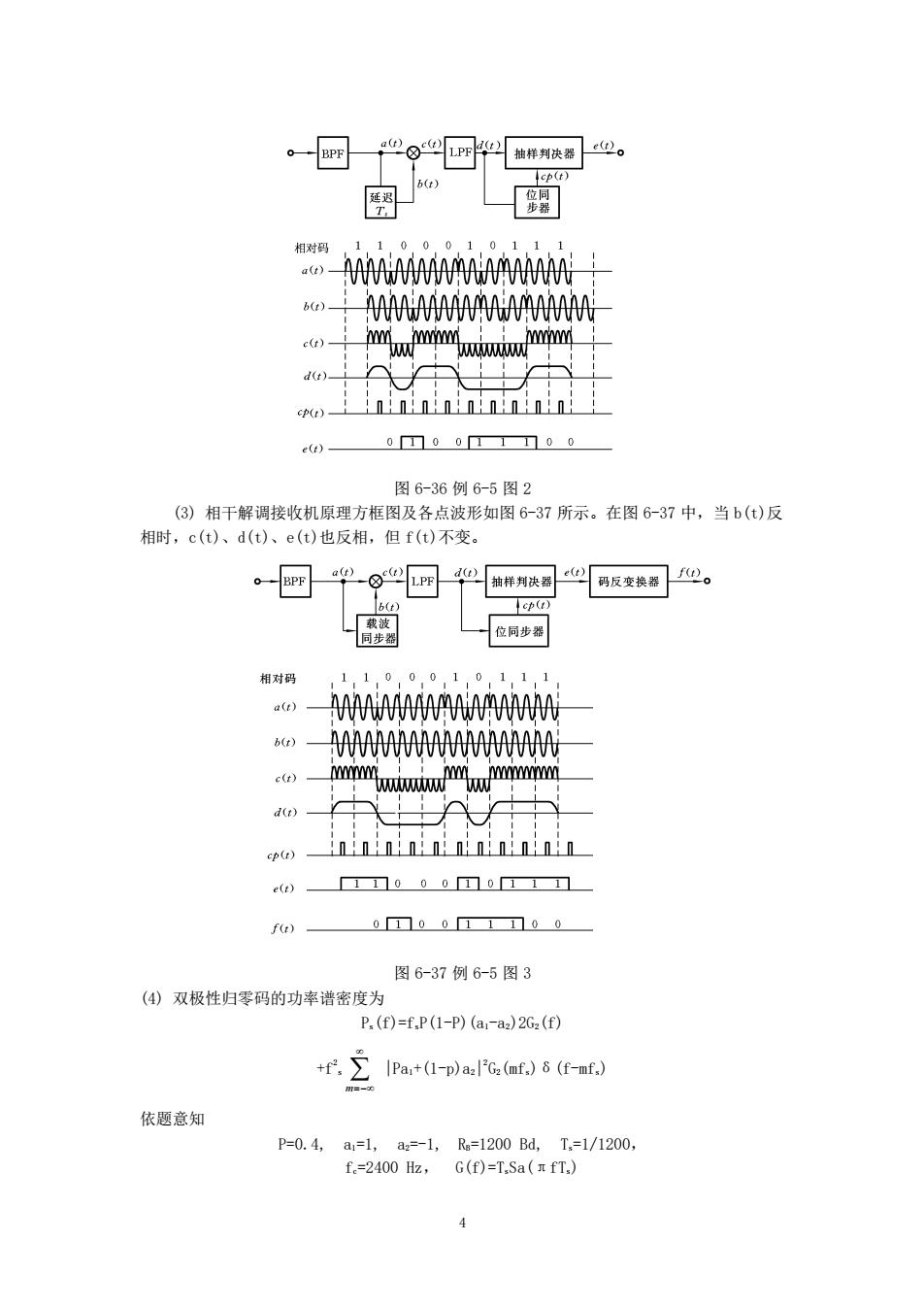
MMM AAAAAAAAAMAAMAAAA c(r) ep(r)- () 0□00I00 图6-36例6-5图2 (3)相干解调接收机原理方框图及各点波形如图6-37所示。在图6-37中,当b()反 相时, c(t)、d(t)、e(t)也反相,但f()不变。 。一PF吧一⑧巴P阳4吧椅样判决器码反变换器®。 儿一位同步器 相对码 1,1,0,0.0,1,0.1.1,1 a() NAW 60) A e() mrimimrmrmnmm ininininini nininininin f)- 01☐00111□00 图6-37例6-5图3 (4④)双极性归零码的功率谱密度为 P,(f)=f,P(1-p)(a1-aa)2G2(f) +f,∑IPa+(1-p)alG(f,)8(f-uf】 依题意知 P=0.4,a=1,a=-1,R=1200Bd,T.=1/1200, f.=2400 Hz,G(f)=T.Sa(x fT.) 4
4 图 6-36 例 6-5 图 2 (3) 相干解调接收机原理方框图及各点波形如图 6-37 所示。在图 6-37 中,当 b(t)反 相时,c(t)、d(t)、e(t)也反相,但 f(t)不变。 图 6-37 例 6-5 图 3 (4) 双极性归零码的功率谱密度为 Ps(f)=fsP(1-P)(a1-a2)2G2(f) +f2 s m=− |Pa1+(1-p)a2| 2 G2(mfs)δ(f-mfs) 依题意知 P=0.4, a1=1, a2=-1, RB=1200 Bd, Ts=1/1200, fc=2400 Hz, G(f)=TsSa(πfTs)
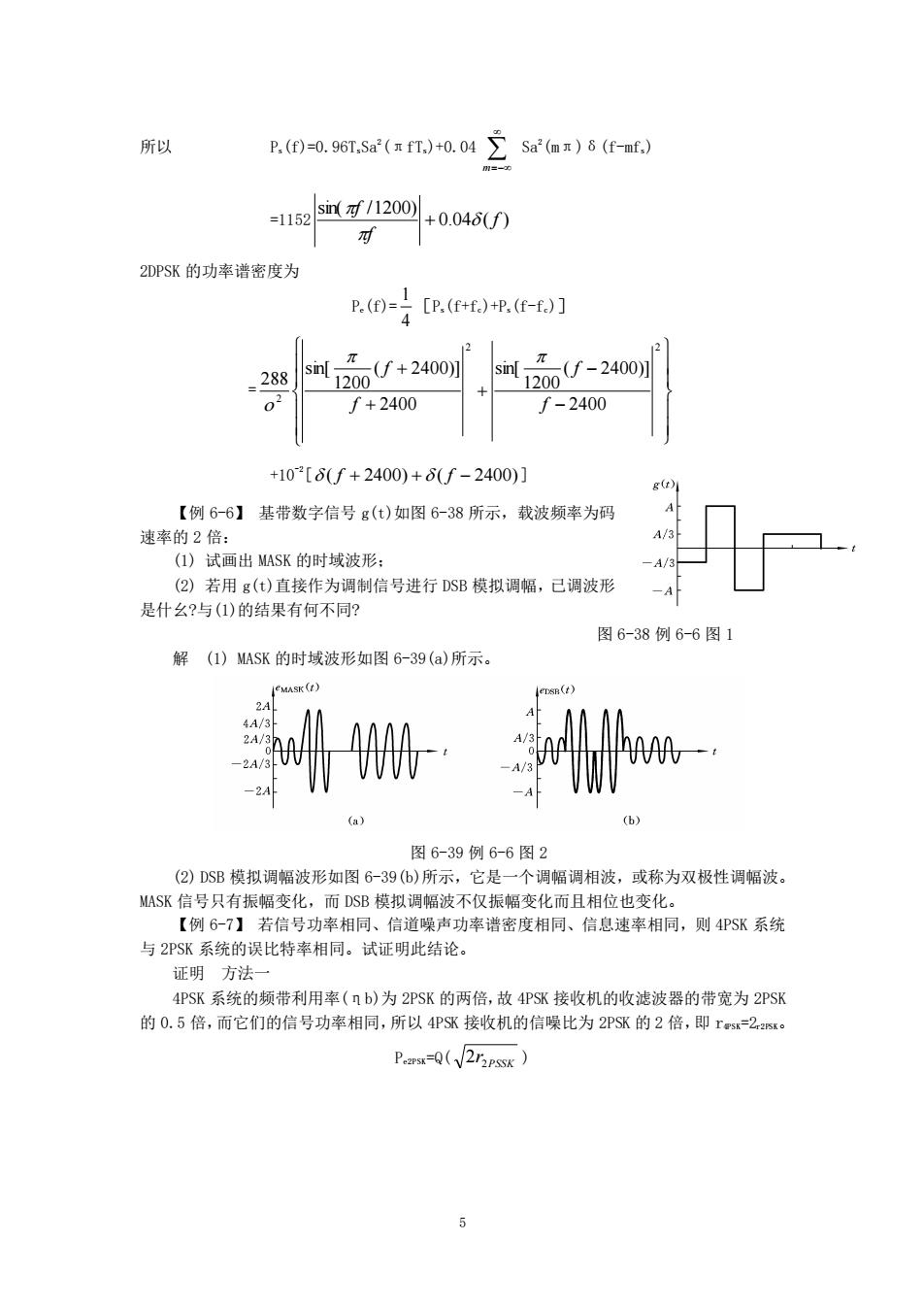
所以 P.(f)=0.96T.Sa(rfT)+0.04Sa(m)8(f-mf) 1152m/200+004 2DPSK的功率谱密度为 Rm-号RER-] 2 288 sm200/+2400列 -240 f+2400 + f-2400 +10[6(f+2400)+6(f-2400)] 【例66】基带数字信号g(t)如图6-38所示,载波频率为码 速率的2倍: A/3 O)试画出MASK的时域波形: (2)若用g(t)直接作为调制信号进行DSB模拟调幅,已调波形 A 是什么?与(1)的结果有何不同? 图6-38例6-6图1 解(1)MASR的时域波形如图6-39(a)所示。 /FMA5K(t》 sn() 2A -2A 图6-39例6-6图2 (2)DSB模拟调幅波形如图6-39(6)所示,它是一个调幅调相波,或称为双极性调幅波。 MASK信号只有振幅变化,而DSB模拟调幅波不仅振幅变化而且相位也变化。 【例6-7】若信号功率相同、信道噪声功率谱密度相同、信息速率相同,则4PSK系统 与2PSR系统的误比特率相同。试证明此结论。 证明方法 4PSR系统的频带利用率(nb)为2PSK的两倍,故4PSX接收机的收滤波器的带宽为2PSK 的0.5倍,而它们的信号功率相同,所以4PSX接收机的信噪比为2PS的2倍,即rs=2。 P.=(
5 所以 Ps(f)=0.96TsSa2 (πfTs)+0.04 m=− Sa2 (mπ)δ(f-mfs) =1152 0.04 ( ) sin( /1200) f f f + 2DPSK 的功率谱密度为 Pe(f)= 4 1 [Ps(f+fc)+Ps(f-fc)] = − − + + + 2 2 2 2400 ( 2400)] 1200 sin[ 2400 ( 2400)] 1200 sin[ 288 f f f f +10-2 [ ( f + 2400) + ( f − 2400) ] 【例 6-6】 基带数字信号 g(t)如图 6-38 所示,载波频率为码 速率的 2 倍: (1) 试画出 MASK 的时域波形; (2) 若用 g(t)直接作为调制信号进行 DSB 模拟调幅,已调波形 是什幺?与(1)的结果有何不同? 图 6-38 例 6-6 图 1 解 (1) MASK 的时域波形如图 6-39(a)所示。 图 6-39 例 6-6 图 2 (2) DSB 模拟调幅波形如图 6-39(b)所示,它是一个调幅调相波,或称为双极性调幅波。 MASK 信号只有振幅变化,而 DSB 模拟调幅波不仅振幅变化而且相位也变化。 【例 6-7】 若信号功率相同、信道噪声功率谱密度相同、信息速率相同,则 4PSK 系统 与 2PSK 系统的误比特率相同。试证明此结论。 证明 方法一 4PSK 系统的频带利用率(ηb)为 2PSK 的两倍,故 4PSK 接收机的收滤波器的带宽为 2PSK 的 0.5 倍,而它们的信号功率相同,所以 4PSK 接收机的信噪比为 2PSK 的 2 倍,即 r4PSK=2r2PSK。 Pe2PSK=Q( PSSK r2 2 )

neo胃}w1-a Paurss-Pars() 方法 PSR解调器由两个正交2PSK解调器构成,每个正交2PSK解调器的误码率即为4PSK解 调器的误比特率。 设信号功率为S,单边噪声谱密度为,2PSK系统的收滤波器带宽为B。则2PSK接收 机的信噪比为S/Bn。4PK接收机两个正交解调器的信号功率为总功率的一半即S'=0.5S, 噪声功率为=0.5B,故信噪比为SNS/B 。可见 4PS接收机的两个正交解 调器的信噪比与25X接收机的相同。由此可见,4P5系统的误比特率与2PSK的相等 【例6-8】若相干2PSX和差分相干2DPSX系统的输入噪声功率相同,系统工作在大信 噪比条件下,试计算它们达到同样误码率所需的相对功率电平(k=s/红):若要求输入信 噪比一样,则系统性能相对比(P/P)为多大。并讨论以上结果。 解()在大信噪比下,可以用近似公式计算2SK系统的误码率,即 P.m-()2 -e-PsK 差分相干2DPSK系统的误码率为 Parsx-P. 得 1 解此方程,得 k=rs PpSK 2hpsK (2)当输入信噪比相同时 由此得 讨论①说明:要达到相同的误码率,差分相干2DPSX系统所需信噪比大于相干2PSK 系统。 ②说明:当信噪比相同时,差分相干2DSR系统的误码率大于相干2PSK系统。 6
6 Pe4PSK=2Q ( 2 ) 2 1 2 ( ) 2 (2 ) 4 2 sin 4 4 2 4 4 2 4 b PSK e PSK PSK PSK PSK PSK P P Q r r Q r Q r = = = = b PSK e PSK PSK Pb PSK P P Q r 4 4 2 2 ( 2 ) 2 1 = = = 方法二 4PSK 解调器由两个正交 2PSK 解调器构成,每个正交 2PSK 解调器的误码率即为 4PSK 解 调器的误比特率。 设信号功率为 S,单边噪声谱密度为 n0,2PSK 系统的收滤波器带宽为 Bc。则 2PSK 接收 机的信噪比为 S/Bcn0。4PSK 接收机两个正交解调器的信号功率为总功率的一半即 S′=0.5S, 噪声功率为 N′=0.5Bcn0,故信噪比为 S′/N′=S/(Bcn0)。可见,4PSK 接收机的两个正交解 调器的信噪比与 2PSK 接收机的相同。由此可见,4PSK 系统的误比特率与 2PSK 的相等。 【例 6-8】 若相干 2PSK 和差分相干 2DPSK 系统的输入噪声功率相同,系统工作在大信 噪比条件下,试计算它们达到同样误码率所需的相对功率电平(k=rDPSK/rPSK);若要求输入信 噪比一样,则系统性能相对比(PePSK/PeDPSK)为多大。并讨论以上结果。 解 (1) 在大信噪比下,可以用近似公式计算 2PSK 系统的误码率,即 Pe2PSK= PSK r PSK e PSK e r Q r 2 2 2 2 1 ( 2 ) − 差分相干 2DPSK 系统的误码率为 DPSK r e DPSK P e 2 2 1 2 − = 令 Pe2PSK=Pe2DPSK 得 PSK DPSK r r PSSK e e r 2 2 2 1 2 1 2 − − = 解此方程,得 1 1 2 ln( ) 2 2 2 2 = = + PSK PSSK PSK DPSK r r r r k (2) 当输入信噪比相同时 Pe2PSK= r e r − 2 1 Pe2DPSK= 1 1 r 由此得 1 1 2 2 = P r P e DPSK e PSSK 讨论 ① 说明:要达到相同的误码率,差分相干 2DPSK 系统所需信噪比大于相干 2PSK 系统。 ② 说明:当信噪比相同时,差分相干 2DPSK 系统的误码率大于相干 2PSK 系统

【例6-9】试证明在大信噪比条件下,当信噪比相同时,相干2DSR系统的误码率是 相干2PSK系统的两倍。 证明2DPSK相干解调原理方框图如图6-40所示 相对码b或b的误码率即为2PS 系统的误码率,绝对码a的误码率即为2DPS系统的误码率。只有当b和b1中仅有一个发 生错误时,a才错,即 Pa =Pah (1-Pa -1)+pch-1(1-P) P.=2P(1-P.) P2DSK=2PS 水台8K帮高对 ⊙地对码a 图6-40例6-8图 【例6-10】己知码元传输速率R=103Bd,接收机输入噪声的双边功率谱密度/2=10 W/z,今要求误码率P.=10,试分别计算出相干0OK、非相干2FSK、差分相干2DPSR以及 2PSK等系统所要求的输入信号功率。 思路只要求出接收机带滤波器输出噪声功率就可以由误码率公式很到P=10的信 噪比,从而得出信号功率。 题中己给出噪声的功率谱密度,但没有给定收滤波器带宽。 6.1节可知,OOK(即2ASK)系统、2DPSK系统、2PSK系统都是线性系统,它们的频带利用号 为1/(1+a)(Bd/Hz)。收滤波器为升余弦滚降特性,其等效噪声带宽为1000Hz,可用此 效带宽求噪声功率。收滤波器的频率特性也可以是带宽为2000z的理想矩形,此时系统所 要求的输入信号功率最大,我们以此为标准进行计算.非相干2FSK解调器由两个非相干2SX 解调器构成,两个收滤波器的带宽与线性系统样。 解设00R、差分相干2DPSR以及2PSX的收滤波器的频率特性是带宽为2000z的理 想矩形,非相干2FSK接收机的两个支路带通滤波器的频率特性也是带宽为2000Hz的理想 矩形。在此条件下,接收机输入噪声功率为 N=(10×2×2000)W=4×107W (1)相于00K(2ASK)系统 由误码率公式 d同r S=(36.13×4×10)=1.45×105W (2)非相干2FSK系统 由误码率公式 r=21.6 S=(21.6×4×10)W=0.86×105W (3)差分相干2DPSR系统
7 【例 6-9】 试证明在大信噪比条件下,当信噪比相同时,相干 2DPSK 系统的误码率是 相干 2PSK 系统的两倍。 证明 2DPSK 相干解调原理方框图如图 6-40 所示。相对码 bk 或 bk-1 的误码率即为 2PSK 系统的误码率,绝对码 ak 的误码率即为 2DPSK 系统的误码率。只有当 bk和 bk-1 中仅有一个发 生错误时,ak 才错,即 k Pea = k peb (1- k peb -1)+ k peb -1(1- k peb ) 所以 Pe2DPSK=2Pe2PSK(1-Pe2PSK) 当 r>>1 时,Pe2PSK<<1,故 Pe2DPSK=2Pe2PSK 图 6-40 例 6-8 图 【例 6-10】已知码元传输速率 RB=103 Bd,接收机输入噪声的双边功率谱密度 n0/2=10-10 W/Hz,今要求误码率 Pe=10-5,试分别计算出相干 OOK、非相干 2FSK、差分相干 2DPSK 以及 2PSK 等系统所要求的输入信号功率。 思路 只要求出接收机带通滤波器输出噪声功率就可以由误码率公式得到 Pe=10-5 的信 噪比,从而得出信号功率。题中已给出噪声的功率谱密度,但没有给定收滤波器带宽。由 6.1 节可知,OOK(即 2ASK)系统、2DPSK 系统、2PSK 系统都是线性系统,它们的频带利用率 为 1/(1+α)(Bd/Hz)。收滤波器为升余弦滚降特性,其等效噪声带宽为 1000 Hz,可用此等 效带宽求噪声功率。收滤波器的频率特性也可以是带宽为 2000 Hz 的理想矩形,此时系统所 要求的输入信号功率最大,我们以此为标准进行计算。非相干 2FSK 解调器由两个非相干 2ASK 解调器构成,两个收滤波器的带宽与线性系统一样。 解 设 OOK、差分相干 2DPSK 以及 2PSK 的收滤波器的频率特性是带宽为 2000 Hz 的理 想矩形,非相干 2FSK 接收机的两个支路带通滤波器的频率特性也是带宽为 2000 Hz 的理想 矩形。在此条件下,接收机输入噪声功率为 N=(10-10×2×2000) W=4×10-7 W (1) 相干 OOK(2ASK)系统 由误码率公式 Pe= 2 r Q =10-5 得 r= N S =36.13 S=(36.13×4×10-7 ) W=1.45×10-5 W (2) 非相干 2FSK 系统 由误码率公式 Pe= 2 1 2 5 10− = r e 得 r=21.6 S=(21.6×4×10-7 ) W=0.86×10-5 W (3) 差分相干 2DPSK 系统

由误码率公式 P.-e=10 r=10.8 S=(10.8×4×10)W=0.43×105W (4)相干2PSK系统 由误码率公式 P.=Q(V2)=10 r=9.03 S-=(9.03×4×10)=0.36×105W 【例6-11】己知2FSX信号的两个频率f,-980Hz,f2=2180Hz,码元速率R=300Bd, (②)非相干解调时的误比特率: (③)相干解调时的误比特率。 解(1)2SK信号的谱零点带宽为 B.-lfa B:=2Rg =600 Hz 信道带宽为3000z,是接收机带通滤波器带宽的5倍,所以接收机带通滤波器输出信 噪比是信道输出信噪比的5倍。当信道输出信噪比为6B时,带通滤波器输出信噪比为 r=5X102=5×4=20 2SR非相干接收机的误比特率为 R=ene2.27x10 (3)同理可得2SR相干接收机的误比特率为 P-Q(VF)=Q(20)-Q(4.47)=3.93×10 【例6-12】己知发送载波幅度A=10V,在4kz带宽的电话信道中分别利用2ASK、 2FSK及2PSK系统进行传输,信道衰减为1dB/km,=10W/z,若采用相干解调,试求解 以下问恩: (1)误比特率为10时冬种传输方式分别传多少公里? (②)若2ASK所用载波幅度AASK=20V,并分别是2FS和2PS的1.4倍和2倍,重倒 思路信道带宽为4k2,为充分利用信道,信道中传输的信号带宽也应该为4kz。 设2ASK及2PSK接收机带通滤波器为4kz带宽的理想矩形、2FSK接收机带通滤波器为2kz 带宽的理想矩形,则可求出接收机的噪声功率,再由各种传输方式的误码率公式求接收机信 号幅度。最后,根据信道衰减及发送载波幅度求传输 离。 解()①2ASR系统 2ASK接收机噪声功率 N=nXB2s=10×4000W=4X103T 2ASR系统的误比特率
8 由误码率公式 Pe= 5 10 2 1 − − = r e 得 r=10.8 S=(10.8×4×10-7 ) W=0.43×10-5 W (4) 相干 2PSK 系统 由误码率公式 Pe=Q( 2r )=10-5 得 r=9.03 S=(9.03×4×10-7 ) W=0.36×10-5 W 【例 6-11】 已知 2FSK 信号的两个频率 f1=980 Hz,f2=2180 Hz,码元速率 RB=300 Bd, 信道有效带宽为 3000 Hz,信道输出端的信噪比为 6 dB。试求: (1) 2FSK 信号的谱零点带宽; (2) 非相干解调时的误比特率; (3) 相干解调时的误比特率。 解 (1) 2FSK 信号的谱零点带宽为 Bs=|f2-f1|+2Rb=(2180-980+2×300) Hz=1800 Hz (2) 设非相干接收机中带通滤波器 BPF1 和 BPF2(见图 6-7)宽度为 BF = 2RB = 600 Hz 信道带宽为 3000 Hz,是接收机带通滤波器带宽的 5 倍,所以接收机带通滤波器输出信 噪比是信道输出信噪比的 5 倍。当信道输出信噪比为 6 dB 时,带通滤波器输出信噪比为 r=5×100.6=5×4=20 2FSK 非相干接收机的误比特率为 Pb= 2 1 e -r/2 = 2 1 e -10=2.27×10-5 (3) 同理可得 2FSK 相干接收机的误比特率为 Pb=Q( r )=Q( 20 )=Q(4.47)=3.93×10-6 【例 6-12】 已知发送载波幅度 A=10 V,在 4 kHz 带宽的电话信道中分别利用 2ASK、 2FSK 及 2PSK 系统进行传输,信道衰减为 1 dB/km,n0=10-8 W/Hz,若采用相干解调,试求解 以下问题: (1) 误比特率为 10-5 时,各种传输方式分别传多少公里? (2) 若 2ASK 所用载波幅度 AASK=20 V,并分别是 2FSK 和 2PSK 的 1.4 倍和 2 倍,重做 (1)。 思路 信道带宽为 4 kHz,为充分利用信道,信道中传输的信号带宽也应该为 4 kHz。 设 2ASK 及 2PSK 接收机带通滤波器为 4 kHz 带宽的理想矩形、2FSK 接收机带通滤波器为 2 kHz 带宽的理想矩形,则可求出接收机的噪声功率,再由各种传输方式的误码率公式求接收机信 号幅度。最后,根据信道衰减及发送载波幅度求传输距离。 解 (1) ① 2ASK 系统 2ASK 接收机噪声功率 N=n0×B2ASK=10-8×4000 W=4×10-5 W 2ASK 系统的误比特率

R母o 由此得 r=36.13 信号功率为 S=36.13×4×103W=144.5×103W 信号幅度为 a=√25=V2×144.5×105V=5.38×102y 由10V衰减到5.38×102V,衰减的分贝(B)数为 [201g(10/(5.38×10)]dD=45.4dB 故2ASK信号传输距离为45.4公里。 ②2FSK系统 2FSK接收机噪声功 N=×B2=10×2000W=2X105T 2PSK系统误比特率 R=Q(V2)=10 由此相 r=18.07 信号功率为 S=18.07×2×105W=36.14×105W 信号幅度为 a=V2s=V2×36.14×105V=2.69×10y 衰减量为 L201g(10/(2.69×10))]dB=51.4dB 故2SK信号传输距离为5L.4公里。 ③2PSK系统 2PSR接收机噪声功率 N=×Bw=10X4000W=4×105W 2PSK系统误比特率 R=Q(2r)=10 由此得 r=9.035 信号功率为 S=9.035×4×103=36.14×107 可见2PSK信号传输距离与2FSK的相同,为51.4公里。 (2)当2ASK载波幅度为20V时,发送功率增大了6dB,故传输距离可由45.4公里增 大到51.4公里. 由2ASX系统和2PSX系统的误比特率公式可知,当噪声功率相等、误比特率相等时,2PSK 接收机的信号功率可以比2ASK的小6B。故在本题给定的条件下,2PSX系统的传输距离 2ASK的相同,为51.4公里。 由2ASK系统和2FSX系统的误比特率公式可知,当2FSX系统的噪声功率为2ASX的0.5 倍、误比特率相等时,2FSK的信号功率可以比2SK的小6dB。本题所给的2FSR发射功率
9 Pb=Q 2 r =10-5 由此得 r=36.13 信号功率为 S=36.13×4×10-5 W=144.5×10-5 W 信号幅度为 a= 2S = -5 2144.510 V=5.38×10-2 V 由 10 V 衰减到 5.38×10-2 V,衰减的分贝(dB)数为 [20lg(10/(5.38×10-2 ))] dB=45.4 dB 故 2ASK 信号传输距离为 45.4 公里。 ② 2FSK 系统 2FSK 接收机噪声功率 N=n0×B2FSK=10-8×2000 W=2×10-5 W 2PSK 系统误比特率 Pb=Q( 2r) =10-5 由此得 r=18.07 信号功率为 S=18.07×2×10-5 W=36.14×10-5 W 信号幅度为 a= 2s = -5 236.1410 V=2.69×10-2 V 衰减量为 [20lg(10/(2.69×10-2 ))] dB=51.4 dB 故 2FSK 信号传输距离为 51.4 公里。 ③ 2PSK 系统 2PSK 接收机噪声功率 N=n0×B2PSK=10-8×4000 W=4×10-5 W 2PSK 系统误比特率 Pb=Q( 2r) =10-5 由此得 r=9.035 信号功率为 S=9.035×4×10-5 W=36.14×10-5 W 可见 2PSK 信号传输距离与 2FSK 的相同,为 51.4 公里。 (2) 当 2ASK 载波幅度为 20 V 时,发送功率增大了 6 dB,故传输距离可由 45.4 公里增 大到 51.4 公里。 由 2ASK 系统和 2PSK 系统的误比特率公式可知,当噪声功率相等、误比特率相等时,2PSK 接收机的信号功率可以比 2ASK 的小 6 dB。故在本题给定的条件下,2PSK 系统的传输距离与 2ASK 的相同,为 51.4 公里。 由 2ASK 系统和 2FSK 系统的误比特率公式可知,当 2FSK 系统的噪声功率为 2ASK 的 0.5 倍、误比特率相等时,2FSK 的信号功率可以比 2ASK 的小 6 dB。本题所给的 2FSK 发射功率

比2ASK的小3dB,故可以比2ASK传输距离远3公里,即2FSR系统的传输距离为54.4公 里 【例6-13】对最高频率为6Mz的模拟信号进行线性O编码,量化电平数为M8 编码信号先通过α=0.2的升余弦滚降滤波器处理,再对载波进行调制: (1)采用2PSK调制,求占用信道带宽和频带利用率: (②)将调制方式改为8PSK,求占用信道带宽和频带利用率。 解()模拟信号的最高频率为,将取样频率取为f,=2。当量化电平数为时 编码位数N10g,8 3。PCM编码后的信息速率为 R=2faN=2×6X10×3bit/s-=36Mbit/s 二进制基带升余弦滚降信号带宽为 B1+0R+02×6L.6 用此信号与载波相乘得到的信号带宽即是占用信道带宽 B=2B,=43.2H 频带利用率为 36×10 .432x100.83ps/他 2PSR系统的频带利用率也可用下式计算: n1+a1+02bps/优0.83bps他 (2)8PSR系统的频带利用率为 .=logM/(1+a )=(log-8/(1+0.2))bps/Hz=2.5 bps/Hz 占用信道带宽 B.=R/n。=36/2.5MHz=14.41Hz 【例6-14】已知电话信道可用的信号传输频带为600~3000z,取载频为1800z, 试说明 (1)采用a=1升余弦滚隆基带信号时,0PSK调制可以传输2400bit/s据 ②)采用a=0.5升余弦滚降基带信号时,8SK调制可以传输4800bit/s数据 (3)画出(1)和(2)传输系统的频率特性草图 解(1)信道带宽为 B,=(3000-600)Hz=2400z a=1时QPSK系统的频带利用率 bps/Hz=1 bps/Hz 1+a 1+1 数据传输速率 R=B.n=2400x1 bit/s=2400 bit/s (2)a=0,5时8PSK系统的频带利用率 =0828 1+0.52ps/B 数据传输速率 R=B.·n=2400×2bit/s=4800bit/s
10 比 2ASK 的小 3 dB,故可以比 2ASK 传输距离远 3 公里,即 2FSK 系统的传输距离为 54.4 公 里。 【例 6-13】 对最高频率为 6 MHz 的模拟信号进行线性 PCM 编码,量化电平数为 M=8, 编码信号先通过α=0.2 的升余弦滚降滤波器处理,再对载波进行调制: (1) 采用 2PSK 调制,求占用信道带宽和频带利用率; (2) 将调制方式改为 8PSK,求占用信道带宽和频带利用率。 解 (1) 模拟信号的最高频率为 fH,将取样频率取为 fs=2fH。当量化电平数为 M=8 时, 编码位数 N=log28=3。PCM 编码后的信息速率为 Rb=2fHN=2×6×106×3 bit/s=36 Mbit/s 二进制基带升余弦滚降信号带宽为 Bs= Rb a 2 1+ = 2 1+ 0.2 ×36 MHz=21.6 MHz 用此信号与载波相乘得到的信号带宽即是占用信道带宽 Bc=2Bs=43.2 MHz 频带利用率为 ηb= 6 6 43.2 10 36 10 = c c B R =0.83 bps/Hz 2PSK 系统的频带利用率也可用下式计算: ηb= 1 0.2 1 1 1 + = + a bps/Hz=0.83 bps/Hz (2) 8PSK 系统的频带利用率为 ηb=log2M/(1+α)=(log28/(1+0.2)) bps/Hz=2.5 bps/Hz 占用信道带宽 Bc=Rb/ηb=36/2.5 MHz=14.4 MHz 【例 6-14】 已知电话信道可用的信号传输频带为 600~3000 Hz,取载频为 1800 Hz, 试说明: (1) 采用α=1 升余弦滚降基带信号时,QPSK 调制可以传输 2400 bit/s 数据; (2) 采用α=0.5 升余弦滚降基带信号时,8PSK 调制可以传输 4800 bit/s 数据; (3) 画出(1)和(2)传输系统的频率特性草图。 解 (1) 信道带宽为 Bc=(3000-600) Hz=2400 Hz α=1 时 QPSK 系统的频带利用率 ηb= 1 1 log 4 1 log 2 2 + = + a M bps/Hz=1 bps/Hz 数据传输速率 Rb=Bc·ηb=2400×1 bit/s=2400 bit/s (2) α=0.5 时 8PSK 系统的频带利用率 ηb= 1 0.5 log 2 8 + =2 bps/Hz 数据传输速率 Rb=Bc·ηb=2400×2 bit/s=4800 bit/s