
第11章同步原理 11.1典型例题 【例11-1】SSB相干解调方框图如图43所示,设载波同步器提取的相干载波与发端 载波的相位误差为中。 (1》求解调器输出信号m(t)的数学表达式和功密: (2)求解调器输出噪声。()的数学表达式和功率 解()设$5B为下边带信号,则相乘器输出为 [Bm0osau+ga0me小ma.+ =m+co(2o,1+w月+4i2o1+0-sa 低通滤波器输出为2m)0sy-m0)sn,)smy使解调输 出失真,解调输出的有用信号为 m.(m(cos 信号功率为 (co (2)设带通滤波器中心频率为“。,令△。=“。,相乘器输入的窄带白噪声为 n(t)coso,t-n(t)sinwot,低通滤波器输出噪声为 n(-()cos(A+)+n()si+w) 输出噪声功率为 N.()co (A(s() +n0n.0-sn2△o1+ =g0+cos2△n+zw1+801-cos2Aon+列1 因为n0=n(0,所以 【例11-2】己知单边带信号的表达式为 s(t)=m(t)cosw.t+m(t)sino.t 试证明不能采用如图11-4(a)所示的平方变换法提取载波。 证明方法 平方器输出信号为 (t)[m().t(]+((]co2w.um() (t)sin2w.t
1 第 11 章 同 步 原 理 11.1 典 型 例 题 【例 11-1】 SSB 相干解调方框图如图 4-3 所示,设载波同步器提取的相干载波与发端 载波的相位误差为φ。 (1) 求解调器输出信号 mo(t)的数学表达式和功率; (2) 求解调器输出噪声 no(t)的数学表达式和功率。 解 (1) 设 SSB 为下边带信号,则相乘器输出为 ˆ( )sin cos( ) 2 1 ( ) cos 2 1 + c + c c m t t m t t ˆ( )[sin( 2 ) sin ] 4 1 ( )[cos cos(2 )] 4 1 = m t + c t + + m t c t + − 低通滤波器输出为 ˆ( )sin 4 1 ˆ( )sin , 4 1 ( ) cos 4 1 m t − m t m t 使解调输 出失真,解调输出的有用信号为 ( ) cos 4 1 m (t) m t o = 信号功率为 S 2 2 0 ( ) cos 16 1 S = m t (2) 设带通滤波器中心频率为ω0,令Δω=ωc-ω0,相乘器输入的窄带白噪声为 nc(t)cosω0t-ns(t)sinω0t,低通滤波器输出噪声为 ( )sin( ) 2 1 ( ) cos( ) 2 1 no (t) = nc t t + + ns t t + 输出噪声功率为 ( ) sin ( ) 4 1 ( ) cos ( ) 4 1 2 2 2 2 No = nc t t + + ns t t + ( ) ( ) sin 2( ) 4 1 + ns t nc t t + ( )[1 cos 2( )] 8 1 ( )[1 cos 2( )] 8 1 2 2 = nc t + t + + ns t − t + 因为 ( ) ( ) 2 2 n t n t c = s ,所以 【例 11-2】 已知单边带信号的表达式为 s(t)=m(t)cosωct+ m ˆ (t)sinωct 试证明不能采用如图 11-4(a)所示的平方变换法提取载波。 证明 方法一 平方器输出信号为 s 2 (t)=[m(t)cosωct+ 2 m ˆ (t)sinωct] 2 = 2 1 [m 2 (t)+ m ˆ (t)]+12[m 2 (t)- 2 m ˆ (t)]cos2wct+m(t) (t)sin2ωct
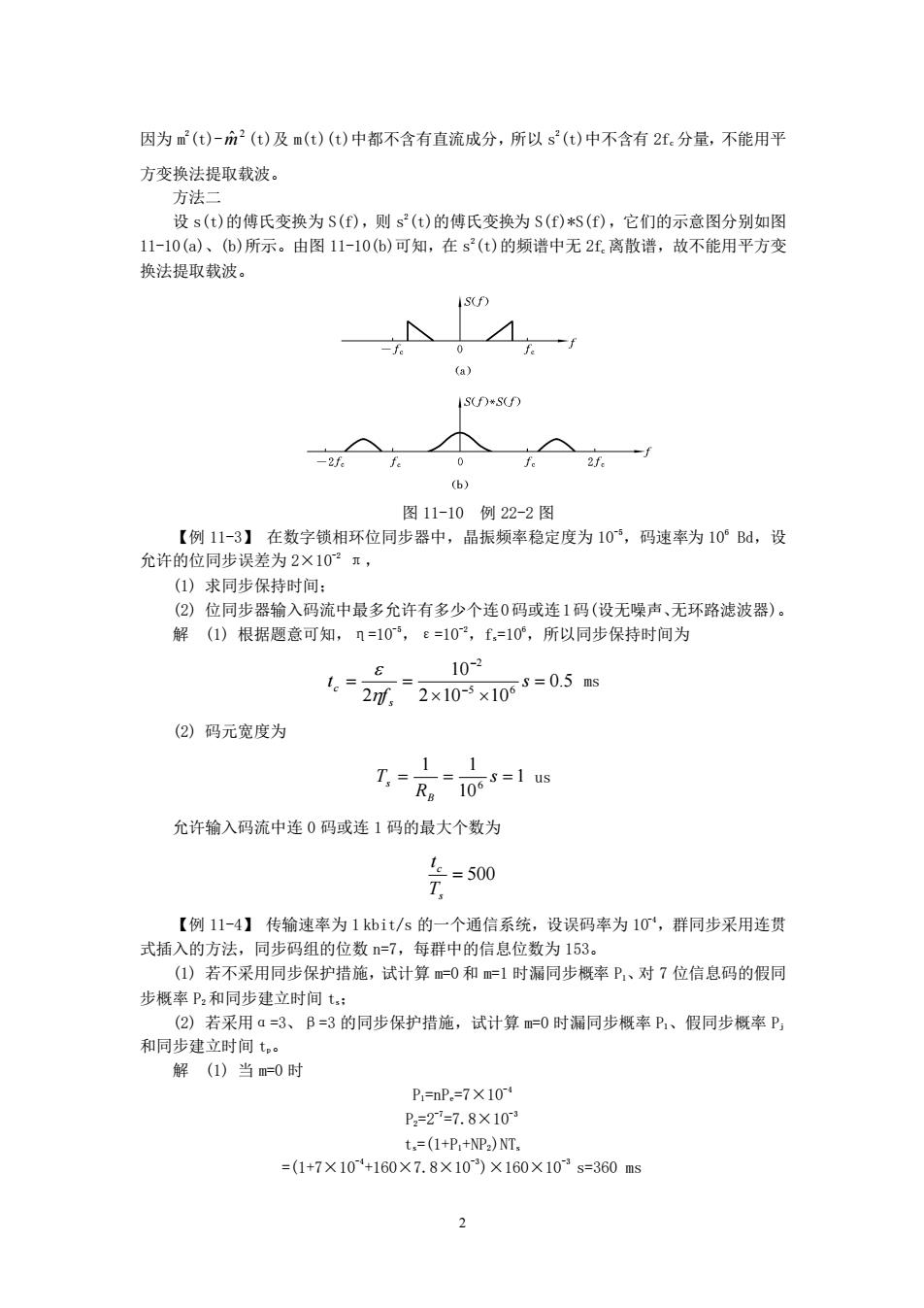
因为m()-m(t)及m(t)(t)中都不含有直流成分,所以s(t)中不含有2.分量,不能用平 方变换法提取载波。 方法二 设s(t)的傅氏变换为S(f),则s(t)的傅氏变换为S(E)5(f),它们的示意图分别如图 11-10(a)、6)所示。由图11-10(6)可知,在s(t)的频谱中无2f.离散谱,故不能用平方变 换法提取载波。 s( a susu 2一 b》 图11-10例22-2图 【例11-3】在数字锁相环位同步器中,晶振频率稳定度为103,码速率为10B,设 允许的位同步误差为2×10° (1)求同步保持时间: (②)位同步器输入码流中最多允许有多少个连0码或连1码(设无噪声、无环路滤波器)。 解(1)根据题意可知,n=10,e=102,f,=10°,所以同步保特时间为 10-2 12-2x10x103=05s (②)码元宽度为 T, R1065=1us 允许输入码流中连0码或连1码的最大个数为 【例11-4】传输速率为1k灿it/s的一个通信系统,设误码率为10,群同步采用连 式插入的方法, 同步码组的位数n=7 每群中的信息位数为153。 (1)若不采用同步保护措施,试计算=0和=1时漏同步概率P,、对7位信息码的假同 步概率P和同步建立时间t: (2)若采用ā=3、B=3的同步保护措施,试计算m=0时漏同步概率P1、假同步概率P: 和同步球立时间t。」 解(1)当0时 P=mP.=7X10 P2=2=7.8×10 t.=(1+P.+NP)NT. =(1+7×10+160×7.8×10×160x×103s=360ms
2 因为 m 2 (t)- 2 m ˆ (t)及 m(t)(t)中都不含有直流成分,所以 s 2 (t)中不含有 2fc 分量,不能用平 方变换法提取载波。 方法二 设 s(t)的傅氏变换为 S(f),则 s 2 (t)的傅氏变换为 S(f)*S(f),它们的示意图分别如图 11-10(a)、(b)所示。由图 11-10(b)可知,在 s 2 (t)的频谱中无 2fc 离散谱,故不能用平方变 换法提取载波。 图 11-10 例 22-2 图 【例 11-3】 在数字锁相环位同步器中,晶振频率稳定度为 10-5,码速率为 106 Bd,设 允许的位同步误差为 2×10-2 π, (1) 求同步保持时间; (2) 位同步器输入码流中最多允许有多少个连0码或连1码(设无噪声、无环路滤波器)。 解 (1) 根据题意可知,η=10-5,ε=10-2,fs=106,所以同步保持时间为 0.5 2 10 10 10 2 5 6 2 = = = − − s f t s c ms (2) 码元宽度为 1 10 1 1 6 = = s = R T B s us 允许输入码流中连 0 码或连 1 码的最大个数为 = 500 s c T t 【例 11-4】 传输速率为 1 kbit/s 的一个通信系统,设误码率为 10-4,群同步采用连贯 式插入的方法,同步码组的位数 n=7,每群中的信息位数为 153。 (1) 若不采用同步保护措施,试计算 m=0 和 m=1 时漏同步概率 P1、对 7 位信息码的假同 步概率 P2 和同步建立时间 ts; (2) 若采用α=3、β=3 的同步保护措施,试计算 m=0 时漏同步概率 Pl、假同步概率 Pj 和同步建立时间 tp。 解 (1) 当 m=0 时 P1=nPe=7×10-4 P2=2-7 =7.8×10-3 ts=(1+P1+NP2)NTs =(1+7×10-4 +160×7.8×10-3 )×160×10-3 s=360 ms

当r1时 Pl-C(1-P.,) =1-C,(1-1097-7×10×(1-10) ≈4.2×10 P=2C:-g+7=624×10 t,=1686ms (2)P=(P.)=(7×10)2=3.43×10 P,=N·2=160×(7.8×101=7.6×10 =)N.(+a)NT 2 2 =+4x160+4×7x10-]x3x160x10g175 2 【例11-5】试证明式(11-13)、(11-14)和(11-15)。 证明当-0时,识别器对一帧内的位帧同步码的漏检测概率为P=,故连续B帧 的帧同步码漏检测概率(即顿同步系统的漏同步概率)为 P=P=(nP) 识别婴对n位数据码元的假同步概率为P=2,连续ā帧对处于相同位置的n位数据码 元都能够检测到同步信号的概率为P°。每个同步帧共有N-位数据,当N时,每个同步帧 可以构成N组位数为的数据,故顿同步系统的假同步概率为 P=N·2a 在a个同步顿中约aN位数据,识别器发生一次假同步的概率为aN·2”。当这个假同 步发生在ā帧中的第一帧时,同步系统的同步建立时间延长一个同步慎:当这个假同步发生 在ā帧中的最后一帧时,则同步建立时间延长a个同步帧,故识别器假同步将同步建立时间 均延长1+a)/2个同步帧。 再考虑到识别器发生 次假同步的概率,则同步建立时间被延 长的同步帧数为(1+a)aN·2/2。 在ā个同步帧时间内,识别器发生一次漏同步概率为aP。,识别器发生一次漏同步将同 步建立时间平均延长(1+α)/2个同步锁。再考虑到识别器发生一次漏同步的概率,则同步 建立时间被延长的同步帧数为a(1+a)nP./2。 当识别器无漏同步和假同步现象时,同步建立时间为α个同步帧,若考虑到识别器的假 同步和漏同步的影响,则幀同步器的同步建立时间为 a+(l+a)aV.2a+ 2 2 -(+a)N.(+a)p aNT, 2 2 命题证毕。 11.2自测自评
3 当 m=1 时 P1=1- n r e r n r C P − = (1− ) 1 0 =1-C 0 7(1-10-4 ) 7 -7×10-4×(1-10-4 ) 6 ≈4.2×10-7 P2=2-n r n r C = 1 0 =2-7 (1+7)≈6.24×10-2 ts=1686 ms (2) Pl=(nPe) β =(7×10-4 ) 3 =3.43×10-10 Pj=N·2 -nα =160×(7.8×10-3 ) 3 =7.6×10-5 s e p n aNT a N a nP t ] 2 (1 ) 2 (1 ) [1 1 + + + = + + ] 3 160 10 s 1.7s 2 4 7 10 2 4 160 [1 3 4 8 + = + − − 【例 11-5】 试证明式(11-13)、(11-14)和(11-15)。 证明 当 m=0 时,识别器对一帧内的 n 位帧同步码的漏检测概率为 P1=nPe,故连续β帧 的帧同步码漏检测概率(即帧同步系统的漏同步概率)为 Pl=Pβ 1=(nPe) β 识别器对 n 位数据码元的假同步概率为 P2=2-n,连续α帧对处于相同位置的 n 位数据码 元都能够检测到同步信号的概率为 P α 2。每个同步帧共有 N-n 位数据,当 Nn 时,每个同步帧 可以构成 N 组位数为 n 的数据,故帧同步系统的假同步概率为 Pj=N·2 -nα 在α个同步帧中约αN 位数据,识别器发生一次假同步的概率为αN·2 -n。当这个假同 步发生在α帧中的第一帧时,同步系统的同步建立时间延长一个同步帧;当这个假同步发生 在α帧中的最后一帧时,则同步建立时间延长α个同步帧,故识别器假同步将同步建立时间 均延长(1+α)/2 个同步帧。再考虑到识别器发生一次假同步的概率,则同步建立时间被延 长的同步帧数为(1+α)αN·2 -n /2。 在α个同步帧时间内,识别器发生一次漏同步概率为αnPe,识别器发生一次漏同步将同 步建立时间平均延长(1+α)/2 个同步帧。再考虑到识别器发生一次漏同步的概率,则同步 建立时间被延长的同步帧数为α(1+α)nPe/2。 当识别器无漏同步和假同步现象时,同步建立时间为α个同步帧,若考虑到识别器的假 同步和漏同步的影响,则帧同步器的同步建立时间为 s e n s e n p aNT a N a nP NT a aN a a nP t a + + + = + + + = + + − 2 (1 ) 2 (1 ) 2 (1 ) 2 (1 ) 2 1 命题证毕。 11.2 自 测 自 评
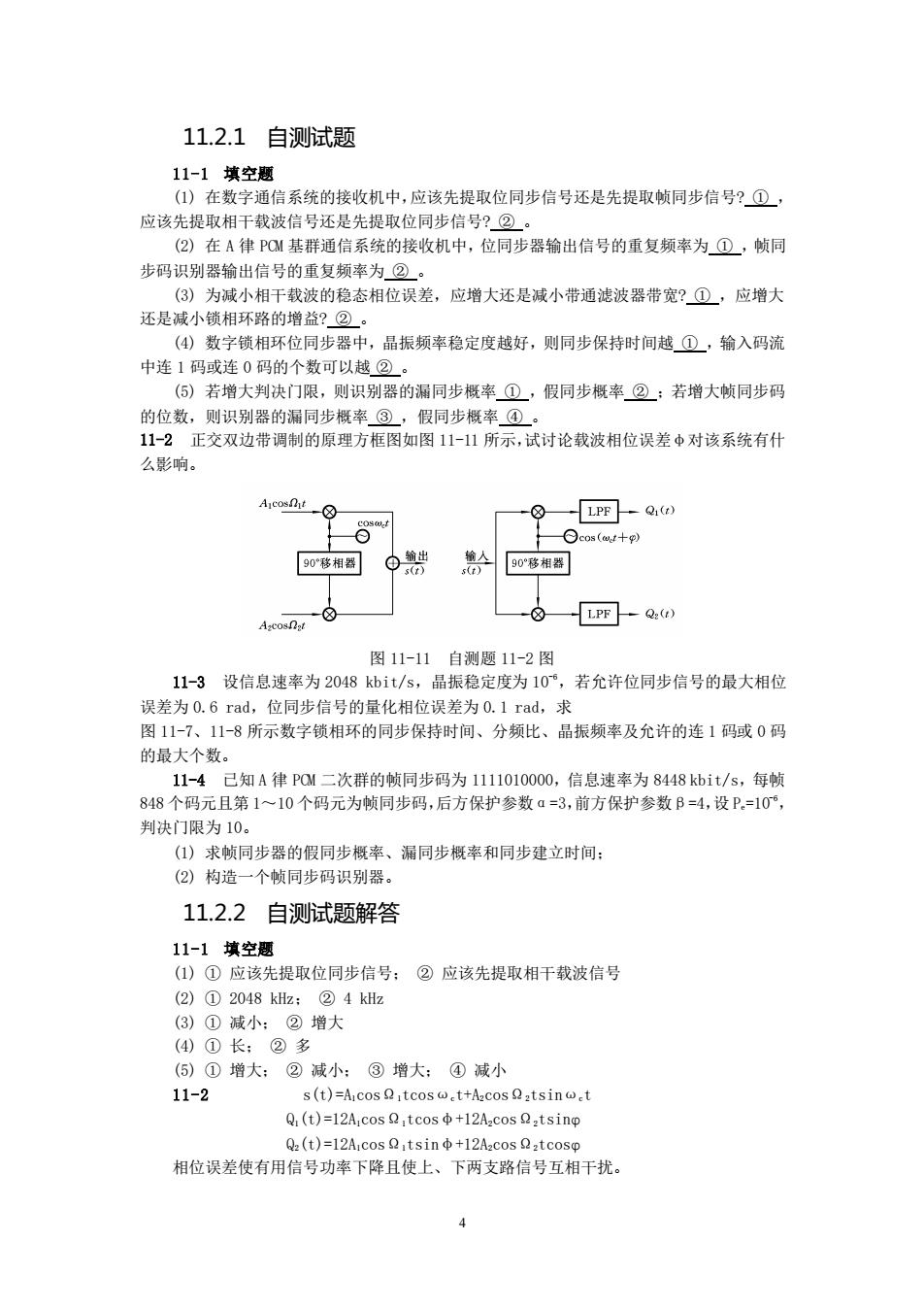
11.2.1自测试题 11-1填空题 (1)在数字通信系统的接收机中,应该先提取位同步信号还是先提取帧同步信号?①, 应该先提取相干载波信号还是先提取位同步信号?②。 (2)在A律P0M基群通信系统的接收机中,位同步器输出信号的重复频率为①,帧同 步码识别器输出信号的重复须率为② (③)为减小相干载波的稳态相位误差,应增大还是减小带通滤波器带宽?①,应增大 还是减小锁相环路的增益?②。 (④)数字锁相环位同步器中,晶振频率稳定度越好,则同步保持时间越①,输入码流 中连1码或连0码的个数可以越②。 (⑤)若增大判决门限,则识别器的漏同步概率①,假同步概率②:若增大顿同步码 假同步概率① 正交双边带调制的原理方框图如图11-所示,试讨论载波相位误差中对该系统有什 么影响。 LPF-Q() B0移湘器 图11-11白测题11-2图 1-3设信总速率为2048灿it/ 晶振稳定度为10,若允许位同步信号的最大相位 误差为0.6rad,位同步信号的量化相位误差为0.1rad,求 图11-7、1-8所示数字锁相环的同步保持时间、分频比、晶振频率及允许的连1码或0码 的最大个数。 11-4己知A律P0M二次群的帧同步码为1111010000,信息速率为8448kbit/s,每帧 848个码元且第1~10个码元为帧同步码,后方保护参数=-3,前方保护参数B=4,设P.=10 判决门限为10 (1)求帧同步器的假同步概率、漏同步概率和同步建立时间: (2)构造一个帧同步码识别器。 11.2.2自测试题解答 11-1填空恩 (1)①应该先提取位同步信号:②应该先提取相干载波信号 (2)①2048kz:②4kHz (3)①减小:②增大 (4)①长:②多 ()①增大:②减小:③增大:④减小 11-2 s(t)=Aicos itcos w:t+Aacos :tsinw: Q(t)=12A,cos Q,tcos+12A,cos Q,tsinp Q(t)=12Acos Qtsin+12Acos Q:tcosp 相位误差使有用信号功率下降且使上、下两支路信号互相干扰, 4
4 11.2.1 自测试题 11-1 填空题 (1) 在数字通信系统的接收机中,应该先提取位同步信号还是先提取帧同步信号? ① , 应该先提取相干载波信号还是先提取位同步信号? ② 。 (2) 在 A 律 PCM 基群通信系统的接收机中,位同步器输出信号的重复频率为 ① ,帧同 步码识别器输出信号的重复频率为 ② 。 (3) 为减小相干载波的稳态相位误差,应增大还是减小带通滤波器带宽? ① ,应增大 还是减小锁相环路的增益? ② 。 (4) 数字锁相环位同步器中,晶振频率稳定度越好,则同步保持时间越 ① ,输入码流 中连 1 码或连 0 码的个数可以越 ② 。 (5) 若增大判决门限,则识别器的漏同步概率 ① ,假同步概率 ② ;若增大帧同步码 的位数,则识别器的漏同步概率 ③ ,假同步概率 ④ 。 11-2 正交双边带调制的原理方框图如图 11-11 所示,试讨论载波相位误差φ对该系统有什 么影响。 图 11-11 自测题 11-2 图 11-3 设信息速率为 2048 kbit/s,晶振稳定度为 10-6,若允许位同步信号的最大相位 误差为 0.6 rad,位同步信号的量化相位误差为 0.1 rad,求 图 11-7、11-8 所示数字锁相环的同步保持时间、分频比、晶振频率及允许的连 1 码或 0 码 的最大个数。 11-4 已知 A 律 PCM 二次群的帧同步码为 1111010000,信息速率为 8448 kbit/s,每帧 848 个码元且第 1~10 个码元为帧同步码,后方保护参数α=3,前方保护参数β=4,设 Pe=10-6, 判决门限为 10。 (1) 求帧同步器的假同步概率、漏同步概率和同步建立时间; (2) 构造一个帧同步码识别器。 11.2.2 自测试题解答 11-1 填空题 (1) ① 应该先提取位同步信号; ② 应该先提取相干载波信号 (2) ① 2048 kHz; ② 4 kHz (3) ① 减小; ② 增大 (4) ① 长; ② 多 (5) ① 增大; ② 减小; ③ 增大; ④ 减小 11-2 s(t)=A1cosΩ1tcosωct+A2cosΩ2tsinωct Q1(t)=12A1cosΩ1tcosφ+12A2cosΩ2tsinφ Q2(t)=12A1cosΩ1tsinφ+12A2cosΩ2tcosφ 相位误差使有用信号功率下降且使上、下两支路信号互相干扰
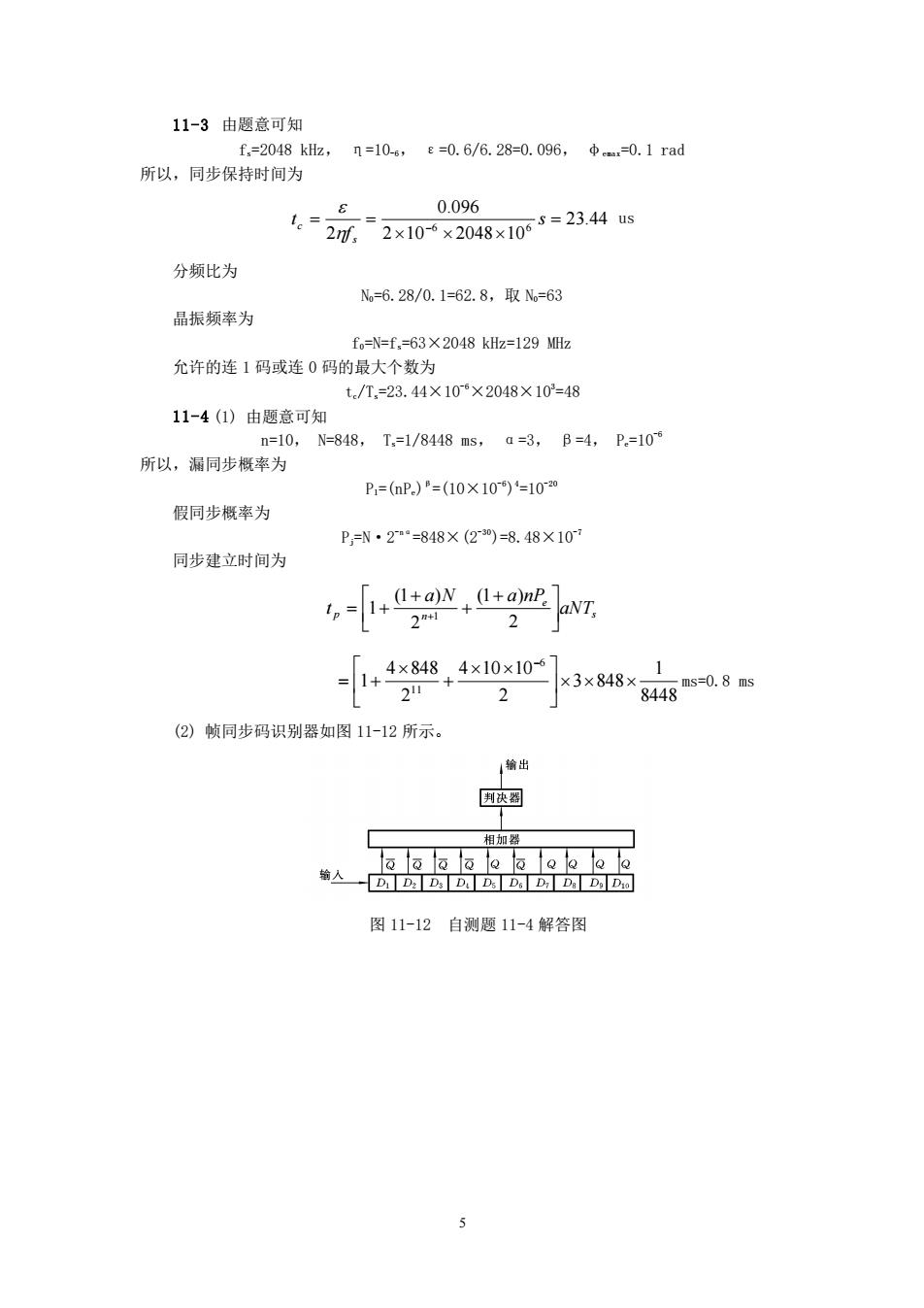
11-3由题意可知 f=2048kHz,1=10-6,e=0.6/6.28=0.096,Φ=0.1rad 所以,同步保持时间为 0.096 2/2x10-6x2048×1005=23.44us 分频比为 N=6.28/0.1=62.8,取N=63 晶振频率为 fo=N=f.=63×2048kz=129MHz 允许的连1码或连0码的最大个数为 t./T,=23.44×106×2048×103=48 11-4(1)由题意可知 n=10,N=848,T,=1/8448ms,a=3,B=4,P.=109 所以,漏同步概率为 P1=(nP.)B=(10×10)=1020 假同步概率为 P=N·2m=848×(230)=8.48×107 同步建立时间为 2+ 1+ 4×848,4×10×106 21 ×3×848× -ms=0.8 ms 8448 (2)帧同步码识别器如图11-12所示。 输出 判决器 相加器 aaaa lo a folo lo lo 输人一D.D:D.D.D:D:D:D.D.D四 图11-12自测题11-4解答图
5 11-3 由题意可知 fs=2048 kHz, η=10-6, ε=0.6/6.28=0.096, φemax=0.1 rad 所以,同步保持时间为 23.44 2 10 2048 10 0.096 2 6 6 = = = − s f t s c us 分频比为 N0=6.28/0.1=62.8,取 N0=63 晶振频率为 f0=N=fs=63×2048 kHz=129 MHz 允许的连 1 码或连 0 码的最大个数为 tc/Ts=23.44×10-6×2048×103 =48 11-4 (1) 由题意可知 n=10, N=848, Ts=1/8448 ms, α=3, β=4, Pe=10-6 所以,漏同步概率为 Pl=(nPe) β =(10×10-6 ) 4 =10-20 假同步概率为 Pj=N·2 -nα =848×(2-30)=8.48×10-7 同步建立时间为 s e p n aNT a N a nP t + + + = + + 2 (1 ) 2 (1 ) 1 1 8448 1 3 848 2 4 10 10 2 4 848 1 6 11 + = + − ms=0.8 ms (2) 帧同步码识别器如图 11-12 所示。 图 11-12 自测题 11-4 解答图