
第2章 确知信号
1 第2章 确 知 信 号

2.1确知信号的类型 ÷信号能量 E=s2) $信号平均功率 P-lim T 能量信号:能量等于一个有限正值,平均功率为零。 ÷功率信号:平均功率等于一个有限正值,能量为无 穷大
2 2.1 确知信号的类型 ❖ 信号能量 ❖ 信号平均功率 ❖ 能量信号:能量等于一个有限正值,平均功率为零。 ❖ 功率信号:平均功率等于一个有限正值,能量为无 穷大。 − E = s (t )dt 2 − → = 2 2 1 2 T / T / T s (t )dt T P lim

2.2确知信号的频域性质 2.2.1功率信号的频谱(单位:V) 周期性功率信号s(),周期To,f=11T0,其傅氏级 数的复系数: 功率信号的频谱, 代表在频率nfo上信 号分量的复振幅 sf)=∑c,e2=2C.e2
3 2.2 确知信号的频域性质 2.2.1功率信号的频谱(单位:V) 周期性功率信号s(t),周期T0,f0=1/ T0,其傅氏级 数的复系数: − − = 2 2 2 0 0 0 0 1 T / T / j n f t n s(t )e dt T C 功率信号的频谱, 代表在频率nf0上信 号分量的复振幅 j n f t n n j n t / T n n s(t ) C e C e 2 0 2 0 =− =− = =

2.2确知信号的频域性质 2.2.2能量信号的频谱(频谱密度,单位VHz) 能量信号s(),其傅氏变换: 能量信号的频谱, Sf)=广nsf1)e2ah 代表在单位频率信 号振幅的分布(相 对大小) s(t)=Sif)edf
4 2.2 确知信号的频域性质 2.2.2能量信号的频谱(频谱密度,单位V/Hz) 能量信号s(t),其傅氏变换: − − S( f ) = s(t )e dt j2ft 能量信号的频谱, 代表在单位频率f信 号振幅的分布(相 对大小) s(t ) S( f )e df j2f t − =
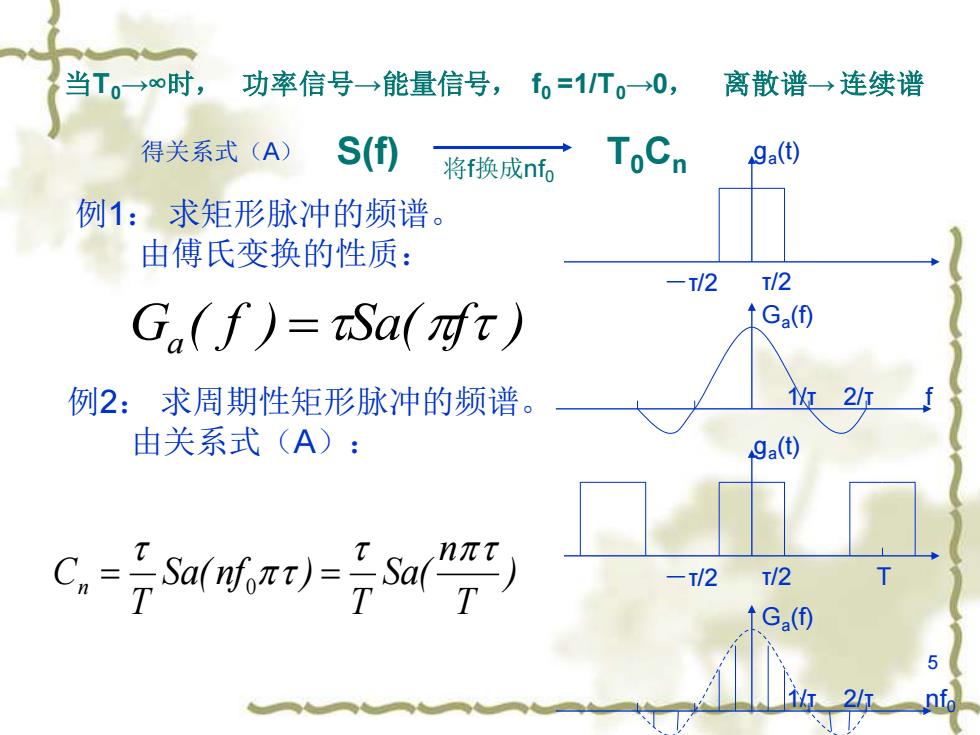
当T0→∞时, 功率信号→能量信号,f0=1T。→0, 离散谱→连续谱 得关系式(A) s(f) 将f换成nf ToCn 9a() 例1:求矩形脉冲的频谱。 由傅氏变换的性质: -/2 /2 Gn(f)=Sa(gt》 ↑Ga(⑤ 例2:求周期性矩形脉冲的频谱。 2/1 由关系式(A): 9a() -T/2 T/2
5 当T0→∞时, 功率信号→能量信号, f0 =1/T0→0, 离散谱→ 连续谱 ) T n Sa( T Sa( nf ) T Cn = 0 = S(f) T0Cn 例1: 求矩形脉冲的频谱。 由傅氏变换的性质: -τ/2 τ/2 1/τ 2/τ f ga (t) Ga (f) 例2: 求周期性矩形脉冲的频谱。 由关系式(A): 得关系式(A) G ( f ) Sa( f ) a = -τ/2 τ/2 ga (t) T 1/τ 2/τ nf0 Ga (f) 将f换成nf0

2.2确知信号的频域性质 2.2.3能量信号的能量谱密度(单位:J/Hz) 由巴塞伐尔定理: 能量谱密度,代表 在单位频率信号能 量的分布 E=Cs2)=心Sf八f 2.2.4功率信号的功率谱密度(单位:WHz) 计算s(①)截短信号s()能量: E=3s)di=∫s,(f小PrfJ=lms,f州 T>00 信号功率 P=P(f)d 功率谱密度,代表在单位 频率f信号功率的分布
6 能量谱密度,代表 在单位频率f信号能 量的分布 2.2 确知信号的频域性质 2.2.3能量信号的能量谱密度(单位:J/Hz) 由巴塞伐尔定理: 2.2.4功率信号的功率谱密度(单位:W/Hz) 计算s(t)截短信号sT (t)能量: E s (t )dt S( f ) df 2 2 − − = = E s (t )dt S ( f ) df T T / T / T 2 2 2 2 − − = = 1 2 S ( f ) T P( f ) T T lim → = 功率谱密度,代表在单位 频率f信号功率的分布 信号功率 P P( f )df − =

÷2.3确知信号的时域性质 ó2.3.1能量信号的自相关函数 定义: R(r)-s()s(t+di -00<T<0 (2.3-1) 必性质: 6自相关函数R()和时间t无关,只和时间差x有关。 6当x=0时,R(O)等于信号的能量: R(O)=[s'(dt=E (2.3-2) 6R()是x的偶函数 R(x)=R(-t) (2.3-3) 6自相关函数R()和其能量谱密度S(OP是一对傅里叶变换: S(f)="R(r)edr R(r)=广Sf)fe2
7 ❖ 2.3 确知信号的时域性质 2.3.1 能量信号的自相关函数 ❖定义: (2.3-1) ❖性质: 自相关函数R()和时间t 无关,只和时间差 有关。 当 = 0时,R(0)等于信号的能量: (2.3-2) R()是 的偶函数 (2.3-3) 自相关函数R()和其能量谱密度|S(f)|2是一对傅里叶变换: − R( ) = s(t)s(t + )dt − R = s t dt = E − (0) ( ) 2 R( ) = R(− ) − − = S f R e d j2 f 2 ( ) ( ) − R = S f e df j f 2 2 ( ) ( )

62.3.2功率信号的自相关函数 定义: 1rT12 s()s(t+)dt R(z)=lm -0<T<0 (2.3-4) 。性质: 6当x=0时,自相关函数R(O)等于信号的平均功率: di-P (2.3-5) ó功率信号的自相关函数也是偶函数。 周期性功率信号: 6自相关函数定义: RC)d 00<t<0 (2.3-6) 6R()和功率谱密度P()之间是傅里叶变换关系: R(t)=["P(N)erdf P(f)=[R(t)edr 8
8 2.3.2 功率信号的自相关函数 ❖定义: (2.3-4) ❖性质: 当 = 0时,自相关函数R(0)等于信号的平均功率: (2.3-5) 功率信号的自相关函数也是偶函数。 ❖周期性功率信号: 自相关函数定义: (2.3-6) R()和功率谱密度P(f)之间是傅里叶变换关系: → − = + − / 2 / 2 ( ) ( ) 1 ( ) lim T T T s t s t dt T R s t dt P T R T T T = = → − / 2 / 2 2 ( ) 1 (0) lim − = + − / 2 / 2 0 0 0 ( ) ( ) 1 ( ) T T s t s t dt T R − R = P f e df j f 2 ( ) ( ) − − = P f R e d j2 f ( ) ( )

例3试求周期性信号s()=Acos(t+)的自相关函数。 解先求功率谱密度,然后对功率谱密度作傅里叶变换, 即可求出其自相关函数。 功率谱密度 CP Ac0St←> af+i8- 由傅氏变换的性质:s(1-t,)S(f)e2% 放有:Acos(1+9)2[8f+6+f-6刀e20
9 ❖例3 试求周期性信号s(t) = Acos(t+)的自相关函数。 解 先求功率谱密度,然后对功率谱密度作傅里叶变换, 即可求出其自相关函数。 功率谱密度 2 Cn [ ( f f ) ( f f )] A Acost 0 0 2 + + − 由傅氏变换的性质: 故有: 0 2 0 j f t s(t t ) S( f )e − − j f [ ( f f ) ( f f )]e A Acos(t ) 2 0 0 2 + + + −

6求功率谱密度: =1-+f- 6求自相关函数: r=PMfe省=于e+en列 对于正弦函数, T,=2n→f6=1/2元 e)=Uewwe+er]esr 10
10 求功率谱密度: 求自相关函数: ( f f ) A ( f f ) A Cn 0 2 0 2 2 4 4 = − + + [ e e ] A R( ) P( f )e df j f j f j f 2 0 2 0 2 2 4 − − = = + cos 2 [ ] 4 ( ) ( ) 2 2 2 A e e A R P f e df j f j j = = + = − − 对于正弦函数, T0 = 2 → f 0 =1/ 2