
第5章模拟调制系统 5.1幅度调制原理 5.2线性调制系统的抗噪声性能 5.3非线性调制原理 5.4调频系统的抗噪声性能 5.5各种模拟调制系统的比较 5.6频分复用和调频立体声
1 第5章 模拟调制系统 5.1 幅度调制原理 5.2 线性调制系统的抗噪声性能 5.3非线性调制原理 5.4 调频系统的抗噪声性能 5.5 各种模拟调制系统的比较 5.6 频分复用和调频立体声
ol 调制按调制信号(基带信号)的变化规律去改变 载波某些参数的过程.使信号转换成适合在信道 中传输的形式。 ● 目的频率变换,信道复用,提高抗干扰性能 ·分类 载波 调制信号 正弦波 数字信号 数字调制 模拟信号 模拟调制 脉冲串 脉冲调制 2
2 ⚫ 调制 按调制信号(基带信号)的变化规律去改变 载波某些参数的过程.使信号转换成适合在信道 中传输的形式。 ⚫ 目的 频率变换,信道复用,提高抗干扰性能 ⚫ 分类 载波 调制信号 正弦波 数字信号 数字调制 模拟信号 模拟调制 脉冲串 脉冲调制

5.1幅度调制(线性调制)的原理 载波 s(t)=Acos(ω.t+p) 已调信号Sm(t)=Am(t)cos(o.t+p。) p。=0 m()调制信号(基带信 cos0.t台πl8(o+0.)+(0-0.)] 设 g02roro m(t)台M(o) 则 S.(@)=FLs.(]=[M(o-a.)+M(@+a.】
3 载波 已调信号 m(t)调制信号 (基带信号) 设 则 ( ) cos( ) = +0 s t A t c ( ) ( )cos( ) = +0 s t Am t t m c m(t) M () [ ( ) ( )] 2 ( ) [ ( )] m m M c M c A S = F s t = − + + 0 = 0 cos [ ( ) ( )] c c c t + + − [ ( ) ( )] 2 1 ( ) ( ) 1 2 1 2 f t f t F F 5.1幅度调制(线性调制)的原理
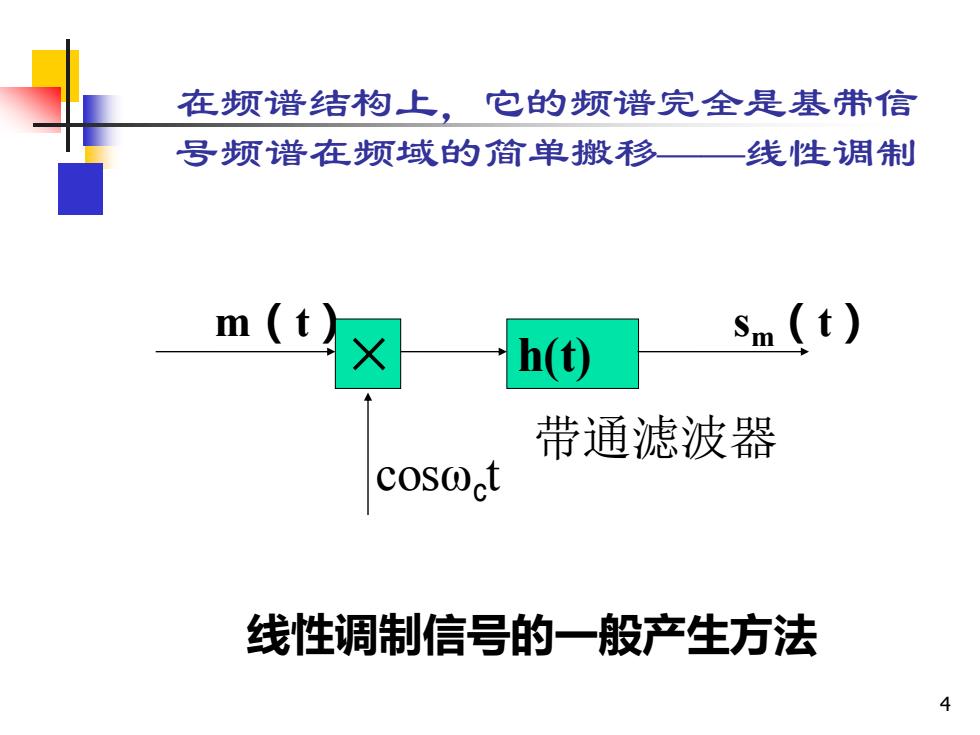
在频谱结构上,它的频谱完全是基带信 号频谱在频域的简单搬移 线性调制 m(t) h() sm(t) 带通滤波器 coso t 线性调制信号的一般产生方法 4
4 在频谱结构上,它的频谱完全是基带信 号频谱在频域的简单搬移——线性调制 m(t) sm(t) 线性调制信号的一般产生方法 cosωc t × h(t) 带通滤波器

s (t)=h(t)m(t-t)cos(@t-w.r)di =cosoth(t)m(t-r)cosordr +sin@th(t)m(t-t)sino rdr S.(o)=,[M(o-o)+M(o+@,月H(o) 适当选择带通滤波器h(t),便可得到 各种凋幅信号
5 s t h m t t d m c c ( ) = ( ) ( − )cos( − ) − t h m t d c c = cos ( ) ( − )cos − t h m t d c c + sin ( ) ( − )sin − [ ( ) ( )] ( ) 2 1 S m () = M − c + M + c H 适当选择带通滤波器 h(t) ,便可得到 各种调幅信号
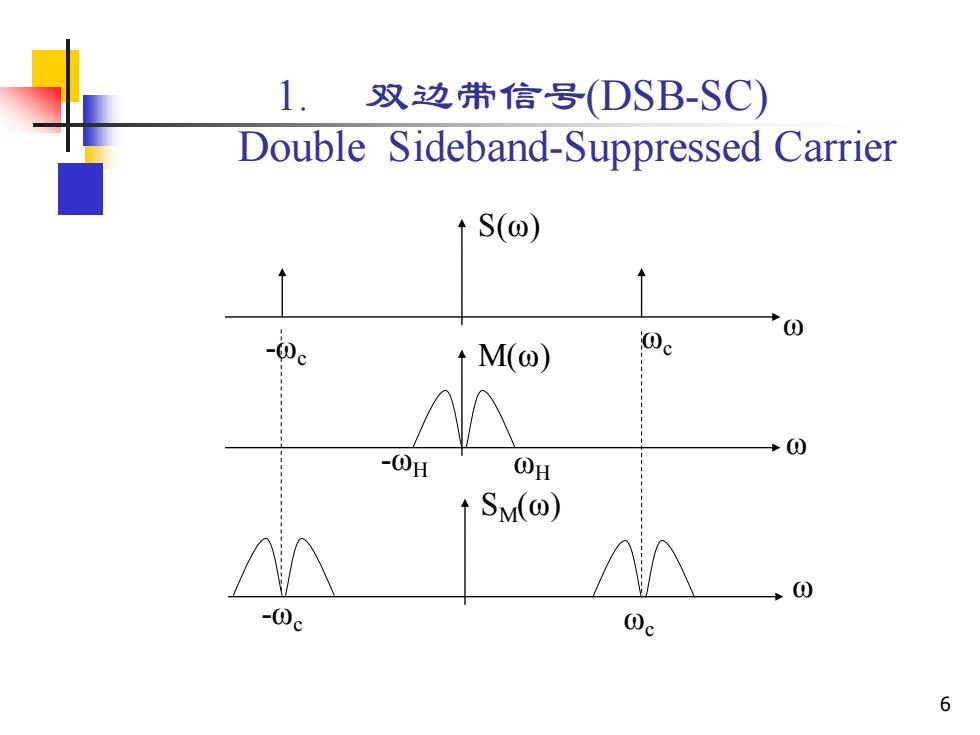
1. 双边带信号(DSB-SC) Double Sideband-Suppressed Carrier S(@) 0 ①c tM(@) Wc N 0 -①H @H SM(@) 0 -①c ①c 6
6 1. 双边带信号(DSB-SC) Double Sideband-Suppressed Carrier S(ω) -ωc ωc -ωc M(ω) ωc ω ω ωH -ωH SM(ω) ω
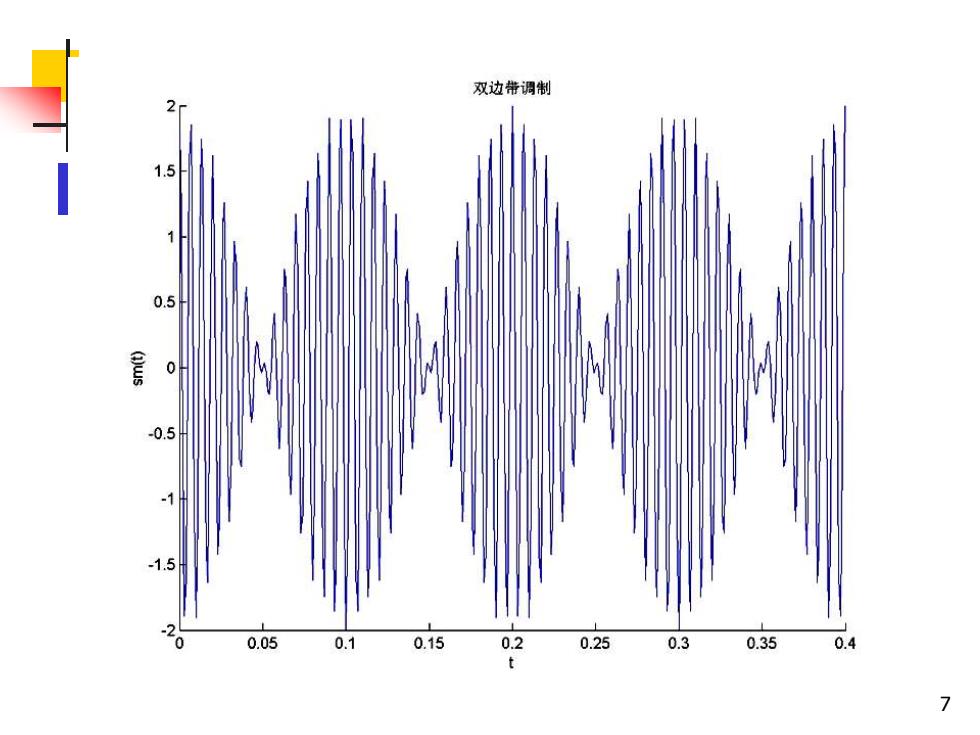
双边带调制 3 1.5 0.5 0.5 1.5 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 t 7
7
m(t) SDSB ( 0 W DSB信号波形 DSB信号的包络与基带信号不 完全相同,因此不能用包络检波 来恢复基带信号 8
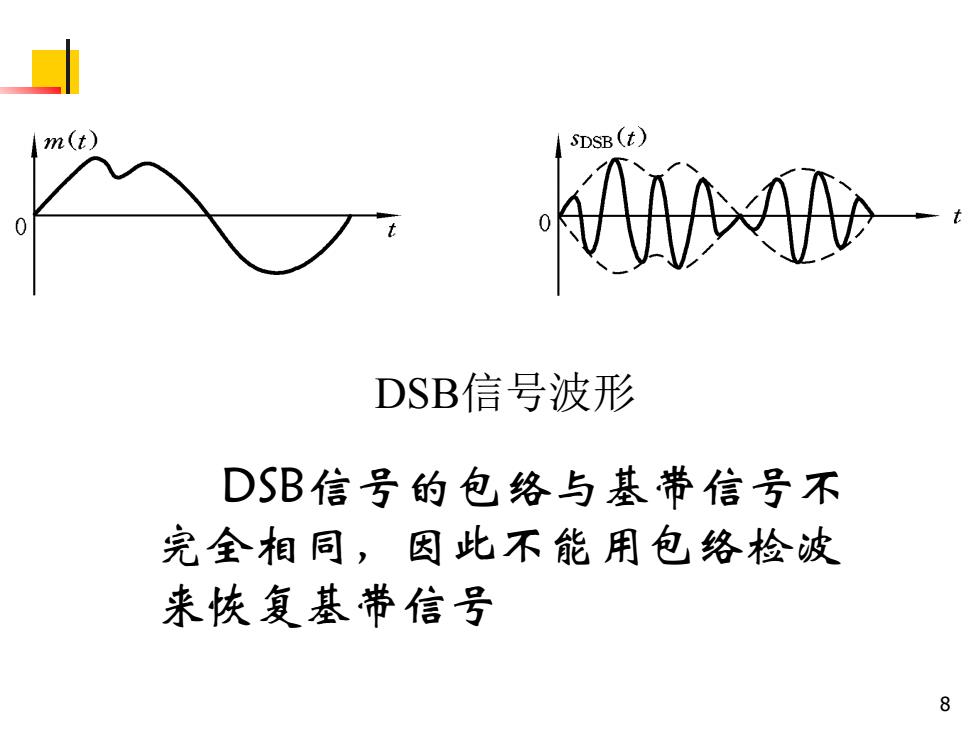
8 DSB信号波形 DSB信号的包络与基带信号不 完全相同,因此不能用包络检波 来恢复基带信号

2.调幅(AM)信号 Amplitude Modulation ◆时域表示式 sav(t)=[4+m(t)]cosot=A cos@t+m(t)cos@t 式中m(t)-调制信号,均值为0; A。~常数,表示叠加的直流分量。 ◆频谱:若m(t)为确知信号,则AM信号的频谱为 Sw(o)=π4[8o+0.)+0-o.】+[M(o+0)+M(o-@.】 若m(t)为随机信号,则已调信号的频域表示式必须 用功率谱描述。 m() s(t) ◆调制器模型 cos@t 9
9 ◆ 时域表示式 式中 m(t) - 调制信号,均值为0; A0 - 常数,表示叠加的直流分量。 ◆ 频谱:若m(t)为确知信号,则AM信号的频谱为 若m(t)为随机信号,则已调信号的频域表示式必须 用功率谱描述。 ◆ 调制器模型 0 0 ( ) [ ( )]cos cos ( )cos AM c c c s t A m t t A t m t t = + = + 0 1 ( ) [ ( ) ( )] [ ( ) ( )] 2 AM c c c c S A M M = + + − + + + − m t( ) s t m ( ) cos c t A0 2.调幅(AM)信号 Amplitude Modulation
◆波形图 m(t) ▣由波形河以看出,当满足条件: m(t)≤Ao A+m(t)外 时,其包络与调制信号波形相同, 因此用包络检波法很容易恢复出原 载波 始调制信号。 。否则,出现“过调幅”现象。这时用 AAAAA 包络检波将发生失真。但是,可以sw()个 采用其他的解调方法,如同步检波。 SAM() SAM( m(t) (a) (b) (c)
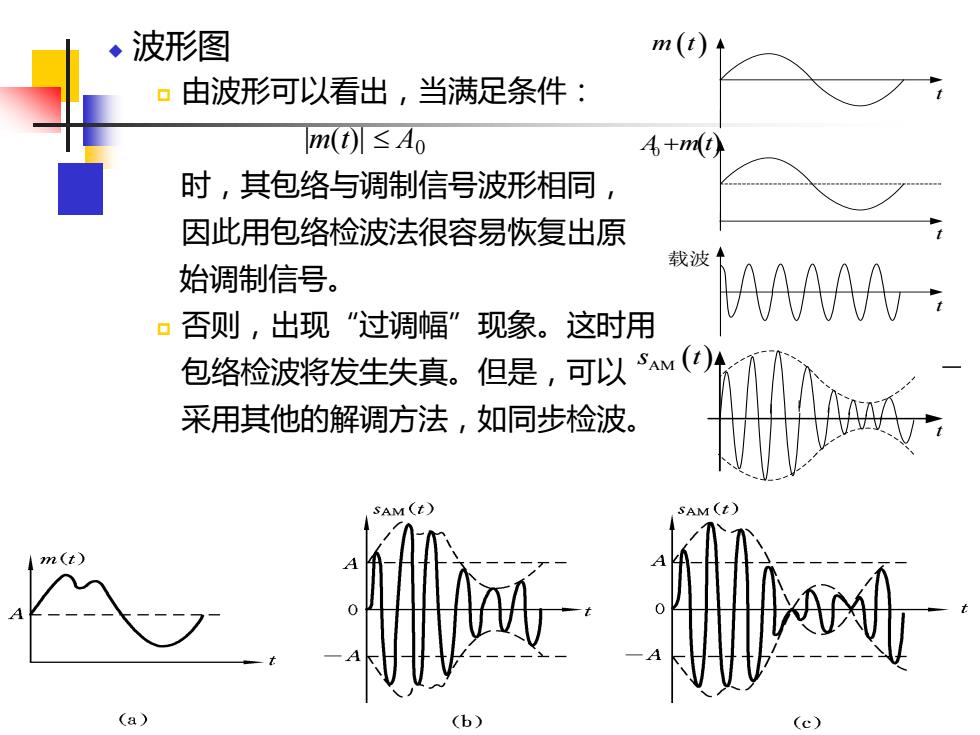
10 ◆ 波形图 由波形可以看出,当满足条件: |m(t)| A0 时,其包络与调制信号波形相同, 因此用包络检波法很容易恢复出原 始调制信号。 否则,出现“过调幅”现象。这时用 包络检波将发生失真。但是,可以 采用其他的解调方法,如同步检波。 t t t t m t( ) A m t 0 + ( ) 载波 s t AM ( ) − H H M () SAM () −c 0 c