
■第三章随机过程 3.1随机过程的基本概念 3.2平稳随机过程 3.3高斯过程 3.4平稳随机过程通过线性系统 3.5窄带随机过程
1 第三章 随机过程 3.1 随机过程的基本概念 3.2 平稳随机过程 3.3 高斯过程 3.4 平稳随机过程通过线性系统 3.5 窄带随机过程

3.1随机过程的基本概念 随机过程是时间t的函数 ■在任意时刻观察,它是一个随机变量 ■随机过程是全部可能实现的总体 2
2 3.1 随机过程的基本概念 ◼ 随机过程是时间t的函数 ◼ 在任意时刻观察,它是一个随机变量 ◼ 随机过程是全部可能实现的总体
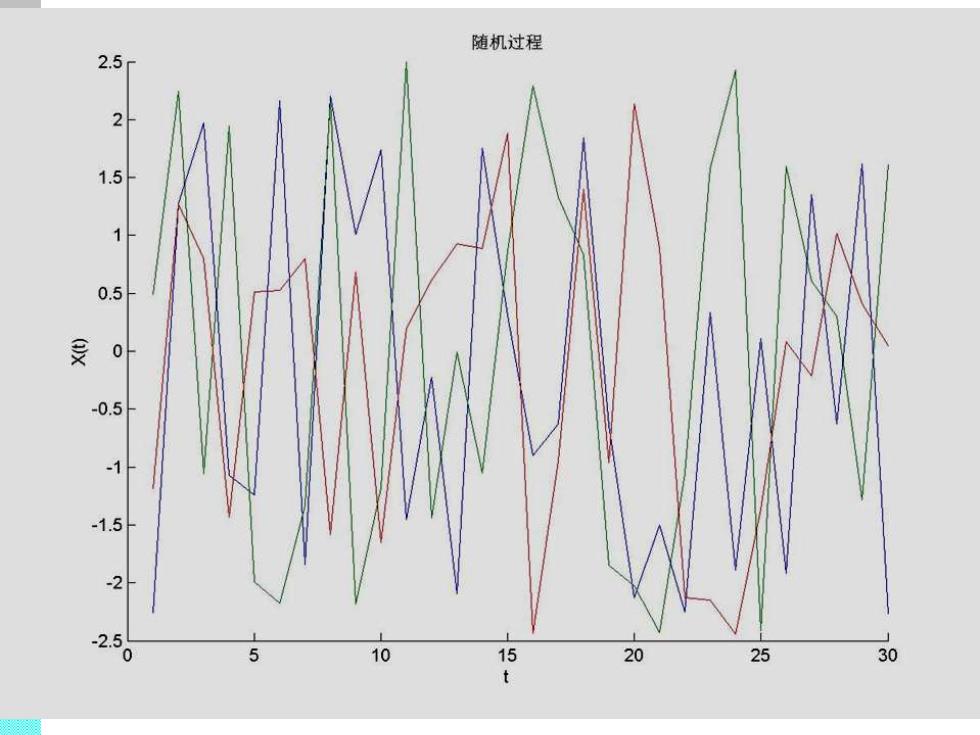
随机过程 2.5 1.5 0.5 0 0.5 15 .25 0 10 15 20 25 30
3

分布函数与概率密度: 设(t)表示一个随机过程,5(t)(t为任意时刻)是一 个随机变量。 F1(X1, t)=P{5(t上x1} 5(t)的一维分布函数 如果存在 aF(x,4) Ox =f(x1,t) 则称之为5(t)的一维概率密度函数
4 分布函数与概率密度: ◼ 设 表示一个随机过程, (t1为任意时刻)是一 个随机变量。 F1(x1,t1)=P{ ≤x1} 的一维分布函数 ◼ 如果存在 ◼ ◼ 则称之为 的一维概率密度函数 (t) ( ) 1 t ( ) 1 t (t) ( , ) ( , ) 1 1 1 1 1 1 1 f x t x F x t = (t)

5(t)的n维分布函数 F(x,x,.,x;t,1,.,t)=P{5()≤x5)≤x,.,5(t)≤x.} n维概率密度函数 aF.(x,x2,.x41)=f(,.X,4,.1) OxOx2.Oxn n越大,Fn,fn描述(t)的统计特性就越充分
5 的n维分布函数 n维概率密度函数 n越大,Fn,fn描述 的统计特性就越充分 n n n n n F (x , x , , x ;t ,t , ,t ) = P{ (t ) x , (t ) x , , (t ) x 1 2 1 2 1 1 2 2 n n n n n x x x F x x x t t t 1 2 1 2 1 2 ( , , ; , , , ) ( , , ; , , , ) n 1 2 n 1 2 n = f x x x t t t (t) (t)
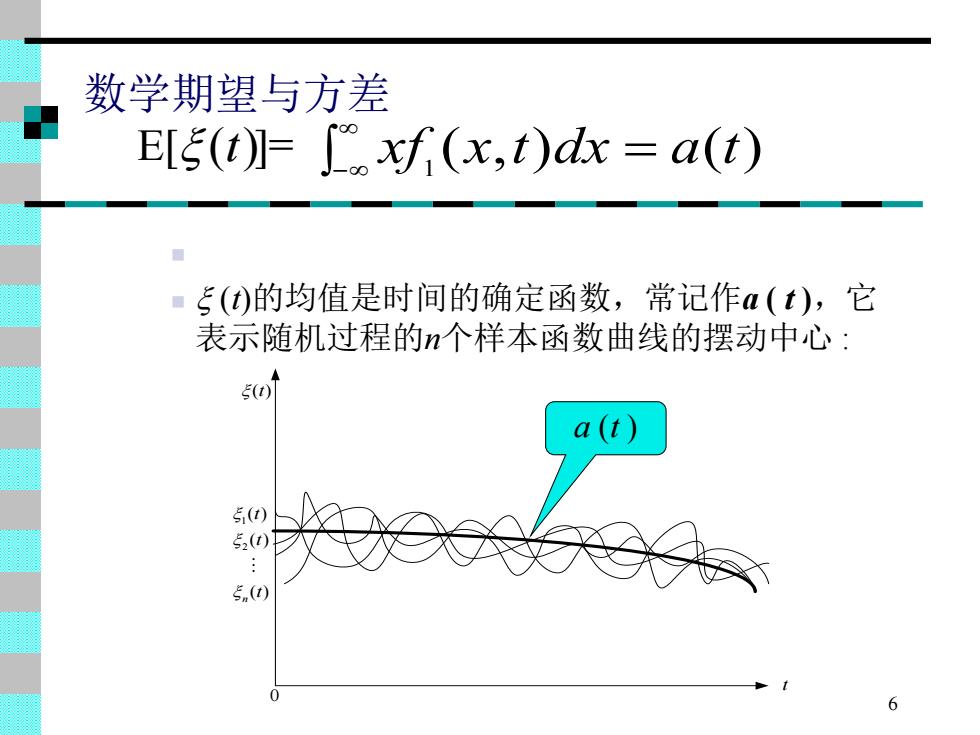
数学期望与方差 E[s(t(x,t)dx=a(t) ■5(t)的均值是时间的确定函数,常记作a(t),它 表示随机过程的n个样本函数曲线的摆动中心: 50 a(t)》 5() 52(t) 5n(0) 6
6 数学期望与方差 E[ ]= ( , ) ( ) 1 xf x t dx = a t − (t) ◼ ◼ (t)的均值是时间的确定函数,常记作a ( t ),它 表示随机过程的n个样本函数曲线的摆动中心 : ()t t 0 1 2 ( ) ( ) ( ) n t t t a (t )

方差 D[5(t)】=E[5(t)-a(t)]2} 方差常记为o2(t)。这里也把任意时刻t,直接写成了t。 因为 D[E5t】=EE2)-2ao0)+a2】 =E[2(t】-2at)E[5(t)]+a2(t) =E[52(t)】-a2(t) =()d-[a 均方值 均值平方 所以,方差等于均方值与均值平方之差,它表示随机过程在时刻对 于均值a(t)的偏离程度
7 ◼方差 方差常记为2 ( t )。这里也把任意时刻t1直接写成了t。 因为 所以,方差等于均方值与均值平方之差,它表示随机过程在时刻 t 对 于均值a ( t )的偏离程度。 2 D[(t)] = E [(t) − a(t)] ( ) ( ) ( ) ( ) ( ) ( ) ( ) [ ( )] ( ) [ ( )] 2 ( ) 2 2 2 2 2 2 2 E ξ t a t E ξ t a t E ξ t a t D ξ t E ξ t a t ξ t a t = − = − + = − + 2 1 2 = x f (x,t)dx −[a(t)] − 均方值 均值平方

协方差函数与相关函数 用来衡量任意两个时刻上获得的随机变量 的统计相关特性 协方差B(t,t2)=E{[5(t)-a(t)][5(t2)-a(t2)]} =xa(t)x,-a(t )f(x2tt)dx dx 8
8 用来衡量任意两个时刻上获得的随机变量 的统计相关特性 协方差 B(t1,t2)=E{[ -a(t1)][ -a(t2)]} = ( ) 1 t ( ) 2 t − − − [ ( )] 1 1 x a t 2 2 2 1 2 1 2 1 2 [x − a(t )] f (x , x ;t ,t )dx dx 协方差函数与相关函数

相关函数R(t,t2)=E[5(t)(t2)] xx(x,x2t,t2)dx dx2 B(t1,2=R(t1,t2)-E5(t)]E[5(t2)] 5(t),7(t) 表示两个随机过程 互协方差函数 Bn(t1,t2)=E{[5(t)-a(t)][7(t2)-an(t2)]} 互相关函数 R(t,t2)=E[5(t)7(t2)]
9 相关函数 R(t1,t2 )=E[ ] = B(t1,t2 )=R(t1,t2 )-E[ ] E[ ] , 表示两个随机过程 互协方差函数 互相关函数 1 2 2 1 2 1 2 1 2 x x f (x , x ;t ,t )dx dx − − ( ) 1 t ( ) 2 t ( ) 1 t ( ) 2 t (t) (t) ( , ) 1 2 B t t = E{[ (t 1 ) − a (t 1 )][(t 2 ) − a (t 2 )]} ( , ) [ ( ) ( )] 1 2 1 2 R t t E t t =

3.2平稳随机过程 任何n维分布函数或概率密度函数与时间起点无关 n(x1,x2.xmt1,t2,.,tn) =f(x,x2,.xnt+t,t2+t,.,tn+T) (1) 任意的n和t因此,一维分布与t无关,二维分布只与t1,2间隔 有关。 均值E[5(t)]=f(x,t)xf(x)dx=a(2) 方差E[5(t)-a(t)]=(x-a)f(x,t)x =(x-a)'f(x)dx=o2 (3) 相关函数R(t,)=x,x2f(x,x2;t1,t2)dx,dx =R(t,-t2)=R(x) 0 (4)
10 3.2 平稳随机过程 任何n维分布函数或概率密度函数与时间起点无关 ( , , ; , , , ) n 1 2 n 1 2 n f x x x t t t ( , , ; , , , ) 1 2 1 2 = + + + n n n f x x x t t t 任意的n和 因此,一维分布与t无关,二维分布只与t1,t2间隔 有关。 均值 (2) 方差 (3) 相关函数 R(t1,t2)= (4) (1) = E[ (t)] − xf (x,t)dx= = − xf (x)dx a 2 E[(t) − a(t)] = − − (x a) f (x,t)dx 2 = − = − 2 2 (x a) f (x)dx 1 2 2 1 2 1 2 1 2 x x f (x , x ;t ,t )dx dx − − ( ) ( ) = R t 1 − t 2 = R