
第9章差错控制编码 9.1典型例题 【例9-1】已知码组集中有8个码组为(000000)、(001110)、(010101)、(011011)、 (100011)、(101101)、(110110)、(111000),若用于检错,能检出几位错码?若用于纠错, 能纠正几位错码? 解最小码距d=3。所以, 用于检错,由d≥c+1得e=2,能检出2位错码: 用于纠错,由d≥2t+1得t=1,能纠正1位错码。 【例9-2】一码长n=15的汉明码,监督位r应为多少?编码 效率为多少? 解汉明码的监督位数目r与码长n满足关系式2-=n。本题中,n=l5,所以=4。 编码效率为 R=1-1-5 1515 【例9-3】已知(亿,4)循环码的全部码组为 0000000000101100101100101100101100001100011100010100010110011101011000 001110101001111101001111010001110101111111 试写出该循环码的生成多项式g(x)和生成矩阵G(x),并将G(x)化为典型矩阵。 解g(x)是一个常数项为1的(-k)次多项式,本题中n=7,k=4,所以r=3。由 码组集可知生成多项式g(x)=x+x+1。 生成矩阵 「x3g(x) 「x6+x4+x3 G(x)=xg(x) x+x+x x g(x) x+x2+x g(x) x3+x+1 1011000 G=/010100 0010110 0001011 将第1行、第3行、 第4行相加(模2加,下同)并用相加结果取代第1行,将第2行与第 行相加并用相加结果取代第2行,得典型矩阵 「10001017 0100111 G= 0010110 L0001011 【例9-4】已知(亿,3)循环码的监督关系式为 astatazta=0 as+aa+a+ao-0
1 第 9 章 差错控制编码 9.1 典 型 例 题 【例 9-1】 已知码组集中有 8 个码组为(000000)、(001110)、(010101)、(011011)、 (100011)、(101101)、(110110)、(111000),若用于检错,能检出几位错码?若用于纠错, 能纠正几位错码? 解 最小码距 dmin=3。所以, 用于检错,由 dmin≥e+1 得 e=2,能检出 2 位错码; 用于纠错,由 dmin≥2t+1 得 t=1,能纠正 1 位错码。 【例 9-2】 一码长 n=15 的汉明码,监督位 r 应为多少?编码 效率为多少? 解 汉明码的监督位数目 r 与码长 n 满足关系式 2 r -1=n。本题中,n=15,所以 r=4。 编码效率为 15 11 15 4 = = 1− = 1− = n r n k Rc 【例 9-3】 已知(7,4)循环码的全部码组为 0000000 0001011 0010110 0101100 1011000 0110001 1100010 1000101 1001110 1011000 0011101 0100111 1101001 1110100 0111010 1111111 试写出该循环码的生成多项式 g(x)和生成矩阵 G(x),并将 G(x)化为典型矩阵。 解 g(x)是一个常数项为 1 的(n-k)次多项式,本题中 n=7,k=4,所以 r=3。由 码组集可知生成多项式 g(x)=x3 +x+1。 生成矩阵 + + + + + + + + = = ( ) 1 ( ) ( ) ( ) ( ) 3 4 2 5 3 2 6 4 3 2 3 x x x x x x x x x x x g x x g x x g x x g x G x 故 = 0001011 0010110 0101100 1011000 G 将第 1 行、第 3 行、第 4 行相加(模 2 加,下同)并用相加结果取代第 1 行,将第 2 行与第 4 行相加并用相加结果取代第 2 行,得典型矩阵 = 0001011 0010110 0100111 1000101 G 【例 9-4】 已知(7,3)循环码的监督关系式为 a6+a3+a2+a1=0 a5+a2+a1+a0=0

ae+a,+a,=0 a-0 )求该循环码的型监督矩阵和具型生成阵 (②)输入信息码元为101001,求编码后的系统码 解(1)由监督关系式得监督矩阵 [1001110 H= 0100111 100010 0110001 典型监督矩阵 T1011000 H= 1110100 1100010 =[PI,] 0110001 典型生成矩阵 G=[,Q] 「1110] 「100 Q=p=01114=010 1101 001 [1110100 所以 G=0111010 0011101 (②)由典型生成矩阵可得 1110100 G=0111010 0011101 「x6+x3+x+x21「x2g(x) 即G(x)=x3+x4+x3+x =x8(x) x4+x3+x2+1 g(x) 所以生成多项式为 g(x)=x+x+x+1 101码的码多项式为x2+1, '(x2+1)/g(x)=x2+x+(x+1)/g(x) 所以信息码101的循环码多项式为x+x+x+1,对应的循环码组为1010011.001码的码多项 式为1, x/g(x)=1+(x+x2+1)/g(x) 所以信息码001的循环码多项式为x+x+x+1,对应的循环码为0011101。由此可得, 对信息码元101001编码后的系统码为 2
2 a6+a5+a1=0 a5+a4+a0=0 (1) 求该循环码的典型监督矩阵和典型生成矩阵; (2) 输入信息码元为 101001,求编码后的系统码。 解 ( 1) 由监督关系式得监督矩阵 = 0110001 1100010 0100111 1001110 H 典型监督矩阵 [ ] 0110001 1100010 1110100 1011000 H = PIr = 典型生成矩阵 G=[IkQ] = = = 001 010 100 , 1101 0111 1110 k T Q P I 所以 = 0011101 0111010 1110100 G (2) 由典型生成矩阵可得 = 0011101 0111010 1110100 G 即 = + + + + + + + + + = ( ) ( ) ( ) 1 ( ) 2 4 3 2 5 4 3 6 5 4 2 g x x g x x g x x x x x x x x x x x x G x 所以生成多项式为 g(x)=x4 +x3 +x2 +1 101 码的码多项式为 x 2 +1, x 4 (x2 +1)/g(x)=x2 +x+(x+1)/g(x) 所以信息码 101 的循环码多项式为 x 6 +x4 +x+1,对应的循环码组为 1010011。001 码的码多项 式为 1, x 4 /g(x)=1+(x3 +x2 +1)/g(x) 所以信息码 001 的循环码多项式为 x 4 +x3 +x2 +1,对应的循环码为 0011101。由此可得, 对信息码元 101001 编码后的系统码为

10100110011101 【例9-5】已知(2,1,2)卷积码编码器的输出与m,和m的关系为 y:=+电 y2=me+mg 试确定: (1)编码器电路: (2)卷积码的码树图、状态图及网格图。 解()编码器电路如 图9-9(a)所不 (2)卷积码的码树图、状态图及网格图分别如图9-9(6)、(c)、()所示。在码树图中 当输入信息为0码时,状态向上变化,当输入信息为1码时,状态向下变化。在状态图及网 格图中,虚线表示输入信息为1码,实线表示输入信总为0码。图中,a、b、c、d分 别表示m画的状态为00、01、10、11,相邻状态之间的二个码元表示编码器的输出YY2: 输入序列M了囚件四 -⑧ ( d 、 0 11 11 d0 01 01 (e) 图99例9-5图 9.2自测自评 9.2.1自测试题 9-1填空题 ()码组0100110的码重为①,它与码组0011011之间的码距是② (2)线性分组码(63,51)的编码效率为①,卷积码(2,1,7)的编码效率为② (3)已知循环码的生成多项式为x+x+x+1,此循环码可纠正①位错误码元,可检出② 位错误码元。 (4)用(7,4)汉明码构成交织深度为5的交织码,此交织码的码长为①,可纠正②位 突发错误 (⑤)若信息码元为100101,则奇监督码为①,偶监督码为② 9-2已知两码组为(00000)、(11111)。若该码集合用于检错,能检出几位错码?若用于 纠错,能纠正几位错码?若同时用于检错与纠错,各能纠、检几位错码? 9-3己知(7,3)码的生成矩阵为
3 10100110011101 【例 9-5】 已知(2,1,2)卷积码编码器的输出与 m1,m2 和 m3 的关系为 y1=m1+m2 y2=m2+m3 试确定: (1) 编码器电路; (2) 卷积码的码树图、状态图及网格图。 解 (1) 编码器电路如图 9-9(a)所示。 (2) 卷积码的码树图、状态图及网格图分别如图 9-9(b)、(c)、(d)所示。在码树图中, 当输入信息为 0 码时,状态向上变化,当输入信息为 1 码时,状态向下变化。在状态图及网 格图中,虚线表示输入信息为 1 码,实线表示输入信息为 0 码。图中,a、b、c、d 分 别表示 m3m2 的状态为 00、01、10、11,相邻状态之间的二个码元表示编码器的输出 Y1Y2。 图 9-9 例 9-5 图 9.2 自 测 自 评 9.2.1 自测试题 9-1 填空题 (1) 码组 0100110 的码重为 ① ,它与码组 0011011 之间的码距是 ② 。 (2) 线性分组码(63,51)的编码效率为 ① ,卷积码(2,1,7)的编码效率为 ② 。 (3) 已知循环码的生成多项式为 x 4 +x2 +x+1,此循环码可纠正① 位错误码元,可检出 ② 位错误码元。 (4) 用(7,4)汉明码构成交织深度为 5 的交织码,此交织码的码长为 ① ,可纠正 ② 位 突发错误。 (5) 若信息码元为 100101,则奇监督码为 ① ,偶监督码为 ② 。 9-2 已知两码组为(00000)、(11111)。若该码集合用于检错,能检出几位错码?若用于 纠错,能纠正几位错码?若同时用于检错与纠错,各能纠、检几位错码? 9-3 已知(7,3)码的生成矩阵为

「1001110 G=010011 10011101 列出所有许用码组,并求监督矩阵。 9-4(②3,12)格雷码能纠正3个随机错误,证明它是完备码。 9-5已知(7,4)循环码的生成多项式为x+x2+1, )求典型生成矩阵和典型监督矩阵 (②)输入信息码为11001011,求编码后的系统码: (3)求此循环码的全部码组: (4)分析此循环码的纠、检错能力: (5)画出编码器的电路图。 96已知码率为1/2的卷积码的生成多项式为(x)=1,8:(x)=1+x, ()画出编码器的电路图 (②)画出卷积码的树状图、状态图及网格图: (3)当输入信息码为110010时,求卷积码。 9.2.2自测试题解答 9-1填空题 1)①3:②5 (2)①51/63:②1/2 (3)①1:②3 (4①35:②5 (5)①0.②1 9-2最小码距d=5,所以 用于检错,由d≥e+1,得e=4,能检出4位错码: 用于纠错,由d.≥2t+1,得t=2,能纠正2位错码: 同时用于纠错与检错,由d.≥e+t+1,得t=1,e=3,能检出3位错码同时纠正1 位错码。 9-3可将G表示为式(9-8)形式,此(,3)码为循环码。将码组(0011101)循环移位得 到7个许用码组,第8个许用码组为全0码。8个许用码组为 0011101,0111010,1110100,1101001,1010011,0100111,1001110,0000000 由生成矩阵得 [1110 Q=0111 1101 101 P-q's 11 110 011 所以监督矩阵为
4 = 10011101 010011 1001110 G 列出所有许用码组,并求监督矩阵。 9-4 (23,12)格雷码能纠正 3 个随机错误,证明它是完备码。 9-5 已知(7,4)循环码的生成多项式为 x 3 +x2 +1, (1) 求典型生成矩阵和典型监督矩阵; (2) 输入信息码为 11001011,求编码后的系统码; (3) 求此循环码的全部码组; (4) 分析此循环码的纠、检错能力; (5) 画出编码器的电路图。 9-6 已知码率为 1/2 的卷积码的生成多项式为 g1(x)=1,g2(x)=1+x, (1) 画出编码器的电路图; (2) 画出卷积码的树状图、状态图及网格图; (3) 当输入信息码为 110010 时,求卷积码。 9.2.2 自测试题解答 9-1 填空题 (1) ① 3; ② 5 (2) ① 51/63; ② 1/2 (3) ① 1; ② 3 (4) ① 35; ② 5 (5) ① 0; ② 1 9-2 最小码距 dmin=5,所以, 用于检错,由 dmin≥e+1,得 e=4,能检出 4 位错码; 用于纠错,由 dmin≥2t+1,得 t=2,能纠正 2 位错码; 同时用于纠错与检错,由 dmin≥e+t+1,得 t=1,e=3,能检出 3 位错码同时纠正 1 位错码。 9-3 可将 G 表示为式(9-8)形式,此(7,3)码为循环码。将码组(0011101)循环移位得 到 7 个许用码组,第 8 个许用码组为全 0 码。8 个许用码组为 0011101,0111010,1110100,1101001,1010011,0100111,1001110,0000000 由生成矩阵得 = 1101 0111 1110 Q P=QT = 011 110 111 101 所以监督矩阵为

[1011000 1110100 =[PL]= 1100010 0110001 9-4r=m-k=23-12=11 11个校正子的状态数为2-1=2-1=2047 发生1个、2个以及3个随机错误的组合种类数为 C4+C5-23+23x22+23+22x21-2047 2 3×2 因此可知,(23,12)格雷码是完备码。 9-5(1)生成矩阵 「x3gx)x6+x3+x G(x)= xg(x)x+x+x xg(x) x+x+x g(x) x3+x2+1 「1101000 所以 c/010100 0011010 0001101 典型生成矩阵为 「1000110 c=/01011 0010111 =[1Q] 0001101 [10117 由于 P=q=1110 0111 所以典型监督矩阵为 「1011100 e[P.]=1110010 0111001 (2)1100的码多项式为x2+x2 x2(x+x)/g(x)=x41+(x+10/gx) 所以信息码1100的循环多项式为X+x+x+1,对应的循环码组为1100101.1011的码多项式 为x+x+1, x2(x+x+1)/g(x)=x+x2+x2/g(x) 所以信息码1011的循环多项式为x+x+x+x2,对应的循环码组为1011100
5 H=[PIr]= 0110001 1100010 1110100 1011000 9-4 r=n-k=23-12=11 11 个校正子的状态数为 2 r -1=2 11 -1=2047 发生 1 个、2 个以及 3 个随机错误的组合种类数为 2047 3 2 23 22 21 2 23 22 23 2 23 1 23 = + + C + C = + 因此可知,(23,12)格雷码是完备码。 9-5 (1) 生成矩阵 G(x)= + + + + + + + + ( ) 1 ( ) ( ) ( ) 3 2 4 3 5 4 2 6 5 4 2 3 x x x x x x x x x x x g x xg x x g x x g x 所以 G= 0001101 0011010 0110100 1101000 典型生成矩阵为 G= 0001101 0010111 0100011 1000110 =[IkQ] 由于 P=QT = 0111 1110 1011 所以典型监督矩阵为 H=[PIr]= 0111001 1110010 1011100 (2) 1100 的码多项式为 x 3 +x2, x 3 (x3 +x2 )/g(x)=x3 +1+(x2 +1)/g(x) 所以信息码 1100 的循环多项式为 x 6 +x5 +x2 +1,对应的循环码组为 1100101。1011 的码多项式 为 x 3 +x+1, x 3 (x3 +x+1)/g(x)=x3 +x2 +x2 /g(x) 所以信息码 1011 的循环多项式为 x 6 +x4 +x3 +x2,对应的循环码组为 1011100
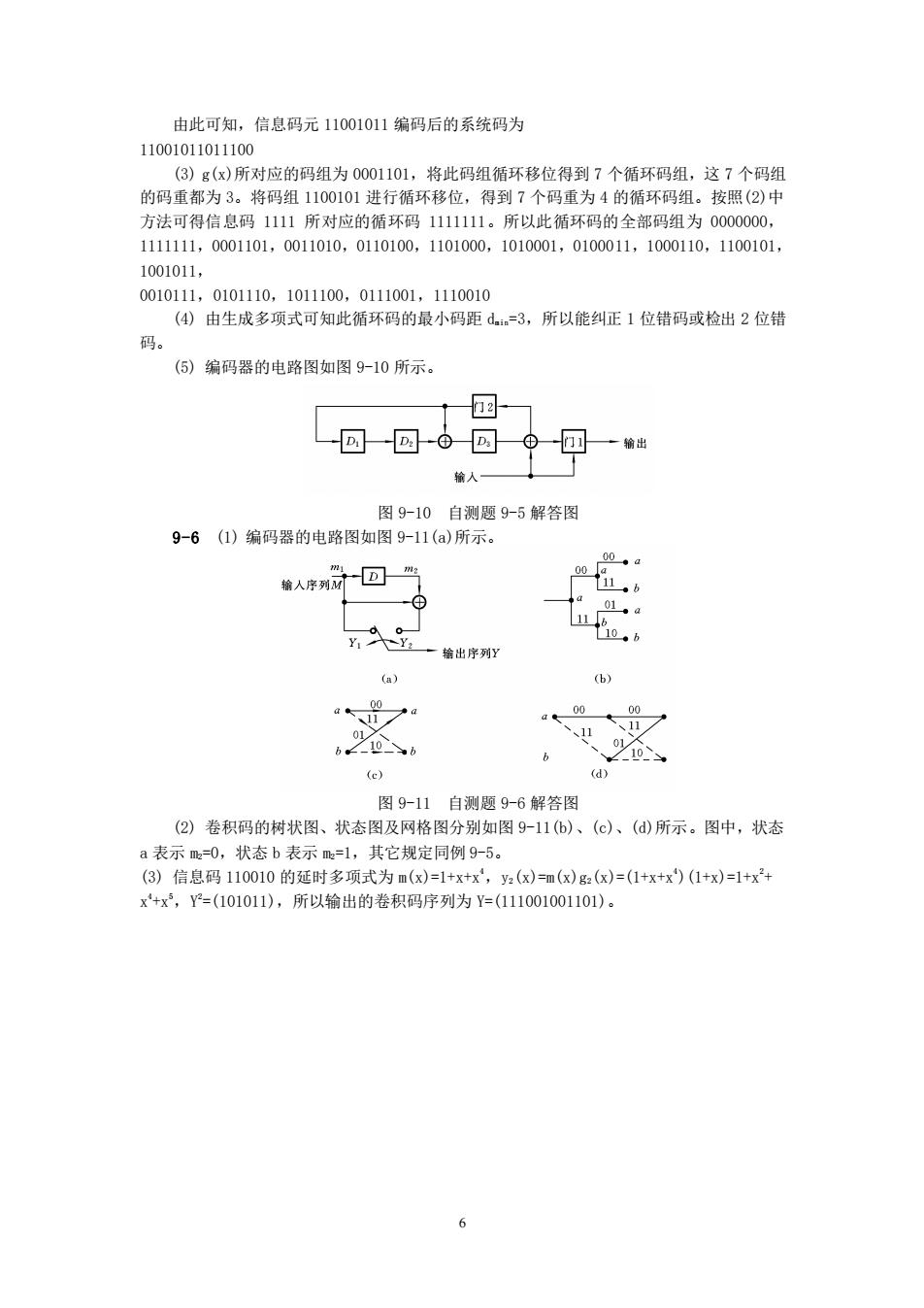
由此可知,信息码元11001011编码后的系统码为 11001011011100 (3)g(x)所对应的码组为0001101,将此码组循环移位得到7个循环码组,这7个码组 的码重都为3。将码组1100101进行循环移位,得到7个码重为4的循环码组。按照(2)中 方法可得信息码1111所对应的循环码1111111。所以此循环码的全部码组为0000000, 1111111,0001101,0011010,0110100,1101000,1010001,0100011,1000110,1100101, 1001011, 0010111,0101110,1011100,0111001,1110010 (4)由生成多项式可知此循环码的最小码距d=3,所以能纠正1位错码或检出2位错 码。 (5)编码器的电路图如图9-10所示。 四 D 门1 ·输出 输人 图9-10自测题9-5解答图 9-6(1)编码器的电路图如图9-11(a)所示。 mi 00◆a 输人序列D m2 00 11。b 01a 10。b 输出序列Y (a) (b) 00 a 00 00 a 01 八11 八11之 6210b 、01 10 (c) (d) 图9-11自测题9-6解答图 (2)卷积码的树状图、状态图及网格图分别如图9-11(b)、(c)、()所示。图中,状态 a表示m=0,状态b表示m=1,其它规定同例9-5。 (3)信息码110010的延时多项式为m(x)=1+x+x',y2(x)=m(x)g2(x)=(1+x+x)(1+x)=1+x2+ x+x,Y=(101011),所以输出的卷积码序列为Y=(111001001101)。 6
6 由此可知,信息码元 11001011 编码后的系统码为 11001011011100 (3) g(x)所对应的码组为 0001101,将此码组循环移位得到 7 个循环码组,这 7 个码组 的码重都为 3。将码组 1100101 进行循环移位,得到 7 个码重为 4 的循环码组。按照(2)中 方法可得信息码 1111 所对应的循环码 1111111。所以此循环码的全部码组为 0000000, 1111111,0001101,0011010,0110100,1101000,1010001,0100011,1000110,1100101, 1001011, 0010111,0101110,1011100,0111001,1110010 (4) 由生成多项式可知此循环码的最小码距 dmin=3,所以能纠正 1 位错码或检出 2 位错 码。 (5) 编码器的电路图如图 9-10 所示。 图 9-10 自测题 9-5 解答图 9-6 (1) 编码器的电路图如图 9-11(a)所示。 图 9-11 自测题 9-6 解答图 (2) 卷积码的树状图、状态图及网格图分别如图 9-11(b)、(c)、(d)所示。图中,状态 a 表示 m2=0,状态 b 表示 m2=1,其它规定同例 9-5。 (3) 信息码 110010 的延时多项式为 m(x)=1+x+x4,y2(x)=m(x)g2(x)=(1+x+x4 )(1+x)=1+x2 + x 4 +x5,Y 2 =(101011),所以输出的卷积码序列为 Y=(111001001101)