
第7章模拟信号的数字传输 7.1典型例题 【例7-1】已知信号m(t)=10cos(20It)cos(200πt),抽样频*E,=250z。 (1)求已抽样信号m()的频谱: (2)要求无失直恢复m(t),试求对m(t)采用的低頫滤波器的截止师率: 3)试求无失真恢复m()情况下的最低抽样频率 解(①)m()=5c0s(220)+5c0s(180rt M(f)=5I[6(f+110)+6(f-110)+6(f+90)+8(f-90)] L(f)=f,∑M(f+nf,)=1250元∑M(f+250m) m(t)的频谱如图7-16所示。 IM.( 图7-16例7-1图 (②)低通滤波器的截止频率为110H2。 (③)根据低通信号抽样定理,最低抽样频率f.=110×2Hz=220Hz。 【例7-2】已知一低通信号m(t)的频谱M(E)为 200 0,其它 (1)假设以300z的速率对m(t)进行理想抽样,试画出已抽样信号m,(t)的频谱草图: (2)若用f.=400Hz的速率抽样,重做上题。 解()■()的频谱如图7-17(a)所示,画()的频谱M()如图7-17)所示。 (2)f.=400z时,m(t)的频谱如图7-17(c)所示
1 第 7 章 模拟信号的数字传输 7.1 典 型 例 题 【例 7-1】 已知信号 m(t)=10cos(20πt)cos(200πt),抽样频率 fs=250 Hz。 (1) 求已抽样信号 ms(t)的频谱; (2) 要求无失真恢复 m(t),试求对 ms(t)采用的低频滤波器的截止频率; (3) 试求无失真恢复 m(t)情况下的最低抽样频率 fs。 解 (1) m(t)=5cos(220πt)+5cos(180πt) M(f)=5π[δ(f+110)+δ(f-110)+δ(f+90)+δ(f-90)] Ms(f)=fs n=− M(f+nfs)=1250π n=− M(f+250n) ms(t)的频谱如图 7-16 所示。 图 7-16 例 7-1 图 (2) 低通滤波器的截止频率为 110 Hz。 (3) 根据低通信号抽样定理,最低抽样频率 fs=110×2 Hz=220 Hz。 【例 7-2】 已知一低通信号 m(t)的频谱 M(f)为 M(f)= − 0,其它 ,| | 200 200 | | 1 f Hz f (1) 假设以 300 Hz 的速率对 m(t)进行理想抽样,试画出已抽样信号 ms(t)的频谱草图; (2) 若用 fs=400 Hz 的速率抽样,重做上题。 解 (1) m(t)的频谱如图 7-17(a)所示,ms(t)的频谱 Ms(f)如图 7-17(b)所示。 (2) fs=400 Hz 时,ms(t)的频谱如图 7-17(c)所示
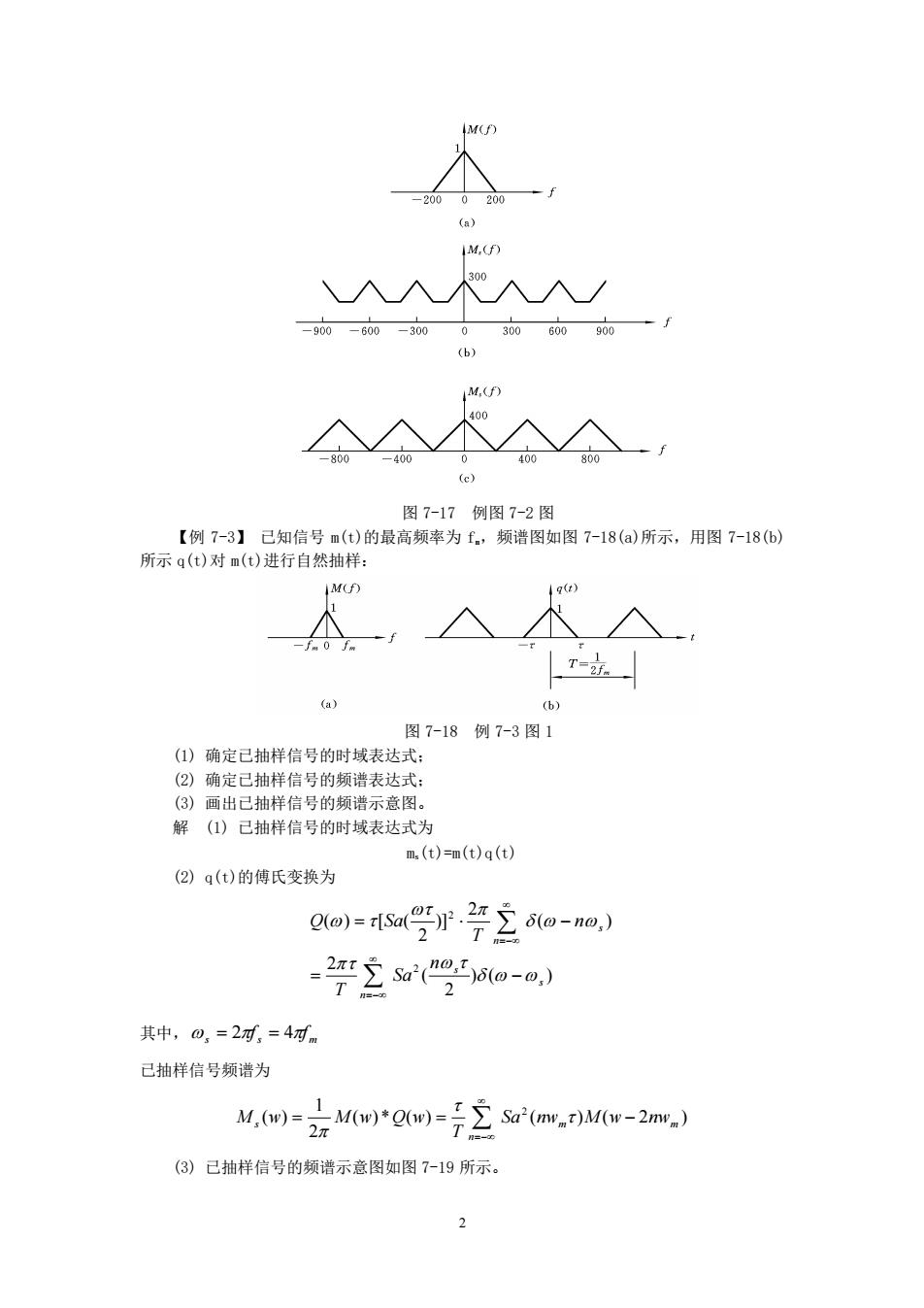
M.( -600-3000 30600900 图7-17例图7-2图 【例7-3】己知信号m()的最高频率为f,频谱图如图7-18(a)所示,用图7-18(b) 所示q(t)对()进行自然抽样 9() T=. w 图7-18例7-3图1 ()确定己抽样信号的时域表达式: (2)确定己抽样信号的频谐表达式: ③)画出己抽样信号的缬谐示意图。 解()已抽样信号的时域表达式为 m.(t)=m(t)q(t) (2)q(t)的傅氏变换为 go)=a(r2立a-nm,) 22%5a-a) 其中,0,=2列,=4河 己抽样信号频谱为 M.()()()(m)M(w-2m) (3)已抽样信号的频谱示意图如图7-19所示
2 图 7-17 例图 7-2 图 【例 7-3】 已知信号 m(t)的最高频率为 fm,频谱图如图 7-18(a)所示,用图 7-18(b) 所示 q(t)对 m(t)进行自然抽样: 图 7-18 例 7-3 图 1 (1) 确定已抽样信号的时域表达式; (2) 确定已抽样信号的频谱表达式; (3) 画出已抽样信号的频谱示意图。 解 (1) 已抽样信号的时域表达式为 ms(t)=m(t)q(t) (2) q(t)的傅氏变换为 ) ( ) 2 ( 2 ( ) 2 )] 2 ( ) [ ( 2 2 s s n s n n Sa T n T Q Sa = − = − =− =− 其中, s s m = 2f = 4f 已抽样信号频谱为 ( ) * ( ) ( ) ( 2 ) 2 1 ( ) 2 m m n s Sa nw M w nw T M w = M w Q w = − =− (3) 已抽样信号的频谱示意图如图 7-19 所示

S02(xr) 图7-19例7-3图2(设=5.) 【例7-4】设m()频谱如图7一18(a)所示,用图7-18)所示q()的单个脉冲对m() 进行瞬时抽样: (1)确定已抽样信号的时域表达式: (②)确定已抽样信号的频域表达式: (③)画出己抽样信号的频谱示意图。 解(Q①)瞬时抽样的原理框图如图7-5(a)所示,已抽样信号的时域表达式为 (2)q(t)的频谱为 9(o)=r5r(9 所以m,()的频谱为 L(o)=号[立Ma+a小q(o)=号s(7)三(o+2) (3)血()的频谱图如图7-20所示。 M.( Sa( 人人人人入 -4f-2f0 2f 图7-20例7-4图 图7-21例7-5例图1 【例7-5】已知模拟信号抽样值的概率密度p(x)如图7-21所示。 ()如果按4电平进行均匀量化,试计算信号与量化噪声功率比: (②)如果按8电平进行均匀量化,试确定量化间隔和量化电平: (③)如果按8电平进行非均匀量化,试确定能使量化信号电平等概的非均匀量化区间, 并画出压缩特性 解(1)分层电平为 x1=-1,x=-0.5,x=0,x=0.5,xg=1 量化电平为 y=-0.75,yg=-0.25,y=0.25,y=0.75 信号功率为 s小布e2时05-团r号 6
3 图 7-19 例 7-3 图 2(设 m 5 f 1 = ) 【例 7-4】 设 m(t)频谱如图 7—18(a)所示,用图 7-18(b)所示 q(t)的单个脉冲对 m(t) 进行瞬时抽样: (1) 确定已抽样信号的时域表达式; (2) 确定已抽样信号的频域表达式; (3) 画出已抽样信号的频谱示意图。 解 (1) 瞬时抽样的原理框图如图 7-5(a)所示,已抽样信号的时域表达式为 ms(t)=[ n=− m(t)δ(t+nT)]*q(t) (2) q(t)的频谱为 Q(ω)=τSa2 ) 2 ( w 所以 ms(t)的频谱为 Ms(ω)= T 1 [ n=− M(ω+2nωm)]·Q(ω)= T Sa2 ) 2 ( w n=− (ω+2nωm) (3) ms(t)的频谱图如图 7-20 所示。 图 7-20 例 7-4 图 图 7-21 例 7-5 例图 1 【例 7-5】 已知模拟信号抽样值的概率密度 p(x)如图 7-21 所示。 (1) 如果按 4 电平进行均匀量化,试计算信号与量化噪声功率比; (2) 如果按 8 电平进行均匀量化,试确定量化间隔和量化电平; (3) 如果按 8 电平进行非均匀量化,试确定能使量化信号电平等概的非均匀量化区间, 并画出压缩特性。 解 (1) 分层电平为 x1=-1, x2=-0.5,x3=0,x4=0.5,x5=1 量化电平为 y1=-0.75, y2=-0.25, y3=0.25, y4=0.75 信号功率为 S= −1 1 x 2 p(x)dx=2 0.5 1 x 2 (1-x)dx= 6 1
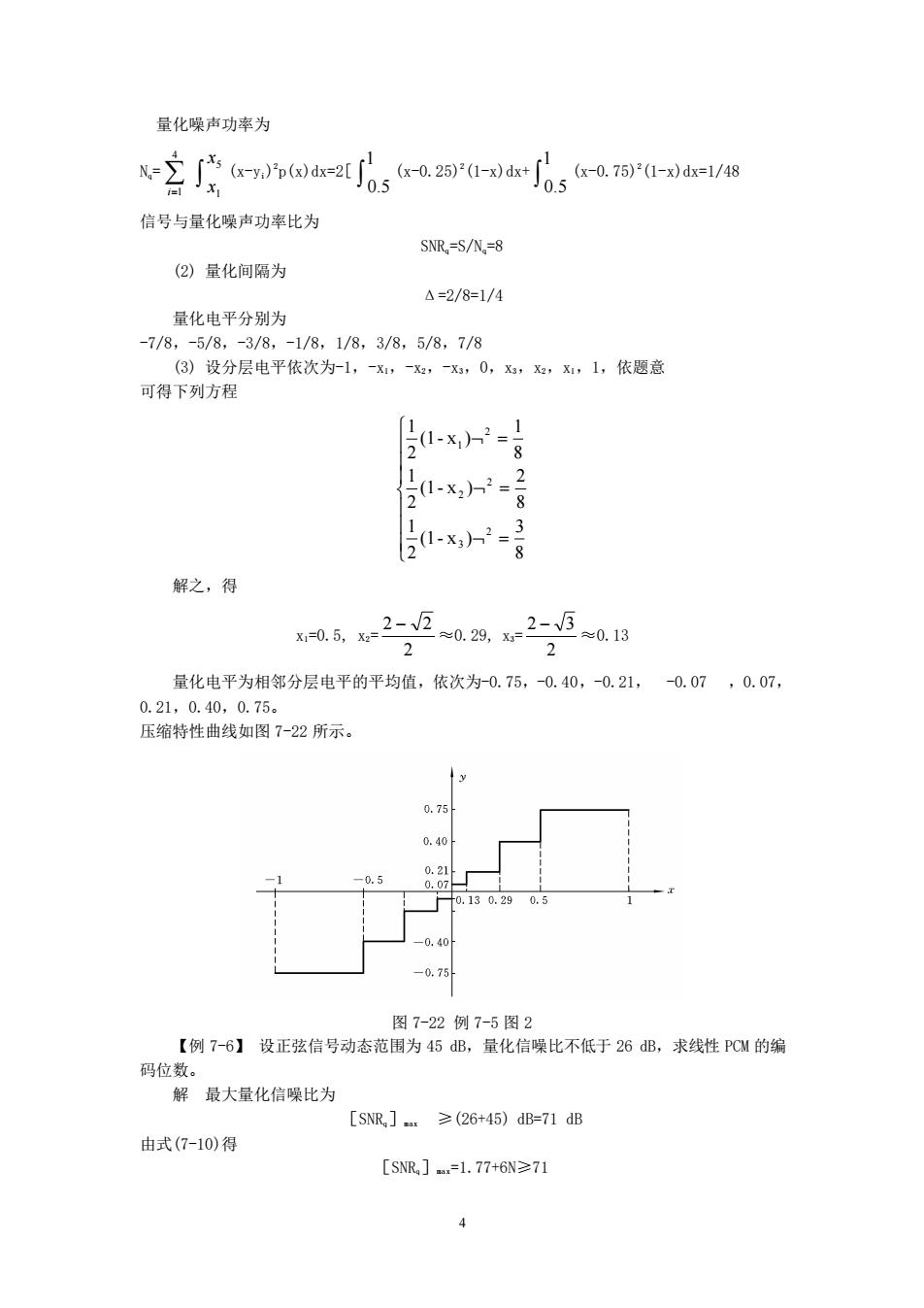
量化噪声功率为 信号与量化噪声功率比为 SNR.=S/N.=8 (②)量化间隔为 △=2/8=1/4 量化电平分别为 -7/8,-5/8,-3/8,-1/8,1/8,3/8,5/8,7/8 (3)设分层电平依次为-1,X,x,-x,0,x,x,1,依题意 可得下列方程 8 x-专 解之,得 2aa25n 2 量化电平为相邻分层电平的平均值,依次为-0.75,0.40,-0.21,-0.07,0.07 0.21,0.40,0.75 压缩特性曲线如图7-22所示。 0.75 0.40 15 .21 .130.290.5 -0.40 7 图7-22例7-5图2 【例7-6】设正弦信号动态范围为45dB,量化信噪比不低于26dB,求线性PCW的编 码位 解最大量化信噪比为 [SNR(26+45)dB=71 dB 由式(7-10)得 [SNR1=1.77+6N≥71
4 量化噪声功率为 Nq= = 1 5 4 1 x x i (x-yi) 2 p(x)dx=2[ 0.5 1 (x-0.25)2 (1-x)dx+ 0.5 1 (x-0.75)2 (1-x)dx=1/48 信号与量化噪声功率比为 SNRq=S/Nq=8 (2) 量化间隔为 Δ=2/8=1/4 量化电平分别为 -7/8,-5/8,-3/8,-1/8,1/8,3/8,5/8,7/8 (3) 设分层电平依次为-1,-x1,-x2,-x3,0,x3,x2,x1,1,依题意 可得下列方程 = = = 8 3 (1- x ) 2 1 8 2 (1- x ) 2 1 8 1 (1- x ) 2 1 2 3 2 2 2 1 解之,得 x1=0.5, x2= 2 2 − 2 ≈0.29, x3= 2 2 − 3 ≈0.13 量化电平为相邻分层电平的平均值,依次为-0.75,-0.40,-0.21, -0.07 ,0.07, 0.21,0.40,0.75。 压缩特性曲线如图 7-22 所示。 图 7-22 例 7-5 图 2 【例 7-6】 设正弦信号动态范围为 45 dB,量化信噪比不低于 26 dB,求线性 PCM 的编 码位数。 解 最大量化信噪比为 [SNRq]max ≥(26+45) dB=71 dB 由式(7-10)得 [SNRq]max=1.77+6N≥71

N>12 即线性PCM的编码位数至少为12才能满足对量化信噪比的要求。 【例7-7】输入信号抽样值x为630个最小量化单位,求A律P0M码、译码输出和量 化误 解(1)先采用逐位比较法确定PCW码组 因为x>0,所以C=1 因为x》128,所以C=1,处于第5一8段落内 因为x0512,所以C= ,处于第7或第8段落内 因为x2×32=64,所以C=1 因为118-64=54>1×32,所以C。=1 即PCM码组为11100011,此码组对应的量化值为512+64+32=608,量化误差为 ©,=630-608=22。编码器的量化误差可大于量化间隔的一半,不是最佳编码器。 (2)译码输出及量化误差 译码输出为编码器的量化电平加上编码器输入信号所处段落的量化间隔的一半,即为 608+32/2=624 译码器输出的量化误差为 630-624=6 讨论译码器首先将对数PCM转换为线性PCM,再进行数模转换。若将A律PCM码11IOOO1I 转换为12位线性码(仅称自然码)101001100000(第1位为符号位) 则译码结果为608,量 化结果不是最佳的(量化误差大于量化间隔的一半)。实际使用的译码器是将A律PCM码按照 表7-2转换为13位线性PC码,再进行数模转换,从而使译码输出(即量化电平)处于量化 区间的中间,实现最佳量化。 出题A律PCy码11100011对应的13位线性PC为1010011100000(第1位为符号位) 对应的十进制数为608×2+32=1248,相当于将编码器的输出电平增大1倍再加上该段落的 量化电平,为了与抽样值进行比较,认为译码吗输出为608+32/2=624。 【例7-8】设简单增量调制器输入的正弦信号频率为3.4kz、幅度为1V,若抽样频 密=32kH2,求量阶0 解正弦信号最大斜率为 Au=1×2×3.4×10 为使△M不过载,必须满足 Au≤0f 由此得 0≥4=20x34x10y=0.6N 32×103 【例7-9】对10路带宽均为300~3400z的模拟信号进行PCM时分复用传输。抽样 速率为8000Hz,抽样后进行8级量化,并编为自然二进制码,码元波形是宽度为ī的矩形 脉冲,且占空比为1。试求传输此时分复用CM信号所需的最小带宽(设码流中无顿同步码 5
5 N≥12 即线性 PCM 的编码位数至少为 12 才能满足对量化信噪比的要求。 【例 7-7】 输入信号抽样值 x 为 630 个最小量化单位,求 A 律 PCM 码、译码输出和量 化误差。 解 (1) 先采用逐位比较法确定 PCM 码组 因为 x>0,所以 C1=1 因为 x>128,所以 C2=1,处于第 5~8 段落内 因为 x>512,所以 C3=1,处于第 7 或第 8 段落内 因为 x2×32=64,所以 C7=1 因为 118-64=54>1×32,所以 C8=1 即 PCM 码组为 11100011,此码组对应的量化值为 512+64+32=608,量化误差为 eq=630-608=22。编码器的量化误差可大于量化间隔的一半,不是最佳编码器。 (2) 译码输出及量化误差 译码输出为编码器的量化电平加上编码器输入信号所处段落的量化间隔的一半,即为 608+32/2=624 译码器输出的量化误差为 630-624=6 讨论 译码器首先将对数PCM转换为线性PCM,再进行数模转换。若将A律PCM码11100011 转换为 12 位线性码(又称自然码)101001100000(第 1 位为符号位),则译码结果为 608,量 化结果不是最佳的(量化误差大于量化间隔的一半)。实际使用的译码器是将 A 律 PCM 码按照 表 7-2 转换为 13 位线性 PCM 码,再进行数模转换,从而使译码输出(即量化电平)处于量化 区间的中间,实现最佳量化。 此题 A 律 PCM 码 11100011 对应的 13 位线性 PCM 码为 1010011100000(第 1 位为符号位), 对应的十进制数为 608×2+32=1248,相当于将编码器的输出电平增大 1 倍再加上该段落的 量化电平,为了与抽样值进行比较,认为译码输出为 608+32/2=624。 【例 7-8】 设简单增量调制器输入的正弦信号频率为 3.4 kHz、幅度为 1 V,若抽样频 率 fs=32 kHz,求量阶σ。 解 正弦信号最大斜率为 Aω=1×2π×3.4×103 为使ΔM 不过载,必须满足 Aω≤σfs 由此得 σ≥ 3 3 32 10 2 3.4 10 = s f A V=0.67V 【例 7-9】 对 10 路带宽均为 300~3400 Hz 的模拟信号进行 PCM 时分复用传输。抽样 速率为 8000 Hz,抽样后进行 8 级量化,并编为自然二进制码,码元波形是宽度为τ的矩形 脉冲,且占空比为 1。试求传输此时分复用 PCM 信号所需的最小带宽(设码流中无帧同步码

等非信号数据)」 解PCM时分复用信号的信息速率为 4-=8×1og8×10khit/s=240khit/ 二进制基带系统的最大频带利用率为 n=2bit/(s·Hz) 所以传输此信号所需最小带宽为 B=R/n=120k 讨论在数字基带传输系统中,信号占空比与正确传输此信号所需带宽无关。信号谱 点带宽与信号占空比有关,占空比越小,信号带宽越大。但信道带宽可以小于信号带宽,只 要无码间串扰,就不会影响信号的正确传输。 【例7-10】计算32电平线性PCM系统在信道误比特率P=10,10,10,10情况下 的最大信噪比SNR。 解SNR 1024 1+4MP1+4096B P=102时,SNR=24.4 P=103时,SNR=200.9 SNR=1019.8 【例7-11】已知正弦信号的频率f,=4k2,试分别设计一个线性PCW系统和一个简单 △M系统,使两个系统的最大量化信噪比都满足30B的要求,比较两个系统的信息速率。 解(1)LPCM系统 [SNR]=(1.76+6N)dB 令1.76+6N=30得 N=5 设抽样频率f,=8kz,则LPOW的信总速率为 R LPCM=8X5 kbit/s=40 kbit/s (2)△M系统 0.04f [SNR.].= -=103 H 令f=4kz,fn=4kz,得 f.=118 kHz 码速率为 R△118kbit/ 可见,当LPO系统和△M系统的量化信噪比相同时,△M系统的信总速率远大于LPC 系统的信息速率。 【例7-12】6路独立信源的最高频率分别为1kz、1kz、2kHz、2kHz、3kz、3 kz,采用时分复用方式进行传输,每路信号均采用8位对数PCW编码。 (1)设计该系统的顿结构和总时隙数,求每个时隙占有的时间宽度及码元宽度 ②)求信道最小传输带宽。 解(1)若选择抽样频率为6kz,则每路信号都符合抽 样定理的要求。不考虑顿同步码、信令码,帧结构如图7-23 TSO TSI TS2 TS3 TS4 TS5 所示。每帧共6个时隙,每个时隙占有的时间宽度为27.8山 166.7 6
6 等非信号数据)。 解 PCM 时分复用信号的信息速率为 Rb=8×log28×10 kbit/s=240 kbit/s 二进制基带系统的最大频带利用率为 ηb=2 bit/(s·Hz) 所以传输此信号所需最小带宽为 Bc=Rb/ηb=120 kHz 讨论 在数字基带传输系统中,信号占空比与正确传输此信号所需带宽无关。信号谱零 点带宽与信号占空比有关,占空比越小,信号带宽越大。但信道带宽可以小于信号带宽,只 要无码间串扰,就不会影响信号的正确传输。 【例 7-10】 计算 M=32 电平线性 PCM 系统在信道误比特率 Pb=10-2 ,10-3 ,10-4 ,10-6 情况下 的最大信噪比 SNR。 解 SNR= M P Pb M 1 4096 1024 1 4 6 2 2 + = + Pb=10-2 时,SNR=24.4 Pb=10-3 时,SNR=200.9 Pb=10-4 时,SNR=726.4 Pb=10-6 时,SNR=1019.8 【例 7-11】 已知正弦信号的频率 fm=4 kHz,试分别设计一个线性 PCM 系统和一个简单 ΔM 系统,使两个系统的最大量化信噪比都满足 30 dB 的要求,比较两个系统的信息速率。 解 (1) LPCM 系统 [SNRq]max=(1.76+6N) dB 令 1.76+6N=30 得 N=5 设抽样频率 fs=8 kHz,则 LPCM 的信息速率为 Rb LPCM=8×5 kbit/s=40 kbit/s (2) ΔM 系统 [SNRq]max= 3 2 3 10 0.04 = f H f k s 令 fk=4 kHz,fH=4 kHz,得 fs=118 kHz 码速率为 Rb ΔM=118 kbit/s 可见,当 LPCM 系统和ΔM 系统的量化信噪比相同时,ΔM 系统的信息速率远大于 LPCM 系统的信息速率。 【例 7-12】 6 路独立信源的最高频率分别为 1 kHz、1 kHz、2 kHz、2 kHz、3 kHz、3 kHz,采用时分复用方式进行传输,每路信号均采用 8 位对数 PCM 编码。 (1) 设计该系统的帧结构和总时隙数,求每个时隙占有的时间宽度及码元宽度; (2) 求信道最小传输带宽。 解 (1) 若选择抽样频率为 6 kHz,则每路信号都符合抽 样定理的要求。不考虑帧同步码、信令码,帧结构如图 7-23 所示。每帧共 6 个时隙,每个时隙占有的时间宽度为 27.8 μ

s,码元宽度为3.5μs。 图7-23例7-12图1 (2)信息速率为 R=(6000帧/秒)×(6时隙/帧)×(8bit/时隙)=288k灿it/s 信道最小传输带宽为 B.=R/2=144kHz 讨论根据抽样定理,这6路信号的抽样频率可以分别为2kH2、2kz、4kⅡz、4kHz 6k、6k 每顿12个时隙,6路信号占有的时隙数分别为 合名、2欧卫个不,每的室定为 、1、2 μs,码元宽度为5.2μs,信息速率为R=(2000帧/秒)×(12时隙/帧)×(⑧bit/时隙)=192 kbit/s,最小传输带宽为96kz。 TSO TSI TS2 TS3 TS4 TS5 TS6 TS7 TS8 TS9 TS1O TSII 人 -500s 7.2自测自评 7.2.1自测试题 7-1填空题 (1)线性PCM的量化噪声与信号功率大小有关吗?①,它适用于动态范围②的信号。 (②)在对数CM中,量化噪声功率与信号功率的定性关系是①,适用动态范围②的 信号。 (3)工程上常用的△M是①,工程上常用的两种对数POM是②和③,中国使用的 是① (4)在对数PM和自适应△M中,抗信道噪声能力较强的是①,量化噪声较小的是 ②。 (5)采用自适应△M的目的是①,采用△-Σ调制的目的是② (6)在对数PCM中采用折叠二进制码的好处是①,线性PM的编码位增加1位,量化 信噪比增大②B。 (?)简单增量调制器输入为单频正弦信号,当信号功率不变而采样频率增大1倍、信号 频率减小1倍时,量化信噪比增大①B:若信号频率不变,采样频率不变,信号幅度减 小1倍,则量化信噪比增大②dB。 (⑧)ADPCM的量化信噪比与对数PCM基本相同,原因是在ADPCM中采取了两个重要措施 它们是①和② (⑨)当输入信号为0电平时,简单增量调制器的输出序列是①,A律13折线脉码调 制器的输出序列是②。 (10)在时分复用系统中,顿同步码的作用是①,用△M传输1路语音是否需要帧同 步码?②。 (1)在时分复用中有两种复接方式,它们是①和②,两者的主要区别是③ 7-2设带通信号的频率范围为2~2.5Mz: (1)求采样频率: (②)作出己抽样信号的频谱示意图。 7-3如图7-25所示,信号频谱为理想矩形,信号通过H()网络后再抽样。 >
7 s,码元宽度为 3.5 μs。 图 7-23 例 7-12 图 1 (2) 信息速率为 Rb=(6000 帧/秒)×(6 时隙/帧)×(8 bit/时隙)=288 kbit/s 信道最小传输带宽为 Bc=Rb/2=144 kHz 讨论 根据抽样定理,这 6 路信号的抽样频率可以分别为 2 kHz、2 kHz、4 kHz、4 kHz、 6 kHz、6 kHz。帧周期为 500 μs,每帧 12 个时隙,6 路信号占有的时隙数分别为 1、1、2、 2、3、3,此时帧结构如图 7-24 所示。每帧共 12 个时隙,每个时隙占用的时间宽度为 41.7 μs,码元宽度为 5.2 μs,信息速率为 Rb=(2000 帧/秒)×(12 时隙/帧)×(8 bit/时隙)=192 kbit/s,最小传输带宽为 96 kHz。 7.2 自 测 自 评 7.2.1 自测试题 7-1 填空题 (1) 线性 PCM 的量化噪声与信号功率大小有关吗? ① ,它适用于动态范围 ② 的信号。 (2) 在对数 PCM 中,量化噪声功率与信号功率的定性关系是 ① ,适用动态范围 ② 的 信号。 (3) 工程上常用的ΔM 是 ① ,工程上常用的两种对数 PCM 是 ② 和 ③ ,中国使用的 是④ 。 (4) 在对数 PCM 和自适应ΔM 中,抗信道噪声能力较强的是 ① ,量化噪声较小的是 ② 。 (5) 采用自适应ΔM 的目的是 ① ,采用Δ-Σ调制的目的是 ② 。 (6) 在对数 PCM 中采用折叠二进制码的好处是 ① ,线性 PCM 的编码位增加 1 位,量化 信噪比增大 ② dB。 (7) 简单增量调制器输入为单频正弦信号,当信号功率不变而采样频率增大 1 倍、信号 频率减小 1 倍时,量化信噪比增大 ① dB;若信号频率不变,采样频率不变,信号幅度减 小 1 倍,则量化信噪比增大 ② dB。 (8) ADPCM 的量化信噪比与对数 PCM 基本相同,原因是在 ADPCM 中采取了两个重要措施, 它们是 ① 和 ② 。 (9) 当输入信号为 0 电平时,简单增量调制器的输出序列是 ① ,A 律 13 折线脉码调 制器的输出序列是 ② 。 (10) 在时分复用系统中,帧同步码的作用是 ① ,用ΔM 传输 1 路语音是否需要帧同 步码? ② 。 (11) 在时分复用中有两种复接方式,它们是 ① 和 ② ,两者的主要区别是 ③ 。 7-2 设带通信号的频率范围为 2~2.5 MHz: (1) 求采样频率; (2) 作出已抽样信号的频谱示意图。 7-3 如图 7-25 所示,信号频谱为理想矩形,信号通过 H1(ω)网络后再抽样

M 0-匹回-9-回w 图7-25自测题7-3图 (1)求抽样角频率: (2)画出已抽样信号的频谱: (3)试分析接收网络品( 应如何设计才没有信号失真。 7-4对正弦信号进行线性脉冲调制编码,如果信号动态范围为40B,要求在整个动 态范围内信噪比不低于30B,问需要几位编码。 7-5采用13折线A律编码,设最小量化间隔为1个量化单位,已知抽样值为95个量 化单位: (①)试求此时编码器输出码组,并计算量化误差 ②)写出对应于该7位码(不包括极性码)的均匀量化1位码和12位码。 7-6若A律13折线编码器的过载电平为V=5V,输入抽样脉冲幅度为0.9375V。 设最小量化间隔为2个单位,最大量化器的分层电平为4096个单位。求编码器的输出码组, 并计算量化误差。 7-7己知△M调制系统中低通滤波器频率范围是300~3400Hz,求在不过载条件下, 该△M系统输出的最大量化信噪比5R,假设抽样频率为10k、16k2、32k2、4格kH26 kz。 7-8对3路信号进行时分复用,这3路信号的最高频率分别是2kH2、4kz和8k2, 信号的量化级都是256。在满足抽样定理所规定的抽样速率下,试求码元传输速率是多少? 购高祥路统将位路信S的员商级均为4进行抽能时分复用,格引 输,信号占空比 ()抽样后信号按8级量化,求PCM信号谱零点带宽及最小信道带宽: (2)抽样后信号按128级量化,求PCM信号谱零点带宽及最小信道带宽。 7-10设信号幅度为均匀分布,最高频率为4kz。对此信号先进行线性PCM编码,再 进行2DPSR调制后传输,要求最大量化信噪比不低于30dB,求此PC/2DPSR系统所需要的 最小信道带宽。 7.2.2自测试题解答 7-1填空题 1)①无关:②小 (2)①信号功率小,量化噪声功率小:②大 ②A律PCM: ③μ律PCM:④A律PCM (4)①自适应△M:②对数PCM (⑤)①提高小信号的量化信噪比:②改普高颜信号的量化信噪比 (6)①小信号的误码噪声功率小:②6 ()①15:②-6 (⑧)①自适应预测:②自适应量化 (9)①101010: ②1000000010000000或0000000000000000 (10)①标明一帧的起始时刻,以便分接信号:②不需要 (11)①同步复接:②准同步复接:③同步复接的各个低次群信号的信息速率完全 相同,而准同步复接的各个低次群信号的信息速率标称值相同,但实际值有一定误差
8 图 7-25 自测题 7-3 图 (1) 求抽样角频率; (2) 画出已抽样信号的频谱; (3) 试分析接收网络 H2(ω)应如何设计才没有信号失真。 7-4 对正弦信号进行线性脉冲调制编码,如果信号动态范围为 40 dB,要求在整个动 态范围内信噪比不低于 30 dB,问需要几位编码。 7-5 采用 13 折线 A 律编码,设最小量化间隔为 1 个量化单位,已知抽样值为-95 个量 化单位: (1) 试求此时编码器输出码组,并计算量化误差; (2) 写出对应于该 7 位码(不包括极性码)的均匀量化 11 位码和 12 位码。 7-6 若 A 律 13 折线编码器的过载电平为 Vmax=5 V,输入抽样脉冲幅度为-0.9375 V。 设最小量化间隔为 2 个单位,最大量化器的分层电平为 4096 个单位。求编码器的输出码组, 并计算量化误差。 7-7 已知ΔM 调制系统中低通滤波器频率范围是 300~3400 Hz,求在不过载条件下, 该ΔM 系统输出的最大量化信噪比 SNRq。假设抽样频率 fs 为 10 kHz、16 kHz、32 kHz、48 kHz64 kHz。 7-8 对 3 路信号进行时分复用,这 3 路信号的最高频率分别是 2 kHz、4 kHz 和 8 kHz, 信号的量化级都是 256。在满足抽样定理所规定的抽样速率下,试求码元传输速率是多少? 7-9 若对 12 路语音信号(每路信号的最高频率均为 4 kHz)进行抽样和时分复用,将所 得脉冲用 PCM 基带系统传输,信号占空比为 1: (1) 抽样后信号按 8 级量化,求 PCM 信号谱零点带宽及最小信道带宽; (2) 抽样后信号按 128 级量化,求 PCM 信号谱零点带宽及最小信道带宽。 7-10 设信号幅度为均匀分布,最高频率为 4 kHz。对此信号先进行线性 PCM 编码,再 进行 2DPSK 调制后传输,要求最大量化信噪比不低于 30 dB,求此 PCM/2DPSK 系统所需要的 最小信道带宽。 7.2.2 自测试题解答 7-1 填空题 (1) ① 无关; ②小 (2) ① 信号功率小,量化噪声功率小; ②大 (3) ① CVSD; ② A 律 PCM; ③ μ律 PCM; ④ A 律 PCM (4) ① 自适应ΔM; ② 对数 PCM (5) ① 提高小信号的量化信噪比; ② 改善高频信号的量化信噪比 (6) ① 小信号的误码噪声功率小; ② 6 (7) ① 15; ② -6 (8) ① 自适应预测; ② 自适应量化 (9) ① 101010.; ②1000000010000000.或 0000000000000000. (10) ① 标明一帧的起始时刻,以便分接信号; ② 不需要 (11) ① 同步复接; ② 准同步复接; ③ 同步复接的各个低次群信号的信息速率完全 相同,而准同步复接的各个低次群信号的信息速率标称值相同,但实际值有一定误差

7-2(1)信号带宽B=(2.5-2)Mmz=0.5Mz f./R=5.N=5.f.=2f./N=1MH2 (②)设带通信号m(t)的频谱如图7-26(a)所示,则己抽样信号m()的频谱如图7-26(c) 所示。图7-266)为抽样冲激序列的频谱。 MO) (a) 3 2 0 1 0 ( 图7-26自测题7-2解答图 -/ 图7-27自测题7-3解答题 7-3①抽样信号角顿率为。≥2。 (2)已抽样信号m()的频谱示意图如图7-27所示(设,=2.) 1 ③H,o)=M,loko. 0,其它 7-4SNR=(4.77+201gD+6NW)d 因为D=A/(2N),A.=V,所以 201gD.=-3dB 动态范围为40B,即 201gD=-43dB 令4.77-43+6N≥30,得 N≥11.37,取=12即可 7-5(1)因为-9564+4×4=80,所以C。=1 因为95>80+4×2=88,所以C= 因为95>88+4×1=92,所以C,=1 输出码组为00110111 量化误差(译码输出量化误差)为 9
9 7-2 (1) 信号带宽 B=(2.5-2) MHz=0.5 MHz fH/B=5,N=5,fs=2fH/N=1 MHz (2) 设带通信号 m(t)的频谱如图 7-26(a)所示,则已抽样信号 ms(t)的频谱如图 7-26(c) 所示。图 7-26(b)为抽样冲激序列的频谱。 图 7-26 自测题 7-2 解答图 图 7-27 自测题 7-3 解答题 7-3 (1) 抽样信号角频率为ωs≥2ωm。 (2) 已抽样信号 ms(t)的频谱示意图如图 7-27 所示(设ωs=2ωm)。 (3) = 0,其它 ,| | ( ) 1 ( ) 2 2 m H M 7-4 SNRq=(4.77+20 lgD+6N) dB 因为 D=A/(2V),Amax=V,所以 20 lgD|max=-3 dB 动态范围为 40 dB,即 20 lgD|min=-43 dB 令 4.77-43+6N≥30,得 N≥11.37, 取 N=12 即可。 7-5 (1) 因为-9564+4×4=80,所以 C6=1 因为 95>80+4×2=88,所以 C7=1 因为 95>88+4×1=92,所以 C8=1 输出码组为 00110111 量化误差(译码输出量化误差)为

95-(92+4/2)=1量化单位 ②7位码01011的均匀量化11位码和12位码分别为00101100和0010110。 7-6用最小量化间隔表示抽样信号 x=-09375×4096-384(绿小量化间隔 5 2 因为-384<0,所以C,=0 因为256<384<512,所以C,C,C,=101 因为384=256+8×16=384,所以C=1,CC,C=000 编码器输出码组为01011000 量化误差为384+32/2-384=16最小量化间隔 7-7[sRJ-004 当f.=300z,£,=64kz时量化信噪比最大 [SNR]-0.04×64 0.32×348.4x10 4k、8k、16k,编码位数为8,故码元传输 速率为 R=(4+8+16)×8kBd=224kBd 7-9(1)R=(12×8×1og:8)kbit/s=288bit/s 频零点带宽为 R-R=288 入 最小信道带宽为 B.=-R=144 kHz (2)R=(12×8×1oga128)kbit/s=672kbit/s =R=672 B-7=36k 7-10[SNR]=6N=30 编码位数N5 选择抽样频率f.=8kz PC信号码速率R=8×5kbit/s=40khit/s 2DPSK系统最大顷带利用率为 n=lbit/(s·Hz) 所需最小信道带宽为 B=R/n=40k2 10
10 95-(92+4/2)=1 量化单位 (2) 7 位码 0110111 的均匀量化 11 位码和 12 位码分别为 00001011100 和 000010111100。 7-6 用最小量化间隔表示抽样信号 xk= 2 4096 5 0.9375 − =-384(最小量化间隔) 因为-384<0,所以 C1=0 因为 256<384<512,所以 C2C3C4=101 因为 384=256+8×16=384,所以 C5=1,C6C7C8=000 编码器输出码组为 01011000 量化误差为 384+32/2-384=16 最小量化间隔 7-7 [SNRq]max= k H s f f f 2 3 0.04 当 fk=300 Hz,fs=64 kHz 时量化信噪比最大 [SNRq]max= 0.3 3.4 0.04 64 2 3 =3.4×104 10lg[SNRq]max=45 dB 7-8 3 路信号的抽样频率分别为 4 kHz、8 kHz、16 kHz,编码位数为 8,故码元传输 速率为 RB=(4+8+16)×8 kBd=224 kBd 7-9 (1) Rb=(12×8×log28) kbit/s=288 kbit/s 频零点带宽为 Bs= 1 =Rb=288 kHz 最小信道带宽为 Bc= 2 1 Rb=144 kHz (2) Rb=(12×8×log2128) kbit/s=672 kbit/s Bs= 1 =Rb=672 kHz Bc= 2 1 Rb=336 kHz 7-10 [SNRq]max=6N=30 编码位数 N=5 选择抽样频率 fs=8 kHz PCM 信号码速率 Rb=8×5 kbit/s=40 kbit/s 2DPSK 系统最大频带利用率为 ηb=1 bit/(s·Hz) 所需最小信道带宽为 Bc=Rb/ηb=40 kHz