海南大学：《通信原理》课程教学资源（习题解答）第1章 绪论、第2章 确知信号与随机信号分析、第3章 信道

第1章绪论 1.1典型例题 【例1-1】进制离散信源输出四个独立符号A、B、C、D。 0人CD出现的概率分别为好名名分家人RCD每个符号所销带 的信息量和信源嫡 (②)A、B、C、D等概，求信源熵 解(1)根据式(1-1)，有 ()=(-log)bit2 bit I(B)=I(C)=(-log)bit=3 bit I(D)=(-log)bit=1 bit 根据式(1-2)，有 (2)根据式(1-3)，有 风0=(1og4)bit/符号=2bit/符号 【例12】某数字道临系统用正弦我波的四个相位Q子、子来传输信息，这 个相位是互相独立的 ()每秒钟内0、无、 兰出现的次数分别为0、1，2，求此适系统 的码速率和信息速率： (②)每秒钟内这四个相位出现的次数都为250，求此通信系统的码速率和信息速率。 解()每秒钟传输1000个相位，即每秒钟传输1000个符号，故 R-=1000Bd 每个特号出现的分为P0-·)片P()(每个号所含 的平均信息量为 信息速率R=100×1子bi/s=1750b1t/6 (②)每秒钟传输的相位数仍为1000，故 R.=1000Bd 此时四个符号出现的概率相等，故 八D=2bit/符号 R=(1000×2)bit/s=2000bit/s 【例1-3】一个由字母A、B、C、D组成的字，对于传输的每一个字母用二进制脉冲编

1 第 1 章 绪 论 1.1 典 型 例 题 【例 1-1】 进制离散信源输出四个独立符号 A、B、C、D。 (1) A、B、C、D 出现的概率分别为 4 1 、 8 1 、 8 1 、 2 1 ，求 A、B、C、D 每个符号所携带 的信息量和信源熵； (2) A、B、C、D 等概，求信源熵。 解 (1) 根据式(1-1)，有 I(A) = (-log2 4 1 )bit=2 bit I(B) = I(C) = (-log2 8 1 )bit=3 bit I(D) = (-log2 2 1 )bit=1 bit 根据式（1-2），有 H(X)=（ 4 1 ×2+ 8 1 8×3+ 8 1 ×3+ 2 1 ×1）bit/符号=1 4 3 bit/符号 (2) 根据式(1-3)，有 H(X)=(log24)bit/符号=2 bit/符号 【例 1-2】 某数字通信系统用正弦载波的四个相位 0、 2  、π、 2 3 来传输信息，这四 个相位是互相独立的。 (1) 每秒钟内 0、 2  、π、 2 3 出现的次数分别为 500、125、125、250，求此通信系统 的码速率和信息速率； (2) 每秒钟内这四个相位出现的次数都为 250，求此通信系统的码速率和信息速率。 解 (1) 每秒钟传输 1000 个相位，即每秒钟传输 1000 个符号，故 RB=1000 Bd 每个符号出现的概率分别为 P(0)= 2 1 ,P       2  = 8 1 ,P(π)= 8 1 ,P       2 3 = 4 1 ，每个符号所含 的平均信息量为 H(X)=( 2 1 ×1+ 8 2 ×3+ 4 1 ×2)bit/符号=1 4 3 bit/符号 信息速率 Rb=(1000×1 4 3 )bit/s=1750 bit/s (2) 每秒钟传输的相位数仍为 1000，故 RB=1000 Bd 此时四个符号出现的概率相等，故 H(X)=2 bit/符号 Rb=(1000×2)bit/s=2000 bit/s 【例 1-3】 一个由字母 A、B、C、D 组成的字，对于传输的每一个字母用二进制脉冲编

码，00代替A,01代替B,10代替C,11代替D,每个脉冲宽度为5s。 (1)不同的字母等概率出现时，试计算传输的平均信息速率： (2)若每个字母出现的概率分别为 e, 试计算传输的平均信息速率。 解()四个字母构成四进制符号，每个符号由两个脉冲构成，故一个符号的持续时间 即码元宽度为2×5。码速率为 R2x5X10B陆100Bd 等概时，平均信总速率为 R=Ralog:4=200 bit/s (2)每个符号的平均信总量为 =(0.2×2.32+0.5×2+0.3×1.74)bit/符号=1.985bit/符号 则平均信息速率为 R=R·0=(100X1.985)bit/s=198.5bit/s 【例1-4】某信源的符号集由A、B、C、D和E组成，设每一符号独立出现，其出现概 率分别为1/4、1/8、1/8、3/16和5/16：信源以1000Bd速率传送信总。 ()求传送1小时的信息量： (2)求传送1小时可能达到的最大信息量。 解(1)信源熵为 5 平均速率为 R=R·l0=(1000×2.23)bit/s=2.23×103bit/s 1小时传输的信息量为 =(2.23×103×3600)bit=8.028hit (②)等概时信源熵为最大值，即 L.=(1og5)bit/符号=2.322bit/符号 1小时传输的最大信息量为 L.=(2.322×1000×3600)bit=8.359Mhit 1.2自测自评 1.2.1自测试题 1-1设载波为正弦信号。 (1)AM信号与4ASK信号在波形上有何区别？ 2)FM信号与4FS信号在波形上有何区别？ (3)W信号与4PSK信号在波形上有何区别 1-2如何衡量模拟通信系统的有效性和可靠性？ 1-3为什么用频带利用率来衡量数字通信系统的有效性？ 1-4在多进制通信系统中，为什么误比特率小于误码率？试以四进制系统

2 码，00 代替 A，01 代替 B，10 代替 C，11 代替 D，每个脉冲宽度为 5 ms。 (1) 不同的字母等概率出现时，试计算传输的平均信息速率； (2) 若每个字母出现的概率分别为 PA= 5 1 15,PB= 4 1 ,PC= 4 1 ,PD= 10 3 试计算传输的平均信息速率。 解 (1) 四个字母构成四进制符号，每个符号由两个脉冲构成，故一个符号的持续时间 即码元宽度为 2×5 ms。码速率为 RB= 3 2 5 10 1 −   Bd=100 Bd 等概时，平均信息速率为 Rb=RBlog24=200 bit/s (2) 每个符号的平均信息量为 H(X)=( 5 1 log25+ 4 2 log24+ 10 3 log2 3 10 )bit/符号 =(0.2×2.32+0.5×2+0.3×1.74) bit/符号=1.985 bit/符号 则平均信息速率为 Rb=RB·H(X)=(100×1.985)bit/s=198.5 bit/s 【例 1-4】 某信源的符号集由 A、B、C、D 和 E 组成，设每一符号独立出现，其出现概 率分别为 1/4、1/8、1/8、3/16 和 5/16；信源以 1000 Bd 速率传送信息。 (1) 求传送 1 小时的信息量； (2) 求传送 1 小时可能达到的最大信息量。 解 (1) 信源熵为 H(X)=（ 4 1 log24+ 8 2 log28+ 16 3 log2 3 16 + 16 5 log2 5 16 ）bit/符号=2.23 bit/符号 平均速率为 Rb=RB·H(X)=(1000×2.23)bit/s=2.23×103 bit/s 1 小时传输的信息量为 I=(2.23×103×3600)bit=8.028 Mbit (2) 等概时信源熵为最大值，即 Hmax=(log25)bit/符号=2.322 bit/符号 1 小时传输的最大信息量为 Imax=(2.322×1000×3600)bit=8.359 Mbit 1.2 自 测 自 评 1.2.1 自测试题 1-1 设载波为正弦信号。 (1) AM 信号与 4ASK 信号在波形上有何区别? (2) FM 信号与 4FSK 信号在波形上有何区别? (3) PM 信号与 4PSK 信号在波形上有何区别? 1-2 如何衡量模拟通信系统的有效性和可靠性? 1-3 为什幺用频带利用率来衡量数字通信系统的有效性? 1-4 在多进制通信系统中，为什幺误比特率小于误码率?试以四进制系统

为例加以说明。 1-5设英文字盘e. x出现的概率分别为0.023、0.105、0.001、0.0 02,试分别求出它们的信息量 1-6已知等概独立的二进制数字信号的信息速率为2400bit/s (1)求此信号的码速率和码元宽度： (②)将此信号变为四进制信号，求此四进制信号的码速率、码元宽度和信息速率。 1-7某4ASK系统的四个振幅值分别为0、1、2、3，这四个振幅是石相种立的。 )振幅0、1、2、3出现的概率分别为0.4、0.3、0.2、0.1，求各种振幅信号的平均 信息量 2)设每个振幅的持续时间（即码元宽度）为1μs,求此系统的信息速率。 1-8一个四进制数字通信系统，码速率为1kBd,连续工作1小时后，接收端收到的错 码为10个。 )求误码率 (②)四个符号独立等概且错一个码元时发生1bit信息错误，求误信率 1.2.2自测试题解答 1-1(1)AM信号的振幅连续变化，振幅的状态个数无限。4SK信号仅有4个振幅，振 幅变化不连续。 (②)FM信号的频率连续变化，频率的状态数无限。4SK信号的频率数仅4个，频率变 化不连续。 (③)PW信号的相位连续变化，相位的状态数无限。4PSK信号仅有4个相位，相位变 化不连续。 1-2用信号带宽来衡量模拟通信系统的有效性，且带宽越小有效性越好。用解调器输出 信噪比来衡量模拟通信系统的可靠性，且信噪比越大可靠性越好。 1-3因为传输数字信号占用的信道带宽可以小于数字信号带宽，频带利用率表示每赫效 带宽信道所能传输的码速率或信息速率。显然，频带利用率越大，数字通信系统的有效性越 f。 1-4在四进制系统中，若四个符号独立等概，且每个符号携带2bt信息量，这四个符 号可以用二进制符号00、01、11、10来表示。当00错为11时有2bit信息量发生错误， 当00错为01或10时仅有1bit信息量错误。只有当1个码元中的2bit全部错误时，误 信率才等于误码率，实际上这种情况出现的概率比较小，故误信率小于误码率。 1-5I(c)=(-1oga0.023)bit=5.44bit /(e)=(-1og0.105)bit=3.25bit /(o)=(-1og,0.001)bit=9.97bit 1)=(-1og0.002)bit=8.96bit 1-6(1) R=R/1og(2400/1og2)Bd=-2400Bd 1 s=0.42ms Rg2400 2 R=(2400/1og4)Bt=1200Bd 1 TR20s0.阳 R=2400b/s

3 为例加以说明。 1-5 设英文字母 c、e、o、x 出现的概率分别为 0.023、0.105、0.001、0.0 02，试分别求出它们的信息量。 1-6 已知等概独立的二进制数字信号的信息速率为 2400 bit/s。 (1) 求此信号的码速率和码元宽度； (2) 将此信号变为四进制信号，求此四进制信号的码速率、码元宽度和信息速率。 1-7 某 4ASK 系统的四个振幅值分别为 0、1、2、3，这四个振幅是互相独立的。 (1) 振幅 0、1、2、3 出现的概率分别为 0.4、0.3、0.2、0.1，求各种振幅信号的平均 信息量； (2) 设每个振幅的持续时间(即码元宽度)为 1 μs，求此系统的信息速率。 1-8 一个四进制数字通信系统，码速率为 1kBd，连续工作 1 小时后，接收端收到的错 码为 10 个。 (1) 求误码率； (2) 四个符号独立等概且错一个码元时发生 1 bit 信息错误，求误信率。 1.2.2 自测试题解答 1-1 (1) AM 信号的振幅连续变化，振幅的状态个数无限。4ASK 信号仅有 4 个振幅，振 幅变化不连续。 (2) FM 信号的频率连续变化，频率的状态数无限。4FSK 信号的频率数仅 4 个，频率变 化不连续。 (3) PM 信号的相位连续变化，相位的状态数无限。4PSK 信号仅有 4 个相位，相位变 化不连续。 1-2 用信号带宽来衡量模拟通信系统的有效性，且带宽越小有效性越好。用解调器输出 信噪比来衡量模拟通信系统的可靠性，且信噪比越大可靠性越好。 1-3 因为传输数字信号占用的信道带宽可以小于数字信号带宽，频带利用率表示每赫兹 带宽信道所能传输的码速率或信息速率。显然，频带利用率越大，数字通信系统的有效性越 好。 1-4 在四进制系统中，若四个符号独立等概，且每个符号携带 2 bit 信息量，这四个符 号可以用二进制符号 00、01、11、10 来表示。当 00 错为 11 时有 2 bit 信息量发生错误， 当 00 错为 01 或 10 时仅有 1 bit 信息量错误。只有当 1 个码元中的 2 bit 全部错误时，误 信率才等于误码率，实际上这种情况出现的概率比较小，故误信率小于误码率。 1-5 I(c)=(-log20.023)bit=5.44 bit I(e)=(-log20.105)bit=3.25 bit I(o)=(-log20.001)bit=9.97 bit I(x)=(-log20.002)bit=8.96 bit 1-6 (1) RB=Rb/log2M=(2400/log22)Bd=2400 Bd T= RB 1 = 2400 1 s=0.42 ms (2) RB=(2400/log24)Bd=1200 Bd T= RB 1 = 1200 1 s=0.83 ms Rb=2400 b/s

1-71)lD=(-0.41og,0.4-0.31og0.3-0.21og,0.2-0.110g,0.1)bit/符号 =(0.4×1.32+0.3×1.74+0.2×2.32+0.1×3.32bit/符号 =1.8 6bit/符号 此即为各种振幅信号的平均信息量。 (2)码速率 R-1 MBd 故信息速率R=R·作(1×10°×1.846)bit/s=l,846Mbit/s 1-8(1)1小时传输的码元数为 1×1000×3600=36×10 误码率为 P.=10/(36×10)=2.8×10 (②)1小时传输的信总量为 (36×10×2)bit=72×103bit 因错误信总量为10bit,故误信率为 R=10/(72×10)=1.4×10 推而广之，若独立等概的M进制信号在传输过程中发生1个码元错误时仅错1bit信息 量，则误信率与误码率之间的关系为 B=P/1ogM

4 1-7 (1)H(X)=(-0.4log20.4-0.3log20.3-0.2log20.2-0.1log20.1)bit/符号 =(0.4×1.32+0.3×1.74+0.2×2.32+0.1×3.32)bit/符号 =1.846 bit/符号 此即为各种振幅信号的平均信息量。 (2) 码速率 RB= T 1 =1 MBd 故信息速率 Rb=RB·H=(1×106×1.846)bit/s=1.846 Mbit/s 1-8 (1) 1 小时传输的码元数为 1×1000×3600=36×105 误码率为 Pe=10/(36×105 )=2.8×10-6 (2) 1 小时传输的信息量为 (36×105×2)bit=72×105 bit 因错误信息量为 10 bit，故误信率为 Pb=10/(72×105 )=1.4×10-6 推而广之，若独立等概的 M 进制信号在传输过程中发生 1 个码元错误时仅错 1 bit 信息 量，则误信率与误码率之间的关系为 Pb=Pe/log2M

第2章确知信号与随机信号分析 2.1典型例题 【例2-1】若信号x(t)=Cos@:t,试求其自相关函数R(t)、功率谱密度P()、信号功率 S 解r)=m Tmaama0+a caa.omo. csemc'+e-me') 根据傅氏变换的频移运算特性，得 P(o)=R(t)e-dr=(ee+emc)e-me'dr =号·2a6@-a,)+o+m,月 -76o-0,)+80+@.】 S=2Podo=226o-a.】 或 【例2-2】若x(t)=D(t),试求其自相关函数R(t)、能量谱密度E(ω)、能量E。 解 R()=[D(1)D(t+r)di=T(t-1) fl-liT.sT R(r) 式中 f()= (0其它 R(t)的图形如图2-6所示。 图26例22图 由表2-2知，三角函数f()的傅氏变换为 根据傅氏变换的时移和放大特性，得

5 第 2 章 确知信号与随机信号分析 2.1 典 型 例 题 【例 2-1】 若信号 x(t)=cosωct，试求其自相关函数 R(τ)、功率谱密度 P(ω)、信号功率 S。 解 R( ) = T →  lim − + / 2 / 2 ( ) ( ) 1 T T x t x t dt T  →  = T lim t t dt T c c T T cos cos ( ) 1 / 2 / 2   + − →  = T lim t dt T c c T T [ cos (2 ) cos ] 2 1 / 2 1 / 2  + +   − = ( ) 4 1 cos 2 1 j r j r c e c e c     − = + 根据傅氏变换的频移运算特性，得    − − −  − −  =   = +      P R e d e c e c e c d j j r j r j r ( ) 4 1 ( ) ( ) = 4 1 · 2 [ ( ) ( )]    −c +  +c = [ ( ) ( )] 2   c   c  − + +    −  − = = [ ( − )] 2 2 1 ( ) 2 1 S P d   c      = 2 1 2 4 1  = 或 S= T →  lim 2 1 cos ( ) 1 2 / 2 / 2 = − t dt T c T T  【例 2-2】 若 x(t)=DT(t)，试求其自相关函数 R(τ)、能量谱密度 E(ω)、能量 E。 解 ( ) = ( ) ( + ) = ( − )   − R D t D t dt Tf t T T 式中 f (t) =    −  其它  0, 1 | t | /T, | t | T R(τ)的图形如图 2-6 所示。 图 2-6 例 2-2 图 由表 2-2 知，三角函数 f(t)的傅氏变换为 )] 2 ( ) [ ( T F T Sa   = 根据傅氏变换的时移和放大特性，得

E)-FISa o)=f产0t=h=T 根据式(2-4)，有 E=Eft=T【a(gTer =T[[SalT'd=T 由此得 [Sa(fT)'df =1/T 【例2-3】求随机相位正弦波：(t)=Cos(“.t+中)的自相关函数、功率谱密度和功率。 =Ecos(u.t+中)[cos(o:t+中)cosa:t-sin(o:t+中)sinwet] =cos(w.t)Ecos2(w.t+)-sin(w.I)E [cos(w.t+)sin(w.t+)] oas(u.te+cos2a1+vl -sin(sin) sinosin. P(o)-R()d-+] s上po)aw-月 小结由例2-1和例2-3可知，确知信号cost和随相信号cos(:t+中)的相关 函数、 功率谱密度是相同的 【例2-4】求乘积信号z(t)=x()y()的自相关函数和功率谱密度。已知x()和y() 是统计独立的平稳随机过程，且它们的自相关函数及功率谱密度函数分别为R(1)、R,(t)、 P,(o)、P(o)。 解 R(r)=E「z(t)·z(t+r)1 =E[x()·y()·x(t+t)·y(t+)] =E[x(t)·x(t+T)·y()·y(t+T)门 因为x(t)与y()是统计独立的平稳随机过程，故x(t)·x(t+t)与y(t)·y(t+t)也是统计 独立的，所以 R(t)=E[x(t)·x(t+t)]·E[y(t)·y(t+t)] 6

6 j T e T E T Sa    2 2 2 ) ] 2 ( ) [ ( − = E f t dt dt T T T = = =  −  − / 2 / 2 2 () ( ) 根据式（2-4），有 E E f df T Sa fT e df j fT  2 2 4 ( ) [ ( )] −  −  −  = = = T Sa fT df = T   − 2 2 [ ( )] 由此得 [Sa( fT)] df 1/T 2 =   −  【例 2-3】 求随机相位正弦波ξ(t)=cos(ωct+φ)的自相关函数、功率谱密度和功率。 式中，ωc 是常数，φ是在区间(0，2π)上均匀分布的随机变量。 解 R(τ)＝E［cos(ωct+φ)cos(ωct+ωcτ+φ)］ =Ecos(ωct+φ)［cos(ωct+φ)cosωcτ-sin(ωct+φ)sinωcτ］ =cos(ωcτ)Ecos2 (ωct+φ)-sin(ωcτ)E［cos(ωct+φ)sin(ωct+φ)］ =cos(ωcτ)E       [1+ cos 2( + )] 2 1 c t  -sin(ωcτ)E 2 1 sin2(ωct+φ) 2 1 =cosωcτ+ 2 1 cosωcτ  2 0 cos2(ωct+φ)   d      2 1 - 2 1 sinωcτ  2 0 sin(2ωct+φ)   d      2 1 = 2 1 cosωcτ P(ω)=  R( ) e -jωτdτ= 2  ［δ(ω-ωc)+δ(ω+ωc)］ S= 2 1   − P(ω)dω= 2 1 小结 由例 2-1 和例 2-3 可知，确知信号 cosωct 和随相信号 cos(ωct+φ)的相关 函数、功率谱密度是相同的。 【例 2-4】 求乘积信号 z(t)=x(t)y(t)的自相关函数和功率谱密度。已知 x(t)和 y(t) 是统计独立的平稳随机过程，且它们的自相关函数及功率谱密度函数分别为 Rx(τ)、Ry(τ)、 Px(ω)、Py(ω)。 解 Rz(τ)=E［z(t)·z(t+τ)］ =E［x(t)·y(t)·x(t+τ)·y(t+τ)］ =E［x(t)·x(t+τ)·y(t)·y(t+τ)］ 因为 x(t)与 y(t)是统计独立的平稳随机过程，故 x(t)·x(t+τ)与 y(t)·y(t+τ)也是统计 独立的，所以 Rz(τ)＝E［x(t)·x(t+τ)］·E［y(t)·y(t+τ)］

=R,(T)·R,() 根据傅氏变换的卷积定理，可得 R.(o)=[P.(u)柳，()] 2π 小结由此例愿可得到一个重要结论：两个独立的平稳随机过程，其乘积的自相关函数等 于它们各自的自相关函数的乘积，其乘积的功率谱密度函数等于各自的功幸谱密度函数的卷 积。可将此结论称为随机信号的卷积定理。在傅氏变换的卷积定理中，并不要求两个时域相 乘的确知信号是独立的 【例2-5】设随机变量中在(0,2)内均匀分布，求Asi中的数学期望和方差，其中A 为常数 a=E(asin中)=(asin中)· A.1 oe[siro]=e[-0-es2wj]- 【例2-6】设z(t)=%coso,t-xasinwot是一随机过程，若x和是彼此独立且具有 均值为0、方差为。的正态随机变量，试求： (1)E[z()]、E[z(t)]: (2)z(t)的一维概率密度函数f(2: (3)B(t,.t)与R(t.t2)。 思路和x是随机变量，而cost、sin,t是随时间变化的。不同取样时刻，co ut、sin“t的值不同，因而z(t)在不同的取样时刻是不同的随机变量，所以z(t)是 随机过程。但每一时刻cos“t、sinwot的值是一个常数，故在对z(t)作统计处理时可认 为coswot、sinot为常数。 (1)E [z(t)]=E(xIcoswot-x'sinwot) oswt.E(x)-sinwt.E(x)=0 E[z,(t)]=E(x,c0 Dot-x:@ot+) ost·E()-sin'wot·E(xxa)+sin2wot·E(x) 因为x1和x2独立，所以 E(xx2)=E(x)·E(x2) 又因为E(x)=E(x)=0,E(x)=E(x)=o,故 E [z'(t)]=o'(cos'wot+sin'wot)=o* (②)因为x、x都是高斯分布，z()是x和的线性组合，所以z()也服从高斯分布 其一维概率密度函数为 = f()= 2m5p(-25》 (3)R(t,t)=E[z(t)·z(ta)] =E [(xcost-xsint).(xicostz-xsinta)] =E(xcos weticoswota+xsinwotlsinwota -X1X2c0su。t1 sinwat.2-x1x2cosu。t2 sinwot:) 1

7 =Rx(τ)·Ry(τ) 根据傅氏变换的卷积定理，可得 Pz(ω)= 2 1 ［Px(ω)*Py(ω)］ 小结由此例题可得到一个重要结论：两个独立的平稳随机过程，其乘积的自相关函数等 于它们各自的自相关函数的乘积，其乘积的功率谱密度函数等于各自的功率谱密度函数的卷 积。可将此结论称为随机信号的卷积定理。在傅氏变换的卷积定理中，并不要求两个时域相 乘的确知信号是独立的。 【例 2-5】 设随机变量φ在(0,2π)内均匀分布，求 Asinφ的数学期望和方差，其中 A 为常数。 解 a=E(Asinφ)=  2 0 (Asinφ)· 2 1 dφ =-A· 2 1 ·cosφ 0 2 =0 σ2 =E［A 2 sin2φ］=E 2 2 2 1 (1 cos 2 ) 2 1 A = A        −  【例 2-6】 设 z(t)=x1cosω0t-x2sinω0t 是一随机过程，若 x1 和 x2 是彼此独立且具有 均值为 0、方差为σ2 的正态随机变量，试求： (1) E［z(t)］、 E［z 2 (t)］; (2) z(t)的一维概率密度函数 f(z)； (3) B(t1,t2)与 R(t1, t2)。 思路 x1 和 x2 是随机变量，而 cosω0t、sinω0t 是随时间变化的。不同取样时刻，cos ω0t、sinω0t 的值不同，因而 z(t)在不同的取样时刻是不同的随机变量，所以 z(t)是一个 随机过程。但每一时刻 cosω0t、sinω0t 的值是一个常数，故在对 z(t)作统计处理时可认 为 cosω0t、sinω0t 为常数。 解 (1) E［z(t)］=E(x1cosω0t-x 2 sinω0t) =cosω0t·E(x1)-sinω0t·E(x2)=0 E［z2(t)］=E(x2 1cos 2ω0t-x1x2sin2ω0t+x2 2sin2ω0t) =cos 2ω0t·E(x2 1)-sin2ω0t·E(x1x2)+sin2ω0t·E(x2 2) 因为 x1 和 x2 独立，所以 E(x1x2)=E(x1)·E(x2) 又因为 E(x1)=E(x2)=0，E(x2 1)=E(x2 2)=σ 2，故 E［z 2 (t)］=σ 2 (cos2ω0t+sin2ω0t)=σ 2 (2) 因为 x1、x2 都是高斯分布，z(t)是 x1 和 x2 的线性组合，所以 z(t)也服从高斯分布， 其一维概率密度函数为 ) 2 exp( 2 1 ( ) 2 2   z f z = − (3) R(t1,t2)=E［z(t1)·z(t2)］ =E［(x1cosω0t1-x2sinω0t1)·(x1cosω0t2-x2sinω0t2)］ =E(x2 1cosω0t1cosω0t2+x2 2sinω0t1sinω0t2 -x1x2cosω0t1sinω0t2-x1x2cosω0t2sinω0t1)

=a(coswot coswot:+sin@tisintz) B(t,ta)=R(ti,ta)-E [z(t)].E [z(ta)]=o'cos 【例2-7】若随机过程z(t)=m(t)cos(oot+中)，其中，m(t)是广义平稳随机过程，且 自相关函数R(T)为 1+t,.-1<t<0 R()1-t0≤t<1 0.,其它 中是服从均匀分布的随机变量，它与m(t)彼此独立。 (1)证明z(t)是广义平稳的： (2)绘出自相关函数R(t)的波形 ()求功率谱密度.()及功率S 解()若E[z()] 常数，R(t,t+t)=R(t),则z(t)为广义平稳的 E[z(t)]=E[m(t)·cos(o。t+φ)] =E[m(t)]·E[cos(wt+中)][m(t)与Φ独立] =E[m(t)]·[2(cos wtcos中-sinwtsin中) =a·0=0 R(t,t)=E[z(t)·z(t)] =E[m(ti)·cos(ut+中)·m(t)·cos(at2+中)] =E[m(t1)·m(t2)]·E[cos(u0t1+Φ)cos(a0t2+Φ)] 5os,+)+2+cosa,6-4) R()·aos@,6+4)+21+osa,4-5川 -()( 可见，z(t)的均值与t无关，自相关函数只与时间间隔ī有关，所以z(t)是广义平稳 的。 (2)R.()=-R-(t)cos.t 其波形如图2-7所示，图中设f。=3。 3)因为 F [cosoT]=[8(0+00)+8(0- )1 F[R(r)]=5a(2 图2-7例2-7图 2‘2玩F[cosu,r]帮[R(t)门 (u)= 1 所以

8 =σ 2 (cosω0t1cosω0t2+sinω0t1sinω0t2) =σ 2 cosω0τ B(t1,t2)=R(t1，t2)-E［z(t1)］·E［z(t2)］=σ 2 cosω0τ 【例 2-7】 若随机过程 z(t)=m(t)cos(ω0t+φ)，其中，m(t)是广义平稳随机过程，且 自相关函数 Rm(τ)为 Rm(τ)=      −   + −   其它   0, 1 , 0 1 1 , 1 0     φ是服从均匀分布的随机变量，它与 m(t)彼此独立。 (1) 证明 z(t)是广义平稳的； (2) 绘出自相关函数 Rz(τ)的波形； (3) 求功率谱密度 Pz(ω)及功率 S。 解 (1) 若 E［z(t)］=常数，Rz(t1,t1+τ)=R(τ)，则 z(t)为广义平稳的。 E［z(t)］=E［m(t)·cos(ω0t+φ)］ =E［m(t)］·E［cos(ω0t+φ)］［m(t)与φ独立］ =E［m(t)］·  2 0 (cosω0tcosφ-sinω0tsinφ) 2 1 dφ =a·0=0 Rz(t1,t2)=E［z(t1)·z(t2)］ =E［m(t1)·cos(ω0t1+φ)·m(t2)·cos(ω0t2+φ)］ =E［m(t1)·m(t2)］·E［cos(ω0t1+φ)cos(ω0t2+φ)］ =Rm(τ)·E       + + + cos ( − ) 2 1 cos[ ( ) 2 ] 2 1 0 1 2 0 1 2  t t   t t =Rm(τ)·       + + + cos ( − )] 2 1 cos[ ( ) 2 ] [ 2 1 [ 0 1 2 0 1 2 E  t t  E  t t =Rm(τ)·       + cos ( − ) 2 1 0 0 1 2  t t = 2 1 cosω0τ·Rm(τ) 可见，z(t)的均值与 t 无关，自相关函数只与时间间隔τ有关，所以 z(t)是广义平稳 的。 (2) Rz(τ)= 2 1 Rm(τ)cosω0τ 其波形如图 2-7 所示，图中设 f0=3。 (3) 因为 F［cosω0τ］=π［δ(ω+ω0)+δ(ω-ω 0)］ F［Rm(τ)］=Sa2       2 w 图 2-7 例 2-7 图 所以 Pz(ω)＝ 2 1 · 2 1 ·F［cosω0τ］*F［Rm(τ)］

6(() ")+s2 2 S=R.(0)=0.5 因为P(o)=7[6(o+w)+6(w-u] R.(o)p[R.(]=5号 立经[suso-门6 04e,0】 2 【例2-8】设信道噪声是一个均值为0、双边功率谱密度为/2的高斯白噪声，接收 机输入端的收滤波器是一个中心角频率为“、带宽为B的理想带通滤波器，且f>B: ()求收滤波器输出噪声时域表达式和双边功率谱密度： (②)求收滤波器输出噪声的自相关函数： (3)求收滤波器输出噪声功率： (④)写出收滤波器输出噪声的一维概率密度函数。 解(1)因为c>B,所以收带通滤波器输出噪声是一个窄带白噪声，它的时域表达式 为 n(t)=v(t)cos [.t+(t)]=n.(t)cosw.t-n.(t)sinw.t n(t)的双边功率谱密度为 .±-B/2≤∫≤±f+B/2 P.(f)=2 0,其它 P.(f)的图形如图2-8所示 P.O B 图2-8例2-8图 ②)P.(o)-2[a(o+u)+n(u-u】

9 = 4 1 π·π［δ(ω+ω0)+δ(ω-ω0)］*Sa2       2 w = )] 2 ) ( 2 [ ( 4 1 2 0 2 w w0 Sa w w Sa − + + S=Rz(0)=0.5 因为 m(t)与 cos(ω0t+φ)不相关，所以也可将 m(t)的功率谱密度 Pm(ω)与 cos(ω0t+φ)的功率谱密度 Pc(ω)进行卷积运算得到 Pz(f)： 因为 Pc(ω)＝ 2  ［δ(ω+ω0)+δ(ω-ω0)］ Pm(ω)=F［Rm(τ)］=Sa2 )` 2 (  所以 Pz(ω)= 2 1 Pc(ω)*Pm(ω) = 2 1 · 2  ［δ(ω+ω0)+δ(ω-ω0)］*Sa2 )` 2 (  = )] 2 ) ( 2 [ ( 4 1 2 0 2 2    − + + Sa Sa 【例 2-8】 设信道噪声是一个均值为 0、双边功率谱密度为 n0/2 的高斯白噪声，接收 机输入端的收滤波器是一个中心角频率为ωc、带宽为 B 的理想带通滤波器，且 fc>>B： (1) 求收滤波器输出噪声时域表达式和双边功率谱密度； (2) 求收滤波器输出噪声的自相关函数； (3) 求收滤波器输出噪声功率； (4) 写出收滤波器输出噪声的一维概率密度函数。 解 (1) 因为 fc>>B，所以收带通滤波器输出噪声是一个窄带白噪声，它的时域表达式 为 n(t)=v(t)cos［ωct+φ(t)］=nc(t)cosωct-ns(t)sinωct n(t)的双边功率谱密度为 Pn(f)=       −    + 其它  0, , / 2 / 2 2 0 f B f f B n c c Pn(f)的图形如图 2-8 所示。 图 2-8 例 2-8 图 (2) Pn(ω)= 2 0 n ［D2πB(ω+ωc)+D2πB(ω-ωc)］

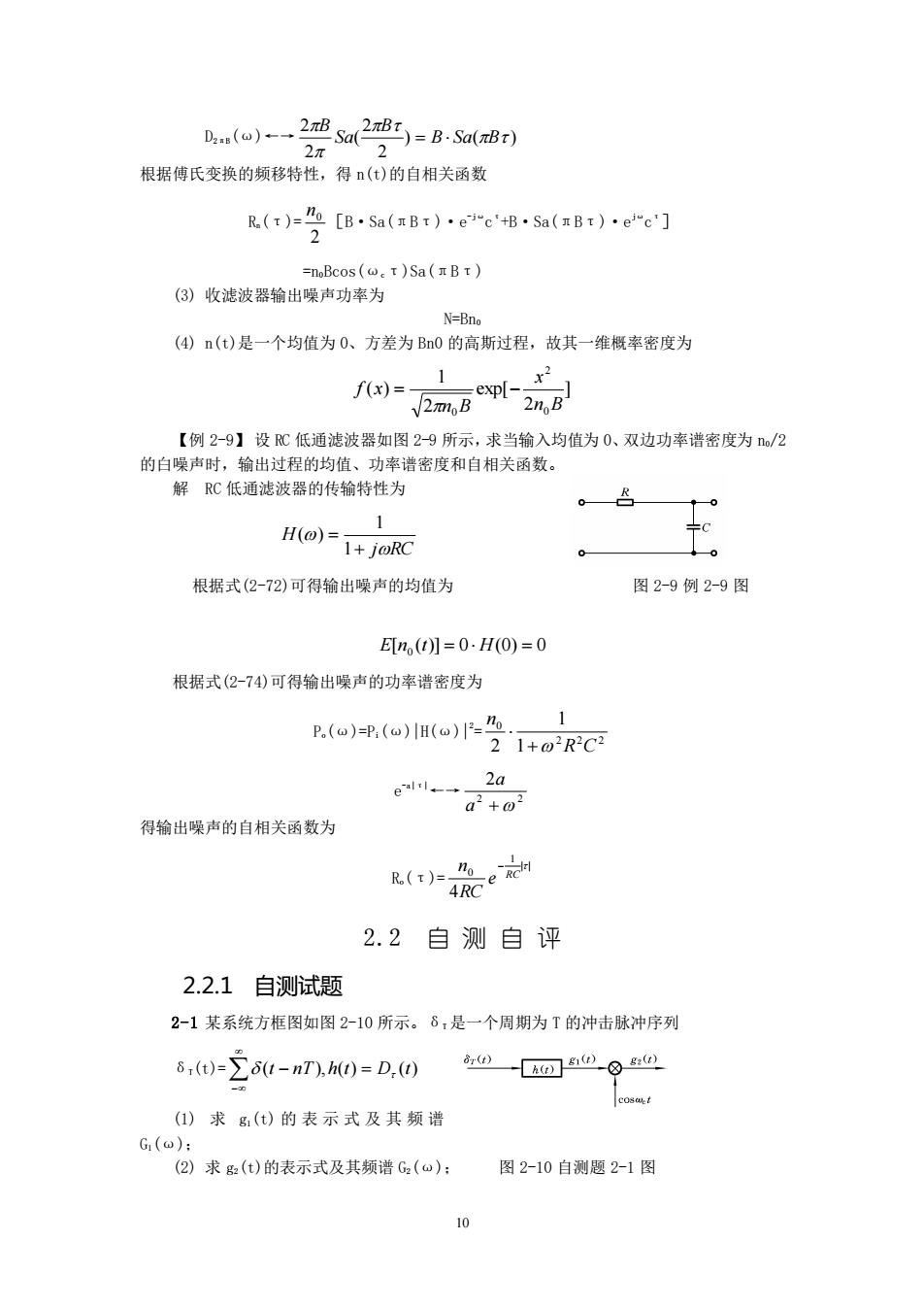
no）-2a25)=B-a(B到） 根据傅氏变换的频移特性，得(t)的自相关函数 R()[BSa(Bt)Sa(Br)] =nBcos(.)Sa(B) (3)收滤波器输出噪声功率为 N=Bno (④)n(t)是一个均值为0、方差为B0的高斯过程，故其一维概率密度为 f(x)= 2mBp-2日 【例2-9】设心低通滤波器如图29所示，求当输入均值为0、双边功率谱密度为/2 的白噪声时，输出过程的均值、功率谱密度和自相关函数。 解RC低通滤波器的传输特性为 。 H()-1+joRC 1 根据式(2-72)可得输出噪声的均值为 图29例2-9图 En(】=0-HO)=0 根据式(2-74)可得输出噪声的功率谱密度为 P(o)=p,(a)H(o)= 21+o2R2C2 ell-→ 2a a+0 得输出噪声的自相关函数为 (归是e 2.2自测自评 2.2.1自测试题 2-1某系统方框图如图2-10所示。6，是一个周期为T的冲击脉冲序列 6(t)=∑81-nT),h0=D.0 (仙)求g()的表示式及其频谐 G(w): (2)求g影(t)的表示式及其频谱G:(u): 图2-10自测题2-1图

10 D2πB(ω)←→ ) ( ) 2 2 ( 2 2       B Sa B B Sa B =  根据傅氏变换的频移特性，得 n(t)的自相关函数 Rn(τ)= 2 0 n ［B·Sa(πBτ)·e -jω c τ +B·Sa(πBτ)·e jω c τ］ =n0Bcos(ωcτ)Sa(πBτ) (3) 收滤波器输出噪声功率为 N=Bn0 (4) n(t)是一个均值为 0、方差为 Bn0 的高斯过程，故其一维概率密度为 ] 2 exp[ 2 1 ( ) 0 2 0 n B x n B f x = −  【例 2-9】 设 RC 低通滤波器如图 2-9 所示，求当输入均值为 0、双边功率谱密度为 n0/2 的白噪声时，输出过程的均值、功率谱密度和自相关函数。 解 RC 低通滤波器的传输特性为 j RC H   + = 1 1 ( ) 根据式(2-72)可得输出噪声的均值为 图 2-9 例 2-9 图 E[n0 (t)] = 0 H(0) = 0 根据式(2-74)可得输出噪声的功率谱密度为 Po(ω)=Pi(ω)|H(ω)|2 = 2 2 2 0 1 1 2 R C n +  e -a|τ|←→ 2 2 2 a + a 得输出噪声的自相关函数为 Ro(τ)= | | 1 0 4  RC e RC n − 2.2 自 测 自 评 2.2.1 自测试题 2-1 某系统方框图如图 2-10 所示。δT 是一个周期为 T 的冲击脉冲序列 δT(t)=   − (t − nT), h(t) = D (t)   (1) 求 g1(t) 的表示式及其频谱 G1(ω)； (2) 求 g2(t)的表示式及其频谱 G2(ω)； 图 2-10 自测题 2-1 图