
第5章数字基带传输系统 5.1典型例题 【例5-1】已知二元信息序列为0100110000100001100000000010,求DB3码,并画出 其波形图。 思路二元信息码中有4组4个连0码,第1、2组之间1码个数为奇数,第2、3组之 间及第3、4组之间1码的个数为偶数。据此,可以进行取代变换。取代变换之后再加符号 就得到HD3码。画波形图时应注意脉冲占空比为O.5,这是国际标准,不能随意画。 解取代变换后原二进制序列变为 010011000V1000V11B00VB00V010 加符号后得HDB,码。HDB,码及其波形图如图5-20所示。 皮形图 图5-20例5-1图 位的有4个连1和4个连0交替出现的序列,画出单极性非归零码、日 思路单极性非归零码、A码的编码规律比较简单。对DB码的编码规律比较熟悉后 即可直接由信息代码求出HDB码,并进而画出波形图。由于序列中4个连1和4个连0是 交替出现的,故相邻的4个连0码组之间1码的个数肯定是偶数个,因此DB码中的每个 取代节都应是BOOv。 解单极性非归零码、AM码、DB3码及其波形图如图521所示 信息代码 NRZ战形 AMm码1-11-100001-11-100001-11-10000 AMI被形 几LrLL HDB码 1-11-1B00V-11-11-B00-V1-11-1B00V waas nnhn 图5-21例5-2图 【例5-3】设随机二进制序列中的1码出现的概率为0.5,对应一个振幅等于1、宽度 等于码元间隔Ts的矩形脉冲,0码对应0电平。 (1)求其功率谱密度及功率,并画出功率谱曲线,求增零点带宽: (②)若1码对应一个占空比等于0.5的矩形脉冲,0码仍为0电平,重新回答(1)中的 问题 3)能否从上述两个信号中用滤波法直接提取码元同步所需的频率s=1/Ts的分量?若 能,给出该分量的功率: (④)分析离散谱£,的功率与1码概率P的关系
1 第 5 章 数字基带传输系统 5.1 典 型 例 题 【例 5-1】 已知二元信息序列为 0100110000100001100000000010,求 HDB3 码,并画出 其波形图。 思路 二元信息码中有 4 组 4 个连 0 码,第 1、2 组之间 1 码个数为奇数,第 2、3 组之 间及第 3、4 组之间 1 码的个数为偶数。据此,可以进行取代变换。取代变换之后再加符号 就得到 HDB3 码。画波形图时应注意脉冲占空比为 0.5,这是国际标准,不能随意画。 解 取代变换后原二进制序列变为 010011000V1000V11B00VB00V010 加符号后得 HDB3 码。HDB3 码及其波形图如图 5-20 所示。 图 5-20 例 5-1 图 【例 5-2】 有 4 个连 1 和 4 个连 0 交替出现的序列,画出单极性非归零码、AMI 码、HDB3 码所对应的波形图。 思路 单极性非归零码、AMI 码的编码规律比较简单。对 HDB3 码的编码规律比较熟悉后 即可直接由信息代码求出 HDB3 码,并进而画出波形图。由于序列中 4 个连 1 和 4 个连 0 是 交替出现的,故相邻的 4 个连 0 码组之间 1 码的个数肯定是偶数个,因此 HDB3 码中的每个 取代节都应是 B00V。 解 单极性非归零码、AMI 码、HDB3 码及其波形图如图 5-21 所示。 图 5-21 例 5-2 图 【例 5-3】 设随机二进制序列中的 1 码出现的概率为 0.5,对应一个振幅等于 1、宽度 等于码元间隔 Ts 的矩形脉冲,0 码对应 0 电平。 (1) 求其功率谱密度及功率,并画出功率谱曲线,求谱零点带宽; (2) 若 1 码对应一个占空比等于 0.5 的矩形脉冲,0 码仍为 0 电平,重新回答(1)中的 问题; (3) 能否从上述两个信号中用滤波法直接提取码元同步所需的频率 fs=1/Ts 的分量?若 能,给出该分量的功率; (4) 分析离散谱 fs 的功率与 1 码概率 P 的关系

思路第一个信号为单极性非归零码,第二个信号为占空比等于0.5的单极性归零码, 它们的基本波形为DT.(t)和D0.5T.()。这两个信号都是相同波形随机序列,可用式(5-3) 求其功率谱。若功率谱中含有=1/的离散语,则可用滤波法直接提取频率为.的他 定时信号,否则不能。 傅氏变换对 D.()-:Sa()=sn/2 0t/2 是本课程中常用公式,此题中t=.或t=0.5T。 解(1)P=0.5,al,a-0 G(f)=T,Sa(fT,)=T,Sa(f/f,) 代入式(5-3)得 P.(f)=f.x0.5X0.5XT*Sa(n f/f.) .'xTSa'(f./)5(f-mf.) =0.25T.Sa(rf/f.)+0.25∑Sa(m)6(f-mf.) 由于 sin(mx)=0 所以 Sa(m)=0 故 P.(f)=0.25t.Sa(mf/) 功率谱密度曲线如图5-22所示。 一0 图5-22例5-3图1 由图5-22可知,谱零点带宽为B.=f。 信号功率为 .s( 0.25f.jrs(/f 根据帕塞瓦尔定理 ar.r (2)P=0.5 G(f)=0.5t.Sa(0.5πfT,)=0.5t.5a(0.5mf/f,) P.(f)=0.0625T.Sa(0.5f/f.)
2 思路 第一个信号为单极性非归零码,第二个信号为占空比等于 0.5 的单极性归零码, 它们的基本波形为 DTs(t)和 D0.5Ts(t)。这两个信号都是相同波形随机序列,可用式(5-3) 求其功率谱。若功率谱中含有 fs=1/Ts 的离散谱,则可用滤波法直接提取频率为 fs=1/Ts 的位 定时信号,否则不能。 傅氏变换对 Dτ(t)←→τSa ) 2 ( =τ / 2 sin / 2 是本课程中常用公式,此题中τ=Ts 或τ=0.5Ts。 解 (1) P=0.5,a1=1,a2=0 G(f)=TsSa(πfTs)=TsSa(πf/fs) 代入式(5-3)得 Ps(f)=fs×0.5×0.5×T 2 sSa2 (πf/fs) +f2 s m=− 0.52×T 2 sSa2 (mπfs/fs)δ(f-mfs) =0.25TsSa2 (πf/fs)+0.25 m=− Sa2 (mπ)δ(f-mfs) 由于 sin(mπ)=0 所以 Sa(mπ)=0 故 Ps(f)=0.25TsSa2 (πf/fs) 功率谱密度曲线如图 5-22 所示。 图 5-22 例 5-3 图 1 由图 5-22 可知,谱零点带宽为 Bs=fs。 信号功率为 S= − Ps(f)df=0.25 − TsSa2 (πf/fs)df =0.25fs − T 2 sSa2 (πf/fs)df 根据帕塞瓦尔定理 − T 2 sSa2 (πf/fs)df= − |G(f)|2 df= − D 2 Ts(t)dt=T2 s 得 (2) P=0.5 G(f)=0.5TsSa(0.5πfTs)=0.5TsSa(0.5πf/fs) Ps(f)=0.0625TsSa2 (0.5πf/fs)
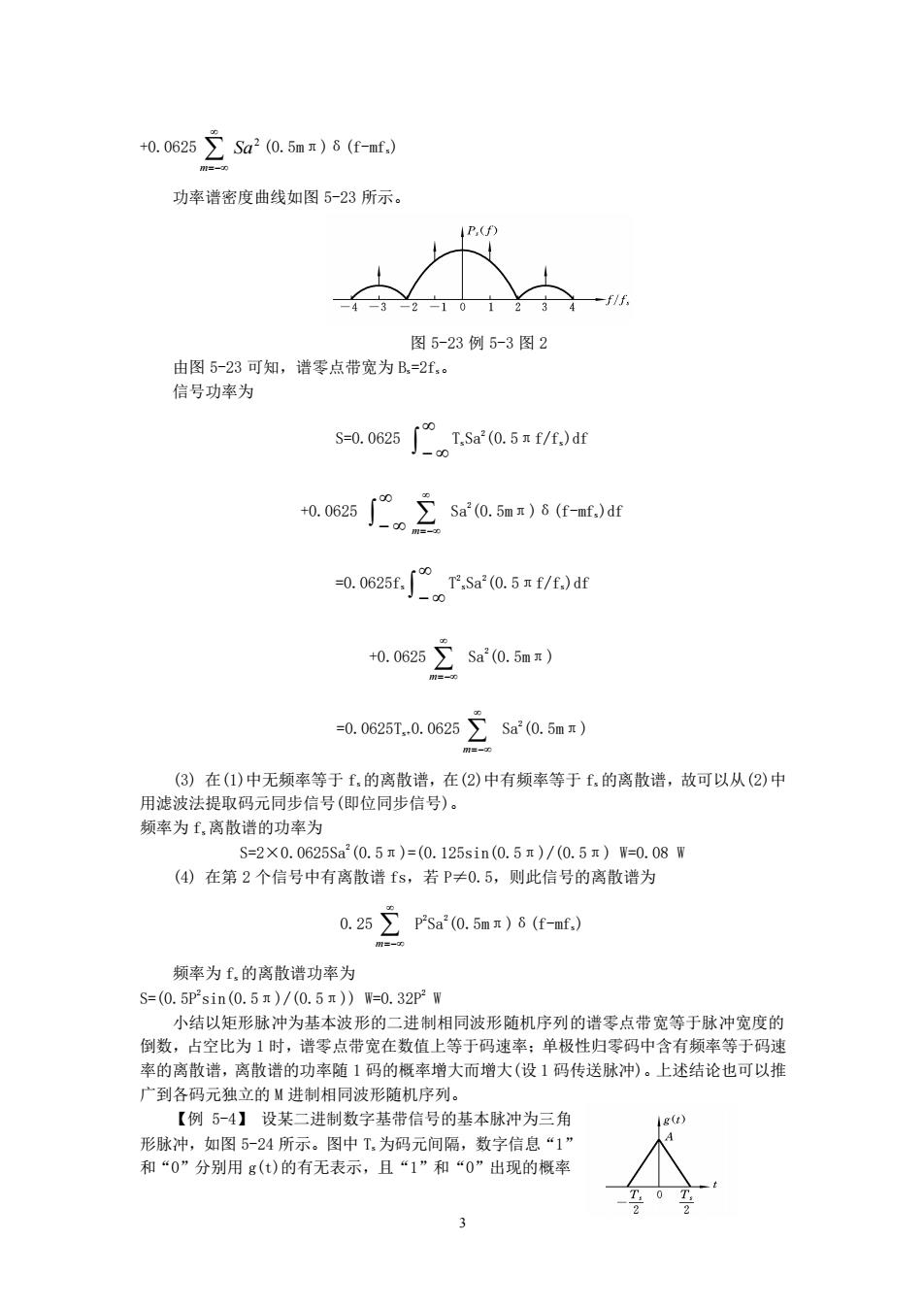
+0.0625∑Sa2(0.5m)6(f-mf,) 功率谱密度曲线如图5-23所示。 RCD 图5-23例5-3图2 由图5-23可知,谱零点带宽为B=2f,。 信号功率为 -.02( aoas三aa6 n0w5trsa.5a/iDdr +0.0625Sa2(0.5mm) -0.06251.06255a.5m (③)在(1)中无频率等于£,的离散谱,在(2)中有频率等于£,的离散谱,故可以从(2)中 用滤波法提取码元同步信号(即位同步信号)。 频率为,离散谱的功率为 S=2×0.0625Sa'(0.5π)=(0.125sin(0.5r)/(0.5r)f=0.08T (4)在第2个信号中有离散谱fs,若P≠0.5,则此信号的离散谱为 0.25∑psa2(0.5mm)6(f-mf,) 频率为£的离散谱功率为 S=(0.5Psin(0.5)/(0.5))W=0.32pW 小结以矩形脉冲为基本波形的二进制相同波形随机序列的谱零点带宽等于脉冲宽度的 倒数,占空比为1时,谱零点带宽在数值上等于码速率:单极性归零码中含有频率等于码速 率的离散谱,离散谱的功率随1码的概率增大而增大(设1码传送脉冲)。上述结论也可以推 广到各码元独立的M进制相同波形随机序列。 【例5-4】设某二进制数字基带信号的基本脉冲为三角 g() 形脉冲,如图5-24所示。图中T,为码元间隔,数字信息“1” 和“0”分别用g(t)的有无表示,且“1”和“0”出现的概率
3 +0.0625 2 Sa m =− (0.5mπ)δ(f-mfs) 功率谱密度曲线如图 5-23 所示。 图 5-23 例 5-3 图 2 由图 5-23 可知,谱零点带宽为 Bs=2fs。 信号功率为 S=0.0625 − TsSa2 (0.5πf/fs)df +0.0625 − m=− Sa2 (0.5mπ)δ(f-mfs)df =0.0625fs − T 2 sSa2 (0.5πf/fs)df +0.0625 m=− Sa2 (0.5mπ) =0.0625Ts+0.0625 m=− Sa2 (0.5mπ) (3) 在(1)中无频率等于 fs 的离散谱,在(2)中有频率等于 fs 的离散谱,故可以从(2)中 用滤波法提取码元同步信号(即位同步信号)。 频率为 fs 离散谱的功率为 S=2×0.0625Sa2 (0.5π)=(0.125sin(0.5π)/(0.5π) W=0.08 W (4) 在第 2 个信号中有离散谱 fs,若 P≠0.5,则此信号的离散谱为 0.25 m=− P 2 Sa2 (0.5mπ)δ(f-mfs) 频率为 fs 的离散谱功率为 S=(0.5P2 sin(0.5π)/(0.5π)) W=0.32P2 W 小结以矩形脉冲为基本波形的二进制相同波形随机序列的谱零点带宽等于脉冲宽度的 倒数,占空比为 1 时,谱零点带宽在数值上等于码速率;单极性归零码中含有频率等于码速 率的离散谱,离散谱的功率随 1 码的概率增大而增大(设 1 码传送脉冲)。上述结论也可以推 广到各码元独立的 M 进制相同波形随机序列。 【例 5-4】 设某二进制数字基带信号的基本脉冲为三角 形脉冲,如图 5-24 所示。图中 Ts 为码元间隔,数字信息“1” 和“0”分别用 g(t)的有无表示,且“1”和“0”出现的概率

相等。 图5-24例5-4图 (1)求该数字基带信号的功率谱密度: (2)能否用滤被法从该数字基带信号中提取码元同步所需的频率=1/T,的分量?若能, 试计算该分量的功率。 思路将底部宽度为t、高度为1的三角形时域函数表示为△t(),傅氏变换对为 4.0-一Ia=5aor14 @r/4 据此式可求得本题中g(t)所对应的G(f),再由式(5-3)即可求解。 解(1 P=0.5,a=l,a=0 2 Rm=f-刊aac0f2laa-刊aeaD5md 4 4 4 -悟立学W 16 (2)频率f.=1/1,离散谱分量为 专iU-#60-0 所以可以用滤波法从该数字基带信号中提取码元同步所需要的频率£.=1/几,的分量,该分量 的功率为 【例5-5】某基带系统的频率特性是截止频率为1z、幅度为1的理想低通滤波器 (1)试根据系统无码间串扰的时域条件求此基带系统无码间串扰的码速率。 (2)设此系统传输信息速率为3Ms,能否无码间串扰? 思路此题需求系统的冲激响应。系统的频率特性是一个幅度为1、宽度为⊙。=4π×10 rad/s的门函数(双边频率特性)Do(u),根据傅氏变换的对称性可得 D,(o)-一%a()-2x10rsa2r×10rt) 2π 2 无码间串扰的时域条件为 C,k=0 MkI,)=0,k0 式中,工,为码元间隔。所以,根据冲激响应波形就可确定此系统无码间串扰的码速率。 设进制数为任意值,根据信息速率与码速率之间的关系求3Mbs所对应的码速率,从 而判断传输3Mbps信号有无码间串扰。 4
4 相等。 图 5-24 例 5-4 图 (1) 求该数字基带信号的功率谱密度; (2) 能否用滤波法从该数字基带信号中提取码元同步所需的频率 fs=1/Ts 的分量?若能, 试计算该分量的功率。 思路 将底部宽度为τ、高度为 1 的三角形时域函数表示为Δτ(t),傅氏变换对为 Δτ(t)←→ 2 2 ] / 4 sin / 4 [ 2 )] 4 [ ( 2 Sa = 据此式可求得本题中 g(t)所对应的 G(f),再由式(5-3)即可求解。 解 (1) P=0.5,a1=1,a2=0 G(f)= ) 2 ( 2 s 2 s fT Sa AT Ps(f)=fsP(1-P)(a1-a2) 2 G 2 (f)+f2 s m=− |Pa1+(1-P)a2| 2 G(mfs)δ(f-mfs) = 4 s f · ) 2 ( 4 4 2 2 s s fT Sa A T + ) 2 ( 4 4 4 2 2 2 s s m s fT Sa f A T =− δ(f-mfs) ) ( ) 2 ( 16 ) 2 ( 16 4 2 2 2 s m s s f mf m Sa fT A Sa A T = + − =− (2) 频率 fs=1/Ts 离散谱分量为 ( ) 0 2 ) ( ) 2 ( 8 4 2 4 2 − s = f − f s A Sa f f A 所以可以用滤波法从该数字基带信号中提取码元同步所需要的频率 fs=1/Ts 的分量,该分量 的功率为 【例 5-5】 某基带系统的频率特性是截止频率为 1 MHz、幅度为 1 的理想低通滤波器。 (1) 试根据系统无码间串扰的时域条件求此基带系统无码间串扰的码速率。 (2) 设此系统传输信息速率为 3 Mbps,能否无码间串扰? 思路 此题需求系统的冲激响应。系统的频率特性是一个幅度为 1、宽度为ω0=4π×106 rad/s 的门函数(双边频率特性)Dω0(ω),根据傅氏变换的对称性可得 Dω0(ω)←→ ) 2 ( 2 0 0 t Sa =2×106 Sa(2π×106 t) 无码间串扰的时域条件为 = = 0, 0 , 0 ( ) k C k h kTs 式中,Ts 为码元间隔。所以,根据冲激响应波形就可确定此系统无码间串扰的码速率。 设进制数为任意值,根据信息速率与码速率之间的关系求 3 Mbps 所对应的码速率,从 而判断传输 3 Mbps 信号有无码间串扰

解(1)h(t)=2×10Sa(2πX10t) 波形如图525所示。由图可知,当T=0.54s/k(k为正整数)时无码间串扰,即此系 统无码间串扰的码速率为 h(r) 图5-25例5-5图 (2)设传输独立等概的M进制信号,则 g:Mm) 3 32 log2 Mk 8=8(n=L,2,.) 即当采用8进制信号时,码速率R(QB),可以满足无码间串扰 n H(oo 条件 例5-6】设某基带传输系统具有图5-26所示的三角形传输函数: ()当R=。/π时,用奈奎斯特准则验证该系统能否实现无码间 0 串扰传输? 图5-26例5-6图1 (②)求该系统接收滤波器输出基本脉冲的时间表达式,并用此来说明(1)中的结论 思路因R=0/T,即R=2f,所以式(5-5)或式(5-6)中的£,=2f。也可将式(5-5)或 式(5-6)表示为角频率的形式 ∑H(unwJ-clo≤g 或∑H(on心)-C。为任意位 若用此两式,则对于此题给定的条件,有 0,=200 根据傅氏变换的对称性,可得 由此式可求得本题所给系统的接收滤波器输出基本脉冲时间表达式,再根据码速率决定 抽样时刻,从而决定有无码间串扰。 解(1)方法一 将H(w)在频率轴上以2u。为间隔切开,由于H(u)的频率范围为(←u,。),故切开、 平移、选加后仍为H(ω),在|w|《o范围内(u)不为常数,故系统有码间串扰
5 解 (1) h(t)=2×106 Sa(2π×106 t) 波形如图 5-25 所示。由图可知,当 Ts=0.5 μs/k(k 为正整数)时无码间串扰,即此系 统无码间串扰的码速率为 图 5-25 例 5-5 图 (2) 设传输独立等概的 M 进制信号,则 RB= log 2 M 3 (MBd) 令 log 2 M 3 = k 2 得 M= k 2 8 =8n (n=1,2,.) 即当采用 8 n 进制信号时,码速率 RB= n 1 (MBd),可以满足无码间串扰 条件。 【例 5-6】设某基带传输系统具有图 5-26 所示的三角形传输函数: (1) 当 RB=ω0/π时,用奈奎斯特准则验证该系统能否实现无码间 串扰传输? 图 5-26 例 5-6 图 1 (2) 求该系统接收滤波器输出基本脉冲的时间表达式,并用此来说明(1)中的结论。 思路 因 RB=ω0/π,即 RB=2f0,所以式(5-5)或式(5-6)中的 fs=2f0。也可将式(5-5)或 式(5-6)表示为角频率的形式 n=− H(ω+nωs)=C,|ω|≤ 2 s 或 n=− H(ω+nωs)=C,ω为任意值 若用此两式,则对于此题给定的条件,有 s = 20 根据傅氏变换的对称性,可得 ΔΩ(ω)←→ 2 2 ] / 4 sin / 4 [ 4 )] 4 [ ( 4 t t t Sa = 由此式可求得本题所给系统的接收滤波器输出基本脉冲时间表达式,再根据码速率决定 抽样时刻,从而决定有无码间串扰。 解 (1) 方法一 将 H(ω)在频率轴上以 2ω0 为间隔切开,由于 H(ω)的频率范围为(-ω0,ω0),故切开、 平移、迭加后仍为 H(ω),在|ω|<ω0 范围内 H(ω)不为常数,故系统有码间串扰
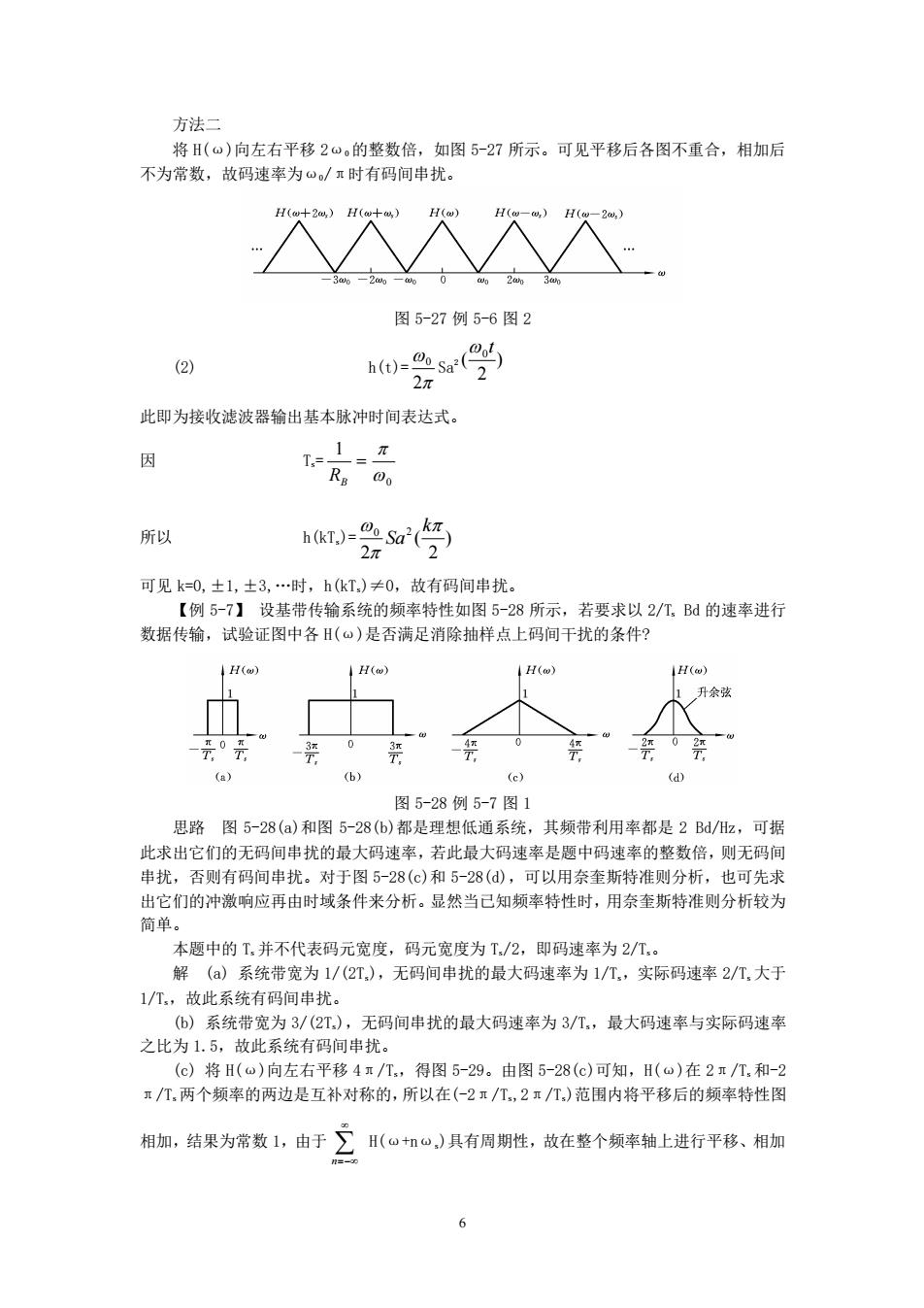
方法二 将H()向左右平移2@,的整数倍,如图5-27所示。可见平移后各图不重合,相加后 不为常数,故码速率为/时有码间串扰。 个入人入 图5-27例5-6图2 (2) -会s(学 此即为接收滤波器输出基本脉冲时间表达式。 1π Rg @o 所以 h-%sa(经) 2π 可见k=0,±1,士3,.时,h(kT,)≠0,故有码间串扰。 【例5-7】设基带传输系统的频率特性如图5-28所示,若要求以2/T.Bd的速率进行 数据传输,试验证图中各H(“)是否满足消除抽样点上码间干扰的条件? H() H(o) .口. 0 (a》 (6) (e) (d) 图5-28例5-7图1 思路图5-28(a)和图528(b)都是理想低通系统,其频带利用率都是2Bd/z,可据 此求出它们的无码间串扰的最大码速率,若此最大码速率是题中码速率的整数倍,则无码间 串扰,否则有码间串扰。对于图5-28(c)和5-28(),可以用奈奎斯特准则分析,也可先求 出它们的冲激响应再由时域条件来分析。显然当己知频率特性时,用奈奎斯特准则分析较为 简单。 本题中的T,并不代表码元宽度,码元宽度为T,/2,即码速率为2/T 解(a)系统带宽为1/(21,),无码间串扰的最大码速率为1/T。,实际码速率2/T,大于 1/T,故此系统有码间串扰。 (6)系统带宽为3/(2T,),无码间串扰的最大码速率为3/T,最大码速率与实际码速率 之比为1.5,故此系统有码间串扰。 (c)将H()向左右平移4/T.,得图5-29。由图5-28(C)可知,H()在2年/T.和-2 /T,两个频率的两边是互补对称的,所以在(-2个,2个,)范围内将平移后的频率特性图 相加,结果为常数1,由于∑(ω+n“,)具有周期性,故在整个频率轴上进行平移、相加 6
6 方法二 将 H(ω)向左右平移 2ω0 的整数倍,如图 5-27 所示。可见平移后各图不重合,相加后 不为常数,故码速率为ω0/π时有码间串扰。 图 5-27 例 5-6 图 2 (2) h(t)= 2 0 Sa2 ) 2 ( 0 t 此即为接收滤波器输出基本脉冲时间表达式。 因 Ts= 0 1 = RB 所以 h(kTs)= ) 2 ( 2 0 2 k Sa 可见 k=0,±1,±3,.时,h(kTs)≠0,故有码间串扰。 【例 5-7】 设基带传输系统的频率特性如图 5-28 所示,若要求以 2/Ts Bd 的速率进行 数据传输,试验证图中各 H(ω)是否满足消除抽样点上码间干扰的条件? 图 5-28 例 5-7 图 1 思路 图 5-28(a)和图 5-28(b)都是理想低通系统,其频带利用率都是 2 Bd/Hz,可据 此求出它们的无码间串扰的最大码速率,若此最大码速率是题中码速率的整数倍,则无码间 串扰,否则有码间串扰。对于图 5-28(c)和 5-28(d),可以用奈奎斯特准则分析,也可先求 出它们的冲激响应再由时域条件来分析。显然当已知频率特性时,用奈奎斯特准则分析较为 简单。 本题中的 Ts 并不代表码元宽度,码元宽度为 Ts/2,即码速率为 2/Ts。 解 (a) 系统带宽为 1/(2Ts),无码间串扰的最大码速率为 1/Ts,实际码速率 2/Ts 大于 1/Ts,故此系统有码间串扰。 (b) 系统带宽为 3/(2Ts),无码间串扰的最大码速率为 3/Ts,最大码速率与实际码速率 之比为 1.5,故此系统有码间串扰。 (c) 将 H(ω)向左右平移 4π/Ts,得图 5-29。由图 5-28(c)可知,H(ω)在 2π/Ts 和-2 π/Ts 两个频率的两边是互补对称的,所以在(-2π/Ts,2π/Ts)范围内将平移后的频率特性图 相加,结果为常数 1,由于 n=− H(ω+nωs)具有周期性,故在整个频率轴上进行平移、相加

处理后也为常数1,所以此系统无码间串扰。 图5-29例5-7图2 (d)将H(u)向左右平移4/T.的整数倍得图5-30。显然不能满足奈奎斯特准则 川+y 图5-30例5-7图3 小结根据(©)的分析结论可知,当给定系统的频率特性H()时,可以找出H(f)的互补 对称频率,最大无码间串扰码速率等于这个互补对称频率的两倍。在(c)中,H()的互补对 称顷率为1/T,故最大码速率为2/T。 在()中,H(f)的互补对称频率为1/(2T),故最大无码间串扰的码速率为1/T,实际码速率 为2/ 码间串扰。 常将这个互补对称频*称为等效矩形带宽W。由()求等效矩形带宽黑,确定无码间串 扰的最大码速率R。ax=2W,再与实际码速率R比较,若Rmx/R为正整数,则无码间串 扰,否则有码间串扰。这是根据系统频率特性()分析码间串扰特性的一个简便方法。 【例5-8】为了传送码元速率R=103B阳的数字基带信号,试问系统采用图5-31中所 画的哪一种传输特性较好?并简要说明其理由。 H(御, -4×10x-2×103x-10x010*x2×10r4×10x 图5-31别5-8图 思路可从码间串扰性能、频带利用率、时域收敛速率以及可实现性等四个方面进行比较,从 而确定选择哪一种传输特性, 解(1)码间串扰性能 (a)因等效矩形带宽W=103Hz,故Bmax=2X103Bd,RDax=2Ra,无码间串扰. (亿b)Rmax=2X103Bd,无码间串扰。 (C)因等效矩形带宽W=500z,故Rmx=l03BdR,无码间串扰 (②)频带利用率 (a)、(⑥)、(c)三种传输特性所占用的信道带宽分别为2×103z、103z、10z,所 以它们的频带利用率分别为0.5Bd/Hz、1Bd/Hz、1Bd/Hz。 (3)时域收敛速率
7 处理后也为常数 1,所以此系统无码间串扰。 图 5-29 例 5-7 图 2 (d) 将 H(ω)向左右平移 4π/Ts 的整数倍得图 5-30。显然不能满足奈奎斯特准则。 图 5-30 例 5-7 图 3 小结 根据(c)的分析结论可知,当给定系统的频率特性 H(f)时,可以找出 H(f)的互补 对称频率,最大无码间串扰码速率等于这个互补对称频率的两倍。在(c)中,H(f)的互补对 称频率为 1/Ts,故最大码速率为 2/Ts。 在(d)中,H(f)的互补对称频率为 1/(2Ts),故最大无码间串扰的码速率为 1/Ts,实际码速率 为 2/Ts,故有码间串扰。 常将这个互补对称频率称为等效矩形带宽 W。由 H(f)求等效矩形带宽 W,确定无码间串 扰的最大码速率 RB max=2W,再与实际码速率 RB 比较,若 RB max/RB 为正整数,则无码间串 扰,否则有码间串扰。这是根据系统频率特性 H(f)分析码间串扰特性的一个简便方法。 【例 5-8】 为了传送码元速率 RB=103 Bd 的数字基带信号,试问系统采用图 5-31 中所 画的哪一种传输特性较好?并简要说明其理由。 图 5-31 例 5-8 图 思路可从码间串扰性能、频带利用率、时域收敛速率以及可实现性等四个方面进行比较,从 而确定选择哪一种传输特性。 解 (1) 码间串扰性能 (a) 因等效矩形带宽 W=103 Hz,故 RB max=2×103 Bd,RB max=2RB,无码间串扰。 (b) RB max=2×103 Bd,无码间串扰。 (c) 因等效矩形带宽 W=500 Hz,故 RB max=103 Bd=RB,无码间串扰。 (2) 频带利用率 (a)、(b)、(c)三种传输特性所占用的信道带宽分别为 2×103 Hz、103 Hz、103 Hz,所 以它们的频带利用率分别为 0.5 Bd/Hz、1 Bd/Hz、1 Bd/Hz。 (3) 时域收敛速率

(a)和(c)的传输特性为三角形,其冲激响应为Sa(x)型,与t2成反比:(b)的传输特性 为矩形,其冲激响应为Sa(x)型,与t成反比。可见(a)、(c)的时域收敛速度快,可以放宽 对位定时信号抖动的要求。 (④)可实现性 (b)为理想矩形,难于实现:(a)、(c)较易于实现 综上所述,洗择传输特性()较好, 小结根据傅氏变换的对称特性,频域收敛速率快的系统,在时域收敛速率慢:反之 频域慢收敛的系统 时域为快收敛 本圈中()在频域为快收敛。 a) ,在频域为慢收敛 故(b)在时域为慢收敛,(@)、()在须域为快收敛。这一特点对于我们定性分析问题提供】 方便。 【例5-9】设二进制基带系统的收滤波器输出噪声功率为0.25。 (①)收滤波器输出信号为峰峰值等于4V的NR2码,求误比特率: N2x025=32 可用两种方法求解P ①查Q函数表或Q函数曲线 R=C1gi6=g4=37x0 ②用近似公式Q(Va)≈er/2m计算 P=Q(16)=e/32I≈3.35×10 (2)BNRZ码的信噪比为 822 N025=16 误比特率为 R=原=i==37xo 小结由上述计算可知,当收滤波器输出的R☑码和BNZ码信号峰峰值相同时,单 极性传输系统的信噪比是双极性的2倍,但它们的误比特率相同。双极性系统的判决门限为 0,与信号大小无关,而单极性系统的判决门限等于信号幅度的一半,随信号大小而变,这 对工程设计带来了不便。基于上述原理,实际使用的往往是双极性系统。 【例5-10】在如图5-15所示的第V类部分响应系统中,设二进制代码为11101001: (1)求无噪声时此系统中其它代码b、ba、C、c',及a': (2)设由于噪声使c',发生2位误码,求ā'。 解(①)各代码之间的关系是 akb c.=b-b-z c=r (kT.),a=[c'] 无噪声时,理想低通网络无码间串扰,c'k=ck。由ak到a'k的全过程如下: ak0011101001 b0011011110 8
8 (a)和(c)的传输特性为三角形,其冲激响应为 Sa2 (x)型,与 t 2 成反比;(b)的传输特性 为矩形,其冲激响应为 Sa(x)型,与 t 成反比。可见(a)、(c)的时域收敛速度快,可以放宽 对位定时信号抖动的要求。 (4) 可实现性 (b)为理想矩形,难于实现;(a)、(c)较易于实现。 综上所述,选择传输特性(c)较好。 小结 根据傅氏变换的对称特性,频域收敛速率快的系统,在时域收敛速率慢;反之, 频域慢收敛的系统,时域为快收敛。本题中(b)在频域为快收敛,(a)、(c)在频域为慢收敛; 故(b)在时域为慢收敛,(a)、(c)在频域为快收敛。这一特点对于我们定性分析问题提供了 方便。 【例 5-9】 设二进制基带系统的收滤波器输出噪声功率为 0.25W。 (1) 收滤波器输出信号为峰 峰值等于 4 V 的 NRZ 码,求误比特率; (2) 收滤波器输出信号为峰 峰值等于 4 V 的 BNRZ 码,求误比特率。 解 (1) NRZ 码的信噪比为 32 2 0.25 4 2 = = N S 可用两种方法求解 Pb: ① 查 Q 函数表或 Q 函数曲线 5 ] ( 16) (4) 3.17 10 2 [ − = Q = Q = N S Pb Q ② 用近似公式 Q( a )≈e -α/2/ 2a 计算 Pb=Q(16)=e-8 /32π≈3.35×10-5 (2) BNRZ 码的信噪比为 16 0.25 2 2 = = N S 误比特率为 5 [ ] ( 16) (4) 3.17 10− = = Q = Q = N S Pb Q 小结 由上述计算可知,当收滤波器输出的 NRZ 码和 BNRZ 码信号峰 峰值相同时,单 极性传输系统的信噪比是双极性的 2 倍,但它们的误比特率相同。双极性系统的判决门限为 0,与信号大小无关,而单极性系统的判决门限等于信号幅度的一半,随信号大小而变,这 对工程设计带来了不便。基于上述原理,实际使用的往往是双极性系统。 【例 5-10】 在如图 5-15 所示的第Ⅳ类部分响应系统中,设二进制代码为 11101001: (1) 求无噪声时此系统中其它代码 bk、bk-2、ck、c′k 及 a′k; (2) 设由于噪声使 c′k 发生 2 位误码,求 a′k。 解 (1) 各代码之间的关系是 bk=akbk-2,ck=bk-bk-2,c’k=r (kTs),a’k=[c′k](mod2) 无噪声时,理想低通网络无码间串扰,c′k=ck。由 ak 到 a′k 的全过程如下: ak 0 0 1 1 1 0 1 0 0 1 bk 0 0 1 1 0 1 1 1 1 0

00110111 11-10100-1 C' a' 11101001 对c',进行模2处理的准则是[1]a=l,[0]m=0,[-1]a=l。 (2)设由于误码,c,的第3个码元由-1变为0,第6个码元由0变为1,则c'、a', c'1100110-1 a'k11001101 可见a',也有2位误码,即无误码传播现象出现。若©中的1(或-1)错为c':的-1(或1), 则进行模2处理后,a',并不发生错误。 小结若a为L电平信号,则相关编码后的c为2L-1电平信号:部分响应系统无误码 传播问恩 【例5-11】设抽样判决器输入信号的信噪比都为16,求二进制双极性系统、四进制 双极性系统及四进制双极性部分响应系统的误码率。 解二进制双极性系统的误码率为 P=Q(16)=3.17×103 四进制双极性系统的误码率为 2-2w-@yn-Q4层6 M =01.79)=3x00367=55x10 四进制双极性部分响应系统的误码率为 -2eg2-1=2ge层 2 -2000-8x0808=015 小结由此题计算结果可知,多进制系统是以牺牲可靠性(即增大误码率)来提高有效性 的(即提高频带利用率nb):部分响应系统的频带利用率可达到基带系统的最大值(B/z), 而且时域收敛速度快,但其抗噪能力却远低于非部分响应系统。 【例5-12】设三抽头横向滤波器的输入信号x()的抽样值为x、x2 其它名=0,抽头增益为e一子、c1、c一了求输出信号y)的抽样值及x付和y) 的峰值畸变。 解由-∑c得 y=c-x-16
9 bk-2 0 0 1 1 0 1 1 1 ck 1 1 -1 0 1 0 0 -1 c ’ k 1 1 -1 0 1 0 0 -1 a ’ k 1 1 1 0 1 0 0 1 对 c′k 进行模 2 处理的准则是[1](mod2)=1,[0](mod2)=0,[-1](mod2)=1。 (2) 设由于误码,ck 的第 3 个码元由-1 变为 0,第 6 个码元由 0 变为 1,则 c′k、a′k 为 c′k1 1 0 0 1 1 0 -1 a′k 1 1 0 0 1 1 0 1 可见 a′k 也有 2 位误码,即无误码传播现象出现。若 ck 中的 1(或-1)错为 c′k 的-1(或 1), 则进行模 2 处理后,a′k 并不发生错误。 小结 若 ak 为 L 电平信号,则相关编码后的 ck为 2L-1 电平信号;部分响应系统无误码 传播问题。 【例 5-11】 设抽样判决器输入信号的信噪比都为 16,求二进制双极性系统、四进制 双极性系统及四进制双极性部分响应系统的误码率。 解 二进制双极性系统的误码率为 Pe=Q( 16 )=3.17×10-5 四进制双极性系统的误码率为 2 2 0.0367 5.5 10 2 3 (1.79) 2 3 16] 15 3 4 3.14 [ 4 6 ( )] 1 3 [ 2( 1) − = = = = − − = Q Q N S M Q M M Pe 四进制双极性部分响应系统的误码率为 0.0808 0.15 60 30 (1.40) 16 30 16] 15 3 4 3.14 [ 16 2 15 ( )] 1 3 4 [ 2( 1) 2 2 2 = = = = − − = Q Q N S L Q L L Pe 小结 由此题计算结果可知,多进制系统是以牺牲可靠性(即增大误码率)来提高有效性 的(即提高频带利用率ηb);部分响应系统的频带利用率可达到基带系统的最大值(Bd/Hz), 而且时域收敛速度快,但其抗噪能力却远低于非部分响应系统。 【例 5-12】 设三抽头横向滤波器的输入信号 x(t)的抽样值为 x-1= 4 1 、x0=1、x1= 2 1 、 其它 xk=0,抽头增益为 c-1=- 4 1 、c0=1、c1=- 2 1 ,求输出信号 y(t)的抽样值及 x(t)和 y(t) 的峰值畸变。 解 由 yk==− 1 i 1 cixk-i 得 y-2=c-1x-1=- 16 1

eo-0 ncaec y=cx=4 之x X00 客月 5.2自测自评 5.2.1自测试题 5-1填空题 (①)设二进制信息代码的码速率为1OO0Bd:则AM虹码的码速率为①Bd:DB,码 的码速率为②Bd:数字双相码的码速率为回Bd:传号反转码的码速率为④Bd。 (2)设二进制信息代码的码速率为10O0B,则HDB码波形、单极性非归零码波形、占 空比为0.4的双极性归零码波形、差分码波形以及传号反转码波形的谱零点带宽依次为① k H H (3)若四进制基带系统中的四个符号独立等概,信息速率为1×10bit/s,则抽样判决 器的位定时信号的重复频率为z。 (④)若第V类部分响应系统的四进制信息序列由代码0、1、2、3构成,则相关器得到 的信息序列包含了以下代码。 5-2问答颗 ()定性说明位定时信号抖动对误码率的影响, (②)设信号功率、进制数以及信道的噪声功率谱密度不变,当传输信息速率增大时误码 率如何变化?为什么? (3)在二进制双极性基带传输系统中,若P(1)>0.5,最佳判决门限应大于0还是小于 0?试根据抽样判决器输入信号的概率密度作定性说明。 (④)采用部分响应系统传输信息有什么优点?付出了什么代价 (⑤)时域均衡器的输入信号的眼图与输出信号的眼图有何区别?为什么? 5-3己知信息代码为1010000011000011,试确定相应的传号差分码、CMI码、数字双 相码、AMI码以及DB,码,并分别画出它们的波形。 5-4双极性归零码的基木信号是一个占空比为0.5、幅度为100mV的矩形脉冲,信息 速率为100kbit/s (1)求其功率谱密度:(②)在什么条件下有频率等于100k的离散谱?(3)当信息速 率增加到1Mbit/s时,功率谱密度将如何变化? 5-5设在某二进制数字基带信号中,数字信息1和0分别由g(t)和-g(t)表示,且1 与0出现的概率相等,g()是升余弦脉冲,即
10 y-1=c-1x0+c0x-1=- 4 1 + 4 1 =0 y0=c-1x1+c0x0+c1x-1=- 8 1 +1- 8 1 = 4 3 y1=c0x1+c1x0= 2 1 - 2 1 =0 y2=c1x1=- 4 1 Dx= 4 3 | | 1 0 0 = =− k k k y x Dy= 12 5 | | 1 0 0 = =− k k k y y 5.2 自 测 自 评 5.2.1 自测试题 5-1 填空题 (1) 设二进制信息代码的码速率为 1000 Bd:则 AMI 码的码速率为 ① Bd;HDB3 码 的码速率为 ② Bd;数字双相码的码速率为 ③ Bd;传号反转码的码速率为 ④ Bd。 (2) 设二进制信息代码的码速率为 1000 Bd,则 HDB3 码波形、单极性非归零码波形、占 空比为 0.4 的双极性归零码波形、差分码波形以及传号反转码波形的谱零点带宽依次为 ① Hz、 ② Hz、 ③ Hz、 ④ Hz、 ⑤ Hz。 (3) 若四进制基带系统中的四个符号独立等概,信息速率为 1×106 bit/s,则抽样判决 器的位定时信号的重复频率为 Hz。 (4) 若第Ⅳ类部分响应系统的四进制信息序列由代码 0、1、2、3 构成,则相关器得到 的信息序列包含了以下代码。 5-2 问答题 (1) 定性说明位定时信号抖动对误码率的影响。 (2) 设信号功率、进制数以及信道的噪声功率谱密度不变,当传输信息速率增大时误码 率如何变化?为什幺? (3) 在二进制双极性基带传输系统中,若 P(1)>0.5,最佳判决门限应大于 0 还是小于 0?试根据抽样判决器输入信号的概率密度作定性说明。 (4) 采用部分响应系统传输信息有什幺优点?付出了什幺代价? (5) 时域均衡器的输入信号的眼图与输出信号的眼图有何区别?为什幺? 5-3 已知信息代码为 1010000011000011,试确定相应的传号差分码、CMI 码、数字双 相码、AMI 码以及 HDB3 码,并分别画出它们的波形。 5-4 双极性归零码的基本信号是一个占空比为 0.5、幅度为 100 mV 的矩形脉冲,信息 速率为 100 kbit/s。 (1) 求其功率谱密度;(2) 在什幺条件下有频率等于 100 kHz 的离散谱?(3) 当信息速 率增加到 1 Mbit/s 时,功率谱密度将如何变化? 5-5 设在某二进制数字基带信号中,数字信息 1 和 0 分别由 g(t)和-g(t)表示,且 1 与 0 出现的概率相等,g(t)是升余弦脉冲,即