
© (多媒体通信》 从变换偏码到单像素相机… 2019年10月13日 甩于工程与后怎科学系
2019年10月13日 《多媒体通信》 从变换编码到单像素相机…

KC从变换编码到单像素相机 ◆漫谈变换编码 ▣为什么不在时域编码而用变换编码? 口傅里叶变换及其变体在应用中遇到的问题 口什么是小波变换? ◆CT图像的常识 ▣CT图像的产生原理 ▣CT图像如何重建? ◆单像素相机 ▣单像素数码相机原理 口压缩感知理论 ◆光场相机 2 ynh.cxh @ustc.edu.cn
{ynh,cxh}@ustc.edu.cn 从变换编码到单像素相机 漫谈变换编码 为什么不在时域编码而用变换编码? 傅里叶变换及其变体在应用中遇到的问题 什么是小波变换? CT图像的常识 CT图像的产生原理 CT图像如何重建? 单像素相机 单像素数码相机原理 压缩感知理论 光场相机 2
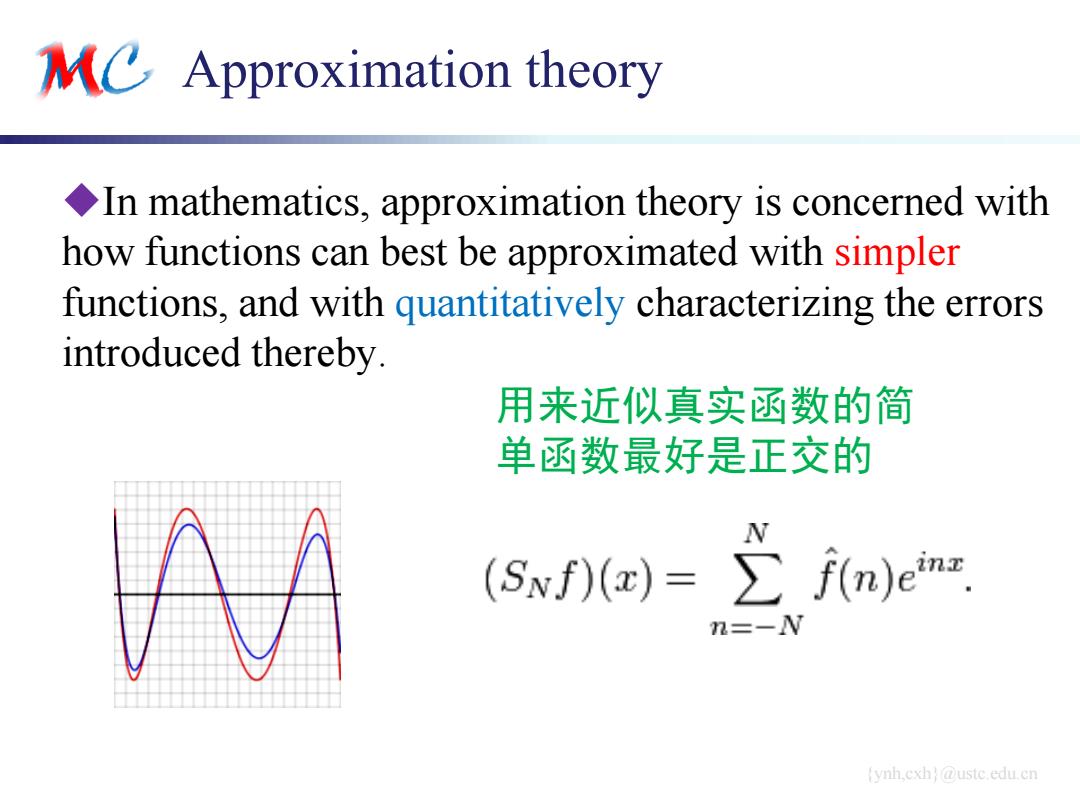
MC Approximation theory In mathematics,approximation theory is concerned with how functions can best be approximated with simpler functions,and with quantitatively characterizing the errors introduced thereby. 用来近似真实函数的简 单函数最好是正交的 (Svf)(r)=∑f(n)emr, n=-N ynh.cxh @ustc.edu.cn
{ynh,cxh}@ustc.edu.cn Approximation theory In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby. 用来近似真实函数的简 单函数最好是正交的
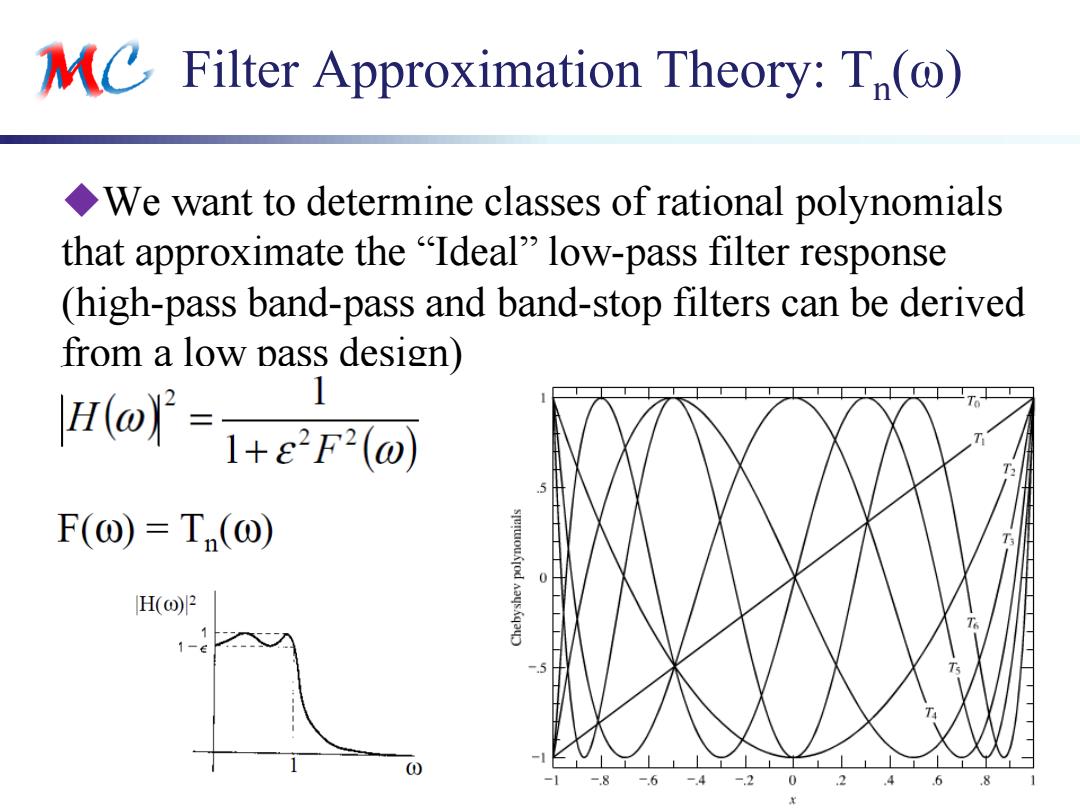
MC Filter Approximation Theory:T(@) We want to determine classes of rational polynomials that approximate the "Ideal"low-pass filter response (high-pass band-pass and band-stop filters can be derived from a low pass design) mtoj=7+o 1 F(⊙)=Tn(⊙) H(o)2 1-6 ① -8 -6-4 -20 2 .4
{ynh,cxh}@ustc.edu.cn Filter Approximation Theory: Tn (ω) We want to determine classes of rational polynomials that approximate the “Ideal” low-pass filter response (high-pass band-pass and band-stop filters can be derived from a low pass design)
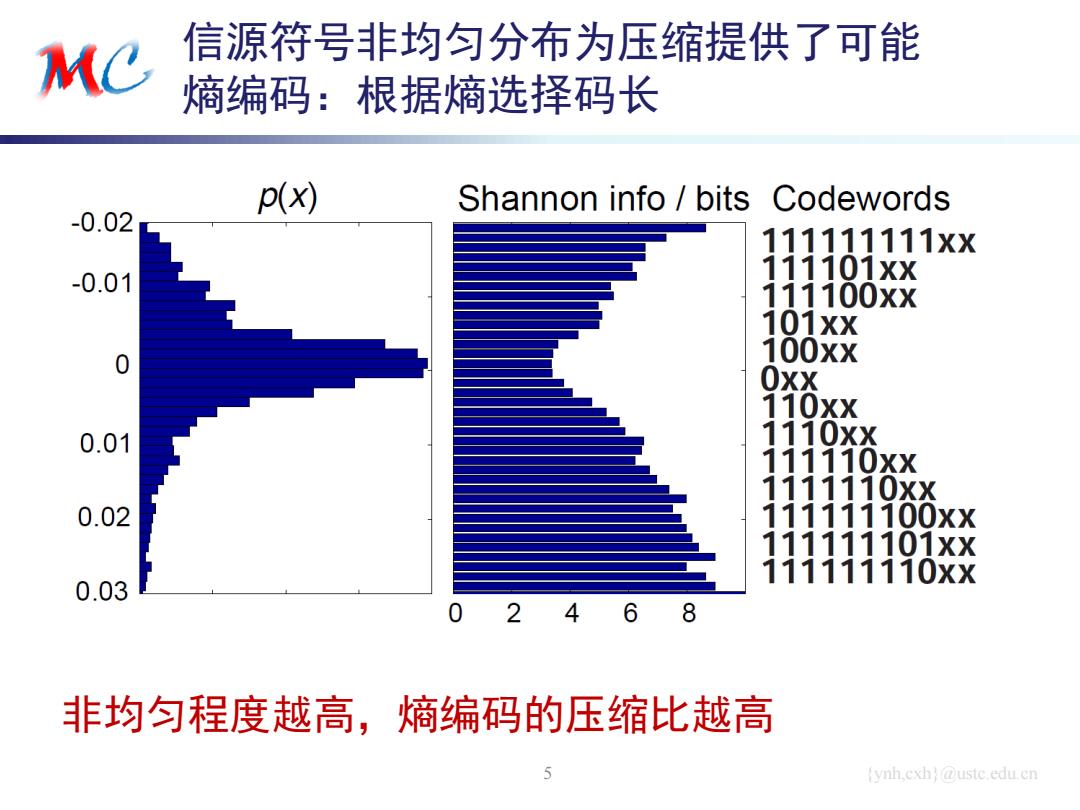
MC 信源符号非均匀分布为压缩提供了可能 熵编码:根据熵选择码长 p(x) Shannon info /bits Codewords -0.02 111111111XX 111 -0.01 01 xx 111100XX 101XX 100xX O 10xx 0.01 0.02 11 XX 01xx 111111110XX 0.03 2 6 8 非均匀程度越高,熵编码的压缩比越高 5 ynh.cxh@ustc.edu.cn
{ynh,cxh}@ustc.edu.cn 信源符号非均匀分布为压缩提供了可能 熵编码:根据熵选择码长 5 非均匀程度越高,熵编码的压缩比越高
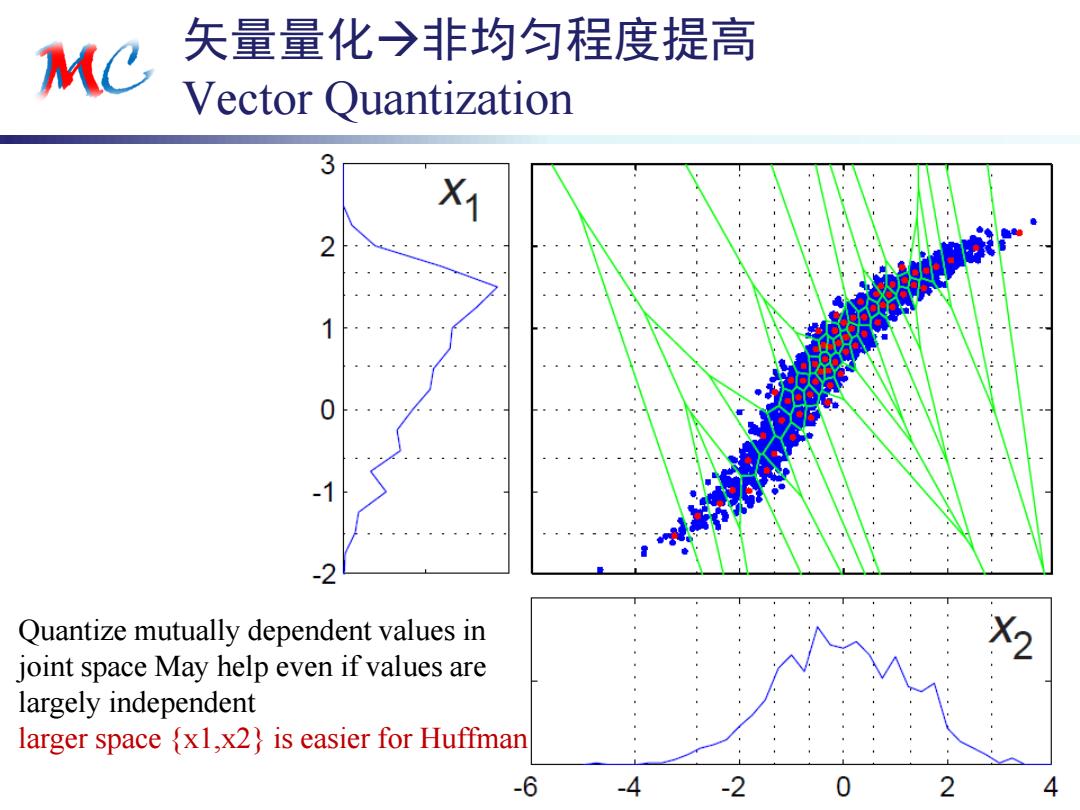
Me 矢量量化→非均匀程度提高 Vector Quantization 3 X1 2 Quantize mutually dependent values in joint space May help even if values are largely independent larger space {x1,x2)is easier for Huffman -6 -4-2 0 2 4
{ynh,cxh}@ustc.edu.cn 矢量量化非均匀程度提高 Vector Quantization 6 Quantize mutually dependent values in joint space May help even if values are largely independent larger space {x1,x2} is easier for Huffman
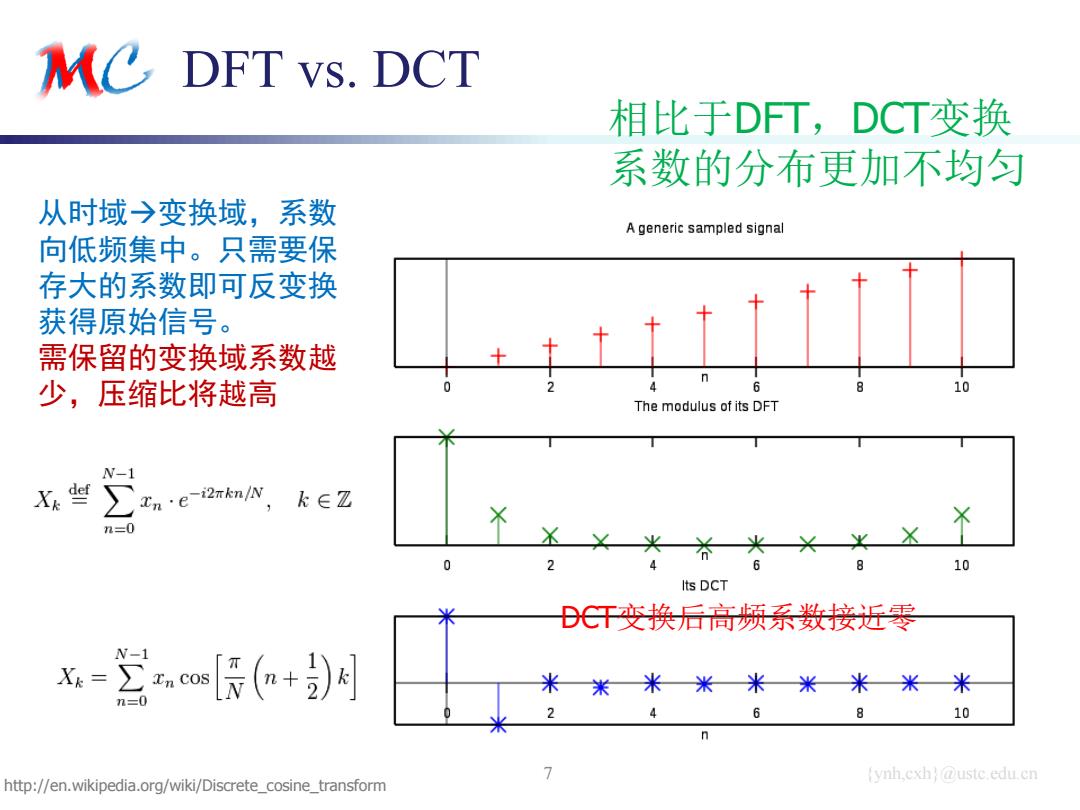
MC DFT vs.DCT 相比于DFT,DCT变换 系数的分布更加不均匀 从时域→变换域,系数 A generic sampled signal 向低频集中。只需要保 存大的系数即可反变换 获得原始信号。 需保留的变换域系数越 少,压缩比将越高 10 The modulus of its DFT N- X些 ∑ne2n,k∈z n=0 0 2 10 Its DCT DC纤变换后高频系数接近零 N-1 Xk= 米米米米米米米米米 n=0 2 6 10 7 ynh.cxh @ustc.edu.cn http://en.wikipedia.org/wiki/Discrete_cosine_transform
{ynh,cxh}@ustc.edu.cn DFT vs. DCT 7 DCT变换后高频系数接近零 http://en.wikipedia.org/wiki/Discrete_cosine_transform 从时域变换域,系数 向低频集中。只需要保 存大的系数即可反变换 获得原始信号。 需保留的变换域系数越 少,压缩比将越高 相比于DFT,DCT变换 系数的分布更加不均匀
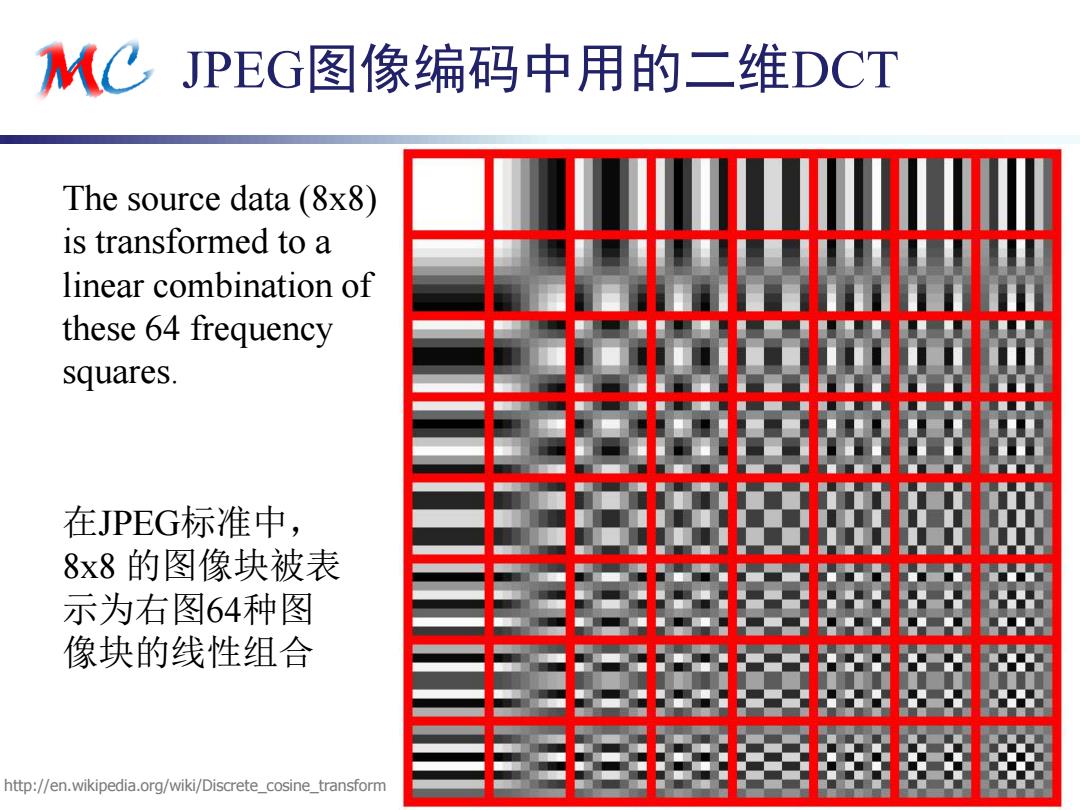
MC JPEG图像编码中用的二维DCT The source data (8x8) is transformed to a linear combination of these 64 frequency squares. 在JPEG标准中, 8x8的图像块被表 示为右图64种图 像块的线性组合 http://en.wikipedia.org/wiki/Discrete_cosine_transform
{ynh,cxh}@ustc.edu.cn JPEG图像编码中用的二维DCT 8 The source data (8x8) is transformed to a linear combination of these 64 frequency squares. 在JPEG标准中, 8x8 的图像块被表 示为右图64种图 像块的线性组合 http://en.wikipedia.org/wiki/Discrete_cosine_transform

KC二维DCT示例 88 A AA 5.1917 0,3911 1.2418 0.岁2 0.1583 0272 -00729 0,2205 0.02里号 05 0.3947 07846 8x8的原始图像块被 表示为右图64种图像 1,28 02214 4.0017-0.2720 0.789 块的线性组合 -0.2640-0.0392-0,2517 0.2750 00226 ,2183 258 6.1924 0.06580.0428-0,4721 0,29u5 4/95 0,31690054g,468-00225-,00550407-0,465001500 http://en.wikipedia.org/wiki/Discrete_cosine_transform -27四-0627 0196000649-0,4u6-01011749
{ynh,cxh}@ustc.edu.cn 二维DCT示例 9 8x8 的原始图像块被 表示为右图64种图像 块的线性组合 http://en.wikipedia.org/wiki/Discrete_cosine_transform

KC图像压缩中的DCT变换 白色代表大的系数;黑色代表接近零的系数 original DFT DCT ynh.cxh @ustc.edu.cn
{ynh,cxh}@ustc.edu.cn 图像压缩中的DCT变换 10 original DFT DCT 白色代表大的系数;黑色代表接近零的系数