
TI-MFA:Keep Calm and Reroute Segments Fast Klaus-Tycho Foerster Mahmoud Parham Marco Chiesa Stefan Schmid IEEE Conference on Computer Communications Workshops 王锋SA19006101 2019.11.29
TI-MFA: Keep Calm and Reroute Segments Fast Klaus-Tycho Foerster Mahmoud Parham Marco Chiesa Stefan Schmid IEEE Conference on Computer Communications Workshops 王锋 SA19006101 2019.11.29

问题描述 ·分段路由的出现是为了解决基于MPLS的流量工程解决方案的运营问题 ·本文的主要问题是关于快速重路由,静态地提前定义故障转移规则,可以无须调用控制平 面或等待最短路径重新收敛 ·有较强鲁棒性的快速重路由计划,可以忍受多个链路的失效
问题描述 • 分段路由的出现是为了解决基于MPLS的流量工程解决方案的运营问题 • 本文的主要问题是关于快速重路由,静态地提前定义故障转移规则,可以无须调用控制平 面或等待最短路径重新收敛 • 有较强鲁棒性的快速重路由计划,可以忍受多个链路的失效
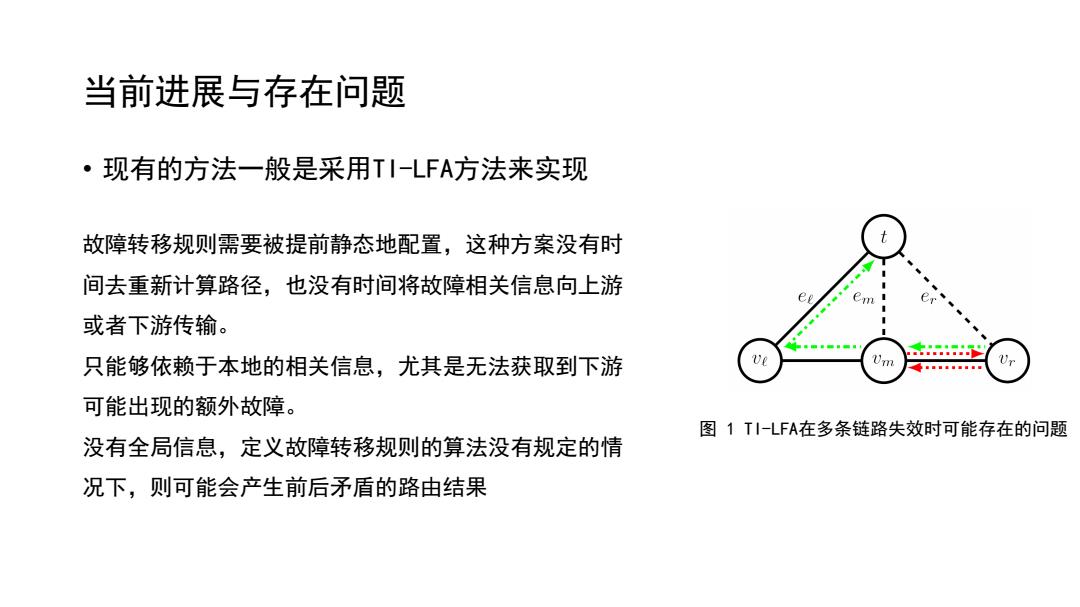
当前进展与存在问题 ·现有的方法一般是采用TI-LFA方法来实现 故障转移规则需要被提前静态地配置,这种方案没有时 间去重新计算路径,也没有时间将故障相关信息向上游 em er 或者下游传输。 只能够依赖于本地的相关信息,尤其是无法获取到下游 U 号■g 可能出现的额外故障。 图1TI-LFA在多条链路失效时可能存在的问题 没有全局信息,定义故障转移规则的算法没有规定的情 况下,则可能会产生前后矛盾的路由结果
当前进展与存在问题 • 现有的方法一般是采用TI-LFA方法来实现 图 1 TI-LFA在多条链路失效时可能存在的问题 故障转移规则需要被提前静态地配置,这种方案没有时 间去重新计算路径,也没有时间将故障相关信息向上游 或者下游传输。 只能够依赖于本地的相关信息,尤其是无法获取到下游 可能出现的额外故障。 没有全局信息,定义故障转移规则的算法没有规定的情 况下,则可能会产生前后矛盾的路由结果

问题的提出与意义 ·首次探索单个故障之外分段路由的快速重路由,对于这个问题,本文对分段路由中的静态 快速故障转移进行了系统的研究 ·关于分段路由中的快速故障转移能够和不能实现什么以及对其可能的权衡方式的见解 ·一个网络能够容忍多个链路同时故障,也意味着网络风险由链路组共同承担,那么它就更 可能用于更大规模的网络中
问题的提出与意义 • 首次探索单个故障之外分段路由的快速重路由,对于这个问题,本文对分段路由中的静态 快速故障转移进行了系统的研究 • 关于分段路由中的快速故障转移能够和不能实现什么以及对其可能的权衡方式的见解 • 一个网络能够容忍多个链路同时故障,也意味着网络风险由链路组共同承担,那么它就更 可能用于更大规模的网络中
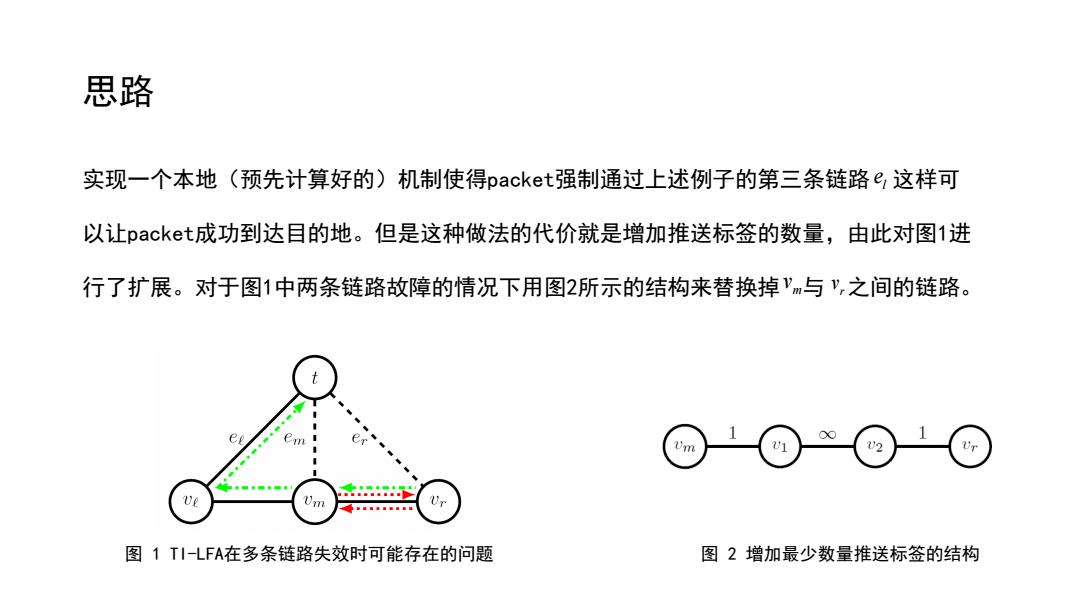
思路 实现一个本地(预先计算好的)机制使得backet强制通过上述例子的第三条链路e,这样可 以让packet.成功到达目的地。但是这种做法的代价就是增加推送标签的数量,由此对图1进 行了扩展。对于图1中两条链路故障的情况下用图2所示的结构来替换掉'm与",之间的链路。 Um 02 图1TI-LFA在多条链路失效时可能存在的问题 图2增加最少数量推送标签的结构
思路 实现一个本地(预先计算好的)机制使得packet强制通过上述例子的第三条链路 这样可 以让packet成功到达目的地。但是这种做法的代价就是增加推送标签的数量,由此对图1进 行了扩展。对于图1中两条链路故障的情况下用图2所示的结构来替换掉 与 之间的链路。 图 1 TI-LFA在多条链路失效时可能存在的问题 图 2 增加最少数量推送标签的结构 l e m v r v

TI-MFA工作原理 从节点V的角度来描述: 1.除了目的地t之外,刷新全部的标签栈 2.根据印acket报头中存储的所有的故障链路信息,在剩余部分网络G中选择到目的地t最 短的路径P 3.在packet的标签栈中添加分段:在路径P上给节点编号为v=y,y2,y=t,然后计算P上 的索引最高的V,,使得从V开始的最短路径在G(有故障链路)和G(无故障链路)中是相 同的,并且将其设置为标签栈的栈顶。如果计算的结果节点是V,将链路(y,2=y,) push到标签栈的栈顶,对于标签栈的第二项,将',作为起始节点重新开始,以此类推直 到y,=t
TI-MFA工作原理 从节点 的角度来描述: 1. 除了目的地t之外,刷新全部的标签栈 2. 根据packet报头中存储的所有的故障链路信息,在剩余部分网络 中选择到目的地t最 短的路径P 3. 在packet的标签栈中添加分段:在路径P上给节点编号为 ,然后计算P上 的索引最高的 ,使得从 开始的最短路径在 (有故障链路)和 (无故障链路)中是相 同的,并且将其设置为标签栈的栈顶。如果计算的结果节点是 ,将链路 push到标签栈的栈顶,对于标签栈的第二项,将 作为起始节点重新开始,以此类推直 到 v ' G 1 2 , , , x v v v v t i v v ' G G 1 2 ( , )i v v v v i v i v t

理论证明 定理一:假设G是一个网络其中有k个链路发生故障,剩余的部分网络G保持连通。TI-MFA成功路由 到目的地。 证明:定理一的证明将通过嵌套的与故障次数有关的归纳讨论进行。 现在假设packet已经遇到了x-I次故障,并且在其路径上遇到了第x次故障。进行以下两种情况的讨 论: 1.x=k:G(有故障链路)和(无故障链路)中的最短路径路由再次相同。 2.x>k:除非接下来遇到某个链路第x+1次故障(前x次故障不会再被遇到),否则目的地是可达的。 然后,再次调用归纳构造:前提是已经遇到的故障不会再被遇到,即最终要么遇到了所有的故障, 要么就成功到达目的地。但是,一旦遇到所有的故障,这意味着通过路径P目的地是可达的
理论证明 定理一:假设 是一个网络其中有k个链路发生故障,剩余的部分网络 保持连通。TI-MFA成功路由 到目的地。 证明:定理一的证明将通过嵌套的与故障次数有关的归纳讨论进行。 现在假设packet已经遇到了 次故障,并且在其路径上遇到了第 次故障。进行以下两种情况的讨 论: 1. (有故障链路)和(无故障链路)中的最短路径路由再次相同。 2. 除非接下来遇到某个链路第 次故障(前 次故障不会再被遇到),否则目的地是可达的。 然后,再次调用归纳构造:前提是已经遇到的故障不会再被遇到,即最终要么遇到了所有的故障, 要么就成功到达目的地。但是,一旦遇到所有的故障,这意味着通过路径P目的地是可达的。 G ' G x 1 x x k : ' G x k : x 1 x

实验与实验分析 ·实验在Rocketfue I拓扑结构上运行,使用其提供的链路权重和延迟变体。 ·实验列举了所有TI-LFA和TI-LMA将遇到两个故障链路的故障情形。 ·实验过程丢弃了所有断开连接的实例。 ·实验过程用程序模拟了TI-LFA和TI-MFA的逐跳行为,并且记录: 1.packet是否成功到达目的地 2.使用的最大标签栈的大小 3.所走路径的长度。 ·分别在是否刷新标签栈的情形下运行TI-LFA和TI-MFA,因此一共有四种算法
实验与实验分析 • 实验在Rocketfuel拓扑结构上运行,使用其提供的链路权重和延迟变体。 • 实验列举了所有TI-LFA和TI-LMA将遇到两个故障链路的故障情形。 • 实验过程丢弃了所有断开连接的实例。 • 实验过程用程序模拟了TI-LFA和TI-MFA的逐跳行为,并且记录: 1. packet是否成功到达目的地 2. 使用的最大标签栈的大小 3. 所走路径的长度。 • 分别在是否刷新标签栈的情形下运行TI-LFA和TI-MFA,因此一共有四种算法

实验与实验分析 ·成功率/可达性分析。两种TI-MFA变体实例在所有实例中都到达了目的地,而TI-LFA(无刷 新)有大约!的实验陷入了无限循环。实验结果如图3所示。(四种算法共进行超过500万次 实验)。 Packet Drop Rates With TI-LFA,double failures 34 no flush 32 2003 T10 flush 028284208 16 14 396 3967 325 weights.intra 3257latencies.intra 175 175 12 12 64 6461 723 2 _weights.intra tencies.intra weights.intra _weights.intra latencies.intra _latencies.intra _weights.intra tencies.intra _weights _latencies.int ntra Backbone Topologies (Rocketfuel) 图3TI-LFA失败率
实验与实验分析 • 成功率/可达性分析。两种TI-MFA变体实例在所有实例中都到达了目的地,而TI-LFA(无刷 新)有大约 的实验陷入了无限循环。实验结果如图3所示。(四种算法共进行超过500万次 实验)。 1 5 图3 TI-LFA失败率

实验与实验分析 ·最大标签栈大小分析。实验结果可以看出TI-MFA在标签栈大小方面的工作是有效的,并且 可以预测在使用刷新的情形下,2k+1就足够处理k个链路故障的情形。 Frequency of Stack Sizes(all 4 algorithms) 100 TI-LFA,no flush 90 TI-LFA,flush TI-MFA,no flush 80 TI-MFA,flush 70 6 40 30 20 10 0 3 Stack Size 图4最大标签栈大小出现的频率
实验与实验分析 • 最大标签栈大小分析。实验结果可以看出TI-MFA在标签栈大小方面的工作是有效的,并且 可以预测在使用刷新的情形下,2k+1就足够处理k个链路故障的情形。 图 4 最大标签栈大小出现的频率