
版权©2019,版权保留,侵犯必究 第十章电路的频率响应 网络函数和频率特性 ●RLC串联电路的频率特性 。串联谐振电路 。并联谐振电路 复旦大学射频集成电路设计研究小组 -012- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -012- 第十章 电路的频率响应 ⚫ 网络函数和频率特性 ⚫ RLC串联电路的频率特性 ⚫ 串联谐振电路 ⚫ 并联谐振电路

版权©2019,版权保留,侵犯必究 网络函数和频率特性 齐性定理 一若线性电路中只有一个电源,则各处电压电流 与此电源的源电压或源电流成正比 一也适用于正弦电流电路的向量模型 电路网络 一激励:单一电源的源电压或源电流 一响应Y:某一电压或电流 复旦大学射频集成电路设计研究小组 -013- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -013- 网络函数和频率特性 • 齐性定理 – 若线性电路中只有一个电源,则各处电压电流 与此电源的源电压或源电流成正比 – 也适用于正弦电流电路的向量模型 • 电路网络 – 激励𝑋ሶ:单一电源的源电压或源电流 – 响应𝑌ሶ:某一电压或电流

版权©2019,版权保留,侵犯必究 网络函数 X X() V 线性无 线性无 y(t) 独立源 独立源 ·网络函数:响应向量与激励向量的比例系数 H0o,-文 复旦大学射频集成电路设计研究小组 -014- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -014- 网络函数 • 网络函数:响应向量与激励向量的比例系数 ( ) Y H ω X j = x(t) v 线性无 独立源 i y(t) 线性无 独立源 Y V • • I • X •

版权©2019,版权保留,侵犯必究 网络函数 ·响应与激励属于同一端口的网络函数 激励 响应 网络函数 电流源 电压 等效阻抗 电压源 电流 等效导纳 复旦大学射频集成电路设计研究小组 -015- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -015- 网络函数 • 响应与激励属于同一端口的网络函数 激励 响应 网络函数 电流源 电压 等效阻抗 电压源 电流 等效导纳
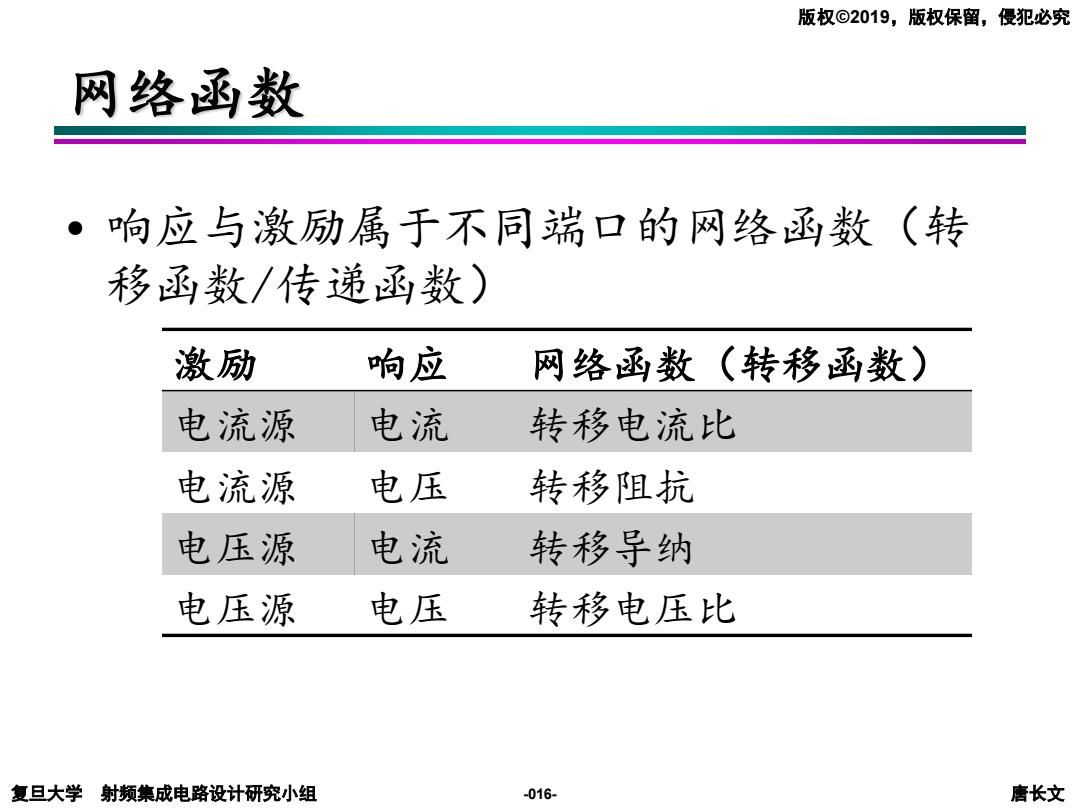
版权©2019,版权保留,侵犯必究 网络函数 响应与激励属于不同端口的网络函数(转 移函数/传递函数) 激励 响应 网络函数(转移函数) 电流源 电流 转移电流比 电流源 电压 转移阻抗 电压源 电流 转移导纳 电压源 电压 转移电压比 复旦大学射频集成电路设计研究小组 -016- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -016- 网络函数 • 响应与激励属于不同端口的网络函数(转 移函数/传递函数) 激励 响应 网络函数(转移函数) 电流源 电流 转移电流比 电流源 电压 转移阻抗 电压源 电流 转移导纳 电压源 电压 转移电压比
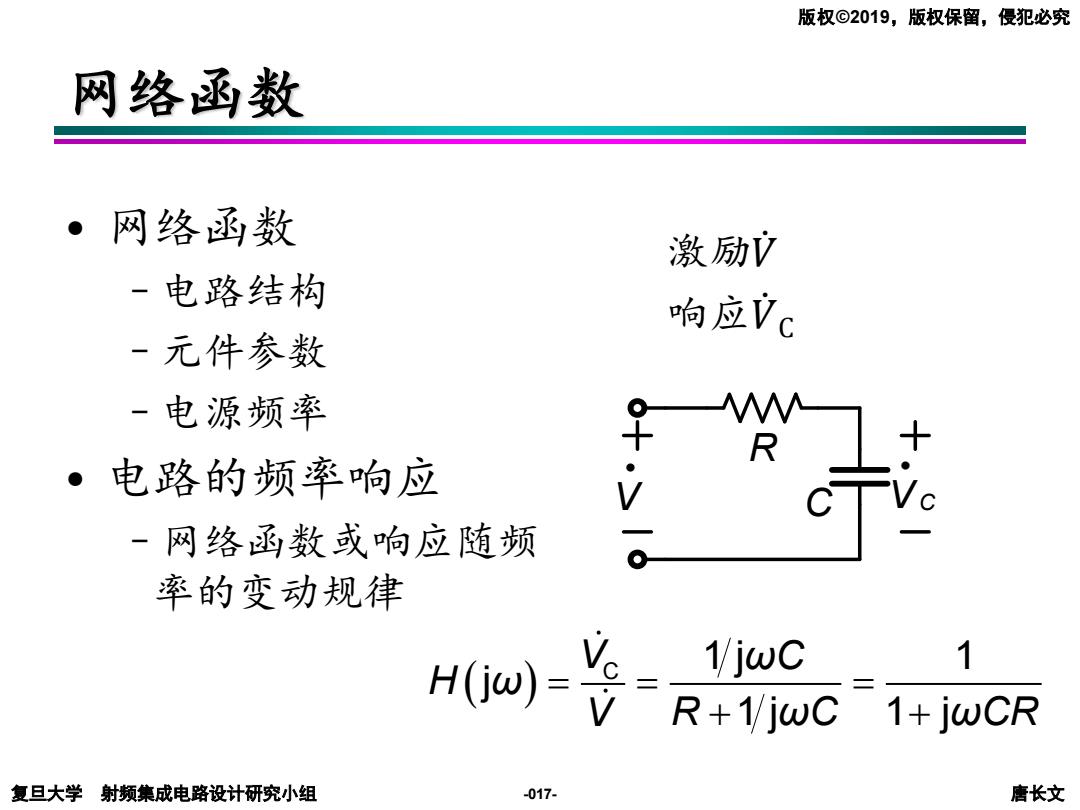
版权©2019,版权保留,侵犯必究 网络函数 ·网络函数 激励 -电路结构 响应Vc -元件参数 -电源频率 R ·电路的频率响应 ● -网络函数或响应随频 率的变动规律 Ho)-¥ VjwC 1 R+1/jwC 1+jwCR 复旦大学射频集成电路设计研究小组 -017- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -017- 网络函数 • 网络函数 –电路结构 –元件参数 –电源频率 • 电路的频率响应 –网络函数或响应随频 率的变动规律 ( ) V ωC H ω V R ωC ωCR 1 1 1 1 = = = + + C j j j j 激励𝑉ሶ 响应𝑉ሶ C R V • V C • C

版权©2019,版权保留,侵犯必究 网络函数 HUw-是Rc 1 jwC 1 1+jwCR ·极坐标形式 Ho8w-长0长4 幅频特性H(jω=VeV (响应和激励有效值 频率 之比与频率的关系) 特性 相频特性(ω)=4c-4 (响应越前于激励的相 位差与频率的关系) 复旦大学射频集成电路设计研究小组 -018- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -018- 网络函数 • 极坐标形式 ( ) V ψ V H ω θ ω ψ ψ V ψ V ( ) ( ) = = − C C C C j H ( ω) =V V C j θ (ω)=ψC −ψ (响应和激励有效值 频率 之比与频率的关系) 特性 幅频特性 相频特性 (响应越前于激励的相 位差与频率的关系) ( ) V ωC H ω V R ωC ωCR 1 1 1 1 = = = + + C j j j j

版权©2019,版权保留,侵犯必究 网络函数 Ho-告R+0c 1 wC 1 1+jwCR ·RC具有时间的量纲,导数具有频率的量纲 ·定义RC电路的固有频率或自然频率 1 W0= RC 1 复旦大学射频集成电路设计研究小组 -019- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -019- ( ) V ωC H ω V R ωC ωCR 1 1 1 1 = = = + + C j j j j 网络函数 • RC具有时间的量纲,导数具有频率的量纲 • 定义RC电路的固有频率或自然频率 0 1 ω RC = ( ) 2 0 0 0 1 1 ( arctan ) 1 j / 1 ( / ) ω ω ω ω ω ω ω == = − + + H j
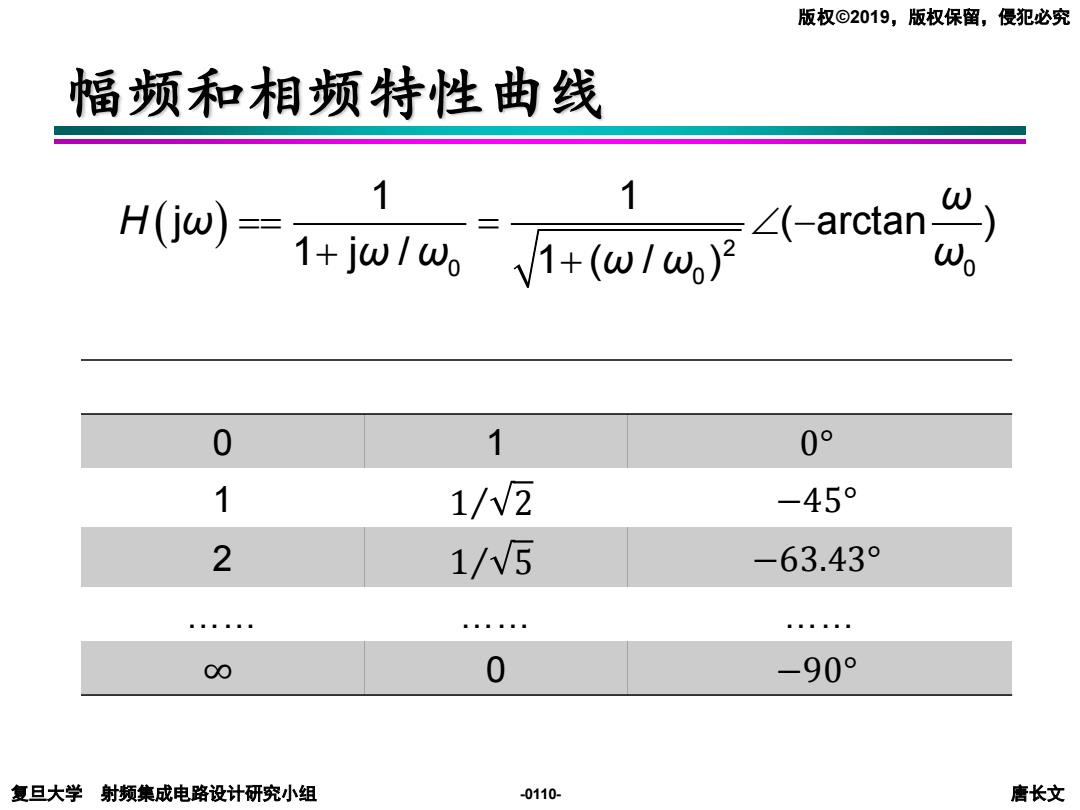
版权©2019,版权保留,侵犯必究 幅频和相频特性曲线 H(jw)= 1 1 n W) 1+jw1w。V1+(ω1ω)2 ∠(-arcta Wo 0 1 0° 1 1/W2 -45° 2 1/W5 -63.43° 00 0 -90° 复旦大学射频集成电路设计研究小组 -0110- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -0110- 幅频和相频特性曲线 0 1 0° 1 1Τ 2 −45° 2 1Τ 5 −63.43° …… …… …… ∞ 0 −90° ( ) ω H ω ω ω0 0 ω ω 2 ω 0 1 1 ( arctan ) 1 j / 1 ( / ) == = − + + j
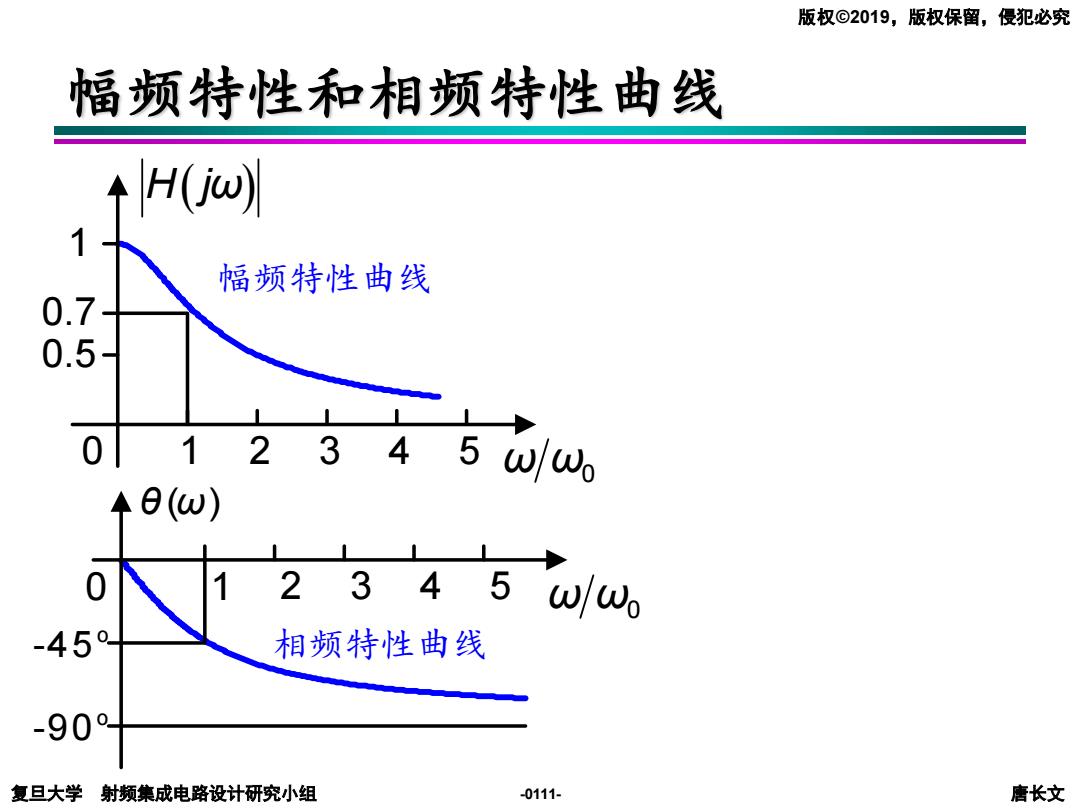
版权©2019,版权保留,侵犯必究 幅频特性和相频特性曲线 H(jw) 幅频特性曲线 0.7 0.5 0 1 2345w/w +8(ω) 2345w/w -45 相频特性曲线 -90t 复旦大学射频集成电路设计研究小组 -0111- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -0111- 幅频特性和相频特性曲线 ω ω0 0 1 2 3 4 5 1 0.7 0.5 H j ( ω) θ ( ) ω o -45o -900 1 2 3 4 5 ω ω0 幅频特性曲线 相频特性曲线