
版权©2019,版权保留,侵犯必究 第三章电阻电路的分析 电路的图 ·支路电流法和支路电压法 ●回路电流法 。节点电压法 复旦大学射频集成电路设计研究小组 -012- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -012- 第三章 电阻电路的分析 ⚫ 电路的图 ⚫ 支路电流法和支路电压法 ⚫ 回路电流法 ⚫ 节点电压法
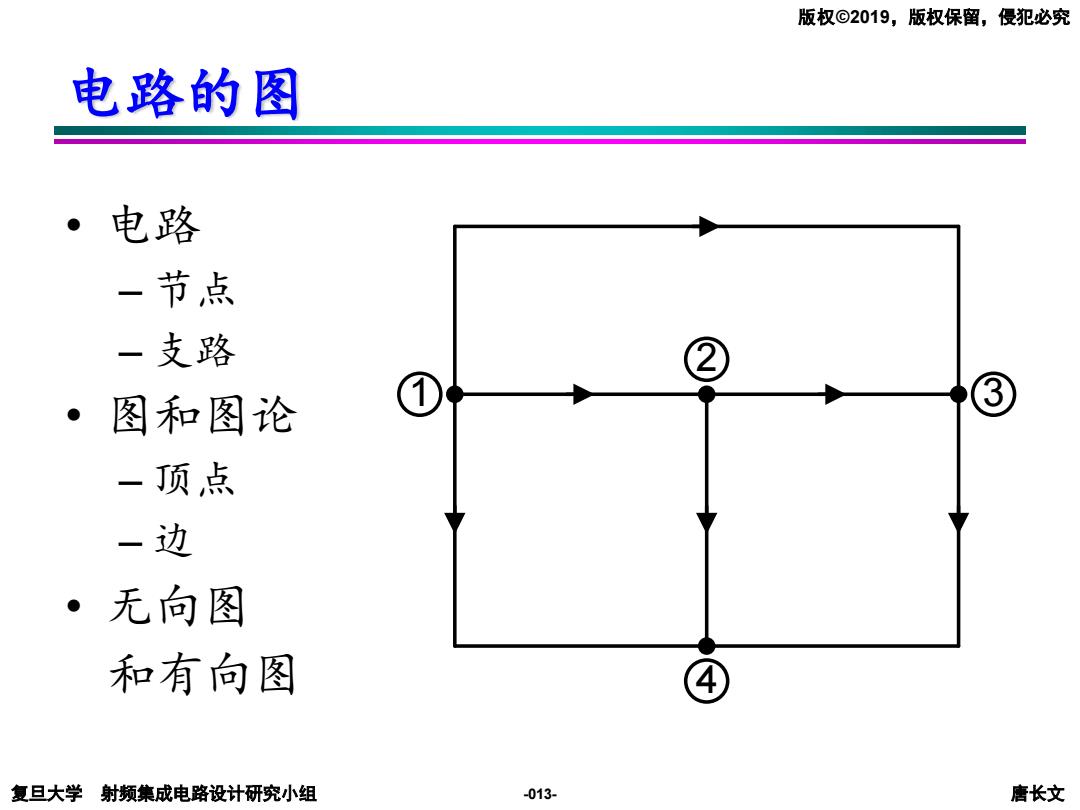
版权©2019,版权保留,侵犯必究 电路的图 。电路 一节点 一支路 ③ 图和图论 ③ 一顶点 一边 ·无向图 和有向图 ④ 复旦大学射频集成电路设计研究小组 -013- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -013- 6 4 5 1 2 3 1 2 3 4 电路的图 • 电路 – 节点 – 支路 • 图和图论 – 顶点 – 边 • 无向图 和有向图 6 4 5 1 2 3 1 2 3 4 6 4 5 1 2 3 1 2 3 4

版权©2019,版权保留,侵犯必究 路径,连通图和回路 ·路径 从一个顶点到另外一个顶点,经过的所有边构 成一条路径。 。连通图 任意两个顶,点之间至少有一条路径的图称为连 通图。 ·回路 如果一条路径的起点和终点重合,且经过的其 他顶,点不出现重复,这条闭合路径就是一个回路。 复旦大学射频集成电路设计研究小组 -014- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -014- 路径,连通图和回路 • 路径 从一个顶点到另外一个顶点,经过的所有边构 成一条路径。 • 连通图 任意两个顶点之间至少有一条路径的图称为连 通图。 • 回路 如果一条路径的起点和终点重合,且经过的其 他顶点不出现重复,这条闭合路径就是一个回路
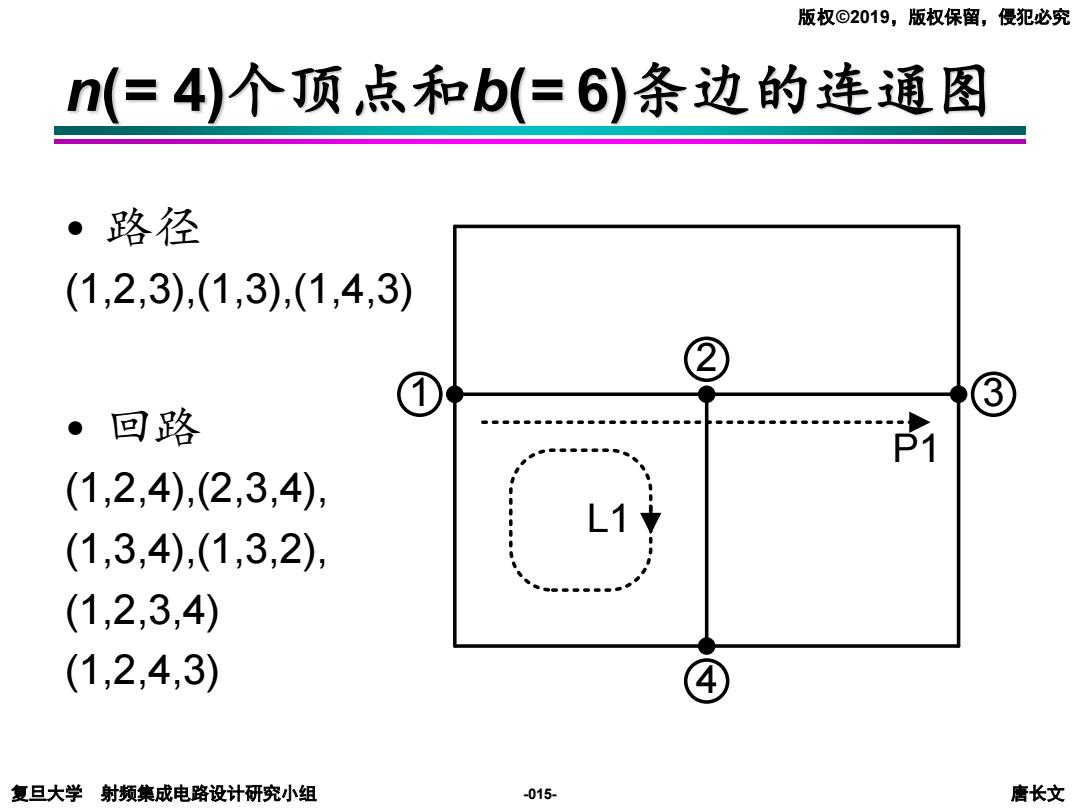
版权©2019,版权保留,侵犯必究 n(仁4)个顶点和b(=6)条边的连通图 ·路径 (1,2,3),(1,3),(1,4,3) ② ③ 回路 (1,2,4),(2,3,4); L1 (1,3,4),(1,3,2), (1,2,3,4) (1,2,4,3) ④ 复旦大学射频集成电路设计研究小组 -015- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -015- • 路径 (1,2,3),(1,3),(1,4,3) • 回路 (1,2,4),(2,3,4), (1,3,4),(1,3,2), (1,2,3,4) (1,2,4,3) n(= 4)个顶点和b(= 6)条边的连通图 6 4 5 1 2 3 1 2 3 4 L1 P1

版权©2019,版权保留,侵犯必究 树,树支和连支 ·树 包含图的全部顶点且不包含任何回路的连通子图。 ·树支 树中包含的边称为该树的树支。 ·连支 图中不包含在树中的边称为树的连支。 n个顶,点和b条边的连通图,其树的树支数为(n-), 连支数为(b-n+1)。 复旦大学射频集成电路设计研究小组 -016- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -016- 树,树支和连支 • 树 包含图的全部顶点且不包含任何回路的连通子图。 • 树支 树中包含的边称为该树的树支。 • 连支 图中不包含在树中的边称为树的连支。 n个顶点和b条边的连通图,其树的树支数为(n − 1), 连支数为(b − n + 1)
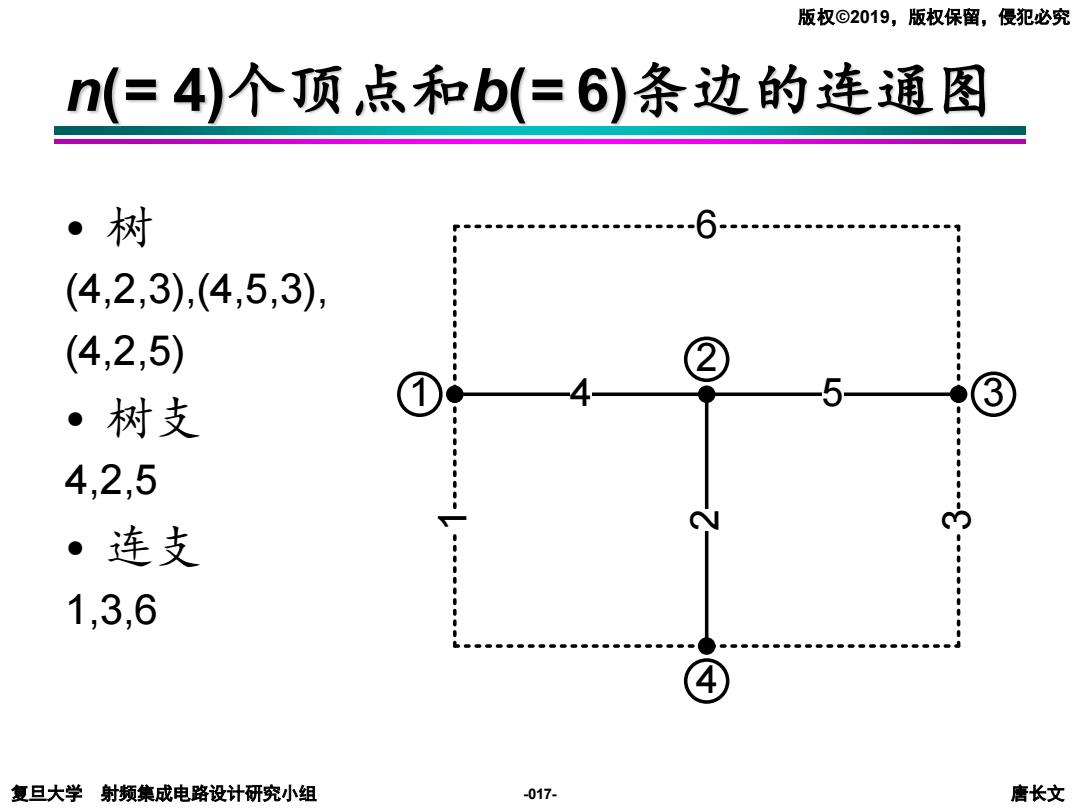
版权©2019,版权保留,侵犯必究 n(=4)个顶点和b(=6)条边的连通图 ·树 -6- (4,2,3),(4,5,3) (4,2,5) ③ 1 4 5 ·树支 4,2,5 ·连支 1,3,6 复旦大学射频集成电路设计研究小组 -017- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -017- • 树 (4,2,3),(4,5,3), (4,2,5) • 树支 4,2,5 • 连支 1,3,6 1 2 4 6 1 2 3 4 3 5 1 2 4 6 1 2 3 4 3 5 1 2 4 6 1 2 3 4 1 2 3 4 6 1 2 3 4 5 1 2 4 6 1 2 3 4 3 5 n(= 4)个顶点和b(= 6)条边的连通图

版权©2019,版权保留,侵犯必究 基本回路,网孔和平面图 ·基本回路 只包含一个连支的回路称为基本回路,也称单 连支回路。基本回路数等于连支数。 。平面图 如果一个图画在平面上,各条边除了连接的点 外不再交叉,这样的图称为平面图。 ·网孔 平面图的单孔回路。内部不存在任何边的网孔 称为内网孔。外部不存在任何边的网孔称为外网孔。 复旦大学射频集成电路设计研究小组 -018- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -018- 基本回路,网孔和平面图 • 基本回路 只包含一个连支的回路称为基本回路,也称单 连支回路。基本回路数等于连支数。 • 平面图 如果一个图画在平面上,各条边除了连接的点 外不再交叉,这样的图称为平面图。 • 网孔 平面图的单孔回路。内部不存在任何边的网孔 称为内网孔。外部不存在任何边的网孔称为外网孔
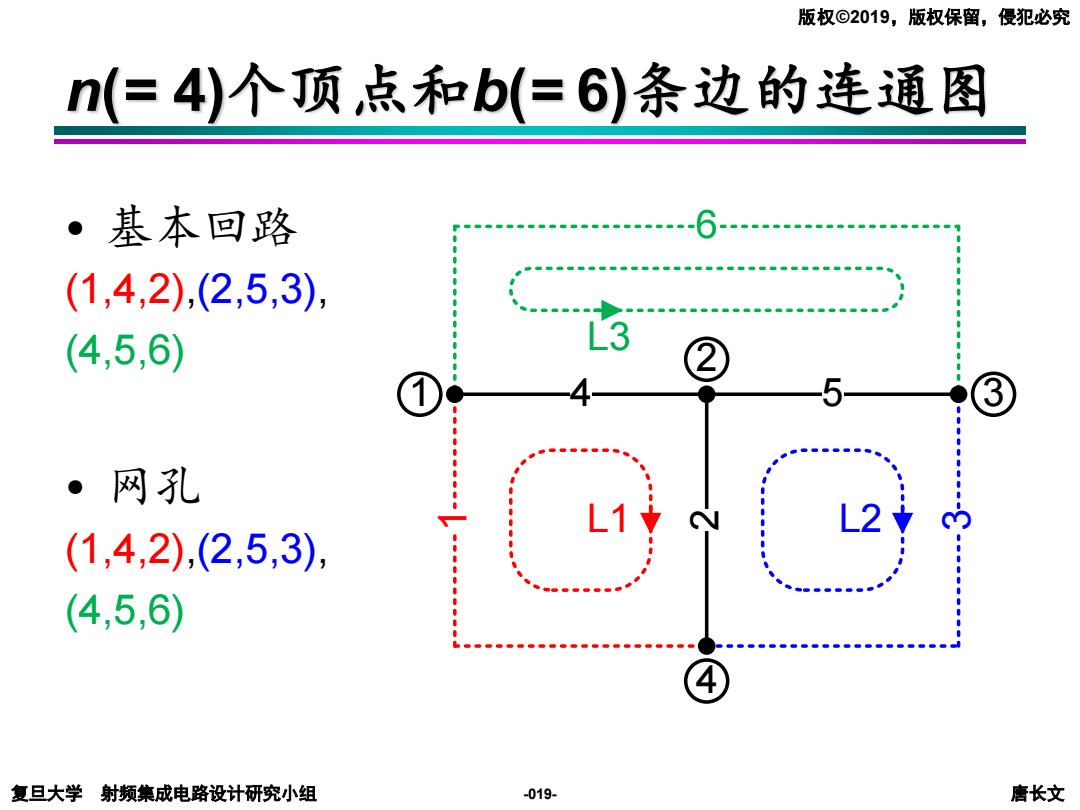
版权©2019,版权保留,侵犯必究 n(=4)个顶点和b(=6)条边的连通图 ·基本回路 (1,4,2),(2,5,3) (4,5,6) ② 。网孔 (1,4,2),(2,5,3) (4,5,6) 复旦大学射频集成电路设计研究小组 -019- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -019- • 基本回路 (1,4,2),(2,5,3), (4,5,6) • 网孔 (1,4,2),(2,5,3), (4,5,6) 1 2 4 6 1 2 3 4 3 5 1 2 4 6 1 2 3 4 L1 3 5 1 2 4 6 1 2 3 4 L2 3 5 1 2 4 6 1 2 3 4 L3 1 2 3 1 4 2 3 4 5 6 L3 L1 L2 n(= 4)个顶点和b(= 6)条边的连通图

版权©2019,版权保留,侵犯必究 电流和电压独立方程 对于具有门个节点和b条支路的电路,基本回路 数等于连支数(b-n+1)。 在任意(n-1)个节点上可以得到(n-)个独立 的KCL方程。 在任意(b-n+)个基本回路上可以得到(b-n +)个独立的KVL方程。 总共b个独立的KCL和KVL方程。 根据每条支路元件的VCR方程又可以列出b个 方程。因此,可由2b个方程解出b个支路电压和b个 支路电流。 复旦大学射频集成电路设计研究小组 -0110- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -0110- 电流和电压独立方程 对于具有n个节点和b条支路的电路,基本回路 数等于连支数(b − n + 1)。 在任意(n − 1)个节点上可以得到(n − 1)个独立 的KCL方程。 在任意(b − n + 1)个基本回路上可以得到(b − n + 1)个独立的KVL方程。 总共b个独立的KCL和KVL方程。 根据每条支路元件的VCR方程又可以列出b个 方程。因此,可由2b个方程解出b个支路电压和b个 支路电流
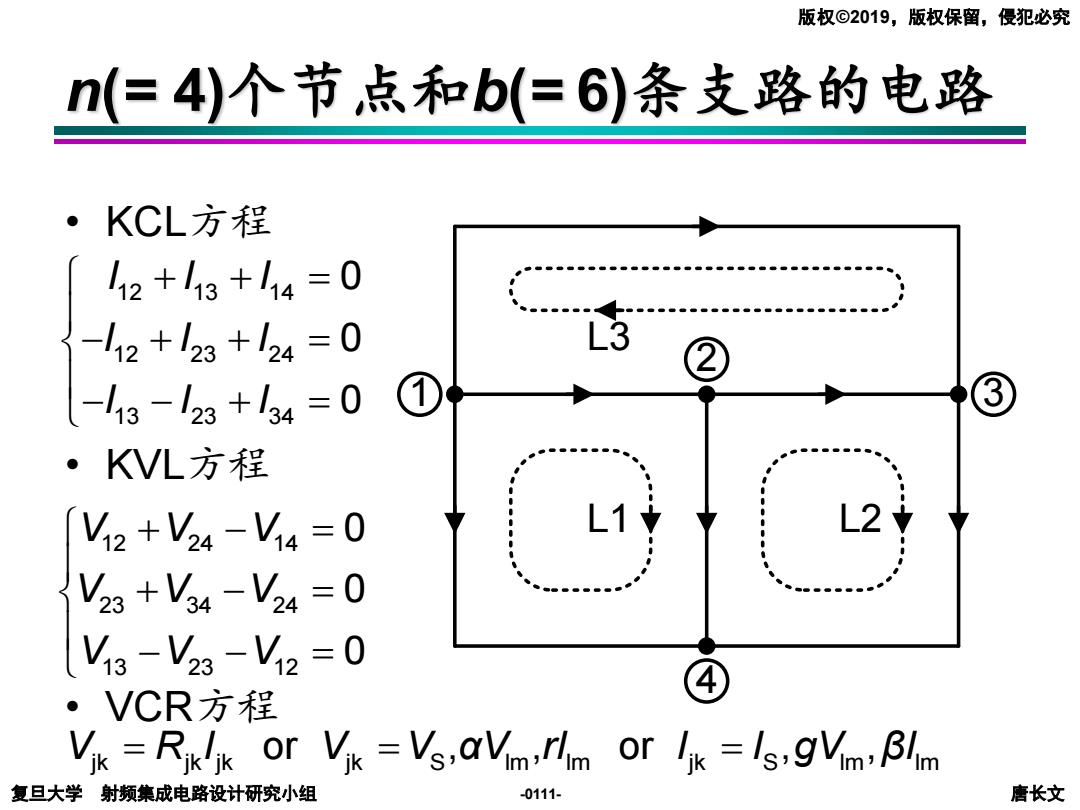
版权©2019,版权保留,侵犯必究 n(=4)个节点和b(=6)条支路的电路 ·KCL方程 12+13+114=0 -12+123+124=0 ② -13-123+134=0 ① ③ ·KVL方程 V2+V24-V4=0 V23+Vg4-V24=0 V34 V3-V23-V2=0 ·VCR方程 Vik =Riklik or Vik =Vs,aVim:rlim or li =Is,gVim:Blim 复旦大学射频集成电路设计研究小组 -0111 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -0111- 6 4 5 1 2 3 1 2 3 4 L3 L1 L2 • KCL方程 • KVL方程 • VCR方程 n(= 4)个节点和b(= 6)条支路的电路 12 13 14 12 23 24 13 23 34 0 0 0 I I I I I I I I I + + = − + + = − − + = 12 24 14 23 34 24 13 23 12 0 0 0 V V V V V V V V V +−= + − = − − = jk jk jk jk S lm lm jk S lm lm V R I V V = = = or , , or , , αV rI I I gV βI 6 1 2 3 4 L3 L1 L2