复旦大学：《电路基础 Fundamental of Electric Circuits》课程教学资源（课件讲稿）二端口网络

第14章二端口网络 提要 本章首先介绍二端口网络的各种参数方程及两种重要 等效电路：T形和Π形等效电路，其次介绍二端口网络的输入、 输出阻抗等概念；最后介绍二端口网络的级联规律。 本章目次 1.二端口网络 4.二端口网络的等效电路 用理 2.导纳方程阻抗方程 5.二端口与电源及负载联结 3.传输参数和混合参数 6.二端口网络的级联

本章首先介绍二端口网络的各种参数方程及两种重要 等效电路：T形和П形等效电路;其次介绍二端口网络的输入、 输出阻抗等概念；最后介绍二端口网络的级联规律。 1.二端口网络 3.传输参数和混合参数 2.导纳方程阻抗方程 4.二端口网络的等效电路 5.二端口与电源及负载联结 6 .二端口网络的级联 本章目次 第14章 二端口网络 提要

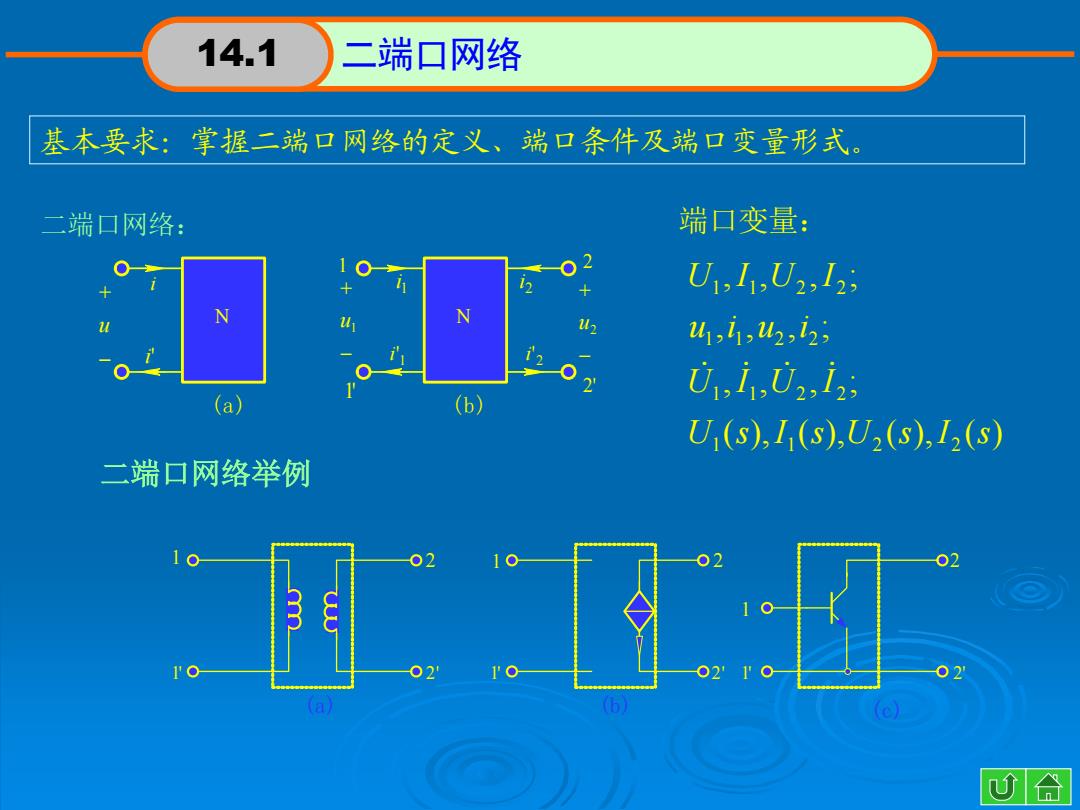
14.1 二端口网络 基本要求：掌握二端口网络的定义、端口条件及端口变量形式。 二端口网络： 端口变量： U1,1,U2,12 N N u 41,71,42,2 0,i,02,12; (a) U(S),I(s),U(s),I2(s) 二端口网络举例 02 02 1● ●21 02 a U合

14.1 二端口网络 基本要求：掌握二端口网络的定义、端口条件及端口变量形式。 二端口网络： N   2 u   1 u 1 i' 1 i 2 i 2 i' 1' 2' 1 2 (b) N   u i' i (a) 二端口网络举例 1' 1 2 2' 2' 1 2 1' 2 2' 1 1' (a) (b) (c) 端口变量： ( ), ( ), ( ), ( ) , , , ; , , , ; , , , ; 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 U s I s U s I s U I U I u i u i U I U I    

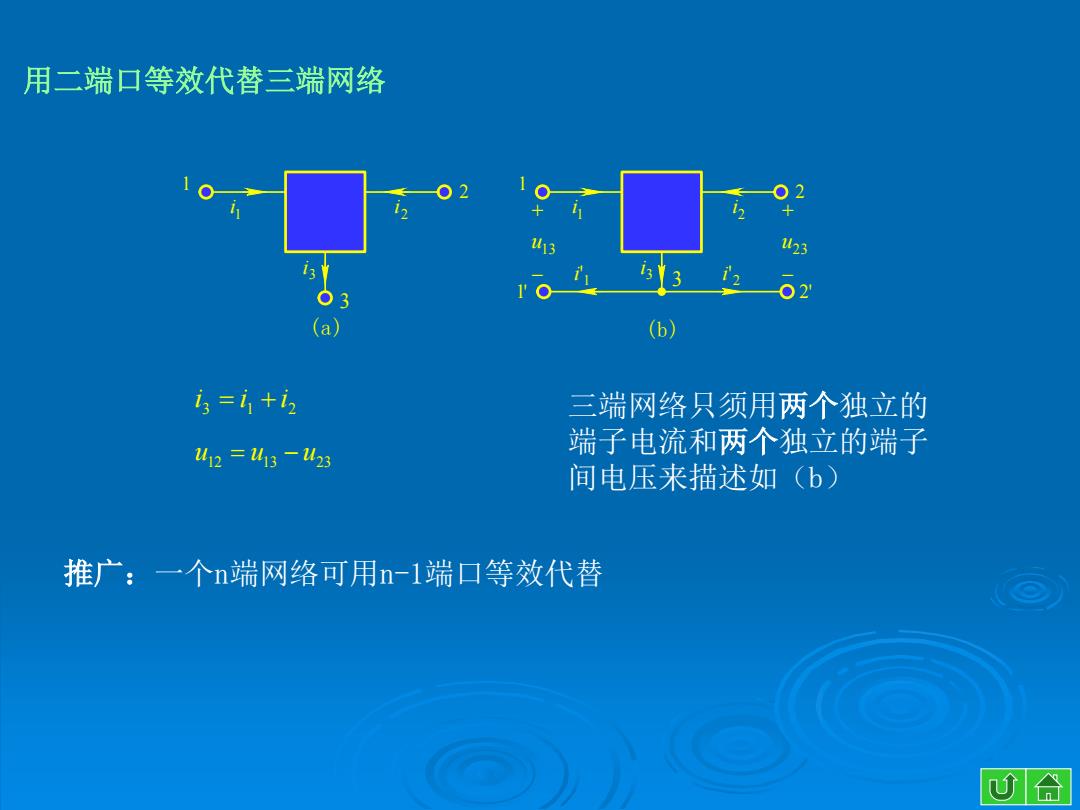
用二端口等效代替三端网络 02 123 3 (a) (b) 13=1+12 三端网络只须用两个独立的 412=413-M23 端子电流和两个独立的端子 间电压来描述如(b) 推广：.一个n端网络可用n-1端口等效代替 心合

推广：一个n端网络可用n-1端口等效代替 用二端口等效代替三端网络 3 1 2 i  i  i u12  u13 u23 三端网络只须用两个独立的 端子电流和两个独立的端子 间电压来描述如（b） 1 2 3 1 i 2 i 3 i 1 2 3 1 i 2 i 3 i 1 i' 2 i' 1' 2'   13 u   23 u (a) (b)

14.2 导纳参数方程和阻抗参数方程 基本要求：熟练掌握二端口网络导纳方程和阻抗参数方程的形式及导纳参数 参数矩阵和阻抗参数矩阵的计算。 1 导纳参数方程 i=YU+Y202 0 端口1 端口2 i,=YU+YU 矩阵形式： &] 相量形式： i=YU 式中：0=心，0，T和i=[山，i,]分别表示端口电压和电流向量 Y (导纳参数矩阵或Y参数矩阵) 心合

1 导纳参数方程 14.2 导纳参数方程和阻抗参数方程 1 Y11U1 Y12U2 I      2 Y21U1 Y22U2 I                             2 1 21 22 11 12 2 1 U U Y Y Y Y I I     矩阵形式： 式中:        21 22 11 12 Y Y Y Y Y U   [U  1 ,U  2 ] T 和 I   [I  1 ,I  2 ] T 分别表示端口电压和电流向量 (导纳参数矩阵或Y 参数矩阵) 相量形式： I  YU  基本要求：熟练掌握二端口网络导纳方程和阻抗参数方程的形式及导纳参数 参数矩阵和阻抗参数矩阵的计算。   U1  1 I  2 I    U2  端口1 端口2 1 1' 2 2

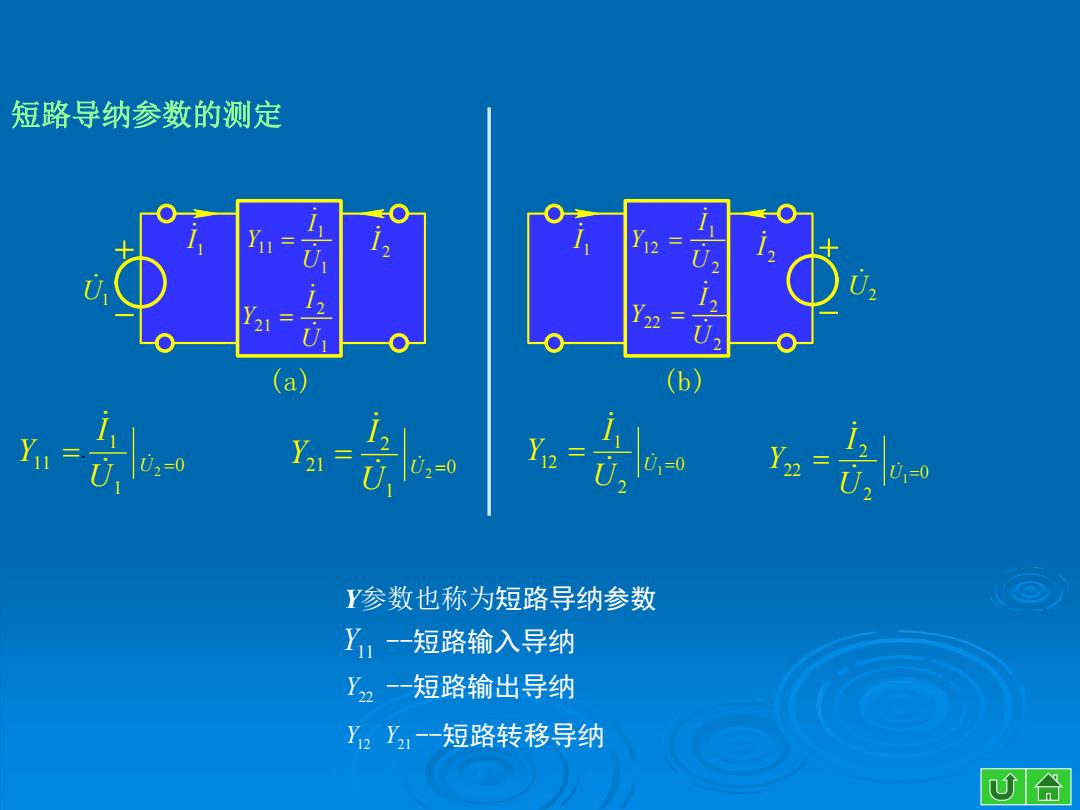
短路导纳参数的测定 12 1 121 122 (a) (b Yn= v.-0 Y参数也称为短路导纳参数 Y一短路输入导纳 Y2-一短路输出导纳 Y2Y,-一短路转移导纳 心合

 0 1 1 11 2   U U I Y    0 1 2 21 2   U U I Y    0 2 1 12 1  U U I Y    0 2 2 22 1  U U I Y    Y参数也称为短路导纳参数 Y11 Y12 Y21 Y22 --短路输入导纳 --短路输出导纳 --短路转移导纳 短路导纳参数的测定 U1  1 1 11 U I Y    1 2 21 U I Y    U2  (a) (b) 1 I  2 I  2 1 1 2 U I Y    2 2 22 U I Y    2 I  1 I 

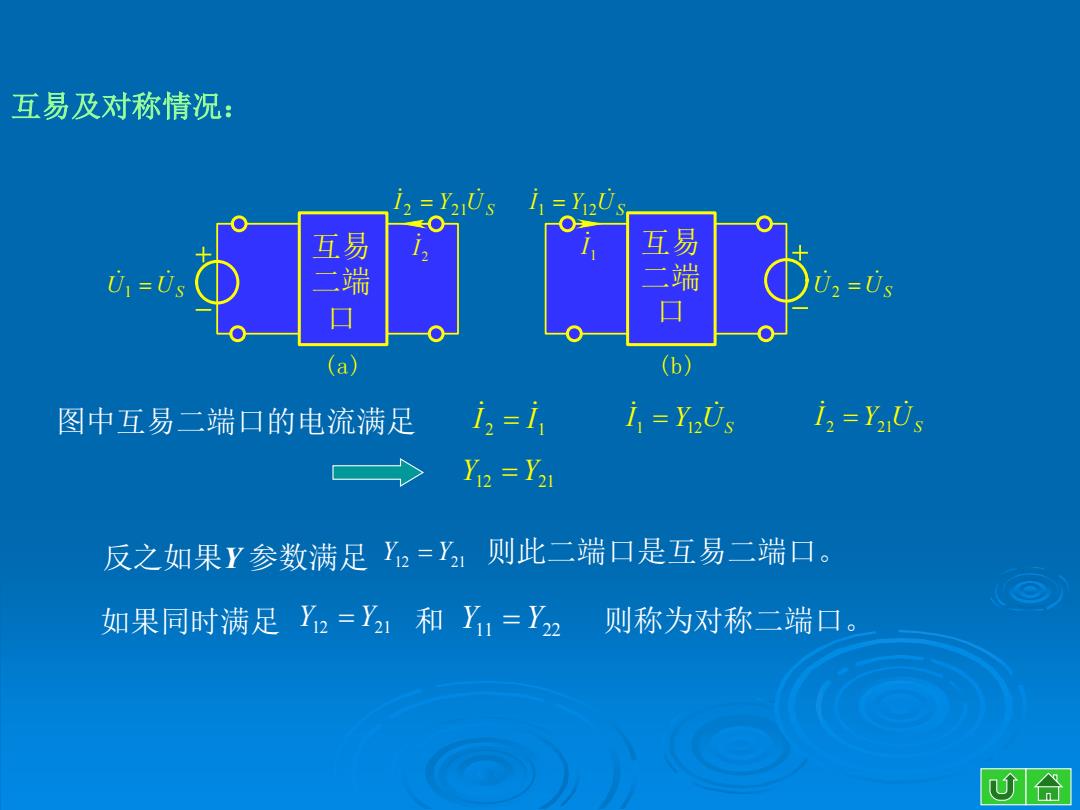
互易及对称情况： 12 =Y2Us 互 互 U1=0s 二端 二端 02=Us 口 (a) (b) 图中互易二端口的电流满足 i,=i i=YUs i,=YUs Y2=Y2 反之如果Y参数满足Y2=Y 则此二端口是互易二端口。 如果同时满足Y2=Y和Y,=Y2 则称为对称二端口。」 心合

图中互易二端口的电流满足 2 1 I I    Y US I   1  12 Y US I   2  21 Y12  Y21 则此二端口是互易二端口。 如果同时满足 Y12  Y21 和 Y11  Y22 则称为对称二端口。 反之如果Y 参数满足 互易及对称情况： Y12  Y21 U US   1  U US   2  (a) (b) 2 I  1 I  Y US I   Y U S 1  12 I   2  2 1 互易 二端 口 互易 二端 口

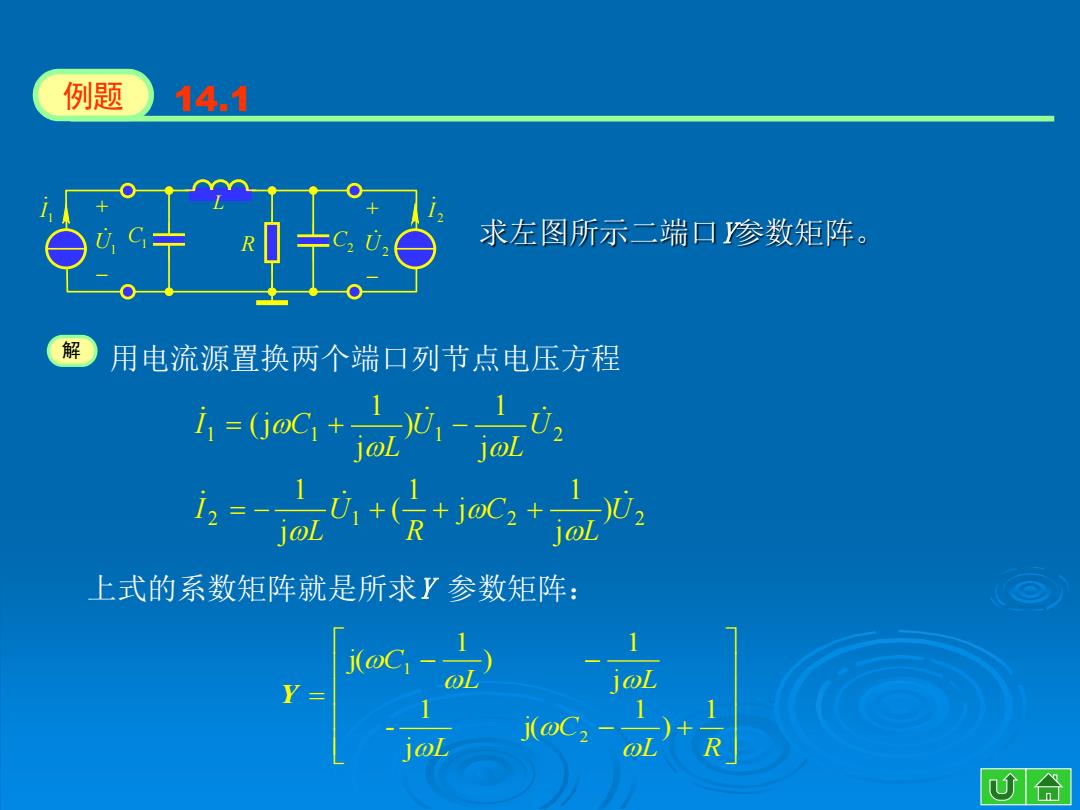
例题 14.1 R 求左图所示二端口参数矩阵。 解 用电流源置换两个端口列节点电压方程 1=ac+a0-: 上式的系数矩阵就是所求Y参数矩阵： 1 joL R 心合

求左图所示二端口Y参数矩阵。 例题 14.1 解 用电流源置换两个端口列节点电压方程 2 1 2 2 1 1 1 2 ) j 1 j 1 ( j 1 j 1 ) j 1 (j U L C R U L I U L U L I C                     上式的系数矩阵就是所求Y 参数矩阵：                  L R C L - L L C 1 ) 1 j( j 1 j 1 ) 1 j( 2 1       Y L C1 R C2   U1    U2  1 I  2 I 

2阻抗参数方程 二端口的阻抗参数方程或☑参数方程 U,Znl Znl, 02=Z1,+Z,2 矩阵形式： -区 相量形式： U-ZI Z- z 二端口阻抗参数 矩阵或Z参数矩 阵 ·互易条件：Z=Z 对称条件：Z2=Z1和Z=Za 心合

2 阻抗参数方程 二端口的阻抗参数方程或Z参数方程 1 11 1 12 2 U Z I Z I      2 21 1 22 2 U Z I Z I      •互易条件: Z12  Z21 •对称条件: Z12  Z21 和 Z11  Z22                        2 1 21 22 11 12 2 1 I I Z Z Z Z U U     矩阵形式：        21 22 11 12 Z Z Z Z Z 二端口阻抗参数 矩阵或Z 参数矩 阵 U ZI 相量形式：   

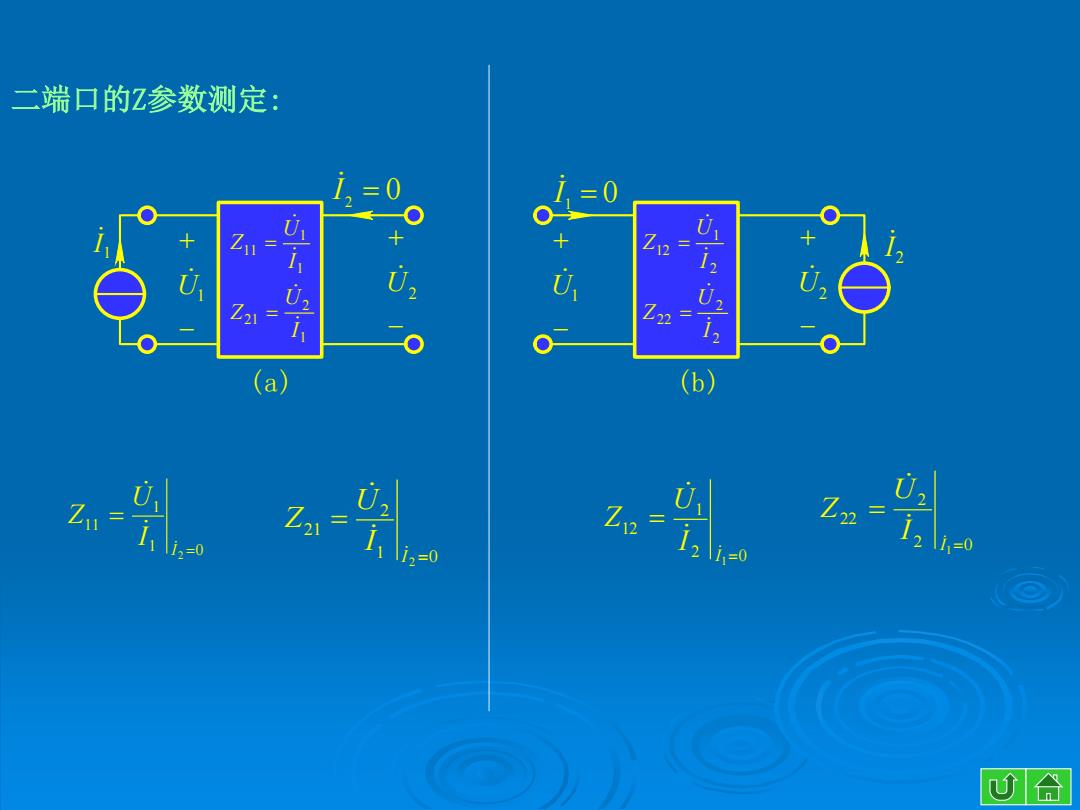
二端口的Z参数测定： 0 + Z + Z Z2 (a) (b) =9 i=0 心合

二端口的Z参数测定: 1 0 1 11 2   I I U Z    1 0 2 21 2   I I U Z    2 0 1 12 1  I I U Z    2 0 2 22 1  I I U Z      U1  (a) (b)   U2  1 I    U1    U2  2 I  1 2 21 1 1 11 I U Z I U Z       2 2 22 2 1 12 I U Z I U Z       I 2  0  I1  0 

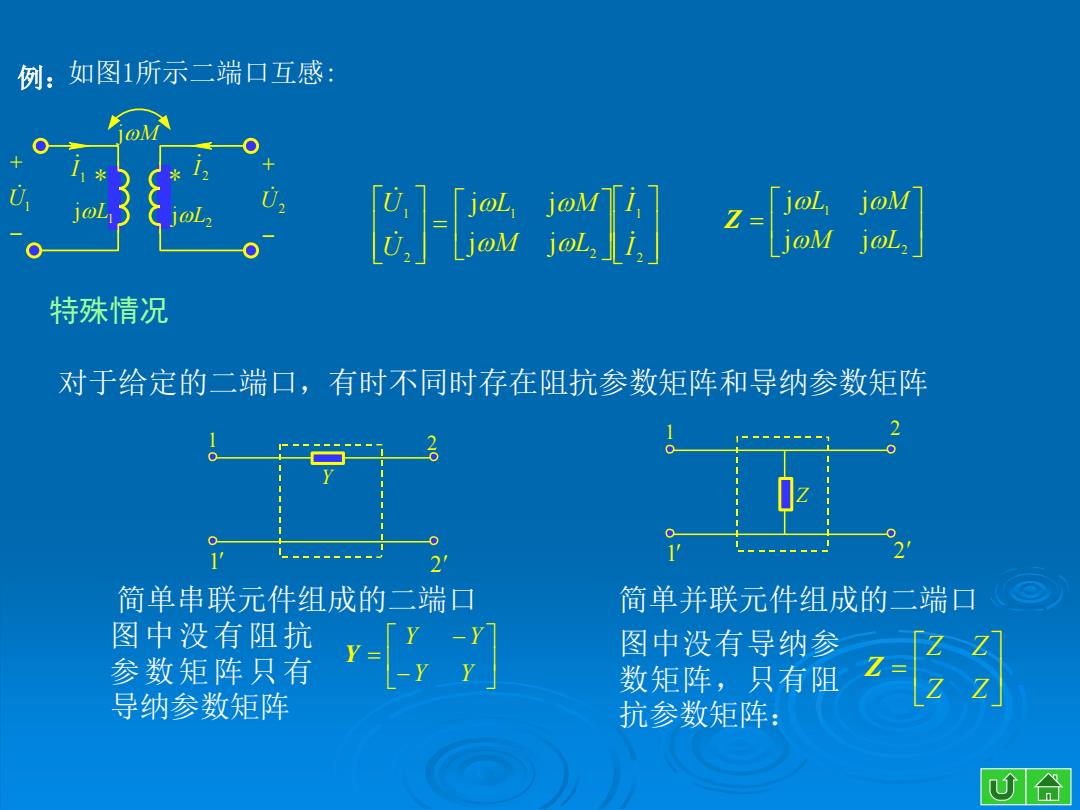
例：如图1所示二端口互感： &[]z 特殊情况 对于给定的二端口，有时不同时存在阻抗参数矩阵和导纳参数矩阵 2 1' 21 2 简单串联元件组成的二端口 简单并联元件组成的二端口 图中没有阻抗 图中没有导纳参 参数矩阵只有 数矩阵，只有阻 Z 导纳参数矩阵 lz 2 抗参数矩阵：

                       2 1 2 1 2 1 j j j j I I M L L M U U                2 1 j j j j M L L M     Z 对于给定的二端口，有时不同时存在阻抗参数矩阵和导纳参数矩阵 特殊情况 例：如图1所示二端口互感:   U1    U2  1 I  2 I  1 jL 2 jL jM * * 图中没有阻抗 参数矩阵只有 导纳参数矩阵          Y Y Y Y Y 简单串联元件组成的二端口 简单并联元件组成的二端口        Z Z Z Z Z 图中没有导纳参 数矩阵，只有阻 抗参数矩阵： 1 1 Z 2 2 1 1 2 2 Y