
版权©2019,版权保留,侵犯必究 第二章电阻电路的等效 。等效电路 。 串联和并联 ·星形和三角形联结的等效 ·电源和电阻的串联与并联 。端口等效电阻 复旦大学射频集成电路设计研究小组 -012- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -012- 第二章 电阻电路的等效 ⚫ 等效电路 ⚫ 串联和并联 ⚫ 星形和三角形联结的等效 ⚫ 电源和电阻的串联与并联 ⚫ 端口等效电阻
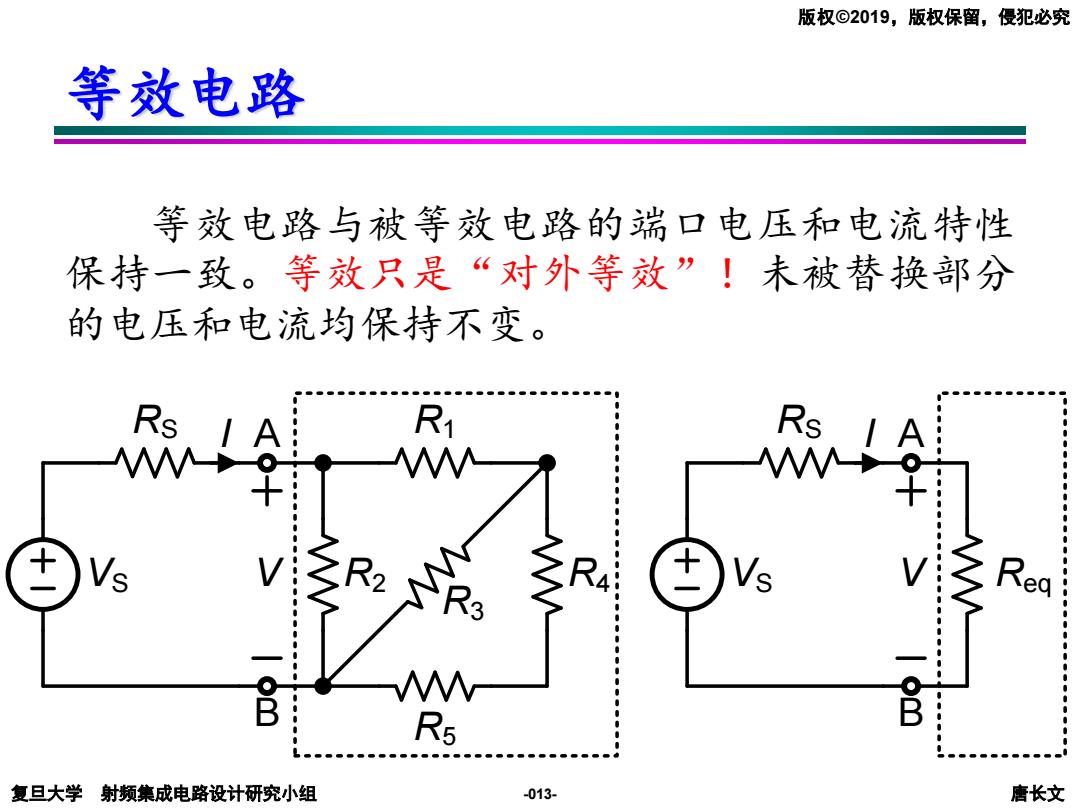
版权©2019,版权保留,侵犯必究 等效电路 等效电路与被等效电路的端口电压和电流特性 保持一致。等效只是“对外等效”!未被替换部分 的电压和电流均保持不变。 Rs R1 Rs R5 复旦大学射频集成电路设计研究小组 -013- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -013- 等效电路 等效电路与被等效电路的端口电压和电流特性 保持一致。等效只是“对外等效”!未被替换部分 的电压和电流均保持不变。 VS RS I V A B R1 R2 R3 R4 R5 VS RS I V A B Req
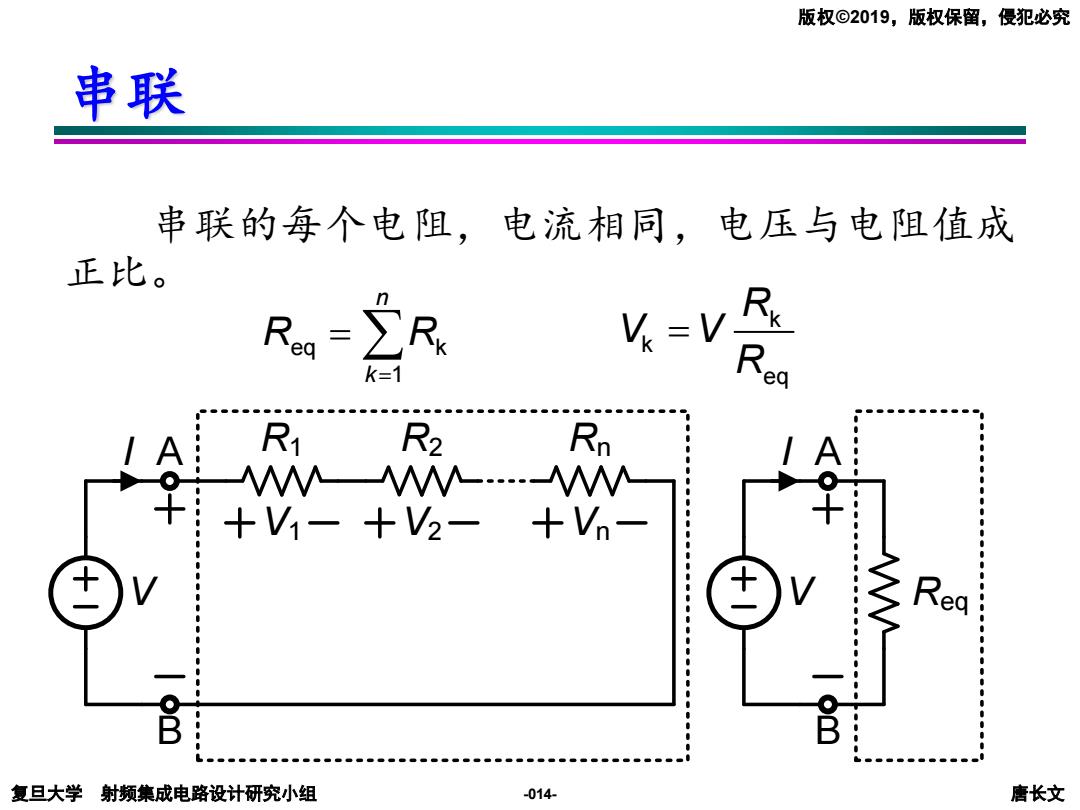
版权©2019,版权保留,侵犯必究 串联 串联的每个电阻,电流相同,电压与电阻值成 正比。 Ro=R V=V k=1 R1 R2 Rn ..-M +V1-+2-+Vn B 复旦大学射频集成电路设计研究小组 -014- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -014- 串联 串联的每个电阻,电流相同,电压与电阻值成 正比。 eq k 1 n k R R = = k k eq R V V R = V I A B R1 Rn V I A B Req V1 Vn R2 V2
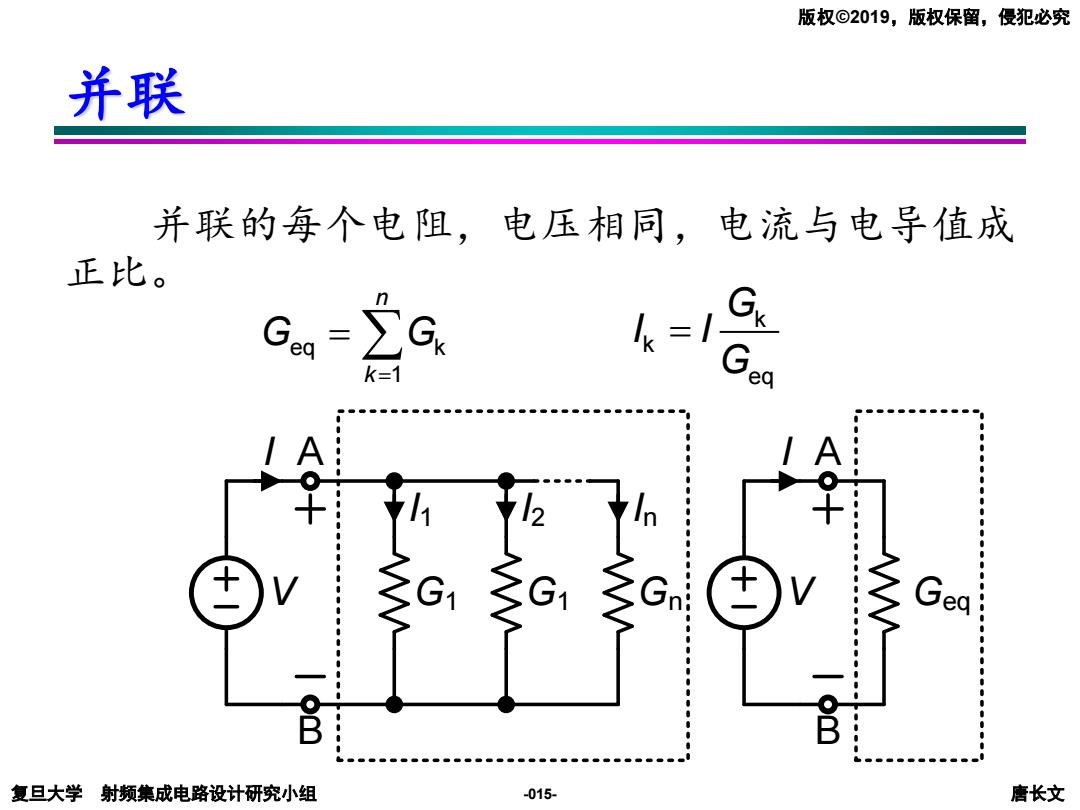
版权©2019,版权保留,侵犯必究 并联 并联的每个电阻,电压相同,电流与电导值成 正比。 k= k=1 eq 复旦大学射频集成电路设计研究小组 -015- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -015- 并联 并联的每个电阻,电压相同,电流与电导值成 正比。 eq k 1 n k G G = = k k eq G I I G = V I A B G1 Gn V I A B G1 Geq I1 I2 In
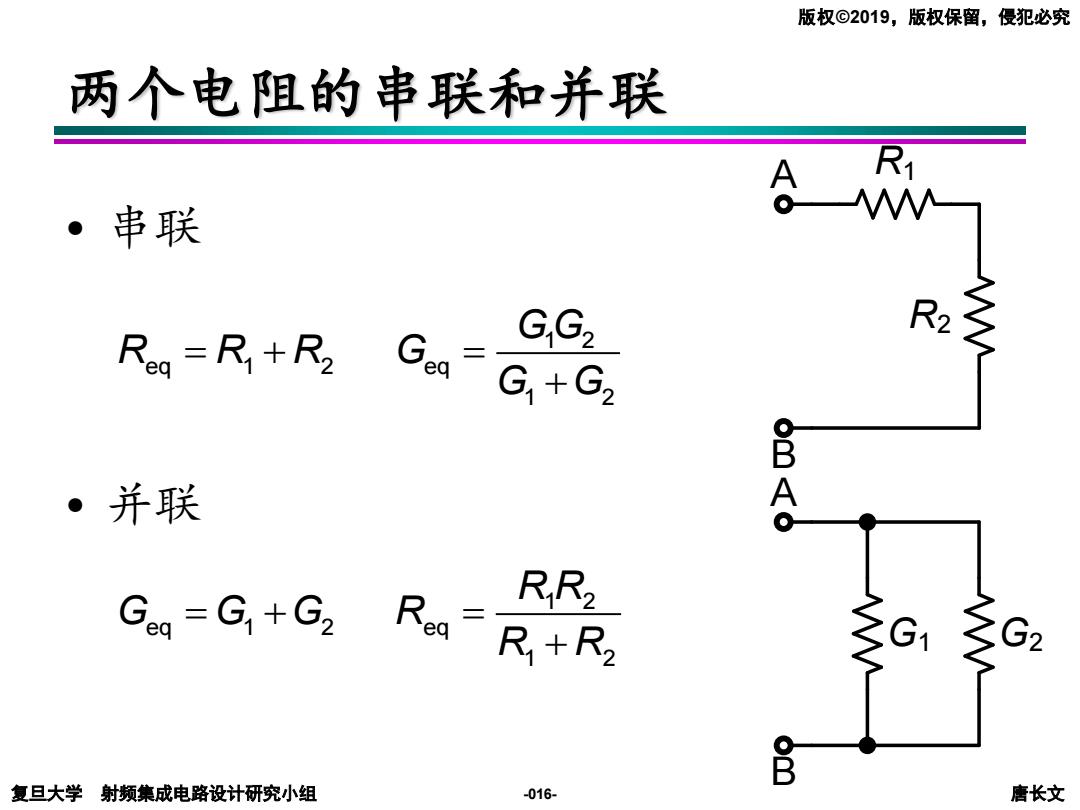
版权©2019,版权保留,侵犯必究 两个电阻的串联和并联 A R1 。串联 Reg =R1+R2 GG R:亨 G,+G2 B 。并联 Geq=G+G2/ RR2 R+R2 G2 复旦大学射频集成电路设计研究小组 -016- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -016- 两个电阻的串联和并联 • 串联 • 并联 A B R1 R2 1 2 eq 1 2 eq 1 2 G G R R R G G G = + = + 1 2 eq 1 2 eq 1 2 R R G G G R R R = + = + A B G1 G2
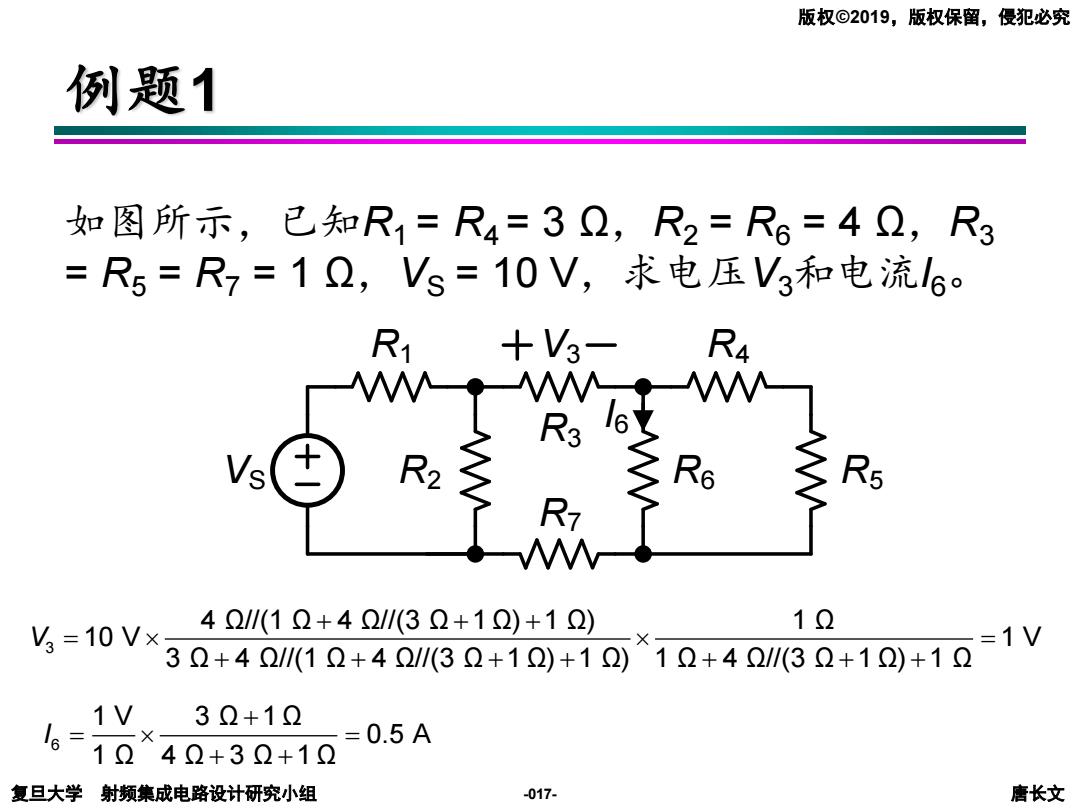
版权©2019,版权保留,侵犯必究 例题1 如图所示,已知R1=R4=32,R2=R6=42,R3 =R5=R7=12,Vs=10V,求电压V3和电流l6。 +V3- R5 12 V=10V× 42/(12+42/(32+12)+12) =1V 32+42l(12+421l(32+12)+12)12+42/32+12)+12 1V32+1 16= =0.5A 1Ω42+3Ω+12 复旦大学射频集成电路设计研究小组 -017- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -017- 例题1 如图所示,已知R1 = R4 = 3 Ω,R2 = R6 = 4 Ω,R3 = R5 = R7 = 1 Ω,VS = 10 V,求电压V3和电流I6。 3 4 Ω//(1 Ω 4 Ω//(3 Ω 1 Ω) 1 Ω) 1 Ω 10 V 1 V 3 Ω 4 Ω//(1 Ω 4 Ω//(3 Ω 1 Ω) 1 Ω) 1 Ω 4 Ω//(3 Ω 1 Ω) 1 Ω V + + + = = + + + + + + + 6 1 V 3 Ω 1 Ω 0.5 A 1 Ω 4 Ω 3 Ω 1 Ω I + = = + + I 6 V3 VS R1 R2 R3 R4 R6 R5 R7
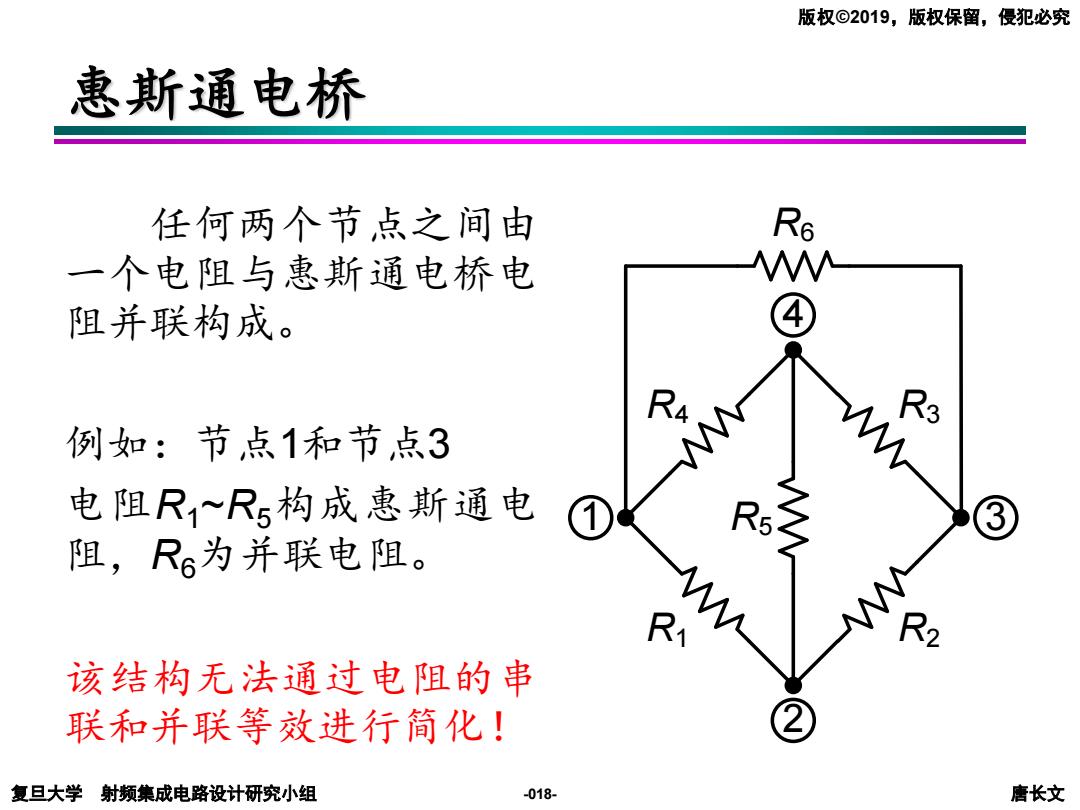
版权©2019,版权保留,侵犯必究 惠斯通电桥 任何两个节点之间由 一个电阻与惠斯通电桥电 M 阻并联构成。 R4 R3 例如:节点1和节点3 电阻R~R构成惠斯通电 5 ③ 阻,R6为并联电阻。 该结构无法通过电阻的串 联和并联等效进行简化! 2 复旦大学射频集成电路设计研究小组 -018- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -018- 惠斯通电桥 任何两个节点之间由 一个电阻与惠斯通电桥电 阻并联构成。 例如:节点1和节点3 电阻R1~R5构成惠斯通电 阻,R6为并联电阻。 该结构无法通过电阻的串 联和并联等效进行简化! 1 2 3 4 R1 R2 R4 R3 R5 R6
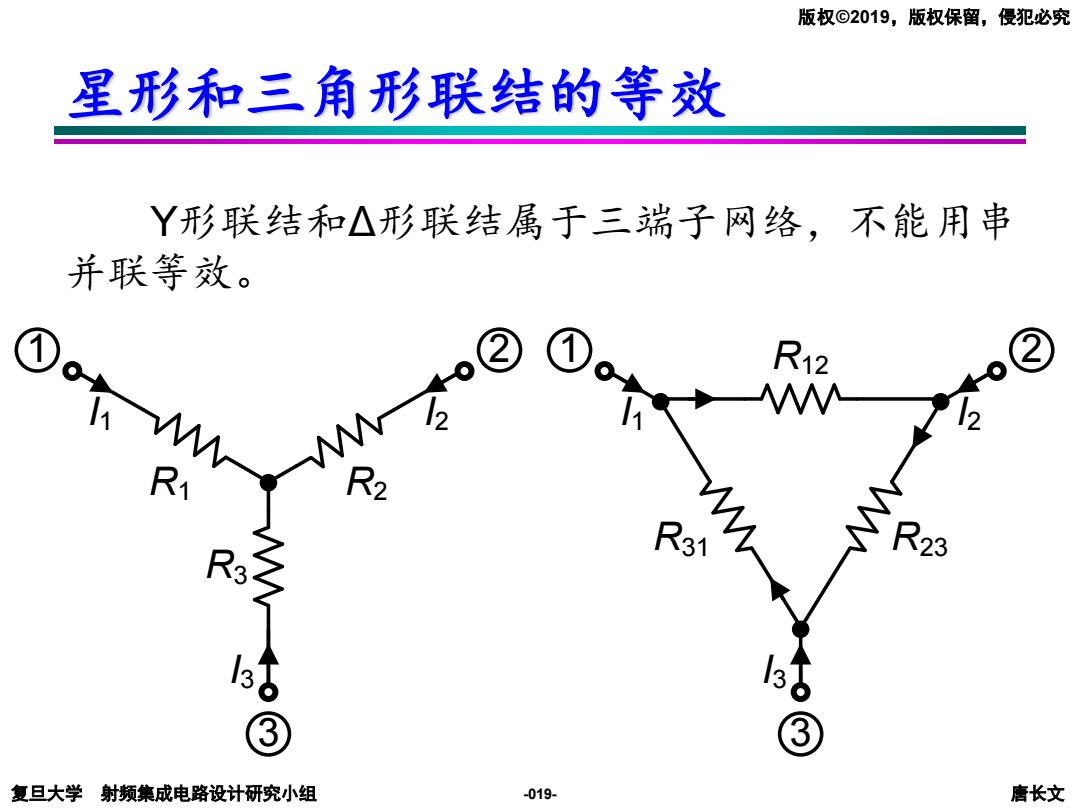
版权©2019,版权保留,侵犯必究 星形和三角形联结的等效 Y形联结和△形联结属于三端子网络,不能用串 并联等效。 1 R2 R31 R23 3 复旦大学射频集成电路设计研究小组 -019- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -019- 星形和三角形联结的等效 R1 R2 R3 R12 R31 R23 I1 I2 I3 1 2 3 I1 I2 I3 1 2 3 Y形联结和Δ形联结属于三端子网络,不能用串 并联等效
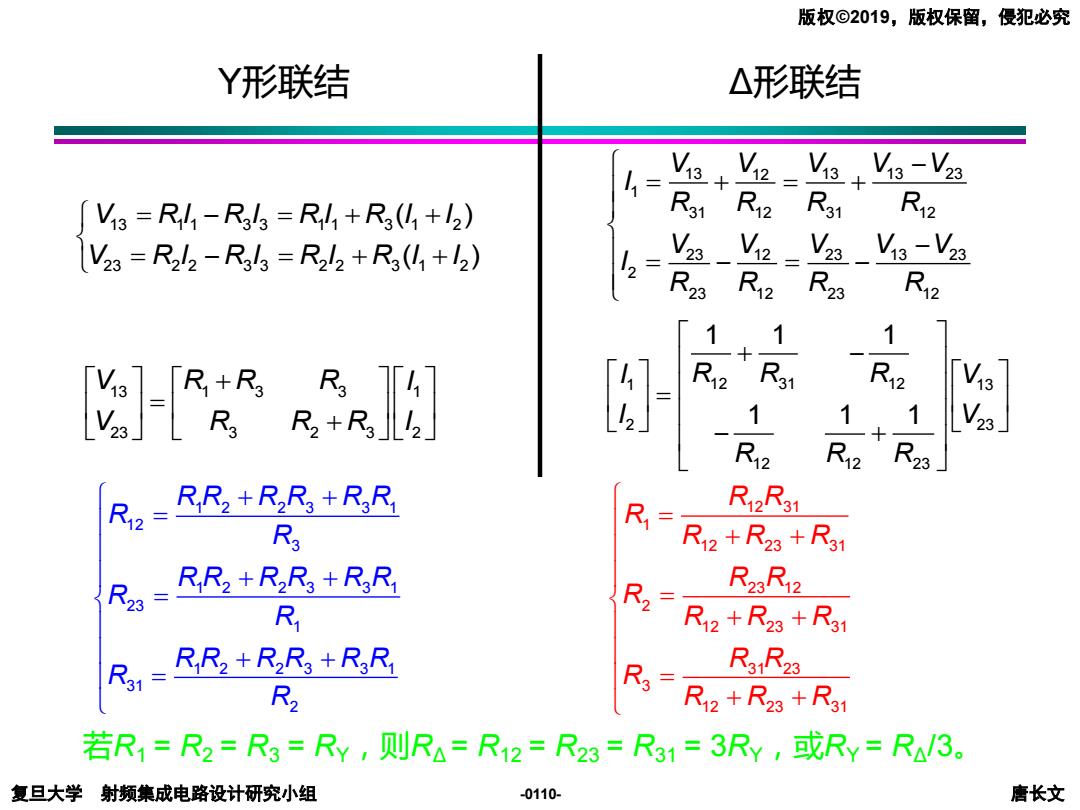
版权©2019,版权保留,侵犯必究 Y形联结 △形联结 11= V3=R41-R53=R4+R3(+12) R12 R3 V23=R252-Rk3=R22+R3(01+12) Vi3-V23 2 R23 12 R23 尺2 12 31 V2 R 23 RR2+R2Rg+R3R R2R31 R3 Ri-RotRa+Ra RR2+R2R3+R3Ri R23R12 R RR2tR+a R31 RR2+R2R3+R3R R3R23 R2 Ra=Ri2+R2+Ran 若R1=R2=R3=RY,则RA=R12=R23=R31=3RY,或Ry=R3。 复旦大学射频集成电路设计研究小组 -0110- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -0110- 1 2 2 3 3 1 12 3 1 2 2 3 3 1 23 1 1 2 2 3 3 1 31 2 R R R R R R R R R R R R R R R R R R R R R R R R + + = + + = + + = 13 1 1 3 3 1 1 3 1 2 23 2 2 3 3 2 2 3 1 2 ( ) ( ) V R I R I R I R I I V R I R I R I R I I = − = + + = − = + + 13 1 3 3 1 23 3 2 3 2 V R R R I V R R R I + = + 13 13 13 23 12 1 31 12 31 12 23 23 13 23 12 2 23 12 23 12 V V V V V I R R R R V V V V V I R R R R − = + = + − = − = − 1 12 31 12 13 2 23 12 12 23 1 1 1 1 1 1 I R R R V I V R R R + − = − + Y形联结 Δ形联结 12 31 1 12 23 31 23 12 2 12 23 31 31 23 3 12 23 31 R R R R R R R R R R R R R R R R R R = + + = + + = + + 若R1 = R2 = R3 = RY,则RΔ = R12 = R23 = R31 = 3RY,或RY = RΔ/3

版权©2019,版权保留,侵犯必究 例题2 如图所示,已知R1=32,R2=122,R3=R4= R5=22,求等效电阻尺ea0 R2 R3 M 3Ω R4 R5 ● Rea Rea 复旦大学射频集成电路设计研究小组 -0111- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -0111- 例题2 如图所示,已知R1 = 3 Ω,R2 = 12 Ω,R3 = R4 = R5 = 2 Ω,求等效电阻Req。 3 Ω 12 Ω 6 Ω 6 Ω 6 Ω Req 2 Ω 4 Ω 6 Ω Req 3 Ω Req 4/7 Ω 12 Ω 6/7 Ω 2 Ω Req 6/7 Ω 6/7 Ω Req 15/7 Ω 3 Ω Req Req R1 R2 R3 R4 R5