
版权©2019,版权保留,侵犯必究 第八章线性动态电路的时域分析 。动态电路的初始值 。一阶电路的零输入响应 ·一阶电路的零状态响应 ·一阶电路的全响应 。一阶电路的三要素法 ·二阶电路的零输入响应 。二阶电路的零状态响应和全响应 复旦大学射频集成电路设计研究小组 -012- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -012- 第八章 线性动态电路的时域分析 ⚫ 动态电路的初始值 ⚫ 一阶电路的零输入响应 ⚫ 一阶电路的零状态响应 ⚫ 一阶电路的全响应 ⚫ 一阶电路的三要素法 ⚫ 二阶电路的零输入响应 ⚫ 二阶电路的零状态响应和全响应

版权©2019,版权保留,侵犯必究 ·阶跃响应 ·冲激响应 ·卷积积分 ·状态变量分析法 复旦大学射频集成电路设计研究小组 -013- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -013- ⚫ 阶跃响应 ⚫ 冲激响应 ⚫ 卷积积分 ⚫ 状态变量分析法
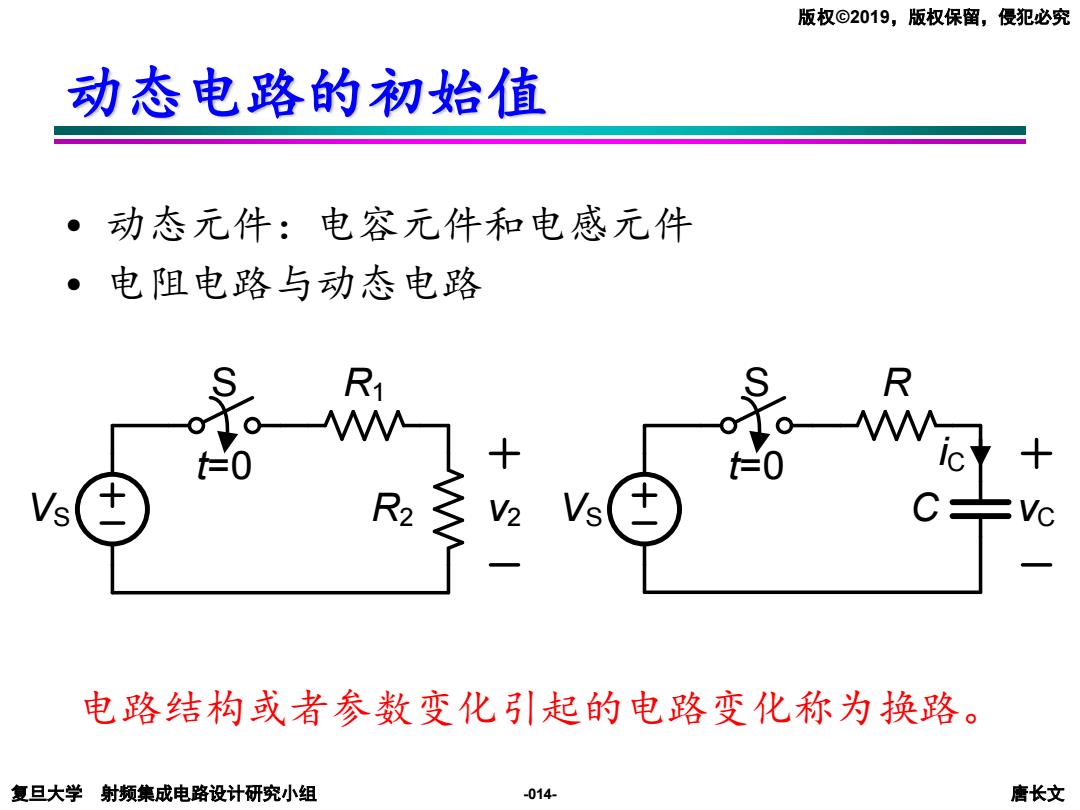
版权©2019,版权保留,侵犯必究 动态电路的初始值 动态元件:电容元件和电感元件 ·电阻电路与动态电路 R2 +2 电路结构或者参数变化引起的电路变化称为换路。 复旦大学射频集成电路设计研究小组 -014 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -014- 动态电路的初始值 • 动态元件:电容元件和电感元件 • 电阻电路与动态电路 电路结构或者参数变化引起的电路变化称为换路。 VS R1 R2 t=0 v2 VS R C t=0 vC S S iC
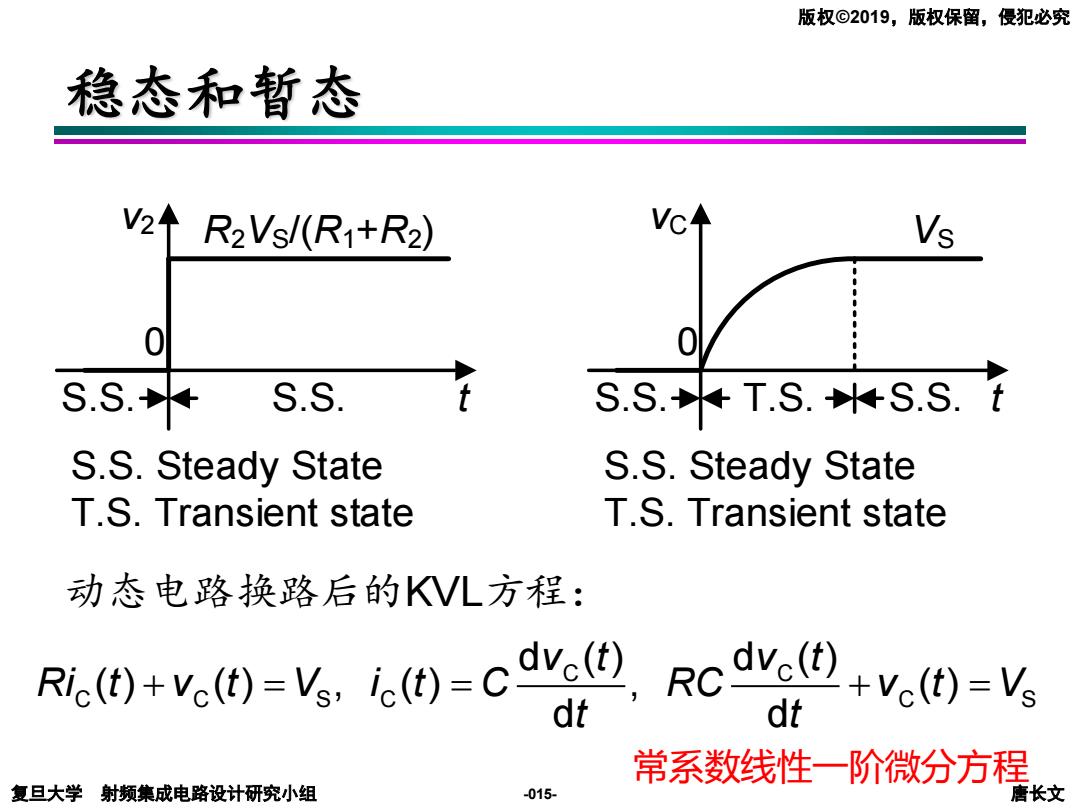
版权©2019,版权保留,侵犯必究 稳态和暂态 2↑R2Vs/(R1+R2) Vc Vs 0 S.S.+ S.S. S.S.+T.S.+S.S.t S.S.Steady State S.S.Steady State T.S.Transient state T.S.Transient state 动态电路换路后的VL方程: R.0+v.0=V,。)=cv,@,Rcdv,②+v.)=V dt dt 常系数线性一阶微分方程 复旦大学射频集成电路设计研究小组 -015- 长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -015- 稳态和暂态 动态电路换路后的KVL方程: C C C C S C C S d ( ) d ( ) ( ) ( ) , ( ) , ( ) d d v t v t Ri t v t V i t C RC v t V t t + = = + = 常系数线性一阶微分方程 t 0 v2 R2 VS/(R1 +R2) S.S. S.S. S.S. Steady State T.S. Transient state t 0 vC T.S. VS S.S. S.S. S.S. Steady State T.S. Transient state

版权©2019,版权保留,侵犯必究 初始值 一阶微分方程求解需要一个初始条件,即待求 变量在换路后瞬间的初始值。 t=0时发生换路,用t=0_和t=0,分别表示换 路前和换路后瞬间,用V(0-)、0-)、q(0)和p(0-)表 示换路之前的稳定值,用V(0+)i0+)、q(0+)和p(0+) 表示换路之后的初始值。 换路之后,电路量将从初始值开始变动。 复旦大学射频集成电路设计研究小组 -016- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -016- 初始值 一阶微分方程求解需要一个初始条件,即待求 变量在换路后瞬间的初始值。 t = 0时发生换路,用t = 0−和t = 0+分别表示换 路前和换路后瞬间,用v(0− )、i(0− )、q(0− )和φ(0− )表 示换路之前的稳定值,用v(0+ )、i(0+ )、q(0+ )和φ(0+ ) 表示换路之后的初始值。 换路之后,电路量将从初始值开始变动

版权©2019,版权保留,侵犯必究 经典时域分析法 根据KCL、KVL和支路的VCR列出以时间为自 变量的阶线性常微分方程,确定待求电路量的0阶 至(门-1)阶在t=0+时的初始值,然后求解常微分方 程得到待求电路量。这种方法称为经典时间域分析 法。 复旦大学射频集成电路设计研究小组 -017- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -017- 经典时域分析法 根据KCL、KVL和支路的VCR列出以时间为自 变量的n阶线性常微分方程,确定待求电路量的0阶 至(n − 1)阶在t = 0+时的初始值,然后求解常微分方 程得到待求电路量。这种方法称为经典时间域分析 法

版权©2019,版权保留,侵犯必究 电容电压的初始值 在=0时刻,线性电容的电荷、电压和电流的 关系为 g0,)-g0.)+0 c()dt.v(,)=.0)+&.0df 如果ic()是有限值, .()df=0 则电容上的电荷和电压就不发生跃变, q(0+)=q(0_),Vc(0)=Vc(0_) 复旦大学射频集成电路设计研究小组 018- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -018- 电容电压的初始值 在t = 0时刻,线性电容的电荷、电压和电流的 关系为 如果iC(t)是有限值, 则电容上的电荷和电压就不发生跃变, 0 0 C C C C 0 0 1 q q i t t v v i t t (0 ) (0 ) ( )d , (0 ) (0 ) ( )d C + + − − + − + − = + = + 0 C 0 i t t ( )d 0 + − = C C q q v v (0 ) (0 ), (0 ) (0 ) + − + − = =

版权©2019,版权保留,侵犯必究 电感电流的初始值 在=0时刻,线性电感的磁通链、电流和电压 的关系为 0)-@)+jv()dt.i(0.)-L(0)1v(dt 如果V(⑤是有限值, v.()dt-o 则电感上的磁通链和电流就不发生跃变, p(0,)=p(0_),i(0)=i(0_) 复旦大学射频集成电路设计研究小组 019 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -019- 电感电流的初始值 在t = 0时刻,线性电感的磁通链、电流和电压 的关系为 如果vL (t)是有限值, 则电感上的磁通链和电流就不发生跃变, 0 0 L L L L 0 0 1 φ(0 ) (0 ) ( )d , (0 ) (0 ) ( )d φ v t t i i v t t L + + − − + − + − = + = + 0 L 0 v t t ( )d 0 + − = L L φ(0 ) (0 ), (0 ) (0 ) φ i i + − + − = =

版权©2019,版权保留,侵犯必究 换路定则 在换路前后电容的电流和电感的电压为有限值 的条件下,换路前后的电容的电压和电感的电流不 能跃变,这种规律称为换路定则。 确定初始值的步骤 1.根据换路前的电路,确定Vc(0-)和i(0-): 2.根据换路定则确定vc(0+)和i(0+): 3.画出t=0时的初始值等效电路,确定其它电路量 的初始值。根据置换定理,电容用Vc(O+)的电压源替 换,电感用i(O+)的电流源替换。 复旦大学射频集成电路设计研究小组 -0110- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -0110- 换路定则 在换路前后电容的电流和电感的电压为有限值 的条件下,换路前后的电容的电压和电感的电流不 能跃变,这种规律称为换路定则。 确定初始值的步骤 1.根据换路前的电路,确定vC(0− )和iL (0− ); 2. 根据换路定则确定vC(0+ )和iL (0+ ); 3. 画出t = 0时的初始值等效电路,确定其它电路量 的初始值。根据置换定理,电容用vC(0+ )的电压源替 换,电感用iL (0+ )的电流源替换
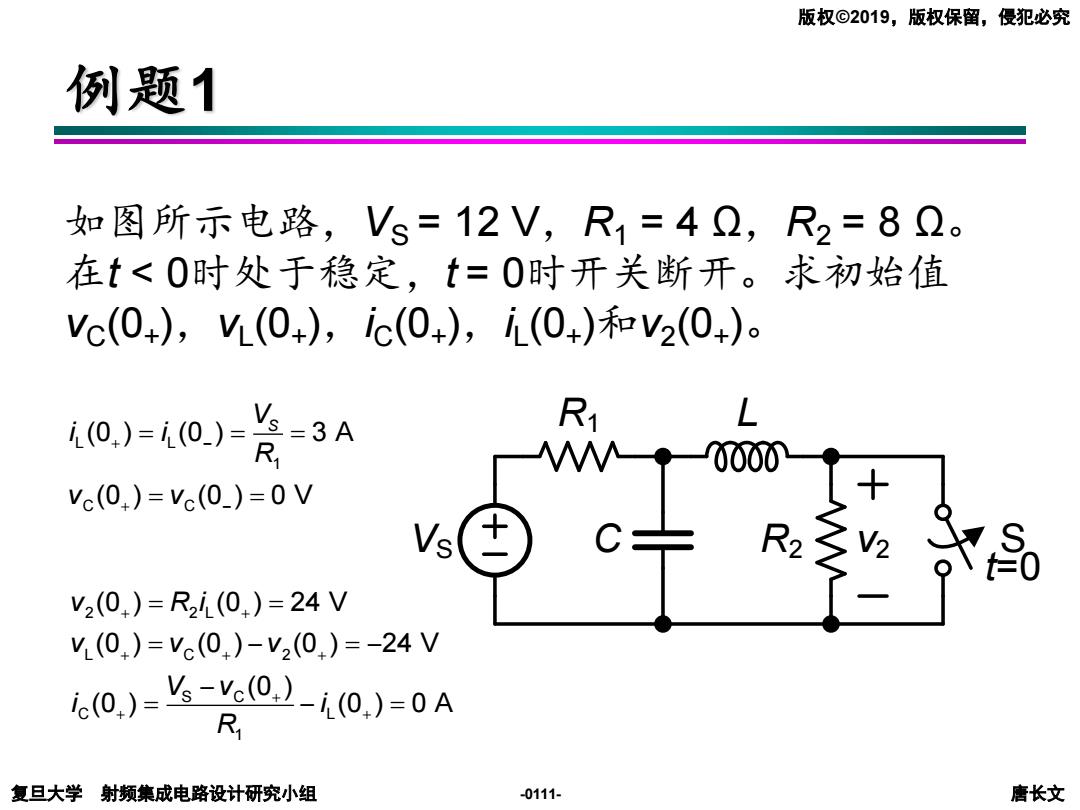
版权©2019,版权保留,侵犯必究 例题1 如图所示电路,Vs=12V,R1=42,R2=82。 在t<0时处于稳定,t=0时开关断开。求初始值 Vc(0+),(0+),ic(0+),i(0+)和V2(0+)。 1(0)=i(0) s=3A L 0000 vc(0)=vc(0)=0V R2 V2(0)=R2i(0)=24V vL(0)=Vc(0)-v2(0)=-24V e0.)=s-Y0l-i(0.)=0A R 复旦大学射频集成电路设计研究小组 -0111- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -0111- R iL(0+) 1 R2 L VS C t=0 v2 S 例题1 如图所示电路,VS = 12 V,R1 = 4 Ω,R2 = 8 Ω。 在t < 0时处于稳定,t = 0时开关断开。求初始值 vC(0+ ),vL (0+ ),iC(0+ ),iL (0+ )和v2 (0+ )。 R1 VS R2 v2(0+) iL(0+) vC(0+) t=0 R iL(0+) 1 R2 L VS C t=0 v2 S L L 1 C C (0 ) (0 ) 3 A (0 ) (0 ) 0 V VS i i R v v + − + − = = = = = 2 2 L L C 2 S C C L 1 (0 ) (0 ) 24 V (0 ) (0 ) (0 ) 24 V (0 ) (0 ) (0 ) 0 A v R i v v v V v i i R + + + + + + + + = = = − = − − = − =