
中南大粤 CENTRAL SOUTH UNIVERSITY 第23章检测算法 23.1常用数字滤波方法 23.2克服系统误差的软件算法 23.3量程自动切换及标度变换
第23章 检测算法 23.1 常用数字滤波方法 23.2 克服系统误差的软件算法 23.3 量程自动切换及标度变换 1

23.检测算法 23.1常用数字滤波方法 23.1.1数字滤波技术特点概述 优点: (1)不需增加硬件,只是一个计算程序,可靠性高,尤其是 可对频率很高或很低的信号滤波。 (2)用软件算法实现,可以使多个输入通道共享一个软件“滤 波器”,降低硬件成本。 (3)改变软件滤波器程序和参数,即可改变滤波特性,对于 抑制低频脉冲干扰、随机噪声特别有效。 主要不足: 需要计算时间,可能影响实时性。 2
23. 检测算法 23.1 常用数字滤波方法 23.1.1 数字滤波技术特点概述 优点: (1) 不需增加硬件,只是一个计算程序,可靠性高,尤其是 可对频率很高或很低的信号滤波。 (2) 用软件算法实现,可以使多个输入通道共享一个软件“滤 波器” ,降低硬件成本。 (3) 改变软件滤波器程序和参数,即可改变滤波特性,对于 抑制低频脉冲干扰、随机噪声特别有效。 主要不足: 需要计算时间,可能影响实时性。 2

23.1常用数字滤波方法 23.1.1数字滤波方法 1)程序判断滤波 △yn=yn-yn- >ym=7n-1或n=2y-1-yn-2 :相邻两个采样值之差的最大可能变化范围。 程序判断滤波又称限幅滤波,很容易用程序判断方法实现。 关键:确定的值。 因过程的动态特性决定其输出参数的变化速度,故可根 据检测实践经验或按参数可能的最大变化速度max及采样周 期T来决定o值,即:o=Tmax 3
23.1 常用数字滤波方法 23.1.1 数字滤波方法 1)程序判断滤波 : 相邻两个采样值之差的最大可能变化范围。 程序判断滤波又称限幅滤波,很容易用程序判断方法实现。 关键:确定的值。 因过程的动态特性决定其输出参数的变化速度,故可根 据检测实践经验或按参数可能的最大变化速度Vmax及采样周 期T来决定值,即: =T·Vmax 3

23.1常用数字滤波方法 23.1.1数字滤波方法 2)中(位)值滤波法 对某一被测参数连续采样n次(一般n=2m+1),把n次采样 值按大小排序,取中间值作为本次的有效采样值 对温度、液位等缓慢变化的被测参数,此法能收到良好 滤波效果,但对压力等快变参数一般不宜采用。 特点:有效抑制脉冲(宽度<)干扰,保持边沿或细节特征。 3)算术平均滤波法 取连续几个采样值的算术均值 作为滤波输出 值。 此方法适用于一般有随机干扰的信号滤波,对信号的平 滑程度完全取决于N。N大,平滑度高,但灵敏度低;N小, 平滑度低,但灵敏度高。 4
23.1 常用数字滤波方法 23.1.1 数字滤波方法 2) 中(位)值滤波法 对某一被测参数连续采样n次(一般n=2m+1),把n次采样 值按大小排序,取中间值作为本次的有效采样值。 对温度、液位等缓慢变化的被测参数,此法能收到良好 滤波效果,但对压力等快变参数一般不宜采用。 特点:有效抑制脉冲(宽度<m)干扰,保持边沿或细节特征。 3) 算术平均滤波法 取连续几个采样值的算术均值 作为滤波输出 值。 此方法适用于一般有随机干扰的信号滤波,对信号的平 滑程度完全取决于N。N大,平滑度高,但灵敏度低;N小, 平滑度低,但灵敏度高。 4

23.1常用数字滤波方法 23.1.1数字滤波方法 4)递推平均滤波法 把N个测量数据看成一个队列,前次所测数据作列尾, 将此数为列尾数的前个测量数据的算术平均值 作为当前滤波输出值。 特点:只需一次测量,就能得到当前的滤波输出值 5)加权递推平均滤波法 其中: 权值确定方法:设τ为对象的纯滞后时间,且 8=1+e +十ew-,则:C。 e(-10a CN- 5
23.1 常用数字滤波方法 23.1.1 数字滤波方法 4) 递推平均滤波法 把N个测量数据看成一个队列,前次所测数据作列尾, 将此数为列尾数的前N个测量数据的算术平均值 作为当前滤波输出值。 特点:只需一次测量,就能得到当前的滤波输出值 5) 加权递推平均滤波法 权值确定方法:设 为对象的纯滞后时间,且 其中: ,则: 5

23.1常用数字滤波方法 23.1.1数字滤波方法 4)复合滤波法 若ySy2≤..Sy,其中,3≤n≤140y1和y.分别是采样值 中的最小值和最大值),则:y,=2+y3++习)(8-2 5)一阶惯性滤波法 以数字形式通过算法实现一阶惯性(动态)RC滤波,能 很好地克服模拟滤波器的缺点。适用于波动频繁的参数滤波, 但带来相位滞后(取决于α值),灵敏度低。算法如下: 其中,a=T(T+D,T为滤波时间常数,T为采样周期。a由实 验定,只要使被测信号不产生明显纹波。 缺点:不能滤除频率高于采样频率二分之一(奈奎斯特频率)的 干扰信号。高于奈奎斯特频率的干扰信号,需模拟滤波。 6
23.1 常用数字滤波方法 23.1.1 数字滤波方法 4) 复合滤波法 若yl≤y2≤…≤yn,其中,3≤n≤14 (y1和yn分别是采样值 中的最小值和最大值),则: 5)一阶惯性滤波法 以数字形式通过算法实现一阶惯性(动态)RC滤波,能 很好地克服模拟滤波器的缺点。适用于波动频繁的参数滤波, 但带来相位滞后(取决于a值),灵敏度低。算法如下: 其中,a=Tf /(Tf+T), Tf为滤波时间常数,T为采样周期。a由实 验定,只要使被测信号不产生明显纹波。 缺点:不能滤除频率高于采样频率二分之一(奈奎斯特频率)的 干扰信号。高于奈奎斯特频率的干扰信号,需模拟滤波。 6

23.2克服系统误差的软件算法 23.2.1系统误差的模型校正法(非线性校正) 校正系统误差的关键是建立误差模型。多数情况下模型 未知,只能通过测量数据建立反映测量值变化的近似模型。 1)代数插值法 设有n+1组离散点:(o,yo),(&,y1),,(X,yn),x∈[a,b] 和未知函数x),并有xo)yo,x1)y1,…,xyn,找一个 函数g(x),使gx)在x(i-0,.,n)处与x)相等。满足此条件 的函数g(x)称为x)的插值函数,x称为插值节点。 用一个n阶代数多项式Pn(X)=ax+an-x-l+. +a x+ao 逼近fx),使P(x)在节点x处满足P(X)=x)=y:i-0,2,,n am0+n-10++a10十@0=0 +十@61十a0=y1 卜十@为n十a0=y为
23.2 克服系统误差的软件算法 23.2.1 系统误差的模型校正法(非线性校正) 校正系统误差的关键是建立误差模型。多数情况下模型 未知,只能通过测量数据建立反映测量值变化的近似模型。 1)代数插值法 设有n+1组离散点: (x0 , y0), (xl, y1), …, (xn , yn),x∈ [a,b] 和未知函数f(x),并有 f(x0)=y0 , f(x1)=y1 , …, f(xn)=yn,找一个 函数g(x),使g(x)在xi(i=0,…,n)处与f(xi)相等。满足此条件 的函数g(x)称为f(x)的插值函数,xi称为插值节点。 用一个n阶代数多项式 Pn(x)=anx n+an-1x n-1+ … +a1x+a0 逼近f(x),使Pn(x)在节点xi处满足Pn(xi) = f(xi) = yi i=0,2, …,n 7

23.2克服系统误差的软件算法 23.2.1系统误差的模型校正法(非线性校正) 1)代数插值法 通常给出离散点总是多于求解插值方程所需的离散数, 因此,用多项式插值法求解离散点的插值函数时,先必须根 据所需的逼近精度决定多项式阶次,该次数与所要逼近的函 数有关。一般常用线性插值和抛物线(二次)插值。 (1)线性插值 在一组数据(X,y)中选两个代表性的点(xyo),(X1,y1), 然后根据插值原理求出插值方程: 0+ y1=a:x+a0 0一1 其中:a= ,80=y0-40 1一0 8
23.2 克服系统误差的软件算法 23.2.1 系统误差的模型校正法(非线性校正) 1)代数插值法 通常给出离散点总是多于求解插值方程所需的离散数, 因此,用多项式插值法求解离散点的插值函数时,先必须根 据所需的逼近精度决定多项式阶次,该次数与所要逼近的函 数有关。一般常用线性插值和抛物线(二次)插值。 (1) 线性插值 在一组数据(xi, yi)中选两个代表性的点(x0 , y0), (x1 , y1), 然后根据插值原理求出插值方程: 其中: 8
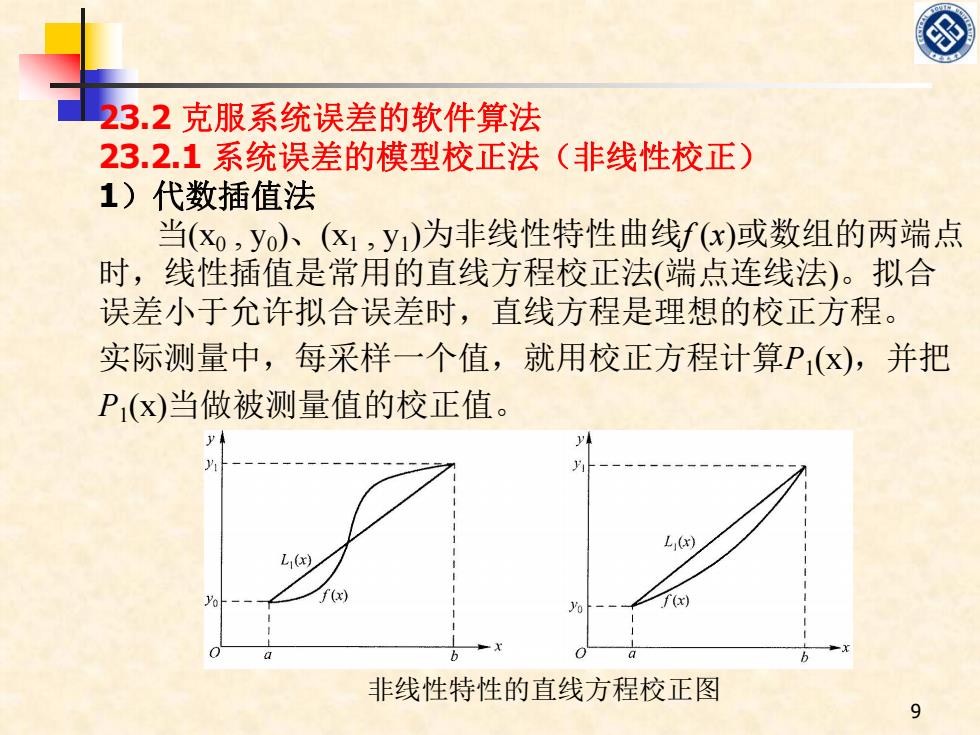
23.2克服系统误差的软件算法 23.2.1系统误差的模型校正法(非线性校正) 1)代数插值法 当(xo,yo)、(x1,y1)为非线性特性曲线f(x)或数组的两端点 时,线性插值是常用的直线方程校正法(端点连线法)。拟合 误差小于允许拟合误差时,直线方程是理想的校正方程。 实际测量中,每采样一个值,就用校正方程计算P(x),并把 P(x)当做被测量值的校正值。 L (x) L1(x) f(x) 非线性特性的直线方程校正图
23.2 克服系统误差的软件算法 23.2.1 系统误差的模型校正法(非线性校正) 1)代数插值法 当(x0 , y0)、(x1 , y1)为非线性特性曲线f (x)或数组的两端点 时,线性插值是常用的直线方程校正法(端点连线法)。拟合 误差小于允许拟合误差时,直线方程是理想的校正方程。 实际测量中,每采样一个值,就用校正方程计算P1(x),并把 P1(x)当做被测量值的校正值。 非线性特性的直线方程校正图 9
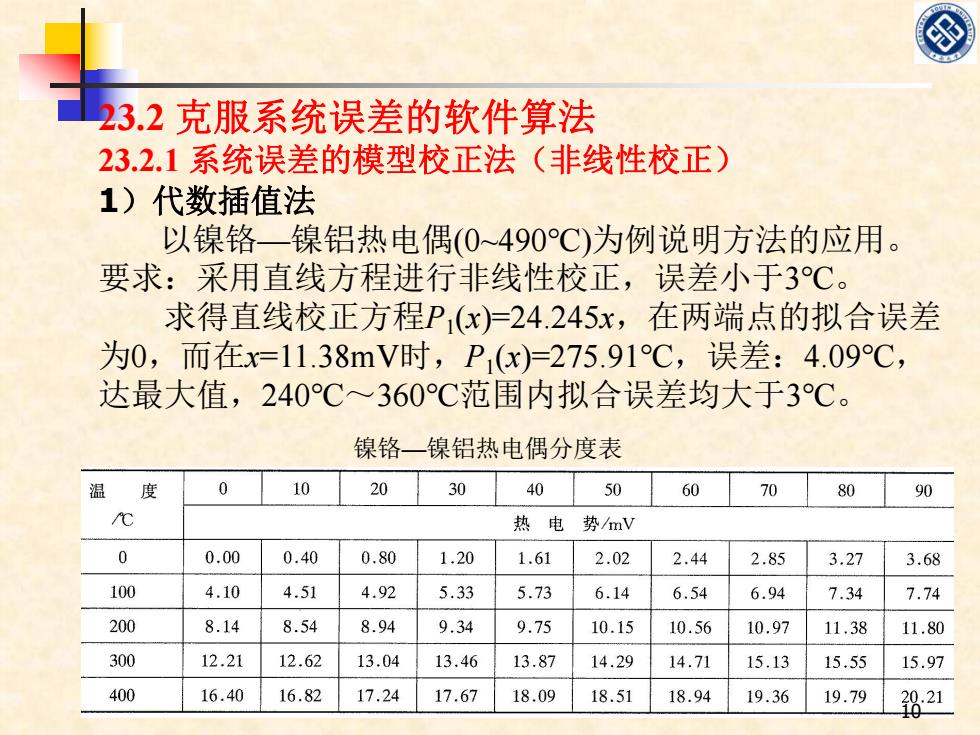
23.2克服系统误差的软件算法 23.2.1系统误差的模型校正法(非线性校正) 1)代数插值法 以镍铬一镍铝热电偶(0~490℃)为例说明方法的应用。 要求:采用直线方程进行非线性校正,误差小于3C。 求得直线校正方程Px)=24.245x,在两端点的拟合误差 为0,而在x=11.38mV时,P1(x)=275.91℃,误差:4.09℃, 达最大值,240℃~360C范围内拟合误差均大于3℃。 镍铬一镍铝热电偶分度表 温 食 0 10 20 30 40 50 60 70 80 90 ℃ 热电势mV 0 0.00 0.40 0.80 1.20 1.61 2.02 2.44 2.85 3.27 3.68 100 4.10 4.51 4.92 5.33 5.73 6.14 6.54 6.94 7.34 7.74 200 8.14 8.54 8.94 9.34 9.75 10.15 10.56 10.97 11.38 11.80 300 12.21 12.62 13.04 13.46 13.87 14.29 14.71 15.13 15.55 15.97 400 16.40 16.82 17.24 17.67 18.09 18.51 18.94 19.36 19.79 821
23.2 克服系统误差的软件算法 23.2.1 系统误差的模型校正法(非线性校正) 1)代数插值法 以镍铬—镍铝热电偶(0~490℃)为例说明方法的应用。 要求:采用直线方程进行非线性校正,误差小于3℃。 求得直线校正方程P1(x)=24.245x,在两端点的拟合误差 为0,而在x=11.38mV时,P1(x)=275.91℃,误差:4.09℃, 达最大值,240℃~360℃范围内拟合误差均大于3℃。 镍铬—镍铝热电偶分度表 10