
第二章电阻电路分析 将仅包含电阻、独立源和受控源的电路称为电阻电路。 2.1图与电路方程 2.6替代定理 一、图的基本概念 一、替代定理 二、KCL和KVL的独立方程◆ 二、替代定理应用举例◆ 2.22b法和支路法 2.7等效电源定理 一、2b法◆ 一、等效电源定理 二、支路法 二、开路电压短路电流的计算 2.3回路法和网孔法 三、等效内阻的计算◆ 一、回路法。 四、定理的应用举例 二、 特殊情况处理◆ 五、 定理应用小结◆ 2.4节点法 六、最大功率传输条件 一、节点法◆ 2.8特勒根定理和互易定理 二、特殊情况处理 一、特勒根定理◆ 2.5齐次定理和叠加定理 二、互易定理◆ 一、 齐次定理 2.9电路的对偶性◆ 二、叠加定理 点击0录中,懂入相关章节
西安电子科技大学电路与系统多媒体室制作 点击目录 ,进入相关章节 2.1 图与电路方程 一、图的基本概念 二、KCL和KVL的独立方程 2.2 2b法和支路法 一、2b法 二、支路法 2.3 回路法和网孔法 一、回路法 二、特殊情况处理 2.4 节点法 一、节点法 二、特殊情况处理 2.5 齐次定理和叠加定理 一、齐次定理 二、叠加定理 2.6 替代定理 一、替代定理 二、替代定理应用举例 2.7 等效电源定理 一、等效电源定理 二、开路电压短路电流的计算 三、等效内阻的计算 四、定理的应用举例 五、定理应用小结 六、最大功率传输条件 2.8 特勒根定理和互易定理 一、特勒根定理 二、互易定理 2.9 电路的对偶性 第 2-1 页 前一页 下一页 退出本章 将仅包含电阻、独立源和受控源的电路称为电阻电路
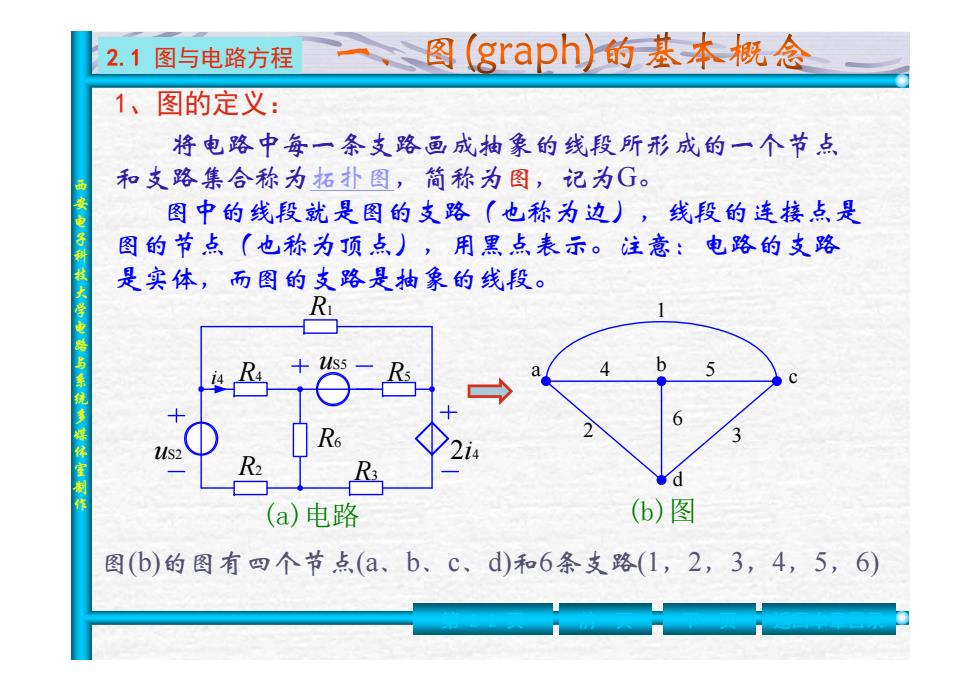
2.1图与电路方程 图(graph)的基本概念 1、图的定义: 将电路中每一条支路画成抽象的线段所形成的一个节点 和支路集合称为拓扑图,简称为图,记为G。 图中的线段就是图的支路(也称为边),线段的连接点是 图的节点(也称为顶点),用黑点表示。注意:电路的支路 是实体,而图的支路是抽象的线段。 R R2 (a)电路 (b)图 图(b)的图有四个节点(a、b、c、d)和6条支路(1,2,3,4,5,6)
西安电子科技大学电路与系统多媒体室制作 2.1 图与电路方程 将电路中每一条支路画成抽象的线段所形成的一个节点 和支路集合称为拓扑图,简称为 图,记为 G 。 图中的线段就是图的支路(也称为边),线段的连接点是 图的节点(也称为顶点),用黑点表示。注意:电路的支路 是实体,而图的支路是抽象的线段。 i4 R1 uS2 uS5 R 2 R 3 R 4 R 5 R 6 2 i 4 (a)电路 (b)图 a b c d 1 2 3 4 5 6 图(b)的图有四个节点(a、b、c、d) 和 6条支路(1,2,3,4,5,6) 第 2-2 页 前一页 下一页 返回本章目录 1、图的定义:
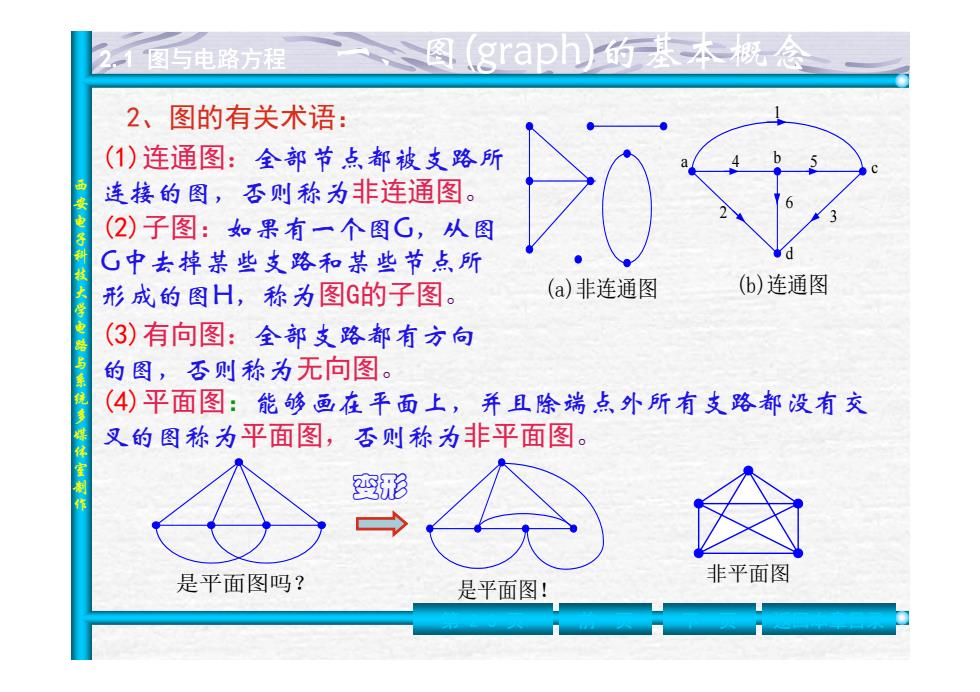
1图与电路方程 grap的基本概念 2、图的有关术语: (1)连通图:全部节点都被支路所 连接的图,否则称为非连通图。 (2)子图:如果有一个图G,从图 G中去掉某些支路和某些节点所 形成的图H,称为图G的子图。 (a)非连通图 (b)连通图 (3)有向图:全部支路都有方向 的图,否则称为无向图。 (④)平面图:能够画在平面上,并且除端点外所有支路都没有交 叉的图称为平面图,否则称为非平面图。 变形 是平面图吗? 非平面图 是平面图!
西安电子科技大学电路与系统多媒体室制作 2.1 图与电路方程 (1)连通图:全部节点都被支路所 连接的图,否则称为非连通图。 (b)连通图 a b c d 1 2 3 4 5 6 (a)非连通图 (3)有向图:全部支路都有方向 的图,否则称为无向图。 (2)子图:如果有一个图G,从图 G中去掉某些支路和某些节点所 形成的图H,称为图G的子图。 (4)平面图:能够画在平面上,并且除端点外所有支路都没有交 叉的图称为平面图,否则称为非平面图。 是平面图吗? 是平面图! 非平面图 变形 第 2-3 页 前一页 下一页 返回本章目录 2、图的有关术语:
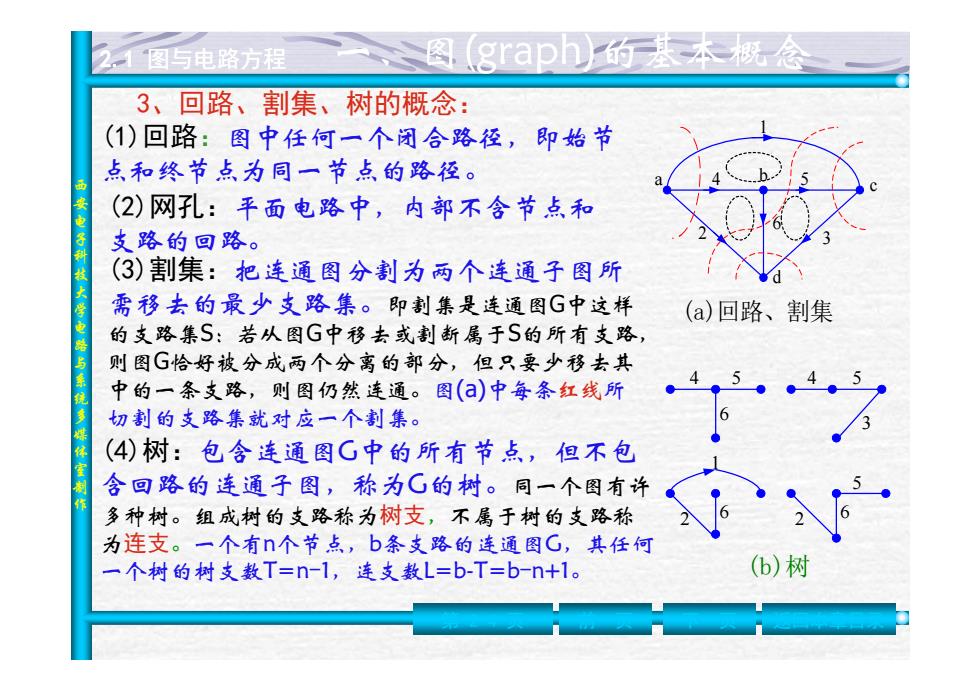
图与电路方程 graph的基本概念 3、回路、割集、树的概念 ()回路:图中任何一个闭合路径,即始节 点和终节点为同一节点的路径。 (2)网孔:平面电路中,内部不含节点和 支路的回路。 (3)割集:把连通图分割为两个连通子图所 需移去的最少支路集。即割集是连通图G中这样 (a)回路、割集 的支路集S:若从图G中移去或割断属于S的所有支路, 则图G恰好被分成两个分离的部分,但只要少移去其 中的一条支路,则图仍然连通。图()中每条红线所 切割的支路集就对应一个割集。 (4)树:包含连通图G中的所有节点,但不包 含回路的连通子图,称为G的树。同一个图有许 多种树。组成树的支路称为树支,不属于树的支路称 为连支。一个有n个节点,b条支路的连通图G,其任何 一个树的树支数T=n-l,连支数L=b-T=b-n+1。 (b)树
西安电子科技大学电路与系统多媒体室制作 2.1 图与电路方程 (1)回路:图中任何一个闭合路径,即始节 点和终节点为同一节点的路径。 (3)割集:把连通图分割为两个连通子图所 需移去的最少支路集。即割集是连通图 G中这样 的支路集 S:若从图 G中移去或割断属于 S的所有支路, 则图 G恰好被分成两个分离的部分,但只要少移去其 中的一条支路,则图仍然连通。 图(a)中每条红线 所 切割的支路集就对应一个割集。 (4)树:包含连通图G中的所有节点,但不包 含回路的连通子图,称为G的树。同一个图有许 多种树。组成树的支路称为树支,不属于树的支路称 为连支 。一个有n个节点,b条支路的连通图G,其任何 一个树的树支数T=n -1,连支数L=b-T=b -n+1。 (a)回路、割集 a b c d 1 2 3 4 5 6 4 5 6 5 3 1 2 6 5 6 2 4 (b)树 (2)网孔:平面电路中,内部不含节点和 支路的回路。 第 2-4 页 前一页 下一页 返回本章目录 3、回路、割集、树的概念:
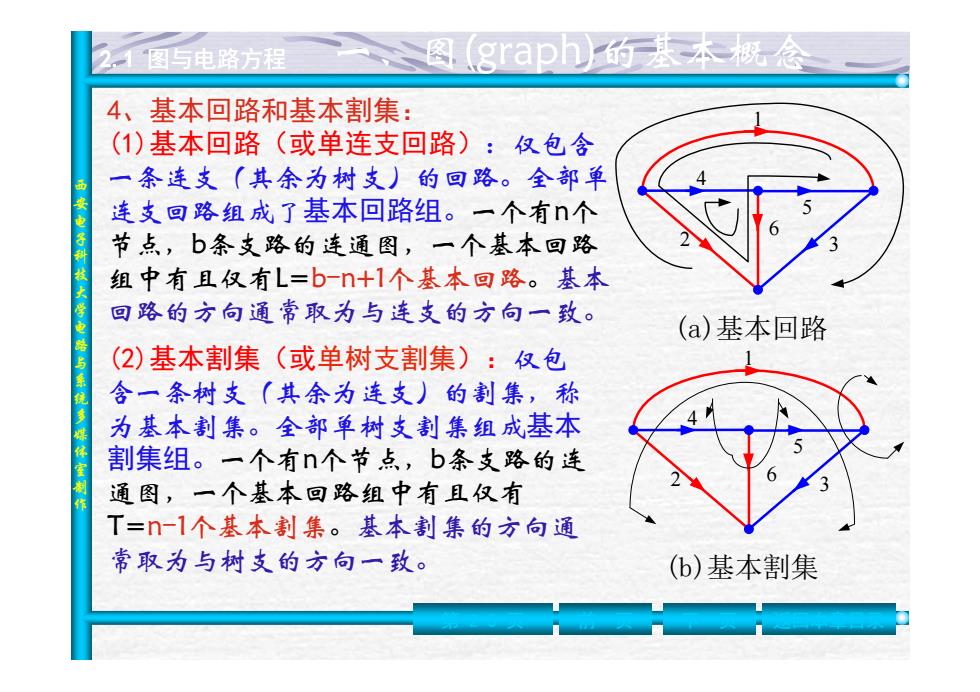
图与电路方程 graph的基本概念 4、基本回路和基本割集: (1)基本回路(或单连支回路):仅包含 一条连支(其余为树支)的回路。全部单 连支回路组成了基本回路组。一个有n个 节点,b条支路的连通图,一个基本回路 组中有且仅有L=b-n+1个基本回路。基本 回路的方向通常取为与连支的方向一致。 (a)基本回路 (2)基本割集(或单树支割集):仅包 会一条树支(其余为连支)的割集,称 为基本割集。全部单树支割集组成基本 割集组。一个有n个节点,b条支路的连 通图,一个基本回路组中有且仅有 T=门-1个基本割集。基本割集的方向通 常取为与树支的方向一致。 (b)基本割集
西安电子科技大学电路与系统多媒体室制作 2.1 图与电路方程 (1)基本回路(或单连支回路):仅包含 一条连支(其余为树支)的回路。全部单 连支回路组成了基本回路组 。一个有n个 节点,b条支路的连通图,一个基本回路 组中有且仅有L= b -n+1个基本回路 。基本 回路的方向通常取为与连支的方向一致。 (2)基本割集(或单树支割集):仅包 含一条树支(其余为连支)的割集,称 为基本割集。全部单树支割集组成基本 割集组 。一个有n个节点,b条支路的连 通图,一个基本回路组中有且仅有 T= n -1个基本割集 。基本割集的方向通 常取为与树支的方向一致。 (a)基本回路 1 2 3 4 5 6 (b)基本割集 1 2 3 4 5 6 第 2-5 页 前一页 下一页 返回本章目录 4、基本回路和基本割集:
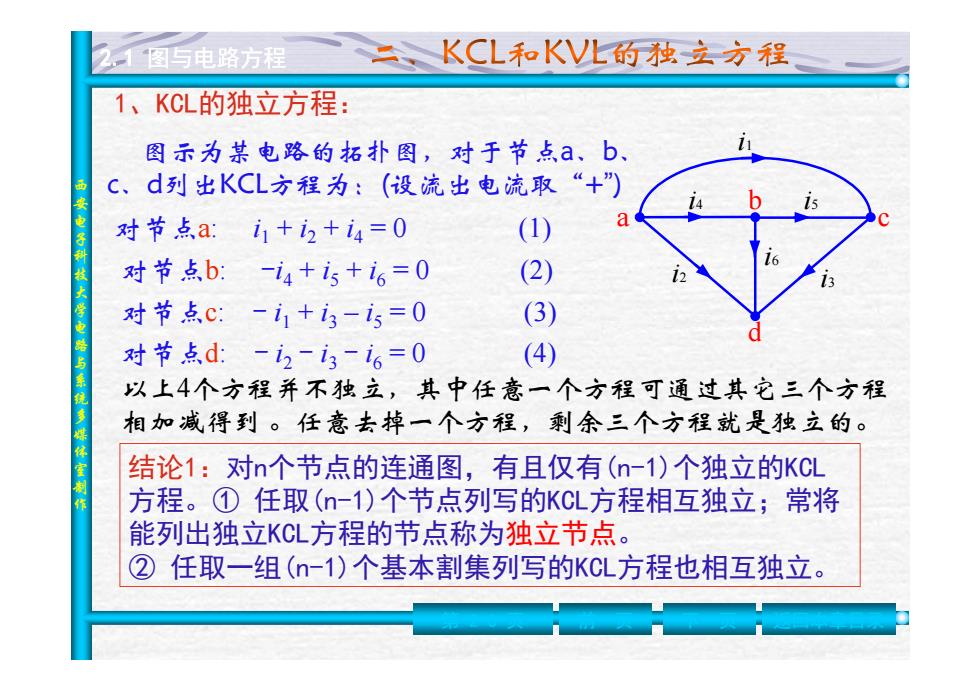
图与电路方程 KCL和KV儿的独立方程 1、KCL的独立方程: 图示为某电路的拓扑图,对于节点a、b、 C、d列出KCL方程为:(设流出电流取“+") 对节点a:i1+i2+i4=0 (1) a 对节点b:-i4+i5+i6=0 (2) 对节点C:-i1+3-i5=0 (3) 对节点d:-i2-3-i6=0 (4) 以上4个方程并不独立,其中任意一个方程可通过其它三个方程 相加减得到。任意去掉一个方程,剩余三个方程就是独立的。 结论1:对n个节点的连通图,有且仅有(n-1)个独立的KC 方程。①任取(-1)个节点列写的KCL方程相互独立;常将 能列出独立KCL方程的节点称为独立节点。 ②任取一组(-1)个基本割集列写的KCL方程也相互独立
西安电子科技大学电路与系统多媒体室制作 2.1 图与电路方程 图示为某电路的拓扑图,对于节点a、b、 c、d列出KCL方程为:(设流出电流取“+ ” ) d b a c i1 i 2 i 3 i 4 i 5 i 6 对节点 a: i1 + i 2 + i 4 = 0 (1) 对节点 b: - i 4 + i 5 + i 6 = 0 (2) 对节点 c: - i1 + i 3 – i 5 = 0 (3) 对节点 d: - i 2 - i 3 - i 6 = 0 (4) 以上 4个方程并不独立,其中任意一个方程可通过其它三个方程 相加减得到 。任意去掉一个方程,剩余三个方程就是独立的。 结论1:对n个节点的连通图,有且仅有(n-1)个独立的KCL 方程。① 任取(n-1)个节点列写的KCL方程相互独立;常将 能列出独立KCL方程的节点称为独立节点 。 ② 任取一组(n-1)个基本割集列写的KCL方程也相互独立。 第 2-6 页 前一页 下一页 返回本章目录 1、KCL的独立方程:
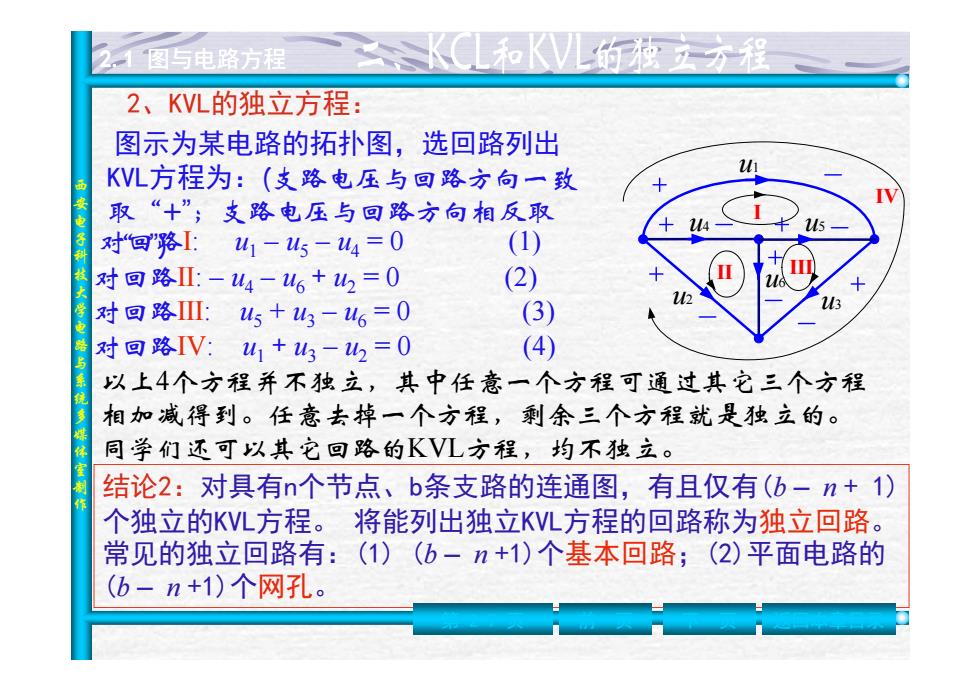
“图与电路方程 2、KL的独立方程: 图示为某电路的拓扑图,选回路列出 KVL方程为:(支路电压与回路方向一致 取“+”;支路电压与回路方句相反取 14 15 对回路:山1-45-44=0 (1) 对回路亚:-4-46+山=0 (2) 12 对回路Ⅲ:山5+山3-46=0 (3) 对回路V:41+山3-42=0 (4) 以上4个方程并不独立,其中任意一个方程可通过其它三个方程 相加减得到。任意去掉一个方程,剩余三个方程就是独立的。 同学们还可以其它回路的KVL方程,均不独立。 结论2:对具有n个节点、b条支路的连通图,有且仅有(b-n+1) 个独立的KVL方程。将能列出独立KVL方程的回路称为独立回路。 常见的独立回路有:(1)(b-n+1)个基本回路;(2)平面电路的 (b-n+1)个网孔
西安电子科技大学电路与系统多媒体室制作 2.1 图与电路方程 图示为某电路的拓扑图,选回路列出 KVL方程为:(支路电压与回路方向一致 取“+ ”;支路电压与回路方向相反取 对回路 “ - ” ) Ⅰ: u1 – u 5 – u 4 = 0 (1) 对回路 Ⅱ: – u 4 – u 6 + u 2 = 0 (2) 对回路 Ⅲ: u 5 + u 3 – u 6 = 0 (3) 对回路 Ⅳ: u1 + u 3 – u 2 = 0 (4) 以上 4个方程并不独立,其中任意一个方程可通过其它三个方程 相加减得到。任意去掉一个方程,剩余三个方程就是独立的。 同学们还可以其它回路的KVL方程,均不独立。 结论2:对具有n个节点、b条支路的连通图,有且仅有(b – n + 1) 个独立的KVL方程。 将能列出独立KVL方程的回路称为独立回路 。 常见的独立回路有:(1) (b – n +1)个基本回路;(2)平面电路的 (b – n +1)个网孔 。 u1 u 2 u 3 u 4 u 5 u 6 Ⅰ Ⅱ Ⅲ Ⅳ 第 2-7 页 前一页 下一页 返回本章目录 2、KVL的独立方程:
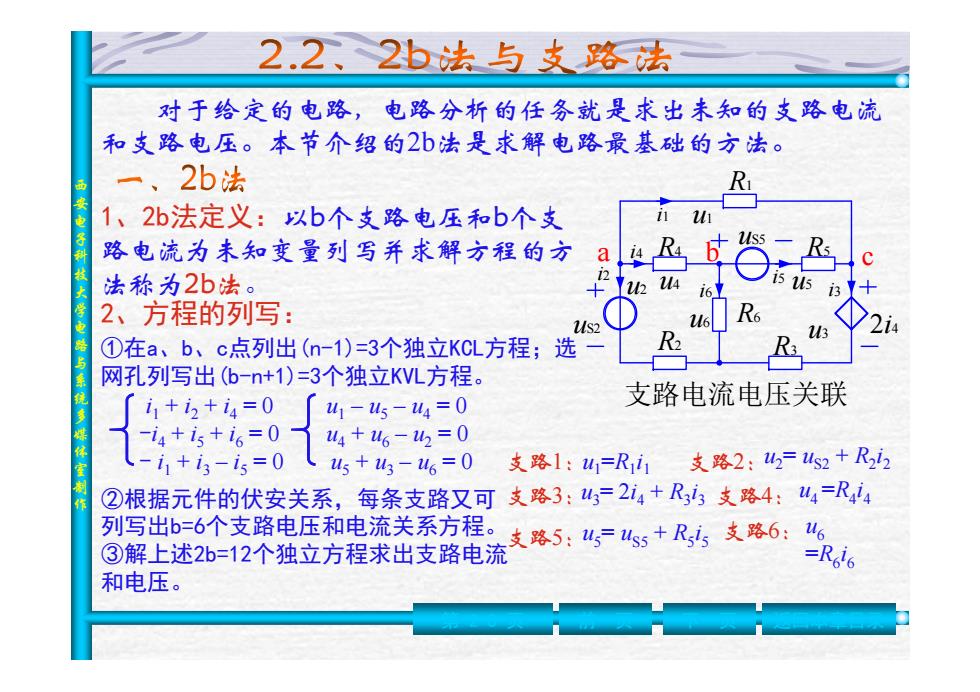
2.2、2b法与支路法 对于给定的电路,电路分析的任务就是求出未知的支路电流 和支路电压。本节介绍的2b法是求解电路最基础的方法。 一、2b法 1、2b法定义:以b个支路电压和b个支 路电流为未知变量列写并求解方程的方 a 法称为2b法。 2、方程的列写: ①在a、b、c点列出(n-1)=3个独立KCL方程;选- 网孔列写出(b-n+1)=3个独立KVL方程。 i1+2+4=0 41-45-w4=0 支路电流电压关联 -i4+i5+i6=0 4+46-4=0 i1+i3-i5=0 45+43-6=0 支路1:山1=R1d1支路2:2=4s2+R22 ②根据元件的伏安关系,每条支路又可支路3:山=2i4+R内支路4:4=R,4 列写出66个支路电压和电流关系方程。支路5:4,=4+R5支路6: ③解上述2b=12个独立方程求出支路电流 =Roio 和电压
西安电子科技大学电路与系统多媒体室制作 对于给定的电路,电路分析的任务就是求出未知的支路电流 和支路电压。本节介绍的2b法是求解电路最基础的方法。 2、方程的列写: i4 R1 uS2 uS5 R 2 R 3 R 4 R 5 R 6 2 i 4 支路电流电压关联 i1 i2 i5 i6 i3 u 4 u 5 u1 u 2 u 6 u 3 a b c ①在a、b、c点列出(n-1)=3个独立KCL方程;选 网孔列写出(b-n+1)=3个独立KVL方程。 i1 + i 2 + i 4 = 0 u1 – u 5 – u 4 = 0 - i 4 + i 5 + i 6 = 0 u 4 + u 6 – u 2 = 0 - i1 + i 3 – i 5 = 0 u 5 + u 3 – u 6 = 0 ②根据元件的伏安关系,每条支路又可 列写出b=6个支路电压和电流关系方程。 支路 1:u1=R1i1 支路 2:u 2= uS2 + R 2 i 2 支路 3:u 3= 2 i 4 + R 3 i 3 支路 4:u4 =R 4 i 4 支路 5:u 5= uS5 + R 5 i 5 支路 6:u6 =R 6 i ③解上述2b=12个独立方程求出支路电流 6 和电压。 第 2-8 页 前一页 下一页 返回本章目录 1、2b法定义:以b个支路电压和b个支 路电流为未知变量列写并求解方程的方 法称为2b法

226法与支路法一二、支路法(b法》 1、支路法定义:以支路电流(或电压)为未知变量列出方程, 求解支路电流(或电压),称为支路电流(或电压)法。简称 支路法。 2、求解思路:(以支路电流法为例说明) ()、选定各支路电流的参考方向; 2)、对(门-1)个独立节点,列出独立KCL方程; ③)、选定(b-+1)个独立回路(基本回路或网孔),指定 回路绕行方向,根据KV儿和OL列出回路电压方程。列 写过程中将支路电压用支路电流来表示。 ()、联立求解上述b个支路电流方程; (⑤)、进而求题中要求的支路电压或功率等
西安电子科技大学电路与系统多媒体室制作 2.2、2b法与支路法 2、求解思路:(以支路电流法为例说明) ⑴、选定各支路电流的参考方向; ⑵、对(n-1)个独立节点,列出独立KCL方程; ⑶、选定(b-n+1)个独立回路(基本回路或网孔),指定 回路绕行方向,根据KVL和OL列出回路电压方程。列 写过程中将支路电压用支路电流来表示。 ⑷、联立求解上述b个支路电流方程; ⑸、进而求题中要求的支路电压或功率等。 第 2-9 页 前一页 下一页 返回本章目录 1、支路法定义:以支路电流(或电压)为未知变量列出方程, 求解支路电流(或电压),称为支路电流(或电压)法。简称 支路法
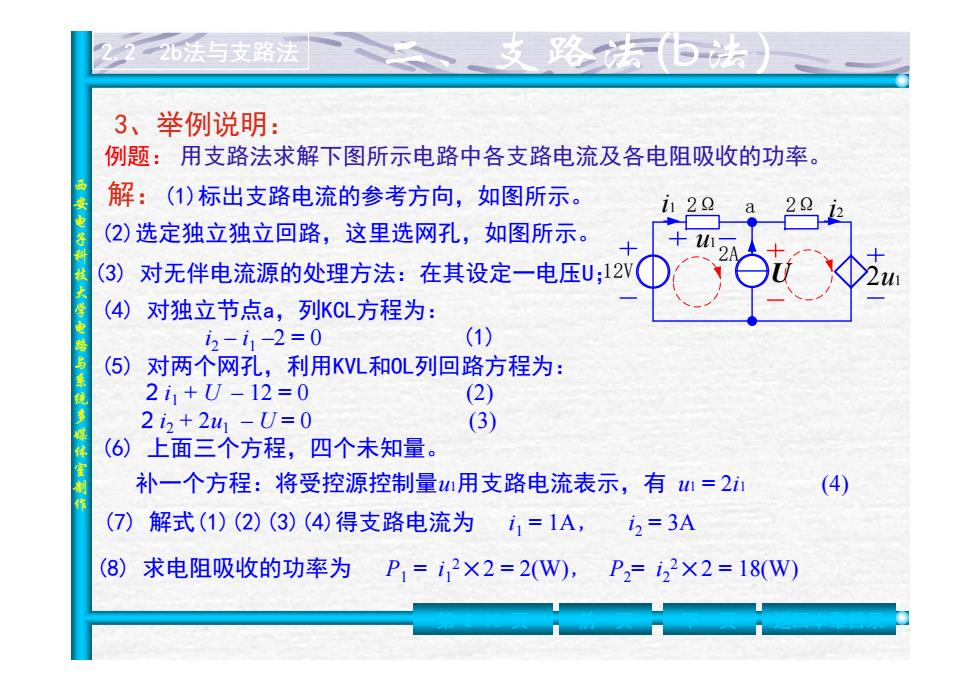
226法与支路法 支路 3、举例说明: 例题:用支路法求解下图所示电路中各支路电流及各电阻吸收的功率。 解:(1)标出支路电流的参考方向,如图所示。 1122 (2)选定独立独立回路,这里选网孔,如图所示。 +11 (3)对无伴电流源的处理方法:在其设定一电压U;12V (4)对独立节点a,列KCL方程为: 2-i1-2=0 (1) (⑤)对两个网孔,利用KVL和0L列回路方程为: 2i1+U-12=0 (2) 2i2+241-U=0 (3) (6)上面三个方程,四个未知量。 补一个方程:将受控源控制量用支路电流表示,有1=2i (4) (⑦)解式(1)(2)(3)(4)得支路电流为1=1A, i2=3A (8)求电阻吸收的功率为 P=i2×2=2(W),P2=22×2=18(W)
西安电子科技大学电路与系统多媒体室制作 2.2 2b法与支路法 例题: 用支路法求解下图所示电路中各支路电流及各电阻吸收的功率。 2A 12V 2Ω 2Ω u1 2u1 i1 a i2 U 解:(1)标出支路电流的参考方向,如图所示。 (2)选定独立独立回路,这里选网孔,如图所示。 (3) 对无伴电流源的处理方法:在其设定一电压U; (4) 对独立节点a,列KCL方程为: i2 – i1 –2 = 0 (1) (5) 对两个网孔,利用KVL和OL列回路方程为: 2 i1 + U – 12 = 0 (2) 2 i2 + 2u1 – U = 0 (3) (6) 上面三个方程,四个未知量。 (7) 解式(1)(2)(3)(4)得支路电流为 i1 = 1A, i2 = 3A (8) 求电阻吸收的功率为 P1 = i12×2 = 2(W), P2= i22×2 = 18(W) 第 2-10 页 前一页 下一页 返回本章目录 3、举例说明: 补一个方程:将受控源控制量u1用支路电流表示,有 u1 = 2i1 (4)