
第四章正弦稳态分析 目录二 4.6互感耦合电路 一、耦合电感 二、耦合电感的VAR 西安电子科技大学电路与系统多媒体室制作 三、去耦等效电路 四、互感电路的计算 4.7变压器 一、理想变压器 二、全耦合变压器 三、实际变压器模型 第2-1页前一页下一页退出本章 点击目录,进入相关章节
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 点击目录 ,进入相关章节 第 2-1 页 前一页 下一页 目录二 4.6 互感耦合电路 一、耦合电感 二、耦合电感的VAR 三、去耦等效电路 四、互感电路的计算 4.7 变压器 一、理想变压器 二、全耦合变压器 三、实际变压器模型 退出本章
4.6互感超合电路 一、耦合电感 耦合电感(互感)是实际互感线圈的理 想化模型。工作原理是单个电感的延伸。 中12 图中两个靠近的线圈,线圈1 有N1匝,线圈2有N2匝。 当线圈1中通电流时,在自身中 激发磁通①1,称自磁通;其中有 一部分也通过N2(①2),称为互磁 通。在线圈密绕的情况下,穿过各自 线圈中每匝的磁通相同,故与两线 圈交链的磁链有 Ψ1=N1Φ1=L1i1 Ni N2 Ψ21=N2①21=M21i1 平1,L1称线圈1的自磁链和自感; Ψ21,M称线圈1电流i对线图2 的互磁链和互感。 同样,线圈2中通电流2时,有平22=N2①22=L2i2,Ψ12=N1①D12=M122
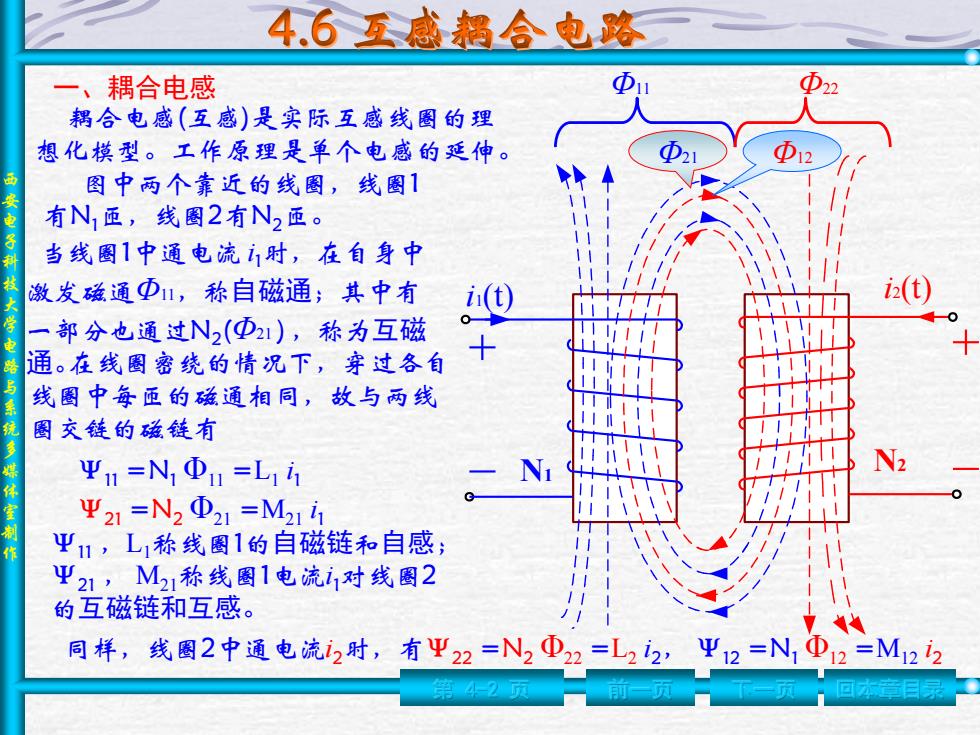
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 4-2 页 前一页 下一页 回本章目录 一、耦合电感 N1 N2 i1(t) Φ11 Φ21 Φ22 Φ12 i2(t) 耦合电感(互感)是实际互感线圈的理 想化模型。工作原理是单个电感的延伸。 图中两个靠近的线圈,线圈1 有N1匝,线圈2有N2匝。 当线圈1中通电流 i 1时,在自身中 激发磁通Φ11,称自磁通;其中有 一部分也通过N2 (Φ21 ),称为互磁 通。在线圈密绕的情况下,穿过各自 线圈中每匝的磁通相同,故与两线 圈交链的磁链有 Ψ11 =N1 Φ11 =L1 i 1 Ψ21 =N2 Φ21 =M21 i 1 Ψ11 ,L1称线圈1的自磁链和自感; Ψ21 , M21称线圈1电流i 1对线圈2 的互磁链和互感。 同样,线圈2中通电流i2时,有Ψ22 =N2 Φ22 =L2 i2, Ψ12 =N1 Φ12 =M12 i2

46感耦合电鸥 对于线性电路,可以证明M12=M21=M,其单位与自感相同, 为亨(H田。 工程上,为了描述两线圈的耦合松紧程度,将两线圈互 磁链与自磁链之比的几何均值定义为耦合系数k,即 de Y12 Y1=N1①1=L1i1,平21=N2①21=M21i1 平2 Ψ22=N2①22=L22,Ψ12=N1①12=M122 将前面的有关式子代入,得: ①2二 M ①22 LL2 由于①21≤①11,①12≤①2,故0≤k≤1,M2LL2 当k=0时,M=0,两线圈互不影响,称无耦合; 当k=1时,M2=LL2,称为全耦合
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 4-3 页 前一页 下一页 回本章目录 工程上,为了描述两线圈的耦合松紧程度,将两线圈互 磁链与自磁链之比的几何均值定义为耦合系数k,即 22 12 11 21 def k 将前面的有关式子代入,得: 2 2 1 2 1 2 1 1 2 1 L L M k Ψ11 =N1 Φ11 =L1 i 1, Ψ21 =N2 Φ21 =M21 i 1 Ψ22 =N2 Φ22 =L2 i2, Ψ12 =N1 Φ12 =M12 i2 由于Φ21 ≤ Φ11 , Φ12≤ Φ22 , 故 0 ≤ k ≤ 1,M2 ≤L1L2 当k = 0时,M = 0,两线圈互不影响,称无耦合; 当k = 1时, M2 = L1L2 ,称为全耦合。 对于线性电路,可以证明 M12 = M21 =M,其单位与自感相同, 为亨(H)
46感超合南跨 二、互感的伏安关系 如图所示两耦合线圈,都通 电流后,其自磁通与互磁通方 向一致,称为磁通相助。 各线圈中的总磁链包含自磁链 i(t) i2( 和互磁链两部分。在磁通相助的 情况下,两线圈的总磁链分别为 Ψ1=Ψ,+平12=L1i+Mi2 () uz(t) Ψ2=Ψ22+Ψ21=L22+Mi1 N2 设两线圈电压、电流参考方句关 联,则根据电磁感应定律,有 山1(t)= dΨ1 di+M- d u2(t)= dΨ2=L2dt z+M d dt
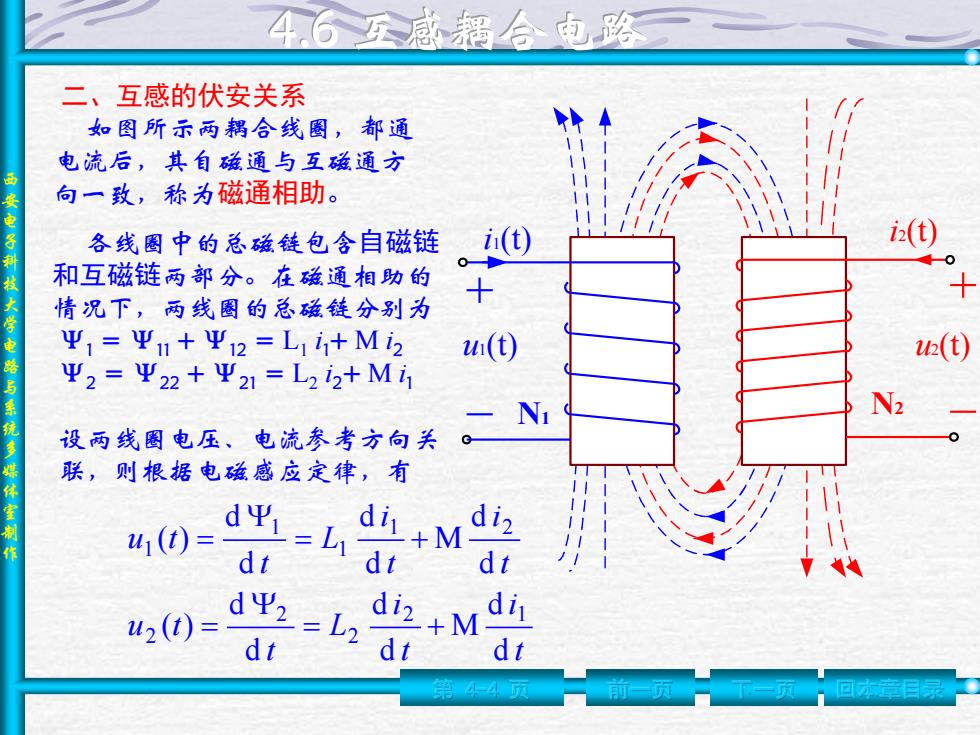
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 4-4 页 前一页 下一页 回本章目录 如图所示两耦合线圈,都通 电流后,其自磁通与互磁通方 向一致,称为磁通相助。 二、互感的伏安关系 N1 N2 i1(t) 各线圈中的总磁链包含自磁链 i2(t) 和互磁链两部分。在磁通相助的 情况下,两线圈的总磁链分别为 Ψ1 = Ψ11 + Ψ12 = L1 i 1+ M i2 Ψ2 = Ψ22 + Ψ21 = L2 i2+ M i 1 设两线圈电压、电流参考方向关 联,则根据电磁感应定律,有 t i t i L t u t t i t i L t u t d d M d d d d ( ) d d M d d d d ( ) 2 1 2 2 2 1 2 1 1 1 u1(t) u2(t)
46乒感耦合电鸭 若改变线圈2的绕向,如图所示。则自磁通与互磁通方向相反,称为磁通相消。 这时,两线圈的总磁链分别为 Ψ1=Ψ1-Ψ2=L1Mi2 Ψ2=Ψ22-Ψ21=L22Mi1 两线圈电压为 in(t) 40s{ di-M diz dt u2(t)= =L2 iz _M i dt dt 上分析表明:耦合电感上的电压等 于自感电压与互感电压的代数和。 在线圈电压、电流参考方向关联的 条件下,自感电压取“+”; 当磁通相助时,互感电压前取“+”; 当磁通相消时,互感电压前取
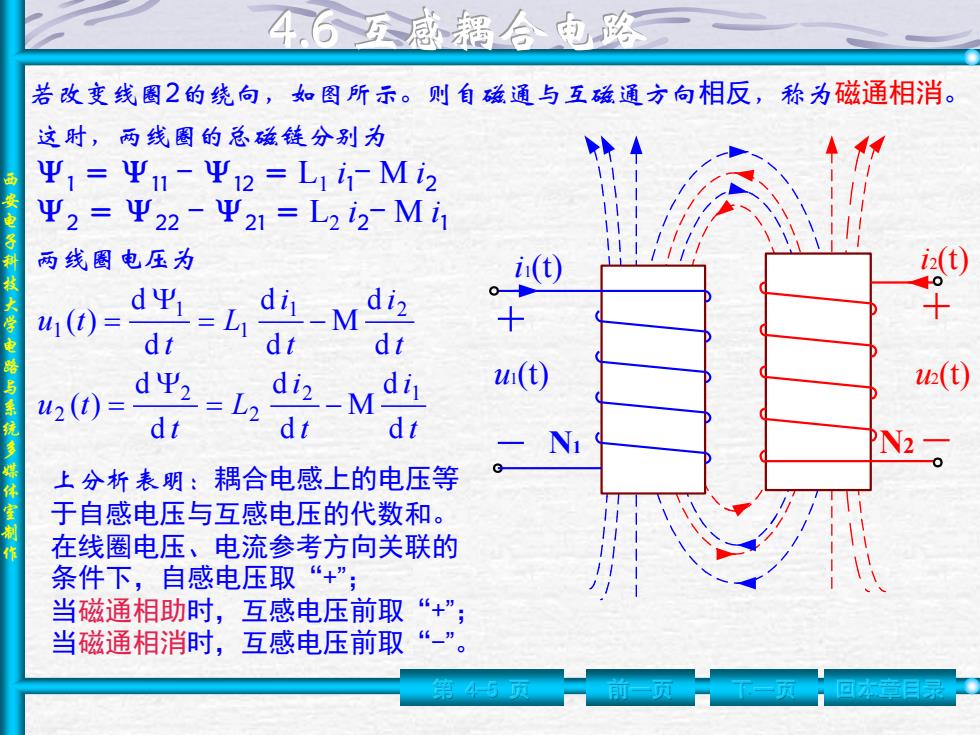
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 4-5 页 前一页 下一页 回本章目录 N1 i1(t) i2(t) u1(t) u2(t) N2 若改变线圈2的绕向,如图所示。则自磁通与互磁通方向相反,称为磁通相消。 这时,两线圈的总磁链分别为 Ψ1 = Ψ11 - Ψ12 = L1 i 1- M i2 Ψ2 = Ψ22 - Ψ21 = L2 i2- M i 1 两线圈电压为 t i t i L t u t t i t i L t u t d d M d d d d ( ) d d M d d d d ( ) 2 1 2 2 2 1 2 1 1 1 上分析表明:耦合电感上的电压等 于自感电压与互感电压的代数和。 在线圈电压、电流参考方向关联的 条件下,自感电压取“+” ; 当磁通相助时,互感电压前取“+” ; 当磁通相消时,互感电压前取“-”
46感韬合电 判断磁通相消还是相助,除与线圈上电流的方向有关外,还与两线圈的 相对绕向有关。 实际中,耦合线圈密封,且电路图不便画出。为此,人们规 定一种称为同名端的标志。根据同名端和电流的参考方向就可 判定磁通相助还是相消。 同名端的规定:当电流从两线圈各自的某端子同时流入(或同时流出) 时,若两线圈产生的磁通相助,则称这两个端子是耦合电感的同名端, 并标记号“。”或 “米” 12 0 2 哪些是同名端? 若从a端流入,i2从c端流入,磁通相助;故ā、C为同名端, 用“。”标出。电路模型如右图。 显然,b、d也是同名端。a、d为异名端,b、c也是异名端
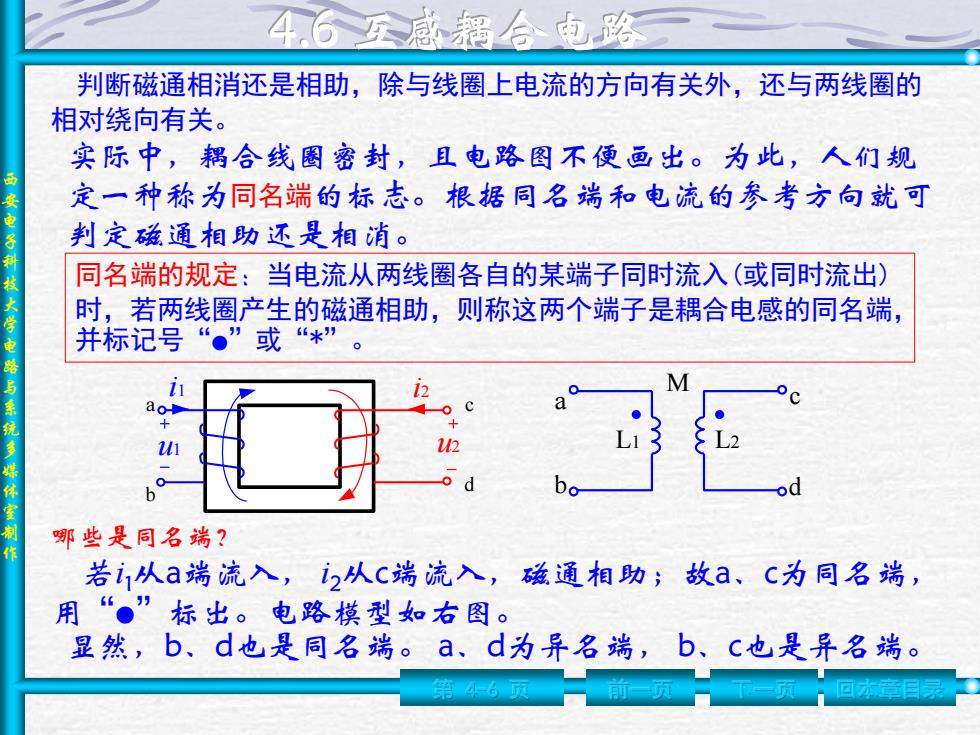
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 4-6 页 前一页 下一页 回本章目录 判断磁通相消还是相助,除与线圈上电流的方向有关外,还与两线圈的 相对绕向有关。 实际中,耦合线圈密封,且电路图不便画出。为此,人们规 定一种称为同名端的标志。根据同名端和电流的参考方向就可 判定磁通相助还是相消。 同名端的规定:当电流从两线圈各自的某端子同时流入(或同时流出) 时,若两线圈产生的磁通相助,则称这两个端子是耦合电感的同名端, 并标记号“ ● ”或“*” 。 哪些是同名端? 若i 1从a端流入, i2从c端流入,磁通相助;故a、c为同名端, 用“ ● ”标出。电路模型如右图。 显然,b、d也是同名端。 a、d为异名端, b、c也是异名端。 b c d a i1 i2 u1 u2 a b c d M L1 L2
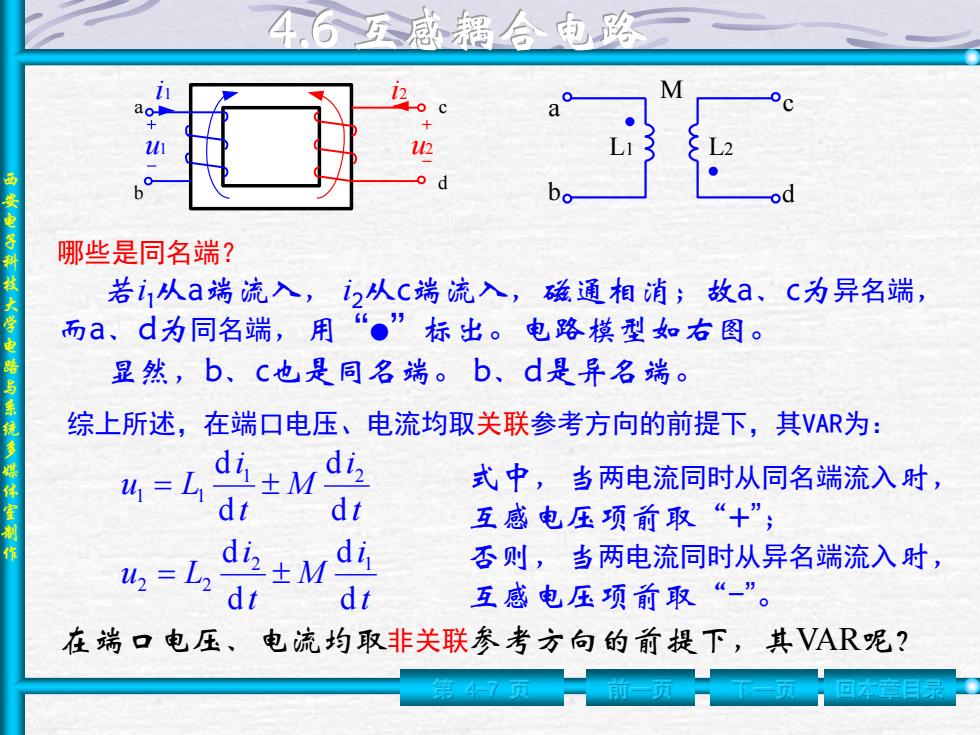
46医感耦合电蹈 ao -o c + 12 o d 哪些是同名端? 若i从a端流入,i从C端流入,磁通相消;故a、C为异名端, 而a、d为同名端,用“。”标出。电路模型如右图。 显然,b、C也是同名端。b、d是异名端。 综上所述,在端口电压、电流均取关联参考方向的前提下,其VAR为: d士Mdh =L 式中,当两电流同时从同名端流入附, dt 互感电压项前取“+”; di±M 4=n 否则,当两电流同时从异名端流入时, i 互感电压项前取“-”。 在端口电压、电流均取非关联参考方向的前提下,其VAR呢?
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 4-7 页 前一页 下一页 回本章目录 a b c d i1 i2 u1 u2 哪些是同名端? 若i 1从a端流入, i2从c端流入,磁通相消;故a、c为异名端, 而a、d为同名端,用“ ● ”标出。电路模型如右图。 显然,b、c也是同名端。 b、d是异名端。 a b c d M L1 L2 综上所述,在端口电压、电流均取关联参考方向的前提下,其VAR为: t i M t i u L t i M t i u L d d d d d d d d 2 1 2 2 1 2 1 1 式中,当两电流同时从同名端流入时, 互感电压项前取“+” ; 否则,当两电流同时从异名端流入时, 互感电压项前取“-” 。 在端口电压、电流均取非关联参考方向的前提下,其VAR呢?

46感超合南路 列写耦合电感VAR的步骤: 4= di dt 42=±L d±Md 当端口电压、电流取关联参考方向时,自感电压项前取“+” 当端口电压、电流取非关联参考方向时,自感电压项前取“-” 当两电流同时从同名端流入时,互感电压项前和自感电压项前同号 当两电流同时从异名端流入时,互感电压项前和自感电压项前异号
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 4-8 页 前一页 下一页 回本章目录 列写耦合电感VAR的步骤: t i M t i u L t i M t i u L d d d d d d d d 2 1 2 2 1 2 1 1 当两电流同时从同名端流入时,互感电压项前和自感电压项前同号 当两电流同时从异名端流入时,互感电压项前和自感电压项前异号 当端口电压、电流取关联参考方向时,自感电压项前取“+” 当端口电压、电流取非关联参考方向时,自感电压项前取“-
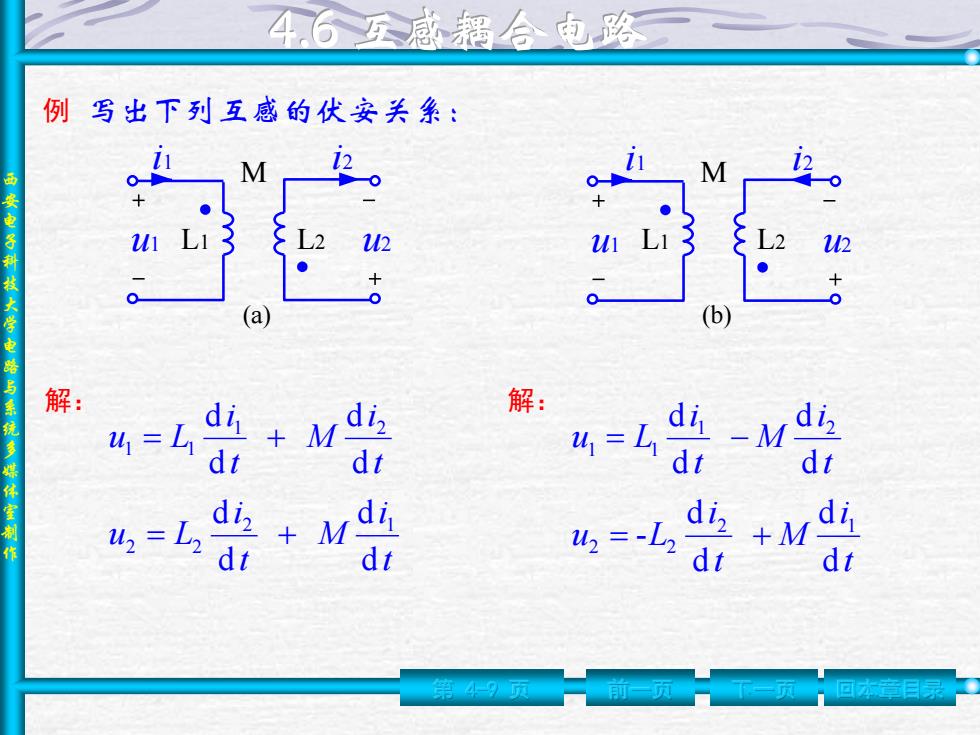
46医感超合电蹈 例写出下列互感的伏安关华: M M 2 安电子科 ,L2 12 ● ● +9 学 (a) (b) 解: diz 解: 4=L dr M dt 4=L diz dt 4=L diz +M u2 =-L di +M di 作 dt dt
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 4-9 页 前一页 下一页 回本章目录 例 写出下列互感的伏安关系: u2 M u1 L1 L2 i1 i2 (a) 解: t i M t i u L t i M t i u L d d d d d d d d 2 1 2 2 1 2 1 1 u2 M u1 L1 L2 i1 i2 (b) 解: t i M t i u L t i M t i u L d d d d - d d d d 2 1 2 2 1 2 1 1
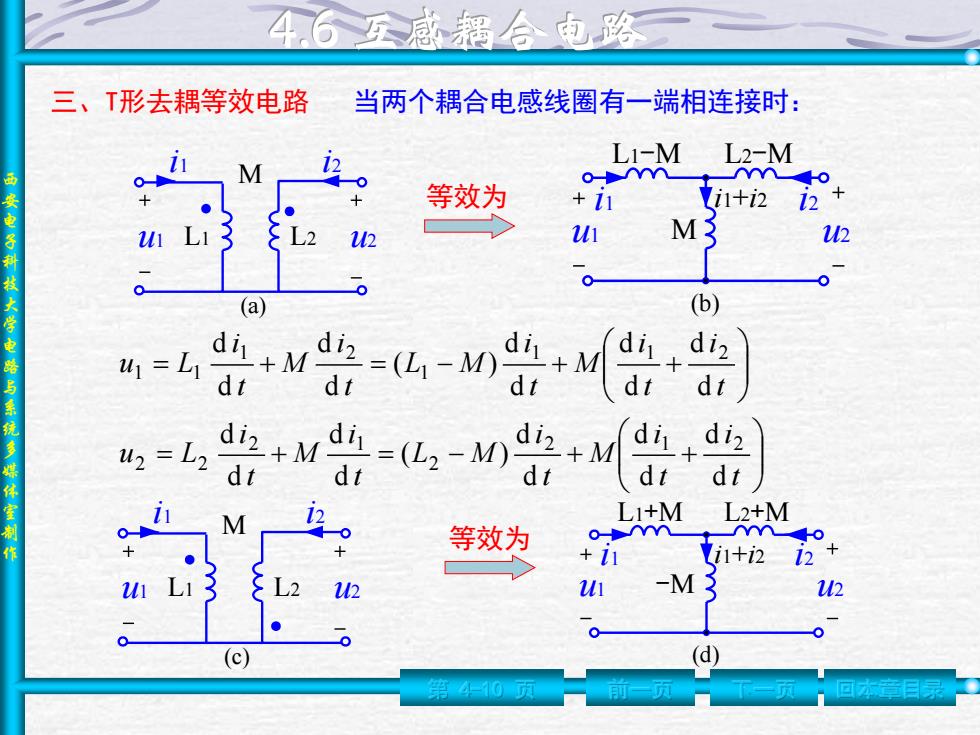
46医感辐合电路 三、T形去耦等效电路 当两个耦合电感线圈有一端相连接时: LI-M L2-M M 等效为 +1 i1+2 12 ui L 2 ui M3 12 0 大学电路 (a) (b) diz 与系统 u=Ldi di =4-M0ai di 42=L2 z+M =(L2-M) iz+M 螺体 di dt dt dt M 12 LI+M L2+M 作 等效为 ● +1 i+2 12+ L2 12 -M3 1l2 ● a (c) (d)
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 4-10 页 前一页 下一页 回本章目录 三、T形去耦等效电路 当两个耦合电感线圈有一端相连接时: u2 M u1 L1 L2 i1 i2 (a) i1 i2 L1-M L2-M u1 M u2 (b) 等效为 i1+i2 t i t i M t i L M t i M t i u L t i t i M t i L M t i M t i u L d d d d d d ( ) d d d d d d d d d d ( ) d d d d 2 1 2 2 2 1 2 2 1 1 2 1 1 2 1 1 u2 M u1 L1 L2 i1 i2 (c) 等效为 i1 i2 L1+M L2+M u1 -M u2 (d) i1+i2