
实验二昆虫种群空间格局测定 一、 实验原理 (一)离散分布的理论拟合 学习昆虫种群空间格局的离散分布型理论拟合方法。 昆虫种群空间格局是一种群内个体在一定的空间内扩散分布的一定形式,由物种的生物学特性以及栖息地 内生物和非生物条件所决定。种群的空间分布型因物种、虫期、虫龄、种群密度以及环境条件而异。研究种群 的空间格局,可以揭示种群的空间结构以及种下结构的状况:有利于确定或改进精确而有效的抽样设计方案: 也可对研究对象资料提出适当的数据统计处理方法:同时对于了解昆虫的猖獗扩散行为也有一定的意义。 离散分布的理论拟合是昆虫种群空间格局研究的重要内容。每个样方出现的个体数量构成随机变量序列, 然后检验此序列可拟合某一个(或不止一个)理论概率分布。过去人们常说的“田间分布型”,并不是指种群 个体在空间的真正排列形式,它只下过是表示在随机抽样中样方出现0、1、2、3个个体的随机变量的频率 分布,究竟属于什么理论概率分布型。昆虫种群主要表现两种类型。 随机分布 在呈随机分布的种群内,个体独立地、随机在分配到可利用的单位中去,每个个体占空 间任何一点的概率是相等的,并且任何一个个体的存在决不影响其他个体的分布。适合于随机公布的理论概率 如潘松分布型。 Pr=。 川 其中,Pr:样方中出现r个体的概率(r=0、1、2n); m:样方中个体平均数。 聚集分布型 种群内个体的分布很少呈随机或均匀性,而大多是聚集性。呈聚集分布的种群,样本平 均数显著小于方差。通常由若干个体组成一定的个体群,最后形成各种不同的类型。适于描述聚集公布的理论 概率型很多。昆虫种群中常见负二项分布型和核心分布型。 负二项分布型 种群内个体分布疏密相嵌,很不均匀。本分布由算术平均数μ和K指数决定。理论 概率为: Pr=K+r-,P产 rl(K-1)! 奈曼分布型 种群内个体形成无数大小相似的核心(个体群)。在核心中的个体数量稠密,呈潘松 公布。在核心与核心之间的个体数量十分稀疏。若将每个核心看作一个单位,则众核心在总体中呈潘松分布。 因此,奈曼分布是潘松公布的特例,是潘松-一潘松分布。分布的理论概率为: Po=em1(1-em2)(r=0) Pr=4%e艺%Pk-r-0 0川 (r>0) 式中,m1=(n+1)x/m2,相当于抽样单位内平均集团数: m2=(n+2)(s2-x)/2x,相当于集团内平均个体数: n=0、1、2、…∞,为参数,n=0时为奈曼A型,昆虫中常见。 (二)聚集强度的测定 学习测量昆虫种群空间聚集程度的基本原理及方法。 由于种群内的每个个体都是不断变化的有机体,它们在任一瞬间的行为习性信赖于种群的遗传结构,以及 若干生物和非生物环境因子的影响,任何一个种群作为一个整体而言,总要因繁殖与死亡、迁进与迁出比例的 变化而产生数量的波动,可以从种群的空间格局中筛选出这样一种可测定、与分布等价的指标,而与种群个体
实验二 昆虫种群空间格局测定 一、 实验原理 (一)离散分布的理论拟合 学习昆虫种群空间格局的离散分布型理论拟合方法。 昆虫种群空间格局是一种群内个体在一定的空间内扩散分布的一定形式,由物种的生物学特性以及栖息地 内生物和非生物条件所决定。种群的空间分布型因物种、虫期、虫龄、种群密度以及环境条件而异。研究种群 的空间格局,可以揭示种群的空间结构以及种下结构的状况;有利于确定或改进精确而有效的抽样设计方案; 也可对研究对象资料提出适当的数据统计处理方法;同时对于了解昆虫的猖獗扩散行为也有一定的意义。 离散分布的理论拟合是昆虫种群空间格局研究的重要内容。每个样方出现的个体数量构成随机变量序列, 然后检验此序列可拟合某一个(或不止一个)理论概率分布。过去人们常说的“田间分布型”,并不是指种群 个体在空间的真正排列形式,它只下过是表示在随机抽样中样方出现0、1、2、3…n个个体的随机变量的频率 分布,究竟属于什么理论概率分布型。昆虫种群主要表现两种类型。 随机分布 在呈随机分布的种群内,个体独立地、随机在分配到可利用的单位中去,每个个体占空 间任何一点的概率是相等的,并且任何一个个体的存在决不影响其他个体的分布。适合于随机公布的理论概率 如潘松分布型。 其中,Pr:样方中出现r个体的概率(r=0、1、2…n); m:样方中个体平均数。 聚集分布型 种群内个体的分布很少呈随机或均匀性,而大多是聚集性。呈聚集分布的种群,样本平 均数显著小于方差。通常由若干个体组成一定的个体群,最后形成各种不同的类型。适于描述聚集公布的理论 概率型很多。昆虫种群中常见负二项分布型和核心分布型。 负二项分布型 种群内个体分布疏密相嵌,很不均匀。本分布由算术平均数μ和Κ指数决定。理论 概率为: 奈曼分布型 种群内个体形成无数大小相似的核心(个体群)。在核心中的个体数量稠密,呈潘松 公布。在核心与核心之间的个体数量十分稀疏。若将每个核心看作一个单位,则众核心在总体中呈潘松分布。 因此,奈曼分布是潘松公布的特例,是潘松---潘松分布。分布的理论概率为: P0=e-m1(1-e-m2) (r=0) (r>0) 式中,m1=(n+1)x/m2,相当于抽样单位内平均集团数; m2=(n+2)(s2-x)/2x,相当于集团内平均个体数; n=0、1、2、…∞,为参数,n=0时为奈曼A型,昆虫中常见。 (二)聚集强度的测定 学习测量昆虫种群空间聚集程度的基本原理及方法。 由于种群内的每个个体都是不断变化的有机体,它们在任一瞬间的行为习性信赖于种群的遗传结构,以及 若干生物和非生物环境因子的影响,任何一个种群作为一个整体而言,总要因繁殖与死亡、迁进与迁出比例的 变化而产生数量的波动,可以从种群的空间格局中筛选出这样一种可测定、与分布等价的指标,而与种群个体
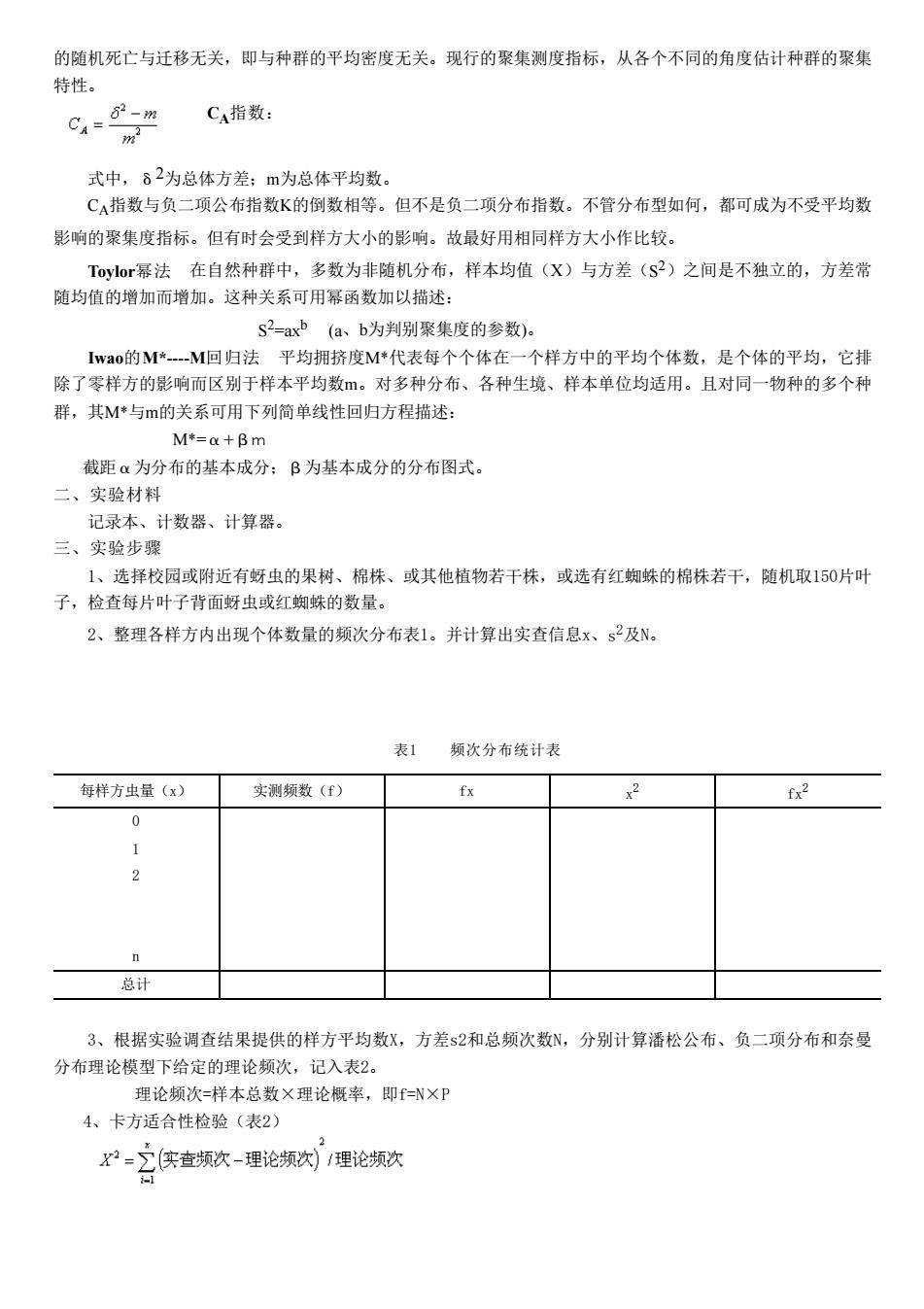
的随机死亡与迁移无关,即与种群的平均密度无关。现行的聚集测度指标,从各个不同的角度估计种群的聚集 特性。 C=-m CA指数: 式中,82为总体方差:m为总体平均数。 CA指数与负二项公布指数K的倒数相等。但不是负二项分布指数。不管分布型如何,都可成为不受平均数 影响的聚集度指标。但有时会受到样方大小的影响。故最好用相同样方大小作比较。 Toylor幂法在自然种群中,多数为非随机分布,样本均值(X)与方差(S2)之间是不独立的,方差常 随均值的增加而增加。这种关系可用幂函数加以描述: s2=axb(a、b为判别聚集度的参数)。 Iwao的M*-M回归法平均拥挤度M*代表每个个体在一个样方中的平均个体数,是个体的平均,它排 除了零样方的影响而区别于样本平均数。对多种分布、各种生境、样本单位均适用。且对同一物种的多个种 群,其M*与m的关系可用下列简单线性回归方程描述: M*=a+Bm 截距α为分布的基本成分:B为基本成分的分布图式。 二、实验材料 记录本、计数器、计算器。 三、实验步骤 1、选择校园或附近有蚜虫的果树、棉株、或其他植物若千株,或选有红蜘蛛的棉株若干,随机取150片叶 子,检查每片叶子背面蚜虫或红蜘蛛的数量。 2、整理各样方内出现个体数量的频次分布表1。并计算出实查信息x、s2及N。 表1 频次分布统计表 每样方虫量(x) 实测频数(f) fx x2 fx2 0 1 2 n 总计 3、根据实验调查结果提供的样方平均数X,方差s2和总频次数N,分别计算潘松公布、负二项分布和奈曼 分布理论模型下给定的理论频次,记入表2。 理论频次=样本总数×理论概率,即f=N×P 4、卡方适合性检验(表2) X2=丁实查频次-理论频次)/理论频次 -1
的随机死亡与迁移无关,即与种群的平均密度无关。现行的聚集测度指标,从各个不同的角度估计种群的聚集 特性。 CA指数: 式中,δ2为总体方差;m为总体平均数。 CA指数与负二项公布指数K的倒数相等。但不是负二项分布指数。不管分布型如何,都可成为不受平均数 影响的聚集度指标。但有时会受到样方大小的影响。故最好用相同样方大小作比较。 Toylor幂法 在自然种群中,多数为非随机分布,样本均值(X)与方差(S 2)之间是不独立的,方差常 随均值的增加而增加。这种关系可用幂函数加以描述: S 2=axb (a、b为判别聚集度的参数)。 Iwao的M*----M回归法 平均拥挤度M*代表每个个体在一个样方中的平均个体数,是个体的平均,它排 除了零样方的影响而区别于样本平均数m。对多种分布、各种生境、样本单位均适用。且对同一物种的多个种 群,其M*与m的关系可用下列简单线性回归方程描述: M*=α+βm 截距α为分布的基本成分;β为基本成分的分布图式。 二、实验材料 记录本、计数器、计算器。 三、实验步骤 1、选择校园或附近有蚜虫的果树、棉株、或其他植物若干株,或选有红蜘蛛的棉株若干,随机取150片叶 子,检查每片叶子背面蚜虫或红蜘蛛的数量。 2、整理各样方内出现个体数量的频次分布表1。并计算出实查信息x、s 2及N。 表1 频次分布统计表 每样方虫量(x) 实测频数(f) fx x 2 fx2 0 1 2 n 总计 3、根据实验调查结果提供的样方平均数X,方差s2和总频次数N,分别计算潘松公布、负二项分布和奈曼 分布理论模型下给定的理论频次,记入表2。 理论频次=样本总数×理论概率,即f=N×P 4、卡方适合性检验(表2)

x2检验在查x2表时的自由度潘松分布为(n-2),负二项分布为(-3),奈曼分布为(n-3)。凡算得的 X2累计值大于自由度下P=0.05时x2值,则其P0.05时,则表示实测频次分布与理论频次分布差异不显著,即可认为服 从该理论分布型。 表2理论频次计算及X之检验表 每样方虫量 实测频次 理论频次(2) 卡方(X2)值 (X) (f) 潘松 负二项 奈曼 潘松 负二项 奈曼 0 2 总计 自由度 概率 适合程度 5、聚集强度指数的计算 1)CA指数的计算与分析 C4=2-m 可用$2、X估计,则: CA=(S2-X)/x2 计算各组的CA值,并以下列规则判别: C=1时,个体为泊松分布: C>1时,个体为聚集分布: C0,(即a>1),且b=l,则种群在一切密度下都是聚集的,但其聚集强度不因种群的改变而变 化: (3)若1oga>0,(即a>1),且b>l,则种群在一切密度下都有是聚集的,聚集强度随种群密度的升高而 增加: (4)若1oga<0,(即0<a<1),且b<1,则种群密度越高,种群分布越均匀。 *=天+天3)MM回归分析与计算: 平均拥挤度
X 2检验在查X 2表时的自由度潘松分布为(n-2),负二项分布为(n-3),奈曼分布为(n-3)。凡算得的 X 2累计值大于自由度下P=0.05时X 2值,则其P0.05时,则表示实测频次分布与理论频次分布差异不显著,即可认为服 从该理论分布型。 表2 理论频次计算及X 2检验表 每样方虫量 (X) 实测频次 (f) 理论频次(f 2) 卡方(X 2)值 潘松 负二项 奈曼 潘松 负二项 奈曼 0 1 2 ┇ ┇ n 总计 自由度 概率 适合程度 5、聚集强度指数的计算 1)CA指数的计算与分析 可用S 2、X估计,则: CA=(S2-X)/X2 计算各组的CA值,并以下列规则判别: C=1时,个体为泊松分布; C>1时,个体为聚集分布; C0,(即a>1),且b=1,则种群在一切密度下都是聚集的,但其聚集强度不因种群的改变而变 化; (3)若loga>0,(即a>1),且b>1,则种群在一切密度下都有是聚集的,聚集强度随种群密度的升高而 增加; (4)若loga<0,(即0<a<1),且b<1,则种群密度越高,种群分布越均匀。 3) M*---M回归分析与计算: 平均拥挤度

式中,x为M:x*为M*的估计值,K值可用矩法估计,则: *+(-0良 式中,Q为抽样数。 计算各组平均拥挤度M*值,并汇总:再全班统一利用最小二乘法建立x*--x回归式:X*=ā+Bx作为 M*=a+BM的估计式,求出参数a、B,并判别。 a:说明分布的基本成份的分布性质: α>0时,个体间相互吸引,分布的基本成分的个体群。 a=0时,分布的基本成分是单个个体。 a1聚集分布, B0,B=1时, 核心分布、泊松分布-正二项分布 (2)a=0,B>1时, 均为聚集分布 负二项分布 (3)a)0,B>1时 负二项分布 四、作业 1、应用经典的理论频次方法,测定蚜虫的分布型。 2、应用三种聚集强度指标计算分析调查结果,判别蚜虫的聚集性和分布概率型。 3、计算并检验调查结果,比较各指数的应用范围
式中,x为M;x*为M*的估计值,K值可用矩法估计,则: 式中,Q为抽样数。 计算各组平均拥挤度M*值,并汇总;再全班统一利用最小二乘法建立x*--x回归式:X*=α+βx作为 M*=α+βM的估计式,求出参数α、β,并判别。 α:说明分布的基本成份的分布性质: α>0时,个体间相互吸引,分布的基本成分的个体群。 α=0时,分布的基本成分是单个个体。 α1聚集分布, β0,β=1时, 核心分布、泊松分布-正二项分布 (2)α=0,β>1时, 均为聚集分布 负二项分布 (3)α>0,β>1时 负二项分布 四、作业 1、应用经典的理论频次方法,测定蚜虫的分布型。 2、应用三种聚集强度指标计算分析调查结果,判别蚜虫的聚集性和分布概率型。 3、计算并检验调查结果,比较各指数的应用范围