
第11卷第3期 智能系统学报 Vol.11 No.3 2016年6月 CAAI Transactions on Intelligent Systems Jun.2016 D0I:10.11992/is.2016030 网s络出版地址:http:/www.cnki.net/kcms/detail/23.1538.TP.20160513.0918.010.html 个体最优共享GEP算法及其气象降水数据预测建模 彭昱忠2,元昌安,李洁,许明涛,陈冰廉 (1.广西师范学院计算机与信息工程学院,广西南宁5300212.广西师范学院北部湾环境演变与资源利用教育 部重点实验室,广西南宁530001:3.广西科技师范学院数计系,广西柳州545004) 摘要:针对基因表达式编程算法存在进化后期收敛慢且容易陷入局部最优而降低其数据建模的性能问题,和降水 量因受诸多自然因素相互影响而难以准确地建模与预测的问题,提出了一种改进的基因表达式编程算法。该算法 具有染色体最优状态记忆功能,在进化过程中可以按条件学习自身的历史经验知识,以加强局部搜索能力和促进收 敛,同时尽量控制个体的趋同化而保持种群的多样性。3组不同区域和不同类型的真实降水数据集的实验验证了其 可以改善传统GEP算法后期收敛慢的问题,寻优能力更强,降水数据拟合和预测效果均显著优于传统GEP算法,BP 神经网络和NAR神经网络等算法。 关键词:基因表达式编程:经验共享:时间序列:气象建模:降水预测:演化计算:演化建模 中图分类号:TP391文献标志码:A文章编号:1673-4785(2016)03-0401-09 中文引用格式:彭昱忠,元昌安,李洁,等.个体最优共享GP算法及其气象降水数据预测建模[J].智能系统学报,2016,11(3): 401-409. 英文引用格式:PENG Yuzhong,YUAN Changan,LI Jie,etal.Individual optimal sharing GEP algorithm and its application in forecast modeling of meteorological precipitation[J].CAAI transactions on intelligent systems,2016,11(3):401-409. Individual optimal sharing GEP algorithm and its application in forecast modeling of meteorological precipitation PENG Yuzhong'2,YUAN Changan',LI Jie',XU Mingtao',CHEN Binglian' (1.College of Computer Information Engineering,Guangxi Normal University,Nanning 530023,China;2.Key Lab of Beibu Gulf Environment Change and Resource Use of ministry of Education,Guangxi Normal University,Nanning 530001,China;3.Department of Mathematics and computer science,Guangxi Science and Technology University,Liuzhou 545004,China) Abstract:Gene expression programming (GEP)is characterized by slow convergence and ease of falling into a lo- cal optimum in the later stages of its evolution.Many methods are difficult to model and use to accurately forecast precipitation because of the simultaneous influence of many natural factors.In this paper,we propose an improved GEP algorithm,which has an optimal state memory function,can learn from historical experience in the process of evolution to strengthen the local search ability,and can thus promote convergence and,at the same time,control the convergence of individuals and maintain the diversity of the population.The experimental results of three groups from different regions and different actual precipitation data sets show that the proposed algorithm can improve the slow convergence problem of the traditional GEP algorithm and has better search ability.Experimental results also show that the proposed algorithm's ability to fit and forecast precipitation data is significantly better than that of tra- ditional GEP algorithm,as well as the BP and NAR neural network algorithms. Keywords:gene expression programming;experience sharing;time series;meteorology modeling;precipitation forecasting;evolutionary computation;evolution modeling 大气系统是个极为复杂的动态巨系统,具有高 维性、多尺度性、复杂性、开放性、混沌性、非平稳性、 收稿日期:2016-03-18.网络出版日期:2016-05-13. 不确定性和动态性等特点。传统上,被主要用于建 基金项目:国家自然科学基金项目(61562008、41575051):广西科学研 立预测模型的常规统计方法难以精确描述大气系统 究与技术开发计划项目(15980191)、广西高校科学技术研 究重点项目(ZD2014083). 的复杂关系,因而预测质量较低。近年来,利用先进 通信作者:李洁.E-mail:lie980522@163.com
第 11 卷第 3 期 智 能 系 统 学 报 Vol.11 №.3 2016 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2016 DOI:10.11992 / tis.2016030 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20160513.0918.010.html 个体最优共享 GEP 算法及其气象降水数据预测建模 彭昱忠1,2 ,元昌安1 ,李洁3 ,许明涛1 ,陈冰廉1 (1.广西师范学院 计算机与信息工程学院,广西 南宁 530021; 2. 广西师范学院 北部湾环境演变与资源利用教育 部重点实验室,广西 南宁 530001; 3.广西科技师范学院 数计系,广西 柳州 545004) 摘 要:针对基因表达式编程算法存在进化后期收敛慢且容易陷入局部最优而降低其数据建模的性能问题,和降水 量因受诸多自然因素相互影响而难以准确地建模与预测的问题,提出了一种改进的基因表达式编程算法。 该算法 具有染色体最优状态记忆功能,在进化过程中可以按条件学习自身的历史经验知识,以加强局部搜索能力和促进收 敛,同时尽量控制个体的趋同化而保持种群的多样性。 3 组不同区域和不同类型的真实降水数据集的实验验证了其 可以改善传统 GEP 算法后期收敛慢的问题,寻优能力更强,降水数据拟合和预测效果均显著优于传统 GEP 算法、BP 神经网络和 NAR 神经网络等算法。 关键词:基因表达式编程;经验共享;时间序列;气象建模;降水预测;演化计算;演化建模 中图分类号:TP391 文献标志码:A 文章编号:1673⁃4785(2016)03⁃0401⁃09 中文引用格式:彭昱忠,元昌安,李洁,等.个体最优共享 GEP 算法及其气象降水数据预测建模[ J]. 智能系统学报, 2016, 11( 3): 401⁃409. 英文引用格式:PENG Yuzhong, YUAN Changan, LI Jie, et al. Individual optimal sharing GEP algorithm and its application in forecast modeling of meteorological precipitation[J]. CAAI transactions on intelligent systems, 2016,11(3): 401⁃409. Individual optimal sharing GEP algorithm and its application in forecast modeling of meteorological precipitation PENG Yuzhong 1,2 , YUAN Changan 1 , LI Jie 3 , XU Mingtao 1 , CHEN Binglian 1 (1. College of Computer & Information Engineering, Guangxi Normal University, Nanning 530023, China; 2. Key Lab of Beibu Gulf Environment Change and Resource Use of ministry of Education, Guangxi Normal University, Nanning 530001, China; 3.Department of Mathematics and computer science, Guangxi Science and Technology University, Liuzhou 545004,China) Abstract:Gene expression programming (GEP) is characterized by slow convergence and ease of falling into a lo⁃ cal optimum in the later stages of its evolution. Many methods are difficult to model and use to accurately forecast precipitation because of the simultaneous influence of many natural factors. In this paper, we propose an improved GEP algorithm, which has an optimal state memory function, can learn from historical experience in the process of evolution to strengthen the local search ability, and can thus promote convergence and, at the same time, control the convergence of individuals and maintain the diversity of the population. The experimental results of three groups from different regions and different actual precipitation data sets show that the proposed algorithm can improve the slow convergence problem of the traditional GEP algorithm and has better search ability. Experimental results also show that the proposed algorithm's ability to fit and forecast precipitation data is significantly better than that of tra⁃ ditional GEP algorithm, as well as the BP and NAR neural network algorithms. Keywords:gene expression programming; experience sharing; time series; meteorology modeling; precipitation forecasting; evolutionary computation; evolution modeling 收稿日期:2016⁃03⁃18. 网络出版日期:2016⁃05⁃13. 基金项目:国家自然科学基金项目( 61562008、41575051);广西科学研 究与技术开发计划项目( 1598019⁃1)、广西高校科学技术研 究重点项目(ZD2014083). 通信作者:李洁. E⁃mail:lijie980522@ 163.com. 大气系统是个极为复杂的动态巨系统,具有高 维性、多尺度性、复杂性、开放性、混沌性、非平稳性、 不确定性和动态性等特点。 传统上,被主要用于建 立预测模型的常规统计方法难以精确描述大气系统 的复杂关系,因而预测质量较低。 近年来,利用先进

·402. 智能系统学报 第11卷 的智能计算和数据挖掘方法,构建和改进气象预测 的参数个数)。GEP的基因有基因型和表现型两种 的方法与模型,帮助对未知气象规律的认识和提高 表现形式,因此,每个基因对应一个K表达式(表示 气象预测能力,已逐渐成为气象、数学和计算机领域 基因编码的有效部分)和一棵表达式树。其中,K表 专家和学者们关注的热点,多个相关国际会议上设 达式就是基因型,表达式树就是表现型,两者之间可 置了相关的专题和Workshop)。 以相互转化。如,以√x+xy为例来说明GEP的染 近年来,被众多学者应用到气象或灾害天气的 色体编码方法,这个式子可以用基因:Q+**xxxy2 预测中的神经网络方法等智能计算方法[2]可有效 表示,该基因对应的表达式树如图1所示。 描述气象要素间的复杂关系,但这些算法结构和参 数难选定、计算量过大而不利于大容量样本学习等 自身固有的缺陷,严重降低了其应用和发展的效果。 基于大量历史数据进行气象数据挖掘与建模预测是 个较有发展前途的研究和应用方向,已吸引了不少 的学者进行研究1)。但用传统数据挖掘算法难 于避免由于气象数据的多层次特性造成的难以建立 准确模型的缺陷,从而降低了气象预报的精度。 基因表达式编程(gene expression programming, 图1表达式树 GEP)是借鉴生物遗传的基因表达规律,融合了遗传 Fig.1 The expression tree 算法(GA)和遗传编程(GP)的优点发展起来的进化 GEP的若干个染色体构成种群,然后通过个体 计算家族中的革命性新成员。GEP不但可以轻易 在种群中不断进化而逐渐逼近问题的解。GEP作 地进化多种形态的复杂计算程序,构建稳健而精确、 可解释性较强的计算模型,而且具有很强的问题表 为进化计算家族的成员,其算法的进化过程类似于 达能力、知识发现能力和寻优能力,可有效进行数据 GA和GP。具体算法过程描述见文献[14]。 挖掘,发现公式、规则或规律,模型的最优化等。 2个体最优共享GEP算法 相关研究表明,GEP能有效克服很多智能计算方法 GEP存在进化后期寻优缓慢且易陷局部最优 和传统数据挖掘与知识发现的不足,求解很多复杂 的问题,已经引起了一些学者的注意,并试图通过控 问题表现更出色,可望是一个具有发展前途的气象 数据建模与预测研究方向。但GEP自身还存在复 制和调节种群结构s1切]、改进和调节遗传操 杂问题建模的进化后期寻优缓慢且易陷入局部最优 作1-0】,改变个体编码结构[2]等方式改进GEP算 的缺陷。针对此问题,本文提出了个体最优共享的 法,并取得了一定的成效。本文借鉴粒子群算法进 化过程中粒子历史最优信息共享的机制促进粒子群 改进GEP算法(best individual shared-based gene ex- 算法快速收敛的思想,对GEP进行了改进,提出了 pression programming,BIS_GEP),能更好地解决后期 寻优缓慢和局部最优问题,并通过3组真实降水案 个体最优共享GEP(BIS_GEP)。 2.1 BIS GEP的基本思想 例的实验验证了其性能。 PS0是模拟鸟群寻找食物过程的动作迁徙和群 1 GEP基本原理概述 聚行为的一种启发式随机搜索的演化计算方法。 GEP和PS0同属仿生演化算法,本质上都是基于自 GEP的个体(染色体)由单个或者多个基因组 然性质和行为规则随机搜索解空间寻求问题最优 成,基因之间可以用函数符号连接起来。GEP的基 因用长度固定的符串来表示,由头和尾两部分组成。 解。PS0具有良好的个体最优信息共享和全局最优 信息共享与更新机制,能充分利用个体自身经验和 其中头部既可以包含函数符号也可以包含终结符 群体经验来调整自身的状态,使其位置与速度的更 号,而尾部则只能包含终结符号。基因中的函数符 新具有很好的导向性。故对局部空间最优解的逼近 号是问题求解过程中的所需要的数学函数和逻辑运 能力很强,收敛速度快,但同时这种导向性也导致其 算等所有候选的函数和操作符的表示,终结符通常 是问题求解过程所需要的候选变量或常量,其中尾 全局搜索能力不强2。相对PS0算法,GEP的各 种遗传操作都缺乏明确的导向性,因此其对空间最 部长度t和头部长度h之间应该满足式(1)的关系: 优解的逼近能力不强,但这同时让GEP算法对空间 t=h×(n-1)+1 (1) 最优解的搜索能力变得很强。经典的社会学理论认 式中n代表函数符集中的最大操目数(可能的最多
的智能计算和数据挖掘方法,构建和改进气象预测 的方法与模型,帮助对未知气象规律的认识和提高 气象预测能力,已逐渐成为气象、数学和计算机领域 专家和学者们关注的热点,多个相关国际会议上设 置了相关的专题和 Workshop [1] 。 近年来,被众多学者应用到气象或灾害天气的 预测中的神经网络方法等智能计算方法[2⁃9] 可有效 描述气象要素间的复杂关系,但这些算法结构和参 数难选定、计算量过大而不利于大容量样本学习等 自身固有的缺陷,严重降低了其应用和发展的效果。 基于大量历史数据进行气象数据挖掘与建模预测是 个较有发展前途的研究和应用方向,已吸引了不少 的学者进行研究[10⁃13] 。 但用传统数据挖掘算法难 于避免由于气象数据的多层次特性造成的难以建立 准确模型的缺陷,从而降低了气象预报的精度。 基因表达式编程( gene expression programming, GEP)是借鉴生物遗传的基因表达规律,融合了遗传 算法(GA)和遗传编程(GP)的优点发展起来的进化 计算家族中的革命性新成员。 GEP 不但可以轻易 地进化多种形态的复杂计算程序,构建稳健而精确、 可解释性较强的计算模型,而且具有很强的问题表 达能力、知识发现能力和寻优能力,可有效进行数据 挖掘,发现公式、规则或规律,模型的最优化等[14] 。 相关研究表明,GEP 能有效克服很多智能计算方法 和传统数据挖掘与知识发现的不足,求解很多复杂 问题表现更出色,可望是一个具有发展前途的气象 数据建模与预测研究方向。 但 GEP 自身还存在复 杂问题建模的进化后期寻优缓慢且易陷入局部最优 的缺陷。 针对此问题,本文提出了个体最优共享的 改进 GEP 算法(best individual shared⁃based gene ex⁃ pression programming,BIS_GEP),能更好地解决后期 寻优缓慢和局部最优问题,并通过 3 组真实降水案 例的实验验证了其性能。 1 GEP 基本原理概述 GEP 的个体(染色体)由单个或者多个基因组 成,基因之间可以用函数符号连接起来。 GEP 的基 因用长度固定的符串来表示,由头和尾两部分组成。 其中头部既可以包含函数符号也可以包含终结符 号,而尾部则只能包含终结符号。 基因中的函数符 号是问题求解过程中的所需要的数学函数和逻辑运 算等所有候选的函数和操作符的表示,终结符通常 是问题求解过程所需要的候选变量或常量,其中尾 部长度 t 和头部长度 h 之间应该满足式(1)的关系: t = h × (n - 1) + 1 (1) 式中 n 代表函数符集中的最大操目数(可能的最多 的参数个数)。 GEP 的基因有基因型和表现型两种 表现形式,因此,每个基因对应一个 K 表达式(表示 基因编码的有效部分)和一棵表达式树。 其中,K 表 达式就是基因型,表达式树就是表现型,两者之间可 以相互转化。 如,以 x 2+xy 为例来说明 GEP 的染 色体编码方法,这个式子可以用基因:Q+∗∗xxxyz 表示,该基因对应的表达式树如图 1 所示。 图 1 表达式树 Fig.1 The expression tree GEP 的若干个染色体构成种群,然后通过个体 在种群中不断进化而逐渐逼近问题的解。 GEP 作 为进化计算家族的成员,其算法的进化过程类似于 GA 和 GP。 具体算法过程描述见文献[14]。 2 个体最优共享 GEP 算法 GEP 存在进化后期寻优缓慢且易陷局部最优 的问题,已经引起了一些学者的注意,并试图通过控 制和 调 节 种 群 结 构[15⁃17] 、 改 进 和 调 节 遗 传 操 作[18⁃20] 、改变个体编码结构[21⁃22]等方式改进 GEP 算 法,并取得了一定的成效。 本文借鉴粒子群算法进 化过程中粒子历史最优信息共享的机制促进粒子群 算法快速收敛的思想,对 GEP 进行了改进,提出了 个体最优共享 GEP(BIS_GEP)。 2.1 BIS_GEP 的基本思想 PSO 是模拟鸟群寻找食物过程的动作迁徙和群 聚行为的一种启发式随机搜索的演化计算方法。 GEP 和 PSO 同属仿生演化算法,本质上都是基于自 然性质和行为规则随机搜索解空间寻求问题最优 解。 PSO 具有良好的个体最优信息共享和全局最优 信息共享与更新机制,能充分利用个体自身经验和 群体经验来调整自身的状态,使其位置与速度的更 新具有很好的导向性。 故对局部空间最优解的逼近 能力很强,收敛速度快,但同时这种导向性也导致其 全局搜索能力不强[23] 。 相对 PSO 算法,GEP 的各 种遗传操作都缺乏明确的导向性,因此其对空间最 优解的逼近能力不强,但这同时让 GEP 算法对空间 最优解的搜索能力变得很强。 经典的社会学理论认 ·402· 智 能 系 统 学 报 第 11 卷

第3期 彭昱忠,等:个体最优共享GEP算法及其气象降水数据预测建模 ·403 为,人类在决策过程时,个体学习和文化传递这两类 个体的趋同化,尽量保持种群的多样性,让种群向全 信息(即自身的经验和其他人的经验)具有极为关 局最优移动。为了实现此目标,需要抑制个体对历 键的作用。对比分析PSO和GEP,GEP在对以往搜 史最佳状态的学习程度,避免所有个体均无节制地 索经验的学习利用上相对较差,因为GEP算法的个 学习历史最佳状态而致个体快速趋同降低了种群的 体并不像PS0那样具有记忆能力,以前的知识随着 多样性。为此BIS_GEP将种群划分为两个子种群, 种群的改变被破坏。本文认为这是导致GEP后期 其中一个子种群的染色体在交叉时按一定的概率与 搜索慢且易陷局部最优的重要原因。BIS_GEP算 自身历史最优状态进行交叉操作,不断迭代进化,并 法正是借鉴了社会学理论和PS0的个体经验学习 每隔给定的step代通过轮盘赌选择二分之一的个 优势而设计的,旨在尽可能保持GEP自身的全局搜 体移到另一个子种群中:而另一个子种群则按常规 索优势,增强局部搜索能力和加快收敛速度。因此, 的GEP算法过程进行进化,并每隔给定的step代排 在BIS_GEP设计上,为每个染色体设计了最优状态 挤出适应度最差的二分之一个体移到另一子种群, 记忆功能,让个体在进化过程中可以充分学习自身 同时接收选自另一子种群的个体,在迭代终止条件 的历史经验知识,以加强局部搜索和促进收敛。同 达到时该子种群中的最优染色体即为本次寻优过程 时还需控制因过度的个体学习历史经验而引起种群 中的最优解。BIS_GEP算法基本思想如图2所示。 个体历史最优 GEP染色 状态参与交叉 优秀GEP 体子群1 轮盘 种群1 轮盘 GEP种群 排挤 赌 择移 移群 移 GEP染色 常规交叉群 优秀GEP 、群 最优GEP 体子群2 种群2 染色体 初始状态i 状态i+step 状态i+n×step 最终态j 图2BIS_GEP算法基本思想示意图 Fig.2 The basic algorithm idea of BIS_GEP 2.2BIS_GEP算法过程 BIS_GEP在经典GEP的基础上,将种群划分为 根据上述主要思想,设计了如图3所描述的 两个等规模的子种群分别按精英保留策略进行进 BIS_GEP算法流程图。 化,然后每隔若干代即对两个相对独立的子种群进 初始化参数和种群 行个体选择与交换,其中的一子种群按常规的GEP 遗传操作进化(详见文献[14]),另一子种群则在常 种群二等分割 规遗传操作的基础上增加按概率进行自身历史最佳 子种群1 子种群2 状态(该染色体的适应度值最高时的编码表示)交 叉的操作。选择个体的标准是按常规的GEP遗传 常规遗 是否达到终止条件 传进化 操作进化的子种群采用轮盘赌选择取余法选择个体 N 个体最优 常规遗 算法结束 (选取没被轮盘赌选择法选中而排挤出的那一半), 状态交叉 传进化 另一种群则按轮盘赌选择法进行需移群交换的个体 选择。该算法通过划分子种群分别进行常规进化和 N 一迭代次数是否ep倍 N 外加个体历史最优交叉进化,然后隔若干代选择个 体移群交换,既可通过充分学习个体自身经验加强 轮盘赌选 轮盘赌排 出二分 移群交换 挤出二分 局部搜索和促进收敛,也能保持种群的多样性,从而 的个体 的个体 改善算法的寻优效果。BIS_GEP算法描述如下: 输入训练数据集T,种群大小Gs、函数集、终 图3BIS_GEP算法流程图 结符集、基因头长HL、移群步数step、各遗传操作率 Fig.3 The algorithm procedure of BIS_GEP 和终止条件等算法的基本参数
为,人类在决策过程时,个体学习和文化传递这两类 信息(即自身的经验和其他人的经验)具有极为关 键的作用。 对比分析 PSO 和 GEP,GEP 在对以往搜 索经验的学习利用上相对较差,因为 GEP 算法的个 体并不像 PSO 那样具有记忆能力,以前的知识随着 种群的改变被破坏。 本文认为这是导致 GEP 后期 搜索慢且易陷局部最优的重要原因。 BIS_GEP 算 法正是借鉴了社会学理论和 PSO 的个体经验学习 优势而设计的,旨在尽可能保持 GEP 自身的全局搜 索优势,增强局部搜索能力和加快收敛速度。 因此, 在 BIS_GEP 设计上,为每个染色体设计了最优状态 记忆功能,让个体在进化过程中可以充分学习自身 的历史经验知识,以加强局部搜索和促进收敛。 同 时还需控制因过度的个体学习历史经验而引起种群 个体的趋同化,尽量保持种群的多样性,让种群向全 局最优移动。 为了实现此目标,需要抑制个体对历 史最佳状态的学习程度,避免所有个体均无节制地 学习历史最佳状态而致个体快速趋同降低了种群的 多样性。 为此 BIS_GEP 将种群划分为两个子种群, 其中一个子种群的染色体在交叉时按一定的概率与 自身历史最优状态进行交叉操作,不断迭代进化,并 每隔给定的 step 代通过轮盘赌选择二分之一的个 体移到另一个子种群中;而另一个子种群则按常规 的 GEP 算法过程进行进化,并每隔给定的 step 代排 挤出适应度最差的二分之一个体移到另一子种群, 同时接收选自另一子种群的个体,在迭代终止条件 达到时该子种群中的最优染色体即为本次寻优过程 中的最优解。 BIS_GEP 算法基本思想如图 2 所示。 图 2 BIS_GEP 算法基本思想示意图 Fig.2 The basic algorithm idea of BIS_GEP 2.2 BIS_GEP 算法过程 根据上述主要思想,设计了如图 3 所描述的 BIS_GEP 算法流程图。 图 3 BIS_GEP 算法流程图 Fig.3 The algorithm procedure of BIS_GEP BIS_GEP 在经典 GEP 的基础上,将种群划分为 两个等规模的子种群分别按精英保留策略进行进 化,然后每隔若干代即对两个相对独立的子种群进 行个体选择与交换,其中的一子种群按常规的 GEP 遗传操作进化(详见文献[14]),另一子种群则在常 规遗传操作的基础上增加按概率进行自身历史最佳 状态(该染色体的适应度值最高时的编码表示) 交 叉的操作。 选择个体的标准是按常规的 GEP 遗传 操作进化的子种群采用轮盘赌选择取余法选择个体 (选取没被轮盘赌选择法选中而排挤出的那一半), 另一种群则按轮盘赌选择法进行需移群交换的个体 选择。 该算法通过划分子种群分别进行常规进化和 外加个体历史最优交叉进化,然后隔若干代选择个 体移群交换,既可通过充分学习个体自身经验加强 局部搜索和促进收敛,也能保持种群的多样性,从而 改善算法的寻优效果。 BIS_GEP 算法描述如下: 输入 训练数据集 T,种群大小 Gs、函数集、终 结符集、基因头长 HL、移群步数 step、各遗传操作率 和终止条件等算法的基本参数 第 3 期 彭昱忠,等:个体最优共享 GEP 算法及其气象降水数据预测建模 ·403·

·404 智能系统学报 第11卷 输出最优函数模型∫及其适应度 用菲波那契(Fibonacci)数列作为时不变线性滤波器 1)生成初始种群: 对输人的气象数据进行滤波抑制高频噪声,然后再 2)种群二等分割为G1和G2: 进行函数挖掘与建模预测。记待测时间序列为 3)种群进化过程: {x(t),t=1,2,…,N},根据Fibonacci数列性质,取 While(终止条件≠true) 线性滤波器H满足式(2)[2: G1.CommGeneticOperatelnProbability ();/ (Fib(Ui)/totalWeight,j≤K∈ h;= ,(2) 子种群1进行常规遗传操作 0,j>K∈N G1.divHistoryBestCrossInProbability(); totalWeight Fib(1)Fib(2)+.+Fib(K) /子种群1进行个体最优状态交叉 (3) G1.CaculateFitness(); 式中:K一般取值为滑动窗口大小减1,则该时不变 //计算子种群1个体适应度 线性滤波器的输出为 G2.CommGeneticOperateInProbability ();/ Y,=(Fib(I)×X,-k+Fib(2)×X-k+1+…+ 子种群2进行常规遗传操作 Fib(K)xX,)/totalWeight G2.CaculateFitness(); 3.2建模方法 //计算子种群2个体适应度 用GEP进行时间序列的建模和预测通常是将 If(generation Modulo step==0)/如果当前 时间序列建模问题转换成符号回归问题,挖掘出对 进化代数是step的倍数 给定时间序列数据拟合度和对未来预测精度较高的 G1Exchdiv=G1.RoulSelectHalf(); 函数模型,将用此函数模型计算未来可能的值。先 /子种群1进行轮盘赌选出一半的个体待交换 求时间序列X(t)的M阶延迟得到矩阵X,如式(4) G2Exchdiv=G2 -G2.RoulSelectHalf(); 所示,矩阵X中的元素与原序列对应关系为X。= /子种群2进行轮盘赌排挤出一半个体待交换 x+1,然后把矩阵X中的第N-M+1列看作是所求函 G1.Add(G2Exchdiv); 数模型的因变量,其余每一列看作所求函数模型的 /个体移群交换 一个自变量,因而窗口大小为N-M+1,而矩阵X的 G2.Add(G1Exchdiv); 每一行即为一个样本数据,则所求的目标函数模型 End if 可记为x-M=f孔xo,x1,…,x-w)。接下来,GEP根据 G1.SelectNextPopulation(); 输入样本,在给定函数符组成的所有可能函数表达 /选择个体构成下一代 空间中寻找拟合样本数据程度较佳的函数表达式。 G2.SelectNextPopulation(); X2 XN-M+1 X10 …X1,N-M generation++; X2 3 XN-M+2 X2.N-M End while 44 4)输出结果。 XM XM+I Xm XM.N-M 3基于BS_GS的气象降水建模与预测 (4) 3.3案例实验与结果分析 3.1数据预处理 3.3.1实验数据与方案 输入数据的质量对数据挖掘与数据建模有着非 本文分别用北京年降水量(1949-2013年,样本 常重要的影响。气象数据资料在收集过程中受到较 长度65,下文简称“北京降水”)、广西桂平冬季月均 多主观因素(如操作员认知程度等)和客观因素(如 降水量(1951-2013年,样本长度63,下文简称“桂 仪器设备的工作状态、环境因素等)的影响,使得气 平降水”)和UNION CITY早季的6月份降水量 象数据不可避免地包含噪声,直接进行数据挖掘和 (1884-2006年,样本长度123,位于美国新泽西州 预测建模必然会导致结果出现偏差。为了提高模型 东北部,下文简称“UNION降水”)这3个典型的不 的有效性和预测结果的准确性,本文在建模前先利 同区域和类型的降水量作为建模预测对象,检验
输出 最优函数模型 f 及其适应度 1)生成初始种群; 2)种群二等分割为 G1 和 G2; 3)种群进化过程: While (终止条件 ≠ true) G1. CommGeneticOperateInProbability ( ); / / 子种群 1 进行常规遗传操作 G1. divHistoryBestCrossInProbability(); / / 子种群 1 进行个体最优状态交叉 G1. CaculateFitness(); / / 计算子种群 1 个体适应度 G2. CommGeneticOperateInProbability ( ); / / 子种群 2 进行常规遗传操作 G2. CaculateFitness(); / / 计算子种群 2 个体适应度 If (generation Modulo step = = 0) / / 如果当前 进化代数是 step 的倍数 G1Exchdiv =G1. RoulSelectHalf(); / / 子种群 1 进行轮盘赌选出一半的个体待交换 G2Exchdiv =G2 - G2. RoulSelectHalf(); / / 子种群 2 进行轮盘赌排挤出一半个体待交换 G1. Add(G2Exchdiv); / / 个体移群交换 G2. Add(G1Exchdiv); End if G1. SelectNextPopulation(); / / 选择个体构成下一代 G2. SelectNextPopulation(); generation ++; End while 4)输出结果。 3 基于 BIS_GIS 的气象降水建模与预测 3.1 数据预处理 输入数据的质量对数据挖掘与数据建模有着非 常重要的影响。 气象数据资料在收集过程中受到较 多主观因素(如操作员认知程度等)和客观因素(如 仪器设备的工作状态、环境因素等)的影响,使得气 象数据不可避免地包含噪声,直接进行数据挖掘和 预测建模必然会导致结果出现偏差。 为了提高模型 的有效性和预测结果的准确性,本文在建模前先利 用菲波那契(Fibonacci)数列作为时不变线性滤波器 对输入的气象数据进行滤波抑制高频噪声,然后再 进行函数挖掘与建模预测。 记待测时间序列为 {x(t),t = 1,2,…,N},根据 Fibonacci 数列性质,取 线性滤波器 H 满足式(2) [24] : hj = Fib(j) / totalWeight, j ≤ K ∈ N 0, j > K ∈ N { , (2) totalWeight = Fib(1) + Fib(2) + … + Fib(K) (3) 式中:K 一般取值为滑动窗口大小减 1,则该时不变 线性滤波器的输出为 Yt = (Fib(1) × Xt-k + Fib(2) × Xt-k+1 + … + Fib(K) × Xt) / totalWeight 3.2 建模方法 用 GEP 进行时间序列的建模和预测通常是将 时间序列建模问题转换成符号回归问题,挖掘出对 给定时间序列数据拟合度和对未来预测精度较高的 函数模型,将用此函数模型计算未来可能的值。 先 求时间序列 X(t)的 M 阶延迟得到矩阵 X,如式(4) 所示,矩阵 X 中的元素与原序列对应关系为 Xji = xj+1 ,然后把矩阵 X 中的第 N-M+1 列看作是所求函 数模型的因变量,其余每一列看作所求函数模型的 一个自变量,因而窗口大小为 N-M+1,而矩阵 X 的 每一行即为一个样本数据,则所求的目标函数模型 可记为 xN-M = f(x0 ,x1 ,…,xN-M )。 接下来,GEP 根据 输入样本,在给定函数符组成的所有可能函数表达 空间中寻找拟合样本数据程度较佳的函数表达式。 X = x1 x2 … xN-M+1 x2 x3 … xN-M+2 … … … … xM xM+1 … xN é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú ≡ x10 x11 … x1,N-M x20 x21 … x2,N-M … … … … xM0 xM1 … xM,N-M é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú (4) 3.3 案例实验与结果分析 3.3.1 实验数据与方案 本文分别用北京年降水量(1949-2013 年,样本 长度 65,下文简称“北京降水”)、广西桂平冬季月均 降水量(1951-2013 年,样本长度 63,下文简称“桂 平降水”) 和 UNION CITY 旱季的 6 月份降水量 (1884-2006 年,样本长度 123,位于美国新泽西州 东北部,下文简称“UNION 降水”)这 3 个典型的不 同区域和类型的降水量作为建模预测对象,检验 ·404· 智 能 系 统 学 报 第 11 卷

第3期 彭昱忠,等:个体最优共享GEP算法及其气象降水数据预测建模 ·405· BIS_GEP预测模型实用效果。这3组降水案例数据 valRatio=15/100,testRatio=15/100 的值分布如图4所示。其中,北京年降水数据逐年 表1实验中的GEP及改进算法的主要参数 变化差异较大,突变点多而尖锐,最大值是最小值的 Tablel Main parameters of GEPs on experiments 6倍之多,数据的分布曲线相当复杂:桂平降水数据 参数名 原始GEP ADF_GEP BIS GEP 尽管最大值是最小值的6倍之多,但其逐年变化曲 最大进化代数 2000 线比北京年降水数据逐年变化曲线平滑,突变点少: UNION CITY降水数据波动幅度较小,数据的分布 群体规模 100 曲线相对平稳。 函数集 +,,X,/,sin,cos,exp,log,sqrt 1.42 终结符集 a,b,c,d,e,f 1.22 1.02 头长/同源基因头长 8/无 8/3 8/无 0.82 桂平冬季月均降水 基因数/同源基因数 5/3 0.62 0.42 北京年降水 交叉率(单点、两点一致) 0.2 0.2 0.2 unioneity6月份降水 0.22 变异率 0.25 0.25 0.25 0.02 年份 基因迁移率(IS和RIS一致) 0.1 0.1 0.1 图4实验案例数据的值分布 适应度函数 MREF Fig.4 The value distribution of experimental data 3.3.2收敛性验证实验与结果分析 本文实验验证的主要方案是,先分别用原始 本文首先对BIS_GEP算法的改进性能进行验 GEP算法、GEP改进算法ADF_GEP和本文所提 证。分别用3种GEP算法对北京降水数据集、桂平 BIS_GEP算法对3个降水案例数据集进行拟合建 降水数据集和UNION CITY降水数据集进行自动建 模,观察和比较3种GEP算法的收敛过程,验证BIS 模,模型评价函数为平均相对误差。本文为避免因 _GEP收敛性能改善效果。然后用这3种方法,以 进化过程中的初始几代的适应度与目标值间的差异 及被大气科学领域运用较多的BP和NAR等神经 过大影响收敛过程曲线图展示效果,在画图时均忽 网络建模预测算法分别对3个降水案例数据集进行 略前5代的收敛过程曲线。桂平降水数据集实验的 建模与预测,比较分析所得结果进而验证BIS_GEP 进化过程(见图6)的前期适应度与中后期的差异较 的建模预测性能。 大,本文根据该收敛过程特点将其进化收敛过程图 3组实验均保留序列中最后10%的样本作为测 拆分成5~125代(见图7(a))和125~2000代(见 图7(b))两部分,以便更清晰地展示算法收敛过程 试样本,其余样本为训练样本,采用逐月/年预报形 式预测测试样本的结果。3组实验中所用的各算法 的效果。 的主要参数保持不变,其中,时间延迟系数都取1, 20.0 19.5 原始GEP平均 嵌入维数取5。GEP相关算法的主要参数如表1所 19.0 BIS GEP平均 ADF GEP平均 示,其中的终结符a,b,c,d,e,…分别代表目标函数 18.5 BIS GEP最佳 ADF GEP最佳 18.0 原始GEP最佳 模型中的变量X。,X,…,X--1。本文实验中的 17.5 BP神经网络和NAR神经网络的均用MATLAB中 17.0 16.5 的神经网络相关类构建,隐层数均为20,BP采用的 出周草兵后发会省信玉兰屋里园 其他主要参数如下:传递函数为tansig,训练函数为 进化代数 traingdm,epochs 10 000,Ir =0.000 1,mc=0.5; NAR采用的其他主要参数如下:trainRatio=70/1O0, 图5北京年降水量建模进化收敛过程 Fig onvergence process of precipitation modeling of Beijing
BIS_GEP 预测模型实用效果。 这 3 组降水案例数据 的值分布如图 4 所示。 其中,北京年降水数据逐年 变化差异较大,突变点多而尖锐,最大值是最小值的 6 倍之多,数据的分布曲线相当复杂;桂平降水数据 尽管最大值是最小值的 6 倍之多,但其逐年变化曲 线比北京年降水数据逐年变化曲线平滑,突变点少; UNION CITY 降水数据波动幅度较小,数据的分布 曲线相对平稳。 图 4 实验案例数据的值分布 Fig.4 The value distribution of experimental data 本文实验验证的主要方案是,先分别用原始 GEP 算法、GEP 改进算法 ADF _GEP 和本文所提 BIS_GEP 算法对 3 个降水案例数据集进行拟合建 模,观察和比较 3 种 GEP 算法的收敛过程,验证 BIS _GEP 收敛性能改善效果。 然后用这 3 种方法,以 及被大气科学领域运用较多的 BP 和 NAR 等神经 网络建模预测算法分别对 3 个降水案例数据集进行 建模与预测,比较分析所得结果进而验证 BIS_GEP 的建模预测性能。 3 组实验均保留序列中最后 10%的样本作为测 试样本,其余样本为训练样本,采用逐月/ 年预报形 式预测测试样本的结果。 3 组实验中所用的各算法 的主要参数保持不变,其中,时间延迟系数都取 1, 嵌入维数取 5。 GEP 相关算法的主要参数如表 1 所 示,其中的终结符 a,b,c,d,e,…分别代表目标函数 模型中的变量 X0 , X1 ,…, XN-M-1 。 本文实验中的 BP 神经网络和 NAR 神经网络的均用 MATLAB 中 的神经网络相关类构建,隐层数均为 20,BP 采用的 其他主要参数如下:传递函数为 tansig,训练函数为 traingdm, epochs = 10 000, lr = 0. 000 1, mc = 0. 5; NAR 采用的其他主要参数如下:trainRatio = 70 / 100, valRatio = 15 / 100,testRatio = 15 / 100。 表 1 实验中的 GEP 及改进算法的主要参数 Table1 Main parameters of GEPs on experiments 参数名 原始 GEP ADF_GEP BIS_GEP 最大进化代数 2 000 群体规模 100 函数集 +,-,×,/ , sin, cos, exp, log, sqrt 终结符集 a,b,c,d,e,f 头长/ 同源基因头长 8 / 无 8 / 3 8 / 无 基因数/ 同源基因数 5 5 / 3 5 交叉率(单点、两点一致) 0.2 0.2 0.2 变异率 0.25 0.25 0.25 基因迁移率( IS 和 RIS 一致) 0.1 0.1 0.1 适应度函数 MREF 3.3.2 收敛性验证实验与结果分析 本文首先对 BIS_GEP 算法的改进性能进行验 证。 分别用 3 种 GEP 算法对北京降水数据集、桂平 降水数据集和 UNION CITY 降水数据集进行自动建 模,模型评价函数为平均相对误差。 本文为避免因 进化过程中的初始几代的适应度与目标值间的差异 过大影响收敛过程曲线图展示效果,在画图时均忽 略前 5 代的收敛过程曲线。 桂平降水数据集实验的 进化过程(见图 6)的前期适应度与中后期的差异较 大,本文根据该收敛过程特点将其进化收敛过程图 拆分成 5~125 代(见图 7( a))和 125 ~ 2 000 代(见 图 7(b))两部分,以便更清晰地展示算法收敛过程 的效果。 图 5 北京年降水量建模进化收敛过程 FigC.5onvergence process of precipitation modeling of Beijing 第 3 期 彭昱忠,等:个体最优共享 GEP 算法及其气象降水数据预测建模 ·405·
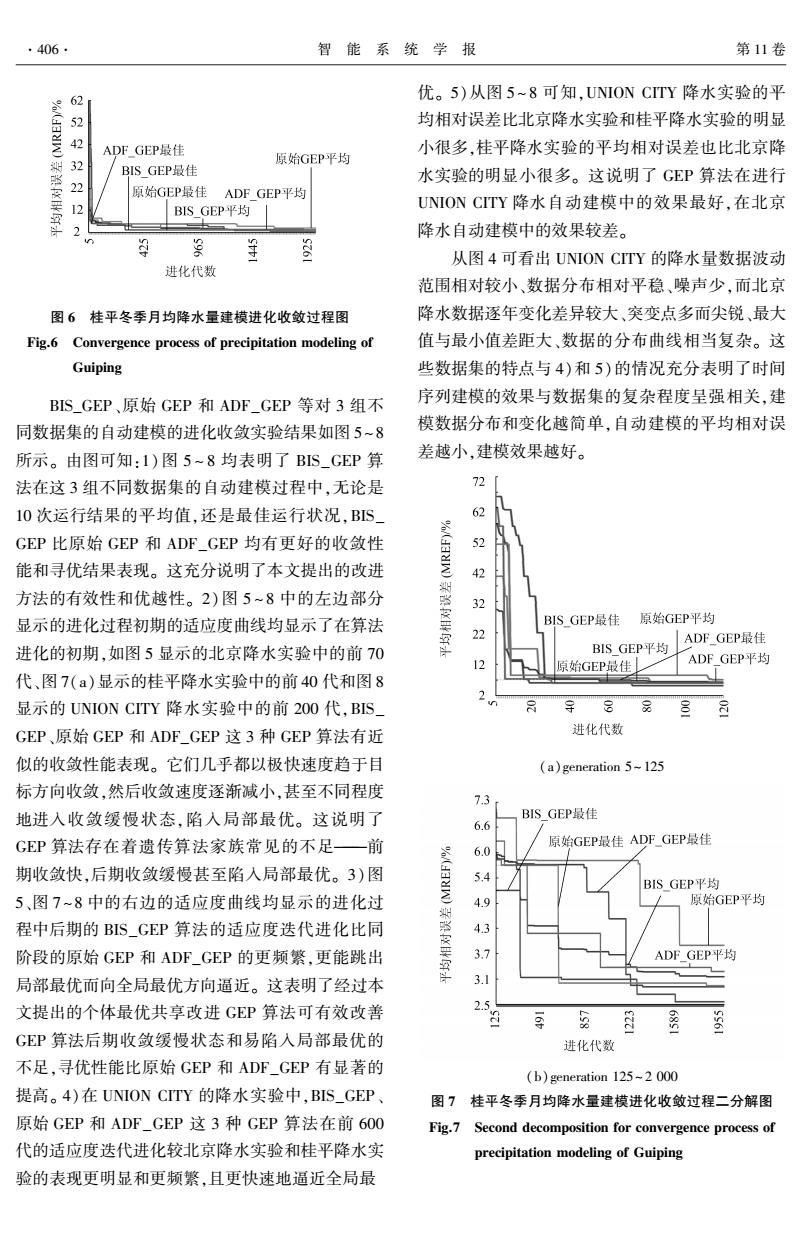
·406· 智能系统学报 第11卷 62 优。5)从图5~8可知,UNION CITY降水实验的平 %/W) 均相对误差比北京降水实验和桂平降水实验的明显 ADF GEP最佳 小很多,桂平降水实验的平均相对误差也比北京降 原始GEP平均 BIS GEP最佳 水实验的明显小很多。这说明了GEP算法在进行 21D 原始GEP最佳 ADF GEP平均 BIS GEP平均 UNION CITY降水自动建模中的效果最好,在北京 降水自动建模中的效果较差。 三 益 从图4可看出UNION CITY的降水量数据波动 进化代数 范围相对较小、数据分布相对平稳、噪声少,而北京 图6桂平冬季月均降水量建模进化收敛过程图 降水数据逐年变化差异较大、突变点多而尖锐、最大 Fig.6 Convergence process of precipitation modeling of 值与最小值差距大、数据的分布曲线相当复杂。这 Guiping 些数据集的特点与4)和5)的情况充分表明了时间 BIS_GEP、原始GEP和ADF_GEP等对3组不 序列建模的效果与数据集的复杂程度呈强相关,建 同数据集的自动建模的进化收敛实验结果如图5~8 模数据分布和变化越简单,自动建模的平均相对误 所示。由图可知:1)图5~8均表明了BIS_GEP算 差越小,建模效果越好。 法在这3组不同数据集的自动建模过程中,无论是 72 10次运行结果的平均值,还是最佳运行状况,BIS 62 GEP比原始GEP和ADF_GEP均有更好的收敛性 52 能和寻优结果表现。这充分说明了本文提出的改进 42 方法的有效性和优越性。2)图5~8中的左边部分 32 显示的进化过程初期的适应度曲线均显示了在算法 BIS GEP最佳 原始GEP平均 22 ADF GEP最佳 进化的初期,如图5显示的北京降水实验中的前70 BIS GEP平均 原始GEP最佳 ADF GEP平均 代、图7(a)显示的桂平降水实验中的前40代和图8 显示的UNION CITY降水实验中的前200代,BIS_ 8 GEP,原始GEP和ADF_GEP这3种GEP算法有近 进化代数 似的收敛性能表现。它们几乎都以极快速度趋于目 (a)generation 5~125 标方向收敛,然后收敛速度逐渐减小,甚至不同程度 7.3 地进入收敛缓慢状态,陷入局部最优。这说明了 BIS GEP最佳 6.6 GEP算法存在着遗传算法家族常见的不足一前 原始GEP最佳ADF_GEP最佳 期收敛快,后期收敛缓慢甚至陷入局部最优。3)图 %/HW) 6.0 5.4 BIS GEP平均 5、图7~8中的右边的适应度曲线均显示的进化过 4.9 原始GEP平均 程中后期的BIS_GEP算法的适应度迭代进化比同 4.3 阶段的原始GEP和ADF_GEP的更频繁,更能跳出 3.7 ADF GEP平均 局部最优而向全局最优方向逼近。这表明了经过本 3.1 文提出的个体最优共享改进GEP算法可有效改善 2.5 安 GEP算法后期收敛缓慢状态和易陷入局部最优的 进化代数 不足,寻优性能比原始GEP和ADF_GEP有显著的 (b)generation 125-2 000 提高。4)在UNION CITY的降水实验中,BIS_GEP、 图7桂平冬季月均降水量建模进化收敛过程二分解图 原始GEP和ADF_GEP这3种GEP算法在前6OO Fig.7 Second decomposition for convergence process of 代的适应度迭代进化较北京降水实验和桂平降水实 precipitation modeling of Guiping 验的表现更明显和更频繁,且更快速地逼近全局最
图 6 桂平冬季月均降水量建模进化收敛过程图 Fig.6 Convergence process of precipitation modeling of Guiping BIS_GEP、原始 GEP 和 ADF_GEP 等对 3 组不 同数据集的自动建模的进化收敛实验结果如图 5~8 所示。 由图可知:1) 图 5 ~ 8 均表明了 BIS_GEP 算 法在这 3 组不同数据集的自动建模过程中,无论是 10 次运行结果的平均值,还是最佳运行状况,BIS_ GEP 比原始 GEP 和 ADF_GEP 均有更好的收敛性 能和寻优结果表现。 这充分说明了本文提出的改进 方法的有效性和优越性。 2)图 5 ~ 8 中的左边部分 显示的进化过程初期的适应度曲线均显示了在算法 进化的初期,如图 5 显示的北京降水实验中的前 70 代、图 7(a)显示的桂平降水实验中的前 40 代和图 8 显示的 UNION CITY 降水实验中的前 200 代,BIS_ GEP、原始 GEP 和 ADF_GEP 这 3 种 GEP 算法有近 似的收敛性能表现。 它们几乎都以极快速度趋于目 标方向收敛,然后收敛速度逐渐减小,甚至不同程度 地进入收敛缓慢状态,陷入局部最优。 这说明了 GEP 算法存在着遗传算法家族常见的不足———前 期收敛快,后期收敛缓慢甚至陷入局部最优。 3)图 5、图 7~8 中的右边的适应度曲线均显示的进化过 程中后期的 BIS_GEP 算法的适应度迭代进化比同 阶段的原始 GEP 和 ADF_GEP 的更频繁,更能跳出 局部最优而向全局最优方向逼近。 这表明了经过本 文提出的个体最优共享改进 GEP 算法可有效改善 GEP 算法后期收敛缓慢状态和易陷入局部最优的 不足,寻优性能比原始 GEP 和 ADF_GEP 有显著的 提高。 4)在 UNION CITY 的降水实验中,BIS_GEP、 原始 GEP 和 ADF_GEP 这 3 种 GEP 算法在前 600 代的适应度迭代进化较北京降水实验和桂平降水实 验的表现更明显和更频繁,且更快速地逼近全局最 优。 5)从图 5 ~ 8 可知,UNION CITY 降水实验的平 均相对误差比北京降水实验和桂平降水实验的明显 小很多,桂平降水实验的平均相对误差也比北京降 水实验的明显小很多。 这说明了 GEP 算法在进行 UNION CITY 降水自动建模中的效果最好,在北京 降水自动建模中的效果较差。 从图 4 可看出 UNION CITY 的降水量数据波动 范围相对较小、数据分布相对平稳、噪声少,而北京 降水数据逐年变化差异较大、突变点多而尖锐、最大 值与最小值差距大、数据的分布曲线相当复杂。 这 些数据集的特点与 4)和 5)的情况充分表明了时间 序列建模的效果与数据集的复杂程度呈强相关,建 模数据分布和变化越简单,自动建模的平均相对误 差越小,建模效果越好。 (a)generation 5~ 125 (b)generation 125~ 2 000 图 7 桂平冬季月均降水量建模进化收敛过程二分解图 Fig.7 Second decomposition for convergence process of precipitation modeling of Guiping ·406· 智 能 系 统 学 报 第 11 卷

第3期 彭昱忠,等:个体最优共享GEP算法及其气象降水数据预测建模 .407. 表2各算法的3组降水案例数据集建模与预测实验结果 Table2 Experimental results of mentioned algorithms of modeling and forecasting on 3 group of precipitation cases BIS_GEP ADF_GEP 原始GEP BP NAR 数据与指标 拟合 预测 拟合 预测 拟合 预测 拟合 预测 拟合 预测 MREF最佳 16.64 23.71 16.85 24.98 16.87 26.78 27.48 47.15 29.17 36.77 北京降水 MREF平均 17.22 24.85 17.34 27.13 17.80 29.17 28.38 51.64 30.42 37.89 MREF最佳 2.57 7.16 2.92 7.83 2.95 8.04 15.69 30.86 10.97 19.65 桂平降水 MREF平均 3.16 10.25 3.28 11.51 3.90 12.18 17.08 32.17 12.29 21.83 MREF最佳0.02120.0347 0.02230.03620.02240.03921.20513.22110.08720.3682 UNION降水 MREF平均0.02230.04160.02410.04340.02370.04671.37843.75630.09650.4113 3.3.3建模与预测效果比较验证 法更好。而BIS_GEP算法在实验上获得较其他算 BIS_GEP算法与其他GEP算法和气象界常用 法更好的数据模型拟合性能和预测性能,模型具有 神经算法进行了自动建模与预测比较实验,取3组 一定的适用性。在UNION CITY降水数据集上的数 降水案例数据集的后10%样本(北京降水和桂平降 据拟合和预测的平均相对误差10次运行得的最佳 水的数据集均取2008-2013年的样本,UNION CITY 值分别达到0.021%和0.034%。据表3数据可知, 降水数据集取1995-2006年样本)作为预测的检验 BIS_GEP比实验中效果第二好的ADF_GEP的相应 样本,其余样本为训练样本。采用逐月/年预报形式 MREF最佳值分别减少了4.93%和5.55%。这比实 预测检验样本的结果,如,用1949-2007年真实的 验中效果最差的BP的相应MREF最佳值分别减少 北京降水数据建模所得模型预测2008年北京降水 了99.45%和99.89%。即使在逐年变化差异较大、 量,接着继续用1949-2008年真实的北京降水数据 突变点多而尖锐、最大值与最小值差距大、数据的分 建模所得模型预测2009年北京降水量,依次类推。 布曲线相当复杂的北京降水数据集上,数据拟合和 同理,用于北京降水、桂平降水和UNION CITY降水 预测时,BIS_GEP算法的平均相对误差也都能分别 实验中。比较结果如表2所示,MREF最佳预测值 保持在18%和25%以内。据表3数据可知BIS 是取10独立运行算法所得的10次各个预测检验样 GEP比实验中效果第二好的ADF_GEP的相应 本预测结果平均值中的最小者,而MREF平均预测 MREF最佳值分别减少了1.25%和5.08%。这比实 值是取10独立运行算法所得的10次各个预测检验 验中拟合效果最差的NAR和预测效果最差的BP 样本预测结果的综合平均值。 的相应MREF最佳值分别减少了42.94%和 ×103 49.71%。这些实验对比结果充分表明了本文提出的 0.0275 BIS_GEP算法较其他算法在降水序列数据自动建 0.0265 模和预测上有较强优势。 0.0255 -ADF GEP平均 ADF GEP最佳 BIS GEP最佳 4 0.0245 结束语 原始GEP最佳 BIS GEP平均 0.0235 原始GEP平均 本文提出了一种个体最优共享的GEP改进算 0.0225 法BIS_GEP,并在3组真实时间序列的自动建模和 0.0215 预测实验中,与原始GEP算法、另一经典的GEP改 “的苦牌学兰的芳学兰的羊兰兰的 进算法ADF_GEP,以及BP神经网络和NAR神经 进化代数 网络进行比较。算法收敛过程实验对比结果表明 图8 UNION CITY每年6月降水量建模进化收敛过程 BIS_GEP能相对改善GEP进化后期收敛缓慢和容 Fig.8 Convergence process of precipitation modeling of 易陷入局部最优的缺陷,具有更强的逼近最优能力: UNION CITY 自动建模能力与预测能力实验对比结果表明,BS GEP在3组不同类型的降水数据的数据拟合和数 从表3可看出,总体上,在3组不同类型和不同 据预测实验中,10次独立运行的最佳平均相对误差 复杂度的真实降水数据集的实验中的3种GEP方 和平均相对误差均比实验中的其他GEP算法和神 法的拟合和预测实验结果均比另外两种神经网络方 经网络算法更小,说明其自动建模能力和模型泛化
表 2 各算法的 3 组降水案例数据集建模与预测实验结果 Table2 Experimental results of mentioned algorithms of modeling and forecasting on 3 group of precipitation cases 数据与指标 BIS_GEP ADF_GEP 原始 GEP BP NAR 拟合 预测 拟合 预测 拟合 预测 拟合 预测 拟合 预测 北京降水 MREF 最佳 16.64 23.71 16.85 24.98 16.87 26.78 27.48 47.15 29.17 36.77 MREF 平均 17.22 24.85 17.34 27.13 17.80 29.17 28.38 51.64 30.42 37.89 桂平降水 MREF 最佳 2.57 7.16 2.92 7.83 2.95 8.04 15.69 30.86 10.97 19.65 MREF 平均 3.16 10.25 3.28 11.51 3.90 12.18 17.08 32.17 12.29 21.83 UNION 降水 MREF 最佳 0.021 2 0.034 7 0.022 3 0.036 2 0.022 4 0.039 2 1.205 1 3.221 1 0.087 2 0.368 2 MREF 平均 0.022 3 0.041 6 0.024 1 0.043 4 0.023 7 0.046 7 1.378 4 3.756 3 0.096 5 0.411 3 3.3.3 建模与预测效果比较验证 BIS_GEP 算法与其他 GEP 算法和气象界常用 神经算法进行了自动建模与预测比较实验,取 3 组 降水案例数据集的后 10%样本(北京降水和桂平降 水的数据集均取 2008-2013 年的样本,UNION CITY 降水数据集取 1995-2006 年样本)作为预测的检验 样本,其余样本为训练样本。 采用逐月/ 年预报形式 预测检验样本的结果,如,用 1949-2007 年真实的 北京降水数据建模所得模型预测 2008 年北京降水 量,接着继续用 1949-2008 年真实的北京降水数据 建模所得模型预测 2009 年北京降水量,依次类推。 同理,用于北京降水、桂平降水和 UNION CITY 降水 实验中。 比较结果如表 2 所示,MREF 最佳预测值 是取 10 独立运行算法所得的 10 次各个预测检验样 本预测结果平均值中的最小者,而 MREF 平均预测 值是取 10 独立运行算法所得的 10 次各个预测检验 样本预测结果的综合平均值。 图 8 UNION CITY 每年 6 月降水量建模进化收敛过程 Fig.8 Convergence process of precipitation modeling of UNION CITY 从表 3 可看出,总体上,在 3 组不同类型和不同 复杂度的真实降水数据集的实验中的 3 种 GEP 方 法的拟合和预测实验结果均比另外两种神经网络方 法更好。 而 BIS_GEP 算法在实验上获得较其他算 法更好的数据模型拟合性能和预测性能,模型具有 一定的适用性。 在 UNION CITY 降水数据集上的数 据拟合和预测的平均相对误差 10 次运行得的最佳 值分别达到 0.021%和 0.034%。 据表 3 数据可知, BIS_GEP 比实验中效果第二好的 ADF_GEP 的相应 MREF 最佳值分别减少了 4.93%和 5.55%。 这比实 验中效果最差的 BP 的相应 MREF 最佳值分别减少 了 99.45%和 99.89%。 即使在逐年变化差异较大、 突变点多而尖锐、最大值与最小值差距大、数据的分 布曲线相当复杂的北京降水数据集上,数据拟合和 预测时,BIS_GEP 算法的平均相对误差也都能分别 保持在 18% 和 25% 以内。 据表 3 数据可知 BIS _ GEP 比实验中效果第二好的 ADF _ GEP 的相应 MREF 最佳值分别减少了 1.25%和 5.08%。 这比实 验中拟合效果最差的 NAR 和预测效果最差的 BP 的 相 应 MREF 最 佳 值 分 别 减 少 了 42. 94% 和 49.71%。这些实验对比结果充分表明了本文提出的 BIS_GEP 算法较其他算法在降水序列数据自动建 模和预测上有较强优势。 4 结束语 本文提出了一种个体最优共享的 GEP 改进算 法 BIS_GEP,并在 3 组真实时间序列的自动建模和 预测实验中,与原始 GEP 算法、另一经典的 GEP 改 进算法 ADF_GEP,以及 BP 神经网络和 NAR 神经 网络进行比较。 算法收敛过程实验对比结果表明 BIS_GEP 能相对改善 GEP 进化后期收敛缓慢和容 易陷入局部最优的缺陷,具有更强的逼近最优能力; 自动建模能力与预测能力实验对比结果表明,BIS_ GEP 在 3 组不同类型的降水数据的数据拟合和数 据预测实验中,10 次独立运行的最佳平均相对误差 和平均相对误差均比实验中的其他 GEP 算法和神 经网络算法更小,说明其自动建模能力和模型泛化 第 3 期 彭昱忠,等:个体最优共享 GEP 算法及其气象降水数据预测建模 ·407·

·408· 智能系统学报 第11卷 能力均有较强的优势。 [7]ZHAO Huasheng,JIN Long,HUANG Ying,et al.An ob- 对3组不同类型和不同复杂度的真实降水数据 jective prediction model for typhoon rainstorm using particle 集的拟合和预测的对比实验结果表明,本文BS_ swarm optimization:neural network ensemble[J].Natural GEP算法对降雨时间序列数据的建模和预测结果 hazards,2014,73(2):427-437. 比传统GEP及其改进算法ADF_GEP、常用的BP和 [8]HE Suhong,FENG Taichen,GONG Yanchun,et al.Pre- dicting extreme rainfall over eastern Asia by using complex NAR神经网络自动建和预测算法的效果好,模型具 networks[J].Chinese physics B,2014,23(5):059202. 有一定的适用性,同时由于该算法模型对资料要求 [9]WU Jiansheng,LONG Jin,LIU Mingzhe.Evolving RBF 比较单一,只需降水历史数据,因而具有广泛的应 neural networks for rainfall prediction using hybrid particle 用价值。 swarm optimization and genetic algorithm[J].Neurocomput- 总之,BIS_GEP的改进是有效的,并为气象时 ing,2015,148:136-142. 间序列预测建模提供了一种切实可行的方法。下一 [10]DHANYA C T,KUMAR D N.Data mining for evolving 步工作是进一步研究和修改BIS_GEP算法,并将其 fuzzy association rules for predicting monsoon rainfall of In- 应用于高维多要素气象预测建模的研究和应用中。 dia[J].Journal of intelligent systems,2009.18(3):193- 另外,该方法若在实际业务中大规模推广应用还有 210. 若干问题有待解决,如海量高维气象数据建模的适 [11]TERZI O.Monthly rainfall estimation using data-mining process[J].Applied computational intelligence and soft 应性和稳定性问题等,都有待进一步研究。 computing,2012,2012:698071. 参考文献: [12]BERNARD E,NAVEAU P,VRAC M,et al.Clustering of maxima:spatial dependencies among heavy rainfall in [1]彭显忠,王谦,元昌安,等.数据挖掘技术在气象预报 France[J].Journal of climate,2013,26(20):7929- 研究中的应用J].干旱气象,2015,33(1):19-27. 7937. PENG Yuzhong,WANG Qian,YUAN Chang'an,et al. [13]TENG Shaohua,FAN Jihui,ZHU Haibin,et al.A cooper- Review of research on data mining in application of meteoro- ative multi-classifier method for local area meteorological logical forecasting[J].Journal of arid meteorology,2015, data mining[C]//Proceedings of the 18th IEEE Interna- 33(1):19-27. tional Conference on Computer Supported Cooperative [2]金龙,吴建生,林开平,等.基于遗传算法的神经网络 Work in Design.Hsinchu,Taiwan,China,2014:435- 短期气候预测模型[J].高原气象,2005,24(6):981- 440. 987 [14]FERREIRA C.Gene expression programming:mathemati- JIN Long,WU Jiansheng,LIN Kaiping,et al.Short-term cal modeling by artificial intelligence[M].Portugal:Angra climate prediction model of neural network based on genetic do Heroismo,2002:1-15. algorithms[J].Plateau meteorology,2005,24(6):981- [15]胡建军,唐常杰,段磊,等.基因表达式编程初始种群 987 的多样化策略[J].计算机学报,2007,30(2):305- [3]EL-SHAFIE A,JAAFER O,AKRAMI S A.Adaptive neu- 310. ro-fuzzy inference system based model for rainfall forecas- HU Jianjun,TANG Changiie,DUAN Lei,et al.The strat- ting in Klang River,Malaysia[J].International journal of egy for diversifying initial population of gene expression the physical sciences,2011,6(12):2875-2885 programming[J].Chinese journal of computers,2007,30 [4]GOSAV S,TIRON G.Artificial neural networks built for the (2):305-310. rainfall estimation using a concatenated database[J].Envi- [16]李太勇,唐常杰,吴江,等.基因表达式编程种群多样 ronmental engineering and management journal,2012,11 性自适应调控算法[J].电子科技大学学报,2010,39 (8):1383-1388. (2):279-283. [5]VENKADESH S,HOOGENBOOM G,POTTER W,et al. LI Taiyong,TANG Changjie,WU Jiang,et al.Adaptive A genetic algorithm to refine input data selection for air tem- population diversity tuning algorithm for gene expression perature prediction using artificial neural networks[J].Ap- programming[].Journal of university of electronic science plied soft computing,2013,13(5):2253-2260. and technology of China,2010,39(2):279-283. [6]RAHMAN M,SAIFUL ISLAM A H M,NADVI S Y M,et [17]宣士斌,刘怡光.基于混合差异度控制的基因表达式编 al.Comparative study of ANFIS and ARIMA model for 程[J].模式识别与人工智能,2012,25(2):186-194. weather forecasting in Dhaka[C]//Proceedings of IEEE in- XUAN Shibin,LIU Yiguang.GEP evolution algorithm ternational conference on informatics,electronics vision. based on control of mixed diversity degree[J].Pattern rec- Dhaka,Bangladesh,2013:1-6. ognition artificial intelligence,2012,25(2):186-194
能力均有较强的优势。 对 3 组不同类型和不同复杂度的真实降水数据 集的拟合和预测的对比实验结果表明,本文 BIS _ GEP 算法对降雨时间序列数据的建模和预测结果 比传统 GEP 及其改进算法 ADF_GEP、常用的 BP 和 NAR 神经网络自动建和预测算法的效果好,模型具 有一定的适用性,同时由于该算法模型对资料要求 比较单一, 只需降水历史数据, 因而具有广泛的应 用价值。 总之,BIS_GEP 的改进是有效的,并为气象时 间序列预测建模提供了一种切实可行的方法。 下一 步工作是进一步研究和修改 BIS_GEP 算法,并将其 应用于高维多要素气象预测建模的研究和应用中。 另外,该方法若在实际业务中大规模推广应用还有 若干问题有待解决,如海量高维气象数据建模的适 应性和稳定性问题等,都有待进一步研究。 参考文献: [1]彭昱忠, 王谦, 元昌安, 等. 数据挖掘技术在气象预报 研究中的应用[J]. 干旱气象, 2015, 33(1): 19⁃27. PENG Yuzhong, WANG Qian, YUAN Chang’ an, et al. Review of research on data mining in application of meteoro⁃ logical forecasting[ J]. Journal of arid meteorology, 2015, 33(1): 19⁃27. [2]金龙, 吴建生, 林开平, 等. 基于遗传算法的神经网络 短期气候预测模型[ J]. 高原气象, 2005, 24( 6): 981⁃ 987. JIN Long, WU Jiansheng, LIN Kaiping, et al. Short⁃term climate prediction model of neural network based on genetic algorithms[ J]. Plateau meteorology, 2005, 24 ( 6): 981⁃ 987 . [3]EL⁃SHAFIE A, JAAFER O, AKRAMI S A. Adaptive neu⁃ ro⁃fuzzy inference system based model for rainfall forecas⁃ ting in Klang River, Malaysia[J]. International journal of the physical sciences, 2011, 6(12): 2875⁃2885. [4]GOSAV S, TIRON G. Artificial neural networks built for the rainfall estimation using a concatenated database[ J]. Envi⁃ ronmental engineering and management journal, 2012, 11 (8): 1383⁃1388. [5] VENKADESH S, HOOGENBOOM G, POTTER W, et al. A genetic algorithm to refine input data selection for air tem⁃ perature prediction using artificial neural networks[ J]. Ap⁃ plied soft computing, 2013, 13(5): 2253⁃2260. [6]RAHMAN M, SAIFUL ISLAM A H M, NADVI S Y M, et al. Comparative study of ANFIS and ARIMA model for weather forecasting in Dhaka[C] / / Proceedings of IEEE in⁃ ternational conference on informatics, electronics & vision. Dhaka, Bangladesh, 2013: 1⁃6. [7]ZHAO Huasheng, JIN Long, HUANG Ying, et al. An ob⁃ jective prediction model for typhoon rainstorm using particle swarm optimization: neural network ensemble [ J]. Natural hazards, 2014, 73(2): 427⁃437. [8]HE Suhong, FENG Taichen, GONG Yanchun, et al. Pre⁃ dicting extreme rainfall over eastern Asia by using complex networks[J]. Chinese physics B, 2014, 23(5): 059202. [9] WU Jiansheng, LONG Jin, LIU Mingzhe. Evolving RBF neural networks for rainfall prediction using hybrid particle swarm optimization and genetic algorithm[J]. Neurocomput⁃ ing, 2015, 148: 136⁃142. [10] DHANYA C T, KUMAR D N. Data mining for evolving fuzzy association rules for predicting monsoon rainfall of In⁃ dia[J]. Journal of intelligent systems, 2009, 18(3): 193⁃ 210. [11] TERZI O. Monthly rainfall estimation using data⁃mining process[ J]. Applied computational intelligence and soft computing, 2012, 2012: 698071. [12]BERNARD E, NAVEAU P, VRAC M, et al. Clustering of maxima: spatial dependencies among heavy rainfall in France[ J]. Journal of climate, 2013, 26 ( 20): 7929⁃ 7937. [13]TENG Shaohua, FAN Jihui, ZHU Haibin, et al. A cooper⁃ ative multi⁃classifier method for local area meteorological data mining[C] / / Proceedings of the 18th IEEE Interna⁃ tional Conference on Computer Supported Cooperative Work in Design. Hsinchu, Taiwan, China, 2014: 435⁃ 440. [14]FERREIRA C. Gene expression programming: mathemati⁃ cal modeling by artificial intelligence[M]. Portugal: Angra do Heroismo, 2002: 1⁃15. [15]胡建军, 唐常杰, 段磊, 等. 基因表达式编程初始种群 的多样化策略[ J]. 计算机学报, 2007, 30 ( 2): 305⁃ 310. HU Jianjun, TANG Changjie, DUAN Lei, et al. The strat⁃ egy for diversifying initial population of gene expression programming[J]. Chinese journal of computers, 2007, 30 (2): 305⁃310. [16]李太勇, 唐常杰, 吴江, 等. 基因表达式编程种群多样 性自适应调控算法[ J]. 电子科技大学学报, 2010, 39 (2): 279⁃283. LI Taiyong, TANG Changjie, WU Jiang, et al. Adaptive population diversity tuning algorithm for gene expression programming[J]. Journal of university of electronic science and technology of China, 2010, 39(2): 279⁃283. [17]宣士斌, 刘怡光. 基于混合差异度控制的基因表达式编 程[J]. 模式识别与人工智能, 2012, 25(2): 186⁃194. XUAN Shibin, LIU Yiguang. GEP evolution algorithm based on control of mixed diversity degree[J]. Pattern rec⁃ ognition & artificial intelligence, 2012, 25(2): 186⁃194. ·408· 智 能 系 统 学 报 第 11 卷

第3期 彭昱忠,等:个体最优共享GEP算法及其气象降水数据预测建模 409· [18]TANG Changjie,DUAN Lei,PENG Jing,et al.The strat- Journal of frontiers of computer science and technology, egies to improve performance of function mining by gene 2014,8(1):90-102. expression programming:genetic modifying,overlapped [24]陈宇,唐常杰,钟义啸,等.基于基因表达式编程和时 gene,backtracking and adaptive mutation[C]//Proceed- 变强度的时间序列预测[J].计算机科学,2005,32(7 ings of the 17th Data Engineering Workshop.Ginowan,Ja- Suppl.B):269-271. pan,2006:100-106. CHEN Yu,TANG Changjie,ZHONG Yixiao,et al.Time [19]BAUTU E,BAUTU A,LUCHIAN H.AdaGEP-an adap- series predication based on gene expression programming tive gene expression programming algorithm[C]//Proceed- and time series vibration intensity[J].Computer science, ings of IEEE International Symposium on Symbolic and Nu- 2005,32(7 Suppl.B):269-271 meric Algorithms for Scientific Computing.Timisoara,Ro- 作者简介: mania,2007:403-406. 彭昱忠,男,1980年生,副教授,主 [20]元昌安,唐常杰,左劫,等.基于基因表达式编程的函 要研究方向为智能计算及数据挖掘。 数挖掘-收敛性分析与残差制导进化算法[J].四川大 主持国家级和省级基金项目4项,发表 学学报:工程科学版,2004,36(6):100-105. 学术论文21篇。 YUAN Chang'an,TANG Changjie,ZUO Jie,et al.Func- tion mining based on gene expression programming-conver- gency analysis and remnant-guided evolution algorithm[J]. Journal of Sichuan university engineering science edition, 元昌安,男,1964年生,教授,主要 2004.36(6):100-105. 研究方向为数据库与知识工程,先后主 [21]RYAN N,HIBLER D.Robust gene expression program- 持国家级和省级基金项目8项,获广西 ming[J].Procedia computer science,2011,6:165-170. 科技进步奖5项,发表学术论文58篇。 [22]ZHONG Jinghui,ONG Y S,CAI Wentong.Self-learning gene expression programming[J].IEEE transactions on ev- olutionary computation,2016,20(1):65-80. [23]张鑫源,胡晓敏,林盈.遗传算法和粒子群优化算法的 李洁,女,1980年生,讲师,主要研 性能对比分析[J].计算机科学与探索,2014,8(1): 究方向为智能计算及数据挖掘,发表学 90-102. 术论文7篇。 ZHANG Xinyuan,HU Xiaomin,LIN Ying.Comparisons of genetic algorithm and particle swarm optimization[J]
[18]TANG Changjie, DUAN Lei, PENG Jing, et al. The strat⁃ egies to improve performance of function mining by gene expression programming: genetic modifying, overlapped gene, backtracking and adaptive mutation[ C] / / Proceed⁃ ings of the 17th Data Engineering Workshop. Ginowan, Ja⁃ pan, 2006: 100⁃106. [19]BAUTU E, BAUTU A, LUCHIAN H. AdaGEP⁃an adap⁃ tive gene expression programming algorithm[C] / / Proceed⁃ ings of IEEE International Symposium on Symbolic and Nu⁃ meric Algorithms for Scientific Computing. Timisoara, Ro⁃ mania, 2007: 403⁃406. [20]元昌安, 唐常杰, 左劼, 等. 基于基因表达式编程的函 数挖掘⁃收敛性分析与残差制导进化算法[ J]. 四川大 学学报:工程科学版, 2004, 36(6): 100⁃105. YUAN Changan, TANG Changjie, ZUO Jie, et al. Func⁃ tion mining based on gene expression programming⁃conver⁃ gency analysis and remnant⁃guided evolution algorithm[J]. Journal of Sichuan university :engineering science edition, 2004, 36(6): 100⁃105. [21] RYAN N, HIBLER D. Robust gene expression program⁃ ming[J]. Procedia computer science, 2011, 6: 165⁃170. [22] ZHONG Jinghui, ONG Y S, CAI Wentong. Self⁃learning gene expression programming[J]. IEEE transactions on ev⁃ olutionary computation, 2016, 20(1): 65⁃80. [23]张鑫源, 胡晓敏, 林盈. 遗传算法和粒子群优化算法的 性能对比分析[ J]. 计算机科学与探索, 2014, 8( 1): 90⁃102. ZHANG Xinyuan, HU Xiaomin, LIN Ying. Comparisons of genetic algorithm and particle swarm optimization[J]. Journal of frontiers of computer science and technology, 2014, 8(1): 90⁃102. [24]陈宇, 唐常杰, 钟义啸, 等. 基于基因表达式编程和时 变强度的时间序列预测[ J]. 计算机科学, 2005, 32(7 Suppl. B): 269⁃271. CHEN Yu, TANG Changjie, ZHONG Yixiao, et al. Time series predication based on gene expression programming and time series vibration intensity[ J]. Computer science, 2005, 32(7 Suppl. B): 269⁃271. 作者简介: 彭昱忠,男,1980 年生,副教授,主 要研究方向为智能计算及数据挖掘。 主持国家级和省级基金项目 4 项,发表 学术论文 21 篇。 元昌安,男,1964 年生,教授,主要 研究方向为数据库与知识工程,先后主 持国家级和省级基金项目 8 项,获广西 科技进步奖 5 项,发表学术论文 58 篇。 李洁,女,1980 年生,讲师,主要研 究方向为智能计算及数据挖掘,发表学 术论文 7 篇。 第 3 期 彭昱忠,等:个体最优共享 GEP 算法及其气象降水数据预测建模 ·409·