
第12卷第1期 智能系统学报 Vol.12 No.1 2017年2月 CAAI Transactions on Intelligent Systems Feb.2017 D0I:10.11992/tis.201603039 网络出版地址:http:/kns.cmki.net/kcms/detail/23.1538.TP.20170227.1800.010.html 基于稀疏表示与线性回归的图像快速超分辨率重建 赵志辉2,赵瑞珍12,岑翼刚2,张凤珍12 (1.北京交通大学信息科学研究所,北京100044;2.北京交通大学现代信息科学与网络技术北京市重点实验室,北京10004) 摘要:单幅图像超分辨率的目的是从一幅低分辨率的图像来重构出高分辨率的图像。基于稀疏表示和邻域嵌入 的超分辨率图像重建方法使得重建图像质量有了极大的改善。但这些方法还很难应用到实际中,因为其重建图像 的速度太慢或者需要调节复杂的参数。目前大多数的方法在图像重建的速度和质量两个方面很难有一个好的权 衡。鉴于以上问题提出了一种基于线性回归的快速图像超分辨率重建算法,将稀疏表示和回归的方法有效地结合 在一起。通过稀疏表示训练的字典,用一种新的方式将整个数据集划分为多个子空间,然后在每一类子空间中独立 地学习高低分辨率图像之间的映射关系,最后通过选择相应的投影矩阵来重建出高分辨图像。实验结果表明,相比 于其他方法,本文提出的算法无论在图像重建速度还是重建质量方面都取得了更好的超分辨率重建效果。 关键词:线性回归:超分辨率:字典训练:稀疏表示;图像重建;特征训练;子空间;邻域嵌入 中图分类号:TP391.41文献标志码:A文章编号:1673-4785(2017)01-0008-07 中文引用格式:赵志辉,赵瑞珍,岑翼刚,等.基于稀疏表示与线性回归的图像快速超分辨率重建[J].智能系统学报,2017,12(1): 8-14. 英文引用格式:ZHAO Zhihui,ZHAO Ruizhen,CEN Yigang,etal.Rapid super-resolution image reconstruction based on sparse representation and linear regression[J].CAAI transactions on intelligent systems,2017,12(1):8-14. Rapid super-resolution image reconstruction based on sparse representation and linear regression ZHAO Zhihui2,ZHAO Ruizhen'2,CEN Yigang'2,ZHANG Fengzhen'2 (1.Institute of Information Science,Beijing Jiaotong University,Beijing 100044,China;2.Beijing Key Laboratory of Advanced Information Science and Network Technology,Beijing Jiaotong University,Beijing 100044,China) Abstract:Single-image super-resolution aims at reconstructing a high-resolution image from a single low-resolution image.Recent methods relying on both neighborhood embedding and sparse coding have led to significant quality improvements.However,the application of these approaches is still practically difficult because they are either too slow or demand tedious parameter tweaks.In most of these methods,the speed and quality of image reconstruction are the two aspects that cannot be balanced easily.With regard to the abovementioned problems,this research proposed a rapid image super-resolution reconstruction algorithm based on linear regression,which effectively combined the sparse representation with the regression method.First,a dictionary was trained using the K-SVD algorithm based on training samples.Subsequently,the entire dataset was divided into a number of subspaces according to the atoms in the dictionary.Moreover,the mapping from low-to-high-resolution images can be independently obtained for each subspace.Finally,the high-resolution image was reconstructed by selecting the corresponding projection matrix.Experimental results demonstrate that both the image reconstruction quality and the speed of the proposed algorithm performed better than other widely used methods. Keywords:linear regression;super-resolution;dictionary learning;sparse representation;image reconstruction; feature learning;subspace;neighborhood embedding 图像超分辨率(super resolution,SR)[I-)重建是 监控,遥感卫星等领域中起着重要的作用,已经得 计算机视觉中一个重要的问题,在医学成像、安全 到了广泛的应用。通常,图像超分辨率的任务就是 从一幅或多幅低分辨率(low resolution,LR)的输入 收稿日期:2016-03-19.网络出版日期:2017-02-27. 基金项目:国家自然科学基金项目(61272028,61572067):国家“863” 图像来重构出一幅高分辨率(high resolution,HR)的 计划项目(2014AA015202):广东省自然科学基金项目 (2016A030313708):北京市自然科学基金项目(4162050). 输出图像。虽然这是一个病态的问题,但由于应用 通信作者:岑翼刚.E-mail:ygcen@bju.cd.cn
第 12 卷第 1 期 智 能 系 统 学 报 Vol.12 №.1 2017 年 2 月 CAAI Transactions on Intelligent Systems Feb. 2017 DOI:10.11992 / tis.201603039 网络出版地址:http: / / kns.cnki.net / kcms/ detail / 23.1538.TP.20170227.1800.010.html 基于稀疏表示与线性回归的图像快速超分辨率重建 赵志辉1,2 ,赵瑞珍1,2 ,岑翼刚1,2 ,张凤珍1,2 (1.北京交通大学 信息科学研究所,北京 100044; 2.北京交通大学 现代信息科学与网络技术北京市重点实验室,北京 100044) 摘 要:单幅图像超分辨率的目的是从一幅低分辨率的图像来重构出高分辨率的图像。 基于稀疏表示和邻域嵌入 的超分辨率图像重建方法使得重建图像质量有了极大的改善。 但这些方法还很难应用到实际中,因为其重建图像 的速度太慢或者需要调节复杂的参数。 目前大多数的方法在图像重建的速度和质量两个方面很难有一个好的权 衡。 鉴于以上问题提出了一种基于线性回归的快速图像超分辨率重建算法,将稀疏表示和回归的方法有效地结合 在一起。 通过稀疏表示训练的字典,用一种新的方式将整个数据集划分为多个子空间,然后在每一类子空间中独立 地学习高低分辨率图像之间的映射关系,最后通过选择相应的投影矩阵来重建出高分辨图像。 实验结果表明,相比 于其他方法,本文提出的算法无论在图像重建速度还是重建质量方面都取得了更好的超分辨率重建效果。 关键词:线性回归;超分辨率;字典训练;稀疏表示;图像重建;特征训练;子空间;邻域嵌入 中图分类号: TP391.41 文献标志码:A 文章编号:1673-4785(2017)01-0008-07 中文引用格式:赵志辉,赵瑞珍,岑翼刚,等. 基于稀疏表示与线性回归的图像快速超分辨率重建[J]. 智能系统学报, 2017, 12(1): 8-14. 英文引用格式:ZHAO Zhihui, ZHAO Ruizhen, CEN Yigang, et al. Rapid super⁃resolution image reconstruction based on sparse representation and linear regression[J]. CAAI transactions on intelligent systems, 2017, 12(1): 8-14. Rapid super⁃resolution image reconstruction based on sparse representation and linear regression ZHAO Zhihui 1,2 , ZHAO Ruizhen 1,2 , CEN Yigang 1,2 , ZHANG Fengzhen 1,2 (1. Institute of Information Science, Beijing Jiaotong University, Beijing 100044, China; 2. Beijing Key Laboratory of Advanced Information Science and Network Technology, Beijing Jiaotong University, Beijing 100044, China) Abstract:Single⁃image super⁃resolution aims at reconstructing a high⁃resolution image from a single low⁃resolution image. Recent methods relying on both neighborhood embedding and sparse coding have led to significant quality improvements. However, the application of these approaches is still practically difficult because they are either too slow or demand tedious parameter tweaks. In most of these methods, the speed and quality of image reconstruction are the two aspects that cannot be balanced easily. With regard to the abovementioned problems, this research proposed a rapid image super⁃resolution reconstruction algorithm based on linear regression, which effectively combined the sparse representation with the regression method. First, a dictionary was trained using the K⁃SVD algorithm based on training samples. Subsequently, the entire dataset was divided into a number of subspaces according to the atoms in the dictionary. Moreover, the mapping from low⁃to⁃high⁃resolution images can be independently obtained for each subspace. Finally, the high⁃resolution image was reconstructed by selecting the corresponding projection matrix. Experimental results demonstrate that both the image reconstruction quality and the speed of the proposed algorithm performed better than other widely used methods. Keywords:linear regression; super⁃resolution; dictionary learning; sparse representation; image reconstruction; feature learning; subspace; neighborhood embedding 收稿日期:2016-03-19. 网络出版日期:2017-02-27. 基金项目:国家自然科学基金项目( 61272028, 61572067);国家“ 863” 计划项 目 ( 2014AA015202 ); 广 东 省 自 然 科 学 基 金 项 目 (2016A030313708);北京市自然科学基金项目(4162050). 通信作者:岑翼刚. E⁃mail:ygcen@ bjtu.edu.cn. 图像超分辨率(super resolution,SR) [1-4]重建是 计算机视觉中一个重要的问题,在医学成像、安全 监控、遥感卫星等领域中起着重要的作用,已经得 到了广泛的应用。 通常,图像超分辨率的任务就是 从一幅或多幅低分辨率( low resolution,LR)的输入 图像来重构出一幅高分辨率(high resolution,HR)的 输出图像。 虽然这是一个病态的问题,但由于应用

第1期 赵志辉,等:基于稀疏表示与线性回归的图像快速超分辨率重建 9· 的需求以及人们研究的兴趣,许多方法相继被提出 数权值,然后利用这K个权值和训练集中HR特征 来解决这个问题。最简单方法就是利用插值算法, 空间对应的K个图像块的线性组合即可重建出HR 比如最邻近插值、双三次线性插值等。虽然这些插 图像块。最终将所有的HR图像块合并到一起,并 值算法运算简单,复杂度低,但重建的图像精度不 且平均相邻图像块重叠区域的像素值得到重建的 高,边缘模糊,很难满足实际应用中图像的需求。 HR图像。 为了提高图像重建的质量,更有效的方法是基 1.2基于稀疏编码的超分辨率图像重建 于学习的方法,利用图像的统计先验s-6)知识或者 邻域嵌入的方法需要在整个训练集中选择邻 机器学习(machine learning,ML)[7-)技术来学习一 近的图像块,当需要提高图像重建的效果时,训练 个从LR图像块到HR图像块的映射函数。最近比 集会变得越来越大,计算的复杂度也将越来越高。 较流行的方法是基于字典或样本学习的方法。其 为了解决这一问题,Yang等)通过字典对的学习 中表现较好的是基于字典学习的超分辨率重建算 将稀疏编码的方法用于图像SR。假设LR图像块 法,它通常是建立在稀疏编码(sparse coding,SC)[uo 和HR图像块有相同的稀疏表示系数,在整个训练 基础上的,其假设自然的图像块可以通过字典原子 集上一起学习高低分辨率字典对,如式(1): 的线性组合来稀疏表示。但这些方法由于在重建 图像的时候需要进行一定时间的稀疏编码,实时性 吧,NIX-DZI呢+y-D,z店+ 1 min 较差。最近,Timofte等山在重建阶段绕开了稀疏 (1) 编码的部分,通过将一个单一的大字典划分为多个 小字典,在保留图像重建精度的前提下,重建速度 式中:N和M分别表示HR图像块和LR图像块的 有了明显的改善。 维数:X.和Y分别表示训练样本中高低分辨率图 受以上文献的启发,本文提出了一种快速重建 像块:D,和D,分别表示高分辨率字典和低分辨率 图像的模型,在提高图像重建速度的同时力争改善 字典:Z是图像块对应的稀疏表示系数。对于输入 图像的重建质量。在我们的算法中,将字典原子和 的LR图像块,计算其在字典D,下相应的稀疏表示 LR特征之间的相关性作为测量依据,将整个数据集 系数:。最终利用这个系数:和学习好的字典D 划分为多个子空间,然后在每一类子空间上独立地 即可重建出HR图像块。 学习高低分辨率图像之间的映射关系。实验结果 这样通过稀疏编码的方式将整个训练集转化 表明,在标准的自然图像测试集上,我们提出的算 成固定大小的字典,避免了训练集变大带来的困 法重建的图像细节更加清晰,效果更好。 难。Zeyde等[]在以上框架的基础上,通过在字典 学习过程中进行的儿个重要的修正改善了运行的 1基于字典对的图像超分辨率重建 速度。由于重建图像时稀疏模型的求解需要消耗 这一部分简要介绍基于字典对的图像SR。主 一定的时间,所以上述所有基于字典对学习的方法 要包括基于邻域嵌入(neighbour embedding,NE)和 中图像重建的速度仍然是相对较慢的。 稀疏编码(SC)的方法。 2快速线性回归的图像超分辨率重建 1.1基于邻域嵌入的超分辨率重建 邻域嵌入的方法假设LR图像块和其对应的 针对以上存在的问题,我们将稀疏表示和回归 HR图像块有着相似的局部几何流形。Chang等[ 的方法结合起来。对于字典训练,本文用一种新的 通过使用局部线性嵌入的流形学习方法,将这个假 相关性的聚类方法来替代K-means聚类方法将整个 设用于图像SR。由于在LR和HR的特征空间中, 训练样本集有效地划分为多个子空间。同时直接 流形被认为有着相似的几何结构,这也就意味着只 利用LR特征和HR特征之间的关系提出了一种新 要有足够的样本,就可以使用在LR特征域中局部 的线性映射模型,避免了重建过程中稀疏编码的求 近邻样本的权重来重建出HR特征域中的图像块。 解。该算法主要包括两个阶段,分别是训练阶段和 对于在LR特征空间中输入的一个图像块,搜 重建阶段。 寻训练集中与其欧氏距离最近的K个图像块作为 2.1训练阶段 它的邻域。通过计算一个带有约束的最小二乘问 首先我们收集包含一一对应的HR图像X.三 题得到该邻域中的样本表示输入图像块的K个系 {X,X2,…,X.}和LR图像Y={Y,Y2,…,Y。}的图
的需求以及人们研究的兴趣,许多方法相继被提出 来解决这个问题。 最简单方法就是利用插值算法, 比如最邻近插值、双三次线性插值等。 虽然这些插 值算法运算简单,复杂度低,但重建的图像精度不 高,边缘模糊,很难满足实际应用中图像的需求。 为了提高图像重建的质量,更有效的方法是基 于学习的方法,利用图像的统计先验[5-6] 知识或者 机器学习(machine learning,ML) [7-9] 技术来学习一 个从 LR 图像块到 HR 图像块的映射函数。 最近比 较流行的方法是基于字典或样本学习的方法。 其 中表现较好的是基于字典学习的超分辨率重建算 法,它通常是建立在稀疏编码(sparse coding,SC) [10] 基础上的,其假设自然的图像块可以通过字典原子 的线性组合来稀疏表示。 但这些方法由于在重建 图像的时候需要进行一定时间的稀疏编码,实时性 较差。 最近,Timofte 等[11] 在重建阶段绕开了稀疏 编码的部分,通过将一个单一的大字典划分为多个 小字典,在保留图像重建精度的前提下,重建速度 有了明显的改善。 受以上文献的启发,本文提出了一种快速重建 图像的模型,在提高图像重建速度的同时力争改善 图像的重建质量。 在我们的算法中,将字典原子和 LR 特征之间的相关性作为测量依据,将整个数据集 划分为多个子空间,然后在每一类子空间上独立地 学习高低分辨率图像之间的映射关系。 实验结果 表明,在标准的自然图像测试集上,我们提出的算 法重建的图像细节更加清晰,效果更好。 1 基于字典对的图像超分辨率重建 这一部分简要介绍基于字典对的图像 SR。 主 要包括基于邻域嵌入( neighbour embedding,NE) 和 稀疏编码(SC)的方法。 1.1 基于邻域嵌入的超分辨率重建 邻域嵌入的方法假设 LR 图像块和其对应的 HR 图像块有着相似的局部几何流形。 Chang 等[12] 通过使用局部线性嵌入的流形学习方法,将这个假 设用于图像 SR。 由于在 LR 和 HR 的特征空间中, 流形被认为有着相似的几何结构,这也就意味着只 要有足够的样本,就可以使用在 LR 特征域中局部 近邻样本的权重来重建出 HR 特征域中的图像块。 对于在 LR 特征空间中输入的一个图像块,搜 寻训练集中与其欧氏距离最近的 K 个图像块作为 它的邻域。 通过计算一个带有约束的最小二乘问 题得到该邻域中的样本表示输入图像块的 K 个系 数权值,然后利用这 K 个权值和训练集中 HR 特征 空间对应的 K 个图像块的线性组合即可重建出 HR 图像块。 最终将所有的 HR 图像块合并到一起,并 且平均相邻图像块重叠区域的像素值得到重建的 HR 图像。 1.2 基于稀疏编码的超分辨率图像重建 邻域嵌入的方法需要在整个训练集中选择邻 近的图像块,当需要提高图像重建的效果时,训练 集会变得越来越大,计算的复杂度也将越来越高。 为了解决这一问题,Yang 等[13] 通过字典对的学习 将稀疏编码的方法用于图像 SR。 假设 LR 图像块 和 HR 图像块有相同的稀疏表示系数,在整个训练 集上一起学习高低分辨率字典对,如式(1): min Dh ,Dl { ,Z} 1 N ‖Xh - DhZ‖2 2 + 1 M ‖Yl - DlZ‖2 2 + λ 1 N + 1 M æ è ç ö ø ÷ ‖Z‖1 (1) 式中:N 和 M 分别表示 HR 图像块和 LR 图像块的 维数;Xh 和 Yl 分别表示训练样本中高低分辨率图 像块;Dh 和 Dl 分别表示高分辨率字典和低分辨率 字典;Z 是图像块对应的稀疏表示系数。 对于输入 的 LR 图像块,计算其在字典 Dl 下相应的稀疏表示 系数 α。 最终利用这个系数 α 和学习好的字典 Dh 即可重建出 HR 图像块。 这样通过稀疏编码的方式将整个训练集转化 成固定大小的字典,避免了训练集变大带来的困 难。 Zeyde 等[14]在以上框架的基础上,通过在字典 学习过程中进行的几个重要的修正改善了运行的 速度。 由于重建图像时稀疏模型的求解需要消耗 一定的时间,所以上述所有基于字典对学习的方法 中图像重建的速度仍然是相对较慢的。 2 快速线性回归的图像超分辨率重建 针对以上存在的问题,我们将稀疏表示和回归 的方法结合起来。 对于字典训练,本文用一种新的 相关性的聚类方法来替代 K⁃means 聚类方法将整个 训练样本集有效地划分为多个子空间。 同时直接 利用 LR 特征和 HR 特征之间的关系提出了一种新 的线性映射模型,避免了重建过程中稀疏编码的求 解。 该算法主要包括两个阶段,分别是训练阶段和 重建阶段。 2.1 训练阶段 首先我们收集包含一一对应的 HR 图像 Xh = {X1 ,X2 ,…,Xu }和 LR 图像 Yl = {Y1 ,Y2 ,…,Yu }的图 第 1 期 赵志辉,等:基于稀疏表示与线性回归的图像快速超分辨率重建 ·9·

·10 智能系统学报 第12卷 像对训练集。将每一幅LR图像Y通过插值,得到 舍弃了对它们的使用,而对于本文的算法这些原始 和HR图像一样大小的LR图像Y,然后对成对的 数据却仍是至关重要的。我们将D中的每个原子 高低分辨率图像分别提取高低分辨率特征。 d作为聚类的中心,按式(6)计算每个原子d与所 为了仅得到图像的高频信息,我们对每一幅 有的LR特征y),的相关性。 HR图像X做如下处理: Ti=(d4yi》 (6) E =X-Y (2) 式中:T{表示第k个原子与第i个LR特征的内积: 然后对仅含有高频信息的图像E进行分块, d表示训练字典D中的第k列原子;y表示整个特 将每一个大小为√x√的图像块作为我们提取的一 征空间I中的第i个LR特征。然后选取对应于T 个n维的HR特征向量xi∈R”。对于每一幅LR图 值最大的M个yi,将这些y作为一类。设d对应 像Y',我们使用其一阶和二阶微分作为图像块的 类中的LR特征为Y={y,帅,…,y},由于在整 梯度特征。本文采用的4个滤波器如下: 个特征空间I中y和x总是成对出现的,从而可以 1=[-101],=f, (3) 得到对应于Y的HR特征X。={x,x,…,}。 f3=[10-201],4=f, 这样即可得到一个含有Y。和X的特征子空间,从 式中T表示转置。通过对图像Y,进行滤波处理,即 而将整个训练的特征空间I划分为K个特征子空 可得到其相应的4幅梯度图像。同样对这4幅梯度 间。相比于传统的聚类方法中某个训练样本只能 图像进行分块,并在各自相同的位置分别取出一个 属于某个特定的类,我们这种新的聚类方式,可以 大小为√n×√n的图像块,将这4个图像块拉直连 将同一个训练样本划分到多个类中共享,进而可以 接起来得到一个4×n维的LR特征向量,记 提高训练的精度使得重建图像的效果更好。 为eR“。 最后,一旦得到了划分后的特征子空间,对每 由于多个滤波器处理后提取的LR特征维数增 一个字典原子d,在其对应的特征子空间上计算相 加会使计算的复杂度提高,我们通过降维的方式来 应的投影矩阵。设x和y分别是HR特征X和 减少后续训练和重建过程中计算的成本。本文采 LR特征Y。中的一对高低分辨率特征向量,它们的 用PCA对LR特征向量进行降维处理,通过一个投 维数分别为n和n。本文通过学习n个线性回归函 影算子B∈Rx4“来降低∈R"的维数,如下式: 数来独立预测HR特征向量中的n个值,在每一个 y片=B阴 (4) 特征子空间上按式(7)来计算从LR特征Y∈R* 式中特征向量yi∈R",n<4n。如此即可得到在图 映射到HR特征X∈RxM的回归投影矩 像Y,和X。相同位置处分别提取的特征y和x组 阵C∈R: 成的一一对应的特征对{y,x},进而将所有训练图 C=min ll X-CYll2 (7) 像提取的特征作为训练集的整个特征空间I={y, 以上的回归问题类似于一个线性最小二乘问 x},其中i=1,2,…,,N,表示整个训练集中特征 题,因此有如下闭式解: 的数量。 C=XY(YY) (8) 不同于式(1)中Yang等]同时训练高低分辨 最终可得到字典D中所有原子对应的投影矩 率字典对,本文仅将LR特征{y}CR作为训练 阵组成的集合P={C}1。在整个训练过程中我 字典的样本,同时不必再训练HR字典。如式(5), 们充分使用了所有的原始高低分辨率图像含有的 我们利用K-SVD训练字典D={d},k=1, 信息来学习回归函数,以提高后续图像重建的精 度。值得一提的是:以上的整个训练过程,包括字 2,…,K0 典的训练、特征空间的划分以及投影矩阵的求解我 D=arg min∑ly-Del,st.laI。≤s,i 们都可以在线下进行计算。 (5) 2.2重建阶段 式中:D∈R*,向量&,是对应于每个训练样本y 通过式(5)和式(8)可以分别得到训练好的字 的稀疏表示系数。 典D={d}1及投影矩阵集P={C}1。在重建 值得注意的是,传统的基于字典对的图像SR 过程中,利用字典原子d和投影矩阵C之间一一 方法在对原始样本数据进行训练得到字典之后便 对应的关系即可快速地重建出HR图像
像对训练集。 将每一幅 LR 图像 Ym 通过插值,得到 和 HR 图像一样大小的 LR 图像 Ym ′,然后对成对的 高低分辨率图像分别提取高低分辨率特征。 为了仅得到图像的高频信息,我们对每一幅 HR 图像 Xm 做如下处理: Em = Xm - Ym ′ (2) 然后对仅含有高频信息的图像 Em 进行分块, 将每一个大小为 n × n的图像块作为我们提取的一 个 n 维的 HR 特征向量 x i h∈R n 。 对于每一幅 LR 图 像 Ym ′,我们使用其一阶和二阶微分作为图像块的 梯度特征。 本文采用的 4 个滤波器如下: f1 = [ - 1 0 1] , f2 = f T 1 , f3 = [1 0 - 2 0 1] , f4 = f Τ 3 , (3) 式中 T 表示转置。 通过对图像 Ym ′ 进行滤波处理,即 可得到其相应的 4 幅梯度图像。 同样对这 4 幅梯度 图像进行分块,并在各自相同的位置分别取出一个 大小为 n × n 的图像块,将这 4 个图像块拉直连 接起来 得 到 一 个 4 × n 维 的 LR 特 征 向 量, 记 为 y ~ i l∈R 4n 。 由于多个滤波器处理后提取的 LR 特征维数增 加会使计算的复杂度提高,我们通过降维的方式来 减少后续训练和重建过程中计算的成本。 本文采 用 PCA 对 LR 特征向量进行降维处理,通过一个投 影算子 B∈R nl ×4n来降低 y ~ i l∈R 4n的维数,如下式: y i l = By ~ i l (4) 式中特征向量 y i l∈R nl,nl <4n。 如此即可得到在图 像 Ym ′和 Xm 相同位置处分别提取的特征 y i l 和 x i h 组 成的一一对应的特征对{y i l,x i h },进而将所有训练图 像提取的特征作为训练集的整个特征空间 I = { y i l, x i h },其中 i = 1,2,…,Ns,Ns 表示整个训练集中特征 的数量。 不同于式(1)中 Yang 等[13] 同时训练高低分辨 率字典对,本文仅将 LR 特征 y i l { } Ns i = 1⊆R nl作为训练 字典的样本,同时不必再训练 HR 字典。 如式(5), 我们利用 K - SVD [15] 训练字典 D = { dk }, k = 1, 2,…,K。 D = arg min {D,αi }∑i ‖y i l - Dαi‖2 2,s.t.‖αi‖0 ≤ s,∀i. (5) 式中:D∈R nl ×K ,向量 αi 是对应于每个训练样本 y i l 的稀疏表示系数。 值得注意的是,传统的基于字典对的图像 SR 方法在对原始样本数据进行训练得到字典之后便 舍弃了对它们的使用,而对于本文的算法这些原始 数据却仍是至关重要的。 我们将 D 中的每个原子 dk 作为聚类的中心,按式(6)计算每个原子 dk 与所 有的 LR 特征 y i l { } Ns i = 1的相关性。 T i k = 〈dk,y i l〉 (6) 式中:T i k表示第 k 个原子与第 i 个 LR 特征的内积; dk 表示训练字典 D 中的第 k 列原子;y i l 表示整个特 征空间 I 中的第 i 个 LR 特征。 然后选取对应于T i k 值最大的 M 个 y i l,将这些 y i l 作为一类。 设 dk 对应 类中的 LR 特征为 Yk = { y k1 l ,y k2 l ,…,y kM l },由于在整 个特征空间 I 中 y i l 和 x i h 总是成对出现的,从而可以 得到对应于 Yk 的 HR 特征 Xk = { x k1 h ,x k2 h ,…,x kM h }。 这样即可得到一个含有 Yk 和 Xk 的特征子空间,从 而将整个训练的特征空间 I 划分为 K 个特征子空 间。 相比于传统的聚类方法中某个训练样本只能 属于某个特定的类,我们这种新的聚类方式,可以 将同一个训练样本划分到多个类中共享,进而可以 提高训练的精度使得重建图像的效果更好。 最后,一旦得到了划分后的特征子空间,对每 一个字典原子 dk,在其对应的特征子空间上计算相 应的投影矩阵。 设 x ki h 和 y ki l 分别是 HR 特征 Xk 和 LR 特征 Yk 中的一对高低分辨率特征向量,它们的 维数分别为 n 和 nl。 本文通过学习 n 个线性回归函 数来独立预测 HR 特征向量中的 n 个值,在每一个 特征子空间上按式(7)来计算从 LR 特征 Yk∈R nl ×M 映 射 到 HR 特 征 Xk ∈ R n×M 的 回 归 投 影 矩 阵C ∗ k ∈R n×nl: C ∗ k = min Ck ‖Xk - CkYk‖2 2 (7) 以上的回归问题类似于一个线性最小二乘问 题,因此有如下闭式解: C ∗ k = XkY T k (YkY T k ) -1 (8) 最终可得到字典 D 中所有原子对应的投影矩 阵组成的集合 P = C ∗ k { } K k = 1 。 在整个训练过程中我 们充分使用了所有的原始高低分辨率图像含有的 信息来学习回归函数,以提高后续图像重建的精 度。 值得一提的是:以上的整个训练过程,包括字 典的训练、特征空间的划分以及投影矩阵的求解我 们都可以在线下进行计算。 2.2 重建阶段 通过式(5)和式(8)可以分别得到训练好的字 典 D = dk { } K k = 1及投影矩阵集 P = C ∗ k { } K k = 1 。 在重建 过程中,利用字典原子 dk 和投影矩阵 C ∗ k 之间一一 对应的关系即可快速地重建出 HR 图像。 ·10· 智 能 系 统 学 报 第 12 卷

第1期 赵志辉,等:基于稀疏表示与线性回归的图像快速超分辨率重建 ·11. 对于输入的一幅LR测试图像Y,同训练阶段中 6)分别在每个d对应的特征子空间上利用式 预处理过程一样,先将其进行bicubic插值得到LR (8)计算各自相应的投影矩阵C:,从而得到投影矩 图像Y,然后将Y进行分块得到图像块s,并提取对 阵集合P={C}1o 应于图像块s的LR特征y,i=1,2,…,J。为了保 由于训练阶段的所有计算过程均可在线下进 证训练和重建过程中整个框架的一致性,重建图像 行,这使得重建阶段更加高效。整个算法的重建阶 时我们仍使用字典原子d和LR特征y之间的相 段总结如下。 关性作为标签。根据训练阶段存储好的字典D,对 输入LR测试图像Y,字典D={d}1,投影 于每个y按照式(6)寻找D中T最大值对应的原 矩阵集P={C=1 子d。然后选择存储的投影矩阵集合P中d对应 输出HR重建图像X。 的投影矩阵C,按式(9)即可重建出HR特征。 I)对图像Y进行bicubic插值放大得到LR图 x'=Cy (9) 像了。 将HR特征x添加到对应的LR图像块s上, 2)对Y进行分块得到图像块s,并提取对应于 就可以得到我们想要的HR图像块sH: 图像块s的LR特征y。 SH=x+si (10) 3)利用式(6)寻找D中和y最邻近的原子d, 最终,通过将所有的图像块s整合到一起,并 得到P中d对应的投影矩阵C:。 且平均每个图像块的重叠区域来得到我们重建的 4)通过式(9)重建出HR特征x,再利用式 HR图像X。 (10)得到HR图像块sH。 从整个重建的过程中可以看出,同基于稀疏表 5)将所有的图像块s整合起来得到最终重建 示字典对的方法相比,我们提出的算法在重建图像 的HR图像X。 时省去了稀疏编码的部分,降低了计算的复杂度, 提高了图像SR重建的速度。 3 实验结果与分析 2.3本文算法的整体流程 实验编程环境为MATLAB2014,计算机的配置 我们将本文提出的算法称为快速线性回归算 为nter(R)Core(TM)i5-4460CPU@3.20Hz,主 法(fast linear regression,FLR)。重建算法的训练阶 段总结如下。 频为3.20GHz,8GB内存,windows7操作系统。 输入训练集中HR图像集X={X,X2,…, 实验选用比较常用的两个标准自然图像测试 集,一个是来自参考文献[16]中包含5幅图像的 X}和LR图像集Y={Y,Y2,…,Y}。 Set5测试集,另一个是来自参考文献[14]中包含14 输出训练字典D={d}1,投影矩阵集 幅图像的Set14测试集作为整个实验的测试图像 P=(C)10 集。同样,为了更好地体现与其他参考文献算法比 1)对Y,中的每一幅LR图像Y。进行插值放 大,得到和HR图像一样像素大小的LR图像Y。 较的公平性,实验中我们使用Yang等)提出的算 法中的91幅图像作为训练集图像,字典的大小同参 2)通过式(2)得到含有高频信息的图像E,并 考文献[11,14]一样为1024列,对LR图像分别进 对其进行分块作为提取的HR特征x。 行2倍和3倍尺度的超分辨率重建。由于人的视觉 3)利用式(3)中的滤波器对图像Y进行滤波提 感知系统对亮度的变化更加敏感,先将彩色图像转 取梯度特征,利用PCA对进行降维得到LR特 换到YUV颜色空间,然后仅对亮度信号Y进行放大 征y,然后得到由一一对应的特征对{,x}组成的 重建,而其他信号通过简单的bicubic插值来放大。 整个特征空间训练集I={y,x}。 整个实验中,我们对比了比较有代表性的基于邻域 4)将LR特征y)二,作为训练字典的样本,利 嵌入和稀疏表示的算法,以及基于回归和快速重建 用式(5)学习字典D={d}10 的算法。除了主观的视觉评价外,本文采用峰值信 5)将D中的每个原子d作为聚类的中心,利 噪比(PSNR)以及图像重建的运行时间分别评价图 用式(6)对特征空间1进行划分,同时得到对应于 像的重建质量和重建速度。 d的LR特征集Y={y,y,…,y"}和HR特征集 由于篇幅有限,这里我们只展示2幅图像通过 X={x,x,…,x}组成的特征子空间。 不同方法进行3倍重建的视觉效果。为了更好地观
对于输入的一幅 LR 测试图像 Y,同训练阶段中 预处理过程一样,先将其进行 bicubic 插值得到 LR 图像 Y ~ ,然后将 Y ~ 进行分块得到图像块 s i L ,并提取对 应于图像块 s i L 的 LR 特征 y i ,i = 1,2,…,J。 为了保 证训练和重建过程中整个框架的一致性,重建图像 时我们仍使用字典原子 dk 和 LR 特征 y i 之间的相 关性作为标签。 根据训练阶段存储好的字典 D,对 于每个 y i 按照式(6)寻找 D 中 T i k 最大值对应的原 子 dk。 然后选择存储的投影矩阵集合 P 中 dk 对应 的投影矩阵 C ∗ k ,按式(9)即可重建出 HR 特征。 x i = C ∗ k y i (9) 将 HR 特征 x i 添加到对应的 LR 图像块 s i L 上, 就可以得到我们想要的 HR 图像块 s i H : s i H = x i + s i L (10) 最终,通过将所有的图像块 s i H 整合到一起,并 且平均每个图像块的重叠区域来得到我们重建的 HR 图像 X。 从整个重建的过程中可以看出,同基于稀疏表 示字典对的方法相比,我们提出的算法在重建图像 时省去了稀疏编码的部分,降低了计算的复杂度, 提高了图像 SR 重建的速度。 2.3 本文算法的整体流程 我们将本文提出的算法称为快速线性回归算 法(fast linear regression,FLR)。 重建算法的训练阶 段总结如下。 输入 训练集中 HR 图像集 Xh = {X1 ,X2 ,…, Xu }和 LR 图像集 Yl = {Y1 ,Y2 ,…,Yu }。 输出 训 练 字 典 D = dk { } K k = 1 , 投 影 矩 阵 集 P = C ∗ k { } K k = 1 。 1)对 Yl 中的每一幅 LR 图像 Ym 进行插值放 大,得到和 HR 图像一样像素大小的 LR 图像 Ym ′。 2)通过式(2)得到含有高频信息的图像 Em ,并 对其进行分块作为提取的 HR 特征 x i h 。 3)利用式(3)中的滤波器对图像 Ym ′进行滤波提 取梯度特征 y ~ i l,利用 PCA 对 y ~ i l 进行降维得到 LR 特 征 y i l,然后得到由一一对应的特征对{y i l,x i h }组成的 整个特征空间训练集 I = {y i l,x i h }。 4)将 LR 特征 y i l { } Ns i = 1作为训练字典的样本,利 用式(5)学习字典 D = dk { } K k = 1 。 5)将 D 中的每个原子 dk 作为聚类的中心,利 用式(6)对特征空间 I 进行划分,同时得到对应于 dk 的 LR 特征集 Yk = {y k1 l ,y k2 l ,…,y kM l }和 HR 特征集 Xk = {x k1 h ,x k2 h ,…,x kM h }组成的特征子空间。 6)分别在每个 dk 对应的特征子空间上利用式 (8)计算各自相应的投影矩阵 C ∗ k ,从而得到投影矩 阵集合 P = C ∗ k { } K k = 1 。 由于训练阶段的所有计算过程均可在线下进 行,这使得重建阶段更加高效。 整个算法的重建阶 段总结如下。 输入 LR 测试图像 Y,字典 D = dk { } K k = 1 ,投影 矩阵集 P = C ∗ k { } K k = 1 。 输出 HR 重建图像 X。 1)对图像 Y 进行 bicubic 插值放大得到 LR 图 像 Y ~ 。 2)对 Y ~ 进行分块得到图像块 s i L ,并提取对应于 图像块 s i L 的 LR 特征 y i 。 3)利用式(6)寻找 D 中和 y i 最邻近的原子 dk, 得到 P 中 dk 对应的投影矩阵 C ∗ k 。 4) 通过式( 9) 重建出 HR 特征 x i ,再利用式 (10)得到 HR 图像块 s i H 。 5)将所有的图像块 s i H 整合起来得到最终重建 的 HR 图像 X。 3 实验结果与分析 实验编程环境为 MATLAB 2014,计算机的配置 为 Inter(R) Core(TM) i5-4460 CPU @ 3.20 Hz,主 频为 3.20 GHz,8 GB 内存,windows 7 操作系统。 实验选用比较常用的两个标准自然图像测试 集,一个是来自参考文献[16] 中包含 5 幅图像的 Set5 测试集,另一个是来自参考文献[14]中包含 14 幅图像的 Set14 测试集作为整个实验的测试图像 集。 同样,为了更好地体现与其他参考文献算法比 较的公平性,实验中我们使用 Yang 等[13] 提出的算 法中的 91 幅图像作为训练集图像,字典的大小同参 考文献[11,14]一样为1 024 列,对 LR 图像分别进 行 2 倍和 3 倍尺度的超分辨率重建。 由于人的视觉 感知系统对亮度的变化更加敏感,先将彩色图像转 换到 YUV 颜色空间,然后仅对亮度信号 Y 进行放大 重建,而其他信号通过简单的 bicubic 插值来放大。 整个实验中,我们对比了比较有代表性的基于邻域 嵌入和稀疏表示的算法,以及基于回归和快速重建 的算法。 除了主观的视觉评价外,本文采用峰值信 噪比(PSNR)以及图像重建的运行时间分别评价图 像的重建质量和重建速度。 由于篇幅有限,这里我们只展示 2 幅图像通过 不同方法进行 3 倍重建的视觉效果。 为了更好地观 第 1 期 赵志辉,等:基于稀疏表示与线性回归的图像快速超分辨率重建 ·11·

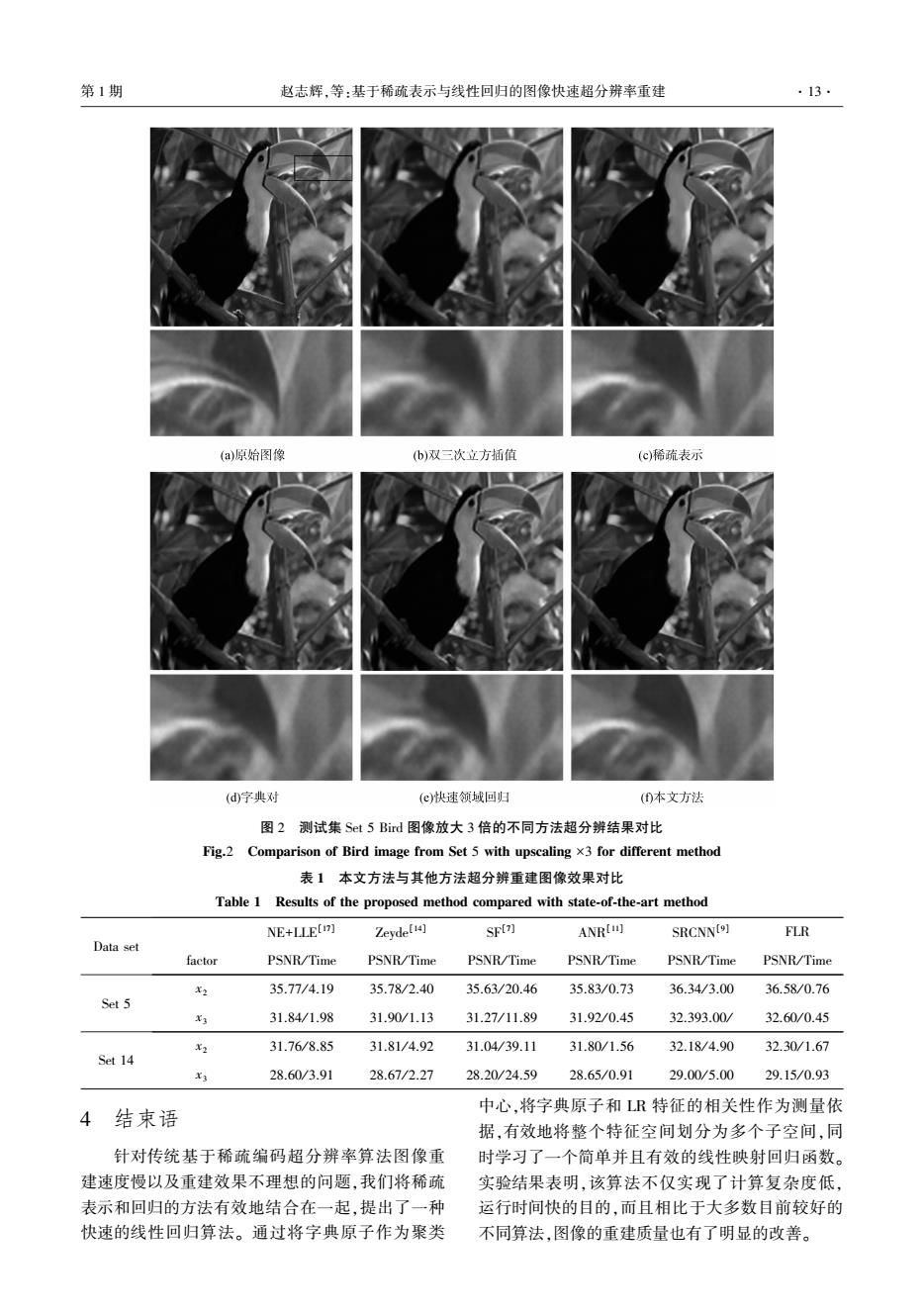
·12. 智能系统学报 第12卷 察图像重建的效果,我们对两幅图像的局部均进行 本文提出的快速线性回归算法(FLR)要明显好于 了放大处理。其中,图1是对来自于测试集St14 基于邻域嵌入和稀疏表示的算法以及其他方法。 中像素大小为768×512的Monarch图像重建的结 其中,图像的重建质量为29.15dB,重建时间仅为 果,图2是对来自于测试集St5中像素大小为288× 0.93s。比基于邻域嵌入的算法(NE+LLE)[6] 288的Bid图像重建的结果。从图1和图2中可以 PSNR值高0.55dB,速度快4.2倍:比Zeyde等 看出,图(b)bicubic插值方法重建的图像过于平滑 PSNR值高0.48dB,速度也要快2.4倍。相比于单 并且存在振铃效应;图(c)Yang等[1)的方法在边缘 独基于线性回归(SF)[)的方法,其实验结果来自于 处有着锯齿效应:图(d)Zeyde等[]与图(e)》 参考文献[18],我们的FLR算法平均PSNR要比其 ANR)的方法相差不多,基本可以保持图像的边缘 高0.95dB,由于两种方法提取的特征不同,我们的 结构,但某些纹理等细节之处仍不是很好:从图() 算法速度上要快26.4倍之多。和目前最快重建算 可见本文的FLR方法在重建纹理细节和消除伪边 法之一的ANR四相比,本文的方法运行时间与其 缘与锯齿两方面均取得了不错的效果,重建的图像 相差不多,但图像重建的PSNR要高0.50dB。另 更加清晰边缘更加锐利,在视觉效果上更接近于原 外,同最近提出的卷积神经网(SRCNN)[)]方法相 始的HR图像。 比,它的实验结果来自于参考文献[19],我们的 表1定量地展示了不同算法在测试图像集 FLR算法PSNR也要高0.15dB,速度提高5.4倍。 Set5和Setl4上针对不同放大因子的平均PSNR 值得一提的是,SRCNN需要通过GPU训练大约 和运行时间。相比于其他评价指标[7),PSNR的 72h,而本文的FLR仅需要花费24min就可以完成 值可以更好地代表人的感知效果。而运行时间的 训练。另外,我们的算法并没有进行优化,也没有 快慢是体现算法能否很好地应用到实际中的重要 通过并行计算来加速,这一切都为以后在实际应用 指标。从表1中最后一行的实验数据可以看出, 中提供了极大的可能性。 (a)原始图像 (b)双三次立方插值 (c)稀疏表示 (d字典对 (e快速领域回归 (①本文方法 图1测试集Set14 Monarch图像放大3倍的不同方法超分辨结果对比 Fig.1 Comparison of Monarch image from Set 14 with upscaling x3 for different method
察图像重建的效果,我们对两幅图像的局部均进行 了放大处理。 其中,图 1 是对来自于测试集 Set 14 中像素大小为 768 × 512 的 Monarch 图像重建的结 果,图 2 是对来自于测试集 Set 5 中像素大小为288× 288 的 Bird 图像重建的结果。 从图 1 和图 2 中可以 看出,图(b) bicubic 插值方法重建的图像过于平滑 并且存在振铃效应;图(c)Yang 等[13]的方法在边缘 处 有 着 锯 齿 效 应; 图 ( d ) Zeyde 等[14] 与 图 ( e ) ANR [11]的方法相差不多,基本可以保持图像的边缘 结构,但某些纹理等细节之处仍不是很好;从图( f) 可见本文的 FLR 方法在重建纹理细节和消除伪边 缘与锯齿两方面均取得了不错的效果,重建的图像 更加清晰边缘更加锐利,在视觉效果上更接近于原 始的 HR 图像。 表 1 定量地展示了不同算法在测试图像集 Set 5和 Set 14 上针对不同放大因子的平均 PSNR 和运行时间。 相比于其他评价指标[17] ,PSNR 的 值可以更好地代表人的感知效果。 而运行时间的 快慢是体现算法能否很好地应用到实际中的重要 指标。 从表 1 中最后一行的实验数据可以看出, 本文提出的快速线性回归算法( FLR) 要明显好于 基于邻域嵌入和稀疏表示的算法以及其他方法。 其中,图像的重建质量为 29.15 dB,重建时间仅为 0.93 s。 比 基 于 邻 域 嵌 入 的 算 法 (NE+LLE) [16] PSNR 值高 0.55 dB,速度快 4.2 倍;比 Zeyde 等[14] PSNR 值高0.48 dB,速度也要快 2.4 倍。 相比于单 独基于线性回归(SF) [7]的方法,其实验结果来自于 参考文献[18],我们的 FLR 算法平均 PSNR 要比其 高 0.95 dB,由于两种方法提取的特征不同,我们的 算法速度上要快 26.4 倍之多。 和目前最快重建算 法之一的 ANR [11] 相比,本文的方法运行时间与其 相差不多,但图像重建的 PSNR 要高0 50 dB。 另 外,同最近提出的卷积神经网( SRCNN) [9] 方法相 比,它的实验结果来自于参考文献[ 19],我们的 FLR 算法 PSNR 也要高0.15 dB,速度提高 5. 4 倍。 值得一提的是, SRCNN 需要通过 GPU 训练大约 72 h,而本文的 FLR 仅需要花费 24 min 就可以完成 训练。 另外,我们的算法并没有进行优化,也没有 通过并行计算来加速,这一切都为以后在实际应用 中提供了极大的可能性。 图 1 测试集 Set 14 Monarch 图像放大 3 倍的不同方法超分辨结果对比 Fig. 1 Comparison of Monarch image from Set 14 with upscaling ×3 for different method ·12· 智 能 系 统 学 报 第 12 卷
第1期 赵志辉,等:基于稀疏表示与线性回归的图像快速超分辨率重建 ·13 (a)原始图像 b)双三次立方插值 (c)稀疏表示 (d字典对 (e)快速领域回归 (①本文方法 图2测试集St5Bird图像放大3倍的不同方法超分辨结果对比 Fig.2 Comparison of Bird image from Set 5 with upscaling x3 for different method 表1本文方法与其他方法超分辨重建图像效果对比 Table 1 Results of the proposed method compared with state-of-the-art method NE+LLE07] Zeyde[4] SF7 ANRU SRCNNI9] FLR Data set factor PSNR/Time PSNR/Time PSNR/Time PSNR/Time PSNR/Time PSNR/Time x2 35.77/4.19 35.78/2.40 35.63/20.46 35.83/0.73 36.34/3.00 36.58/0.76 Set5 33 31.84/1.98 31.90/1.13 31.27/11.89 31.92/0.45 32.393.00/ 32.60/0.45 2 31.76/8.85 31.81/4.92 31.04/39.11 31.80/1.56 32.18/4.90 32.30/1.67 Set 14 28.60/3.91 28.67/2.27 28.20/24.59 28.65/0.91 29.00/5.00 29.15/0.93 4结束语 中心,将字典原子和LR特征的相关性作为测量依 据,有效地将整个特征空间划分为多个子空间,同 针对传统基于稀疏编码超分辨率算法图像重 时学习了一个简单并且有效的线性映射回归函数。 建速度慢以及重建效果不理想的问题,我们将稀疏 实验结果表明,该算法不仅实现了计算复杂度低, 表示和回归的方法有效地结合在一起,提出了一种 运行时间快的目的,而且相比于大多数目前较好的 快速的线性回归算法。通过将字典原子作为聚类 不同算法,图像的重建质量也有了明显的改善
图 2 测试集 Set 5 Bird 图像放大 3 倍的不同方法超分辨结果对比 Fig.2 Comparison of Bird image from Set 5 with upscaling ×3 for different method 表 1 本文方法与其他方法超分辨重建图像效果对比 Table 1 Results of the proposed method compared with state⁃of⁃the⁃art method Data set NE+LLE [17] Zeyde [14] SF [7] ANR [11] SRCNN [9] FLR factor PSNR/ Time PSNR/ Time PSNR/ Time PSNR/ Time PSNR/ Time PSNR/ Time Set 5 x2 35.77 / 4.19 35.78 / 2.40 35.63 / 20.46 35.83 / 0.73 36.34 / 3.00 36.58 / 0.76 x3 31.84 / 1.98 31.90 / 1.13 31.27 / 11.89 31.92 / 0.45 32.393.00 / 32.60 / 0.45 Set 14 x2 31.76 / 8.85 31.81 / 4.92 31.04 / 39.11 31.80 / 1.56 32.18 / 4.90 32.30 / 1.67 x3 28.60 / 3.91 28.67 / 2.27 28.20 / 24.59 28.65 / 0.91 29.00 / 5.00 29.15 / 0.93 4 结束语 针对传统基于稀疏编码超分辨率算法图像重 建速度慢以及重建效果不理想的问题,我们将稀疏 表示和回归的方法有效地结合在一起,提出了一种 快速的线性回归算法。 通过将字典原子作为聚类 中心,将字典原子和 LR 特征的相关性作为测量依 据,有效地将整个特征空间划分为多个子空间,同 时学习了一个简单并且有效的线性映射回归函数。 实验结果表明,该算法不仅实现了计算复杂度低, 运行时间快的目的,而且相比于大多数目前较好的 不同算法,图像的重建质量也有了明显的改善。 第 1 期 赵志辉,等:基于稀疏表示与线性回归的图像快速超分辨率重建 ·13·

·14· 智能系统学报 第12卷 参考文献: [14]ZEYDE R,ELAD M,PROTTER M.On single image scale- up using sparse-representations M]//BOISSONNAT J D, [1]BHAVSAR A V.Range image super-resolution via reconstruction CHENIN P,COHEN A,et al.Curves and Surfaces.Berlin of sparse range data[C]//Proceedings of the 2013 Intemational Heidelberg:Springer,2012:711-730. Conference on Intelligent Systems and Signal Processing.Gujarat. [15]AHARON M,ELAD M,BRUCKSTEIN A.rmK-SVD: ndia.2013:198-20B. an algorithm for designing overcomplete dictionaries for [2]YANG Minchun,WANG Y C F.A self-learning approach to sparse representation [J].IEEE transactions on signal single image super-resolution J].IEEE transactions on processing,2006,54(11):4311-4322. nultimedia,2013,15(3):498-508. [16]BEVILACQUA M,ROUMY A,GUILLEMOT C,et al. [3]PARK S C,PARK M K,KANG M G.Super-resolution Low-complexity single-image super-resolution based on image reconstruction:a technical overview[J].IEEE signal nonnegative neighbor embedding C ]//Proceedings of processing magazine,2003,20(3):21-36. British Machine Vision Conference 2012.Guildford, [4]LI Xin,ORCHARD M T.New edge-directed interpolation Surrey,UK,2012:1-10. [J].IEEE transactions on image processing,2001,10 [17]YANG C Y,MA C,YANG M H.Single-image super-resolution: (10):1521-1527. a benchmark[M]//FLEET D,PAJDLA T,SCHIELE B. [5]FATTAL R.Image upsampling via imposed edge statistics et al.Computer Vision-ECCV 2014.Switzerland:Springer, [J].ACM transactions on graphics (TOG),2007,26 2014:372-386. (3):95. [18]TIMOFTE R,DE SMET V,VAN GOOL L.A+:adjusted [6]FREEMAN W T,JONES T R,PASZTOR E C.Example- anchored neighborhood regression for fast super-resolution based super-resolution[].IEEE computer graphics and [M]//CREMERS D.REID I,SAITO H,et al.Computer applications,2002,22(2):56-65. Vision-ACCV 2014.Switzerland:Springer,2014:111-126. [7]YANG C Y,YANG M H.Fast direct super-resolution by [19]SCHULTER S,LEISTNER C,BISCHOF H.Fast and simple functions C ]//Proceedings of 2013 IEEE accurate image upscaling with super-resolution forests International Conference on Computer Vision.Sydney, [C]//Proceedings of 2015 IEEE Conference on Computer Australia,2013:561-568. Vision and Pattern Recognition.Boston,MA,USA, [8 SUN Jian,XU Zongben,SHUM H Y,et al.Image 2015:3791-3799 super-resolution using gradient profile prior [C]/ 作者简介: Proceedings of 2008 IEEE Conference on Computer Vision 赵志辉,男,1990年生,硕士研究 and Pattern Recognition.Anchorage,USA,2008:1-8. 生,主要研究方向为稀疏表示与图像超 [9]DONG Chao,LOY CC,HE Kaiming,et al.Learning a 分辨率。 deep convolutional network for image super-resolution M ]//FLEET D,PAJDLA T,SCHIELE B,et al. Computer Vision-ECCV 2014.Switzerland:Springer, 2014:184-199. [10]OLSHAUSEN B A,FIELD D J.Sparse coding with an 赵瑞珍,男.1975年生,教授,博士 overcomplete basis set:a strategy employed by V1[J]. 生导师,博士,主要研究方向为图像与 Vision research,1997,37(23):3311-3325. 信号处理算法、压缩感知与稀疏表示、 [11]TIMOFTE R.DE V,VAN GOOL L.Anchored neighborhood 信息感知域智能信息处理。主持参与 regression for fast example-based super-resolution [C]/ 国家自然科学基金、“863”计划等多项 Proceedings of 2013 IEEE Intemational Conference on Computer 项目。 Vision.Sydney,Australia,2013:190-1927. [12]CHANG Hong,YEUNG D Y,XIONG Yimin.Super-resolution through neighbor embedding [C]//Proceedings of the 2004 岑翼刚,男,1978年生,教授,博土 IEEE Conference on Computer Vision and Patter Recognition. 生导师,博士,主要研究方向为小波分 Washington,DC.USA,2004. 析、压缩感知、图像处理。发表学术论 [13]YANG Jianchao,WRIGHT J,HUANG T S,et al.Image 文40余篇。 super-resolution via sparse representation [J].IEEE transactions on image processing,2010,19 (11); 2861-2873
参考文献: [1]BHAVSAR A V. Range image super⁃resolution via reconstruction of sparse range data[C] / / Proceedings of the 2013 International Conference on Intelligent Systems and Signal Processing. Gujarat, India, 2013: 198-203. [2]YANG Minchun, WANG Y C F. A self⁃learning approach to single image super⁃resolution [ J ]. IEEE transactions on multimedia, 2013, 15(3): 498-508. [3] PARK S C, PARK M K, KANG M G. Super⁃resolution image reconstruction: a technical overview[J]. IEEE signal processing magazine, 2003, 20(3): 21-36. [4] LI Xin, ORCHARD M T. New edge⁃directed interpolation [J]. IEEE transactions on image processing, 2001, 10 (10): 1521-1527. [5] FATTAL R. Image upsampling via imposed edge statistics [J]. ACM transactions on graphics ( TOG), 2007, 26 (3): 95. [6] FREEMAN W T, JONES T R, PASZTOR E C. Example⁃ based super⁃resolution [ J ]. IEEE computer graphics and applications, 2002, 22(2): 56-65. [7] YANG C Y, YANG M H. Fast direct super⁃resolution by simple functions [ C ] / / Proceedings of 2013 IEEE International Conference on Computer Vision. Sydney, Australia, 2013: 561-568. [8 ] SUN Jian, XU Zongben, SHUM H Y, et al. Image super⁃resolution using gradient profile prior [ C ] / / Proceedings of 2008 IEEE Conference on Computer Vision and Pattern Recognition. Anchorage, USA, 2008: 1-8. [9] DONG Chao, LOY C C, HE Kaiming, et al. Learning a deep convolutional network for image super⁃resolution [ M ] / / FLEET D, PAJDLA T, SCHIELE B, et al. Computer Vision⁃ECCV 2014. Switzerland: Springer, 2014: 184-199. [10] OLSHAUSEN B A, FIELD D J. Sparse coding with an overcomplete basis set: a strategy employed by V1 [ J]. Vision research, 1997, 37(23): 3311-3325. [11] TIMOFTE R, DE V, VAN GOOL L. Anchored neighborhood regression for fast example⁃based super⁃resolution [ C ] / / Proceedings of 2013 IEEE International Conference on Computer Vision. Sydney, Australia, 2013: 1920-1927. [12]CHANG Hong, YEUNG D Y, XIONG Yimin. Super⁃resolution through neighbor embedding [C] / / Proceedings of the 2004 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC, USA, 2004. [13]YANG Jianchao, WRIGHT J, HUANG T S, et al. Image super⁃resolution via sparse representation [ J ]. IEEE transactions on image processing, 2010, 19 ( 11 ): 2861-2873. [14]ZEYDE R, ELAD M, PROTTER M. On single image scale⁃ up using sparse⁃representations [ M] / / BOISSONNAT J D, CHENIN P, COHEN A, et al. Curves and Surfaces. Berlin Heidelberg: Springer, 2012: 711-730. [15] AHARON M, ELAD M, BRUCKSTEIN A. rmK—SVD: an algorithm for designing overcomplete dictionaries for sparse representation [ J ]. IEEE transactions on signal processing, 2006, 54(11): 4311-4322. [16] BEVILACQUA M, ROUMY A, GUILLEMOT C, et al. Low⁃complexity single⁃image super⁃resolution based on nonnegative neighbor embedding [ C ] / / Proceedings of British Machine Vision Conference 2012. Guildford, Surrey, UK, 2012: 1-10. [17]YANG C Y, MA C, YANG M H. Single⁃image super⁃resolution: a benchmark[M] / / FLEET D, PAJDLA T, SCHIELE B, et al. Computer Vision⁃ECCV 2014. Switzerland: Springer, 2014:372-386. [18] TIMOFTE R, DE SMET V, VAN GOOL L. A+: adjusted anchored neighborhood regression for fast super⁃resolution [M] / / CREMERS D, REID I, SAITO H, et al. Computer Vision—ACCV 2014. Switzerland: Springer, 2014: 111-126. [19] SCHULTER S, LEISTNER C, BISCHOF H. Fast and accurate image upscaling with super⁃resolution forests [C] / / Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA, USA, 2015: 3791-3799. 作者简介: 赵志辉,男,1990 年生,硕士研究 生,主要研究方向为稀疏表示与图像超 分辨率。 赵瑞珍,男,1975 年生,教授,博士 生导师,博士,主要研究方向为图像与 信号处理算法、压缩感知与稀疏表示、 信息感知域智能信息处理。 主持参与 国家自然科学基金、“863”计划等多项 生导师,博士,主要研究方向为小波 岑翼刚,男,1978 年生,教授,博士 分 析、压缩感知、图像处理。 发表学术论 文 40 余篇。 ·14· 智 能 系 统 学 报 第 12 卷 项目