
第11卷第4期 智能系统学报 Vol.11 No.4 2016年8月 CAAI Transactions on Intelligent Systems Aug.2016 D0I:10.11992/6is.201606008 网络出版地址:http:/www.cnki.net/kcms/detail/23.1538.TP.20160808.0830.016.html 横向拆分形势背景下的快速规则提取方法 温云霞1,王俊红12 (1.山西大学计算机与信息技术学院,山西太原030006:2.计算智能与中文信息处理教育部重点实验室,山西太原030006) 摘要:概念格是进行数据挖掘和规则提取的一种有效工具。目前已经提出的概念格上的规则提取方法大多是针 对整个形式背景,得到的规则数目较多,规则集规模较大,且这种规则结构不便于两个规则集的合并。针对这个问 题,本文提出一种伪规则的概念,并给出渐近式获取伪规则的方法:同时证明了通过伪规则集,用户可以根据自己的 兴趣有选择地从伪规则集合中产生出所需的蕴含规则:提出了将两个伪规则集进行合并的方法,从而用户可以通过 拆分合并的思想来获取规则集:最后通过实验分析验证了算法的有效性。 关键词:概念格:形式背景:子背景:规则提取:伪规则:规则合并 中图分类号:TP18文献标志码:A文章编号:1673-4785(2016)04-0526-08 中文引用格式:温云覆,王俊红.横向拆分形势背景下的快速规则提取方法[J].智能系统学报,2016,11(4):526-533. 英文引用格式:WEN Yunxia,WANG Junhong.Research on a fast method for extracting rules based on horizontal splitting[J]. CAAI Transactions on Intelligent Systems,2016,11(4):526-533. Research on a fast method for extracting rules based on horizontal splitting WEN Yunxia',WANG Junhong'2 (1.School of Computer and Information Technology,Shanxi University,Taiyuan 030006,China;2.Key Laboratory of Computational Intelligence and Chinese Information Processing of Ministry of Education,Taiyuan 030006,China) Abstract:The concept lattice is a valid tool for data mining and rule extraction.The methods of extracting rules from the concept lattice are based mainly on the whole formal context,but this results in a large number of rules and rule sets,and it is difficult to combine the rule sets subsets with the original structure.In this paper,the con- cept of a pseudo rule set and its incremental determination method is given;users can get the needed implication rules from the pseudo rule set,according to their interests.A method of combining two pseudo rule sets is then giv- en.Users may therefore get their rule sets by dividing or combining these sets.The effectiveness of this method is proven through experiment analysis. Keywords:concept lattice;formal context;subcontext;extracting rules;pseudo rule;combination of the rule set 概念格[-)是数据分析和知识处理的一种有力的形式背景下概念格构造的复杂度很高,一个可行 工具,由Wl)在1982年提出。近年来获得了飞的方法是把形式背景拆分成多个子形式背景) 速的发展,概念格理论)已经被广泛地应用于软件 分别存储和处理。这种方法的思想是在每个子形式 工程、知识工程、数据挖掘和信息检索等领域。 背景上构造概念格并通过子概念格的合并得到所需 在多源信息系统和数据分布式存储与并行处理 的概念格。概念格的分布式处理大大减少了概念格 中,数据都是分别存储和处理的。另一方面,在较大 的构造复杂度,但对子概念格上获得的规则集之间 的联系,以及不通过子概念格合并直接利用规则集 收稿日期:2016-06-02.网络出版日期:2016-08-08. 基金项目:国家自然科学基金项目(612022018,61303008). 融合产生新规则的研究还较少。 通信作者:王俊红.E-mail:wjhwjh@sxu.cd.em 概念格表明了概念之间的泛化和例化关系,这
第 11 卷第 4 期 智 能 系 统 学 报 Vol.11 №.4 2016 年 8 月 CAAI Transactions on Intelligent Systems Aug. 2016 DOI:10.11992 / tis.201606008 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20160808.0830.016.html 横向拆分形势背景下的快速规则提取方法 温云霞1 , 王俊红1,2 (1. 山西大学 计算机与信息技术学院,山西 太原 030006; 2. 计算智能与中文信息处理教育部重点实验室,山西 太原 030006) 摘 要:概念格是进行数据挖掘和规则提取的一种有效工具。 目前已经提出的概念格上的规则提取方法大多是针 对整个形式背景,得到的规则数目较多,规则集规模较大,且这种规则结构不便于两个规则集的合并。 针对这个问 题,本文提出一种伪规则的概念,并给出渐近式获取伪规则的方法;同时证明了通过伪规则集,用户可以根据自己的 兴趣有选择地从伪规则集合中产生出所需的蕴含规则;提出了将两个伪规则集进行合并的方法,从而用户可以通过 拆分合并的思想来获取规则集;最后通过实验分析验证了算法的有效性。 关键词:概念格; 形式背景; 子背景; 规则提取; 伪规则; 规则合并 中图分类号: TP18 文献标志码:A 文章编号:1673-4785(2016)04-0526-08 中文引用格式:温云霞, 王俊红. 横向拆分形势背景下的快速规则提取方法[J]. 智能系统学报, 2016, 11(4): 526-533. 英文引用格式:WEN Yunxia, WANG Junhong. Research on a fast method for extracting rules based on horizontal splitting[ J]. CAAI Transactions on Intelligent Systems, 2016, 11(4): 526-533. Research on a fast method for extracting rules based on horizontal splitting WEN Yunxia 1 , WANG Junhong 1,2 (1. School of Computer and Information Technology, Shanxi University, Taiyuan 030006, China; 2. Key Laboratory of Computational Intelligence and Chinese Information Processing of Ministry of Education, Taiyuan 030006, China) Abstract:The concept lattice is a valid tool for data mining and rule extraction. The methods of extracting rules from the concept lattice are based mainly on the whole formal context, but this results in a large number of rules and rule sets, and it is difficult to combine the rule sets subsets with the original structure. In this paper, the con⁃ cept of a pseudo rule set and its incremental determination method is given; users can get the needed implication rules from the pseudo rule set, according to their interests. A method of combining two pseudo rule sets is then giv⁃ en. Users may therefore get their rule sets by dividing or combining these sets. The effectiveness of this method is proven through experiment analysis. Keywords: concept lattice; formal context; subcontext; extracting rules; pseudo rule; combination of the rule set 收稿日期:2016-06-02. 网络出版日期:2016-08-08. 基金项目:国家自然科学基金项目(612022018,61303008). 通信作者:王俊红. E⁃mail:wjhwjh@ sxu.edu.cn. 概念格[1-3]是数据分析和知识处理的一种有力 工具,由 Wille [1] 在 1982 年提出。 近年来获得了飞 速的发展,概念格理论[2] 已经被广泛地应用于软件 工程、知识工程、数据挖掘和信息检索等领域。 在多源信息系统和数据分布式存储与并行处理 中,数据都是分别存储和处理的。 另一方面,在较大 的形式背景下概念格构造的复杂度很高,一个可行 的方法是把形式背景拆分成多个子形式背景[4-5] , 分别存储和处理。 这种方法的思想是在每个子形式 背景上构造概念格并通过子概念格的合并得到所需 的概念格。 概念格的分布式处理大大减少了概念格 的构造复杂度,但对子概念格上获得的规则集之间 的联系,以及不通过子概念格合并直接利用规则集 融合产生新规则的研究还较少。 概念格表明了概念之间的泛化和例化关系,这

第4期 温云霞,等:横向拆分形势背景下的快速规则提取方法 ·527· 种层次关系有利于规则提取[6-10。在概念格的规则 例化关系,可作为数据分析与知识获取的一种有效 提取方面学者们进行了一定的研究,王志海等[6-刃 工具。形式背景1上对应的概念格如图1。 提出了概念格上规则提取的一般算法和渐近式算法 表1形式背景 并研究了概念格与关联规则发现。针对不同的形式 Table 1 Formal context 背景有不同的规则提取方法,如李金海等[8]提出的 AU a b c d e f g h i 在决策形式背景上的规则提取。还有一些提取规则 1110000100 的改进方法,如梁吉业等)提出的基于概念格的规 2110000110 则产生集挖掘算法等。近来对概念格的研究也主要 3111 00011 0 是围绕概念格的约简、缩小概念格的构造和规则提 41010001 取的复杂度[-]。但上述规则提取方法,一方面大 5110101000 都是针对一个形式背景,且得到的规则集数量较多、 规模较大。而用户有时可能只需要一部分感兴趣的 (12345,a) 规则信息,而从规模较大的规则集中找出这些感兴 (1235.ab) (1234,g) 趣的规则信息也是一个难题。另一方面规则形式大 (123,abg (234,ag 都是文献[6]和文献[10]提出的规则形式,这种规 则结构不便于两个规则集之间的合并研究。 (23.abgh) (34.acgh) 针对上述问题,本文提出一种伪规则的概念,给 (3.abcgh) (4.acgh0) 出渐近式获取伪规则的方法。同时说明了通过伪规 (5abdf) 则集,用户可以得到原概念格上的蕴含规则。伪规 则集的规模相对较小,其结构适于两个规则集的合 (o.abcdefghi) 并。用户可以根据自己的兴趣有选择地从伪规则集 1 L(U,(a,b,c,dffg,h,i,) 合中产生出所需的蕴含规则。在伪规则集的基础 Fig.1 L(U,a,b,c,df,g,h,i],I) 上,提出了将两个伪规则集进行合并的方法,通过此 1.2规则提取 方法用户可以直接利用伪规则集得到范围更大的规 下面简要介绍由文献[6]提出的规则提取方法 则集。最后通过实验验证了该方法的有效性。 的主要依据定理,该方法的基本思想是依据其双亲 1基本定义 节点即直接泛化的个数及形式来对格中每个节点生 成其无冗余的所有规则。关于此方法的详细描述可 1.1概念格 参考文献[6]。 在形式概念分析】中,形式背景用一个三元组 定理1[6]如果格中节点H=(X1,Y)只有一 K=(U,A,I)表示,如表1所示,其中U是对象集 个双亲节点M=(X2,Y2),则H所产生的规则前件 合,A是属性集合,I是U和A之间定义的一个二元 只能为单个描述符,且Hp∈{Y,-Y2},都存在一 关系。对于Hx∈U,Hy∈A,若x具有属性y,那 条无冗余规则p一Y,-P。 么x与y之间具有关系1,记为x山。关系I与一个 定理26]如果格中节点H=(X1,Y)具有d 偏序集合对应,并且这偏序集合产生一种格结构如 个双亲节点M(X2,Y2),M2(X3,Y),…,M(X, 图1所示。这种由I诱导的格L就称为一个概念 Y),则对于任意一个描述符p∈{Y,-(Y2UY3U 格。格中的每个节点是一个序偶,记为(X,),称 …UY)},都存在一条规则p→Y-p。 X是概念(X,)的外延,Y是概念(X,Y)的内涵。 定理36]若果格中节点H=(X1,Y)具有两 两者之间满足如下两个映射函数∫和g: 个双亲节点M(X2,Y2)和M2(X,Y),则对于每个 fx)={y∈A|Hx∈X,xy} 元素P1∈{Y2-Y2∩Y}和Hp2∈{Y,-Y2∩ g(y)={x∈U1Hy∈Y,xly} 格中所有概念的集合用L(K)表示。给定格中 Y3},都存在一条规则P1P2→Y-PP2。 注:只有当‖X‖>k时,才可能有前件至多 两个概念C,=(X1,Y),C2=(X2,Y2),满足X,C 为k个描述符的规则,并且规则前件的描述符个数 X2,则称(X,Y)是(X2,Y2)的子概念,记为 至多为其双亲节点的数目。除了前件为单个描述符 (X1,Y)≤(X2,Y2)。根据此偏序关系可以生成 的规则之外,其他规则的形式与数目仅仅依赖于其 Hasse图,揭示了概念的内涵和外延之间的范化和 双亲节点
种层次关系有利于规则提取[6-10] 。 在概念格的规则 提取方面学者们进行了一定的研究,王志海等[6-7] 提出了概念格上规则提取的一般算法和渐近式算法 并研究了概念格与关联规则发现。 针对不同的形式 背景有不同的规则提取方法,如李金海等[8] 提出的 在决策形式背景上的规则提取。 还有一些提取规则 的改进方法,如梁吉业等[9] 提出的基于概念格的规 则产生集挖掘算法等。 近来对概念格的研究也主要 是围绕概念格的约简、缩小概念格的构造和规则提 取的复杂度[11-23] 。 但上述规则提取方法,一方面大 都是针对一个形式背景,且得到的规则集数量较多、 规模较大。 而用户有时可能只需要一部分感兴趣的 规则信息,而从规模较大的规则集中找出这些感兴 趣的规则信息也是一个难题。 另一方面规则形式大 都是文献[6]和文献[10]提出的规则形式,这种规 则结构不便于两个规则集之间的合并研究。 针对上述问题,本文提出一种伪规则的概念,给 出渐近式获取伪规则的方法。 同时说明了通过伪规 则集,用户可以得到原概念格上的蕴含规则。 伪规 则集的规模相对较小,其结构适于两个规则集的合 并。 用户可以根据自己的兴趣有选择地从伪规则集 合中产生出所需的蕴含规则。 在伪规则集的基础 上,提出了将两个伪规则集进行合并的方法,通过此 方法用户可以直接利用伪规则集得到范围更大的规 则集。 最后通过实验验证了该方法的有效性。 1 基本定义 1.1 概念格 在形式概念分析[1] 中,形式背景用一个三元组 K = (U,A,I) 表示,如表 1 所示,其中 U 是对象集 合, A 是属性集合, I 是 U 和 A 之间定义的一个二元 关系。 对于 ∀x ∈ U , ∀y ∈ A ,若 x 具有属性 y ,那 么 x 与 y 之间具有关系 I ,记为 xIy 。 关系 I 与一个 偏序集合对应,并且这偏序集合产生一种格结构如 图 1 所示。 这种由 I 诱导的格 L 就称为一个概念 格。 格中的每个节点是一个序偶,记为 (X,Y) ,称 X 是概念 (X,Y) 的外延, Y 是概念 (X,Y) 的内涵。 两者之间满足如下两个映射函数 f 和 g : f(x) = {y ∈ A | ∀x ∈ X,xIy} g(y) = {x ∈ U | ∀y ∈ Y,xIy} 格中所有概念的集合用 L(K) 表示。 给定格中 两个概念 C1 = X1 ,Y1 ( ) , C2 = X2 ,Y2 ( ) ,满足 X1 ⊆ X2 , 则 称 X1 ,Y1 ( ) 是 X2 ,Y2 ( ) 的 子 概 念, 记 为 X1 ,Y1 ( ) ≤ X2 ,Y2 ( ) 。 根据此偏序关系可以生成 Hasse 图,揭示了概念的内涵和外延之间的范化和 例化关系,可作为数据分析与知识获取的一种有效 工具。 形式背景 1 上对应的概念格如图 1。 表 1 形式背景 Table 1 Formal context AU a b c d e f g h i 1 1 1 0 0 0 0 1 0 0 2 1 1 0 0 0 0 1 1 0 3 1 1 1 0 0 0 1 1 0 4 1 0 1 0 0 0 1 1 1 5 1 1 0 1 0 1 0 0 0 图 1 L(U,{a,b,c,d,f,g,h,i},I) Fig.1 L(U,{a,b,c,d,f,g,h,i},I) 1.2 规则提取 下面简要介绍由文献[6]提出的规则提取方法 的主要依据定理,该方法的基本思想是依据其双亲 节点即直接泛化的个数及形式来对格中每个节点生 成其无冗余的所有规则。 关于此方法的详细描述可 参考文献[6]。 定理 1 [ 6 ] 如果格中节点 H = (X1 ,Y1 ) 只有一 个双亲节点 M = (X2 ,Y2 ) ,则 H 所产生的规则前件 只能为单个描述符,且 ∀p ∈ {Y1 - Y2 } ,都存在一 条无冗余规则 p → Y1 - p 。 定理 2 [ 6 ] 如果格中节点 H = (X1 ,Y1 ) 具有 d 个双亲节点 M1(X2 ,Y2 ) , M2(X3 ,Y3 ) ,…, Md(Xd , Yd ) ,则对于任意一个描述符 p ∈ {Y1 - (Y2 ∪ Y3 ∪ … ∪ Yd )} ,都存在一条规则 p → Y1 - p 。 定理 3 [ 6 ] 若果格中节点 H = (X1 ,Y1 ) 具有两 个双亲节点 M1(X2 ,Y2 ) 和 M2(X3 ,Y3 ) ,则对于每个 元素 ∀p1 ∈ {Y2 - Y2 ∩ Y3 } 和 ∀p2 ∈ {Y3 - Y2 ∩ Y3 } ,都存在一条规则 p1 p2 → Y1 - p1 p2 。 注:只有当 ‖X′‖ > k 时,才可能有前件至多 为 k 个描述符的规则,并且规则前件的描述符个数 至多为其双亲节点的数目。 除了前件为单个描述符 的规则之外,其他规则的形式与数目仅仅依赖于其 双亲节点。 第 4 期 温云霞,等:横向拆分形势背景下的快速规则提取方法 ·527·

.528. 智能系统学报 第11卷 例1对图1用上述定理,获得的蕴含规则为 再记录。剩下的没有变更的节点规则全部原样进行 b→a,g→a,d→abf,f→abd,bg→a,bh→ag,h→ 记录。下面给出在已建好的格上提取规则的算法。 ag,c→agh,bc→agh,i→acgh。 该算法采用基于对象的渐近式构造思想,函数 1.3形式背景拆分思想 generaterule(N=(X,Y))生成节点之间的伪规则。 通过对形式背景的拆分,形成多个子背景,分别 算法 构造概念格,然后再将子概念格合并是概念格分布 输入已有的格L与规则集R,要追加的概念 处理的中心思想。 ({x}f{x})); 目前对形式背景的拆分有纵向和横向之分,对 输出更新后的格L'与规则集R。 应的有两种合并方法。横向拆分是指对象域相同, BEGIN 属性项不同的拆分。纵向拆分是指对象域不同,属 R'←一p/*规则集合米/ 性项相同的拆分。本文将采用横向拆分的方式。 FOR每个节点H=(X,X)∈L 2伪规则及其渐近式提取 IF X'C f()THEN 把x加到X中,将节点H加人到Modify(记录更 在一个形式背景上通过文献「61提出的方法以 新节点)中 及其他的一些改进方法所得到的规则数目较多,规 IF X'=f(x)THEN continue; 模较大,其规则形式不便于两个规则集之间的合并 ELSE 操作。因此,我们提出一种新的规则形式及其渐近 new=X'∩f({x})/*生成新节点*/ 式提取方法。其基本思想是对格中每个节点生成与 IF new在L THEN: 其直接关系的父节点之间的一种关系,包括属性集 新增节点N=(XUx,new)并加入 之间的关系和对象集之间的关系,并证明通过伪规 Modify中,增加边N→H; 则集可以推导出全部的蕴含规则。 FOR Modify中的海个节点M=(X.,Yn) 2.1伪规则基本定义 IFY.new THEN加入边M→N, 定义1在形式背景K=(U,A,I)上,概念C1= IFM是H的双亲THEN (X,Y),C2=(X2,Y2),概念C1是概念C2的父亲 删去边M→H; 节点,则概念C,和C2之间产生规则r:Y2/Y,→Y1, R'[H]generaterule(H)R'=R'[H]UR'; 称π为一个伪规则。每个伪规则同时附有其对应的 R'[N]generaterule(N)R'=R'[N]UR'; 对象集表示如:X2→X,/X2。 ENDFOR 注:上述伪规则不是真正的蕴含规则,是一种便 ENDFOR 于规则集合并和产生蕴含规则的一种规则形式。 FOR每个规则p一q∈R 定理4由伪规则集可以推导出全部蕴含规则。 FN的任意子节点N'=(Xn,Yn) 证明通过上述定理1~3可知,对于一个子节 都有Y.≠P Uq THEN 点,根据其父节点的数量采取不同的方法来获取蕴 R′'=R'Up→q/*记录原来的规则*/ 含规则。上述提出的伪规则是子节点与其直接父节 ENDFOR 点之间的一个关系。对于一个子节点找到与其直接 R=R'/*记录新的规则集* 相关的父亲节点对应的伪规则,运用定理1~3即可 END 得到其对应的全部蕴含规则。 Function generaterule(N=(X,Y)) 例如:图1所示格结构中获得的伪规则 BEGIN g(123)→ab(5)和b(123)→ag(4),由此伪规则 FORN的每个父亲节点F=(X,Y:)产生规则: 可以得出子节点为abg,父亲节点为ab和ag。则 Y/Y(X:)→Y(X,/X) 通过定理2和定理3可以得到如下的蕴含规则: ENDFOR bg+a。 END 2.2伪规则的渐近式提取方法 3 伪规则集合并 采用基于对象的概念格渐近式构造思想,对每 个新生成的节点产生其对应的伪规则。并对更新节 概念格的构造一直是影响其应用的主要因素, 点判断其对应的原伪规则是否已经失效,如失效不 文献[4]和文献[5]提出了拆分和合并的思想。将
例 1 对图 1 用上述定理,获得的蕴含规则为 b →a,g → a,d → abf,f → abd,bg → a,bh → ag,h → ag,c → agh,bc → agh,i → acgh。 1.3 形式背景拆分思想 通过对形式背景的拆分,形成多个子背景,分别 构造概念格,然后再将子概念格合并是概念格分布 处理的中心思想。 目前对形式背景的拆分有纵向和横向之分,对 应的有两种合并方法。 横向拆分是指对象域相同, 属性项不同的拆分。 纵向拆分是指对象域不同,属 性项相同的拆分。 本文将采用横向拆分的方式。 2 伪规则及其渐近式提取 在一个形式背景上通过文献[6]提出的方法以 及其他的一些改进方法所得到的规则数目较多,规 模较大,其规则形式不便于两个规则集之间的合并 操作。 因此,我们提出一种新的规则形式及其渐近 式提取方法。 其基本思想是对格中每个节点生成与 其直接关系的父节点之间的一种关系,包括属性集 之间的关系和对象集之间的关系,并证明通过伪规 则集可以推导出全部的蕴含规则。 2.1 伪规则基本定义 定义 1 在形式背景 K = (U,A,I) 上,概念 C1 = X1 ,Y1 ( ) , C2 = X2 ,Y2 ( ) ,概念 C1 是概念 C2 的父亲 节点,则概念 C1 和 C2 之间产生规则 r : Y2 / Y1 → Y1 , 称 r 为一个伪规则。 每个伪规则同时附有其对应的 对象集表示如: X2 → X1 / X2 。 注:上述伪规则不是真正的蕴含规则,是一种便 于规则集合并和产生蕴含规则的一种规则形式。 定理 4 由伪规则集可以推导出全部蕴含规则。 证明 通过上述定理 1 ~ 3 可知,对于一个子节 点,根据其父节点的数量采取不同的方法来获取蕴 含规则。 上述提出的伪规则是子节点与其直接父节 点之间的一个关系。 对于一个子节点找到与其直接 相关的父亲节点对应的伪规则,运用定理 1 ~ 3 即可 得到其对应的全部蕴含规则。 例 如: 图 1 所 示 格 结 构 中 获 得 的 伪 规 则 g(123) →ab(5) 和 b(123) → ag(4) ,由此伪规则 可以得出子节点为 abg ,父亲节点为 ab 和 ag 。 则 通过定理 2 和定理 3 可以得到如下的蕴含规则: bg →a 。 2.2 伪规则的渐近式提取方法 采用基于对象的概念格渐近式构造思想,对每 个新生成的节点产生其对应的伪规则。 并对更新节 点判断其对应的原伪规则是否已经失效,如失效不 再记录。 剩下的没有变更的节点规则全部原样进行 记录。 下面给出在已建好的格上提取规则的算法。 该算法 采 用 基 于 对 象 的 渐 近 式 构 造 思 想, 函 数 generaterule(N = (X,Y)) 生成节点之间的伪规则。 算法 输入 已有的格 L 与规则集 R ,要追加的概念 ({x},f({x})) ; 输出 更新后的格 L′ 与规则集 R。 BEGIN R′ ← φ / ∗规则集合∗/ FOR 每个节点 H = (X,X′) ∈ L IF X′ ⊆ f({x}) THEN 把 x 加到 X 中,将节点 H 加入到 Modify(记录更 新节点)中 IF X′ = f({x}) THEN continue; ELSE new = X′ ∩ f({x}) / ∗生成新节点∗/ IF new ∉ L THEN; 新增节点 N = (X ∪ x,new) 并加入 Modify 中,增加边 N → H ; FOR Modify 中的每个节点M = (Xm,Ym) IF Ym ⊆ new THEN 加入边 M → N , IF M 是 H 的双亲 THEN 删去边 M → H ; R′[H] = generaterule(H) R′ = R′[H] ∪R′ ; R′[N] = generaterule(N) R′ = R′[N] ∪R′ ; ENDFOR ENDFOR FOR 每个规则 p → q ∈ R IF N 的任意子节点 N′ = (Xn ,Yn ) 都有 Yn ≠ p ∪ q THEN R′ = R′ ∪ p → q / ∗记录原来的规则∗/ ENDFOR R = R′ / ∗记录新的规则集∗/ END Function generaterule(N = (X,Y)) BEGIN FOR N 的每个父亲节点 F = (Xi,Yi) 产生规则: Y / Yi(Xi) → Yi(Xi / X) ENDFOR END 3 伪规则集合并 概念格的构造一直是影响其应用的主要因素, 文献[4]和文献[5]提出了拆分和合并的思想。 将 ·528· 智 能 系 统 学 报 第 11 卷

第4期 温云霞,等:横向拆分形势背景下的快速规则提取方法 .529. 形式背景拆分成多个子形式背景,分别构造概念格 O2)∩(03U0:),(BUD)}是两个节点的子节点 并对其进行合并。但是,目前提出的合并都是针对 当原概念格节点中不存在此节点,因此依据伪规则 子概念格的合并,而每个子概念格上都可以提取规 生成方法,可以生成BD/B→B,BD/D→D。且 则,因而可以将直接利用两个规则集进行合并,直接 (03U0,)与(0,U02)的所有子节点的交集都不 产生所需的规则信息。对于两个子规则集直接进行 是new,保证生成正确的规则。记录new。 合并,相关研究还较少。下面提出通过伪规则集来 定理8(0,U02)∩(03U0)=p,如果p 实现两个规则的合并。 在原概念格节点集中不存在,则直接生成前者子节 两个对应概念格上的伪规则集合并的主要思想 点与新节点之间的规则。 是通过伪规则中包含的概念属性和对象信息,运用 证明因为如果两规则的父节点与父节点的交 一定的合并原理来生成新的规则。在合并的过程中 集是空集,那么前者对应的子节点与后者父节点的 产生新的节点概念信息,记录新生概念信息。因此 交集也一定是空集,则记录ABD/AB→AB,ABD/D 规则合并后也就得到了合并后的一个概念格的结 →D记录新节点P。 构。合并规则依据的是概念格横向合并的思想,根 注:在每个规则集中增加一个辅助规则,即内涵 据合并时新规则产生的信息来判断是否是新生成的 最大的节点自身生成一个辅助规则:Y→Y,保证在 规则,比较与原规则之间的关系来判断是否要更改 规则合并时可以访问到概念格中的每个节点。在合 原规则。因格中的节点在规则中既可以是前件也可 并的过程中会产生新的概念节点,也要对这些新产 以是后件,因此合并时只考虑其作为后件的情况,避 生的概念节点判断它们之间是否可以产生伪规则。 免重复规则。 同时判断更新节点与新生节点之间是否产生新的规 例如给定两个伪规则A(O,)→B(O,)和 则,可以防止重复地生成规则。 C(O3)→D(0),则有如下合并规则: 例2给定的形式背景如表1所示。图2和图 定理5(0,U02)≤(0,U0.),则更新原 3是对形式背景横向拆分每3个属性为一个子形式 有规则:A→BD。 背景所对应的概念格。在图2上提取的伪规则集 证明因为节点C={(0,U02),B}对象集包 R1为:b(1235)→a(4),c(34)→a(125), 含于节点C'={(O,U0,),D对象集,则节点C同 c(3)→ab(125),b(3)→ac(4),abc(3)→ 样具有节点C的属性,同时C的子节点也具有节点 abc(3)。图3对应的伪规则集R2为:h(234)一 C'的属性,因此节点C及其子节点的属性变为 g(1),i(4)→gh(23),ghi(4)→ghi(4)。 {BD,ABD,则规则更新为A→BD。 (12345.a) 实际操作中每次都记录更新节点(0,UO2), 以便后续合并处理重复的问题。 (1235,ab) (34,ac) 定理6若有01二(03U04),02¢(03U O,),则更新原有规则:AD→B。 (3,abc) 证明因为节点C={O,(AUB)}对象集包 图2子概念格L(U,{a,b,c},) 含于节点C'={(03U04),D},而02¢(03U0) Fig.2 Sub-concept lattice L(U,a,b,c,I) 即说明节点C的父亲节点的对象集并不包含于节 点C'。因此只将C的属性变为{AUDUB},其父 (1234g) 亲节点的属性不变,则原规则更新为AD→B。记 录更新节点01 (234.gh) 定理7(0,U02)∩(0U0,)≠p,则生 成new=(01U02)∩(03U04),是(0,U02)和 (O3UO,)与的子集,如果new在原概念格节点集 (4gh) 中不存在,且(03U0,)与(01U02)的所有子节 点的交集都不是new,则生的规则有:BD/B→B, 图3子概念格L(U,{g,h,i,) Fig.3 Sub-concept lattice L(U,g,,i,I) BD/D→D。 合并过程如下:首先判断要加入的伪规则对应 证明两个概念节点C={(01UO2),B}和 C'={(O3UOa),D}产生的新节点new={(O1U 的节点信息是否已经存在,若存在不做任何操作
形式背景拆分成多个子形式背景,分别构造概念格 并对其进行合并。 但是,目前提出的合并都是针对 子概念格的合并,而每个子概念格上都可以提取规 则,因而可以将直接利用两个规则集进行合并,直接 产生所需的规则信息。 对于两个子规则集直接进行 合并,相关研究还较少。 下面提出通过伪规则集来 实现两个规则的合并。 两个对应概念格上的伪规则集合并的主要思想 是通过伪规则中包含的概念属性和对象信息,运用 一定的合并原理来生成新的规则。 在合并的过程中 产生新的节点概念信息,记录新生概念信息。 因此 规则合并后也就得到了合并后的一个概念格的结 构。 合并规则依据的是概念格横向合并的思想,根 据合并时新规则产生的信息来判断是否是新生成的 规则,比较与原规则之间的关系来判断是否要更改 原规则。 因格中的节点在规则中既可以是前件也可 以是后件,因此合并时只考虑其作为后件的情况,避 免重复规则。 例如 给 定 两 个 伪 规 则 A(O1 ) → B(O2 ) 和 C(O3 ) → D(O4 ) ,则有如下合并规则: 定理 5 (O1 ∪ O2 ) ⊆ (O3 ∪ O4 ) ,则更新原 有规则: A → BD 。 证明 因为节点 C = {(O1 ∪ O2 ),B} 对象集包 含于节点 C′ = {(O3 ∪ O4 ),D} 对象集,则节点 C 同 样具有节点 C′ 的属性,同时 C 的子节点也具有节点 C′ 的属性, 因此节点 C 及其子节点的属性变为 {BD,ABD} ,则规则更新为 A → BD 。 实际操作中每次都记录更新节点 (O1 ∪ O2 ) , 以便后续合并处理重复的问题。 定理 6 若有 O1 ⊆ (O3 ∪ O4 ) , O2 ⊄ (O3 ∪ O4 ) ,则更新原有规则: AD → B 。 证明 因为节点 C = {O1 ,(A ∪ B)} 对象集包 含于节点 C′ = {(O3 ∪O4 ),D} ,而 O2 ⊄ (O3 ∪O4 ) 即说明节点 C 的父亲节点的对象集并不包含于节 点 C′ 。 因此只将 C 的属性变为 {A∪D∪B} ,其父 亲节点的属性不变,则原规则更新为 AD → B 。 记 录更新节点 O1 定理 7 (O1 ∪ O2 ) ∩ (O3 ∪ O4 ) ≠ φ ,则生 成 new = (O1 ∪O2 ) ∩(O3 ∪O4 ) ,是 (O1 ∪O2 ) 和 (O3 ∪ O4 ) 与的子集,如果 new 在原概念格节点集 中不存在,且 (O3 ∪ O4 ) 与 (O1 ∪ O2 ) 的所有子节 点的交集都不是 new ,则生的规则有: BD/ B → B , BD/ D → D 。 证明 两个概念节点 C = {(O1 ∪ O2 ),B} 和 C′ ={(O3 ∪ O4 ),D} 产生的新节点 new = {(O1 ∪ O2 ) ∩ (O3 ∪ O4 ),(B ∪ D)} 是两个节点的子节点 当原概念格节点中不存在此节点,因此依据伪规则 生成方法,可以生成 BD/ B → B , BD/ D → D 。 且 (O3 ∪ O4 ) 与 (O1 ∪ O2 ) 的所有子节点的交集都不 是 new ,保证生成正确的规则。 记录 new 。 定理 8 (O1 ∪ O2 ) ∩ (O3 ∪ O4 ) = φ ,如果 φ 在原概念格节点集中不存在,则直接生成前者子节 点与新节点之间的规则。 证明 因为如果两规则的父节点与父节点的交 集是空集,那么前者对应的子节点与后者父节点的 交集也一定是空集,则记录 ABD/ AB → AB , ABD/ D → D 记录新节点 φ 。 注:在每个规则集中增加一个辅助规则,即内涵 最大的节点自身生成一个辅助规则: Y → Y ,保证在 规则合并时可以访问到概念格中的每个节点。 在合 并的过程中会产生新的概念节点,也要对这些新产 生的概念节点判断它们之间是否可以产生伪规则。 同时判断更新节点与新生节点之间是否产生新的规 则,可以防止重复地生成规则。 例 2 给定的形式背景如表 1 所示。 图 2 和图 3 是对形式背景横向拆分每 3 个属性为一个子形式 背景所对应的概念格。 在图 2 上提取的伪规则集 R1 为: b(1235) → a(4) , c(34) → a(125) , c(3) →ab(125) , b(3) → ac(4) , abc(3) → abc(3) 。 图 3 对应的伪规则集 R2 为: h(234) → g(1) , i(4) → gh(23) , ghi(4) → ghi(4) 。 图 2 子概念格 L(U,{a,b,c },l) Fig.2 Sub⁃concept lattice L(U,{a,b,c },I) 图 3 子概念格 L(U,{g,h,i},I) Fig.3 Sub⁃concept lattice L(U,{g,h,i},I) 合并过程如下:首先判断要加入的伪规则对应 的节点信息是否已经存在,若存在不做任何操作。 第 4 期 温云霞,等:横向拆分形势背景下的快速规则提取方法 ·529·
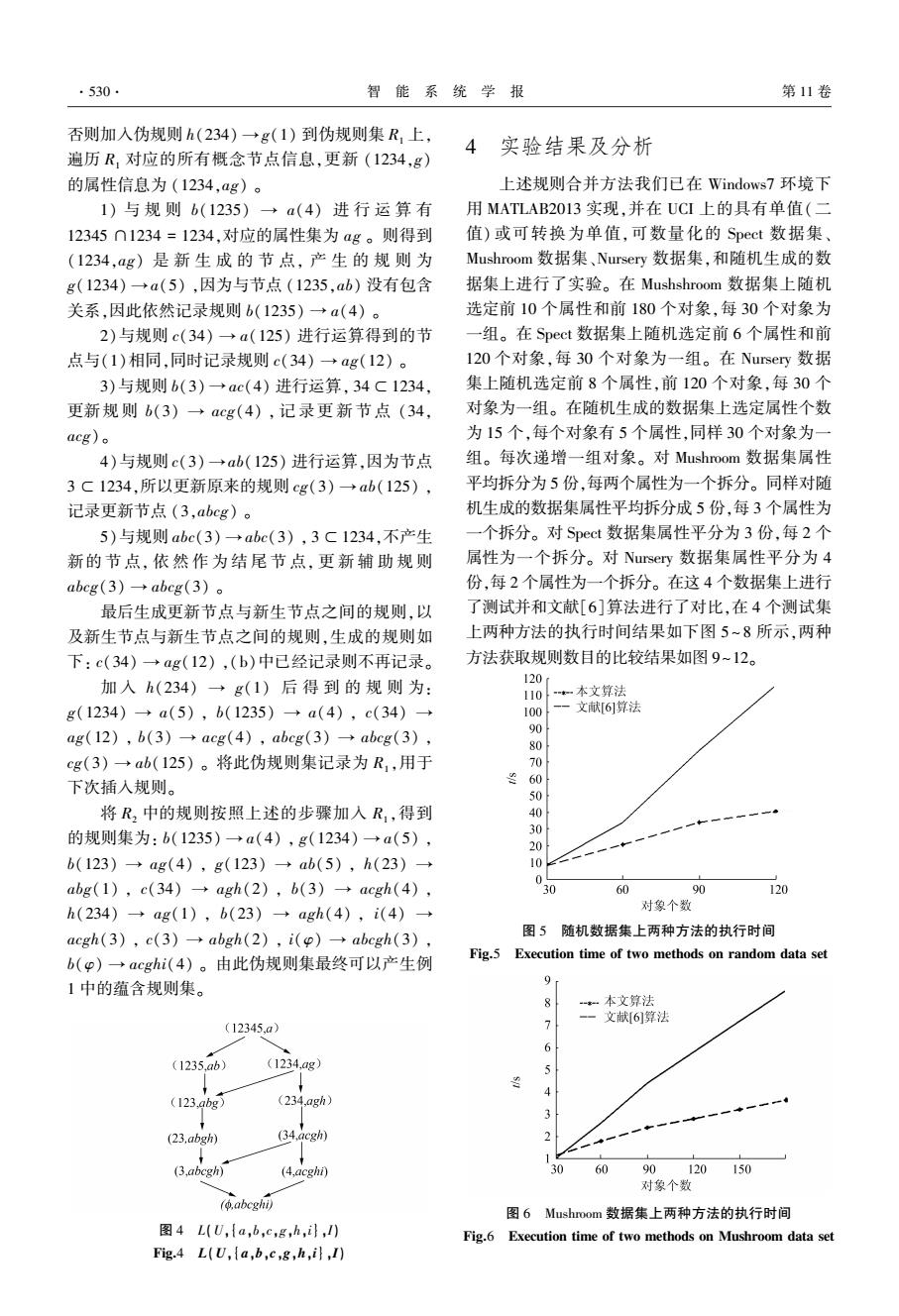
.530 智能系统学报 第11卷 否则加入伪规则h(234)→g(1)到伪规则集R,上, 4 实验结果及分析 遍历R,对应的所有概念节点信息,更新(1234,g) 的属性信息为(1234,ag))。 上述规则合并方法我们已在Windows7环境下 1)与规则b(1235)→a(4)进行运算有 用MATLAB2013实现,并在UCI上的具有单值(二 12345∩1234=1234,对应的属性集为ag。则得到 值)或可转换为单值,可数量化的Spect数据集 (1234,ag)是新生成的节点,产生的规则为 Mushroom数据集、Nursery数据集,和随机生成的数 g(1234)→a(5),因为与节点(1235,ab)没有包含 据集上进行了实验。在Mushshroom数据集上随机 关系,因此依然记录规则b(1235)→a(4)。 选定前10个属性和前180个对象,每30个对象为 2)与规则c(34)→a(125)进行运算得到的节 一组。在Spect数据集上随机选定前6个属性和前 点与(1)相同,同时记录规则c(34)→g(12)。 120个对象,每30个对象为一组。在Nursery数据 3)与规则b(3)→ac(4)进行运算,34C1234, 集上随机选定前8个属性,前120个对象,每30个 更新规则b(3)→acg(4),记录更新节点(34, 对象为一组。在随机生成的数据集上选定属性个数 acg)。 为15个,每个对象有5个属性,同样30个对象为一 4)与规则c(3)→ab(125)进行运算,因为节点 组。每次递增一组对象。对Mushroom数据集属性 3C1234,所以更新原来的规则cg(3)→ab(125), 平均拆分为5份,每两个属性为一个拆分。同样对随 记录更新节点(3,abcg)。 机生成的数据集属性平均拆分成5份,每3个属性为 5)与规则abc(3)+abc(3),3C1234,不产生 一个拆分。对Spect数据集属性平分为3份,每2个 新的节点,依然作为结尾节点,更新辅助规则 属性为一个拆分。对Nursery数据集属性平分为4 abcg(3)→abcg(3)。 份,每2个属性为一个拆分。在这4个数据集上进行 最后生成更新节点与新生节点之间的规则,以 了测试并和文献[6]算法进行了对比,在4个测试集 及新生节点与新生节点之间的规则,生成的规则如 上两种方法的执行时间结果如下图5~8所示,两种 下:c(34)→ag(12),(b)中已经记录则不再记录。 方法获取规则数目的比较结果如图9~12。 加入h(234)→g(1)后得到的规则为: 120 110 *本文算法 g(1234)→a(5),b(1235)→a(4),c(34)→ 100 文献6]算法 ag(12),b(3)→acg(4),abcg(3)→abcg(3), 90 80 cg(3)→ab(125)。将此伪规则集记录为R,用于 0 下次插入规则。 6 50 将R,中的规则按照上述的步骤加入R,得到 40 一 的规则集为:b(1235)→a(4),g(1234)→a(5), 30 20 b(123)→ag(4),g(123)→ab(5),,h(23)→ 10 abg(1),c(34)→agh(2),b(3)→acgh(4), 0 0 60 90 120 h(234)→ag(1),b(23)→agh(4),i(4)→ 对象个数 acgh(3),c(3)→abgh(2),i(p)→abcgh(3), 图5随机数据集上两种方法的执行时间 b(p)一acghi(4)。由此伪规则集最终可以产生例 Fig.5 Execution time of two methods on random data set 1中的蕴含规则集。 9 f *一本文算法 一文献[6]算法 (12345,a) 6 (1235.ab) (1234,ag) (123,abg) (234,agh) (23.abgh) (34.acgh) ◆ (3.abcgh) (4,acghi) 30 60 90120150 对象个数 (.abcghi) 图6 Mushroom数据集上两种方法的执行时间 4 L(U,(a,b,c,g,h,i,) Fig.6 Execution time of two methods on Mushroom data set Fig.4 L(U,a,b,c,g,h,i)
否则加入伪规则 h(234) → g(1) 到伪规则集 R1 上, 遍历 R1 对应的所有概念节点信息,更新 (1234,g) 的属性信息为 (1234,ag) 。 1) 与 规 则 b(1235) → a(4) 进 行 运 算 有 12345 ∩1234 = 1234,对应的属性集为 ag 。 则得到 (1234,ag) 是 新 生 成 的 节 点, 产 生 的 规 则 为 g(1234) → a(5) ,因为与节点 (1235,ab) 没有包含 关系,因此依然记录规则 b(1235) → a(4) 。 2)与规则 c(34) → a(125) 进行运算得到的节 点与(1)相同,同时记录规则 c(34) → ag(12) 。 3)与规则 b(3) → ac(4) 进行运算, 34 ⊂1234, 更新规 则 b(3) → acg(4) , 记 录 更 新 节 点 (34, acg)。 4)与规则 c(3) →ab(125) 进行运算,因为节点 3 ⊂ 1234,所以更新原来的规则 cg(3) → ab(125) , 记录更新节点 (3,abcg) 。 5)与规则 abc(3) → abc(3) , 3 ⊂1234,不产生 新的 节 点, 依 然 作 为 结 尾 节 点, 更 新 辅 助 规 则 abcg(3) → abcg(3) 。 最后生成更新节点与新生节点之间的规则,以 及新生节点与新生节点之间的规则,生成的规则如 下: c(34) → ag(12) ,(b)中已经记录则不再记录。 加 入 h(234) → g(1) 后 得 到 的 规 则 为: g(1234) → a(5) , b(1235) → a(4) , c(34) → ag(12) , b(3) → acg(4) , abcg(3) → abcg(3) , cg(3) → ab(125) 。 将此伪规则集记录为 R1 ,用于 下次插入规则。 将 R2 中的规则按照上述的步骤加入 R1 ,得到 的规则集为: b(1235) → a(4) , g(1234) → a(5) , b(123) → ag(4) , g(123) → ab(5) , h(23) → abg(1) , c(34) → agh(2) , b(3) → acgh(4) , h(234) → ag(1) , b(23) → agh(4) , i(4) → acgh(3) , c(3) → abgh(2) , i(φ) → abcgh(3) , b(φ) → acghi(4) 。 由此伪规则集最终可以产生例 1 中的蕴含规则集。 图 4 L(U,{a,b,c,g,h,i},I) Fig.4 L(U,{a,b,c,g,h,i},I) 4 实验结果及分析 上述规则合并方法我们已在 Windows7 环境下 用 MATLAB2013 实现,并在 UCI 上的具有单值(二 值) 或可转换为单值,可数量化的 Spect 数据集、 Mushroom 数据集、Nursery 数据集,和随机生成的数 据集上进行了实验。 在 Mushshroom 数据集上随机 选定前 10 个属性和前 180 个对象,每 30 个对象为 一组。 在 Spect 数据集上随机选定前 6 个属性和前 120 个对象,每 30 个对象为一组。 在 Nursery 数据 集上随机选定前 8 个属性,前 120 个对象,每 30 个 对象为一组。 在随机生成的数据集上选定属性个数 为 15 个,每个对象有 5 个属性,同样 30 个对象为一 组。 每次递增一组对象。 对 Mushroom 数据集属性 平均拆分为 5 份,每两个属性为一个拆分。 同样对随 机生成的数据集属性平均拆分成 5 份,每 3 个属性为 一个拆分。 对 Spect 数据集属性平分为 3 份,每 2 个 属性为一个拆分。 对 Nursery 数据集属性平分为 4 份,每 2 个属性为一个拆分。 在这 4 个数据集上进行 了测试并和文献[6]算法进行了对比,在 4 个测试集 上两种方法的执行时间结果如下图 5 ~ 8 所示,两种 方法获取规则数目的比较结果如图 9~12。 图 5 随机数据集上两种方法的执行时间 Fig.5 Execution time of two methods on random data set 图 6 Mushroom 数据集上两种方法的执行时间 Fig.6 Execution time of two methods on Mushroom data set ·530· 智 能 系 统 学 报 第 11 卷
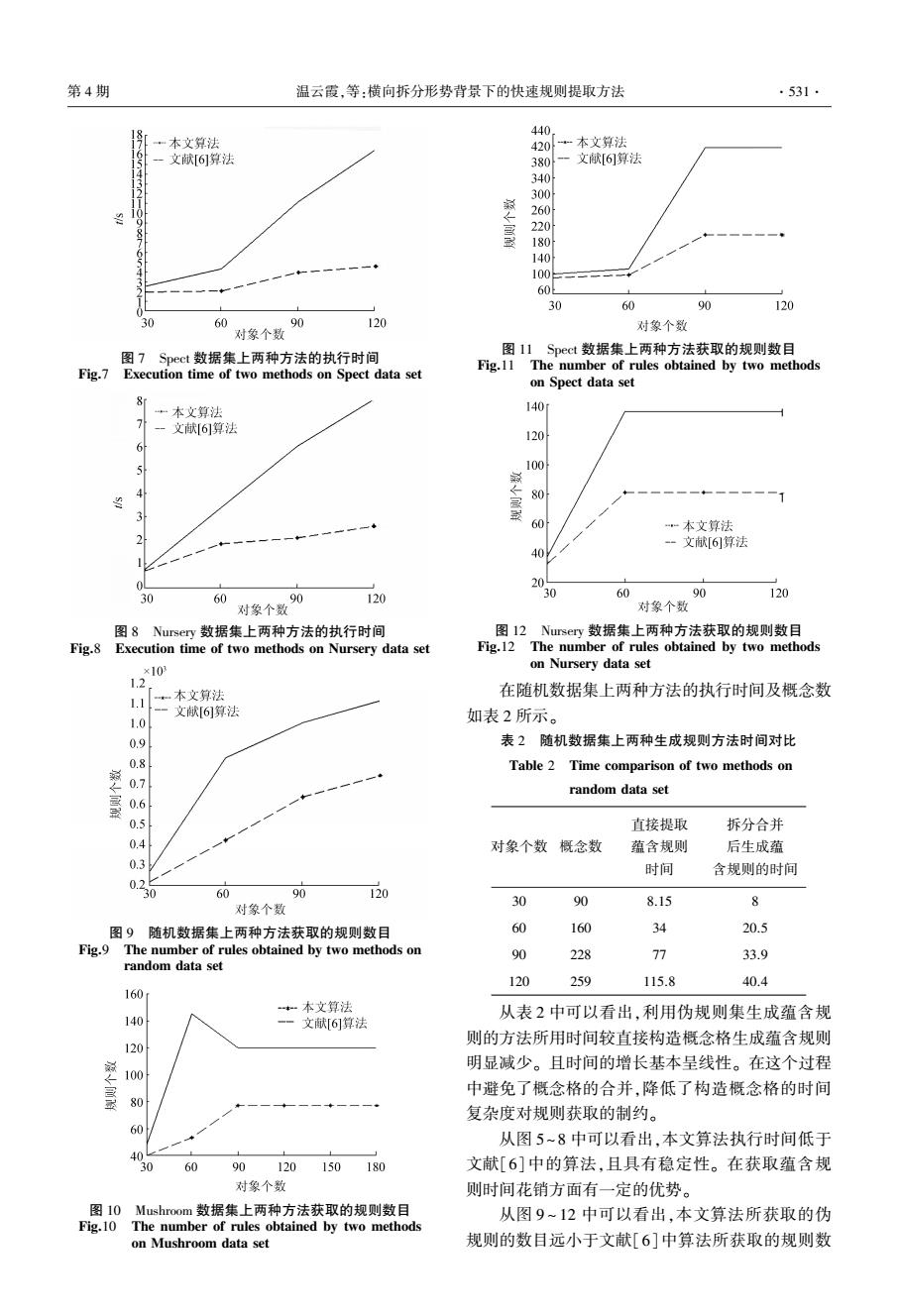
第4期 温云霞,等:横向拆分形势背景下的快速规则提取方法 .531. 440 一本文算法 420 ·本文算法 文献[6算法 380 文献[6]算法 5432 340 300 10 人联 260 220 180 654 140 100 60 30 60 90 120 30 60 90 120 对象个数 对象个数 图7 Spect数据集上两种方法的执行时间 图11 Spect数据集上两种方法获取的规则数目 Fig.11 The number of rules obtained by two methods Fig.7 Execution time of two methods on Spect data set on Spect data set “本文算法 140 7升 文献6)算法 120 6 100 80 "1 一一◆ 60 一本文算法 文献[6算法 40 2 30 60 90 120 30 60 90 120 对象个数 对象个数 图8 Nursery数据集上两种方法的执行时间 图12 Nursery数据集上两种方法获取的规则数目 Fig.8 Execution time of two methods on Nursery data set Fig.12 The number of rules obtained by two methods 10 on Nursery data set 1.2 1.1 本文算法 在随机数据集上两种方法的执行时间及概念数 -一文献[6]算法 1.0 如表2所示。 0.9 表2随机数据集上两种生成规则方法时间对比 0.8 Table 2 Time comparison of two methods on 0.7 random data set 0.6 0.5 直接提取 拆分合并 0.4 对象个数概念数 蕴含规则 后生成蕴 0.3 时间 含规则的时间 0.2 0 60 90 120 对象个数 30 90 8.15 P 图9随机数据集上两种方法获取的规则数目 60 160 20.5 Fig.9 The number of rules obtained by two methods on 90 228 77 33.9 random data set 120 259 115.8 40.4 160 *本文算法 从表2中可以看出,利用伪规则集生成蕴含规 140 文献[6]算法 则的方法所用时间较直接构造概念格生成蕴含规则 120 明显减少。且时间的增长基本呈线性。在这个过程 100 中避免了概念格的合并,降低了构造概念格的时间 复杂度对规则获取的制约。 60 从图5~8中可以看出,本文算法执行时间低于 4 30 60 90120 150 180 文献[6]中的算法,且具有稳定性。在获取蕴含规 对象个数 则时间花销方面有一定的优势。 图10 Mushroom数据集上两种方法获取的规则数目 从图9~12中可以看出,本文算法所获取的伪 Fig.10 The number of rules obtained by two methods on Mushroom data set 规则的数目远小于文献[6]中算法所获取的规则数
图 7 Spect 数据集上两种方法的执行时间 Fig.7 Execution time of two methods on Spect data set 图 8 Nursery 数据集上两种方法的执行时间 Fig.8 Execution time of two methods on Nursery data set 图 9 随机数据集上两种方法获取的规则数目 Fig.9 The number of rules obtained by two methods on random data set 图 10 Mushroom 数据集上两种方法获取的规则数目 Fig.10 The number of rules obtained by two methods on Mushroom data set 图 11 Spect 数据集上两种方法获取的规则数目 Fig.11 The number of rules obtained by two methods on Spect data set 图 12 Nursery 数据集上两种方法获取的规则数目 Fig.12 The number of rules obtained by two methods on Nursery data set 在随机数据集上两种方法的执行时间及概念数 如表 2 所示。 表 2 随机数据集上两种生成规则方法时间对比 Table 2 Time comparison of two methods on random data set 对象个数 概念数 直接提取 蕴含规则 时间 拆分合并 后生成蕴 含规则的时间 30 90 8.15 8 60 160 34 20.5 90 228 77 33.9 120 259 115.8 40.4 从表 2 中可以看出,利用伪规则集生成蕴含规 则的方法所用时间较直接构造概念格生成蕴含规则 明显减少。 且时间的增长基本呈线性。 在这个过程 中避免了概念格的合并,降低了构造概念格的时间 复杂度对规则获取的制约。 从图 5~8 中可以看出,本文算法执行时间低于 文献[6]中的算法,且具有稳定性。 在获取蕴含规 则时间花销方面有一定的优势。 从图 9 ~ 12 中可以看出,本文算法所获取的伪 规则的数目远小于文献[6]中算法所获取的规则数 第 4 期 温云霞,等:横向拆分形势背景下的快速规则提取方法 ·531·

,532 智能系统学报 第11卷 目,得到的伪规则集的规模较小,用户可以根据所需 HU Keyun,LU Yuchang,SHI Chunyi.Advances in concept 灵活地通过伪规则生成部分和全部的蕴含规则。在 lattice and its application[.Journal of Tsinghua universi- 随机数据集以及Spect数据集上,获取的概念数与 ty:science technology,2004,40(9):77-81. 规则数对比如表3所示。 [4]李云,刘宗田,陈鲮,等.多概念格的横向合并算法[J] 表3随机数据集上蕴含规则与伪规则数的对比 电子学报,2004,32(11):1849-1854. Table 3 The comparison of amount between rule and LI Yun,LIU Zongtian,CHEN Ling,et al.Horizontal union pseudo rule on random data set algorithm of multiple concept lattices[].Acta electronica 对象个数 概念数 蕴含规则数 伪规则数 sinica,2004,32(11):1849-1854. 30 263 214 [5]智慧来,智东杰,刘宗田.概念格合并原理与算法[J]: 90 60 160 845 426 电子学报,2010,38(2):455-459. 90 228 1024 645 ZHI Huilai,ZHI Dongiie,LIU Zongtian.Theory and algo- 120 259 1135 755 rithm of concept lattice union[J].Acta electronica sinica, 2010.38(2):455-459. 表4 Spect数据集上蕴含规则与伪规则数的对比 [6]王志海,胡可云,胡学钢,等.概念格上规则提取的一 Table 4 The comparison of amount between rule and 般算法与渐近式算法[J].计算机学报,1999,22(1): pseudo rule on Spect data set 66-70. 对象个数 概念数 蕴含规则数 伪规则数 WANG Zhihai,HU Keyun,HU Xuegang,et al.General 30 37 98 89 and incremental algorithms of rule extraction based on Con- 42 96 111 cept lattice[J].Chinese journal of computers,1999,22 90 64 416 197 (1):66-70. 120 64 416 197 [7]谢志鹏,刘宗田.概念格与关联规则发现[J].计算机研 究与发展,2000,37(12):1415-1421 从表3和表4中可以看出,当概念数量较多时, XIE Zhipeng,LIU Zongtian.Concept lattice and association 所获得的伪规则集的数量明显小于所获取的蕴含规 rule discovery[].Journal of computer research develop- 则集的数量。在规模较小的伪规则中,用户能够更 ment,2000,37(12):1415-1421. 好地选取感兴趣的属性并生成全部的蕴含规则。 [8]李金海,吕跃进.基于概念格的决策形式背景属性约简 6结论 及规则提取[J刀.数学的实践与认识,2009,39(7):182 -188. 本文在横向拆分的形式背景下,对基于概念格 LI Jinhai,LV Yuejin.Attribute reduction and rules extrac- 的规则提取进行了研究。1)首先提出了伪规则的 tion in decision formal context based on concept lattice[J]. 概念,并给出了伪规则的渐近式提取方法,证明了通 Mathematics in practice and theory,2009,39(7):182- 过伪规则集可以生成全部的蕴含规则:2)本文基于 188 伪规则形式,给出了伪规则合并的法则及快速规则 [9]梁吉业,王俊红.基于概念格的规则产生集挖掘算法 [J].计算机研究与展,2004,41(8):1339-1344. 获取方法,通过理论推理和实验验证说明了本文方 LIANG Jiye,WANG Junhong.An algorithm for extracting 法的有效性:3)本文所提的规则获取方法主要是针 rule-generating sets based on Concept lattice[J].Journal of 对于横向拆分的形式背景,但是对形式背景的拆分 computer research and development,2004,41(8):1339- 有多种拆分方式,对于不同的拆分方式下的规则获 1344. 取是进一步需要研究的工作。 [10]GODIN R,MISSAOUI R.An incremental concept forma- 参考文献: tion approach for learning from databases[].Theoretical computer science,1994,133(2):387-419. [1]GANTER B,WILLE R.Formal concept analysis:mathe- [11]李进金,张燕兰,吴伟志,等.形式背景与协调决策形 matical foundations[M].Berlin Heidelberg:Springer-Ver- 式背景属性约简与概念格生成[J].计算机学报,2014. lag,1999. 37(8):1768-1774 [2]WILLE R.Restructuring lattice theory:an approach based LI Jinjin,ZHANG Yanlan,WU Weizhi,et al.Attribute on Hierarchies of concepts M]//RIVAL I.Ordered Sets. reduction for formal context and consistent decision formal Netherlands:Springer,1982:445-470. context and Concept lattice generation[]].Chinese journal [3]胡可云,陆玉昌,石纯一·概念格及其应用进展[J].清 of computers,2014,37(8):1768-1774. 华大学学报:自然科学版,2000,40(9):77-81. [12]MA Jianmin,LEUNG Y,ZHANG Wenxiu.Attribute re-
目,得到的伪规则集的规模较小,用户可以根据所需 灵活地通过伪规则生成部分和全部的蕴含规则。 在 随机数据集以及 Spect 数据集上,获取的概念数与 规则数对比如表 3 所示。 表 3 随机数据集上蕴含规则与伪规则数的对比 Table 3 The comparison of amount between rule and pseudo rule on random data set 对象个数 概念数 蕴含规则数 伪规则数 30 90 263 214 60 160 845 426 90 228 1 024 645 120 259 1 135 755 表 4 Spect 数据集上蕴含规则与伪规则数的对比 Table 4 The comparison of amount between rule and pseudo rule on Spect data set 对象个数 概念数 蕴含规则数 伪规则数 30 37 98 89 60 42 96 111 90 64 416 197 120 64 416 197 从表 3 和表 4 中可以看出,当概念数量较多时, 所获得的伪规则集的数量明显小于所获取的蕴含规 则集的数量。 在规模较小的 伪规则中,用户能够更 好地选取感兴趣的属性并生成全部的蕴含规则。 6 结论 本文在横向拆分的形式背景下,对基于概念格 的规则提取进行了研究。 1) 首先提出了伪规则的 概念,并给出了伪规则的渐近式提取方法,证明了通 过伪规则集可以生成全部的蕴含规则;2)本文基于 伪规则形式,给出了伪规则合并的法则及快速规则 获取方法,通过理论推理和实验验证说明了本文方 法的有效性;3)本文所提的规则获取方法主要是针 对于横向拆分的形式背景,但是对形式背景的拆分 有多种拆分方式,对于不同的拆分方式下的规则获 取是进一步需要研究的工作。 参考文献: [1] GANTER B, WILLE R. Formal concept analysis: mathe⁃ matical foundations[M]. Berlin Heidelberg: Springer⁃Ver⁃ lag, 1999. [2]WILLE R. Restructuring lattice theory: an approach based on Hierarchies of concepts [ M] / / RIVAL I. Ordered Sets. Netherlands: Springer, 1982: 445-470. [3]胡可云, 陆玉昌, 石纯一. 概念格及其应用进展[ J]. 清 华大学学报: 自然科学版, 2000, 40(9): 77-81. HU Keyun, LU Yuchang, SHI Chunyi. Advances in concept lattice and its application[J]. Journal of Tsinghua universi⁃ ty: science & technology, 2004, 40(9): 77-81. [4]李云, 刘宗田, 陈崚, 等. 多概念格的横向合并算法[J]. 电子学报, 2004, 32(11): 1849-1854. LI Yun, LIU Zongtian, CHEN Ling, et al. Horizontal union algorithm of multiple concept lattices[ J]. Acta electronica sinica, 2004, 32(11): 1849-1854. [5]智慧来, 智东杰, 刘宗田. 概念格合并原理与算法[ J]. 电子学报, 2010, 38(2): 455-459. ZHI Huilai, ZHI Dongjie, LIU Zongtian. Theory and algo⁃ rithm of concept lattice union[ J]. Acta electronica sinica, 2010, 38(2): 455-459. [6]王志海, 胡可云, 胡学钢, 等. 概念格上规则提取的一 般算法与渐近式算法[ J]. 计算机学报, 1999, 22( 1): 66-70. WANG Zhihai, HU Keyun, HU Xuegang, et al. General and incremental algorithms of rule extraction based on Con⁃ cept lattice [ J]. Chinese journal of computers, 1999, 22 (1): 66-70. [7]谢志鹏, 刘宗田. 概念格与关联规则发现[ J]. 计算机研 究与发展, 2000, 37(12): 1415-1421. XIE Zhipeng, LIU Zongtian. Concept lattice and association rule discovery[J]. Journal of computer research & develop⁃ ment, 2000, 37(12): 1415-1421. [8]李金海, 吕跃进. 基于概念格的决策形式背景属性约简 及规则提取[J]. 数学的实践与认识, 2009, 39(7): 182 -188. LI Jinhai, LV Yuejin. Attribute reduction and rules extrac⁃ tion in decision formal context based on concept lattice[ J]. Mathematics in practice and theory, 2009, 39 ( 7): 182 - 188. [9]梁吉业, 王俊红. 基于概念格的规则产生集挖掘算法 [J]. 计算机研究与展, 2004, 41(8): 1339-1344. LIANG Jiye, WANG Junhong. An algorithm for extracting rule⁃generating sets based on Concept lattice[ J]. Journal of computer research and development, 2004, 41(8): 1339- 1344. [10]GODIN R, MISSAOUI R. An incremental concept forma⁃ tion approach for learning from databases[ J]. Theoretical computer science, 1994, 133(2): 387-419. [11]李进金, 张燕兰, 吴伟志, 等. 形式背景与协调决策形 式背景属性约简与概念格生成[J]. 计算机学报, 2014, 37(8): 1768-1774. LI Jinjin, ZHANG Yanlan, WU Weizhi, et al. Attribute reduction for formal context and consistent decision formal context and Concept lattice generation[J]. Chinese journal of computers, 2014, 37(8): 1768-1774. [12] MA Jianmin, LEUNG Y, ZHANG Wenxiu. Attribute re⁃ ·532· 智 能 系 统 学 报 第 11 卷

第4期 温云霞,等:横向拆分形势背景下的快速规则提取方法 ·533· ductions in object-oriented concept lattices[J].Interna- HU Keyun,LU Yuchang,SHI Chunyi.An integrated min- tional journal of machine learning and cybernetics,2014, ing approach for classification and association rule based on 5(5):789-813. Concept lattice[J].Journal of software,2000,11 (11): [13]LI Jinhai,MEI Changlin,WANG Junhong,et al.Rule- 1478-1484. preserved object compression in Formal decision contexts [19]MAO Hua.Characterization and reduction of concept lat- tices through matroid theory[].Information sciences, using concept lattices [J].Knowledge-based systems, 2014.281:338-354. 2014,71:435-445. [20]YANG Yafeng.Parallel construction of variable precision [14]CORNEJO M E.MEDINA J,RAMIREZ-POUSSA E.At- concept lattice in fuzzy formal context[J.AASRI Proce- tribute reduction in multi-adjoint concept lattices[J].In- dia,2013,5:214-219. formation sciences,2015,294:41-56. [21]DiAZ-MORENO J C,MEDINA J.Using concept lattice [15]TAN Anhui,LI Jinjin,LIN Guoping.Connections between theory to obtain the set of Solutions of multi-adjoint rela- covering-based rough sets and concept lattices[J].Interna- tion equations[J].Information sciences,2014,266:218 tional journal of approximate reasoning,2015,56(Part -225. A):43-58. [22]ISHIGURE H,MUTOH A,MATSUI T,et al.Concept lat- [16]张文修,魏玲,祁建军.概念格的属性约简理论与方法 tice reduction using attribute inference [C]//Proceedings of the IEEE 4th Global Conference on Consumer Electron- [J】.中国科学E辑:信息科学,2005,35(6):628- ic8.0saka:IEEE.2015:108-111. 639. [23]CHEN Jinkun,LI Jinjin,LIN Yaojin,et al.Relations of ZHANG Wenxiu,WEI Ling,QI Jianjun.Attribute reduc- reduction between covering generalized rough sets and Con- tion theory and approach to concept lattice[.Science in cept lattices[J].Information sciences,2015,304:16- China series F:information sciences,2005,48(6):713- 27. 726. 作者简介: [17]张磊,张宏莉,殷丽华,等.概念格的属性渐减原理与 温云霞,女,1986年生,硕士研究 算法研究[J刀.计算机研究与发展,2013,50(2):248- 生,主要研究方向为概念格与数据挖 掘。 259. ZHANG Lei,ZHANG Hongli,YIN Lihua,et al.Theory and algorithms of attribute decrement for Concept lattice [J].Journal of computer research and development, 2013,50(2):248-259. 王俊红,女,1979年生,副教授,博 [18]胡可云,陆玉昌,石纯一.基于概念格的分类和关联规 士,硕士生导师,主要研究方向为粒计 则的集成挖掘方法[J].软件学报,2000,11(11): 算、概念格与数据挖掘。 1478-1484
ductions in object⁃oriented concept lattices [ J]. Interna⁃ tional journal of machine learning and cybernetics, 2014, 5(5): 789-813. [13] LI Jinhai, MEI Changlin, WANG Junhong, et al. Rule⁃ preserved object compression in Formal decision contexts using concept lattices [ J ]. Knowledge⁃based systems, 2014, 71: 435-445. [14]CORNEJO M E, MEDINA J, RAMíREZ⁃POUSSA E. At⁃ tribute reduction in multi⁃adjoint concept lattices[ J]. In⁃ formation sciences, 2015, 294: 41-56. [15]TAN Anhui, LI Jinjin, LIN Guoping. Connections between covering⁃based rough sets and concept lattices[J]. Interna⁃ tional journal of approximate reasoning, 2015, 56 ( Part A): 43-58. [16]张文修, 魏玲, 祁建军. 概念格的属性约简理论与方法 [J]. 中国科学 E 辑: 信息科学, 2005, 35( 6): 628- 639. ZHANG Wenxiu, WEI Ling, QI Jianjun. Attribute reduc⁃ tion theory and approach to concept lattice[ J]. Science in China series F: information sciences, 2005, 48(6): 713- 726. [17]张磊, 张宏莉, 殷丽华, 等. 概念格的属性渐减原理与 算法研究[J]. 计算机研究与发展, 2013, 50(2): 248- 259. ZHANG Lei, ZHANG Hongli, YIN Lihua, et al. Theory and algorithms of attribute decrement for Concept lattice [ J ]. Journal of computer research and development, 2013, 50(2): 248-259. [18]胡可云, 陆玉昌, 石纯一. 基于概念格的分类和关联规 则的集成挖掘方法 [ J]. 软件学报, 2000, 11 ( 11): 1478-1484. HU Keyun, LU Yuchang, SHI Chunyi. An integrated min⁃ ing approach for classification and association rule based on Concept lattice[ J]. Journal of software, 2000, 11( 11): 1478-1484. [19]MAO Hua. Characterization and reduction of concept lat⁃ tices through matroid theory [ J ]. Information sciences, 2014, 281: 338-354. [20] YANG Yafeng. Parallel construction of variable precision concept lattice in fuzzy formal context[ J]. AASRI Proce⁃ dia, 2013, 5: 214-219. [21] DíAZ⁃MORENO J C, MEDINA J. Using concept lattice theory to obtain the set of Solutions of multi⁃adjoint rela⁃ tion equations[J]. Information sciences, 2014, 266: 218 -225. [22]ISHIGURE H, MUTOH A, MATSUI T, et al. Concept lat⁃ tice reduction using attribute inference [ C] / / Proceedings of the IEEE 4th Global Conference on Consumer Electron⁃ ics. Osaka: IEEE, 2015: 108-111. [23]CHEN Jinkun, LI Jinjin, LIN Yaojin, et al. Relations of reduction between covering generalized rough sets and Con⁃ cept lattices [ J]. Information sciences, 2015, 304: 16 - 27. 作者简介: 温云霞,女,1986 年生,硕士研究 生,主要研究方向为概念格与数据挖 掘。 王俊红,女,1979 年生,副教授,博 士,硕士生导师,主要研究方向为粒计 算、概念格与数据挖掘。 第 4 期 温云霞,等:横向拆分形势背景下的快速规则提取方法 ·533·