
第12卷第4期 智能系统学报 Vol.12 No.4 2017年8月 CAAI Transactions on Intelligent Systems Aug.2017 D0I:10.11992/is.201605001 改进D-S证据理论在 电动汽车锂电池故障诊断中的应用 夏飞23,马茜2,张浩23,彭道刚2,孙朋2,罗志疆2 (1.上海电力学院自动化工程学院,上海200090:2.上海发电过程智能管控工程技术研究中心,上海200090:3.同 济大学电子与信息工程学院,上海201804) 摘要:针对电动汽车电池系统的故障采用基于神经网络的改进DS证据理论组合规则完成诊断过程。为了避免 单一途径的诊断可能造成故障漏检误检的状况,决策层采用D-S证据理论组合规则来确定基于BP网络和RBF网络 两种故障诊断算法结果。然而为了克服D$证据理论处理高度冲突证据的缺陷,本文提出了一种基于神经网络改 进的D-$证据理论组合规则。首先,采用神经网络对电池故障进行初步诊断,结合网络诊断准确率来分配不确定信 息并构造证据体,又引入了证据间的支持矩阵来确定新的加权证据体。然后,把各个焦元的信任度融入D-S证据理 论组合规则,从而融合神经网络证据体及新加权证据体。最后,依据决策准则确定锂电池系统的故障状态。通过仿 真实验验证了本文提出的改进DS证据理论融合诊断方法在电动汽车锂电池故障诊断中的有效性。 关键词:故障诊断:电动汽车:锂电池:改进证据理论:信息融合 中图分类号:TP301文献标志码:A文章编号:1673-4785(2017)04-0526-12 中文引用格式:马茜,夏飞,张浩,等.改进D-S证据理论在电动汽车锂电池故障诊断中的应用[J].智能系统学报,2017,12(4): 526-537. 英文引用格式:MAXi,XIA Fei,.ZHANG Hao,etal.Application of improved D-S evidence theory in fault diagnosis of lithium batteries in electric vehicles[J].CAAI transactions on intelligent systems,2017,12(4):526-537. Application of improved D-S evidence theory in fault diagnosis of lithium batteries in electric vehicles XIA Fei3,MA Xi2,ZHANG Hao23,PENG Daogang'2,SUN Peng'2,LUO Zhijiang'2 (1.College of Automation Engineering,Shanghai University of Electric Power,Shanghai 200090,China;2.Shanghai Engineering Research Center of Intelligent Management and Control for Power Process,Shanghai 200090,China;3.College of Electronics and Information Engineering,Tongji University,Shanghai 201804,China) Abstract:In this study,we used the improved Dempster-Shafer (D-S)evidence theory combination rules based on the neural network to construct a fault diagnosis process for an electric vehicle battery system.To avoid misdiagnoses and missed diagnoses caused by a single fault diagnosis method,we applied the D-S evidence theory combination principle to determine the result based on the back-propagation (BP)network and radial basis function (RBF) network fault diagnosis algorithm.However,to overcome the defects in the D-S evidence theory in dealing with highly conflicting evidence,we propose a D-S evidence theory combination principle based on an improved neural network.First,we apply a neural network to perform a preliminary diagnosis regarding battery failure and the accuracy of the network diagnosis.Then,we distribute indefinite information and construct a body of evidence.We also introduce a support matrix of this evidence to determine a new weighted body of evidence.We then integrate the credibility of every focal element into the D-S evidence theory combination rules to fuse the neural network body of evidence with the new weighted body of evidence.Lastly,based on the decision criterion,we determine the failure state of the lithium battery system.Our simulation results show that our proposed improved D-S evidence theory fusion diagnosis method is effective in the fault diagnosis of electric vehicles with lithium batteries. Keywords:fault diagnosis;electric vehicle;lithium battery;improved evidence theory;information fusion 电动汽车的动力锂电池系统对于整个电动汽 车而言,是保证汽车正常行驶和准确预估续驶里程 的基础。当前制约电动汽车发展的核心技术就是 收稿日期:2016-05-03 在行车过程中电池系统能否准确切实提供动力,确 基金项目:上海市“科技创新行动计划”高新技术领域科研项目 (15111106800):上海市发电过程智能管控工程技术研究中 保安全出行。由于目前国内动力电池技术并非完 心项目(14DZ2251100):上海市电站自动化技术重点实验室 全成熟,电池故障在初期征兆不易察觉,因此对电 开放课题(13D72273800). 通信作者:张浩.E-mail:hzhangk@163.com
第 12 卷第 4 期 智 能 系 统 学 报 Vol.12 №.4 2017 年 8 月 CAAI Transactions on Intelligent Systems Aug. 2017 DOI:10.11992 / tis.201605001 改进 D⁃S 证据理论在 电动汽车锂电池故障诊断中的应用 夏飞1,2,3 ,马茜1,2 ,张浩1,2,3 ,彭道刚1,2 ,孙朋1,2 ,罗志疆1,2 (1.上海电力学院 自动化工程学院 , 上海 200090; 2.上海发电过程智能管控工程技术研究中心, 上海 200090; 3.同 济大学 电子与信息工程学院,上海 201804) 摘 要:针对电动汽车电池系统的故障采用基于神经网络的改进 D⁃S 证据理论组合规则完成诊断过程。 为了避免 单一途径的诊断可能造成故障漏检误检的状况,决策层采用 D⁃S 证据理论组合规则来确定基于 BP 网络和 RBF 网络 两种故障诊断算法结果。 然而为了克服 D⁃S 证据理论处理高度冲突证据的缺陷,本文提出了一种基于神经网络改 进的 D⁃S 证据理论组合规则。 首先,采用神经网络对电池故障进行初步诊断,结合网络诊断准确率来分配不确定信 息并构造证据体,又引入了证据间的支持矩阵来确定新的加权证据体。 然后,把各个焦元的信任度融入 D⁃S 证据理 论组合规则,从而融合神经网络证据体及新加权证据体。 最后,依据决策准则确定锂电池系统的故障状态。 通过仿 真实验验证了本文提出的改进 D⁃S 证据理论融合诊断方法在电动汽车锂电池故障诊断中的有效性。 关键词:故障诊断;电动汽车;锂电池;改进证据理论;信息融合 中图分类号:TP301 文献标志码:A 文章编号:1673-4785(2017)04-0526-12 中文引用格式:马茜,夏飞,张浩,等.改进 D⁃S 证据理论在电动汽车锂电池故障诊断中的应用[ J]. 智能系统学报, 2017, 12( 4): 526-537. 英文引用格式:MA Xi, XIA Fei, ZHANG Hao,et al. Application of improved D⁃S evidence theory in fault diagnosis of lithium batteries in electric vehicles[J]. CAAI transactions on intelligent systems, 2017, 12(4): 526-537. Application of improved D⁃S evidence theory in fault diagnosis of lithium batteries in electric vehicles XIA Fei 1,2,3 , MA Xi 1,2 ,ZHANG Hao 1,2,3 , PENG Daogang 1,2 , SUN Peng 1,2 , LUO Zhijiang 1,2 (1. College of Automation Engineering, Shanghai University of Electric Power, Shanghai 200090, China; 2. Shanghai Engineering Research Center of Intelligent Management and Control for Power Process, Shanghai 200090, China; 3. College of Electronics and Information Engineering, Tongji University, Shanghai 201804, China) Abstract:In this study, we used the improved Dempster⁃Shafer (D⁃S) evidence theory combination rules based on the neural network to construct a fault diagnosis process for an electric vehicle battery system. To avoid misdiagnoses and missed diagnoses caused by a single fault diagnosis method, we applied the D⁃S evidence theory combination principle to determine the result based on the back⁃propagation (BP) network and radial basis function (RBF) network fault diagnosis algorithm. However, to overcome the defects in the D⁃S evidence theory in dealing with highly conflicting evidence, we propose a D⁃S evidence theory combination principle based on an improved neural network. First, we apply a neural network to perform a preliminary diagnosis regarding battery failure and the accuracy of the network diagnosis. Then, we distribute indefinite information and construct a body of evidence. We also introduce a support matrix of this evidence to determine a new weighted body of evidence. We then integrate the credibility of every focal element into the D⁃S evidence theory combination rules to fuse the neural network body of evidence with the new weighted body of evidence. Lastly, based on the decision criterion, we determine the failure state of the lithium battery system. Our simulation results show that our proposed improved D⁃S evidence theory fusion diagnosis method is effective in the fault diagnosis of electric vehicles with lithium batteries. Keywords: fault diagnosis; electric vehicle; lithium battery; improved evidence theory; information fusion 收稿日期:2016-05-03. 基金项目: 上 海 市 “ 科 技 创 新 行 动 计 划” 高 新 技 术 领 域 科 研 项 目 (15111106800);上海市发电过程智能管控工程技术研究中 心项目(14DZ2251100);上海市电站自动化技术重点实验室 开放课题(13DZ2273800). 通信作者:张浩.E⁃mail: hzhangk@ 163.com. 电动汽车的动力锂电池系统对于整个电动汽 车而言,是保证汽车正常行驶和准确预估续驶里程 的基础。 当前制约电动汽车发展的核心技术就是 在行车过程中电池系统能否准确切实提供动力,确 保安全出行。 由于目前国内动力电池技术并非完 全成熟,电池故障在初期征兆不易察觉,因此对电

第4期 夏飞,等:改进DS证据理论在电动汽车锂电池故障诊断中的应用 ·527· 池系统进行故障诊断研究,从而确保电池处于正常 的权重因子来修正证据源山。文献[12]提出了矛 运作状态,具有非常重要的现实意义。 盾系数来确定证据的权重。文献[13]综合了证据 电池在工作中不能避免颠簸碰撞等状况发生, 体可信度和证据源可靠度给出了证据可信度的计 导致电池电压过高或过低,电流过大或过小等。目 算公式,但是对于两个支持度的权重大小如何选择 前电动汽车电池系统故障诊断主要的研究方向集 仍然没有客观的计算方法。这些改进方法仅仅采 中在专家诊断和神经网络两个方面。文献[1]中结 用证据间每个焦元被赋予的基本概率分配函数值 合了模糊数学、神经网络和专家系统,通过专家系 的差值来衡量证据间的距离,但是没有考虑在某一 统搭建整体框架,采用模糊数学和神经网络的方法 个证据体中相应焦元之间的关联性,在证据源不确 实现电池故障诊断:文献[2]通过电池系统的仿真 定的情况下,证据之间的距离描述得不够准确。 模型,提取传感器的信号特征建立BP神经网络完 2)对组合规则的改进。Yagert首先提出了冲 成故障模式识别;文献[3]采用小波包对电池特征 突信息的分配,将不能起到正面效果的冲突信息赋 提取,设计B神经网络对电池故障进行诊断,同时 值给辨识框架,处理方法保守。文献[15]认为冲突 设计上位机,提供直接显示和数据分析支持。由于 信息也具有有用信息,对其进行了利用和分配。这 动力锂电池系统自身的复杂性和容易受到周围环 两种方法在处理多个证据与一个证据高度冲突时, 境影响等不确定性因素,将导致故障诊断的准确性 使未知项获得较大的支持度,无法做出正确决策。 下降。为了提高电动汽车锂电池故障诊断的准确 文献[16]依据命题的平均支持度进行加权分配冲 性,避免单一诊断方法可能造成漏检误检的情况发 突信息,但是该方法只是简单的平均加权整合,降 生,需要对同一故障对应的不同故障征兆进行融合 低了有用证据的可信度;文献[17]中对辨识框架下 处理得到合理判定结果。D-S证据理论作为一种处 不同目标进行了单独考虑,按照证据关于不同目标 理不确定性的推理方法,可以将其应用于锂电池的 的冲突程度进行分配:文献[18]根据部分与整体之 故障诊断技术中。同时D-S证据理论在信息融合方 间的相似性,将每一个命题的BPA的总和看作系统 面得到了广泛应用。基于D-S证据理论和BP神经 的确定性程度,作为信任度转换的权重。当目标的 网络的信息融合改进了多传感器信息融合[):基于 确定度较大时变换结果应该相对乐观,相反,它还 改进D-S证据理论融合量子粒子群优化BP神经网 是很保守的。 络的诊断方法提高了水电机组振动故障诊断效 针对以上改进算法的问题,本文提出了一种新 果[):基于小波神经网络和概率神经网络结合D-S 的改进算法应用于电动汽车的故障诊断中。应用 证据理论完成了对汽轮机组故障诊断分析。 神经网络对电池进行初步诊断,根据诊断的准确率 然而经典D-S证据理论在处理冲突证据时往往 将不确定性信息进行重新分配,保证了证据信息的 得到悖于常理的结论。经典的Zadeh悖论中指出, 完整性。引入证据之间的支持矩阵确定证据体的 两位目击者都认为C是嫌疑犯的可能性极低,应该 加权系数,构造新的加权证据体,赋予可靠性低证 支持率最低。而经过数据融合后得到结果为目标 据较小的权重以降低对结果的不良影响。为了改 C,得到与实际相悖的结果。由此发现D-S证据理 进D-$证据理论对于冲突证据处理的不足,不仅考 论对于高度冲突的证据信息无法得到正确的融合 虑到证据关于不同焦元的冲突程度,而且进一步地 结果,因此需要对D-S证据理论在处理冲突信息方 将证据焦元目标的信任度融入组合规则中,不仅保 面作出改进。针对冲突证据的情况,国内外学者做 证了辨识框架的完整性,也对冲突信息进行了合理 了大量研究探索,可分为以下两种方法: 有效地分配。根据改进的D-S证据理论融合方法, 1)对数据模型的修改。由于传感器处于外界 将由神经网络诊断得到的两条证据及其加权证据 环境,经常受到周围自然环境、人为因素的干扰以 进行融合。最后,依据决策准则得符合常理的电池 及传感器自身性能的影响,常常需要对传感器得到 故障类型。 的证据数据修改其权重信息。目前对证据修正其 1 权重可以快速有效地识别出系统存在的冲突证据。 证据理论的改进 通常是利用证据距离函数表达证据体之间的距离 1.1加权证据体生成 及相似性程度],同时还有证据距离函数和其他函 对电池组和单体电池的电压、电流和温度等状 数联合共同修正证据源,包括了证据体的可靠 态参数的在线监测、估计和预测借助于传感器完 度[8】、方向相似度函数[)等。利用证据体间贴近 成,但是电动汽车在锂电池方面,由于电池系统功 度[]及贴近度概率转换规则的相关系数确定不同 率高、结构复杂,运行环境受到温度和颠簸等不确
池系统进行故障诊断研究,从而确保电池处于正常 运作状态,具有非常重要的现实意义。 电池在工作中不能避免颠簸碰撞等状况发生, 导致电池电压过高或过低,电流过大或过小等。 目 前电动汽车电池系统故障诊断主要的研究方向集 中在专家诊断和神经网络两个方面。 文献[1]中结 合了模糊数学、神经网络和专家系统,通过专家系 统搭建整体框架,采用模糊数学和神经网络的方法 实现电池故障诊断;文献[2]通过电池系统的仿真 模型,提取传感器的信号特征建立 BP 神经网络完 成故障模式识别;文献[3]采用小波包对电池特征 提取,设计 BP 神经网络对电池故障进行诊断,同时 设计上位机,提供直接显示和数据分析支持。 由于 动力锂电池系统自身的复杂性和容易受到周围环 境影响等不确定性因素,将导致故障诊断的准确性 下降。 为了提高电动汽车锂电池故障诊断的准确 性,避免单一诊断方法可能造成漏检误检的情况发 生,需要对同一故障对应的不同故障征兆进行融合 处理得到合理判定结果。 D⁃S 证据理论作为一种处 理不确定性的推理方法,可以将其应用于锂电池的 故障诊断技术中。 同时 D⁃S 证据理论在信息融合方 面得到了广泛应用。 基于 D⁃S 证据理论和 BP 神经 网络的信息融合改进了多传感器信息融合[4] ;基于 改进 D⁃S 证据理论融合量子粒子群优化 BP 神经网 络的诊断方法提高了水电机组振动故障诊断效 果[5] ;基于小波神经网络和概率神经网络结合 D⁃S 证据理论完成了对汽轮机组故障诊断分析[6] 。 然而经典 D⁃S 证据理论在处理冲突证据时往往 得到悖于常理的结论。 经典的 Zadeh 悖论中指出, 两位目击者都认为 C 是嫌疑犯的可能性极低,应该 支持率最低。 而经过数据融合后得到结果为目标 C,得到与实际相悖的结果。 由此发现 D⁃S 证据理 论对于高度冲突的证据信息无法得到正确的融合 结果,因此需要对 D⁃S 证据理论在处理冲突信息方 面作出改进。 针对冲突证据的情况,国内外学者做 了大量研究探索,可分为以下两种方法: 1)对数据模型的修改。 由于传感器处于外界 环境,经常受到周围自然环境、人为因素的干扰以 及传感器自身性能的影响,常常需要对传感器得到 的证据数据修改其权重信息。 目前对证据修正其 权重可以快速有效地识别出系统存在的冲突证据。 通常是利用证据距离函数表达证据体之间的距离 及相似性程度[7] ,同时还有证据距离函数和其他函 数联合 共 同 修 正 证 据 源, 包 括 了 证 据 体 的 可 靠 度[8] 、方向相似度函数[9] 等。 利用证据体间贴近 度[10]及贴近度概率转换规则的相关系数确定不同 的权重因子来修正证据源[11] 。 文献[12]提出了矛 盾系数来确定证据的权重。 文献[13] 综合了证据 体可信度和证据源可靠度给出了证据可信度的计 算公式,但是对于两个支持度的权重大小如何选择 仍然没有客观的计算方法。 这些改进方法仅仅采 用证据间每个焦元被赋予的基本概率分配函数值 的差值来衡量证据间的距离,但是没有考虑在某一 个证据体中相应焦元之间的关联性,在证据源不确 定的情况下,证据之间的距离描述得不够准确。 2)对组合规则的改进。 Yager [14] 首先提出了冲 突信息的分配,将不能起到正面效果的冲突信息赋 值给辨识框架,处理方法保守。 文献[15]认为冲突 信息也具有有用信息,对其进行了利用和分配。 这 两种方法在处理多个证据与一个证据高度冲突时, 使未知项获得较大的支持度,无法做出正确决策。 文献[16]依据命题的平均支持度进行加权分配冲 突信息,但是该方法只是简单的平均加权整合,降 低了有用证据的可信度;文献[17]中对辨识框架下 不同目标进行了单独考虑,按照证据关于不同目标 的冲突程度进行分配;文献[18]根据部分与整体之 间的相似性,将每一个命题的 BPA 的总和看作系统 的确定性程度,作为信任度转换的权重。 当目标的 确定度较大时变换结果应该相对乐观,相反,它还 是很保守的。 针对以上改进算法的问题,本文提出了一种新 的改进算法应用于电动汽车的故障诊断中。 应用 神经网络对电池进行初步诊断,根据诊断的准确率 将不确定性信息进行重新分配,保证了证据信息的 完整性。 引入证据之间的支持矩阵确定证据体的 加权系数,构造新的加权证据体,赋予可靠性低证 据较小的权重以降低对结果的不良影响。 为了改 进 D⁃S 证据理论对于冲突证据处理的不足,不仅考 虑到证据关于不同焦元的冲突程度,而且进一步地 将证据焦元目标的信任度融入组合规则中,不仅保 证了辨识框架的完整性,也对冲突信息进行了合理 有效地分配。 根据改进的 D⁃S 证据理论融合方法, 将由神经网络诊断得到的两条证据及其加权证据 进行融合。 最后,依据决策准则得符合常理的电池 故障类型。 1 证据理论的改进 1.1 加权证据体生成 对电池组和单体电池的电压、电流和温度等状 态参数的在线监测、估计和预测借助于传感器完 成,但是电动汽车在锂电池方面,由于电池系统功 率高、结构复杂,运行环境受到温度和颠簸等不确 第 4 期 夏飞,等:改进 D⁃S 证据理论在电动汽车锂电池故障诊断中的应用 ·527·
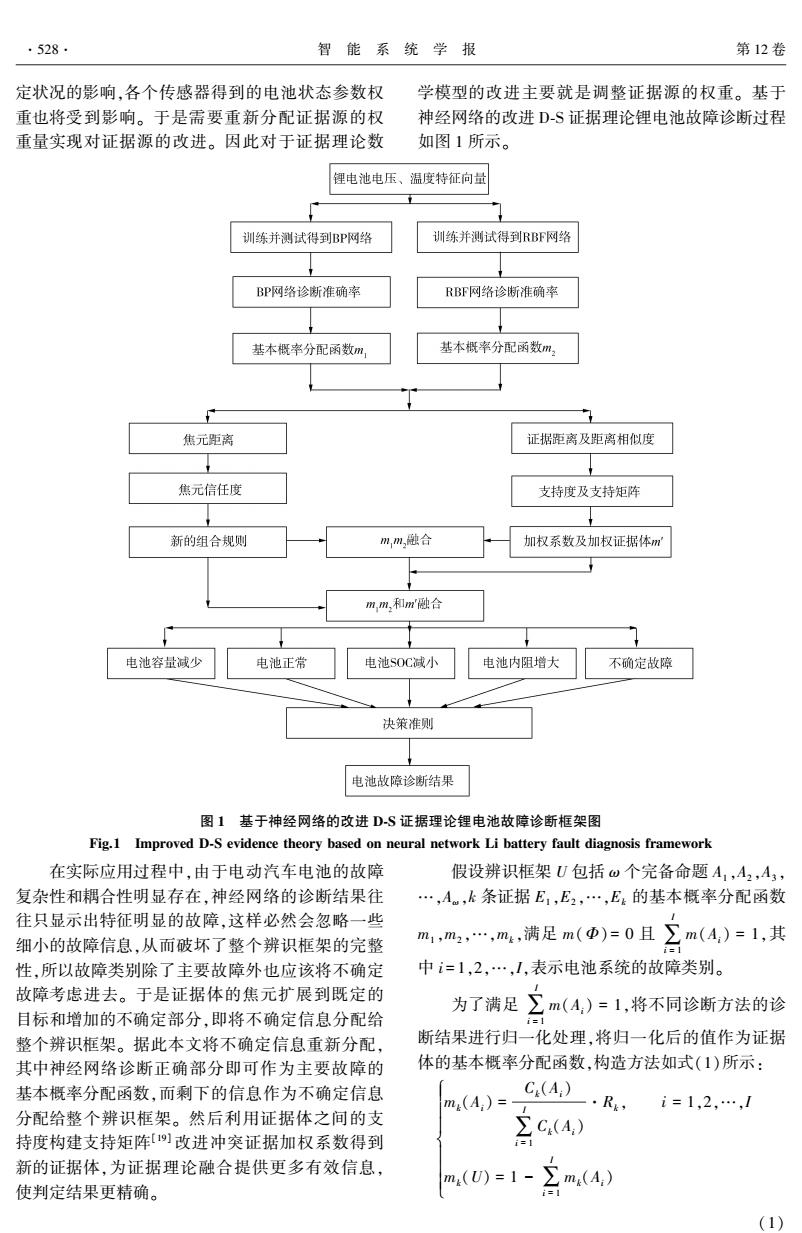
.528. 智能系统学报 第12卷 定状况的影响,各个传感器得到的电池状态参数权 学模型的改进主要就是调整证据源的权重。基于 重也将受到影响。于是需要重新分配证据源的权 神经网络的改进D-S证据理论锂电池故障诊断过程 重量实现对证据源的改进。因此对于证据理论数 如图1所示。 锂电池电压、温度特征向量 训练并测试得到BP网络 训练并测试得到RBF网络 BP网络诊断准确率 RBF网络诊断谁确率 基本概率分配函数m, 基本概率分配函数m? 焦元距离 证据距离及距离相似度 焦元信任度 支持度及支持矩阵 新的组合规则 m,m,融合 加权系数及加权证据体m m,m,和m'融合 电池容量减少 电池正常 电池S0C减小 电池内阻增大 不确定故障 决策准则 电池故障诊断结果 图1基于神经网络的改进DS证据理论锂电池故障诊断框架图 Fig.1 Improved D-S evidence theory based on neural network Li battery fault diagnosis framework 在实际应用过程中,由于电动汽车电池的故障 假设辨识框架U包括w个完备命题A1,A2,A3, 复杂性和耦合性明显存在,神经网络的诊断结果往 …,A,k条证据E1,E2,…,E:的基本概率分配函数 往只显示出特征明显的故障,这样必然会忽略一些 细小的故障信息,从而破坏了整个辨识框架的完整 m,m…,m,满足m()=0且三m(4)=1,其 性,所以故障类别除了主要故障外也应该将不确定 中i=1,2,…,1,表示电池系统的故障类别。 故障考虑进去。于是证据体的焦元扩展到既定的 为了满足∑m(4,)=1,将不同诊断方法的诊 目标和增加的不确定部分,即将不确定信息分配给 整个辨识框架。据此本文将不确定信息重新分配, 断结果进行归一化处理,将归一化后的值作为证据 其中神经网络诊断正确部分即可作为主要故障的 体的基本概率分配函数,构造方法如式(1)所示: 基本概率分配函数,而剩下的信息作为不确定信息 C(A) m(A:)= -·R4,i=1,2,…,1 分配给整个辨识框架。然后利用证据体之间的支 持度构建支持矩阵[]改进冲突证据加权系数得到 三c 新的证据体,为证据理论融合提供更多有效信息, 使判定结果更精确。 (0=1-三m4) (1)
定状况的影响,各个传感器得到的电池状态参数权 重也将受到影响。 于是需要重新分配证据源的权 重量实现对证据源的改进。 因此对于证据理论数 学模型的改进主要就是调整证据源的权重。 基于 神经网络的改进 D⁃S 证据理论锂电池故障诊断过程 如图 1 所示。 图 1 基于神经网络的改进 D⁃S 证据理论锂电池故障诊断框架图 Fig.1 Improved D⁃S evidence theory based on neural network Li battery fault diagnosis framework 在实际应用过程中,由于电动汽车电池的故障 复杂性和耦合性明显存在,神经网络的诊断结果往 往只显示出特征明显的故障,这样必然会忽略一些 细小的故障信息,从而破坏了整个辨识框架的完整 性,所以故障类别除了主要故障外也应该将不确定 故障考虑进去。 于是证据体的焦元扩展到既定的 目标和增加的不确定部分,即将不确定信息分配给 整个辨识框架。 据此本文将不确定信息重新分配, 其中神经网络诊断正确部分即可作为主要故障的 基本概率分配函数,而剩下的信息作为不确定信息 分配给整个辨识框架。 然后利用证据体之间的支 持度构建支持矩阵[19] 改进冲突证据加权系数得到 新的证据体,为证据理论融合提供更多有效信息, 使判定结果更精确。 假设辨识框架 U 包括 ω 个完备命题 A1 ,A2 ,A3 , …,Aω,k 条证据 E1 ,E2 ,…,Ek 的基本概率分配函数 m1 ,m2 ,…,mk,满足 m(Φ) = 0 且 ∑ I i = 1 m(Ai) = 1,其 中 i = 1,2,…,I,表示电池系统的故障类别。 为了满足 ∑ I i = 1 m(Ai) = 1,将不同诊断方法的诊 断结果进行归一化处理,将归一化后的值作为证据 体的基本概率分配函数,构造方法如式(1)所示: mk(Ai) = Ck(Ai) ∑ I i = 1 Ck(Ai) ·Rk, i = 1,2,…,I mk(U) = 1 - ∑ I i = 1 mk(Ai) ì î í ï ï ï ï ï ï (1) ·528· 智 能 系 统 学 报 第 12 卷

第4期 夏飞,等:改进DS证据理论在电动汽车锂电池故障诊断中的应用 ·529 式中:C,(A:)表示应用第k种诊断方法检测锂电池 数如式(6)所示: 故障状态时,诊断出电池处于A故障类型,此时的 B= k -,k=1,2,…,n (6 诊断结果输出。其中R表示第k种锂电池故障诊 断方法的诊断正确率,如式(2)所示: k=1 4)利用权重系数对证据进行修正,得到新的证 名 (x:-y:)2 据体: R=1- (2) (x:-x)2 m'= B()Xm (7) i=1 k=1 式中:x:表示第i组测试数据应用该诊断方法得到 综上,对于证据源的修正主要是利用不同诊断 的诊断结果值,一共有n组测试数据;y:表示第i组 方法的诊断正确率将不确定信息重新分配,在得到 测试数据的期望输出值:x.表示n组测试数据得到 辨识框架下各目标的基本概率分配函数后,计算两 的实验结果均值。 条证据的支持度,借助支持矩阵的特征向量得到加 在得到不同故障诊断方法对于锂电池故障的 权系数,生成新的证据体。 基本概率分配函数之后,按照以下步骤借助证据体 1.2证据理论组合规则的改进 之间支持矩阵生成加权证据体。 1.2.1经典D-S证据理论及改进 1)计算证据体间距离以及距离相似度。辨识 辨识框架U={A1,A2,A3…},n条证据对辨 框架上相互独立的两个证据体距离和距离相似度 识目标的支持率可以用基本概率分配函数来表 可以表示为 示,函数值越大表示对该目标的支持率越大,反 之越小。 doa(m:m)=(m -m)D(m -m)(3) 经典D-S证据理论的组合规则表示为 DS(m:,m;)=1-drA(m:,m;),i,j=1,2,,n ∑m,(4,)m,(4)m,(4)… (4) m(A)= 4n4nr…=A A≠Φ,U 1-k 式中:D表示2×2矩阵;N表示辨识框架的元素 个数。 (8) 2)计算证据m:的支持度。证据体m:的支持度 式中:k=∑m,(A)m2(4)m,(A)…,称k为 A,nA,nAr·=w 表示为 1 sup(m:)=∑DS(m,m,) (5) 证据冲突系数,1一为归一化因子。 经典的证据理论在处理高度冲突证据时会得 3)计算权重系数。构建证据E1,E2,…,En的支 到悖于常理的结论,因此需要进行冲突分析,将冲 持矩阵R=(sup(m:,m;))nxm 突系数重新分配。在此基础上,Yager首先提出分 式中:特征向量V=[u2,]T满足R=Aw,即 析,既然冲突系数对最终结果判定的影响最大,那 入:=T1·+r2·t…+打a·a。将A:作为证据 可以将其分配给整个辨识框架。文献[14]的组合 E,E2,…,En对证据E的支持度归一化,其权重系 规则表示为 (m(A)=m (A)m2(A )m3(A)... ADADAr…=A (9) m(U)= ∑m,(A)m2(4)m(A)…=k AiOAOAr…= 融合结果显示,绝大部分的支持率都赋给了辨 判定结果没有很好帮助。 识框架,对于冲突证据没有起到有效作用,仍然对 文献[15]中将冲突系数重新分配,组合规则为 m(A)= ∑m,(4)m,(4)m,(A,)…+k··q(A)A≠重,U A,n8ncr…=A (10) m(U)=】 ,m1(A:)m2(A)m3(A)…+k·e·q(U)+k(1-e) AinBinC..=U 式中:8=e是可信度,=,1 ∑k,是冲 n(n-1)1 突程度,q(A)=二∑m,(A)是目标A的支持度。 n1i运m 2 文献[16]同样对冲突系数修正,组合规则为
式中:Ck(Ai)表示应用第 k 种诊断方法检测锂电池 故障状态时,诊断出电池处于 Ai 故障类型,此时的 诊断结果输出。 其中 Rk 表示第 k 种锂电池故障诊 断方法的诊断正确率,如式(2)所示: Rk = 1 - ∑ n i = 1 (xi - yi) 2 ∑ n i = 1 (xi - xv) 2 (2) 式中:xi 表示第 i 组测试数据应用该诊断方法得到 的诊断结果值,一共有 n 组测试数据;yi 表示第 i 组 测试数据的期望输出值;xv 表示 n 组测试数据得到 的实验结果均值。 在得到不同故障诊断方法对于锂电池故障的 基本概率分配函数之后,按照以下步骤借助证据体 之间支持矩阵生成加权证据体。 1)计算证据体间距离以及距离相似度。 辨识 框架上相互独立的两个证据体距离和距离相似度 可以表示为 dBPA(mi,mj) = 1 2 (mi - mj)D(mi - mj) (3) DS(mi,mj) = 1 - dBPA(mi,mj), i,j = 1,2,…,n (4) 式中:D 表示 2 N ×2 N 矩阵;N 表示辨识框架的元素 个数。 2)计算证据 mi 的支持度。 证据体 mi 的支持度 表示为 sup(mi) = ∑i = 1 j≠i DS(mi,mj) (5) 3)计算权重系数。 构建证据 E1 ,E2 ,…,En 的支 持矩阵 R = (sup(mi,mj))n×n 式中:特征向量 V = v1 v2…vn [ ] T 满足 Rv = λv, 即 λvk = rk1·v1 +rk2·v2 +…+rkn·vn 。 将 λvk 作为证据 E1 ,E2 ,…,En 对证据 Ek 的支持度归一化,其权重系 数如式(6)所示: βk = vk ∑ n k = 1 vk , k = 1,2,…,n (6) 4)利用权重系数对证据进行修正,得到新的证 据体: m′ = ∑ n k = 1 β(k) × mk (7) 综上,对于证据源的修正主要是利用不同诊断 方法的诊断正确率将不确定信息重新分配,在得到 辨识框架下各目标的基本概率分配函数后,计算两 条证据的支持度,借助支持矩阵的特征向量得到加 权系数,生成新的证据体。 1.2 证据理论组合规则的改进 1.2.1 经典 D⁃S 证据理论及改进 辨识框架 U = { A1 ,A2 ,A3 …} , n 条证据对辨 识目标的支持率可以用基本概率分配函数来表 示,函数值越大表示对该目标的支持率越大,反 之越小。 经典 D⁃S 证据理论的组合规则表示为 m(A) = A ∑i∩Aj∩Al… = A m1(Ai)m2(Aj)m3(Al)… 1 - k A ≠ Φ,U (8) 式中: k = A ∑i∩Aj∩Al… = Φ m1(Ai)m2(Aj)m3(Al)…,称 k 为 证据冲突系数, 1 1 - k 为归一化因子。 经典的证据理论在处理高度冲突证据时会得 到悖于常理的结论,因此需要进行冲突分析,将冲 突系数重新分配。 在此基础上,Yager 首先提出分 析,既然冲突系数对最终结果判定的影响最大,那 可以将其分配给整个辨识框架。 文献[14] 的组合 规则表示为 m(A) = A ∑i∩Aj∩Al… = A m1(Ai)m2(Aj)m3(Al)… m(U) = A ∑i∩Aj∩Al… = Φ m1(Ai)m2(Aj)m3(Al)… = k ì î í ï ï ï ï (9) 融合结果显示,绝大部分的支持率都赋给了辨 识框架,对于冲突证据没有起到有效作用,仍然对 判定结果没有很好帮助。 文献[15]中将冲突系数重新分配,组合规则为 m(A) = A ∑i∩Bj∩Cl… = A m1(Ai)m2(Aj)m3(Al)… + k·ε·q(A) A ≠ Φ,U m(U) = A ∑i∩Bj∩Cl ... = U m1(Ai)m2(Aj)m3(Al)… + k·ε·q(U) + k(1 - ε) ì î í ï ï ï ï (10) 式中: ε = e - k ~ 是可信度,k ~ = 1 n(n - 1) 2 1≤∑i≤j≤n kij 是冲 突程度, q(A) = 1 n 1∑≤i≤n mi(A) 是目标 A 的支持度。 文献[16]同样对冲突系数修正,组合规则为 第 4 期 夏飞,等:改进 D⁃S 证据理论在电动汽车锂电池故障诊断中的应用 ·529·

·530· 智能系统学报 第12卷 m(A)=∑m,(A:)m2(4)m3(A)…+k·q(A),A≠重,U (11) An4nAr…=A 式中:g(4)=∑m(A)是目标A的支持度。 有效信息,很难达到预期良好效果。 n1运m 文献[17]认为传感器得到的冲突数据并不 文献[15]和文献[16]认为冲突系数并非完全 是针对所有的目标,而是对于某一个目标存在冲 没用,同样携带有用信息,将冲突系数重新分配,如 突。在得到目标的基本概率分配函数时,不仅考 式(10)~(11)表示。当证据存在高度冲突时,冲突 虑证据间关于这一目标的冲突情况,目标之间的 系数k较大,利用这样的改进方法进行组合,融合结 冲突信息也要考虑,提出一种新的合成法则,表 果会偏重于不确定信息部分,不能为正确结论提供 示为 m(Φ)=0 m(A)=∑m,(A,)m2(4)m(A)…+fA),A≠Φ, (12) n4nAr…=A 1 取f4)=(∑m,(4,)m,(4,)m,(4)…+ 可靠度也不是完全相同的。对组合规则的改进不 n4n4,nun=Φ 能只考虑全局层面上,而把目标本身的可靠度忽 m2(A)m1(A)m3(A)…+…),式中:n 略。证据的信任度和焦元的信任度是不同的,为了 AnA,nAkn…= 为证据数,i,j,k,l,s…=1,2,3,…,n。 降低信任度低的焦元对结果的影响,在文献[22]的 1.2.2改进的D-S证据理论组合规则 基础上,将焦元信任度加入到组合规则的改进中, 在经典证据理论的优势下关于证据理论组合 这样参与融合的每一个焦元都有一个分配系数。新 规则的改进就是按照一定的规则将证据冲突系数 的合成法则处理了证据对目标存在的一致性信息及冲 合理有效分配,体现冲突证据的有效融合[202]。从 突信息。依旧遵循D-S证据理论处理目标一致性理 全局角度分析,一些人为原因或者自然原因造成某 论,而对于冲突信息借鉴一致性信息的融合,将焦元的 些证据体与其他证据体冲突。从局部角度分析,引 信任度考虑进去,得到了合理充分的利用。 起冲突的可能是某一目标,不同证据体的同一目标 本文提出的新组合规则表示为 m(A)=m,(A.)mz (A )m3(A,)+f(A) A040An.=4 (13) m(U)=∑m,(4)m,(A,)m,(A) An4ynAn…=U 取 f4)=∑ D(A:)·m(A:) nnn=D(4)m(A)+D,(4)·m(A)+D,(A)·m,(A)+·mA)·m,A)·m(4,)+ D2(4)·m2(4) nunn=D.4)m4)+D,(4)·m(4,)+D,(4)·m(4)+·m,4)·m4,)·m(M,)+… 式中:f(A)表示冲突信息的分配,D,(A)表示第i条 焦元之间的距离,这里可以利用不同证据体与加权 证据中目标A:信任度。将证据中存在的冲突按照 证据体同一焦元的距离来表示,如式(14)所示。 焦元的冲突程度进行分配,归一化处理的分配因子 FD[m,(A)]=m.(A)-mAE(A)(14) 是焦元的可信度。 式中:mE(A:)是加权证据体。在得到焦元距的基 计算焦元的信任度可以效仿证据体的信任度。 础上获得每一个焦元的信任度2],并将其归一化。 利用不同证据体与加权证据体同一焦元的距离得 定义焦元的信任度,如式(15)所示,归一化的结果 到各条证据不同焦元的距离FD[m,(A)],再在焦 如式(16)所示。 元距的基础上得到各焦元的信任度。首先要得到 2m;(A:)mAVE(A:) Fcrd[m;(Ag)]=[1 -FD[m;(Ag)]] [m,(4)]2+[me(A)]2 i=1,2,…,n;k=1,2,…,K(15)
m(A) = A ∑i∩Aj∩Al… = A m1(Ai)m2(Aj)m3(Al)… + k·q(A),A ≠ Φ,U (11) 式中: q(A) = 1 n 1∑≤i≤n mi(A) 是目标 A 的支持度。 文献[15]和文献[16]认为冲突系数并非完全 没用,同样携带有用信息,将冲突系数重新分配,如 式(10) ~ (11)表示。 当证据存在高度冲突时,冲突 系数 k 较大,利用这样的改进方法进行组合,融合结 果会偏重于不确定信息部分,不能为正确结论提供 有效信息,很难达到预期良好效果。 文献[ 17] 认为传感器得到的冲突数据并不 是针对所有的目标,而是对于某一个目标存在冲 突。 在得到目标的基本概率分配函数时,不仅考 虑证据间关于这一目标的冲突情况,目标之间的 冲突信息也要考虑,提出一种新的合成法则,表 示为 m(Φ) = 0 m(A) = A ∑i∩Aj∩Al… = A { m1(Ai)m2(Aj)m3(Al)… + f(A),A ≠ Φ,U (12) 取f(A)= 1 n ( A ∑i∩As∩Ak∩… = Φ m1(Ai)m2(As)m3(Ak)… + A ∑ j∩As∩Ak∩… = Φ m2(Aj)m1(As)m3(Ak)… + …), 式中:n 为证据数,i,j,k,l,s… = 1,2,3,…,n 。 1.2.2 改进的 D⁃S 证据理论组合规则 在经典证据理论的优势下关于证据理论组合 规则的改进就是按照一定的规则将证据冲突系数 合理有效分配,体现冲突证据的有效融合[20-21] 。 从 全局角度分析,一些人为原因或者自然原因造成某 些证据体与其他证据体冲突。 从局部角度分析,引 起冲突的可能是某一目标,不同证据体的同一目标 可靠度也不是完全相同的。 对组合规则的改进不 能只考虑全局层面上,而把目标本身的可靠度忽 略。 证据的信任度和焦元的信任度是不同的,为了 降低信任度低的焦元对结果的影响,在文献[22]的 基础上,将焦元信任度加入到组合规则的改进中, 这样参与融合的每一个焦元都有一个分配系数。 新 的合成法则处理了证据对目标存在的一致性信息及冲 突信息。 依旧遵循 D⁃S 证据理论处理目标一致性理 论,而对于冲突信息借鉴一致性信息的融合,将焦元的 信任度考虑进去,得到了合理充分的利用。 本文提出的新组合规则表示为 m(A) = A ∑i∩Aj∩Al∩… = A m1(Ai)m2(Aj)m3(Al) + f(A) m(U) = A ∑i∩Aj∩Al∩… = U m1(Ai)m2(Aj)m3(Al) ì î í ï ï ï ï (13) 取 f(A) = A ∑i∩As∩Ak∩… = Φ D1(Ai)·m1(Ai) D1(Ai)·m1(Ai) + D2(As)·m2(As) + D3(Ak)·m3(Ak) + … ·m1(Ai)·m2(As)·m3(Ak)… + A ∑ j∩As∩Ak∩… = Φ D2(Aj)·m2(Aj) D2(Aj)·m2(Aj) + D1(As)·m1(As) + D3(Ak)·m3(Ak) + … ·m2(Aj)·m1(As)·m3(Ak)… + … 式中:f(A)表示冲突信息的分配,Di(Ak)表示第 i 条 证据中目标 Ak 信任度。 将证据中存在的冲突按照 焦元的冲突程度进行分配,归一化处理的分配因子 是焦元的可信度。 计算焦元的信任度可以效仿证据体的信任度。 利用不同证据体与加权证据体同一焦元的距离得 到各条证据不同焦元的距离 FD[mi(Ak)],再在焦 元距的基础上得到各焦元的信任度。 首先要得到 焦元之间的距离,这里可以利用不同证据体与加权 证据体同一焦元的距离来表示,如式(14)所示。 FD[mi(Ak)] = mi(Ak) - mAVE(Ak) (14) 式中:mAVE(Ak)是加权证据体。 在得到焦元距的基 础上获得每一个焦元的信任度[23] ,并将其归一化。 定义焦元的信任度,如式(15) 所示,归一化的结果 如式(16)所示。 Fcrd[mi(Ak)] = [1 - FD[mi(Ak)]]· 2mi(Ak)mAVE(Ak) [mi(Ak)] 2 + [mAVE(Ak)] 2 i = 1,2,…,n;k = 1,2,…,K (15) ·530· 智 能 系 统 学 报 第 12 卷

第4期 夏飞,等:改进DS证据理论在电动汽车锂电池故障诊断中的应用 ·531· Ferd[m;(A:) D(A)= i=1,2,…,n;k=1,2,…,K 名会adaa小 (16) 由式(16)得到了不同证据体各焦元的信任度 表1不同组合规则的融合结果比较(m1⊕m2) 后,将其带入新的组合规则式(13)中,计算出分配 Table 1 Comparison of the fusion results of different 给产生冲突的各焦元信息。这样证据间不同目标 combination rules (mm2) 产生的冲突因子采用焦元的可信度,而不是该条证 方法 m2(A,) m2(A2) m2(A,)m2(U) 据的可信度,新的方法合理地融合了一致性信息和 DS证据理论 0.0000 0.0000 1.0000 0.0000 冲突信息。 文献「121方法0.4055 0.0045 0.5900 0.0000 1.3决策规则 文献[13]方法0.2152 0.0035 0.5501 0.2312 事实上,合理的决策规则是一个信息融合系统 文献「141方法0.0000 0.0000 0.0990 0.9010 的关键部分,不但可以借助有效的决策规则在面对 文献[15]方法0.2336 0.0025 0.3819 0.3817 多属性决策时做出正确选择,而且有效地降低决策 风险2]。本文对于确定锂电池故障类型的融合诊 文献[16]方法0.4055 0.0045 0.5900 0.0000 断结果进行决策时,应用基于决策焦元属性的证据 文献[17]方法0.4500 0.00500.5450 0.0000 结构决策规则。依据决策焦元的基本概率函数值, 本文组合方法0.4388 0.00020.56100.0000 本文选取基本概率函数最大规则,同时满足以下规 表2不同组合规则的融合结果比较(m,①m,①m,) 则才能确认最终的锂电池故障类型。 Table 2 Comparison of the fusion results of different 1)锂电池故障类型存在最大的基本概率分配 combination rules(m,⊕m,⊕m,】 函数值,即某故障类型的基本概率分配函数输出值 方法 mi2(A1) m12s(A2)m2s(A3)m12(U) 是所有故障类型输出值中的最大值。 DS证据理论 0.0000 0.0000 1.0000 1.0000 m(A)=max{m(A:),A:C} (17) 文献[12]方法0.4832 0.0642 0.45260.0000 2)某故障类型与其他故障类型的基本概率分 文献[13]方法 0.3685 0.0332 0.5220 0.0763 配函数值差异足够大时,才能选择确认锂电池处于 文献[141方法0.0000 0.0000 0.0297 0.9703 该故障状态。 文献[15]方法 0.2609 0.0391 0.2887 0.4111 m(A2)-m(A,)>E1 (18) 文献[16]方法0.4528 0.0679 0.4792 0.0000 (m(A2)=max{m(A;),A:C0,A:A) 文献[171方法0.47500.1025 0.42250.0000 3)不确定的基本概率函数值应该小于一定的 阈值。 本文组合方法0.50150.05720.44130.0000 m(0)<62 (19) 从证据的基本概率分配函数可以直观地看出, E1、62一般根据经验取得,本文取E,=0.2,E2= 前两条证据体明显是相互冲突的,证据体1对目标 0.5。当融合后的BPA同时满足以上3条决策规则 A,支持率较大,而证据体2却几乎完全支持目标 时,可以准确得到锂电池故障的最终诊断结果。 4A,。加入第3条证据后,目标A,的支持率应该大于 1.4算例验证与对比分析 目标A的支持率。在处理冲突证据时,第2条证据 下面通过一组算例对本文提出的改进算法进 对目标A,的支持度为0,使得在D-S证据理论的融 行验证,并和D-S证据理论方法及其他改进方法进 合结果中对目标A,的支持度依然是0,D-S证据理 行比较。 论有着明显的“一票否决”的弊端,致使决策失效。 设U={A1,A2,43},有: 文献[12]通过矛盾系数确定证据的加权系数,但依 m1:m1(A1)=0.9,m1(A2)=0,m1(A3)=0.1 然遵循D-S证据理论的组合规则,融合方法显得保 m2:m2(A1)=0,m2(A2)=0.01,m2(A3)=0.99 守。文献[13]综合证据体的支持度和证据源可靠 m3:m3(A)=0.5,m3(A2)=0.2,m3(A3)=0.3 度,但是并没有给出具体两者权重调整方法,缺乏 将本文改进算法的计算结果与另外几种改进 实际应用的准确性,没有得到正确结果。文献[14] 算法的计算结果比较,得到表1和表2。 也无法得到正确决策,而是将冲突分配给了未知
Di(Ak) = Fcrd[mi(Ak)] ∑ n i = 1 ∑ K k = 1 Fcrd[mi(Ak)] i = 1,2,…,n;k = 1,2,…,K (16) 由式(16)得到了不同证据体各焦元的信任度 后,将其带入新的组合规则式(13) 中,计算出分配 给产生冲突的各焦元信息。 这样证据间不同目标 产生的冲突因子采用焦元的可信度,而不是该条证 据的可信度,新的方法合理地融合了一致性信息和 冲突信息。 1.3 决策规则 事实上,合理的决策规则是一个信息融合系统 的关键部分,不但可以借助有效的决策规则在面对 多属性决策时做出正确选择,而且有效地降低决策 风险[24] 。 本文对于确定锂电池故障类型的融合诊 断结果进行决策时,应用基于决策焦元属性的证据 结构决策规则。 依据决策焦元的基本概率函数值, 本文选取基本概率函数最大规则,同时满足以下规 则才能确认最终的锂电池故障类型。 1)锂电池故障类型存在最大的基本概率分配 函数值,即某故障类型的基本概率分配函数输出值 是所有故障类型输出值中的最大值。 m(A1 ) = max{m(Ai),Ai ⊂ θ} (17) 2)某故障类型与其他故障类型的基本概率分 配函数值差异足够大时,才能选择确认锂电池处于 该故障状态。 m(A2 ) - m(A1 ) > ε1 m(A2 ) = max m(Ai),Ai ⊂ θ,Ai ≠ A1 { { } (18) 3)不确定的基本概率函数值应该小于一定的 阈值。 m(θ) < ε2 (19) ε1 、ε2 一般根据经验取得,本文取 ε1 = 0.2,ε2 = 0.5。 当融合后的 BPA 同时满足以上 3 条决策规则 时,可以准确得到锂电池故障的最终诊断结果。 1.4 算例验证与对比分析 下面通过一组算例对本文提出的改进算法进 行验证,并和 D⁃S 证据理论方法及其他改进方法进 行比较。 设 U= A1 ,A2 ,A3 { } ,有: m1 :m1(A1 ) = 0.9,m1(A2 ) = 0,m1(A3 ) = 0.1 m2 :m2(A1 ) = 0,m2(A2 ) = 0.01,m2(A3 ) = 0.99 m3 :m3(A1 ) = 0.5,m3(A2 ) = 0.2,m3(A3 ) = 0.3 将本文改进算法的计算结果与另外几种改进 算法的计算结果比较,得到表 1 和表 2。 表 1 不同组合规则的融合结果比较(m1m2 ) Table 1 Comparison of the fusion results of different combination rules (m1m2 ) 方法 m12(A1 ) m12(A2 ) m12(A3 ) m12(U) D⁃S 证据理论 0.000 0 0.000 0 1.000 0 0.000 0 文献[12]方法 0.405 5 0.004 5 0.590 0 0.000 0 文献[13]方法 0.215 2 0.003 5 0.550 1 0.231 2 文献[14]方法 0.000 0 0.000 0 0.099 0 0.901 0 文献[15]方法 0.233 6 0.002 5 0.381 9 0.381 7 文献[16]方法 0.405 5 0.004 5 0.590 0 0.000 0 文献[17]方法 0.450 0 0.005 0 0.545 0 0.000 0 本文组合方法 0.438 8 0.000 2 0.561 0 0.000 0 表 2 不同组合规则的融合结果比较(m1m2m3 ) Table 2 Comparison of the fusion results of different combination rules (m1m2m3 ) 方法 m123(A1 ) m123(A2 ) m123(A3 ) m123(U) D⁃S 证据理论 0.000 0 0.000 0 1.000 0 1.000 0 文献[12]方法 0.483 2 0.064 2 0.452 6 0.000 0 文献[13]方法 0.368 5 0.033 2 0.522 0 0.076 3 文献[14]方法 0.000 0 0.000 0 0.029 7 0.970 3 文献[15]方法 0.260 9 0.039 1 0.288 7 0.411 1 文献[16]方法 0.452 8 0.067 9 0.479 2 0.000 0 文献[17]方法 0.475 0 0.102 5 0.422 5 0.000 0 本文组合方法 0.501 5 0.057 2 0.441 3 0.000 0 从证据的基本概率分配函数可以直观地看出, 前两条证据体明显是相互冲突的,证据体 1 对目标 A1 支持率较大,而证据体 2 却几乎完全支持目标 A3 。 加入第 3 条证据后,目标 A1 的支持率应该大于 目标 A3 的支持率。 在处理冲突证据时,第 2 条证据 对目标 A1 的支持度为 0,使得在 D⁃S 证据理论的融 合结果中对目标 A1 的支持度依然是 0,D⁃S 证据理 论有着明显的“一票否决”的弊端,致使决策失效。 文献[12]通过矛盾系数确定证据的加权系数,但依 然遵循 D⁃S 证据理论的组合规则,融合方法显得保 守。 文献[13]综合证据体的支持度和证据源可靠 度,但是并没有给出具体两者权重调整方法,缺乏 实际应用的准确性,没有得到正确结果。 文献[14] 也无法得到正确决策,而是将冲突分配给了未知 第 4 期 夏飞,等:改进 D⁃S 证据理论在电动汽车锂电池故障诊断中的应用 ·531·

.532. 智能系统学报 第12卷 项,虽然没有随便支持其他目标,但同时提高了决 所示。 策难度。文献[15]绝大部分的支持率赋给了未知 表3S0C为80%时各类电池电压信号能量值归一化 项,很大程度上会干扰融合结果,决策精度较低。 Table 3 SOC=80%energy values of various types of 文献[16]按照各命题的平均支持度分配冲突信息, battery voltage signal normalization 需要更多的证据才能得到正确的结果,融合效果不 电压能量值Cell_Norm Cell_Cap Cell Rt Cell SOC 太理想。文献[17]忽略了多条数据源的权重,加强 E'(3.0) 0.5060 0.5046 0.5020 0.4872 了冲突信息对融合结果的不利影响,存在一定缺陷。 E'(3.1) 0.4054 0.4023 0.7298 0.3758 本文所提出的方法可以解决“一票否决”的问 E'(3,2) 0.4007 0.3971 0.7337 0.3788 题,通过初步诊断方法的诊断准确率及证据之间的 E'(3,3) 0.4085 0.4057 0.7212 0.3853 支持矩阵来确定证据的加权系数,降低了冲突证据 E'(3,4) 0.4005 0.3969 0.7340 0.3786 对融合结果的影响,同时考虑了焦元的信任度加入 E'(3,5) 0.4003 0.3968 0.7344 0.3781 到组合规则中,把冲突从证据之间扩展到焦元之 间,合理有效地利用冲突证据的有用信息。本文的 E'(3.6) 0.4068 0.4035 0.7247 0.3827 组合规则同时处理了一致性信息和焦元冲突信息, E(3,7) 0.3980 0.3942 0.73840.3754 大大降低了信任度低的目标A,的支持率,对于目标 表4S0C为80%时各类电池温度信号能量值归一化 A,和A,的支持同样符合常理,较好处理了冲突信 Table 4 SOC=80%all kinds of battery temperature signal 息,融合结果的精度也非常理想,在较少证据下得 energy value normalization 到符合常理的决策结果。通过表1和表2的比较可 温度能量值Cell_Norm Cell_Cap Cell Rt Cell SOC 知,本文改进方法的融合结果更精确、更贴合实际 E'(3,0) 0.4914 0.4893 0.5349 0.4827 情况。 E(3,1) 0.1154 0.1149 0.9801 0.1133 2锂电池故障诊断 E'(3,2) 0.0076 0.0076 0.9999 0.0075 E'(3,3) 0.0132 0.0132 0.9997 0.0130 如前文所述,锂电池的状态参数容易受到周围 E'(3.4) 0.0391 0.0391 0.9977 0.0390 环境温度和颠簸碰撞等不确定状况的影响,将会导 E'(3.5) 0.0048 0.0048 1.0000 0.0048 致单一诊断方法诊断的不确定性。为提高其故障 诊断的准确性,采用本文提出的改进D-S证据理论 E(3,6) 0.0009 0.0009 1.0000 0.0009 融合方法对电动汽车电池进行故障诊断。首先,应 E'(3,7) 0.1015 0.1015 0.98440.1015 用BP和RBF神经网络对锂电池分别进行初步诊 为了对电动汽车锂电池进行准确的故障诊断, 断,将两者的诊断结果构造成证据体m1、m2。再引 本文提出了一种基于BP和RBF神经网络的改进 入证据体之间的支持矩阵得到m1m2的加权系数, D-S证据理论方法。利用BP网络和RBF网络计算 并由此生成加权证据体m'。然后在组合规则中考 速度快、内存小、可用于实时监测和诊断的特点[5), 虑了每个焦元的信任度,充分利用了证据间的一致 将锂电池4种故障状态的电压和温度特征向量通过 性信息和冲突信息,得到组合规则。证据体融合 训练得到BP和RBF神经网络模型,并对电池故障 后,依据决策规则判定锂电池的故障类别。 进行初步诊断。Cell_Nom、Cell_Cap、Cell_Rt、Cell 2.1神经网络初步诊断 S0C4种故障类型在诊断网络中的输出分别用矢量 电池系统主要的故障状态主要包括容量减少、 (1,0,0,0)、(0,1,0,0)、(0,0,1,0)、(0,0,0,1)来 内阻增大、S0C减小等3种。在实际诊断中为了表 表示。 示电池的所有状态,加入了电池的正常状态。将这 在BP神经网络中,训练函数取L-M优化算法 4种故障状态分别记为Cell_Norm、Cell_Cap、Cel_Rt (rainlm),学习率为0.3,输入节点为8,输出节点为 和Cell_s0C。设初始SOC为80%,可以得到Cell_ 4。由于隐含层节点对神经网络诊断精度有较大影 Nom、Cell_Cap、Cell_Rt、Cel_SOC4种故障类型的电 响,但是由于其没有具体选择准则,本文中通过经 池单体仿真电压和温度。将这些故障信号进行小 验公式取隐含层节点数为17,同时在节点17附近 波包分解,得到锂电池的故障特征),如表3和表4 取值,比较不同节点下诊断误差的大小,如图2所
项,虽然没有随便支持其他目标,但同时提高了决 策难度。 文献[15]绝大部分的支持率赋给了未知 项,很大程度上会干扰融合结果,决策精度较低。 文献[16]按照各命题的平均支持度分配冲突信息, 需要更多的证据才能得到正确的结果,融合效果不 太理想。 文献[17]忽略了多条数据源的权重,加强 了冲突信息对融合结果的不利影响,存在一定缺陷。 本文所提出的方法可以解决“一票否决” 的问 题,通过初步诊断方法的诊断准确率及证据之间的 支持矩阵来确定证据的加权系数,降低了冲突证据 对融合结果的影响,同时考虑了焦元的信任度加入 到组合规则中,把冲突从证据之间扩展到焦元之 间,合理有效地利用冲突证据的有用信息。 本文的 组合规则同时处理了一致性信息和焦元冲突信息, 大大降低了信任度低的目标 A2 的支持率,对于目标 A1 和 A3 的支持同样符合常理,较好处理了冲突信 息,融合结果的精度也非常理想,在较少证据下得 到符合常理的决策结果。 通过表 1 和表 2 的比较可 知,本文改进方法的融合结果更精确、更贴合实际 情况。 2 锂电池故障诊断 如前文所述,锂电池的状态参数容易受到周围 环境温度和颠簸碰撞等不确定状况的影响,将会导 致单一诊断方法诊断的不确定性。 为提高其故障 诊断的准确性,采用本文提出的改进 D⁃S 证据理论 融合方法对电动汽车电池进行故障诊断。 首先,应 用 BP 和 RBF 神经网络对锂电池分别进行初步诊 断,将两者的诊断结果构造成证据体 m1 、m2 。 再引 入证据体之间的支持矩阵得到 m1 、m2 的加权系数, 并由此生成加权证据体 m′。 然后在组合规则中考 虑了每个焦元的信任度,充分利用了证据间的一致 性信息和冲突信息,得到组合规则。 证据体融合 后,依据决策规则判定锂电池的故障类别。 2.1 神经网络初步诊断 电池系统主要的故障状态主要包括容量减少、 内阻增大、SOC 减小等 3 种。 在实际诊断中为了表 示电池的所有状态,加入了电池的正常状态。 将这 4 种故障状态分别记为 Cell_Norm、Cell_Cap、Cell_Rt 和 Cell_SOC。 设初始 SOC 为 80%,可以得到 Cell_ Norm、Cell_Cap、Cell_Rt、Cell_SOC4 种故障类型的电 池单体仿真电压和温度。 将这些故障信号进行小 波包分解,得到锂电池的故障特征[3] ,如表 3 和表 4 所示。 表 3 SOC 为 80%时各类电池电压信号能量值归一化 Table 3 SOC = 80% energy values of various types of battery voltage signal normalization 电压能量值 Cell_Norm Cell_Cap Cell_Rt Cell_SOC E′(3,0) 0.506 0 0.504 6 0.502 0 0.487 2 E′(3,1) 0.405 4 0.402 3 0.729 8 0.375 8 E′(3,2) 0.400 7 0.397 1 0.733 7 0.378 8 E′(3,3) 0.408 5 0.405 7 0.721 2 0.385 3 E′(3,4) 0.400 5 0.396 9 0.734 0 0.378 6 E′(3,5) 0.400 3 0.396 8 0.734 4 0.378 1 E′(3,6) 0.406 8 0.403 5 0.724 7 0.382 7 E′(3,7) 0.398 0 0.394 2 0.738 4 0.375 4 表 4 SOC 为 80%时各类电池温度信号能量值归一化 Table 4 SOC= 80% all kinds of battery temperature signal energy value normalization 温度能量值 Cell_Norm Cell_Cap Cell_Rt Cell_SOC E′(3,0) 0.491 4 0.489 3 0.534 9 0.482 7 E′(3,1) 0.115 4 0.114 9 0.980 1 0.113 3 E′(3,2) 0.007 6 0.007 6 0.999 9 0.007 5 E′(3,3) 0.013 2 0.013 2 0.999 7 0.013 0 E′(3,4) 0.039 1 0.039 1 0.997 7 0.039 0 E′(3,5) 0.004 8 0.004 8 1.000 0 0.004 8 E′(3,6) 0.000 9 0.000 9 1.000 0 0.000 9 E′(3,7) 0.101 5 0.101 5 0.984 4 0.101 5 为了对电动汽车锂电池进行准确的故障诊断, 本文提出了一种基于 BP 和 RBF 神经网络的改进 D⁃S 证据理论方法。 利用 BP 网络和 RBF 网络计算 速度快、内存小、可用于实时监测和诊断的特点[25] , 将锂电池 4 种故障状态的电压和温度特征向量通过 训练得到 BP 和 RBF 神经网络模型,并对电池故障 进行初步诊断。 Cell_Norm、Cell_Cap、Cell_Rt、Cell_ SOC4 种故障类型在诊断网络中的输出分别用矢量 (1,0,0,0)、(0,1,0,0)、(0,0,1,0)、(0,0,0,1)来 表示。 在 BP 神经网络中,训练函数取 L⁃M 优化算法 (trainlm),学习率为 0.3,输入节点为 8,输出节点为 4。 由于隐含层节点对神经网络诊断精度有较大影 响,但是由于其没有具体选择准则,本文中通过经 验公式取隐含层节点数为 17,同时在节点 17 附近 取值,比较不同节点下诊断误差的大小,如图 2 所 ·532· 智 能 系 统 学 报 第 12 卷
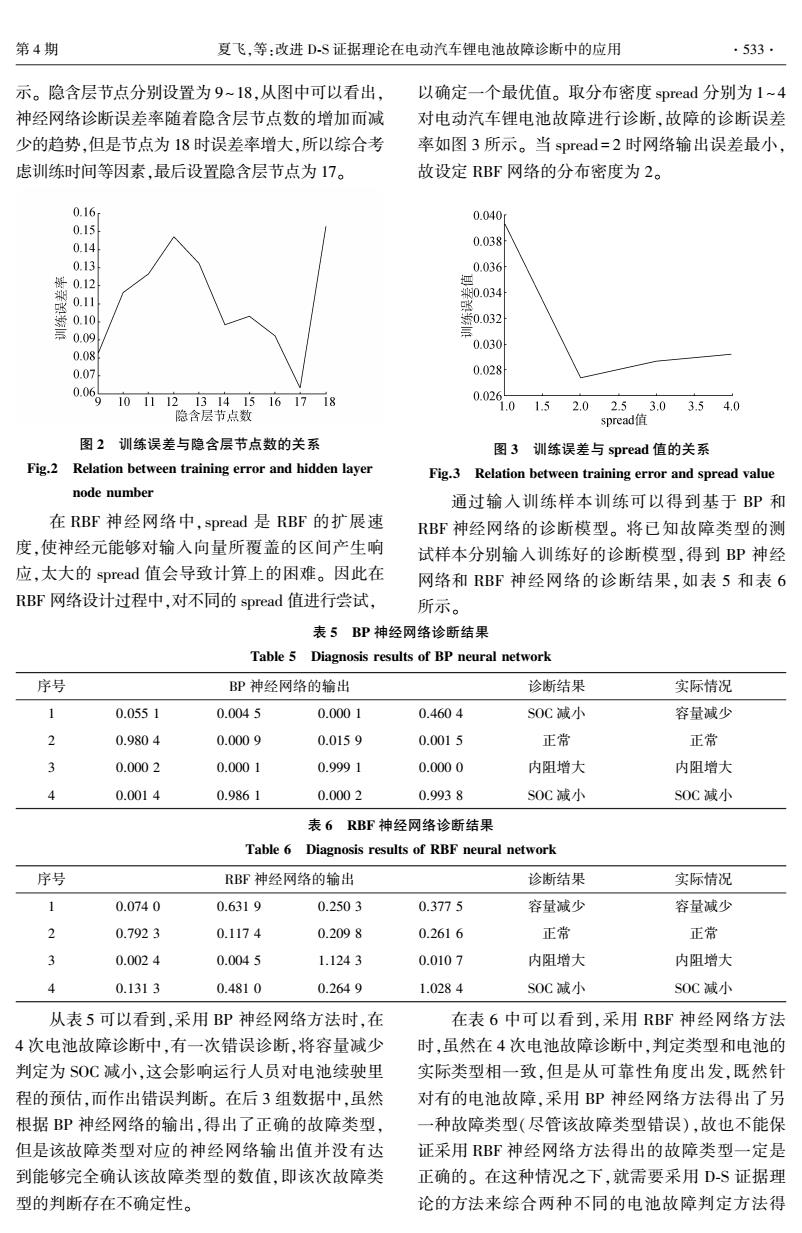
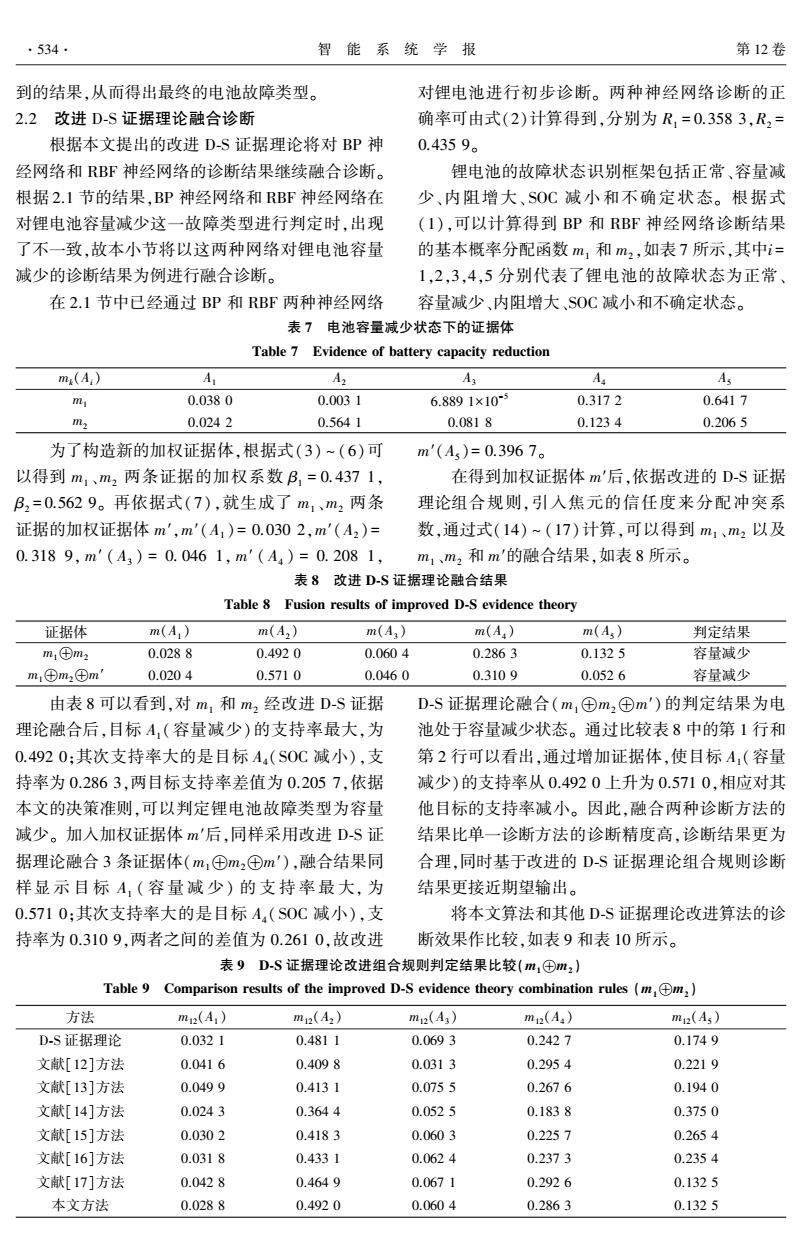
第4期 夏飞,等:改进DS证据理论在电动汽车锂电池故障诊断中的应用 ·533. 示。隐含层节点分别设置为9~18,从图中可以看出, 以确定一个最优值。取分布密度spread分别为1~4 神经网络诊断误差率随着隐含层节点数的增加而减 对电动汽车锂电池故障进行诊断,故障的诊断误差 少的趋势,但是节点为18时误差率增大,所以综合考 率如图3所示。当spread=2时网络输出误差最小, 虑训练时间等因素,最后设置隐含层节点为17。 故设定RBF网络的分布密度为2。 0.16 0.040 0.15 0.14 0.038 0.13 0.036 0.12 0.034 0.11 言0.09 002 0.030 0.08 0.07 0.028 0.0 9101112131415161718 0.026 1.0 1.5 2.02.5.3.03.54.0 隐含层节点数 spread值 图2训练误差与隐含层节点数的关系 图3训练误差与spread值的关系 Fig.2 Relation between training error and hidden layer Fig.3 Relation between training error and spread value node number 通过输入训练样本训练可以得到基于BP和 在RBF神经网络中,spread是RBF的扩展速 RBF神经网络的诊断模型。将已知故障类型的测 度,使神经元能够对输入向量所覆盖的区间产生响 试样本分别输入训练好的诊断模型,得到BP神经 应,太大的spread值会导致计算上的困难。因此在 网络和RBF神经网络的诊断结果,如表5和表6 RBF网络设计过程中,对不同的spread值进行尝试, 所示。 表5BP神经网络诊断结果 Table 5 Diagnosis results of BP neural network 序号 BP神经网络的输出 诊断结果 实际情况 1 0.0551 0.0045 0.0001 0.4604 SOC减小 容量减少 3 0.9804 0.0009 0.0159 0.0015 正常 正常 0.0002 0.0001 0.9991 0.0000 内阻增大 内阻增大 0.0014 0.9861 0.0002 0.9938 S0C减小 SOC减小 表6RBF神经网络诊断结果 Table 6 Diagnosis results of RBF neural network 序号 RBF神经网络的输出 诊断结果 实际情况 1 0.0740 0.6319 0.2503 0.3775 容量减少 容量减少 2 0.7923 0.1174 0.2098 0.2616 正常 正常 0.0024 0.0045 1.1243 0.0107 内阻增大 内阻增大 0.1313 0.4810 0.2649 1.0284 SOC减小 SOC减小 从表5可以看到,采用BP神经网络方法时,在 在表6中可以看到,采用RBF神经网络方法 4次电池故障诊断中,有一次错误诊断,将容量减少 时,虽然在4次电池故障诊断中,判定类型和电池的 判定为SOC减小,这会影响运行人员对电池续驶里 实际类型相一致,但是从可靠性角度出发,既然针 程的预估,而作出错误判断。在后3组数据中,虽然 对有的电池故障,采用BP神经网络方法得出了 根据BP神经网络的输出,得出了正确的故障类型, 一种故障类型(尽管该故障类型错误),故也不能保 但是该故障类型对应的神经网络输出值并没有达 证采用RBF神经网络方法得出的故障类型一定是 到能够完全确认该故障类型的数值,即该次故障类 正确的。在这种情况之下,就需要采用D-S证据理 型的判断存在不确定性。 论的方法来综合两种不同的电池故障判定方法得
示。 隐含层节点分别设置为 9~18,从图中可以看出, 神经网络诊断误差率随着隐含层节点数的增加而减 少的趋势,但是节点为 18 时误差率增大,所以综合考 虑训练时间等因素,最后设置隐含层节点为 17。 图 2 训练误差与隐含层节点数的关系 Fig.2 Relation between training error and hidden layer node number 在 RBF 神经网络中,spread 是 RBF 的扩展速 度,使神经元能够对输入向量所覆盖的区间产生响 应,太大的 spread 值会导致计算上的困难。 因此在 RBF 网络设计过程中,对不同的 spread 值进行尝试, 以确定一个最优值。 取分布密度 spread 分别为 1~4 对电动汽车锂电池故障进行诊断,故障的诊断误差 率如图 3 所示。 当 spread = 2 时网络输出误差最小, 故设定 RBF 网络的分布密度为 2。 图 3 训练误差与 spread 值的关系 Fig.3 Relation between training error and spread value 通过输入训练样本训练可以得到基于 BP 和 RBF 神经网络的诊断模型。 将已知故障类型的测 试样本分别输入训练好的诊断模型,得到 BP 神经 网络和 RBF 神经网络的诊断结果,如表 5 和表 6 所示。 表 5 BP 神经网络诊断结果 Table 5 Diagnosis results of BP neural network 序号 BP 神经网络的输出 诊断结果 实际情况 1 0.055 1 0.004 5 0.000 1 0.460 4 SOC 减小 容量减少 2 0.980 4 0.000 9 0.015 9 0.001 5 正常 正常 3 0.000 2 0.000 1 0.999 1 0.000 0 内阻增大 内阻增大 4 0.001 4 0.986 1 0.000 2 0.993 8 SOC 减小 SOC 减小 表 6 RBF 神经网络诊断结果 Table 6 Diagnosis results of RBF neural network 序号 RBF 神经网络的输出 诊断结果 实际情况 1 0.074 0 0.631 9 0.250 3 0.377 5 容量减少 容量减少 2 0.792 3 0.117 4 0.209 8 0.261 6 正常 正常 3 0.002 4 0.004 5 1.124 3 0.010 7 内阻增大 内阻增大 4 0.131 3 0.481 0 0.264 9 1.028 4 SOC 减小 SOC 减小 从表 5 可以看到,采用 BP 神经网络方法时,在 4 次电池故障诊断中,有一次错误诊断,将容量减少 判定为 SOC 减小,这会影响运行人员对电池续驶里 程的预估,而作出错误判断。 在后 3 组数据中,虽然 根据 BP 神经网络的输出,得出了正确的故障类型, 但是该故障类型对应的神经网络输出值并没有达 到能够完全确认该故障类型的数值,即该次故障类 型的判断存在不确定性。 在表 6 中可以看到,采用 RBF 神经网络方法 时,虽然在 4 次电池故障诊断中,判定类型和电池的 实际类型相一致,但是从可靠性角度出发,既然针 对有的电池故障,采用 BP 神经网络方法得出了另 一种故障类型(尽管该故障类型错误),故也不能保 证采用 RBF 神经网络方法得出的故障类型一定是 正确的。 在这种情况之下,就需要采用 D⁃S 证据理 论的方法来综合两种不同的电池故障判定方法得 第 4 期 夏飞,等:改进 D⁃S 证据理论在电动汽车锂电池故障诊断中的应用 ·533·
.534. 智能系统学报 第12卷 到的结果,从而得出最终的电池故障类型。 对锂电池进行初步诊断。两种神经网络诊断的正 2.2改进D-S证据理论融合诊断 确率可由式(2)计算得到,分别为R,=0.3583,R2= 根据本文提出的改进D-S证据理论将对BP神 0.4359. 经网络和RBF神经网络的诊断结果继续融合诊断。 锂电池的故障状态识别框架包括正常、容量减 根据2.1节的结果,BP神经网络和RBF神经网络在 少、内阻增大、SOC减小和不确定状态。根据式 对锂电池容量减少这一故障类型进行判定时,出现 (I),可以计算得到BP和RBF神经网络诊断结果 了不一致,故本小节将以这两种网络对锂电池容量 的基本概率分配函数m1和m2,如表7所示,其中i= 减少的诊断结果为例进行融合诊断。 1,2,3,4,5分别代表了锂电池的故障状态为正常、 在2.1节中已经通过BP和RBF两种神经网络 容量减少、内阻增大、S0C减小和不确定状态。 表7电池容量减少状态下的证据体 Table 7 Evidence of battery capacity reduction m(A) A A2 A A A mi 0.0380 0.0031 6.8891×10- 0.3172 0.6417 m2 0.0242 0.5641 0.0818 0.1234 0.2065 为了构造新的加权证据体,根据式(3)~(6)可 m'(A)=0.3967。 以得到m1、m2两条证据的加权系数B,=0.4371, 在得到加权证据体m'后,依据改进的D-S证据 B2=0.5629。再依据式(7),就生成了m1m2两条 理论组合规则,引入焦元的信任度来分配冲突系 证据的加权证据体m',m'(A1)=0.0302,m'(A2)= 数,通过式(14)~(17)计算,可以得到m1、m2以及 0.3189,m'(A3)=0.0461,m'(A4)=0.2081, m1、m2和m'的融合结果,如表8所示。 表8改进D-S证据理论融合结果 Table 8 Fusion results of improved D-S evidence theory 证据体 m(A:) m(A,) m(A.) m(A4) m(As) 判定结果 m1⊕m2 0.0288 0.4920 0.0604 0.2863 0.1325 容量减少 m,①m2⊕m1 0.0204 0.5710 0.0460 0.3109 0.0526 容量减少 由表8可以看到,对m,和m,经改进D-S证据 D-S证据理论融合(m,①m,⊕m')的判定结果为电 理论融合后,目标A,(容量减少)的支持率最大,为 池处于容量减少状态。通过比较表8中的第1行和 0.4920:其次支持率大的是目标A(S0C减小),支 第2行可以看出,通过增加证据体,使目标A(容量 持率为0.2863,两目标支持率差值为0.2057,依据 减少)的支持率从0.4920上升为0.5710,相应对其 本文的决策准则,可以判定锂电池故障类型为容量 他目标的支持率减小。因此,融合两种诊断方法的 减少。加入加权证据体m'后,同样采用改进D-S证 结果比单一诊断方法的诊断精度高,诊断结果更为 据理论融合3条证据体(m1⊕m2⊕m'),融合结果同 合理,同时基于改进的D-S证据理论组合规则诊断 样显示目标A(容量减少)的支持率最大,为 结果更接近期望输出。 0.5710:其次支持率大的是目标A,(S0C减小),支 将本文算法和其他D-S证据理论改进算法的诊 持率为0.3109,两者之间的差值为0.2610,故改进 断效果作比较,如表9和表10所示。 表9D-S证据理论改进组合规则判定结果比较(m1①m,】 Table 9 Comparison results of the improved D-S evidence theory combination rules (mm) 方法 m2(A) m12(A2) m12(A3) m12(A) m12(A5) D-S证据理论 0.0321 0.4811 0.0693 0.2427 0.1749 文献[12]方法 0.0416 0.4098 0.0313 0.2954 0.2219 文献[13]方法 0.0499 0.4131 0.0755 0.2676 0.1940 文献[14]方法 0.0243 0.3644 0.0525 0.1838 0.3750 文献[15]方法 0.0302 0.4183 0.0603 0.2257 0.2654 文献[16]方法 0.0318 0.4331 0.0624 0.2373 0.2354 文献[17]方法 0.0428 0.4649 0.0671 0.2926 0.1325 本文方法 0.0288 0.4920 0.0604 0.2863 0.1325
到的结果,从而得出最终的电池故障类型。 2.2 改进 D⁃S 证据理论融合诊断 根据本文提出的改进 D⁃S 证据理论将对 BP 神 经网络和 RBF 神经网络的诊断结果继续融合诊断。 根据 2.1 节的结果,BP 神经网络和 RBF 神经网络在 对锂电池容量减少这一故障类型进行判定时,出现 了不一致,故本小节将以这两种网络对锂电池容量 减少的诊断结果为例进行融合诊断。 在 2.1 节中已经通过 BP 和 RBF 两种神经网络 对锂电池进行初步诊断。 两种神经网络诊断的正 确率可由式(2)计算得到,分别为 R1 = 0.358 3,R2 = 0.435 9。 锂电池的故障状态识别框架包括正常、容量减 少、内阻增大、 SOC 减小和不确定状态。 根据式 (1),可以计算得到 BP 和 RBF 神经网络诊断结果 的基本概率分配函数 m1 和 m2 ,如表 7 所示,其中i = 1,2,3,4,5 分别代表了锂电池的故障状态为正常、 容量减少、内阻增大、SOC 减小和不确定状态。 表 7 电池容量减少状态下的证据体 Table 7 Evidence of battery capacity reduction mk(Ai) A1 A2 A3 A4 A5 m1 0.038 0 0.003 1 6.889 1×10 -5 0.317 2 0.641 7 m2 0.024 2 0.564 1 0.081 8 0.123 4 0.206 5 为了构造新的加权证据体,根据式(3) ~ (6)可 以得到 m1 、m2 两条证据的加权系数 β1 = 0.437 1, β2 = 0.562 9。 再依据式(7),就生成了 m1 、m2 两条 证据的加权证据体 m′,m′(A1 ) = 0.030 2,m′(A2 ) = 0. 318 9, m′ ( A3 ) = 0. 046 1, m′ ( A4 ) = 0. 208 1, m′(A5 )= 0.396 7。 在得到加权证据体 m′后,依据改进的 D⁃S 证据 理论组合规则,引入焦元的信任度来分配冲突系 数,通过式(14) ~ (17)计算,可以得到 m1 、m2 以及 m1 、m2 和 m′的融合结果,如表 8 所示。 表 8 改进 D⁃S 证据理论融合结果 Table 8 Fusion results of improved D⁃S evidence theory 证据体 m(A1 ) m(A2 ) m(A3 ) m(A4 ) m(A5 ) 判定结果 m1m2 0.028 8 0.492 0 0.060 4 0.286 3 0.132 5 容量减少 m1m2m′ 0.020 4 0.571 0 0.046 0 0.310 9 0.052 6 容量减少 由表 8 可以看到,对 m1 和 m2 经改进 D⁃S 证据 理论融合后,目标 A1(容量减少)的支持率最大,为 0.492 0;其次支持率大的是目标 A4( SOC 减小),支 持率为 0.286 3,两目标支持率差值为 0.205 7,依据 本文的决策准则,可以判定锂电池故障类型为容量 减少。 加入加权证据体 m′后,同样采用改进 D⁃S 证 据理论融合 3 条证据体(m1m2m′),融合结果同 样显 示 目 标 A1 ( 容 量 减 少) 的 支 持 率 最 大, 为 0.571 0;其次支持率大的是目标 A4( SOC 减小),支 持率为 0.310 9,两者之间的差值为 0.261 0,故改进 D⁃S 证据理论融合(m1m2m′)的判定结果为电 池处于容量减少状态。 通过比较表 8 中的第 1 行和 第 2 行可以看出,通过增加证据体,使目标 A1(容量 减少)的支持率从 0.492 0 上升为 0.571 0,相应对其 他目标的支持率减小。 因此,融合两种诊断方法的 结果比单一诊断方法的诊断精度高,诊断结果更为 合理,同时基于改进的 D⁃S 证据理论组合规则诊断 结果更接近期望输出。 将本文算法和其他 D⁃S 证据理论改进算法的诊 断效果作比较,如表 9 和表 10 所示。 表 9 D⁃S 证据理论改进组合规则判定结果比较(m1m2 ) Table 9 Comparison results of the improved D⁃S evidence theory combination rules (m1m2 ) 方法 m12(A1 ) m12(A2 ) m12(A3 ) m12(A4 ) m12(A5 ) D⁃S 证据理论 0.032 1 0.481 1 0.069 3 0.242 7 0.174 9 文献[12]方法 0.041 6 0.409 8 0.031 3 0.295 4 0.221 9 文献[13]方法 0.049 9 0.413 1 0.075 5 0.267 6 0.194 0 文献[14]方法 0.024 3 0.364 4 0.052 5 0.183 8 0.375 0 文献[15]方法 0.030 2 0.418 3 0.060 3 0.225 7 0.265 4 文献[16]方法 0.031 8 0.433 1 0.062 4 0.237 3 0.235 4 文献[17]方法 0.042 8 0.464 9 0.067 1 0.292 6 0.132 5 本文方法 0.028 8 0.492 0 0.060 4 0.286 3 0.132 5 ·534· 智 能 系 统 学 报 第 12 卷
第4期 夏飞,等:改进DS证据理论在电动汽车锂电池故障诊断中的应用 ·535. 由表9可知,当融合两条证据体时(m,①m2), 果精度较低。文献[17]仅考虑了融合规则,忽略了 文献[12]遵循D-S证据理论的组合规则,虽然加入 多条数据源获取数据时的权重,加强了冲突信息对 了矛盾系数权重,但融合结果精度不太理想。文献 融合结果的不利影响,存在一定缺陷。由此可知, [13]对未知项支持率较大,在实际应用中对权重的 在列举的几种方法中对目标A,的支持率都不是很 选择分配仍然是该算法的弊端。文献[14]改进算 理想。在此基础上,本文先从全局信息出发,根据 法融合结果显示目标A(不确定故障)支持率最大, 支持矩阵确定了每条证据的加权系数,对冲突信息 为0.3750。这是因为文献[14]的方法中将冲突信 进行合理分配。同时考虑了每条证据中各个焦元 息分配给未知项,对决策结果产生极大干扰。依据 的信任度,从局部角度出发,充分利用每个焦元的 决策规则,采用文献[14]的方法无法确定电池的故 有用信息,降低了冲突焦元对融合结果的影响。对 障类型。文献[15]将冲突信息分配给未知项的程 A1(容量减少)支持率达到了0.4920,融合结果区分 度较大,证据高度冲突时融合结果不太理想。文献 能力高于其他方法。表明本方法具有良好的可靠 [16]在处理冲突证据时,常常需要多条证据提供有 性,提高了诊断结果的准确性。 用信息才能辨识出目标,两条证据融合时,融合结 表10D-S证据理论改进组合规则判定结果比较(m1①m2①m') Table 10 Comparison results of the improved D-S evidence theory combination rules(mmm') 方法 m1(A) m2(A2) m12s(A3) mx(A:) m1(A3)) D-S证据理论 0.0267 0.5633 0.0546 0.2579 0.0977 文献[12]方法 0.0399 0.4520 0.0411 0.2383 0.2087 文献[13]方法 0.0513 0.4437 0.0800 0.2059 0.2191 文献[14]方法 0.0217 0.3804 0.0405 0.1892 0.3682 文献[15]方法 0.0269 0.4578 0.0496 0.2351 0.2306 文献[16]方法 0.0291 0.4865 0.0531 0.2526 0.1787 文献[17]方法 0.0470 0.5052 0.0730 0.3222 0.0526 本文方法 0.0204 0.5710 0.0460 0.3109 0.0526 从表10可以看出,当增加新的证据体后,利用 一方面从局部出发,对每条证据的各个焦元目标进 3条证据m,④m,①m'融合,采用上述几种方法均可 行可信度分析,在组合规则中为各焦元分配了信任 以判定电池处于容量减少状态。采用本文提出的 度,降低冲突焦元对融合结果的影响,使得最终诊 改进算法,当加入加权证据体后,目标A,的支持率 断结果更精确。本文的改进算法同时处理了证据 稳定提高,从两条证据体的0.4920增加到3条证据 一致性信息和焦元冲突信息,使电动汽车锂电池的 体的0.5710,并相应降低了其他目标对最终决策的 故障诊断结果更精确,更接近实际。 干扰。且支持率较大的两目标一A,、A,的支持率 3 结束语 之差从融合两条证据体的0.2057增加到融合3条 证据体的0.2601,增大了第一目标和第2目标支持 基于电动汽车锂电池故障的复杂性和不确定 率的差值,使目标A,的支持率更具可靠性,同时使 性,本文提出一种基于BP和RBF神经网络的改进 决策结果更接近事实。 D-S证据理论故障诊断方法。本方法首先通过BP 由此可见,通过增加加权证据体以及改进D-S 和RBF神经网络对锂电池故障特征向量进行初步 融合规则的方法,一方面对冲突信息进行合理有效 诊断,利用诊断正确率重新分配不确定信息,转化 分配,依据局部诊断方法的准确率将不确定信息重 为证据的基本概率分配函数。然后将支持矩阵考 新分配,并构造了加权证据体,成功避免了“一票否 虑进加权系数中,生成新的加权证据体。考虑到冲 决”和冲突信息较大程度分配给未知项等问题: 突不仅存在于证据之间,也存在于不同焦元之间
由表 9 可知,当融合两条证据体时(m1m2 ), 文献[12]遵循 D⁃S 证据理论的组合规则,虽然加入 了矛盾系数权重,但融合结果精度不太理想。 文献 [13]对未知项支持率较大,在实际应用中对权重的 选择分配仍然是该算法的弊端。 文献[14] 改进算 法融合结果显示目标 A5(不确定故障)支持率最大, 为 0.375 0。 这是因为文献[14]的方法中将冲突信 息分配给未知项,对决策结果产生极大干扰。 依据 决策规则,采用文献[14]的方法无法确定电池的故 障类型。 文献[15]将冲突信息分配给未知项的程 度较大,证据高度冲突时融合结果不太理想。 文献 [16]在处理冲突证据时,常常需要多条证据提供有 用信息才能辨识出目标,两条证据融合时,融合结 果精度较低。 文献[17]仅考虑了融合规则,忽略了 多条数据源获取数据时的权重,加强了冲突信息对 融合结果的不利影响,存在一定缺陷。 由此可知, 在列举的几种方法中对目标 A1 的支持率都不是很 理想。 在此基础上,本文先从全局信息出发,根据 支持矩阵确定了每条证据的加权系数,对冲突信息 进行合理分配。 同时考虑了每条证据中各个焦元 的信任度,从局部角度出发,充分利用每个焦元的 有用信息,降低了冲突焦元对融合结果的影响。 对 A1(容量减少)支持率达到了 0.492 0,融合结果区分 能力高于其他方法。 表明本方法具有良好的可靠 性,提高了诊断结果的准确性。 表 10 D⁃S 证据理论改进组合规则判定结果比较(m1m2m′) Table 10 Comparison results of the improved D⁃S evidence theory combination rules (m1m2m′) 方法 m123(A1 ) m123(A2 ) m123(A3 ) m123(A4 ) m123(A5 ) D⁃S 证据理论 0.026 7 0.563 3 0.054 6 0.257 9 0.097 7 文献[12]方法 0.039 9 0.452 0 0.041 1 0.238 3 0.208 7 文献[13]方法 0.051 3 0.443 7 0.080 0 0.205 9 0.219 1 文献[14]方法 0.021 7 0.380 4 0.040 5 0.189 2 0.368 2 文献[15]方法 0.026 9 0.457 8 0.049 6 0.235 1 0.230 6 文献[16]方法 0.029 1 0.486 5 0.053 1 0.252 6 0.178 7 文献[17]方法 0.047 0 0.505 2 0.073 0 0.322 2 0.052 6 本文方法 0.020 4 0.571 0 0.046 0 0.310 9 0.052 6 从表 10 可以看出,当增加新的证据体后,利用 3 条证据 m1m2m′融合,采用上述几种方法均可 以判定电池处于容量减少状态。 采用本文提出的 改进算法,当加入加权证据体后,目标 A1 的支持率 稳定提高,从两条证据体的 0.492 0 增加到 3 条证据 体的 0.571 0,并相应降低了其他目标对最终决策的 干扰。 且支持率较大的两目标———A1 、A4 的支持率 之差从融合两条证据体的 0.205 7 增加到融合 3 条 证据体的 0.260 1,增大了第一目标和第 2 目标支持 率的差值,使目标 A1 的支持率更具可靠性,同时使 决策结果更接近事实。 由此可见,通过增加加权证据体以及改进 D⁃S 融合规则的方法,一方面对冲突信息进行合理有效 分配,依据局部诊断方法的准确率将不确定信息重 新分配,并构造了加权证据体,成功避免了“一票否 决”和冲突信息较大程度分配给未知项等问题;另 一方面从局部出发,对每条证据的各个焦元目标进 行可信度分析,在组合规则中为各焦元分配了信任 度,降低冲突焦元对融合结果的影响,使得最终诊 断结果更精确。 本文的改进算法同时处理了证据 一致性信息和焦元冲突信息,使电动汽车锂电池的 故障诊断结果更精确,更接近实际。 3 结束语 基于电动汽车锂电池故障的复杂性和不确定 性,本文提出一种基于 BP 和 RBF 神经网络的改进 D⁃S 证据理论故障诊断方法。 本方法首先通过 BP 和 RBF 神经网络对锂电池故障特征向量进行初步 诊断,利用诊断正确率重新分配不确定信息,转化 为证据的基本概率分配函数。 然后将支持矩阵考 虑进加权系数中,生成新的加权证据体。 考虑到冲 突不仅存在于证据之间,也存在于不同焦元之间。 第 4 期 夏飞,等:改进 D⁃S 证据理论在电动汽车锂电池故障诊断中的应用 ·535·