【知识工程】在线学习的大规模网络流量分类研究编辑部

第11卷第3期 智能系统学报 Vol.11 No.3 2016年6月 CAAI Transactions on Intelligent Systems Jun.2016 D0:10.3969/j.issn.1673-4785.201603033 网络出版地址：http://www.cnki.net/kcms/detail/23.1538.tp.20150930.1557.028.html 在线学习的大规模网络流量分类研究 易磊，潘志松，邱俊洋，薛胶，任会峰 (中国人民解放军理工大学指挥信息系统学院，江苏南京210007) 摘要：传统的批处理机器学习方法在面对大规模网络流量分类问题时存在分类器训练速度慢、计算复杂度高的缺 陷。近年来迅速发展的在线学习方法是解决大规模问题的有效途径。本文针对高速骨干网上的大规模网络流量分 类问题，提出了一个基于在线学习的分类框架，并应用了8种在线学习算法。在真实数据集上的实验表明，在分类精 度相当的情况下，在线学习算法与支持向量机(SVM)相比空间开销小、模型训练时间显著缩短。同时，为了考察网 络流量中样本顺序对分类效果的影响，本文对比了样本按时序处理与随机处理两种方式的差异，验证了网络流量样 本存在着时序上的相关性。 关键词：在线学习；大规模；网络流量分类；时序相关性；数据流；随机优化 中图分类号：TP181文献标志码：A文章编号：1673-4785(2016)03-0318-10 中文引用格式：易磊，潘志松，邱俊洋，等.在线学习的大规模网络流量分类研究[J].智能系统学报，2016,11(2)：318-327. 英文引用格式：YI Lei,PAN Zhisong,QIU Junyang,etal.Large-scale network traffic classification based on online learning[J]. CAAI transactions on intelligent systems,2016,11(3):318-327. Large-scale network traffic classification based on online learning YI Lei,PAN Zhisong,QIU Junyang,XUE Jiao,REN Huifeng (Institute of Command Information System,PLA University of Science and Technology,Nanjing 210007,China) Abstract:Facing the challenges of large-scale network traffic classification problem,traditional batch machine learning algorithms suffer from slow training process and high computational complexity.In recent years,the rapid developing online learning technology is an effective way to solve large-scale problems.To address the issue of large-scale network traffic classification problem on a high-speed backbone network,we proposed a traffic classifi- cation scheme based on online learning and applied eight online learning algorithms.Experiments on real network traffic data sets showed that in the classification accuracy similar situation,online learning algorithm has less space overhead and training time than the support vector machine.Meanwhile,to examine the impact of the order of net- work traffic samples on the classification results,this paper compared the difference between the two ways of pro- cessing samples,sequentially and random,we verified that the presence of timing correlation in network traffic sam- ples by comparing online learning and stochastic optimization. Keywords:online learning;large-scale;traffic classification;timing correlation;data stream;stochastic optimiza- tion 网络流量分类是指识别网络中的各种应用与协 侵检测等方面具有重大的作用。近年来，基于网络 议并对相关的网络流量进行分类的过程。网路流量 流量统计特征的机器学习分类方法受到了研究者的 分类是现代网络管理与安全系统中最基本的功 极大关注[)]。这类方法主要是利用网络流量在传 能)，在QOS服务质量控制、网络应用趋势分析、入 输层的统计特征，根据实验或经验提取相关的特征 属性再运用机器学习的方法进行分类。传统的机器 收稿日期：2016-03-18.网络出版日期：2016-05-13 基金项目：国家自然科学基金项目(61473149). 学习方法在网络流量分类领域已有了应用，但依然 通信作者：易磊.E-mail:vileinjut(@163.com. 存在如下问题：随着日益扩大的网络带宽与互联网

第 １１ 卷第 ３ 期 智 能 系 统 学 报 Ｖｏｌ．１１ №．３ ２０１６ 年 ６ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ｊｕｎ． ２０１６ ＤＯＩ：１０．３９６９ ／ ｊ．ｉｓｓｎ．１６７３⁃４７８５．２０１６０３０３３ 网络出版地址：ｈｔｔｐ： ／ ／ ｗｗｗ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｅｔａｉｌ ／ ２３．１５３８．ｔｐ．２０１５０９３０．１５５７．０２８．ｈｔｍｌ 在线学习的大规模网络流量分类研究 易磊，潘志松，邱俊洋，薛胶，任会峰 （中国人民解放军理工大学 指挥信息系统学院，江苏 南京 ２１０００７） 摘 要：传统的批处理机器学习方法在面对大规模网络流量分类问题时存在分类器训练速度慢、计算复杂度高的缺 陷。 近年来迅速发展的在线学习方法是解决大规模问题的有效途径。 本文针对高速骨干网上的大规模网络流量分 类问题，提出了一个基于在线学习的分类框架，并应用了 ８ 种在线学习算法。 在真实数据集上的实验表明，在分类精 度相当的情况下，在线学习算法与支持向量机（ ＳＶＭ）相比空间开销小、模型训练时间显著缩短。 同时，为了考察网 络流量中样本顺序对分类效果的影响，本文对比了样本按时序处理与随机处理两种方式的差异，验证了网络流量样 本存在着时序上的相关性。 关键词：在线学习；大规模；网络流量分类；时序相关性；数据流；随机优化 中图分类号：ＴＰ１８１ 文献标志码：Ａ 文章编号：１６７３⁃４７８５（２０１６）０３⁃０３１８⁃１０ 中文引用格式：易磊，潘志松，邱俊洋，等．在线学习的大规模网络流量分类研究［Ｊ］． 智能系统学报， ２０１６， １１（２）： ３１８⁃３２７． 英文引用格式：ＹＩ Ｌｅｉ， ＰＡＮ Ｚｈｉｓｏｎｇ， ＱＩＵ Ｊｕｎｙａｎｇ， ｅｔ ａｌ． Ｌａｒｇｅ⁃ｓｃａｌｅ ｎｅｔｗｏｒｋ ｔｒａｆｆｉｃ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ｂａｓｅｄ ｏｎ ｏｎｌｉｎｅ ｌｅａｒｎｉｎｇ ［Ｊ］． ＣＡＡＩ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｉｎｔｅｌｌｉｇｅｎｔ ｓｙｓｔｅｍｓ， ２０１６，１１（３）： ３１８⁃３２７． Ｌａｒｇｅ⁃ｓｃａｌｅ ｎｅｔｗｏｒｋ ｔｒａｆｆｉｃ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ｂａｓｅｄ ｏｎ ｏｎｌｉｎｅ ｌｅａｒｎｉｎｇ ＹＩ Ｌｅｉ， ＰＡＮ Ｚｈｉｓｏｎｇ， ＱＩＵ Ｊｕｎｙａｎｇ， ＸＵＥ Ｊｉａｏ， ＲＥＮ Ｈｕｉｆｅｎｇ （Ｉｎｓｔｉｔｕｔｅ ｏｆ Ｃｏｍｍａｎｄ Ｉｎｆｏｒｍａｔｉｏｎ Ｓｙｓｔｅｍ， ＰＬＡ Ｕｎｉｖｅｒｓｉｔｙ ｏｆ Ｓｃｉｅｎｃｅ ａｎｄ Ｔｅｃｈｎｏｌｏｇｙ，Ｎａｎｊｉｎｇ ２１０００７， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｆａｃｉｎｇ ｔｈｅ ｃｈａｌｌｅｎｇｅｓ ｏｆ ｌａｒｇｅ⁃ｓｃａｌｅ ｎｅｔｗｏｒｋ ｔｒａｆｆｉｃ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ｐｒｏｂｌｅｍ， ｔｒａｄｉｔｉｏｎａｌ ｂａｔｃｈ ｍａｃｈｉｎｅ ｌｅａｒｎｉｎｇ ａｌｇｏｒｉｔｈｍｓ ｓｕｆｆｅｒ ｆｒｏｍ ｓｌｏｗ ｔｒａｉｎｉｎｇ ｐｒｏｃｅｓｓ ａｎｄ ｈｉｇｈ ｃｏｍｐｕｔａｔｉｏｎａｌ ｃｏｍｐｌｅｘｉｔｙ． Ｉｎ ｒｅｃｅｎｔ ｙｅａｒｓ， ｔｈｅ ｒａｐｉｄ ｄｅｖｅｌｏｐｉｎｇ ｏｎｌｉｎｅ ｌｅａｒｎｉｎｇ ｔｅｃｈｎｏｌｏｇｙ ｉｓ ａｎ ｅｆｆｅｃｔｉｖｅ ｗａｙ ｔｏ ｓｏｌｖｅ ｌａｒｇｅ⁃ｓｃａｌｅ ｐｒｏｂｌｅｍｓ． Ｔｏ ａｄｄｒｅｓｓ ｔｈｅ ｉｓｓｕｅ ｏｆ ｌａｒｇｅ⁃ｓｃａｌｅ ｎｅｔｗｏｒｋ ｔｒａｆｆｉｃ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ｐｒｏｂｌｅｍ ｏｎ ａ ｈｉｇｈ⁃ｓｐｅｅｄ ｂａｃｋｂｏｎｅ ｎｅｔｗｏｒｋ， ｗｅ ｐｒｏｐｏｓｅｄ ａ ｔｒａｆｆｉｃ ｃｌａｓｓｉｆｉ⁃ ｃａｔｉｏｎ ｓｃｈｅｍｅ ｂａｓｅｄ ｏｎ ｏｎｌｉｎｅ ｌｅａｒｎｉｎｇ ａｎｄ ａｐｐｌｉｅｄ ｅｉｇｈｔ ｏｎｌｉｎｅ ｌｅａｒｎｉｎｇ ａｌｇｏｒｉｔｈｍｓ． Ｅｘｐｅｒｉｍｅｎｔｓ ｏｎ ｒｅａｌ ｎｅｔｗｏｒｋ ｔｒａｆｆｉｃ ｄａｔａ ｓｅｔｓ ｓｈｏｗｅｄ ｔｈａｔ ｉｎ ｔｈｅ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ａｃｃｕｒａｃｙ ｓｉｍｉｌａｒ ｓｉｔｕａｔｉｏｎ， ｏｎｌｉｎｅ ｌｅａｒｎｉｎｇ ａｌｇｏｒｉｔｈｍ ｈａｓ ｌｅｓｓ ｓｐａｃｅ ｏｖｅｒｈｅａｄ ａｎｄ ｔｒａｉｎｉｎｇ ｔｉｍｅ ｔｈａｎ ｔｈｅ ｓｕｐｐｏｒｔ ｖｅｃｔｏｒ ｍａｃｈｉｎｅ． Ｍｅａｎｗｈｉｌｅ， ｔｏ ｅｘａｍｉｎｅ ｔｈｅ ｉｍｐａｃｔ ｏｆ ｔｈｅ ｏｒｄｅｒ ｏｆ ｎｅｔ⁃ ｗｏｒｋ ｔｒａｆｆｉｃ ｓａｍｐｌｅｓ ｏｎ ｔｈｅ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ｒｅｓｕｌｔｓ， ｔｈｉｓ ｐａｐｅｒ ｃｏｍｐａｒｅｄ ｔｈｅ ｄｉｆｆｅｒｅｎｃｅ ｂｅｔｗｅｅｎ ｔｈｅ ｔｗｏ ｗａｙｓ ｏｆ ｐｒｏ⁃ ｃｅｓｓｉｎｇ ｓａｍｐｌｅｓ， ｓｅｑｕｅｎｔｉａｌｌｙ ａｎｄ ｒａｎｄｏｍ， ｗｅ ｖｅｒｉｆｉｅｄ ｔｈａｔ ｔｈｅ ｐｒｅｓｅｎｃｅ ｏｆ ｔｉｍｉｎｇ ｃｏｒｒｅｌａｔｉｏｎ ｉｎ ｎｅｔｗｏｒｋ ｔｒａｆｆｉｃ ｓａｍ⁃ ｐｌｅｓ ｂｙ ｃｏｍｐａｒｉｎｇ ｏｎｌｉｎｅ ｌｅａｒｎｉｎｇ ａｎｄ ｓｔｏｃｈａｓｔｉｃ ｏｐｔｉｍｉｚａｔｉｏｎ． Ｋｅｙｗｏｒｄｓ：ｏｎｌｉｎｅ ｌｅａｒｎｉｎｇ； ｌａｒｇｅ⁃ｓｃａｌｅ； ｔｒａｆｆｉｃ ｃｌａｓｓｉｆｉｃａｔｉｏｎ； ｔｉｍｉｎｇ ｃｏｒｒｅｌａｔｉｏｎ； ｄａｔａ ｓｔｒｅａｍ； ｓｔｏｃｈａｓｔｉｃ ｏｐｔｉｍｉｚａ⁃ ｔｉｏｎ 收稿日期：２０１６⁃０３⁃１８． 网络出版日期：２０１６⁃０５⁃１３． 基金项目：国家自然科学基金项目（６１４７３１４９）． 通信作者：易磊．Ｅ⁃ｍａｉｌ：ｙｉｌｅｉｎｊｕｔ＠ １６３．ｃｏｍ． 网络流量分类是指识别网络中的各种应用与协 议并对相关的网络流量进行分类的过程。 网路流量 分类是现代网络管理与安全系统中最基本的功 能［１］ ，在 ＱＯＳ 服务质量控制、网络应用趋势分析、入 侵检测等方面具有重大的作用。 近年来，基于网络 流量统计特征的机器学习分类方法受到了研究者的 极大关注［２］ 。 这类方法主要是利用网络流量在传 输层的统计特征，根据实验或经验提取相关的特征 属性再运用机器学习的方法进行分类。 传统的机器 学习方法在网络流量分类领域已有了应用，但依然 存在如下问题：随着日益扩大的网络带宽与互联网

第3期 易磊，等：在线学习的大规模网络流量分类研究 ·319· 用户规模，各类网络流量呈现出爆炸式的增长。现 EM算法的无监督贝叶斯分类器。Eman等山使用 有的批处理方法在处理大规模网络流量分类问题 了EM聚类方法来解决流量分类问题，与贝叶斯分 时，其分类准确率与模型训练速率等通常难以取得 类方法相比有更高的分类准确率。这些算法都属于 平衡，模型训练时间将随着样本数量的增大而急剧 批处理的方法，在解决大规模网络流量分类问题时， 上升。如何解决大规模网络流量分类问题已成为学 存在着分类器训练慢、计算复杂度高的缺陷。 者和业界人士面临的重大挑战。 在线学习是一种解决大规模问题的有效手段。 在机器学习领域中，在线学习代表着一类利用 在线学习自提出以来，已应用于许多实际的应用场 一组有序的样本建立预测模型的高效的、大规模的 景中，例如垃圾邮件检测、在线广告推送、多媒体检 算法。在线学习算法按时序一次处理一个或者一小 索和金融时间序列预测。研究者们提出了大量的在 批样本，处理过的样本不再处理也不再保存，这使得 线学习算法并进行了理论性证明。Rosenblatt于 在线学习方法计算迅速且高效，更适合样本规模大 1958年提出的感知机算法[2]是最为人熟知的在线 且样本按时序到达并动态变化的应用场景。有些研 学习算法。Crammer等tis]提出的Passive-Aggressive 究者认为，在线学习能够敏锐地捕捉到数据变化的 (PA)算法也是一种著名的在线学习算法。为了提 趋势，进而解决数据非同分布和实时学习问题)。 高在线学习算法的效率，研究者们提出了一系列的 针对高速骨干网上的大规模网络流量分类问 二阶在线学习算法[。与一阶算法不同，二阶算法 题，本文将在线学习方法应用于网络流量分类问题， 通常假定权重向量服从一个高斯分布，并在每次迭 主要贡献有： 代时尝试更新高斯分布的均值与方差。Confidence 1)提出了一种基于在线学习的网络流量分类 Weighted(CW)算法[s是一种典型的二阶算法。 框架，在分类精度相当的条件下，在线学习方法比传 此外，还有许多基于CW算法的改进算法，Crammer 统的支持向量机(SVM)方法有更好的分类效率： 等16]提出了一种改进CW算法鲁棒性的AROW算 2)对比了8种不同在线学习算法在网络流量 法，Wang等I)]提出了Soft Confidence-weighted 分类应用中的分类性能差异，为应用打下了基础： (SCW)算法。 3)为了考察网络流量中样本顺序对分类效果 本文提出的在线学习网络流量分类框架应用了 的影响，对比了样本按时序处理与随机处理两种方 8种在线学习算法。其中，一阶算法有感知机算法、 式的差异，验证了网络流量样本存在着时序上的相 在线梯度下降算法(OGD)、Passive--Aggressive算法 关性。 (PA)以及两种基于PA的改进算法：PA-I、PA-Ⅱ算 法；二阶算法则选用了3种：Confidence-Weighted 1 相关研究 (CW)算法，以及基于CW算法改进的2种Soft Con- 近年来，基于流量统计特征的机器学习分类方 fidence-weighted(SCW)算法：SCW-I、SCW-算法。 法受到了研究者的极大关注。这类方法主要是 2在线学习的网络流量分类框架 利用网络流量在传输层的统计特征，根据实验或经 验提取相关的特征属性再运用机器学习的方法进行 2.1在线学习网络流量分类框架 分类。基于统计特征的机器学习网络流量分类方法 在线学习概念自提出以来发展出了一系列的算 主要分为监督学习和无监督学习两类。监督学习方 法，既能处理二分类问题又能处理多分类问题。为 面，Moore等提出了一种使用朴素贝叶斯的分类 了验证在线学习方法在网络流量分类问题中的有 方法，分类准确率能达到约65%。Auld等)使用了 效性，本文将网络流量分类简化为一个二分类问题。 贝叶斯神经网络的方法，并对特征集合进行了特征 下面将由在线学习二分类算法的一般流程出发，提 选择，使得分类精度得到了提高，分类准确率达到了 出在线学习网络流量分类框架。 95%。此外，还有一系列监督学习方法运用到了网 在线学习处理的数据是一种带有时序性的样本 络流量分类问题中：文献[6-7]将支持向量机运用到 序列，其优化目标通常是最小化在整个样本序列下 了网络流量分类问题：文献[8-9]运用了决策树理 产生的累积误差。对于一个二分类问题，样本的特 论。无监督学习方面，Zander等[o提出了基于Au- 征X属于一个d维的特征空间，X=R:样本的类标 toClass的无监督网络流量分类方法，是一种基于 Y为-1与+1，Y={-1,+1}。在t时刻，分类器接收

用户规模，各类网络流量呈现出爆炸式的增长。 现 有的批处理方法在处理大规模网络流量分类问题 时，其分类准确率与模型训练速率等通常难以取得 平衡，模型训练时间将随着样本数量的增大而急剧 上升。 如何解决大规模网络流量分类问题已成为学 者和业界人士面临的重大挑战。 在机器学习领域中，在线学习代表着一类利用 一组有序的样本建立预测模型的高效的、大规模的 算法。 在线学习算法按时序一次处理一个或者一小 批样本，处理过的样本不再处理也不再保存，这使得 在线学习方法计算迅速且高效，更适合样本规模大 且样本按时序到达并动态变化的应用场景。 有些研 究者认为，在线学习能够敏锐地捕捉到数据变化的 趋势，进而解决数据非同分布和实时学习问题［３］ 。 针对高速骨干网上的大规模网络流量分类问 题，本文将在线学习方法应用于网络流量分类问题， 主要贡献有： １）提出了一种基于在线学习的网络流量分类 框架，在分类精度相当的条件下，在线学习方法比传 统的支持向量机（ＳＶＭ）方法有更好的分类效率； ２）对比了 ８ 种不同在线学习算法在网络流量 分类应用中的分类性能差异，为应用打下了基础； ３）为了考察网络流量中样本顺序对分类效果 的影响，对比了样本按时序处理与随机处理两种方 式的差异，验证了网络流量样本存在着时序上的相 关性。 １ 相关研究 近年来，基于流量统计特征的机器学习分类方 法受到了研究者的极大关注［２］ 。 这类方法主要是 利用网络流量在传输层的统计特征，根据实验或经 验提取相关的特征属性再运用机器学习的方法进行 分类。 基于统计特征的机器学习网络流量分类方法 主要分为监督学习和无监督学习两类。 监督学习方 面，Ｍｏｏｒｅ 等［４］提出了一种使用朴素贝叶斯的分类 方法，分类准确率能达到约 ６５％。 Ａｕｌｄ 等［５］ 使用了 贝叶斯神经网络的方法，并对特征集合进行了特征 选择，使得分类精度得到了提高，分类准确率达到了 ９５％。 此外，还有一系列监督学习方法运用到了网 络流量分类问题中：文献［６⁃７］将支持向量机运用到 了网络流量分类问题；文献［８⁃９］ 运用了决策树理 论。 无监督学习方面，Ｚａｎｄｅｒ 等［１０］ 提出了基于 Ａｕ⁃ ｔｏＣｌａｓｓ 的无监督网络流量分类方法，是一种基于 ＥＭ 算法的无监督贝叶斯分类器。 Ｅｒｍａｎ 等［１１］ 使用 了 ＥＭ 聚类方法来解决流量分类问题，与贝叶斯分 类方法相比有更高的分类准确率。 这些算法都属于 批处理的方法，在解决大规模网络流量分类问题时， 存在着分类器训练慢、计算复杂度高的缺陷。 在线学习是一种解决大规模问题的有效手段。 在线学习自提出以来，已应用于许多实际的应用场 景中，例如垃圾邮件检测、在线广告推送、多媒体检 索和金融时间序列预测。 研究者们提出了大量的在 线学习算法并进行了理论性证明。 Ｒｏｓｅｎｂｌａｔｔ 于 １９５８ 年提出的感知机算法［１２］ 是最为人熟知的在线 学习算法。 Ｃｒａｍｍｅｒ 等［１３］ 提出的 Ｐａｓｓｉｖｅ⁃Ａｇｇｒｅｓｓｉｖｅ （ＰＡ）算法也是一种著名的在线学习算法。 为了提 高在线学习算法的效率，研究者们提出了一系列的 二阶在线学习算法［１４］ 。 与一阶算法不同，二阶算法 通常假定权重向量服从一个高斯分布，并在每次迭 代时尝试更新高斯分布的均值与方差。 Ｃｏｎｆｉｄｅｎｃｅ⁃ Ｗｅｉｇｈｔｅｄ （ＣＷ） 算法［１５］ 是一种典型的二阶算法。 此外，还有许多基于 ＣＷ 算法的改进算法， Ｃｒａｍｍｅｒ 等［１６］提出了一种改进 ＣＷ 算法鲁棒性的 ＡＲＯＷ 算 法， Ｗａｎｇ 等［１７］ 提 出 了 Ｓｏｆｔ Ｃｏｎｆｉｄｅｎｃｅ⁃ｗｅｉｇｈｔｅｄ （ＳＣＷ）算法。 本文提出的在线学习网络流量分类框架应用了 ８ 种在线学习算法。 其中，一阶算法有感知机算法、 在线梯度下降算法（ＯＧＤ）、Ｐａｓｓｉｖｅ⁃Ａｇｇｒｅｓｓｉｖｅ 算法 （ＰＡ）以及两种基于 ＰＡ 的改进算法：ＰＡ⁃Ｉ、ＰＡ⁃ＩＩ 算 法；二阶算法则选用了 ３ 种： Ｃｏｎｆｉｄｅｎｃｅ⁃Ｗｅｉｇｈｔｅｄ （ＣＷ）算法，以及基于 ＣＷ 算法改进的 ２ 种 Ｓｏｆｔ Ｃｏｎ⁃ ｆｉｄｅｎｃｅ⁃ｗｅｉｇｈｔｅｄ（ＳＣＷ）算法：ＳＣＷ⁃Ｉ、ＳＣＷ⁃ＩＩ 算法。 ２ 在线学习的网络流量分类框架 ２．１ 在线学习网络流量分类框架 在线学习概念自提出以来发展出了一系列的算 法，既能处理二分类问题又能处理多分类问题。 为 了验证在线学习方法在网络流量分类 问题中的有 效性，本文将网络流量分类简化为一个二分类问题。 下面将由在线学习二分类算法的一般流程出发，提 出在线学习网络流量分类框架。 在线学习处理的数据是一种带有时序性的样本 序列，其优化目标通常是最小化在整个样本序列下 产生的累积误差。 对于一个二分类问题，样本的特 征 Ｘ 属于一个 ｄ 维的特征空间，Ｘ ＝ Ｒ ｄ ；样本的类标 Ｙ 为－１ 与＋１，Ｙ ＝ {－１，＋１} 。 在 ｔ 时刻，分类器接收 第 ３ 期 易磊，等：在线学习的大规模网络流量分类研究 ·３１９·

.320. 智能系统学报 第11卷 一个训练样本x,∈X,并计算样本的类标的预测值： 异。另一方面，有研究者认为在线学习按顺序选择 .=sgn(f(x,:w))=sgn(w,·x,)∈Y(1) 样本的方式能敏锐捕捉到数据变化的趋势。为了考 在做出预测后，分类器从环境中获取到样本的 察网络流量中样本顺序对分类效果的影响，本文在 真实类标y,∈Y,并通过一定的准则计算预测的损失 SCW-I算法的基础上将顺序抽取样本的方式改为随 (y,)。当损失大于0时，分类模型将按如下原则 机抽取的方式，实验对比了两者在网络流量分类问 更新： 题中的差异，两种方法之间的效果差异表明了网络 w,+1←△(w,;(xy,)) (2) 流量样本存在着时序上的相关性。 在线学习不再区分训练阶段与测试阶段，在接 2.2在线学习二分类算法 收到新样本后对样本类别进行预测同时按照需要更 为了检验本文提出的在线学习分类框架，我们 新模型，其模型始终处于一个动态变化的过程，具有 选取了8种在线学习方法进行验证。所有的在线学 良好的实时性，能够跟踪数据流的变化趋势。在线 习算法均满足表1所示的在线学习算法一般流程， 学习需要在模型对样本进行预测后，能够即时获取 但由于理论基础不同，它们在损失函数、学习率、模 到样本的真实类别。网络流量样本虽然是流式数 型的更新条件以及方式有差异。 据，但是样本的真实类别无法实时获取。为此，提出 2.2.1一阶算法 了一种按照在线学习方法训练分类器的网络流量分 感知机算法感知机算法[2)]于1958年提出， 类框架，如图1所示。训练阶段，该框架首先对实时 是最早最简单的一阶在线学习算法，其优化目标是： 网络流量进行抽样并通过特征提取与样本标记产生 最小化学习到的分类器由当前样本带来的损失。感 训练数据集，然后使用在线学习算法对分类模型进 知机算法采用0-1损失作为损失函数，当损失大于 行训练。特征提取可使用Moore]提出的248维网 0时，按照梯度下降的方式更新模型，其学习率恒 络流统计特征，样本标记可使用深度包检测工具 为1。 nDPI以及开源工具Tstat。测试阶段，该框架使用训 OGD算法在线梯度下降算法(OGD)[18]也是 练完成的模型对实时网络流量进行分类。将模型分 一种一阶算法，其优化目标与感知机算法一致，也是 类结果与nDPI与Tstat等工具的结果对比，当偏差 采用梯度下降的更新方式来优化由不同损失函数产 达到一定阈值时对模型进行重新训练。 生的优化目标。其与感知机算法的区别在于：OGD 训练过程 算法学习率n,设定为S,其中C是大于0的学习率 样本标记 训练 抽样 特征提取 在线分类器 常数，t为迭代轮数。在OGD算法的实现中我们使 实时 分类 用了4种损失函数，分别为0-1损失、hinge损失、lo- 特征提取 分类器 网络流量 结果 gistic损失和平方损失。在实验中可以发现，当使用 hinge损失时，模型的分类效果最佳，因此我们在实 图1在线网络流量分类框架 验中均采用hinge损失。 Fig.1 Online traffic classification scheme PA算法Passive-Aggressive算法[B]是一种比 本框架在获取到完整训练集后离线训练在线学 感知机算法和OGD算法更加复杂的一阶在线学习 习分类模型。在线学习方法在优化理论中被称作增 量算法。增量算法的主要思路是：当目标函数由一 算法，其优化目标是如下两个目标的权衡：最小化学 习到的分类器与之前的分类器的距离、最小化学习 些子函数之和组成时，可以通过每次仅对一个子函 数进行“首尾相接”依次传递式的梯度优化迭代而 到的分类器由当前样本带来的损失。PA算法可以 看作为如下的在线优化问题： 最终得到原问题的最优解。当按照随机的方式挑选 子函数而不是按照顺序依次进行优化时，增量式方 w=argmin 2 lw-w3, 法可以称为随机优化方法)。在线学习与随机优 化有很紧密的关系，在很多情况下，两者甚至等同使 s.t.(w;(x,y,))=max(0,1-y,(w·x,))=0 用[]。在线和随机优化形式上虽然只是抽取样本 (3) 方式上的区别，但研究表明，它们的收敛性存在着差 式中目标函数项为Passive项，表示最小化学习到的 分类器与之前的分类器的距离，约束项为Aggressive

一个训练样本 ｘｔ∈Ｘ，并计算样本的类标的预测值： ｙ ( ｔ ＝ ｓｇｎ ｆ ｘｔ；ｗｔ ( ( ) ) ＝ ｓｇｎ ｗｔ·ｘｔ ( ) ∈ Ｙ （１） 在做出预测后，分类器从环境中获取到样本的 真实类标 ｙｔ∈Ｙ，并通过一定的准则计算预测的损失 ｙｔ，ｙ ( ｔ ( ) 。 当损失大于 ０ 时，分类模型将按如下原则 更新： ｗｔ＋１ ← Δ ｗｔ； ｘｔ，ｙｔ ( ( ) ) （２） 在线学习不再区分训练阶段与测试阶段，在接 收到新样本后对样本类别进行预测同时按照需要更 新模型，其模型始终处于一个动态变化的过程，具有 良好的实时性，能够跟踪数据流的变化趋势。 在线 学习需要在模型对样本进行预测后，能够即时获取 到样本的真实类别。 网络流量样本虽然是流式数 据，但是样本的真实类别无法实时获取。 为此，提出 了一种按照在线学习方法训练分类器的网络流量分 类框架，如图 １ 所示。 训练阶段，该框架首先对实时 网络流量进行抽样并通过特征提取与样本标记产生 训练数据集，然后使用在线学习算法对分类模型进 行训练。 特征提取可使用 Ｍｏｏｒｅ ［３］ 提出的 ２４８ 维网 络流统计特征，样本标记可使用深度包检测工具 ｎＤＰＩ 以及开源工具 Ｔｓｔａｔ。 测试阶段，该框架使用训 练完成的模型对实时网络流量进行分类。 将模型分 类结果与 ｎＤＰＩ 与 Ｔｓｔａｔ 等工具的结果对比，当偏差 达到一定阈值时对模型进行重新训练。 图 １ 在线网络流量分类框架 Ｆｉｇ．１ Ｏｎｌｉｎｅ ｔｒａｆｆｉｃ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ｓｃｈｅｍｅ 本框架在获取到完整训练集后离线训练在线学 习分类模型。 在线学习方法在优化理论中被称作增 量算法。 增量算法的主要思路是：当目标函数由一 些子函数之和组成时，可以通过每次仅对一个子函 数进行“首尾相接”依次传递式的梯度优化迭代而 最终得到原问题的最优解。 当按照随机的方式挑选 子函数而不是按照顺序依次进行优化时，增量式方 法可以称为随机优化方法［３］ 。 在线学习与随机优 化有很紧密的关系，在很多情况下，两者甚至等同使 用［１９］ 。 在线和随机优化形式上虽然只是抽取样本 方式上的区别，但研究表明，它们的收敛性存在着差 异。 另一方面，有研究者认为在线学习按顺序选择 样本的方式能敏锐捕捉到数据变化的趋势。 为了考 察网络流量中样本顺序对分类效果的影响，本文在 ＳＣＷ⁃Ｉ 算法的基础上将顺序抽取样本的方式改为随 机抽取的方式，实验对比了两者在网络流量分类问 题中的差异，两种方法之间的效果差异表明了网络 流量样本存在着时序上的相关性。 ２．２ 在线学习二分类算法 为了检验本文提出的在线学习分类框架，我们 选取了 ８ 种在线学习方法进行验证。 所有的在线学 习算法均满足表 １ 所示的在线学习算法一般流程， 但由于理论基础不同，它们在损失函数、学习率、模 型的更新条件以及方式有差异。 ２．２．１ 一阶算法 感知机算法 感知机算法［１２］ 于 １９５８ 年提出， 是最早最简单的一阶在线学习算法，其优化目标是： 最小化学习到的分类器由当前样本带来的损失。 感 知机算法采用 ０－１ 损失作为损失函数，当损失大于 ０ 时，按照梯度下降的方式更新模型，其学习率恒 为 １。 ＯＧＤ 算法 在线梯度下降算法（ＯＧＤ） ［１８］ 也是 一种一阶算法，其优化目标与感知机算法一致，也是 采用梯度下降的更新方式来优化由不同损失函数产 生的优化目标。 其与感知机算法的区别在于：ＯＧＤ 算法学习率 ηｔ 设定为 Ｃ ｔ ，其中 Ｃ 是大于 ０ 的学习率 常数，ｔ 为迭代轮数。 在 ＯＧＤ 算法的实现中我们使 用了 ４ 种损失函数，分别为 ０－１ 损失、ｈｉｎｇｅ 损失、ｌｏ⁃ ｇｉｓｔｉｃ 损失和平方损失。 在实验中可以发现，当使用 ｈｉｎｇｅ 损失时，模型的分类效果最佳，因此我们在实 验中均采用 ｈｉｎｇｅ 损失。 ＰＡ 算法 Ｐａｓｓｉｖｅ⁃Ａｇｇｒｅｓｓｉｖｅ 算法［１３］是一种比 感知机算法和 ＯＧＤ 算法更加复杂的一阶在线学习 算法，其优化目标是如下两个目标的权衡：最小化学 习到的分类器与之前的分类器的距离、最小化学习 到的分类器由当前样本带来的损失。 ＰＡ 算法可以 看作为如下的在线优化问题： ｗｔ＋１ ＝ ａｒｇ ｍｉｎ ｗ １ ２ ‖ｗ － ｗｔ‖２ ， ｓ．ｔ． ｗ； ｘｔ，ｙｔ ( ( ) ) ＝ ｍａｘ ０，１ － ｙｔ ｗ·ｘｔ ( ( ) ) ＝ ０ （３） 式中目标函数项为 Ｐａｓｓｉｖｅ 项，表示最小化学习到的 分类器与之前的分类器的距离，约束项为 Ａｇｇｒｅｓｓｉｖｅ ·３２０· 智 能 系 统 学 报 第 １１ 卷

第3期 易磊，等：在线学习的大规模网络流量分类研究 ·321· 项，表示学习到的分类器由当前样本带来的损失。 束。尽管这种方式有非常迅速的学习速率，但是在 PA算法的损失函数采用了hinge损失，模型的更新 处理标记错误的样本时会导致分布的参数误修改。 方式为梯度下降，学习率为1。此外，PA算法还能 这就使CW算法在应用于有大量噪声的真实问题中 扩展成PA-I算法与PA-Ⅱ算法，这两种算法能更 时效果不理想。 好地处理不可分或者有噪声的数据。 SCW算法的提出克服CW算法的上述缺陷，具 PA-算法可以看作如下优化问题： 体的形式如下： 1 w=argminww+C(w:() u+1,∑+i)=argminDx.(Nu,)‖Nu,E))+ CP(N,);(x,y,)) (9) (4) 式中C是权衡passiveness与aggressiveness的参数。 式中：(0；(x,y)=max(0,1-y,(w·x,),C大于 式(9)表示的是SCW-I算法。此外，若使用平方惩 0,用以权衡passive项与aggressive项。 罚项，则变成了SCW-Ⅱ算法： PA-Ⅱ算法可以看作如式(5)形式 +1E+i)=argminD.(NGw,)‖Nu,Σ))+ 1 =arg minlw-+C (w;())2 Cr (N();(x.))2 (10) (5) 阶算法方面，感知机算法优化目标是最小化 式中：(0；(x,y)=max(0,1-y,(w·x,),C大于 学习到的分类器由当前样本带来的损失，损失函数 0,用以权衡passive项与aggressive项。 采用0-1损失，以定步长的梯度下降的方式来更新 2.2.2二阶算法 模型：OGD算法与感知机算法优化目标一致，但采 为了更好地探索特征之间的深层结构，二阶算 用了4种不同的损失函数，梯度下降迭代的步长随 法通常假定权重向量服从一个高斯分布ω~N 迭代轮数增长而缩短：PA算法的优化目标是最小化 (u,),其中均值向量u∈R,协方差矩阵Σ∈R。 学习到的分类器与之前的分类器的距离、最小化学 二阶算法在每次迭代时尝试更新高斯分布的均值与 习到的分类器由当前样本带来的损失。PA算法也 方差。 使用了梯度下降来更新模型。PA-I算法与PA-Ⅱ CW算法CW算法由Crammer等[1)于2008 算法类似，均使用了一个参数C来调节两个目标的 年提出，该算法的权重分布N(μ，)通过最小化新 权重，只是PA-Ⅱ算法使用了平方约束项。 旧分布权重的KL散度来更新，并确保分类正确的 二阶算法则是假定权重向量服从高斯分布，每 概率大于一个阈值，可以看作如下优化问题： 次迭代使用梯度下降尝试更新均值与方差。CW算 +1,2i)=argninD(N,2),N,2,)） 法的优化目标是最小化新旧分布权重的KL散度来 s.t.Py。~Nu,)[y,(w·xΣ，)≥0]≥0 更新，并确保分类正确的概率大于一个阈值。SCW (6) 算法在CW算法中引入了新的损失函数，并使用了 式中：目标函数项表示最小化新旧分布权重的KL 参数C来调节两个目标的权重。SCW-I算法与 散度，约束项表示分类正确的概率大于某个阈值。 SCW-Ⅱ算法区别在于PA-Ⅱ算法使用了平方约 SCW算法针对CW算法的局限，Wang等I 束项。 于20l3年提出了Soft Confidence-weighted算法。首 3网络流量分类实验 先引入一种新的损失函数： 3.1实验数据集 P(Nu,);(x,y))=max(0,p√xx,-yu·x,) 为了检验本文提出的在线学习分类框架的性 (7) 能，本实验采用了Moore等在文献)中所使用的网 式中p=Φ-()。原始CW算法的优化问题，可以 络流量数据集，每个样本均是由一条完整的双向 改写成如下形式： TCP流提取248维流量统计特征而来，实验中我们 w+1,Σ+i)=argminDK(Nw,)‖Nu,E)) μ，2 直接使用了完整的248维属性作为样本特征。该数 s.t.°(Nu,);(x,y,))=0,p>0(8) 据集采集了某网络出口24h内10个时间段的双向 原始的CW算法采取了一种非常激进的更新策 流量数据，每个时间段的平均抽样时间约为 略，即尽可能地改变分布以满足当前样本带来的约 1680s。该数据集共包含10种类别的377526个

项，表示学习到的分类器由当前样本带来的损失。 ＰＡ 算法的损失函数采用了 ｈｉｎｇｅ 损失，模型的更新 方式为梯度下降，学习率为 １。 此外，ＰＡ 算法还能 扩展成 ＰＡ－Ｉ 算法与 ＰＡ－ＩＩ 算法，这两种算法能更 好地处理不可分或者有噪声的数据。 ＰＡ⁃Ｉ 算法可以看作如下优化问题： ｗｔ＋１ ＝ ａｒｇｍｉｎ ｗ １ ２ ‖ｗ － ｗｔ‖２ ＋ Ｃ ｗ； ｘｔ，ｙｔ ( ( ) ) （４） 式中： ｗ； ｘｔ，ｙｔ ( ( ) ) ＝ ｍａｘ ０，１－ｙｔ（ｗ·ｘ ( ｔ） ) ， Ｃ 大于 ０，用以权衡 ｐａｓｓｉｖｅ 项与 ａｇｇｒｅｓｓｉｖｅ 项。 ＰＡ⁃Ⅱ算法可以看作如式（５）形式： ｗｔ＋１ ＝ ａｒｇ ｍｉｎ ｗ １ ２ ‖ｗ － ｗｔ‖２ ＋ Ｃ ｗ； ｘｔ，ｙｔ ( ( ) ) ２ （５） 式中： ｗ； ｘｔ，ｙｔ ( ( ) ) ＝ ｍａｘ ０，１－ｙｔ（ｗ·ｘ ( ｔ） ) ， Ｃ 大于 ０，用以权衡 ｐａｓｓｉｖｅ 项与 ａｇｇｒｅｓｓｉｖｅ 项。 ２．２．２ 二阶算法 为了更好地探索特征之间的深层结构，二阶算 法通常假定权重向量服从一个高斯分布 ω ～ Ｎ (μ，Σ ) ，其中均值向量 μ∈Ｒ ｄ ，协方差矩阵Σ∈Ｒ ｄ×ｄ 。 二阶算法在每次迭代时尝试更新高斯分布的均值与 方差。 ＣＷ 算法 ＣＷ 算法由 Ｃｒａｍｍｅｒ 等［１５］ 于 ２００８ 年提出，该算法的权重分布 Ｎ(μ，Σ ) 通过最小化新 旧分布权重的 ＫＬ 散度来更新，并确保分类正确的 概率大于一个阈值，可以看作如下优化问题： μｔ＋１ ，Σｔ＋１ ( ) ＝ ａｒｇｍｉｎ μ，Σ ＤＫＬ Ｎ(μ，Σ ) ，Ｎ μｔ，Σｔ ( ( ) ) ｓ．ｔ． Ｐγｗ ～ Ｎ(μ，Σ ) ｙｔ ｗ·ｘΣｔ [ ( ) ≥ ０] ≥ ０ （６） 式中：目标函数项表示最小化新旧分布权重的 ＫＬ 散度，约束项表示分类正确的概率大于某个阈值。 ＳＣＷ 算法 针对 ＣＷ 算法的局限，Ｗａｎｇ 等［１７］ 于 ２０１３ 年提出了 Ｓｏｆｔ Ｃｏｎｆｉｄｅｎｃｅ⁃ｗｅｉｇｈｔｅｄ 算法。 首 先引入一种新的损失函数： ｌ φ Ｎ(μ，Σ) ； ｘｔ，ｙｔ ( ( ) ) ＝ ｍａｘ ０，φ ｘ Ｔ ｔ Σｘｔ － ｙｔμ·ｘｔ ( ) （７） 式中 φ ＝ Φ －１ (η ) 。 原始 ＣＷ 算法的优化问题，可以 改写成如下形式： μｔ＋１，Σｔ＋１ ( ) ＝ ａｒｇｍｉｎ μ，∑ ＤＫＬ Ｎ(μ，Σ) ‖Ｎ μｔ，Σｔ ( ( ) ) ｓ．ｔ． ｌ φ Ｎ(μ，Σ ) ； ｘｔ，ｙｔ ( ( ) ) ＝ ０，φ ＞ ０ （８） 原始的 ＣＷ 算法采取了一种非常激进的更新策 略，即尽可能地改变分布以满足当前样本带来的约 束。 尽管这种方式有非常迅速的学习速率，但是在 处理标记错误的样本时会导致分布的参数误修改。 这就使 ＣＷ 算法在应用于有大量噪声的真实问题中 时效果不理想。 ＳＣＷ 算法的提出克服 ＣＷ 算法的上述缺陷，具 体的形式如下： μｔ＋１，Σｔ＋１ ( ) ＝ ａｒｇｍｉｎ μ，Σ ＤＫＬ Ｎ(μ，Σ) ‖Ｎ μｔ，Σｔ ( ( ) ) ＋ Ｃｌ φ Ｎ(μ，Σ ) ； ｘｔ，ｙｔ ( ( ) ) （９） 式中 Ｃ 是权衡 ｐａｓｓｉｖｅｎｅｓｓ 与 ａｇｇｒｅｓｓｉｖｅｎｅｓｓ 的参数。 式（９）表示的是 ＳＣＷ⁃Ｉ 算法。 此外，若使用平方惩 罚项，则变成了 ＳＣＷ⁃ＩＩ 算法： μｔ＋１，Σｔ＋１ ( ) ＝ ａｒｇｍｉｎ μ，Σ ＤＫＬ Ｎ(μ，Σ) ‖Ｎ μｔ，Σｔ ( ( ) ) ＋ Ｃｌ φ Ｎ(μ，Σ ) ； ｘｔ，ｙｔ ( ( ) ) ２ （１０） 一阶算法方面，感知机算法优化目标是最小化 学习到的分类器由当前样本带来的损失，损失函数 采用 ０－１ 损失，以定步长的梯度下降的方式来更新 模型；ＯＧＤ 算法与感知机算法优化目标一致，但采 用了 ４ 种不同的损失函数，梯度下降迭代的步长随 迭代轮数增长而缩短；ＰＡ 算法的优化目标是最小化 学习到的分类器与之前的分类器的距离、最小化学 习到的分类器由当前样本带来的损失。 ＰＡ 算法也 使用了梯度下降来更新模型。 ＰＡ⁃Ⅰ算法与 ＰＡ⁃Ⅱ 算法类似，均使用了一个参数 Ｃ 来调节两个目标的 权重，只是 ＰＡ⁃Ⅱ算法使用了平方约束项。 二阶算法则是假定权重向量服从高斯分布，每 次迭代使用梯度下降尝试更新均值与方差。 ＣＷ 算 法的优化目标是最小化新旧分布权重的 ＫＬ 散度来 更新，并确保分类正确的概率大于一个阈值。 ＳＣＷ 算法在 ＣＷ 算法中引入了新的损失函数，并使用了 参数 Ｃ 来调节两个目标的权重。 ＳＣＷ⁃Ⅰ算法与 ＳＣＷ⁃Ⅱ算法区别在于 ＰＡ⁃Ⅱ 算法使用了平方约 束项。 ３ 网络流量分类实验 ３．１ 实验数据集 为了检验本文提出的在线学习分类框架的性 能，本实验采用了 Ｍｏｏｒｅ 等在文献［３］ 中所使用的网 络流量数据集，每个样本均是由一条完整的双向 ＴＣＰ 流提取 ２４８ 维流量统计特征而来，实验中我们 直接使用了完整的 ２４８ 维属性作为样本特征。 该数 据集采集了某网络出口 ２４ ｈ 内 １０ 个时间段的双向 流量 数 据， 每 个 时 间 段 的 平 均 抽 样 时 间 约 为 １ ６８０ ｓ。 该数据集共包含 １０ 种类别的 ３７７ ５２６ 个 第 ３ 期 易磊，等：在线学习的大规模网络流量分类研究 ·３２１·

322. 智能系统学报 第11卷 网络流量样本，每种类别包含的流量和所占比例如 3.2实验环境 表1。 为了验证本文提出的在线学习网络分类框架的 表1 Moore数据集样本类别分布 有效性，本文使用MATLAB2015a用于数值计算， Table 1 Statistics of Moore datasets SVM的实现采用了Libsvm软件包，在线学习算法的 类别 数量 比例/% 实现采用了的LB0L算法库0。实验采用普通台 WWW 328091 86.91 式电脑，操作系统为Windows7旗舰版，其中CPU MAIL 28567 7.567 为Intel i5处理器，内存4GB。 BULK 11539 3.056 DATABASE 3.3评价指标 2648 0.701 SERVICE 2099 0.556 网络流量分类系统的评价指标主要有两个方 P2P 2094 0.555 面：分类系统的效率与精度，效率意味着分类模型的 ATTACK 1793 0.475 训练时间足够短，消耗的存储空间能够被接受，精度 MEDIA 1152 0.305 意味着分类准确率较高，且漏报率与误报率控制在 INT 110 0.029 一定范围内。为了对比批处理方法与在线学习方法 GAME 8 0.002 在网络流量分类问题中的性能差异，参考了文献[2如 总计 377526 100 的做法，将在线学习算法与SVM算法进行对比，采 由表1可以看出，数据集中各类数据数量分布 用了模型训练时间、分类精度和F-measure为评价 极不平均，WWW流量占据了数据集中的很高的比 指标。 例。样本数量不平均问题对分类器的效果会有很大 的影响，这是网络流量分类问题中的一个难点。本 对于在线学习，模型训练过程中的支持向量数 文重点不在于此，因此我们将数据集的样本分类简 量也是一项重要的评价指标。支持向量是指在线学 化为两类：一类为WWW流，另一类为其他应用。 习模型训练过程中产生损失，并导致模型发生更新 如表2所示，本次实验所用实验数据集分为两组，一 的样本。支持向量数量过少导致模型训练比较粗 组是将10个子集独立的作为实验数据集，记为： 糙，可能无法达到相应的精度：数量过多则会导致计 Moore1~Moore10:另一组将10个子集按顺序合成 算量增加，降低模型训练的效率。因此，在对比不同 为一个数据集，记为：MooreSet。为了模拟网络流量 在线学习方法的性能时，增加了模型训练过程的支 按序到达的特点，我们将数据集的前90%样本为训 持向量数。在对比样本按时序处理与随机处理的训 练集训练分类模型，后10%为测试集来测试模型效 练过程的差异时，还采用了模型训练的累积错误率 果。每个数据集的样本分布如表2所示。 表2数据集样本分布 作为评价指标。 Table 2 Sample size of Moore datasets 3.4实验与分析 训练集 测试集 为了评估本文提出的在线学习网络流量分类框 数据集 数量 WWW 其他 WWW 其他 架，本节设计了两个实验。实验1侧重于对比在线 Moorel 24863 16130 6247 2081 405 学习算法与SVM以及不同在线学习方法之间的性 Moore2 23801 16841 4580 1718 662 能差异。实验2侧重于考察网络流量中样本顺序对 Moore3 22932 16036 4603 2029 264 分类效果的影响，对比样本时序处理方式与随机处 Moore4 22285 17647 2410 1994 234 理方式的性能差异。 Moore5 21645 17183 2301 1435 729 3.4.1性能对比实验 Moore6 19384 15505 1941 1387 551 性能对比实验在10个数据子集与1个完整的 Moore7 55835 46682 3570 5300 283 数据集上，分别运行SVM算法与8种在线学习算 Moore8 5549446526 3419 5169 380 Moore9 法，使用每个数据集的前90%的样本作为训练集训 66248 53782 5842 6211 413 Moorel0 65 036 48386 10147 6050 453 练模型，使用后10%的样本作为测试集模拟模型实 MooreSet 37752629737042404 30722 7030 时运行的性能。实验结果及分析如下：

网络流量样本，每种类别包含的流量和所占比例如 表 １。 表 １ Ｍｏｏｒｅ 数据集样本类别分布 Ｔａｂｌｅ １ Ｓｔａｔｉｓｔｉｃｓ ｏｆ Ｍｏｏｒｅ ｄａｔａｓｅｔｓ 类别 数量 比例／ ％ ＷＷＷ ３２８ ０９１ ８６．９１ ＭＡＩＬ ２８ ５６７ ７．５６７ ＢＵＬＫ １１ ５３９ ３．０５６ ＤＡＴＡＢＡＳＥ ２ ６４８ ０．７０１ ＳＥＲＶＩＣＥ ２ ０９９ ０．５５６ Ｐ２Ｐ ２ ０９４ ０．５５５ ＡＴＴＡＣＫ １ ７９３ ０．４７５ ＭＥＤＩＡ １ １５２ ０．３０５ ＩＮＴ １１０ ０．０２９ ＧＡＭＥ ８ ０．００２ 总计 ３７７ ５２６ １００ 由表 １ 可以看出，数据集中各类数据数量分布 极不平均，ＷＷＷ 流量占据了数据集中的很高的比 例。 样本数量不平均问题对分类器的效果会有很大 的影响，这是网络流量分类问题中的一个难点。 本 文重点不在于此，因此我们将数据集的样本分类简 化为两类：一类为 ＷＷＷ 流，另一类为其他应用。 如表 ２ 所示，本次实验所用实验数据集分为两组，一 组是将 １０ 个子集独立的作为实验数据集，记为： Ｍｏｏｒｅ１～ Ｍｏｏｒｅ１０；另一组将 １０ 个子集按顺序合成 为一个数据集，记为：ＭｏｏｒｅＳｅｔ。 为了模拟网络流量 按序到达的特点，我们将数据集的前 ９０％样本为训 练集训练分类模型，后 １０％为测试集来测试模型效 果。 每个数据集的样本分布如表 ２ 所示。 表 ２ 数据集样本分布 Ｔａｂｌｅ ２ Ｓａｍｐｌｅ ｓｉｚｅ ｏｆ Ｍｏｏｒｅ ｄａｔａｓｅｔｓ 数据集 数量 训练集 测试集 ＷＷＷ 其他 ＷＷＷ 其他 Ｍｏｏｒｅ１ ２４ ８６３ １６ １３０ ６ ２４７ ２ ０８１ ４０５ Ｍｏｏｒｅ２ ２３ ８０１ １６ ８４１ ４ ５８０ １ ７１８ ６６２ Ｍｏｏｒｅ３ ２２ ９３２ １６ ０３６ ４ ６０３ ２ ０２９ ２６４ Ｍｏｏｒｅ４ ２２ ２８５ １７ ６４７ ２ ４１０ １ ９９４ ２３４ Ｍｏｏｒｅ５ ２１ ６４５ １７ １８３ ２ ３０１ １ ４３５ ７２９ Ｍｏｏｒｅ６ １９ ３８４ １５ ５０５ １ ９４１ １ ３８７ ５５１ Ｍｏｏｒｅ７ ５５ ８３５ ４６ ６８２ ３ ５７０ ５ ３００ ２８３ Ｍｏｏｒｅ８ ５５ ４９４ ４６ ５２６ ３ ４１９ ５ １６９ ３８０ Ｍｏｏｒｅ９ ６６ ２４８ ５３ ７８２ ５ ８４２ ６ ２１１ ４１３ Ｍｏｏｒｅ１０ ６５ ０３６ ４８ ３８６ １０１４７ ６ ０５０ ４５３ ＭｏｏｒｅＳｅｔ ３７７ ５２６ ２９７ ３７０ ４２ ４０４ ３０ ７２２ ７ ０３０ ３．２ 实验环境 为了验证本文提出的在线学习网络分类框架的 有效性，本文使用 ＭＡＴＬＡＢ ２０１５ａ 用于数值计算， ＳＶＭ 的实现采用了 Ｌｉｂｓｖｍ 软件包，在线学习算法的 实现采用了的 ＬＩＢＯＬ 算法库［２０］ 。 实验采用普通台 式电脑，操作系统为 Ｗｉｎｄｏｗｓ ７ 旗舰版，其中 ＣＰＵ 为 Ｉｎｔｅｌ ｉ５ 处理器，内存４ ＧＢ。 ３．３ 评价指标 网络流量分类系统的评价指标主要有两个方 面：分类系统的效率与精度，效率意味着分类模型的 训练时间足够短，消耗的存储空间能够被接受，精度 意味着分类准确率较高，且漏报率与误报率控制在 一定范围内。 为了对比批处理方法与在线学习方法 在网络流量分类问题中的性能差异，参考了文献［２１］ 的做法，将在线学习算法与 ＳＶＭ 算法进行对比，采 用了模型训练时间、分类精度和 Ｆ⁃ｍｅａｓｕｒｅ 为评价 指标。 对于在线学习，模型训练过程中的支持向量数 量也是一项重要的评价指标。 支持向量是指在线学 习模型训练过程中产生损失，并导致模型发生更新 的样本。 支持向量数量过少导致模型训练比较粗 糙，可能无法达到相应的精度；数量过多则会导致计 算量增加，降低模型训练的效率。 因此，在对比不同 在线学习方法的性能时，增加了模型训练过程的支 持向量数。 在对比样本按时序处理与随机处理的训 练过程的差异时，还采用了模型训练的累积错误率 作为评价指标。 ３．４ 实验与分析 为了评估本文提出的在线学习网络流量分类框 架，本节设计了两个实验。 实验 １ 侧重于对比在线 学习算法与 ＳＶＭ 以及不同在线学习方法之间的性 能差异。 实验 ２ 侧重于考察网络流量中样本顺序对 分类效果的影响，对比样本时序处理方式与随机处 理方式的性能差异。 ３．４．１ 性能对比实验 性能对比实验在 １０ 个数据子集与 １ 个完整的 数据集上，分别运行 ＳＶＭ 算法与 ８ 种在线学习算 法，使用每个数据集的前 ９０％的样本作为训练集训 练模型，使用后 １０％的样本作为测试集模拟模型实 时运行的性能。 实验结果及分析如下： ·３２２· 智 能 系 统 学 报 第 １１ 卷

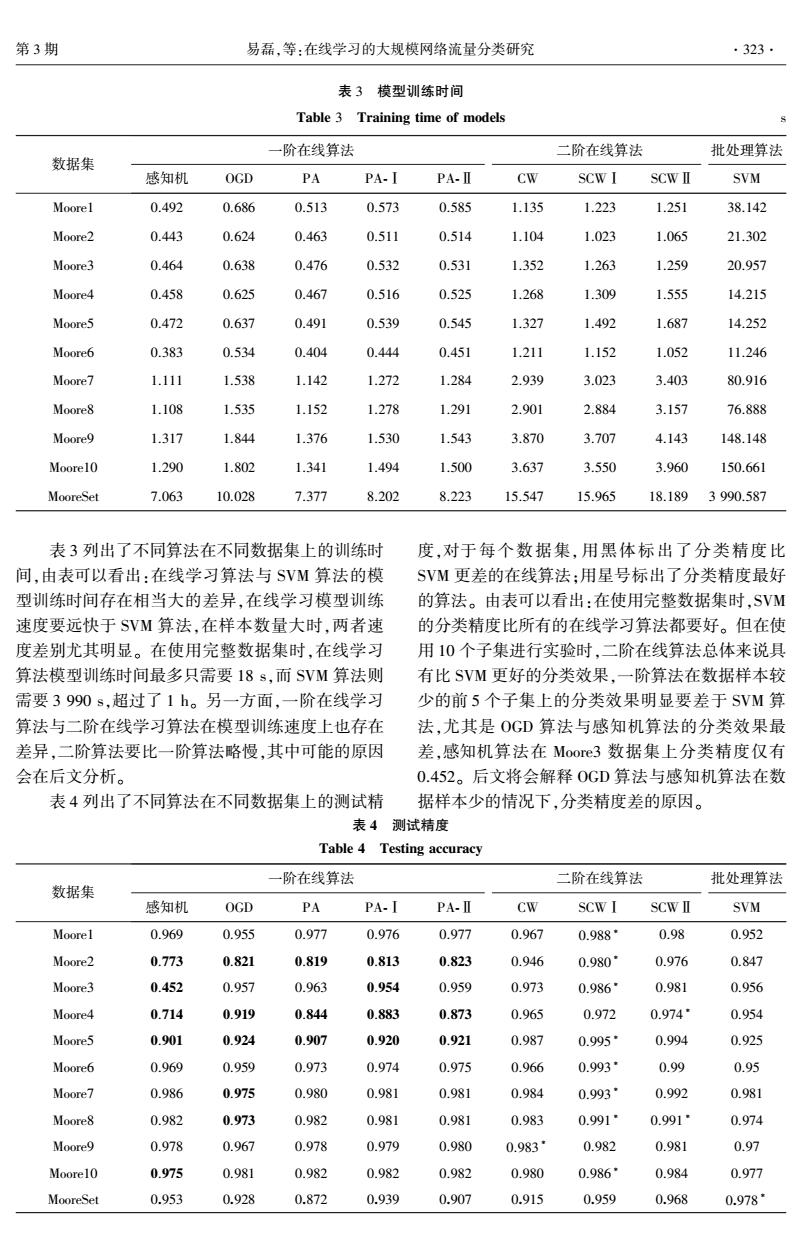
第3期 易磊，等：在线学习的大规模网络流量分类研究 ·323 表3模型训练时间 Table 3 Training time of models 一阶在线算法 二阶在线算法 批处理算法 数据集 感知机 OGD PA PA-I PA-Ⅱ Cw SCW I SCWⅡ SVM Moorel 0.492 0.686 0.513 0.573 0.585 1.135 1.223 1.251 38.142 Moore2 0.443 0.624 0.463 0.511 0.514 1.104 1.023 1.065 21.302 Moore3 0.464 0.638 0.476 0.532 0.531 1.352 1.263 1.259 20.957 Moore4 0.458 0.625 0.467 0.516 0.525 1.268 1.309 1.555 14.215 Moore5 0.472 0.637 0.491 0.539 0.545 1.327 1.492 1.687 14.252 Moore6 0.383 0.534 0.404 0.444 0.451 1.211 1.152 1.052 11.246 Moore7 1.111 1.538 1.142 1.272 1.284 2.939 3.023 3.403 80.916 Moore8 1.108 1.535 1.152 1.278 1.291 2.901 2.884 3.157 76.888 Moore9 1.317 1.844 1.376 1.530 1.543 3.870 3.707 4.143 148.148 Moorel0 1.290 1.802 1.341 1.494 1.500 3.637 3.550 3.960 150.661 MooreSet 7.063 10.028 7.377 8.202 8.223 15.547 15.965 18.189 3990.587 表3列出了不同算法在不同数据集上的训练时 度，对于每个数据集，用黑体标出了分类精度比 间，由表可以看出：在线学习算法与SVM算法的模 SVM更差的在线算法：用星号标出了分类精度最好 型训练时间存在相当大的差异，在线学习模型训练 的算法。由表可以看出：在使用完整数据集时，SVM 速度要远快于SVM算法，在样本数量大时，两者速 的分类精度比所有的在线学习算法都要好。但在使 度差别尤其明显。在使用完整数据集时，在线学习 用10个子集进行实验时，二阶在线算法总体来说具 算法模型训练时间最多只需要18s,而SVM算法则 有比SVM更好的分类效果，一阶算法在数据样本较 需要3990s,超过了1h。另一方面，一阶在线学习 少的前5个子集上的分类效果明显要差于SVM算 算法与二阶在线学习算法在模型训练速度上也存在 法，尤其是OGD算法与感知机算法的分类效果最 差异，二阶算法要比一阶算法略慢，其中可能的原因 差，感知机算法在Moore.3数据集上分类精度仅有 会在后文分析。 0.452。后文将会解释0GD算法与感知机算法在数 表4列出了不同算法在不同数据集上的测试精 据样本少的情况下，分类精度差的原因。 表4 测试精度 Table 4 Testing accuracy 一阶在线算法 二阶在线算法 批处理算法 数据集 感知机 OGD PA PA-I PA-Ⅱ CW SCW I SCWⅡ SVM Moorel 0.969 0.955 0.977 0.976 0.977 0.967 0.988 0.98 0.952 Moore2 0.773 0.821 0.819 0.813 0.823 0.946 0.980 0.976 0.847 Moore3 0.452 0.957 0.963 0.954 0.959 0.973 0.986 0.981 0.956 Moore4 0.714 0.919 0.844 0.883 0.873 0.965 0.972 0.974 0.954 Moore5 0.901 0.924 0.907 0.920 0.921 0.987 0.995 0.994 0.925 Moore6 0.969 0.959 0.973 0.974 0.975 0.966 0.993· 0.99 0.95 Moore7 0.986 0.975 0.980 0.981 0.981 0.984 0.993· 0.992 0.981 Moore8 0.982 0.973 0.982 0.981 0.981 0.983 0.991" 0.991· 0.974 Moore9 0.978 0.967 0.978 0.979 0.980 0.983 0.982 0.981 0.97 Moore10 0.975 0.981 0.982 0.982 0.982 0.980 0.986 0.984 0.977 MooreSet 0.953 0.928 0.872 0.939 0.907 0.915 0.959 0.968 0.978

表 ３ 模型训练时间 Ｔａｂｌｅ ３ Ｔｒａｉｎｉｎｇ ｔｉｍｅ ｏｆ ｍｏｄｅｌｓ ｓ 数据集 一阶在线算法 二阶在线算法 批处理算法 感知机 ＯＧＤ ＰＡ ＰＡ⁃Ⅰ ＰＡ⁃Ⅱ ＣＷ ＳＣＷⅠ ＳＣＷⅡ ＳＶＭ Ｍｏｏｒｅ１ ０．４９２ ０．６８６ ０．５１３ ０．５７３ ０．５８５ １．１３５ １．２２３ １．２５１ ３８．１４２ Ｍｏｏｒｅ２ ０．４４３ ０．６２４ ０．４６３ ０．５１１ ０．５１４ １．１０４ １．０２３ １．０６５ ２１．３０２ Ｍｏｏｒｅ３ ０．４６４ ０．６３８ ０．４７６ ０．５３２ ０．５３１ １．３５２ １．２６３ １．２５９ ２０．９５７ Ｍｏｏｒｅ４ ０．４５８ ０．６２５ ０．４６７ ０．５１６ ０．５２５ １．２６８ １．３０９ １．５５５ １４．２１５ Ｍｏｏｒｅ５ ０．４７２ ０．６３７ ０．４９１ ０．５３９ ０．５４５ １．３２７ １．４９２ １．６８７ １４．２５２ Ｍｏｏｒｅ６ ０．３８３ ０．５３４ ０．４０４ ０．４４４ ０．４５１ １．２１１ １．１５２ １．０５２ １１．２４６ Ｍｏｏｒｅ７ １．１１１ １．５３８ １．１４２ １．２７２ １．２８４ ２．９３９ ３．０２３ ３．４０３ ８０．９１６ Ｍｏｏｒｅ８ １．１０８ １．５３５ １．１５２ １．２７８ １．２９１ ２．９０１ ２．８８４ ３．１５７ ７６．８８８ Ｍｏｏｒｅ９ １．３１７ １．８４４ １．３７６ １．５３０ １．５４３ ３．８７０ ３．７０７ ４．１４３ １４８．１４８ Ｍｏｏｒｅ１０ １．２９０ １．８０２ １．３４１ １．４９４ １．５００ ３．６３７ ３．５５０ ３．９６０ １５０．６６１ ＭｏｏｒｅＳｅｔ ７．０６３ １０．０２８ ７．３７７ ８．２０２ ８．２２３ １５．５４７ １５．９６５ １８．１８９ ３ ９９０．５８７ 表 ３ 列出了不同算法在不同数据集上的训练时 间，由表可以看出：在线学习算法与 ＳＶＭ 算法的模 型训练时间存在相当大的差异，在线学习模型训练 速度要远快于 ＳＶＭ 算法，在样本数量大时，两者速 度差别尤其明显。 在使用完整数据集时，在线学习 算法模型训练时间最多只需要 １８ ｓ，而 ＳＶＭ 算法则 需要 ３ ９９０ ｓ，超过了 １ ｈ。 另一方面，一阶在线学习 算法与二阶在线学习算法在模型训练速度上也存在 差异，二阶算法要比一阶算法略慢，其中可能的原因 会在后文分析。 表 ４ 列出了不同算法在不同数据集上的测试精 度，对于每个数据集， 用黑体标出了分类精度比 ＳＶＭ 更差的在线算法；用星号标出了分类精度最好 的算法。 由表可以看出：在使用完整数据集时，ＳＶＭ 的分类精度比所有的在线学习算法都要好。 但在使 用 １０ 个子集进行实验时，二阶在线算法总体来说具 有比 ＳＶＭ 更好的分类效果，一阶算法在数据样本较 少的前 ５ 个子集上的分类效果明显要差于 ＳＶＭ 算 法，尤其是 ＯＧＤ 算法与感知机算法的分类效果最 差，感知机算法在 Ｍｏｏｒｅ３ 数据集上分类精度仅有 ０．４５２。 后文将会解释 ＯＧＤ 算法与感知机算法在数 据样本少的情况下，分类精度差的原因。 表 ４ 测试精度 Ｔａｂｌｅ ４ Ｔｅｓｔｉｎｇ ａｃｃｕｒａｃｙ 数据集 一阶在线算法 二阶在线算法 批处理算法 感知机 ＯＧＤ ＰＡ ＰＡ⁃Ⅰ ＰＡ⁃Ⅱ ＣＷ ＳＣＷⅠ ＳＣＷⅡ ＳＶＭ Ｍｏｏｒｅ１ ０．９６９ ０．９５５ ０．９７７ ０．９７６ ０．９７７ ０．９６７ ０．９８８ ∗ ０．９８ ０．９５２ Ｍｏｏｒｅ２ ０．７７３ ０．８２１ ０．８１９ ０．８１３ ０．８２３ ０．９４６ ０．９８０ ∗ ０．９７６ ０．８４７ Ｍｏｏｒｅ３ ０．４５２ ０．９５７ ０．９６３ ０．９５４ ０．９５９ ０．９７３ ０．９８６ ∗ ０．９８１ ０．９５６ Ｍｏｏｒｅ４ ０．７１４ ０．９１９ ０．８４４ ０．８８３ ０．８７３ ０．９６５ ０．９７２ ０．９７４ ∗ ０．９５４ Ｍｏｏｒｅ５ ０．９０１ ０．９２４ ０．９０７ ０．９２０ ０．９２１ ０．９８７ ０．９９５ ∗ ０．９９４ ０．９２５ Ｍｏｏｒｅ６ ０．９６９ ０．９５９ ０．９７３ ０．９７４ ０．９７５ ０．９６６ ０．９９３ ∗ ０．９９ ０．９５ Ｍｏｏｒｅ７ ０．９８６ ０．９７５ ０．９８０ ０．９８１ ０．９８１ ０．９８４ ０．９９３ ∗ ０．９９２ ０．９８１ Ｍｏｏｒｅ８ ０．９８２ ０．９７３ ０．９８２ ０．９８１ ０．９８１ ０．９８３ ０．９９１ ∗ ０．９９１ ∗ ０．９７４ Ｍｏｏｒｅ９ ０．９７８ ０．９６７ ０．９７８ ０．９７９ ０．９８０ ０．９８３ ∗ ０．９８２ ０．９８１ ０．９７ Ｍｏｏｒｅ１０ ０．９７５ ０．９８１ ０．９８２ ０．９８２ ０．９８２ ０．９８０ ０．９８６ ∗ ０．９８４ ０．９７７ ＭｏｏｒｅＳｅｔ ０．９５３ ０．９２８ ０．８７２ ０．９３９ ０．９０７ ０．９１５ ０．９５９ ０．９６８ ０．９７８ ∗ 第 ３ 期 易磊，等：在线学习的大规模网络流量分类研究 ·３２３·

324. 智能系统学报 第11卷 表5列出了不同算法在不同数据集上的F 释上文中发现的二阶算法训练时间比一阶算法慢 measure,对于每个数据集，用黑体标出了F-measure 但是效果比一阶算法好的现象。二阶算法的模型更 比SVM更差的在线算法；用星号标出了F-measure 加复杂，模型每次更新的计算量更大，由表6可以看 最好的算法。从表5可以得出与表4一致的结论。 出，二阶算法的支持向量数比一阶算法略多，这就导 表6列出了8种不同在线算法在不同数据集上训练 致了二阶算法比一阶算法模型训练所需时间更长。 时的支持向量数。支持向量是指在线学习模型训练 感知机与OGD算法的支持向量数明显要少于其他 过程中产生损失，并导致模型发生更新的样本。支 在线算法，这导致了模型没有得到有效的训练，达不 持向量越多表示模型更新次数越多，模型训练越充 到其他算法相当的分类精度。我们注意到感知机算 分，相应的计算量也越大。反之，则计算量更少，模 法的支持向量数最少，这可能是其分类精度极不稳 型训练可能不够。这里尝试从支持向量数的角度解 定甚至分类精度非常低的原因。 表5F-measure Table 5 F-measure 一阶在线算法 二阶在线算法 批处理算法 数据集 感知机 OGD PA PA-I PA-II CW SCW I SCWⅡ SVM Moorel 0.982 0.973 0.987 0.986 0.986 0.980 0.993 0.993 0.971 Moore2 0.849 0.850 0.851 0.852 0.853 0.854 0.855 0.856 0.857 Moore3 0.552 0.975 0.979 0.974 0.976 0.985 0.992· 0.992· 0.986 Moore4 0.812 0.954 0.906 0.931 0.925 0.981 0.985 0.985 0.975 Moore5 0.925 0.943 0.930 0.941 0.941 0.990 0.996 0.996 0.946 Moore6 0.978 0.972 0.981 0.982 0.983 0.976 0.9951 0.9951 0.966 Moore7 0.992 0.987 0.990 0.990 0.990 0.991 0.996 0.996 0.991 Moore8 0.990 0.985 0.991 0.990 0.990 0.991 0.995· 0.995 0.986 Moore9 0.988 0.982 0.988 0.989 0.989 0.991 0.991 0.991 0.984 Moore10 0.987 0.990 0.991 0.990 0.991 0.989 0.992· 0.992 0.988 MooreSet 0.971 0.958 0.915 0.962 0.940 0.950 0.975 0.975 0.987 表6支持向量数 Table 6 Number of support vectors 一阶在线算法 二阶在线算法 数据集 感知机 OGD PA PA-1 PA-2 cw SCW1 SCW2 Moorel 277 947 1056 1099 1621 895 863 1063 Moore2 209 847 864 888 1139 844 744 812 Moore3 210 819 921 933 1366 812 594 746 Moore4 244 772 954 982 1452 882 768 1127 Moore5 237 609 953 960 1385 796 812 1304 Moore6 206 585 844 862 1214 735 663 555 Moore7 405 1624 1475 1591 2384 1405 1332 2149 Moore8 393 1318 1446 1489 2167 1317 1160 2102 Moore9 837 1672 2426 2515 3476 2120 2071 3242 Moore10 531 1542 1924 1962 2954 1787 1590 2645 MooreSet 2904 7716 10074 9892 14344 9525 6265 15825

表 ５ 列出了不同算法在不同数据集上的 Ｆ⁃ ｍｅａｓｕｒｅ，对于每个数据集，用黑体标出了 Ｆ⁃ｍｅａｓｕｒｅ 比 ＳＶＭ 更差的在线算法；用星号标出了 Ｆ⁃ｍｅａｓｕｒｅ 最好的算法。 从表 ５ 可以得出与表 ４ 一致的结论。 表 ６ 列出了 ８ 种不同在线算法在不同数据集上训练 时的支持向量数。 支持向量是指在线学习模型训练 过程中产生损失，并导致模型发生更新的样本。 支 持向量越多表示模型更新次数越多，模型训练越充 分，相应的计算量也越大。 反之，则计算量更少，模 型训练可能不够。 这里尝试从支持向量数的角度解 释上文中发现的二阶算法训练时间比一阶算法慢， 但是效果比一阶算法好的现象。 二阶算法的模型更 加复杂，模型每次更新的计算量更大，由表 ６ 可以看 出，二阶算法的支持向量数比一阶算法略多，这就导 致了二阶算法比一阶算法模型训练所需时间更长。 感知机与 ＯＧＤ 算法的支持向量数明显要少于其他 在线算法，这导致了模型没有得到有效的训练，达不 到其他算法相当的分类精度。 我们注意到感知机算 法的支持向量数最少，这可能是其分类精度极不稳 定甚至分类精度非常低的原因。 表 ５ Ｆ⁃ｍｅａｓｕｒｅ Ｔａｂｌｅ ５ Ｆ⁃ｍｅａｓｕｒｅ 数据集 一阶在线算法 二阶在线算法 批处理算法 感知机 ＯＧＤ ＰＡ ＰＡ⁃Ⅰ ＰＡ⁃Ⅱ ＣＷ ＳＣＷⅠ ＳＣＷⅡ ＳＶＭ Ｍｏｏｒｅ１ ０．９８２ ０．９７３ ０．９８７ ０．９８６ ０．９８６ ０．９８０ ０．９９３ ∗ ０．９９３ ∗ ０．９７１ Ｍｏｏｒｅ２ ０．８４９ ０．８５０ ０．８５１ ０．８５２ ０．８５３ ０．８５４ ０．８５５ ０．８５６ ０．８５７ ∗ Ｍｏｏｒｅ３ ０．５５２ ０．９７５ ０．９７９ ０．９７４ ０．９７６ ０．９８５ ０．９９２ ∗ ０．９９２ ∗ ０．９８６ Ｍｏｏｒｅ４ ０．８１２ ０．９５４ ０．９０６ ０．９３１ ０．９２５ ０．９８１ ０．９８５ ∗ ０．９８５ ∗ ０．９７５ Ｍｏｏｒｅ５ ０．９２５ ０．９４３ ０．９３０ ０．９４１ ０．９４１ ０．９９０ ０．９９６ ∗ ０．９９６ ∗ ０．９４６ Ｍｏｏｒｅ６ ０．９７８ ０．９７２ ０．９８１ ０．９８２ ０．９８３ ０．９７６ ０．９９５ ∗ ０．９９５ ∗ ０．９６６ Ｍｏｏｒｅ７ ０．９９２ ０．９８７ ０．９９０ ０．９９０ ０．９９０ ０．９９１ ０．９９６ ∗ ０．９９６ ∗ ０．９９１ Ｍｏｏｒｅ８ ０．９９０ ０．９８５ ０．９９１ ０．９９０ ０．９９０ ０．９９１ ０．９９５ ∗ ０．９９５ ∗ ０．９８６ Ｍｏｏｒｅ９ ０．９８８ ０．９８２ ０．９８８ ０．９８９ ０．９８９ ０．９９１ ０．９９１ ∗ ０．９９１ ∗ ０．９８４ Ｍｏｏｒｅ１０ ０．９８７ ０．９９０ ０．９９１ ０．９９０ ０．９９１ ０．９８９ ０．９９２ ∗ ０．９９２ ∗ ０．９８８ ＭｏｏｒｅＳｅｔ ０．９７１ ０．９５８ ０．９１５ ０．９６２ ０．９４０ ０．９５０ ０．９７５ ０．９７５ ０．９８７ ∗ 表 ６ 支持向量数 Ｔａｂｌｅ ６ Ｎｕｍｂｅｒ ｏｆ ｓｕｐｐｏｒｔ ｖｅｃｔｏｒｓ 数据集 一阶在线算法 二阶在线算法 感知机 ＯＧＤ ＰＡ ＰＡ⁃１ ＰＡ⁃２ ＣＷ ＳＣＷ１ ＳＣＷ２ ＳＶＭ Ｍｏｏｒｅ１ ２７７ ９４７ １ ０５６ １ ０９９ １ ６２１ ８９５ ８６３ １ ０６３ Ｍｏｏｒｅ２ ２０９ ８４７ ８６４ ８８８ １ １３９ ８４４ ７４４ ８１２ Ｍｏｏｒｅ３ ２１０ ８１９ ９２１ ９３３ １ ３６６ ８１２ ５９４ ７４６ Ｍｏｏｒｅ４ ２４４ ７７２ ９５４ ９８２ １ ４５２ ８８２ ７６８ １ １２７ Ｍｏｏｒｅ５ ２３７ ６０９ ９５３ ９６０ １ ３８５ ７９６ ８１２ １ ３０４ Ｍｏｏｒｅ６ ２０６ ５８５ ８４４ ８６２ １ ２１４ ７３５ ６６３ ５５５ Ｍｏｏｒｅ７ ４０５ １ ６２４ １ ４７５ １ ５９１ ２ ３８４ １ ４０５ １ ３３２ ２ １４９ Ｍｏｏｒｅ８ ３９３ １ ３１８ １ ４４６ １ ４８９ ２ １６７ １ ３１７ １ １６０ ２ １０２ Ｍｏｏｒｅ９ ８３７ １ ６７２ ２ ４２６ ２ ５１５ ３ ４７６ ２ １２０ ２ ０７１ ３ ２４２ Ｍｏｏｒｅ１０ ５３１ １ ５４２ １ ９２４ １ ９６２ ２ ９５４ １ ７８７ １ ５９０ ２ ６４５ ＭｏｏｒｅＳｅｔ ２ ９０４ ７ ７１６ １０ ０７４ ９ ８９２ １４ ３４４ ９ ５２５ ６ ２６５ １５ ８２５ ·３２４· 智 能 系 统 学 报 第 １１ 卷

第3期 易磊，等：在线学习的大规模网络流量分类研究 ·325. 通过性能对比实验可以发现，在8种在线学习 在线学习算法去训练模型。本实验使用10个数据 分类算法中，二阶算法的分类效果普遍优于一阶算 子集作为实验数据集，将分类性能最好的SCW-I算 法，与SVM分类效果相当：SCW-I算法有着较好的 法分别用样本按时序处理与随机处理的方式进行训 分类精度与分类效率，具有良好的应用前景。 练，然后使用测试集进行测试。其中，随机处理方式 3.4.2时序相关性实验 按照不同的随机顺序重复实验20次，对实验结果取 为了考察网络流量中样本顺序对分类效果的影 平均。实验还使用了模型训练过程中的累积错误率 响，我们将训练数据集中样本的顺序随机打乱，再用 作为评价指标。时序方式与随机方式对比见表7。 表7时序方式与随机方式对比 Table 7 Comparison of sequentially and random 训练错误率 测试精度 F-measure 训练时间/s 数据集 时序 随机 时序 随机 时序 随机 时序 随机 Moorel 0.008 0.010 0.988 0.982 0.993 0.989 1.223 1.189 Moore2 0.010 0.006 0.98 0.976 0.855 0.984 1.023 1.091 Moore3 0.004 0.006 0.986 0.986 0.992 0.992 1.263 1.274 Moore4 0.008 0.008 0.972 0.976 0.985 0.987 1.309 1.467 Moore5 0.007 0.007 0.995 0.993 0.996 0.995 1.492 1.510 Moore6 0.006 0.007 0.993 0.992 0.995 0.994 1.152 1.327 Moore7 0.008 0.006 0.993 0.994 0.996 0.997 3.023 3.686 Moore8 0.005 0.006 0.991 0.991 0.995 0.995 2.884 3.479 Moore9 0.010 0.011 0.982 0.984 0.991 0.992 3.707 4.685 Moore10 0.008 0.010 0.986 0.985 0.992 0.992 3.550 4.311 MooreSet 0.007 0.008 0.959 0.967 0.975 0.980 15.965 17.692 表7对比了SCW-I算法时序方式与随机方式 ×102 在不同数据集下的性能指标，用黑体标出了较好的 3.0 -Stochastic 指标。由表可以看出：在网络流量分类问题中，时序 2.5 +Onlinc 方式比随机方式有更低的训练累积错误率、较好的 2.0 测试精度与F-measure、更快的模型训练时间。这表 1.5 明网络流量的样本顺序对分类效果有正面影响，因 1.0 此可以认为网络流量样本存在着一种时间上的相关 性，这种特性对分类效率的提高有积极意义。 0.5 为了说明此种相关性，在模型训练过程中按照 ×10 02040.60.81.01.21.41.61.8 样本数量间隔设置了15个采样点，记录了在线方式 样本数量 与随机方式训练过程中训练错误率的变化趋势。我 们选取了第4、6、8、10个子集的一次实验结果，绘制 (b)Moore6 了模型训练累积错误率的趋势，如图2所示。 ×102 1.6 ×102 3.0 1.4 -Stochastic →Stochastic +Online 2.5 +Online 12 1.0 2.0 0.8 1.5 0.6 0.4 1.0 0.2 0.5 0510520253035404550*10 10 样本数量 0.5 1.0 1.5 2.0 2.5 样本数量 (c)Moore8 (a)Moore4

通过性能对比实验可以发现，在 ８ 种在线学习 分类算法中，二阶算法的分类效果普遍优于一阶算 法，与 ＳＶＭ 分类效果相当；ＳＣＷ⁃Ⅰ算法有着较好的 分类精度与分类效率，具有良好的应用前景。 ３．４．２ 时序相关性实验 为了考察网络流量中样本顺序对分类效果的影 响，我们将训练数据集中样本的顺序随机打乱，再用 在线学习算法去训练模型。 本实验使用 １０ 个数据 子集作为实验数据集，将分类性能最好的 ＳＣＷ－Ｉ 算 法分别用样本按时序处理与随机处理的方式进行训 练，然后使用测试集进行测试。 其中，随机处理方式 按照不同的随机顺序重复实验 ２０ 次，对实验结果取 平均。 实验还使用了模型训练过程中的累积错误率 作为评价指标。 时序方式与随机方式对比见表 ７。 表 ７ 时序方式与随机方式对比 Ｔａｂｌｅ ７ Ｃｏｍｐａｒｉｓｏｎ ｏｆ ｓｅｑｕｅｎｔｉａｌｌｙ ａｎｄ ｒａｎｄｏｍ 数据集 训练错误率 测试精度 Ｆ⁃ｍｅａｓｕｒｅ 训练时间／ ｓ 时序 随机 时序 随机 时序 随机 时序 随机 Ｍｏｏｒｅ１ ０．００８ ０．０１０ ０．９８８ ０．９８２ ０．９９３ ０．９８９ １．２２３ １．１８９ Ｍｏｏｒｅ２ ０．０１０ ０．００６ ０．９８ ０．９７６ ０．８５５ ０．９８４ １．０２３ １．０９１ Ｍｏｏｒｅ３ ０．００４ ０．００６ ０．９８６ ０．９８６ ０．９９２ ０．９９２ １．２６３ １．２７４ Ｍｏｏｒｅ４ ０．００８ ０．００８ ０．９７２ ０．９７６ ０．９８５ ０．９８７ １．３０９ １．４６７ Ｍｏｏｒｅ５ ０．００７ ０．００７ ０．９９５ ０．９９３ ０．９９６ ０．９９５ １．４９２ １．５１０ Ｍｏｏｒｅ６ ０．００６ ０．００７ ０．９９３ ０．９９２ ０．９９５ ０．９９４ １．１５２ １．３２７ Ｍｏｏｒｅ７ ０．００８ ０．００６ ０．９９３ ０．９９４ ０．９９６ ０．９９７ ３．０２３ ３．６８６ Ｍｏｏｒｅ８ ０．００５ ０．００６ ０．９９１ ０．９９１ ０．９９５ ０．９９５ ２．８８４ ３．４７９ Ｍｏｏｒｅ９ ０．０１０ ０．０１１ ０．９８２ ０．９８４ ０．９９１ ０．９９２ ３．７０７ ４．６８５ Ｍｏｏｒｅ１０ ０．００８ ０．０１０ ０．９８６ ０．９８５ ０．９９２ ０．９９２ ３．５５０ ４．３１１ ＭｏｏｒｅＳｅｔ ０．００７ ０．００８ ０．９５９ ０．９６７ ０．９７５ ０．９８０ １５．９６５ １７．６９２ 表 ７ 对比了 ＳＣＷ⁃Ⅰ算法时序方式与随机方式 在不同数据集下的性能指标，用黑体标出了较好的 指标。 由表可以看出：在网络流量分类问题中，时序 方式比随机方式有更低的训练累积错误率、较好的 测试精度与 Ｆ⁃ｍｅａｓｕｒｅ、更快的模型训练时间。 这表 明网络流量的样本顺序对分类效果有正面影响，因 此可以认为网络流量样本存在着一种时间上的相关 性，这种特性对分类效率的提高有积极意义。 为了说明此种相关性，在模型训练过程中按照 样本数量间隔设置了 １５ 个采样点，记录了在线方式 与随机方式训练过程中训练错误率的变化趋势。 我 们选取了第 ４、６、８、１０ 个子集的一次实验结果，绘制 了模型训练累积错误率的趋势，如图 ２ 所示。 （ａ）Ｍｏｏｒｅ４ （ｂ）Ｍｏｏｒｅ６ （ｃ）Ｍｏｏｒｅ８ 第 ３ 期 易磊，等：在线学习的大规模网络流量分类研究 ·３２５·

.326· 智能系统学报 第11卷 ×103 work traffic classification J].IEEE/ACM transactions on 3.0 -Stochastic networking,2015,23(4):1257-1270. Online [2]NGUYEN T TT,ARMITAGE G.A survey of techniques for 2 internet traffic classification using machine learning [J]. 5 IEEE communications surveys tutorials,2008,10(4): 56-76. 1.0 [3]陶卿，高乾坤，姜纪远，等.稀疏学习优化问题的求解 0.5 综述[J].软件学报，2013,24(11)：2498-2507. ×10 TAO Qing,GAO Qiankun,JIANG Jiyuan,et al.Survey of 34 6 solving the optimization problems for sparse learning[]. 样本数量 Journal of software,2013,24(11):2498-2507. (d)Moorel0 [4]MOORE A W,ZUEV D.Internet traffic classification using 图2训练累积错误率 bayesian analysis techniques[J].ACM sigmetrics perform- Fig.2 Training cumulative mistake rate ance evaluation review,2005,33(1):50-60. [5]AULD T,MOORE A W,GULL S F.Bayesian neural net- 由图2可以看出，模型训练过程中，随机方式与 works for internet traffic classification[].IEEE transactions 时序方式的累积错误率的变化趋势有很大的不同。 on neural networks,2007,18(1):223-239 两种方法不仅是收敛速度的差异，随机方式的累积 [6]ESTE A,GRINGOLI F,SALGARELLI L.Support vector 错误率的变化趋势是一个缓慢下降的过程，而在线 machines for TCP traffic classification[J].Computer net- 方式的变化趋势却是一个曲折上升的过程，且每个 works,2009,53(14):2476-2490. 数据集的曲线都有各自的结构特点。 [7]SCHATZMANN D,MuHLBAUER W,SPYROPOULOS T, 由此可以发现，网络流量样本中存在着一种时 et al.Digging into HTTPS:flow-based classification of web- 间上的相关性，对模型的分类效果有一定的正面影 mail traffic[C]//Proceedings of the 10th ACM SIGCOMM 响。但这种特性还缺乏理论性的分析，同时如何运 conference on internet measurement.New York,NY,USA, 2010:322.327. 用这种特性还需要进一步研究。 [8]WANG Yu,YU Shunzheng.Supervised learning real-time 4结束语 traffic classifiers[J].Journal of networks,2009,4(7): 622-629. 本文针对高速骨干网大规模网络流量分类问题 [9]NGUYEN TT T,ARMITAGE G,BRANCH P,et al.Time- 提出了一种基于在线学习的网络流量分类框架，并 ly and continuous machine-learning-based classification for 将8种在线学习方法运用到网络流量分类问题中。 interactive IP traffic [J].IEEE/ACM transactions on net- 对比在线算法与批处理方法SVM的性能差异，实验 working,2012,20(6):1880-1894. 表明在分类精度相当的情况下，在线学习算法与 [10]ZANDER S,NGUYEN T,ARMITAGE G.Automated traf- SVM相比空间开销小、模型训练时间显著缩短：对 fic classification and application identification using ma- 比不同在线学习方法的分类性能，实验表明SCW- chine learning[C]//Proceedings of the IEEE conference I算法在8种在线学习算法中有最好的分类效果： on local computer networks 30th anniversary.Sydney, 对比样本时序处理方式与随机处理方式的差异，实 NSW,Australia,2005:250-257. 验表明网络流量样本中存在着一种时间序列上的相 [11]ERMAN J,ARLITT M,MAHANTI A.Traffic classifica- 关性。 tion using clustering algorithms [C]//Proceedings of the 2006 SIGCOMM workshop on mining network data.New 本文发现的网络流量样本的相关性只是通过实 York,NY,USA,2006:281-286. 验来验证，缺乏理论分析，也没有找到合适的利用方 [12]ROSENBLATT F.The perception:a probabilistic model for 法。另一方面，本文仅使用了二分类在线算法在实 information storage and organization in the brain[.Psy- 验数据集上进行验证，如何把算法扩展到多分类并 chological review,1958,65(6):386-408. 实际应用于大规模网络环境是下一步工作的重点。 [13]CRAMMER K,DEKEL O,KESHET J,et al.Online pas- 参考文献： sive-aggressive algorithms[].Journal of machine learning research,2006,7(3):551-585. [1]ZHANG Jun,CHEN Xiao,XIANG Yang,et al.Robust net- [14]CESA-BIANCHI N,CONCONI A,GENTILE C.A second-

（ｄ）Ｍｏｏｒｅ１０ 图 ２ 训练累积错误率 Ｆｉｇ．２ Ｔｒａｉｎｉｎｇ ｃｕｍｕｌａｔｉｖｅ ｍｉｓｔａｋｅ ｒａｔｅ 由图 ２ 可以看出，模型训练过程中，随机方式与 时序方式的累积错误率的变化趋势有很大的不同。 两种方法不仅是收敛速度的差异，随机方式的累积 错误率的变化趋势是一个缓慢下降的过程，而在线 方式的变化趋势却是一个曲折上升的过程，且每个 数据集的曲线都有各自的结构特点。 由此可以发现，网络流量样本中存在着一种时 间上的相关性，对模型的分类效果有一定的正面影 响。 但这种特性还缺乏理论性的分析，同时如何运 用这种特性还需要进一步研究。 ４ 结束语 本文针对高速骨干网大规模网络流量分类问题 提出了一种基于在线学习的网络流量分类框架，并 将 ８ 种在线学习方法运用到网络流量分类问题中。 对比在线算法与批处理方法 ＳＶＭ 的性能差异，实验 表明在分类精度相当的情况下，在线学习算法与 ＳＶＭ 相比空间开销小、模型训练时间显著缩短；对 比不同在线学习方法的分类性能，实验表明 ＳＣＷ⁃ Ⅰ算法在 ８ 种在线学习算法中有最好的分类效果； 对比样本时序处理方式与随机处理方式的差异，实 验表明网络流量样本中存在着一种时间序列上的相 关性。 本文发现的网络流量样本的相关性只是通过实 验来验证，缺乏理论分析，也没有找到合适的利用方 法。 另一方面，本文仅使用了二分类在线算法在实 验数据集上进行验证，如何把算法扩展到多分类并 实际应用于大规模网络环境是下一步工作的重点。 参考文献： ［１］ＺＨＡＮＧ Ｊｕｎ， ＣＨＥＮ Ｘｉａｏ， ＸＩＡＮＧ Ｙａｎｇ， ｅｔ ａｌ． Ｒｏｂｕｓｔ ｎｅｔ⁃ ｗｏｒｋ ｔｒａｆｆｉｃ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ［ Ｊ］． ＩＥＥＥ／ ＡＣＭ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｎｅｔｗｏｒｋｉｎｇ， ２０１５， ２３（４）： １２５７⁃１２７０． ［２］ＮＧＵＹＥＮ Ｔ Ｔ Ｔ， ＡＲＭＩＴＡＧＥ Ｇ． Ａ ｓｕｒｖｅｙ ｏｆ ｔｅｃｈｎｉｑｕｅｓ ｆｏｒ ｉｎｔｅｒｎｅｔ ｔｒａｆｆｉｃ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ｕｓｉｎｇ ｍａｃｈｉｎｅ ｌｅａｒｎｉｎｇ ［ Ｊ ］． ＩＥＥＥ ｃｏｍｍｕｎｉｃａｔｉｏｎｓ ｓｕｒｖｅｙｓ ＆ ｔｕｔｏｒｉａｌｓ， ２００８， １０ （ ４）： ５６⁃７６． ［３］陶卿， 高乾坤， 姜纪远， 等． 稀疏学习优化问题的求解 综述［Ｊ］． 软件学报， ２０１３， ２４（１１）： ２４９８⁃２５０７． ＴＡＯ Ｑｉｎｇ， ＧＡＯ Ｑｉａｎｋｕｎ， ＪＩＡＮＧ Ｊｉｙｕａｎ， ｅｔ ａｌ． Ｓｕｒｖｅｙ ｏｆ ｓｏｌｖｉｎｇ ｔｈｅ ｏｐｔｉｍｉｚａｔｉｏｎ ｐｒｏｂｌｅｍｓ ｆｏｒ ｓｐａｒｓｅ ｌｅａｒｎｉｎｇ ［ Ｊ］． Ｊｏｕｒｎａｌ ｏｆ ｓｏｆｔｗａｒｅ， ２０１３， ２４（１１）： ２４９８⁃２５０７． ［４］ＭＯＯＲＥ Ａ Ｗ， ＺＵＥＶ Ｄ． Ｉｎｔｅｒｎｅｔ ｔｒａｆｆｉｃ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ｕｓｉｎｇ ｂａｙｅｓｉａｎ ａｎａｌｙｓｉｓ ｔｅｃｈｎｉｑｕｅｓ［ Ｊ］． ＡＣＭ ｓｉｇｍｅｔｒｉｃｓ ｐｅｒｆｏｒｍ⁃ ａｎｃｅ ｅｖａｌｕａｔｉｏｎ ｒｅｖｉｅｗ， ２００５， ３３（１）： ５０⁃６０． ［５］ＡＵＬＤ Ｔ， ＭＯＯＲＥ Ａ Ｗ， ＧＵＬＬ Ｓ Ｆ． Ｂａｙｅｓｉａｎ ｎｅｕｒａｌ ｎｅｔ⁃ ｗｏｒｋｓ ｆｏｒ ｉｎｔｅｒｎｅｔ ｔｒａｆｆｉｃ ｃｌａｓｓｉｆｉｃａｔｉｏｎ［Ｊ］． ＩＥＥＥ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｎｅｕｒａｌ ｎｅｔｗｏｒｋｓ， ２００７， １８（１）： ２２３⁃２３９． ［６］ ＥＳＴＥ Ａ， ＧＲＩＮＧＯＬＩ Ｆ， ＳＡＬＧＡＲＥＬＬＩ Ｌ． Ｓｕｐｐｏｒｔ ｖｅｃｔｏｒ ｍａｃｈｉｎｅｓ ｆｏｒ ＴＣＰ ｔｒａｆｆｉｃ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ［ Ｊ］． Ｃｏｍｐｕｔｅｒ ｎｅｔ⁃ ｗｏｒｋｓ， ２００９， ５３（１４）： ２４７６⁃２４９０． ［７］ＳＣＨＡＴＺＭＡＮＮ Ｄ， ＭüＨＬＢＡＵＥＲ Ｗ， ＳＰＹＲＯＰＯＵＬＯＳ Ｔ， ｅｔ ａｌ． Ｄｉｇｇｉｎｇ ｉｎｔｏ ＨＴＴＰＳ： ｆｌｏｗ⁃ｂａｓｅｄ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ｏｆ ｗｅｂ⁃ ｍａｉｌ ｔｒａｆｆｉｃ［Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ １０ｔｈ ＡＣＭ ＳＩＧＣＯＭＭ ｃｏｎｆｅｒｅｎｃｅ ｏｎ ｉｎｔｅｒｎｅｔ ｍｅａｓｕｒｅｍｅｎｔ． Ｎｅｗ Ｙｏｒｋ， ＮＹ， ＵＳＡ， ２０１０： ３２２⁃３２７． ［８］ ＷＡＮＧ Ｙｕ， ＹＵ Ｓｈｕｎｚｈｅｎｇ． Ｓｕｐｅｒｖｉｓｅｄ ｌｅａｒｎｉｎｇ ｒｅａｌ⁃ｔｉｍｅ ｔｒａｆｆｉｃ ｃｌａｓｓｉｆｉｅｒｓ ［ Ｊ］． Ｊｏｕｒｎａｌ ｏｆ ｎｅｔｗｏｒｋｓ， ２００９， ４ （ ７）： ６２２⁃６２９． ［ ９］ＮＧＵＹＥＮ Ｔ Ｔ Ｔ， ＡＲＭＩＴＡＧＥ Ｇ， ＢＲＡＮＣＨ Ｐ， ｅｔ ａｌ． Ｔｉｍｅ⁃ ｌｙ ａｎｄ ｃｏｎｔｉｎｕｏｕｓ ｍａｃｈｉｎｅ⁃ｌｅａｒｎｉｎｇ⁃ｂａｓｅｄ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ｆｏｒ ｉｎｔｅｒａｃｔｉｖｅ ＩＰ ｔｒａｆｆｉｃ ［ Ｊ］． ＩＥＥＥ／ ＡＣＭ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｎｅｔ⁃ ｗｏｒｋｉｎｇ， ２０１２， ２０（６）： １８８０⁃１８９４． ［１０］ＺＡＮＤＥＲ Ｓ， ＮＧＵＹＥＮ Ｔ， ＡＲＭＩＴＡＧＥ Ｇ． Ａｕｔｏｍａｔｅｄ ｔｒａｆ⁃ ｆｉｃ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ａｎｄ ａｐｐｌｉｃａｔｉｏｎ ｉｄｅｎｔｉｆｉｃａｔｉｏｎ ｕｓｉｎｇ ｍａ⁃ ｃｈｉｎｅ ｌｅａｒｎｉｎｇ ［ Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ＩＥＥＥ ｃｏｎｆｅｒｅｎｃｅ ｏｎ ｌｏｃａｌ ｃｏｍｐｕｔｅｒ ｎｅｔｗｏｒｋｓ ３０ｔｈ ａｎｎｉｖｅｒｓａｒｙ． Ｓｙｄｎｅｙ， ＮＳＷ， Ａｕｓｔｒａｌｉａ， ２００５： ２５０⁃２５７． ［１１］ＥＲＭＡＮ Ｊ， ＡＲＬＩＴＴ Ｍ， ＭＡＨＡＮＴＩ Ａ． Ｔｒａｆｆｉｃ ｃｌａｓｓｉｆｉｃａ⁃ ｔｉｏｎ ｕｓｉｎｇ ｃｌｕｓｔｅｒｉｎｇ ａｌｇｏｒｉｔｈｍｓ ［ Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ２００６ ＳＩＧＣＯＭＭ ｗｏｒｋｓｈｏｐ ｏｎ ｍｉｎｉｎｇ ｎｅｔｗｏｒｋ ｄａｔａ． Ｎｅｗ Ｙｏｒｋ， ＮＹ， ＵＳＡ， ２００６： ２８１⁃２８６． ［１２］ＲＯＳＥＮＢＬＡＴＴ Ｆ． Ｔｈｅ ｐｅｒｃｅｐｔｉｏｎ： ａ ｐｒｏｂａｂｉｌｉｓｔｉｃ ｍｏｄｅｌ ｆｏｒ ｉｎｆｏｒｍａｔｉｏｎ ｓｔｏｒａｇｅ ａｎｄ ｏｒｇａｎｉｚａｔｉｏｎ ｉｎ ｔｈｅ ｂｒａｉｎ［ Ｊ］． Ｐｓｙ⁃ ｃｈｏｌｏｇｉｃａｌ ｒｅｖｉｅｗ， １９５８， ６５（６）： ３８６⁃４０８． ［１３］ＣＲＡＭＭＥＲ Ｋ， ＤＥＫＥＬ Ｏ， ＫＥＳＨＥＴ Ｊ， ｅｔ ａｌ． Ｏｎｌｉｎｅ ｐａｓ⁃ ｓｉｖｅ⁃ａｇｇｒｅｓｓｉｖｅ ａｌｇｏｒｉｔｈｍｓ［Ｊ］． Ｊｏｕｒｎａｌ ｏｆ ｍａｃｈｉｎｅ ｌｅａｒｎｉｎｇ ｒｅｓｅａｒｃｈ， ２００６， ７（３）： ５５１⁃５８５． ［１４］ＣＥＳＡ⁃ＢＩＡＮＣＨＩ Ｎ， ＣＯＮＣＯＮＩ Ａ， ＧＥＮＴＩＬＥ Ｃ． Ａ ｓｅｃｏｎｄ⁃ ·３２６· 智 能 系 统 学 报 第 １１ 卷

第3期 易磊，等：在线学习的大规模网络流量分类研究 ·327. order perceptron algorithm[J].SIAM journal on compu- [21]LU Jing,HOI S C H,WANG Jialei,et al.Large scale on- ing,2005,34(3):640-668. line kernel learning[J].Journal of machine learning re- [15]CRAMMER K,DREDZE M,PEREIRA F.Exact convex search,2014,1:1-48 confidence-weighted learning[C]//Advances in neural in- 作者简介： formation processing systems 21.Mountain View,CA, 易磊，男，1991年生，硕士研究生， USA.2008:345-352. 主要研究方向为机器学习及其在大规 [16]CRAMMER K,KULESZA A,DREDZE M.Adaptive regu- 模网络流量分类中的应用。 larization of weight vectors[J].Machine learning,2013, 91(2)：:155-187. [17]WANG Jialei,ZHAO Peilin,HOI S C H.Exact soft confi- dence-weighted learning[C]//Proceedings of the 29th in- ternational conference on machine learning.Edinburgh, 潘志松.男.1973年生，教授，博士 Scotland,UK,2012. 生导师，江苏省计算机学会模式识别与 [18]ZINKEVICH M.Online convex programming and general- 人工智能专委会委员，主要研究方向为 ized infinitesimal gradient ascent[C]//Proceedings of the 模式识别、机器学习、网络安全。主持 international conference on machine learning.Washington, 国家科研项目多项，发表学术论文30 DC.USA,2003:928-936. 余篇。 [19]CESA-BIANCHI N,CONCONI A,GENTILE C.On the generalization ability of on-line learning algorithms[J]. 邱俊洋，男，1989年生，博士研究 IEEE transactions on information theory,2004,50(9): 生，主要研究方向为机器学习及其在大 2050-2057. 规模网络数据流异常检测中的应用，发 [20]HOI S C H,WANG Jialei,ZHAO Peilin.LIBOL:a li- 表学术论文2篇。 brary for online learning algorithms[J].Journal of machine learning research,2014,15(1):495-499

ｏｒｄｅｒ ｐｅｒｃｅｐｔｒｏｎ ａｌｇｏｒｉｔｈｍ ［ Ｊ］． ＳＩＡＭ ｊｏｕｒｎａｌ ｏｎ ｃｏｍｐｕ⁃ ｔｉｎｇ， ２００５， ３４（３）： ６４０⁃６６８． ［１５］ ＣＲＡＭＭＥＲ Ｋ， ＤＲＥＤＺＥ Ｍ， ＰＥＲＥＩＲＡ Ｆ． Ｅｘａｃｔ ｃｏｎｖｅｘ ｃｏｎｆｉｄｅｎｃｅ⁃ｗｅｉｇｈｔｅｄ ｌｅａｒｎｉｎｇ［Ｃ］ ／ ／ Ａｄｖａｎｃｅｓ ｉｎ ｎｅｕｒａｌ ｉｎ⁃ ｆｏｒｍａｔｉｏｎ ｐｒｏｃｅｓｓｉｎｇ ｓｙｓｔｅｍｓ ２１． Ｍｏｕｎｔａｉｎ Ｖｉｅｗ， ＣＡ， ＵＳＡ， ２００８： ３４５⁃３５２． ［１６］ＣＲＡＭＭＥＲ Ｋ， ＫＵＬＥＳＺＡ Ａ， ＤＲＥＤＺＥ Ｍ． Ａｄａｐｔｉｖｅ ｒｅｇｕ⁃ ｌａｒｉｚａｔｉｏｎ ｏｆ ｗｅｉｇｈｔ ｖｅｃｔｏｒｓ［ Ｊ］． Ｍａｃｈｉｎｅ ｌｅａｒｎｉｎｇ， ２０１３， ９１（２）： １５５⁃１８７． ［１７］ＷＡＮＧ Ｊｉａｌｅｉ， ＺＨＡＯ Ｐｅｉｌｉｎ， ＨＯＩ Ｓ Ｃ Ｈ． Ｅｘａｃｔ ｓｏｆｔ ｃｏｎｆｉ⁃ ｄｅｎｃｅ⁃ｗｅｉｇｈｔｅｄ ｌｅａｒｎｉｎｇ［Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ２９ｔｈ ｉｎ⁃ ｔｅｒｎａｔｉｏｎａｌ ｃｏｎｆｅｒｅｎｃｅ ｏｎ ｍａｃｈｉｎｅ ｌｅａｒｎｉｎｇ． Ｅｄｉｎｂｕｒｇｈ， Ｓｃｏｔｌａｎｄ， ＵＫ， ２０１２． ［１８］ ＺＩＮＫＥＶＩＣＨ Ｍ． Ｏｎｌｉｎｅ ｃｏｎｖｅｘ ｐｒｏｇｒａｍｍｉｎｇ ａｎｄ ｇｅｎｅｒａｌ⁃ ｉｚｅｄ ｉｎｆｉｎｉｔｅｓｉｍａｌ ｇｒａｄｉｅｎｔ ａｓｃｅｎｔ［Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ｉｎｔｅｒｎａｔｉｏｎａｌ ｃｏｎｆｅｒｅｎｃｅ ｏｎ ｍａｃｈｉｎｅ ｌｅａｒｎｉｎｇ． Ｗａｓｈｉｎｇｔｏｎ， ＤＣ， ＵＳＡ， ２００３： ９２８⁃９３６． ［１９］ ＣＥＳＡ⁃ＢＩＡＮＣＨＩ Ｎ， ＣＯＮＣＯＮＩ Ａ， ＧＥＮＴＩＬＥ Ｃ． Ｏｎ ｔｈｅ ｇｅｎｅｒａｌｉｚａｔｉｏｎ ａｂｉｌｉｔｙ ｏｆ ｏｎ⁃ｌｉｎｅ ｌｅａｒｎｉｎｇ ａｌｇｏｒｉｔｈｍｓ ［ Ｊ ］． ＩＥＥＥ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｉｎｆｏｒｍａｔｉｏｎ ｔｈｅｏｒｙ， ２００４， ５０ （ ９）： ２０５０⁃２０５７． ［２０］ＨＯＩ Ｓ Ｃ Ｈ， ＷＡＮＧ Ｊｉａｌｅｉ， ＺＨＡＯ Ｐｅｉｌｉｎ． ＬＩＢＯＬ： ａ ｌｉ⁃ ｂｒａｒｙ ｆｏｒ ｏｎｌｉｎｅ ｌｅａｒｎｉｎｇ ａｌｇｏｒｉｔｈｍｓ［Ｊ］． Ｊｏｕｒｎａｌ ｏｆ ｍａｃｈｉｎｅ ｌｅａｒｎｉｎｇ ｒｅｓｅａｒｃｈ， ２０１４， １５（１）： ４９５⁃４９９． ［２１］ＬＵ Ｊｉｎｇ， ＨＯＩ Ｓ Ｃ Ｈ， ＷＡＮＧ Ｊｉａｌｅｉ， ｅｔ ａｌ． Ｌａｒｇｅ ｓｃａｌｅ ｏｎ⁃ ｌｉｎｅ ｋｅｒｎｅｌ ｌｅａｒｎｉｎｇ ［ Ｊ］． Ｊｏｕｒｎａｌ ｏｆ ｍａｃｈｉｎｅ ｌｅａｒｎｉｎｇ ｒｅ⁃ ｓｅａｒｃｈ， ２０１４， １： １⁃４８． 作者简介： 易磊，男，１９９１ 年生，硕士研究生， 主要研究方向为机器学习及其在大规 模网络流量分类中的应用。 潘志松，男，１９７３ 年生，教授，博士 生导师，江苏省计算机学会模式识别与 人工智能专委会委员，主要研究方向为 模式识别、机器学习、网络安全。 主持 国家科研项目多项，发表学术论文 ３０ 余篇。 邱俊洋，男，１９８９ 年生，博士研究 生，主要研究方向为机器学习及其在大 规模网络数据流异常检测中的应用，发 表学术论文 ２ 篇。 第 ３ 期 易磊，等：在线学习的大规模网络流量分类研究 ·３２７·