【智能系统】PSO优化的六自由度机械臂全局快速终端滑模控制

第12卷第2期 智能系统学报 Vol.12 No.2 2017年4月 CAAI Transactions on Intelligent Systems Apr.2017 D0I:10.11992/is.201605024 网络出版地址：http://www.cmki.net/kcms/detail,/23.1538.tp.20170217.0954.004.html P$0优化的六自由度机械臂 全局快速终端滑模控制 王琥，胡立坤，谭颖 (广西大学电气工程学院，广西南宁530004)】 摘要：针对六自由度机械臂控制系统，提出一种基于粒子群优化(PS0)算法的全局快速终端滑模控制方法，以更大 程度地减小系统的抖振，提高系统的响应速度。对于机械臂多输入多输出的特点，为了方便设计，将系统划分为6个 二阶子系统，对各个关节进行设计，分析克服控制律的奇异性，同时运用Lyapunov理论证明系统的稳定性，并基于 PS0算法完成控制参数的优化。实验结果表明：优化后的控制方法不仅可以提高系统的快速性，还可以明显减小系 统的抖振，使系统具有良好的动静态性能。 关键词：自动控制技术：六自由度机械臂：李雅普诺夫理论；PS0算法；全局快速终端滑模；控制律：抖振 中图分类号：TP24文献标志码：A文章编号：1673-4785(2017)02-0266-06 中文引用格式：王琥，胡立坤，谭颖.PS0优化的六自由度机械臂全局快速终端滑模控制[J].智能系统学报，2017,12(2)：266- 271. 英文引用格式：WANG Hu,HULikun,TAN Ying..APSO-based global fast terminal sliding mode controller for6-DOF manipula- tors[J].CAAI transactions on intelligent systems,2017,12(2):266-271. A PSO-based global fast terminal sliding mode controller for 6-DOF manipulators WANG Hu,HU Likun,TAN Ying College of Electrical Engineering,Guangxi University,Nanning 530004,China) Abstract:In this paper,we propose a global fast terminal sliding mode (GFTSM)control method based on particle swarm optimization(PSO)for the 6-DOF (degrees of freedom)manipulator control system to reduce chattering and improve response times of the system.We divided the multi-input multi-output (MIMO)6-DOF system into six sec- ond-order subsystems,each joint designed and analyzed to overcome the singularity of control law.Further,we demonstrated the stability of our system using Lyapunov theory and optimized the control parameters based on the PSO algorithm.Our simulation results show that the optimized control method not only improves the speed and re- sponse times of the system,but also reduces the chattering,thus producing a system with good dynamics and static performance. Keywords:automatic control technology:6-DOF manipulator;Lyapunov theory;PSO algorithm;global fast termi- nal sliding mode;control law;chattering 随着德国工业4.0普及，机器人被广泛应用在 制问题的解决方法已有很多，如文献[1-4]提出的 各个领域，成为国内外学者关注的热点之一。其控 自适应鲁棒控制和模糊PID控制等。滑模被广泛 应用在机器人控制、电机控制、航天发动机等方面。 收稿日期：2016-05-24.网络出版日期：2017-02-17. 其原理主要为利用输入的控制信号不断做切换，使 基金项目：广西自然科学基金项目(2012 GXNSFBA053144). 通信作者：胡立坤.E-mail:hk3 email(@163.com. 得系统不断逼近预设好的滑模面，从而使误差逐渐

第 １２ 卷第 ２ 期 智 能 系 统 学 报 Ｖｏｌ．１２ №．２ ２０１７ 年 ４ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ａｐｒ． ２０１７ ＤＯＩ：１０．１１９９２ ／ ｔｉｓ．２０１６０５０２４ 网络出版地址：ｈｔｔｐ： ／ ／ ｗｗｗ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｅｔａｉｌ ／ ２３．１５３８．ｔｐ．２０１７０２１７．０９５４．００４．ｈｔｍｌ ＰＳＯ 优化的六自由度机械臂 全局快速终端滑模控制 王琥，胡立坤，谭颖 （广西大学 电气工程学院，广西 南宁 ５３０００４） 摘 要：针对六自由度机械臂控制系统，提出一种基于粒子群优化（ＰＳＯ）算法的全局快速终端滑模控制方法，以更大 程度地减小系统的抖振，提高系统的响应速度。 对于机械臂多输入多输出的特点，为了方便设计，将系统划分为 ６ 个 二阶子系统，对各个关节进行设计，分析克服控制律的奇异性，同时运用 Ｌｙａｐｕｎｏｖ 理论证明系统的稳定性，并基于 ＰＳＯ 算法完成控制参数的优化。 实验结果表明：优化后的控制方法不仅可以提高系统的快速性，还可以明显减小系 统的抖振，使系统具有良好的动静态性能。 关键词：自动控制技术；六自由度机械臂；李雅普诺夫理论；ＰＳＯ 算法；全局快速终端滑模；控制律；抖振 中图分类号： ＴＰ２４ 文献标志码：Ａ 文章编号：１６７３－４７８５（２０１７）０２－０２６６－０６ 中文引用格式：王琥，胡立坤，谭颖． ＰＳＯ 优化的六自由度机械臂全局快速终端滑模控制［ Ｊ］． 智能系统学报， ２０１７， １２（２）： ２６６－ ２７１． 英文引用格式：ＷＡＮＧ Ｈｕ， ＨＵ Ｌｉｋｕｎ， ＴＡＮ Ｙｉｎｇ． Ａ ＰＳＯ⁃ｂａｓｅｄ ｇｌｏｂａｌ ｆａｓｔ ｔｅｒｍｉｎａｌ ｓｌｉｄｉｎｇ ｍｏｄｅ ｃｏｎｔｒｏｌｌｅｒ ｆｏｒ ６⁃ＤＯＦ ｍａｎｉｐｕｌａ⁃ ｔｏｒｓ［Ｊ］． ＣＡＡＩ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｉｎｔｅｌｌｉｇｅｎｔ ｓｙｓｔｅｍｓ， ２０１７， １２（２）： ２６６－２７１． Ａ ＰＳＯ⁃ｂａｓｅｄ ｇｌｏｂａｌ ｆａｓｔ ｔｅｒｍｉｎａｌ ｓｌｉｄｉｎｇ ｍｏｄｅ ｃｏｎｔｒｏｌｌｅｒ ｆｏｒ ６⁃ＤＯＦ ｍａｎｉｐｕｌａｔｏｒｓ ＷＡＮＧ Ｈｕ， ＨＵ Ｌｉｋｕｎ， ＴＡＮ Ｙｉｎｇ （Ｃｏｌｌｅｇｅ ｏｆ Ｅｌｅｃｔｒｉｃａｌ Ｅｎｇｉｎｅｅｒｉｎｇ， Ｇｕａｎｇｘｉ Ｕｎｉｖｅｒｓｉｔｙ， Ｎａｎｎｉｎｇ ５３０００４， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｉｎ ｔｈｉｓ ｐａｐｅｒ， ｗｅ ｐｒｏｐｏｓｅ ａ ｇｌｏｂａｌ ｆａｓｔ ｔｅｒｍｉｎａｌ ｓｌｉｄｉｎｇ ｍｏｄｅ （ＧＦＴＳＭ） ｃｏｎｔｒｏｌ ｍｅｔｈｏｄ ｂａｓｅｄ ｏｎ ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ （ＰＳＯ） ｆｏｒ ｔｈｅ ６⁃ＤＯＦ （ｄｅｇｒｅｅｓ ｏｆ ｆｒｅｅｄｏｍ） ｍａｎｉｐｕｌａｔｏｒ ｃｏｎｔｒｏｌ ｓｙｓｔｅｍ ｔｏ ｒｅｄｕｃｅ ｃｈａｔｔｅｒｉｎｇ ａｎｄ ｉｍｐｒｏｖｅ ｒｅｓｐｏｎｓｅ ｔｉｍｅｓ ｏｆ ｔｈｅ ｓｙｓｔｅｍ． Ｗｅ ｄｉｖｉｄｅｄ ｔｈｅ ｍｕｌｔｉ⁃ｉｎｐｕｔ ｍｕｌｔｉ⁃ｏｕｔｐｕｔ （ＭＩＭＯ） ６⁃ＤＯＦ ｓｙｓｔｅｍ ｉｎｔｏ ｓｉｘ ｓｅｃ⁃ ｏｎｄ⁃ｏｒｄｅｒ ｓｕｂｓｙｓｔｅｍｓ， ｅａｃｈ ｊｏｉｎｔ ｄｅｓｉｇｎｅｄ ａｎｄ ａｎａｌｙｚｅｄ ｔｏ ｏｖｅｒｃｏｍｅ ｔｈｅ ｓｉｎｇｕｌａｒｉｔｙ ｏｆ ｃｏｎｔｒｏｌ ｌａｗ． Ｆｕｒｔｈｅｒ， ｗｅ ｄｅｍｏｎｓｔｒａｔｅｄ ｔｈｅ ｓｔａｂｉｌｉｔｙ ｏｆ ｏｕｒ ｓｙｓｔｅｍ ｕｓｉｎｇ Ｌｙａｐｕｎｏｖ ｔｈｅｏｒｙ ａｎｄ ｏｐｔｉｍｉｚｅｄ ｔｈｅ ｃｏｎｔｒｏｌ ｐａｒａｍｅｔｅｒｓ ｂａｓｅｄ ｏｎ ｔｈｅ ＰＳＯ ａｌｇｏｒｉｔｈｍ． Ｏｕｒ ｓｉｍｕｌａｔｉｏｎ ｒｅｓｕｌｔｓ ｓｈｏｗ ｔｈａｔ ｔｈｅ ｏｐｔｉｍｉｚｅｄ ｃｏｎｔｒｏｌ ｍｅｔｈｏｄ ｎｏｔ ｏｎｌｙ ｉｍｐｒｏｖｅｓ ｔｈｅ ｓｐｅｅｄ ａｎｄ ｒｅ⁃ ｓｐｏｎｓｅ ｔｉｍｅｓ ｏｆ ｔｈｅ ｓｙｓｔｅｍ， ｂｕｔ ａｌｓｏ ｒｅｄｕｃｅｓ ｔｈｅ ｃｈａｔｔｅｒｉｎｇ， ｔｈｕｓ ｐｒｏｄｕｃｉｎｇ ａ ｓｙｓｔｅｍ ｗｉｔｈ ｇｏｏｄ ｄｙｎａｍｉｃｓ ａｎｄ ｓｔａｔｉｃ ｐｅｒｆｏｒｍａｎｃｅ． Ｋｅｙｗｏｒｄｓ： ａｕｔｏｍａｔｉｃ ｃｏｎｔｒｏｌ ｔｅｃｈｎｏｌｏｇｙ； ６⁃ＤＯＦ ｍａｎｉｐｕｌａｔｏｒ； Ｌｙａｐｕｎｏｖ ｔｈｅｏｒｙ； ＰＳＯ ａｌｇｏｒｉｔｈｍ； ｇｌｏｂａｌ ｆａｓｔ ｔｅｒｍｉ⁃ ｎａｌ ｓｌｉｄｉｎｇ ｍｏｄｅ； ｃｏｎｔｒｏｌ ｌａｗ； ｃｈａｔｔｅｒｉｎｇ 收稿日期：２０１６－０５－２４． 网络出版日期：２０１７－０２－１７． 基金项目：广西自然科学基金项目（２０１２ＧＸＮＳＦＢＡ０５３１４４）． 通信作者：胡立坤． Ｅ⁃ｍａｉｌ：ｈｌｋ３ｅｍａｉｌ＠ １６３．ｃｏｍ． 随着德国工业 ４．０ 普及，机器人被广泛应用在 各个领域，成为国内外学者关注的热点之一。 其控 制问题的解决方法已有很多，如文献［１－４］提出的 自适应鲁棒控制和模糊 ＰＩＤ 控制等。 滑模被广泛 应用在机器人控制、电机控制、航天发动机等方面。 其原理主要为利用输入的控制信号不断做切换，使 得系统不断逼近预设好的滑模面，从而使误差逐渐

第2期 王琥，等：基于PS0优化的六自由度机械臂全局快速终端滑模控制 ·267. 减小。文献[5]提出了一种积分次优化的二阶滑 G(0)∈Rx1代表重力加速度矩阵。r(0)代表各个 模，利用其在三自由度的工业机器人上的轨迹跟踪， 关节的输入力矩矢量。当机械臂处于非高速运动状 并与典型的PD控制器、次优化的二阶滑模三者进 态时，式(1)中的离心力和哥氏力对机械臂系统几 行比较。文献[6]利用非线性阻尼和终端滑模对机 乎不产生任何影响，因此，是可以完全忽略不计 械手进行控制，使其稳定性得于提高：文献[7]利用 的]，即式(1)可以简化为 高阶滑模对单自由度机械手进行控制：文献[8]提 M(0)0+G(0)=r(t) (2) 出了融合自适应模糊算法和滑模，对机器人进行控 由于六自由度机器人具有MMO特性，为了实 制，提高了被控系统的鲁棒性。然而，传统滑模的控 现对其控制的目标，将其分解成单关节的子系统，由 制机理是在不同的控制逻辑之间来回切换，因此，势 式(2)可有 必存在时间滞后、空间滞后、系统惯性等因素，导致 0=M(0)(r(t)-G(0)) (3) 被控系统容易出现抖振现象。抖振的存在，使得系 统状态在平衡状态之间来回切换，导致被控系统出 a16 现跟踪误差。工业机器人控制对于精确性有着严苛 : (4) 的要求，对于末端执行器的跟踪误差应达到工业要 a61 求，否则会降低被控系统的准确度。当跟踪误差过 由式(3)、(4)可得单关节的角加速度为 大时，甚至会激发高频未建模态，使工业机器人处于 6 不受控状态。近年来，诸多学者针对抖振现象提出 0:=amT:+ (agr-aG)-aaG (5) j=1*i 了不同的改进方法，从而有效的减小被控系统的抖 式中G:为i轴的重力加速度，i=1,2,…,6。 振问题，主要包括趋近律方法，观测方法，智能控制 令： 方法，动态滑模方法等。在人工智能迅速崛起的基 x1=0 础上，大多的学者主要采用智能控制与不同形式的 x2=0 滑模相结合的控制方法，如文献[9]提出的改进神 经网络自适应滑模控制；文章[10-11]采用基于智 )=2(a5-a,G)-aG j=1j-i 能算法(GA,PSO)的滑模控制。全局快速终端滑模 g(x）=aa 是在传统滑模的基础上引入非线性函数，既保证了 则有 系统在有限时间内到达滑模面，又使得系统在有限 时间内达到平衡点时，误差可以快速收敛至零，达到 1=X2 (6) 全局快速收敛的目的。具有减小系统抖振，提高系 x3=f八x)+g(x)r 统动静态的优点。 式中：f(x)g(x)为R域中光滑的连续函数。 为了提高系统的响应速度和减小系统抖振等动 如式(6)所示的二阶非线性方程即表示为六自 静态性能，本文提出一种基于P$0优化的全局快速 由度机械臂的各个关节子系统。此法好处在于将六 终端滑模的六自由度机器臂控制，分析与克服全局 自由度机械臂模型转换成相互独立的子系统，方便 快速终端滑模的奇异性，给出了系统的响应时间，并 后期的设计与优化。 通过仿真和实验两方面验证该控制策略的准确性和 1.2滑模控制器设计 可行性。 设单关节的常规全局快速终端滑模控制器的滑 模面函数为 1机械臂滑模控制系统 s:=e:ae:+Be (7) 1.1六自由度机械臂数学模型 式中p<q且都为互质的正奇数，取值分别为：P= 利用Euler-Lagrange方法，不考虑外部未知干扰 3,g-5,i=1,2,…,6,e为误差信号]，即有 力作用，在关节坐标中建立六自由度机械臂的动力 e:=0°(t)-0(t) 学模型如下： e=0(t)-0.(t) (8) M(0)0+C(0,0)0+G(0)=r(t)(1) e:=0(t)-0.(t) 式中：0、0、0∈Rx1分别代表关节角度、角速度、角 由式(7)求导可得 加速度矢量：M(0)∈R6x6代表正定对称惯性矩 (9) 阵，C(0,0)∈Rx1代表离心力和哥氏力矢量， 5,=e+a,+B,·Pee,p-g/9 9

减小。 文献［５］ 提出了一种积分次优化的二阶滑 模，利用其在三自由度的工业机器人上的轨迹跟踪， 并与典型的 ＰＤ 控制器、次优化的二阶滑模三者进 行比较。 文献［６］利用非线性阻尼和终端滑模对机 械手进行控制，使其稳定性得于提高；文献［７］利用 高阶滑模对单自由度机械手进行控制；文献［８］ 提 出了融合自适应模糊算法和滑模，对机器人进行控 制，提高了被控系统的鲁棒性。 然而，传统滑模的控 制机理是在不同的控制逻辑之间来回切换，因此，势 必存在时间滞后、空间滞后、系统惯性等因素，导致 被控系统容易出现抖振现象。 抖振的存在，使得系 统状态在平衡状态之间来回切换，导致被控系统出 现跟踪误差。 工业机器人控制对于精确性有着严苛 的要求，对于末端执行器的跟踪误差应达到工业要 求，否则会降低被控系统的准确度。 当跟踪误差过 大时，甚至会激发高频未建模态，使工业机器人处于 不受控状态。 近年来，诸多学者针对抖振现象提出 了不同的改进方法，从而有效的减小被控系统的抖 振问题，主要包括趋近律方法，观测方法，智能控制 方法，动态滑模方法等。 在人工智能迅速崛起的基 础上，大多的学者主要采用智能控制与不同形式的 滑模相结合的控制方法，如文献［９］提出的改进神 经网络自适应滑模控制；文章［１０－１１］采用基于智 能算法（ＧＡ，ＰＳＯ）的滑模控制。 全局快速终端滑模 是在传统滑模的基础上引入非线性函数，既保证了 系统在有限时间内到达滑模面，又使得系统在有限 时间内达到平衡点时，误差可以快速收敛至零，达到 全局快速收敛的目的。 具有减小系统抖振，提高系 统动静态的优点。 为了提高系统的响应速度和减小系统抖振等动 静态性能，本文提出一种基于 ＰＳＯ 优化的全局快速 终端滑模的六自由度机器臂控制，分析与克服全局 快速终端滑模的奇异性，给出了系统的响应时间，并 通过仿真和实验两方面验证该控制策略的准确性和 可行性。 １ 机械臂滑模控制系统 １．１ 六自由度机械臂数学模型 利用 Ｅｕｌｅｒ⁃Ｌａｇｒａｎｇｅ 方法，不考虑外部未知干扰 力作用，在关节坐标中建立六自由度机械臂的动力 学模型如下： Ｍ（θ）θ ¨ ＋ Ｃ（θ，θ · ）θ · ＋ Ｇ（θ） ＝ τ（ｔ） （１） 式中： θ、θ · 、θ ¨ ∈ Ｒ ６×１ 分别代表关节角度、角速度、角 加速度矢量； Ｍ（θ） ∈ Ｒ ６×６ 代表正定对称惯性矩 阵， Ｃ（θ，θ · ） ∈ Ｒ ６×１ 代表离心力和哥氏力矢量， Ｇ（θ） ∈ Ｒ ６×１ 代表重力加速度矩阵。 τ（θ） 代表各个 关节的输入力矩矢量。 当机械臂处于非高速运动状 态时，式（１）中的离心力和哥氏力对机械臂系统几 乎不产生任何影响， 因此， 是可以完全忽略不计 的［１２］ ，即式（１）可以简化为 Ｍ（θ）θ ¨ ＋ Ｇ（θ） ＝ τ（ｔ） （２） 由于六自由度机器人具有 ＭＩＭＯ 特性，为了实 现对其控制的目标，将其分解成单关节的子系统，由 式（２）可有 θ ¨ ＝ Ｍ －１ （θ）（τ（ｔ） － Ｇ（θ）） （３） 令 Ｍ －１ ＝ ａ１１ … ａ１６ ︙ ︙ ａ６１ … ａ６６ é ë ê ê êê ù û ú ú úú （４） 由式（３）、（４）可得单关节的角加速度为 θ ¨ ｉ ＝ ａｉｉτｉ ＋ ∑ ６ ｊ ＝ １，ｊ≠ｉ （ａｉｊτｊ － ａｉｊＧｊ） － ａｉｉＧｉ （５） 式中 Ｇｉ 为 ｉ 轴的重力加速度， ｉ ＝ １，２，…，６。 令： ｘ１ ＝ θｉ ｘ２ ＝ θ · ｉ ｆ（ｘ） ＝ ∑ ６ ｊ ＝ １，ｊ≠ｉ （ａｉｊτｊ － ａｉｊＧｊ） － ａｉｉＧｉ ｇ（ｘ） ＝ ａｉｉ ì î í ï ï ïï ï ï ï 则有 ｘ · １ ＝ ｘ２ ｘ · ２ { ＝ ｆ（ｘ） ＋ ｇ（ｘ）τ ｉ （６） 式中： ｆ（ｘ）、ｇ（ｘ） 为 Ｒ 域中光滑的连续函数。 如式（６）所示的二阶非线性方程即表示为六自 由度机械臂的各个关节子系统。 此法好处在于将六 自由度机械臂模型转换成相互独立的子系统，方便 后期的设计与优化。 １．２ 滑模控制器设计 设单关节的常规全局快速终端滑模控制器的滑 模面函数为 ｓｉ ＝ ｅ · ｉ ＋ αｉ ｅｉ ＋ βｉ ｅ ｐ ／ ｑ ｉ （７） 式中 ｐ ＜ ｑ 且都为互质的正奇数，取值分别为： ｐ ＝ ３，ｑ ＝ ５，ｉ ＝ １，２，…，６， ｅｉ 为误差信号［１３］ ，即有 ｅｉ ＝ θｉ ∗ （ｔ） － θｉ（ｔ） ｅ · ｉ ＝ θ · ｉ ∗ （ｔ） － θ · ｉ（ｔ） ｅ ¨ ｉ ＝ θ ¨ ｉ ∗ （ｔ） － θ ¨ ｉ（ｔ） ì î í ï ï ï ï （８） 由式（７）求导可得 ｓ · ｉ ＝ ｅ ¨ ｉ ＋ αｉ ｅ · ｉ ＋ βｉ· ｐ ｑ ｅ · ｉ ｅｉ ｐ － ｑ ／ ｑ （９） 第 ２ 期 王琥，等：基于 ＰＳＯ 优化的六自由度机械臂全局快速终端滑模控制 ·２６７·

·268 智能系统学报 第12卷 由式(6)、(8)、(9)可得 2PS0优化机械臂滑模控制系统 =0:-fx)-g(x)T+ae+BLe PSO算法是Kennedy博士和Eberhart博士通过 (10) 对鸟群觅食的集体协作行为的研究，于20世纪90 故此选取位置控制规律为 年代首次提出的计算优化算法。该算法是基于群体 T:=(8-f八x)+a,e:+ 迭代，追求解空间中的最优粒子，具有简单易实现、 B.·Pe,+h(s)/g(x) 收敛速度快、全局搜索能力强等优点，适用于科研以 (11) 及工程应用。算法的搜索机制可描述为，以解空间 式中h为指数趋近律，定义为 中的任意一点为出发点，基于设定的适应度函数为 h(s)=s;+Yis;n/m,n =3,m=5 (12) 个体最优解保留标准，通过群体的更新迭代，寻求出 由位置控制律式(11)可知，当系统的状态接近 解空间中的最优解。假设，问题的解空间为D维， 至设定值时，即e≈0之时，因为p-q/g<0,则 初始的粒子群体规模为，以初始种群中的一点为 e-接近于无穷大，及证明式(11)存在奇异问题。 寻求解的出发点，以适应度函数为评价标准，通过粒 在实际的控制中，奇异的存在容易被控系统失调。 子迭代更新，寻求出个体极值以及全局最优值。粒 为了克服奇异问题，选取滑模面为 子的迭代更新规则如下所示。 s:=ei+ae:+Be:q/p (13) +=w·+c(p-X)+ 同理，可得控制律为 car2(S-X) (19) T:=(0-f八x)+a,e:+ X+=X++ B.·9e,egn+h(s)/g(x) 式中：k为迭代次数，w为惯性权重，c1c2分别为局 (14) 部学习因子和全局学习因子。随机数11,12∈[0， 通过解方程(7)s:=0得，系统滑动模态上任意 1]。p为个体极值，S,为当前整种群最优值。 状态e,(0)≠0至平衡状态的时间为 基于PSO优化的全局快速终端滑模控制的六 4.=Pn&e(0)p-9)p+B (15) 自由度工业机械臂系统如图1所示。由图1可知， x(P-q) B 以六自由度机械臂的各个关节的角度和其输入的控 通过解h(s)=0得，系统从状态空间任意一点 制量作为PS0的输人项，通过迭代优化，调整α：、 到达滑动模态上的时间为 B:、P:y:参数，从而达到改善系统性能的目的。 m In 9s (0)m n/m +y: aB t,= (16) PSO优化 i(m-n) Y s=e+ae+Ber 0, 由式(15)、(16)可知，单关节系统的响应时间 由到达时间和滑模运动时间决定；时间参数与α：、 全局快速终端 6-DIF B:、y:、P:4个参数息息相关，因此对于控制律参数 滑模控制 机械臂 的优化有重要的意义。 为了使滑模面在被控系统发生滑动模式，则必 图1基于PS0优化的全局快速终端滑模控制系统 须满足Lyapunov稳定性。证明如下。选取Lya- Fig.1 Controlled 6-DOF manipulator via PSO-GFTSM punov函数为 为保证被控系统拥有良好的动静态性能，同时 V=s2/2 (17) 防止系统控制量的输出过大。因此，PS0优化的最 则有 小目标函数的参数选定为：误差的绝对值的时间积 V=s 5i (18) 分和系统控制量输出的平方，参照文献[13]，单关 综合式(7)、(8)、(13)、(14)有 节最优目标函数定为 =-s·h(s)= J(t)=J(@:le.(t)+:(t))dt+st -s:·(9:+Ysm)=-(9+y+mm) 式中：w1、ω2w3为权重系数，e,(t)为i关节的跟踪 因为m,n互质奇数，则m+n为偶数，参数p、y: 误差，t为i关节上升时间。同时，为了避免超调对 为大于零的实数，即可得V<0,所以系统是稳定的。 系统的影响，在优化函数中加入惩罚函数，即当系统 出现超调σ，时，改写为

由式（６）、（８）、（９）可得 ｓ · ｉ ＝ θ ¨ ∗ ｉ － ｆ（ｘ） － ｇ（ｘ）τｉ ＋ αｉ ｅ · ｉ ＋ βｉ· ｐ ｑ ｅ · ｉ ｅ ｐ－ｑ ／ ｑ ｉ （１０） 故此选取位置控制规律为 τｉ ＝ （θ ¨ ∗ ｉ － ｆ（ｘ） ＋ αｉ ｅ · ｉ ＋ βｉ· ｐ ｑ ｅ · ｉ ｅ ｐ－ｑ ／ ｑ ｉ ＋ ｈ（ｓ）） ／ ｇ（ｘ） （１１） 式中 ｈ 为指数趋近律，定义为 ｈ（ｓ） ＝ φｉ ｓｉ ＋ γｉ ｓｉ ｎ ／ ｍ，ｎ ＝ ３，ｍ ＝ ５ （１２） 由位置控制律式（１１）可知，当系统的状态接近 至设定值时，即 ｅ ≈ ０ 之时，因为 ｐ － ｑ ／ ｑ ＜ ０，则 ｅ ｐ－ｑ ／ ｑ 接近于无穷大，及证明式（１１）存在奇异问题。 在实际的控制中，奇异的存在容易被控系统失调。 为了克服奇异问题，选取滑模面为 ｓｉ ＝ ｅ · ｉ ＋ αｉ ｅｉ ＋ βｉ ｅｉ ｑ ／ ｐ （１３） 同理，可得控制律为 τｉ ＝ （θ ¨ ∗ ｉ － ｆ（ｘ） ＋ αｉ ｅ · ｉ ＋ βｉ· ｑ ｐ ｅ · ｉ ｅ ｑ－ｐ ／ ｐ ｉ ＋ ｈ（ｓ）） ／ ｇ（ｘ） （１４） 通过解方程（７） ｓｉ ＝ ０ 得，系统滑动模态上任意 状态 ｅｉ（０） ≠ ０ 至平衡状态的时间为 ｔ ｓ ＝ ｐ αｉ（ｐ － ｑ） ｌｎ αｉ ｅｉ （０）（ｐ － ｑ） ／ ｐ ＋ βｉ βｉ （１５） 通过解 ｈ（ｓ） ＝ ０ 得，系统从状态空间任意一点 到达滑动模态上的时间为 ｔ ｒ ＝ ｍ φｉ（ｍ － ｎ） ｌｎ φｉ ｓｉ （０）ｍ － ｎ ／ ｍ ＋ γｉ γｉ （１６） 由式（１５）、（１６）可知，单关节系统的响应时间 由到达时间和滑模运动时间决定；时间参数与 αｉ、 βｉ、γｉ、φｉ ４ 个参数息息相关，因此对于控制律参数 的优化有重要的意义。 为了使滑模面在被控系统发生滑动模式，则必 须满足 Ｌｙａｐｕｎｏｖ 稳定性。 证明如下。 选取 Ｌｙａ⁃ ｐｕｎｏｖ 函数为 Ｖ ＝ ｓｉ ２ ／ ２ （１７） 则有 Ｖ · ＝ ｓｉ ｓ · ｉ （１８） 综合式（７）、（８）、（１３）、（１４）有 Ｖ · ＝ － ｓｉ·ｈ（ｓ） ＝ － ｓｉ·（φｉ ｓｉ ＋ γｉ ｓ ｎ／ ｍ ｉ ） ＝ － （φｉ ｓ ２ ｉ ＋ γｉ ｓ ｎ＋ｍ／ ｍ ｉ ） 因为 ｍ、ｎ 互质奇数，则 ｍ ＋ ｎ 为偶数，参数 φ、γｉ 为大于零的实数，即可得 Ｖ · ＜ ０，所以系统是稳定的。 ２ ＰＳＯ 优化机械臂滑模控制系统 ＰＳＯ 算法是 Ｋｅｎｎｅｄｙ 博士和 Ｅｂｅｒｈａｒｔ 博士通过 对鸟群觅食的集体协作行为的研究，于 ２０ 世纪 ９０ 年代首次提出的计算优化算法。 该算法是基于群体 迭代，追求解空间中的最优粒子，具有简单易实现、 收敛速度快、全局搜索能力强等优点，适用于科研以 及工程应用。 算法的搜索机制可描述为，以解空间 中的任意一点为出发点，基于设定的适应度函数为 个体最优解保留标准，通过群体的更新迭代，寻求出 解空间中的最优解。 假设，问题的解空间为 Ｄ 维， 初始的粒子群体规模为 ｎ， 以初始种群中的一点为 寻求解的出发点，以适应度函数为评价标准，通过粒 子迭代更新，寻求出个体极值以及全局最优值。 粒 子的迭代更新规则如下所示。 Ｖ ｋ＋１ ｉ ＝ ω·Ｖ ｋ ｉ ＋ ｃ１ ｒ１（ｐ ｋ ｉ － Ｘ ｋ ｉ ） ＋ ｃ２ ｒ２（Ｓ ｋ ｉ － Ｘ ｋ ｉ ） Ｘ ｋ＋１ ｉ ＝ Ｘ ｋ ｉ ＋ Ｖ ｋ＋１ ｉ （１９） 式中：ｋ 为迭代次数， ω 为惯性权重， ｃ１ 、ｃ２ 分别为局 部学习因子和全局学习因子。 随机数 ｒ１ ，ｒ２ ∈ ［０， １］ 。 ｐ 为个体极值， Ｓｉ 为当前整种群最优值。 基于 ＰＳＯ 优化的全局快速终端滑模控制的六 自由度工业机械臂系统如图 １ 所示。 由图 １ 可知， 以六自由度机械臂的各个关节的角度和其输入的控 制量作为 ＰＳＯ 的输入项，通过迭代优化，调整 αｉ、 βｉ、φｉ、γｉ 参数，从而达到改善系统性能的目的。 图 １ 基于 ＰＳＯ 优化的全局快速终端滑模控制系统 Ｆｉｇ．１ Ｃｏｎｔｒｏｌｌｅｄ ６⁃ＤＯＦ ｍａｎｉｐｕｌａｔｏｒ ｖｉａ ＰＳＯ⁃ＧＦＴＳＭ 为保证被控系统拥有良好的动静态性能，同时 防止系统控制量的输出过大。 因此，ＰＳＯ 优化的最 小目标函数的参数选定为：误差的绝对值的时间积 分和系统控制量输出的平方，参照文献［１３］，单关 节最优目标函数定为 Ｊｉ（ｔ） ＝ ∫ ¥ ０ （ω１ ｅｉ（ｔ） ＋ ω２ τ ２ ｉ （ｔ））ｄｔ ＋ ω３ ｔ ｉｕ 式中： ω１ 、ω２ 、ω３ 为权重系数， ｅｉ（ｔ） 为 ｉ 关节的跟踪 误差， ｔ ｉｕ 为 ｉ 关节上升时间。 同时，为了避免超调对 系统的影响，在优化函数中加入惩罚函数，即当系统 出现超调 σｉ 时，改写为 ·２６８· 智 能 系 统 学 报 第 １２ 卷

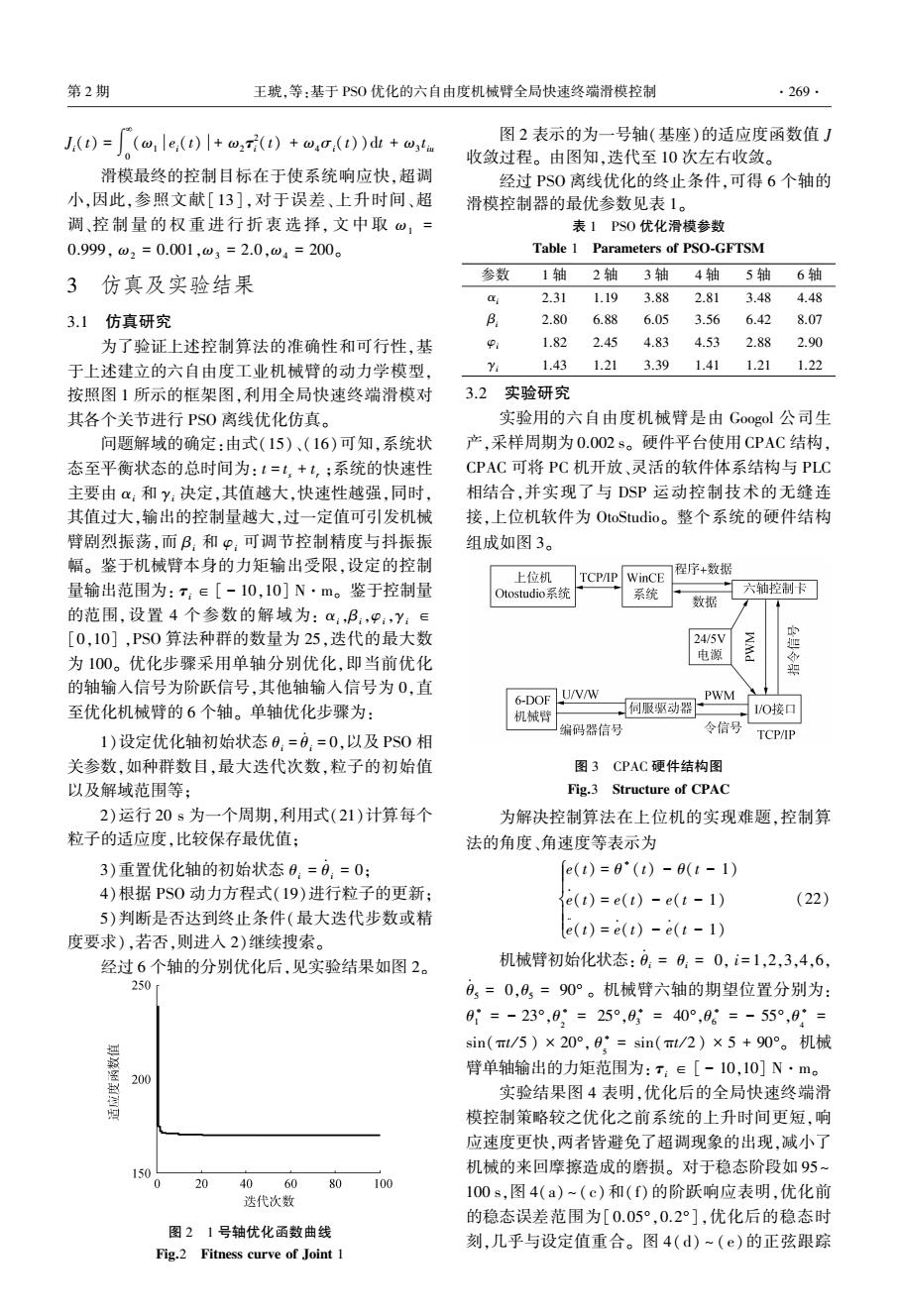
第2期 王琥，等：基于PS0优化的六自由度机械臂全局快速终端滑模控制 ·269. J)=(@.le.(t)+()+.()dt+ 图2表示的为一号轴（基座）的适应度函数值J 收敛过程。由图知，迭代至10次左右收敛。 滑模最终的控制目标在于使系统响应快，超调 经过PS0离线优化的终止条件，可得6个轴的 小，因此，参照文献[13]，对于误差、上升时间、超 滑模控制器的最优参数见表1。 调、控制量的权重进行折衷选择，文中取ω，= 表1PS0优化滑模参数 0.999,w2=0.001,w3=2.0,w4=200。 Table 1 Parameters of PSO-GFTSM 3仿真及实验结果 参数 1轴 2轴3轴4轴 5轴6轴 2.311.193.88 2.813.48 4.48 3.1仿真研究 B 2.80 6.88 6.05 3.56 6.42 8.07 为了验证上述控制算法的准确性和可行性，基 9 1.82 2.45 4.83 4.53 2.88 2.90 于上述建立的六自由度工业机械臂的动力学模型， 之 1.43 1.21 3.39 1.41 1.21 1.22 按照图1所示的框架图，利用全局快速终端滑模对 3.2实验研究 其各个关节进行PS0离线优化仿真。 实验用的六自由度机械臂是由Googol公司生 问题解域的确定：由式(15)、(16)可知，系统状 产，采样周期为0.002s。硬件平台使用CPAC结构， 态至平衡状态的总时间为：1=1，+1，；系统的快速性 CPAC可将PC机开放、灵活的软件体系结构与PLC 主要由α：和y:决定，其值越大，快速性越强，同时， 相结合，并实现了与DSP运动控制技术的无缝连 其值过大，输出的控制量越大，过一定值可引发机械 接，上位机软件为OtoStudio。整个系统的硬件结构 臂剧烈振荡，而B,和P:可调节控制精度与抖振振 组成如图3。 幅。鉴于机械臂本身的力矩输出受限，设定的控制 上位机 程序+数据 TCP/IP WinCE 量输出范围为：T;∈[-10,10]N·m。鉴于控制量 Otostudio系统 系统 六轴控制卡 数据 的范围，设置4个参数的解域为：：，B:,P,Y:∈ [0,10],PS0算法种群的数量为25，迭代的最大数 24/5V 的 为100。优化步骤采用单轴分别优化，即当前优化 电源 的轴输入信号为阶跃信号，其他轴输入信号为0，直 6-D0F U/V/W PWM 至优化机械臂的6个轴。单轴优化步骤为： 机械臂 口伺服驱动器 I/O接▣ 编码器信号 令信号 1)设定优化轴初始状态8，=0，=0，以及PS0相 TCP/IP 关参数，如种群数目，最大迭代次数，粒子的初始值 图3CPAC硬件结构图 以及解域范围等； Fig.3 Structure of CPAC 2)运行20s为一个周期，利用式(21)计算每个 为解决控制算法在上位机的实现难题，控制算 粒子的适应度，比较保存最优值： 法的角度、角速度等表示为 3)重置优化轴的初始状态0，=0：=0： e(t)=0'(t)-9(t-1) 4)根据PS0动力方程式(19)进行粒子的更新： e(t)=e(t)-e(t-1) (22) 5)判断是否达到终止条件（最大迭代步数或精 e(t)=e(t)-e(t-1) 度要求)，若否，则进入2)继续搜索。 经过6个轴的分别优化后，见实验结果如图2。 机械臂初始化状态：0=0：=0，i=1,2,3,4,6, 250 0,=0,0=90°。机械臂六轴的期望位置分别为： 01=-23°，0，=25°，03=40°，06=-55°，0= sin(Tt/5)×20°，0=sin(rt/2)×5+90°。机械 200 臂单轴输出的力矩范围为：T:∈[-10,10]N·m。 实验结果图4表明，优化后的全局快速终端滑 模控制策略较之优化之前系统的上升时间更短，响 应速度更快，两者皆避免了超调现象的出现，减小了 150 机械的来回摩擦造成的磨损。对于稳态阶段如95~ 0 20 4060 80 100 100s,图4(a)~(c)和(f)的阶跃响应表明，优化前 迭代次数 的稳态误差范围为[0.05°，0.2°]，优化后的稳态时 图21号轴优化函数曲线 刻，几乎与设定值重合。图4(d)~(e)的正弦跟踪 Fig.2 Fitness curve of Joint 1

Ｊｉ（ｔ） ＝ ∫ ¥ ０ （ω１ ｅｉ（ｔ） ＋ ω２ τ ２ ｉ （ｔ） ＋ ω４σｉ（ｔ））ｄｔ ＋ ω３ ｔ ｉｕ 滑模最终的控制目标在于使系统响应快，超调 小，因此，参照文献［ １３］，对于误差、上升时间、超 调、控 制 量 的 权 重 进 行 折 衷 选 择， 文 中 取 ω１ ＝ ０．９９９， ω２ ＝ ０．００１，ω３ ＝ ２．０，ω４ ＝ ２００。 ３ 仿真及实验结果 ３．１ 仿真研究 为了验证上述控制算法的准确性和可行性，基 于上述建立的六自由度工业机械臂的动力学模型， 按照图 １ 所示的框架图，利用全局快速终端滑模对 其各个关节进行 ＰＳＯ 离线优化仿真。 问题解域的确定：由式（１５）、（１６）可知，系统状 态至平衡状态的总时间为： ｔ ＝ ｔ ｓ ＋ ｔ ｒ ；系统的快速性 主要由 αｉ 和 γｉ 决定，其值越大，快速性越强，同时， 其值过大，输出的控制量越大，过一定值可引发机械 臂剧烈振荡，而 βｉ 和 φｉ 可调节控制精度与抖振振 幅。 鉴于机械臂本身的力矩输出受限，设定的控制 量输出范围为： τｉ ∈ ［ － １０，１０］ Ｎ·ｍ。 鉴于控制量 的范围，设置 ４ 个参数的解域为： αｉ，βｉ，φｉ，γｉ ∈ ［０，１０］ ，ＰＳＯ 算法种群的数量为 ２５，迭代的最大数 为 １００。 优化步骤采用单轴分别优化，即当前优化 的轴输入信号为阶跃信号，其他轴输入信号为 ０，直 至优化机械臂的 ６ 个轴。 单轴优化步骤为： １）设定优化轴初始状态 θｉ ＝ θ · ｉ ＝ ０，以及 ＰＳＯ 相 关参数，如种群数目，最大迭代次数，粒子的初始值 以及解域范围等； ２）运行 ２０ ｓ 为一个周期，利用式（２１）计算每个 粒子的适应度，比较保存最优值； ３）重置优化轴的初始状态 θｉ ＝ θ · ｉ ＝ ０； ４）根据 ＰＳＯ 动力方程式（１９）进行粒子的更新； ５）判断是否达到终止条件（最大迭代步数或精 度要求），若否，则进入 ２）继续搜索。 经过 ６ 个轴的分别优化后，见实验结果如图 ２。 图 ２ １ 号轴优化函数曲线 Ｆｉｇ．２ Ｆｉｔｎｅｓｓ ｃｕｒｖｅ ｏｆ Ｊｏｉｎｔ １ 图 ２ 表示的为一号轴（基座）的适应度函数值 Ｊ 收敛过程。 由图知，迭代至 １０ 次左右收敛。 经过 ＰＳＯ 离线优化的终止条件，可得 ６ 个轴的 滑模控制器的最优参数见表 １。 表 １ ＰＳＯ 优化滑模参数 Ｔａｂｌｅ １ Ｐａｒａｍｅｔｅｒｓ ｏｆ ＰＳＯ⁃ＧＦＴＳＭ 参数 １ 轴 ２ 轴 ３ 轴 ４ 轴 ５ 轴 ６ 轴 αｉ ２．３１ １．１９ ３．８８ ２．８１ ３．４８ ４．４８ βｉ ２．８０ ６．８８ ６．０５ ３．５６ ６．４２ ８．０７ φｉ １．８２ ２．４５ ４．８３ ４．５３ ２．８８ ２．９０ γｉ １．４３ １．２１ ３．３９ １．４１ １．２１ １．２２ ３．２ 实验研究 实验用的六自由度机械臂是由 Ｇｏｏｇｏｌ 公司生 产，采样周期为 ０．００２ ｓ。 硬件平台使用 ＣＰＡＣ 结构， ＣＰＡＣ 可将 ＰＣ 机开放、灵活的软件体系结构与 ＰＬＣ 相结合，并实现了与 ＤＳＰ 运动控制技术的无缝连 接，上位机软件为 ＯｔｏＳｔｕｄｉｏ。 整个系统的硬件结构 组成如图 ３。 图 ３ ＣＰＡＣ 硬件结构图 Ｆｉｇ．３ Ｓｔｒｕｃｔｕｒｅ ｏｆ ＣＰＡＣ 为解决控制算法在上位机的实现难题，控制算 法的角度、角速度等表示为 ｅ（ｔ） ＝ θ ∗ （ｔ） － θ（ｔ － １） ｅ · （ｔ） ＝ ｅ（ｔ） － ｅ（ｔ － １） ｅ ¨ （ｔ） ＝ ｅ · （ｔ） － ｅ · （ｔ － １） ì î í ï ï ï ï （２２） 机械臂初始化状态： θ · ｉ ＝ θｉ ＝ ０， ｉ ＝ １，２，３，４，６， θ · ５ ＝ ０，θ５ ＝ ９０° 。 机械臂六轴的期望位置分别为： θ ∗ １ ＝ － ２３°，θ ∗ ２ ＝ ２５°，θ ∗ ３ ＝ ４０°，θ ∗ ６ ＝ － ５５°，θ ∗ ４ ＝ ｓｉｎ（πｔ ／ ５ ） × ２０°， θ ∗ ５ ＝ ｓｉｎ（πｔ ／ ２ ） × ５ ＋ ９０°。 机械 臂单轴输出的力矩范围为： τｉ ∈ ［ － １０，１０］ Ｎ·ｍ。 实验结果图 ４ 表明，优化后的全局快速终端滑 模控制策略较之优化之前系统的上升时间更短，响 应速度更快，两者皆避免了超调现象的出现，减小了 机械的来回摩擦造成的磨损。 对于稳态阶段如 ９５～ １００ ｓ，图 ４（ａ） ～ （ｃ）和（ ｆ）的阶跃响应表明，优化前 的稳态误差范围为［０．０５°，０．２°］，优化后的稳态时 刻，几乎与设定值重合。 图 ４（ ｄ） ～ （ ｅ）的正弦跟踪 第 ２ 期 王琥，等：基于 ＰＳＯ 优化的六自由度机械臂全局快速终端滑模控制 ·２６９·

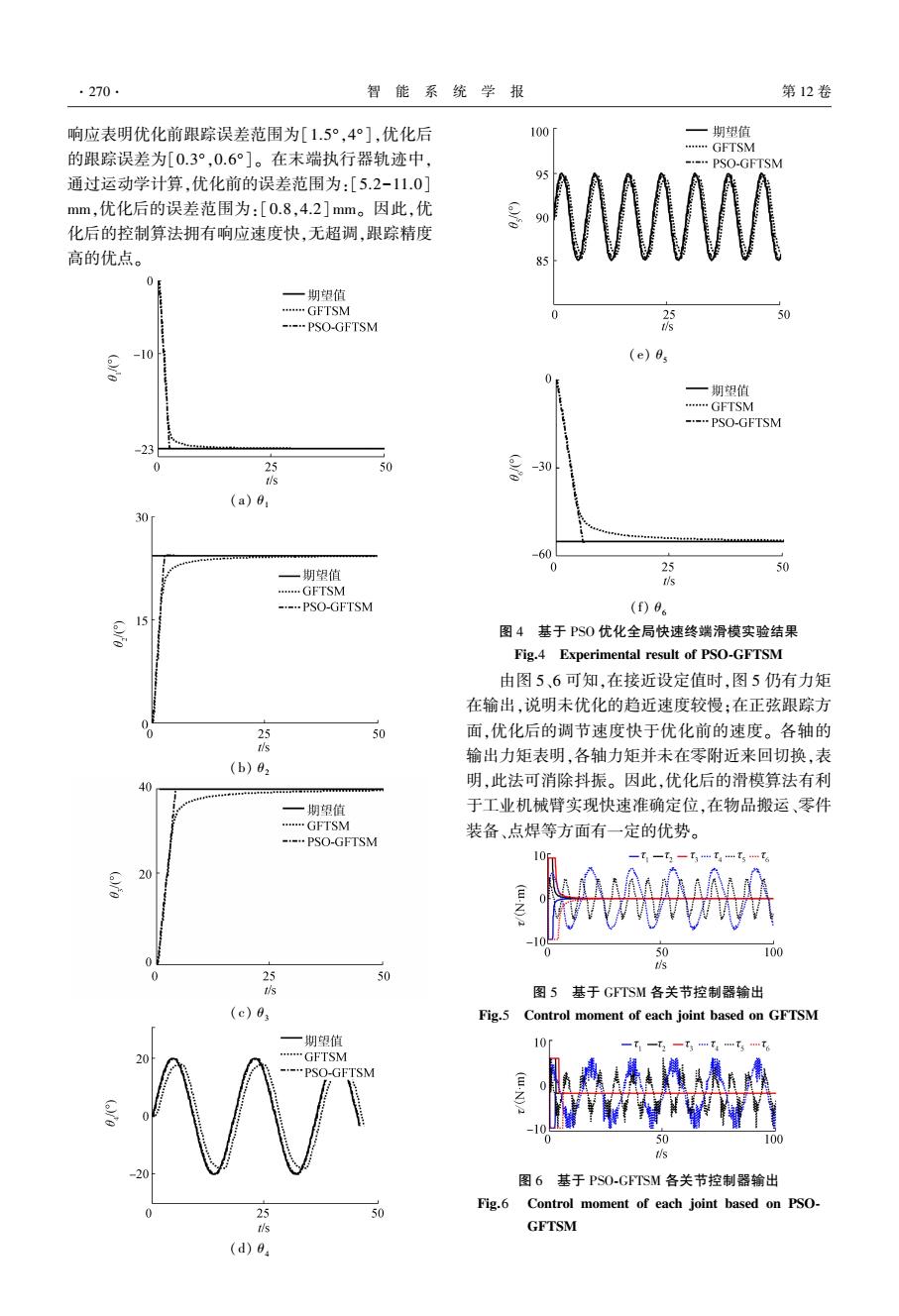
·270 智能系统学报 第12卷 响应表明优化前跟踪误差范围为[1.5°，4°]，优化后 100 一期望值 GFTSM 的跟踪误差为[0.3°，0.6°]。在末端执行器轨迹中， PSO-GFTSM 通过运动学计算，优化前的误差范围为：[5.2-11.0] 95 mm,优化后的误差范围为：[0.8,4.2]mm。因此，优 90 化后的控制算法拥有响应速度快，无超调，跟踪精度 W 高的优点。 0 一期望值 …GFTSM 50 --…PSO-GFTSM -10 (.)o (e)0s —一期望值 …GFTSM --…PSO-GFTSM -23 25 50 -30 s (a)8, 3) -60 一期望值 0 25 0 .…GFTSM -.--PSO-GFTSM (f)9。 15 图4基于PS0优化全局快速终端滑模实验结果 Fig.4 Experimental result of PSO-GFTSM 由图5、6可知，在接近设定值时，图5仍有力矩 在输出，说明未优化的趋近速度较慢：在正弦跟踪方 25 50 面，优化后的调节速度快于优化前的速度。各轴的 s 输出力矩表明，各轴力矩并未在零附近来回切换，表 (b)82 40 明，此法可消除抖振。因此，优化后的滑模算法有利 一期望值 于工业机械臂实现快速准确定位，在物品搬运、零件 …GFTSM 装备、点焊等方面有一定的优势。 --…PSO-GFTSM 20 50 100 0 0 25 50 s 图5基于GFTSM各关节控制器输出 (c)0, Fig.5 Control moment of each joint based on GFTSM 一期望值 10r GFTSM -PSO-GFTSM 50 100 s 图6基于PSO-GFTSM各关节控制器输出 50 Fig.6 Control moment of each joint based on PSO- GFTSM (d)

响应表明优化前跟踪误差范围为［１．５°，４°］，优化后 的跟踪误差为［０．３°，０．６°］。 在末端执行器轨迹中， 通过运动学计算，优化前的误差范围为：［５．２－１１．０］ ｍｍ，优化后的误差范围为：［０．８，４．２］ｍｍ。 因此，优 化后的控制算法拥有响应速度快，无超调，跟踪精度 高的优点。 （ａ） θ １ （ｂ） θ ２ （ｃ） θ ３ （ｄ） θ ４ （ｅ） θ ５ （ｆ） θ ６ 图 ４ 基于 ＰＳＯ 优化全局快速终端滑模实验结果 Ｆｉｇ．４ Ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔ ｏｆ ＰＳＯ⁃ＧＦＴＳＭ 由图 ５、６ 可知，在接近设定值时，图 ５ 仍有力矩 在输出，说明未优化的趋近速度较慢；在正弦跟踪方 面，优化后的调节速度快于优化前的速度。 各轴的 输出力矩表明，各轴力矩并未在零附近来回切换，表 明，此法可消除抖振。 因此，优化后的滑模算法有利 于工业机械臂实现快速准确定位，在物品搬运、零件 装备、点焊等方面有一定的优势。 图 ５ 基于 ＧＦＴＳＭ 各关节控制器输出 Ｆｉｇ．５ Ｃｏｎｔｒｏｌ ｍｏｍｅｎｔ ｏｆ ｅａｃｈ ｊｏｉｎｔ ｂａｓｅｄ ｏｎ ＧＦＴＳＭ 图 ６ 基于 ＰＳＯ⁃ＧＦＴＳＭ 各关节控制器输出 Ｆｉｇ．６ Ｃｏｎｔｒｏｌ ｍｏｍｅｎｔ ｏｆ ｅａｃｈ ｊｏｉｎｔ ｂａｓｅｄ ｏｎ ＰＳＯ⁃ ＧＦＴＳＭ ·２７０· 智 能 系 统 学 报 第 １２ 卷

第2期 王琥，等：基于PS0优化的六自由度机械臂全局快速终端滑模控制 ·271. [9]付涛，王大镇，弓清忠，等.改进神经网络自适应滑模 4 结束语 控制的机器人轨迹跟踪控制[J].大连理工大学学报， 针对六自由度工业机械臂控制问题，考虑机械 2014.54(5):523-530. 臂本身的MIM0特性，将其分解成单关节SS0系 FU Tao,WANG Dazhen,GONG Qingzhong,et al.Robot 统，在全局快速终端变结构滑模控制的基础上，分析 trajectory tracking control of improved neural network adap- 并克服了全局快速终端滑模控制的奇异性，同时采 tive sliding mode control[]]Journal of Dalian university of 用PS0优化其控制律参数。实验结果表明：相比于 technology,2014,54(5):523-530. 优化前的滑模控制，基于PS0优化的全局快速终端 「10]王艳敏，冯勇，陆启良.基于遗传算法的柔性机械手高 滑模算法可以更加有效地减小被控系统的抖振问 阶终端滑模控制[J].吉林大学学报：工学版，2009,39 题，减小系统的上升时间，跟踪误差更小，可缩短滑 (6):1563-1567 模系统收敛时间，提高系统的动静态性能。 WANG Yanmin,FENG Yong,LU Qiliang.High-order ter- 参考文献： minal sliding mode control of flexible manipulators based on genetic algorithm[].Journal of Jilin university:engi- [1]JASIM I F,PLAPPER P W.Stable robust adaptive control neering and technology edition,2009,39(6):1563- of robotic manipulators with switched constraints[C]//Pro- 1567. ceedings of 2013 IEEE International Conference on Mecha- [11]SHARAF A M,EL-GAMMAL AAA.A variable structure tronics and Automation.Takamatsu:IEEE,2013:755- sliding mode Particle Swarm Optimization-PSO optimal reg- 760. ulating controller for industrial PMDC motor drives[C]/ [2]SHOJAEI K,SHAHRI A M.Adaptive robust time-varying Proceedings of 2009 IEEE International Electric Machines control of uncertain non-holonomic robotic systems[].IET control theory applications,2012,6(1):90-102. and Drives Conference.Miami,FL:IEEE,2009:337- [3]JAISWAL N K,KUMAR V.Comparison between conven- 343. tional PID and Fuzzy PID supervisor for 3-DOF Scara type [12]NIKU S B.机器人学导论：分析、系统及应用[M].孙富 robot manipulator[C]//Proceedings of 2014 IEEE Students' 春，译.北京：电子工业出版社，2004. Conference on Electrical,Electronics and Computer Sci- [13]王瑞明，蒋静坪.基于适应性遗传算法的滑模控制感应 ence.Bhopal:IEEE,2014:1-5. 电机伺服驱动系统研究[J].中国电机工程学报，2005， [4]CAPISANI L M.,FERRARA A,FERREIRA DE LOZA A, 25(17):136-141 et al.Manipulator fault diagnosis via higher order sliding- WANG Ruiming,JIANG Jingping.Sliding-mode controlled mode observers[J].IEEE transactions on industrial elec- induction motor servo drive system via AGA optimization tronics,2012,59(10):3979-3986. [5]FERRARA A,INCREMONA G P.Design of an integral su- [J].Proceedings of the CSEE,2005,25(17):136-141. boptimal second-order sliding mode controller for the robust 作者简介： motion control of robot manipulators[J].IEEE transactions 王琥.男，1990年生，硕士生，研究 on control systems technology,2015,23(6):2316-2325. 方向为机器人视觉、机器人控制以及轨 [6]JIN Yi,CHANG P H,JIN Maolin,et al.Stability guaran- 迹规划。 teed time-delay control of manipulators using nonlinear damping and terminal sliding mode[J].IEEE transactions on industrial electronics,2013,60(8):3304-3317. [7]ARISOY A,BAYRAKCEKEN M K,BASTURK S,et al. High order sliding mode control of a space robot manipulator 胡立坤，男，1977年生，研究生导 [C]//Proceedings of the 2011 5th International Conference 师，主要研究方向是非线性系统动力学 on Recent Advances in Space Technologies.Istanbul: 与控制、光/风/蓄分布式电源转换与控 EEE,2011:833-838. 制、工业测控网络应用。已发表核心期 [8]SOLTANPOUR M R,OTADOLAJAM P,KHOOBAN M H. 刊学术论文50余篇，其中SCI收录2 Robust control strategy for electrically driven robot manipu- 篇，收录14篇：获得软件著作权1项：获得实用新型专利 lators:adaptive fuzzy sliding mode[J.IET science,meas- 1项：申请发明专利8项。 urement technology,2015,9(3):322-334

４ 结束语 针对六自由度工业机械臂控制问题，考虑机械 臂本身的 ＭＩＭＯ 特性，将其分解成单关节 ＳＩＳＯ 系 统，在全局快速终端变结构滑模控制的基础上，分析 并克服了全局快速终端滑模控制的奇异性，同时采 用 ＰＳＯ 优化其控制律参数。 实验结果表明：相比于 优化前的滑模控制，基于 ＰＳＯ 优化的全局快速终端 滑模算法可以更加有效地减小被控系统的抖振问 题，减小系统的上升时间，跟踪误差更小，可缩短滑 模系统收敛时间，提高系统的动静态性能。 参考文献： ［１］ＪＡＳＩＭ Ｉ Ｆ， ＰＬＡＰＰＥＲ Ｐ Ｗ． Ｓｔａｂｌｅ ｒｏｂｕｓｔ ａｄａｐｔｉｖｅ ｃｏｎｔｒｏｌ ｏｆ ｒｏｂｏｔｉｃ ｍａｎｉｐｕｌａｔｏｒｓ ｗｉｔｈ ｓｗｉｔｃｈｅｄ ｃｏｎｓｔｒａｉｎｔｓ［Ｃ］ ／ ／ Ｐｒｏ⁃ ｃｅｅｄｉｎｇｓ ｏｆ ２０１３ ＩＥＥＥ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｍｅｃｈａ⁃ ｔｒｏｎｉｃｓ ａｎｄ Ａｕｔｏｍａｔｉｏｎ． Ｔａｋａｍａｔｓｕ： ＩＥＥＥ， ２０１３： ７５５ － ７６０． ［２］ ＳＨＯＪＡＥＩ Ｋ， ＳＨＡＨＲＩ Ａ Ｍ． Ａｄａｐｔｉｖｅ ｒｏｂｕｓｔ ｔｉｍｅ⁃ｖａｒｙｉｎｇ ｃｏｎｔｒｏｌ ｏｆ ｕｎｃｅｒｔａｉｎ ｎｏｎ⁃ｈｏｌｏｎｏｍｉｃ ｒｏｂｏｔｉｃ ｓｙｓｔｅｍｓ［ Ｊ］． ＩＥＴ ｃｏｎｔｒｏｌ ｔｈｅｏｒｙ ＆ ａｐｐｌｉｃａｔｉｏｎｓ， ２０１２， ６（１）： ９０－１０２． ［３］ ＪＡＩＳＷＡＬ Ｎ Ｋ， ＫＵＭＡＲ Ｖ． Ｃｏｍｐａｒｉｓｏｎ ｂｅｔｗｅｅｎ ｃｏｎｖｅｎ⁃ ｔｉｏｎａｌ ＰＩＤ ａｎｄ Ｆｕｚｚｙ ＰＩＤ ｓｕｐｅｒｖｉｓｏｒ ｆｏｒ ３⁃ＤＯＦ Ｓｃａｒａ ｔｙｐｅ ｒｏｂｏｔ ｍａｎｉｐｕｌａｔｏｒ［Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ２０１４ ＩＥＥＥ Ｓｔｕｄｅｎｔｓ＇ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｅｌｅｃｔｒｉｃａｌ， Ｅｌｅｃｔｒｏｎｉｃｓ ａｎｄ Ｃｏｍｐｕｔｅｒ Ｓｃｉ⁃ ｅｎｃｅ． Ｂｈｏｐａｌ： ＩＥＥＥ， ２０１４： １－５． ［４］ＣＡＰＩＳＡＮＩ Ｌ Ｍ， ＦＥＲＲＡＲＡ Ａ， ＦＥＲＲＥＩＲＡ ＤＥ ＬＯＺＡ Ａ， ｅｔ ａｌ． Ｍａｎｉｐｕｌａｔｏｒ ｆａｕｌｔ ｄｉａｇｎｏｓｉｓ ｖｉａ ｈｉｇｈｅｒ ｏｒｄｅｒ ｓｌｉｄｉｎｇ⁃ ｍｏｄｅ ｏｂｓｅｒｖｅｒｓ ［ Ｊ］． ＩＥＥＥ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｉｎｄｕｓｔｒｉａｌ ｅｌｅｃ⁃ ｔｒｏｎｉｃｓ， ２０１２， ５９（１０）： ３９７９－３９８６． ［５］ＦＥＲＲＡＲＡ Ａ， ＩＮＣＲＥＭＯＮＡ Ｇ Ｐ． Ｄｅｓｉｇｎ ｏｆ ａｎ ｉｎｔｅｇｒａｌ ｓｕ⁃ ｂｏｐｔｉｍａｌ ｓｅｃｏｎｄ⁃ｏｒｄｅｒ ｓｌｉｄｉｎｇ ｍｏｄｅ ｃｏｎｔｒｏｌｌｅｒ ｆｏｒ ｔｈｅ ｒｏｂｕｓｔ ｍｏｔｉｏｎ ｃｏｎｔｒｏｌ ｏｆ ｒｏｂｏｔ ｍａｎｉｐｕｌａｔｏｒｓ［ Ｊ］． ＩＥＥＥ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｃｏｎｔｒｏｌ ｓｙｓｔｅｍｓ ｔｅｃｈｎｏｌｏｇｙ， ２０１５， ２３（６）： ２３１６－２３２５． ［６］ＪＩＮ Ｙｉ， ＣＨＡＮＧ Ｐ Ｈ， ＪＩＮ Ｍａｏｌｉｎ， ｅｔ ａｌ． Ｓｔａｂｉｌｉｔｙ ｇｕａｒａｎ⁃ ｔｅｅｄ ｔｉｍｅ⁃ｄｅｌａｙ ｃｏｎｔｒｏｌ ｏｆ ｍａｎｉｐｕｌａｔｏｒｓ ｕｓｉｎｇ ｎｏｎｌｉｎｅａｒ ｄａｍｐｉｎｇ ａｎｄ ｔｅｒｍｉｎａｌ ｓｌｉｄｉｎｇ ｍｏｄｅ［ Ｊ］． ＩＥＥＥ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｉｎｄｕｓｔｒｉａｌ ｅｌｅｃｔｒｏｎｉｃｓ， ２０１３， ６０（８）： ３３０４－３３１７． ［７］ ＡＲＩＳＯＹ Ａ， ＢＡＹＲＡＫＣＥＫＥＮ Ｍ Ｋ， ＢＡＳＴＵＲＫ Ｓ， ｅｔ ａｌ． Ｈｉｇｈ ｏｒｄｅｒ ｓｌｉｄｉｎｇ ｍｏｄｅ ｃｏｎｔｒｏｌ ｏｆ ａ ｓｐａｃｅ ｒｏｂｏｔ ｍａｎｉｐｕｌａｔｏｒ ［Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ２０１１ ５ｔｈ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｒｅｃｅｎｔ Ａｄｖａｎｃｅｓ ｉｎ Ｓｐａｃｅ Ｔｅｃｈｎｏｌｏｇｉｅｓ． Ｉｓｔａｎｂｕｌ： ＩＥＥＥ， ２０１１： ８３３－８３８． ［８］ＳＯＬＴＡＮＰＯＵＲ Ｍ Ｒ， ＯＴＡＤＯＬＡＪＡＭ Ｐ， ＫＨＯＯＢＡＮ Ｍ Ｈ． Ｒｏｂｕｓｔ ｃｏｎｔｒｏｌ ｓｔｒａｔｅｇｙ ｆｏｒ ｅｌｅｃｔｒｉｃａｌｌｙ ｄｒｉｖｅｎ ｒｏｂｏｔ ｍａｎｉｐｕ⁃ ｌａｔｏｒｓ： ａｄａｐｔｉｖｅ ｆｕｚｚｙ ｓｌｉｄｉｎｇ ｍｏｄｅ［Ｊ］． ＩＥＴ ｓｃｉｅｎｃｅ， ｍｅａｓ⁃ ｕｒｅｍｅｎｔ ＆ ｔｅｃｈｎｏｌｏｇｙ， ２０１５， ９（３）： ３２２－３３４． ［９］付涛， 王大镇， 弓清忠， 等． 改进神经网络自适应滑模 控制的机器人轨迹跟踪控制［ Ｊ］． 大连理工大学学报， ２０１４， ５４（５）： ５２３－５３０． ＦＵ Ｔａｏ， ＷＡＮＧ Ｄａｚｈｅｎ， ＧＯＮＧ Ｑｉｎｇｚｈｏｎｇ， ｅｔ ａｌ． Ｒｏｂｏｔ ｔｒａｊｅｃｔｏｒｙ ｔｒａｃｋｉｎｇ ｃｏｎｔｒｏｌ ｏｆ ｉｍｐｒｏｖｅｄ ｎｅｕｒａｌ ｎｅｔｗｏｒｋ ａｄａｐ⁃ ｔｉｖｅ ｓｌｉｄｉｎｇ ｍｏｄｅ ｃｏｎｔｒｏｌ［Ｊ］． Ｊｏｕｒｎａｌ ｏｆ Ｄａｌｉａｎ ｕｎｉｖｅｒｓｉｔｙ ｏｆ ｔｅｃｈｎｏｌｏｇｙ， ２０１４， ５４（５）： ５２３－５３０． ［１０］王艳敏， 冯勇， 陆启良． 基于遗传算法的柔性机械手高 阶终端滑模控制［Ｊ］． 吉林大学学报： 工学版， ２００９， ３９ （６）： １５６３－１５６７． ＷＡＮＧ Ｙａｎｍｉｎ， ＦＥＮＧ Ｙｏｎｇ， ＬＵ Ｑｉｌｉａｎｇ． Ｈｉｇｈ⁃ｏｒｄｅｒ ｔｅｒ⁃ ｍｉｎａｌ ｓｌｉｄｉｎｇ ｍｏｄｅ ｃｏｎｔｒｏｌ ｏｆ ｆｌｅｘｉｂｌｅ ｍａｎｉｐｕｌａｔｏｒｓ ｂａｓｅｄ ｏｎ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ［ Ｊ］． Ｊｏｕｒｎａｌ ｏｆ Ｊｉｌｉｎ ｕｎｉｖｅｒｓｉｔｙ： ｅｎｇｉ⁃ ｎｅｅｒｉｎｇ ａｎｄ ｔｅｃｈｎｏｌｏｇｙ ｅｄｉｔｉｏｎ， ２００９， ３９ （ ６ ）： １５６３ － １５６７． ［１１］ＳＨＡＲＡＦ Ａ Ｍ， ＥＬ⁃ＧＡＭＭＡＬ Ａ Ａ Ａ． Ａ ｖａｒｉａｂｌｅ ｓｔｒｕｃｔｕｒｅ ｓｌｉｄｉｎｇ ｍｏｄｅ Ｐａｒｔｉｃｌｅ Ｓｗａｒｍ Ｏｐｔｉｍｉｚａｔｉｏｎ⁃ＰＳＯ ｏｐｔｉｍａｌ ｒｅｇ⁃ ｕｌａｔｉｎｇ ｃｏｎｔｒｏｌｌｅｒ ｆｏｒ ｉｎｄｕｓｔｒｉａｌ ＰＭＤＣ ｍｏｔｏｒ ｄｒｉｖｅｓ［Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ２００９ ＩＥＥＥ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｅｌｅｃｔｒｉｃ Ｍａｃｈｉｎｅｓ ａｎｄ Ｄｒｉｖｅｓ Ｃｏｎｆｅｒｅｎｃｅ． Ｍｉａｍｉ， ＦＬ： ＩＥＥＥ， ２００９： ３３７ － ３４３． ［１２］ＮＩＫＵ Ｓ Ｂ． 机器人学导论： 分析、系统及应用［Ｍ］． 孙富 春， 译． 北京： 电子工业出版社， ２００４． ［１３］王瑞明， 蒋静坪． 基于适应性遗传算法的滑模控制感应 电机伺服驱动系统研究［Ｊ］． 中国电机工程学报， ２００５， ２５（１７）： １３６－１４１． ＷＡＮＧ Ｒｕｉｍｉｎｇ， ＪＩＡＮＧ Ｊｉｎｇｐｉｎｇ． Ｓｌｉｄｉｎｇ⁃ｍｏｄｅ ｃｏｎｔｒｏｌｌｅｄ ｉｎｄｕｃｔｉｏｎ ｍｏｔｏｒ ｓｅｒｖｏ ｄｒｉｖｅ ｓｙｓｔｅｍ ｖｉａ ＡＧＡ ｏｐｔｉｍｉｚａｔｉｏｎ ［Ｊ］． Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ＣＳＥＥ， ２００５， ２５（１７）： １３６－１４１． 作者简介： 王琥，男，１９９０ 年生，硕士生，研究 方向为机器人视觉、机器人控制以及轨 迹规划。 胡立坤，男，１９７７ 年生，研究生导 师，主要研究方向是非线性系统动力学 与控制、光／ 风／ 蓄分布式电源转换与控 制、工业测控网络应用。 已发表核心期 刊学术论文 ５０ 余篇，其中 ＳＣＩ 收录 ２ 篇，Ｅｉ 收录 １４ 篇；获得软件著作权 １ 项；获得实用新型专利 １ 项；申请发明专利 ８ 项。 第 ２ 期 王琥，等：基于 ＰＳＯ 优化的六自由度机械臂全局快速终端滑模控制 ·２７１·