【智能系统】联合连通拓扑下的二阶多自主体系统有限时间包容控制

第12卷第2期 智能系统学报 Vol.12 No.2 2017年4月 CAAI Transactions on Intelligent Systems Apr.2017 D0I:10.11992/6is.201605013 网络出版地址：http://www.cmki.net/kcms/detail,/23.1538.tp.20170111.1705.020.html 联合连通拓扑下的二阶多自主体系统 有限时间包容控制 庄昊，杨洪勇 (鲁东大学信息与电气工程学院，山东烟台264025) 摘要：针对具有多领航者的二阶网络化系统群集运动问题，提出了一种有限时间收敛的包容控制算法。在此基础 上，运用现代控制理论、代数图论和矩阵论等分析工具对所提出的控制算法进行理论分析，得到了当通信拓扑为动 态联合连通时，二阶网络化系统在有限时间内实现群集运动的收敛条件。通过此包容控制算法，使得系统在静态拓 扑和联合连通条件下均在有限时间内收敛到目标区域内。最后，应用系统仿真验证了所得结论的正确性。 关键词：多领航者：群集运动：有限时间：联合连通：包容控制 中图分类号：TP391文献标志码：A文章编号：1673-4785(2017)02-0188-08 中文引用格式：庄吴，杨洪勇.联合连通拓扑下的二阶多自主体系统有限时间包容控制[J].智能系统学报，2017,12(2)：188-195. 英文引用格式：ZHUANG Hao,YANG Hongyong.Finite-time containment control of second-order multi-agent systems with jointly connected topologies[].CAAI transactions on intelligent systems,2017,12(2):188-195. Finite-time containment control of second-order multi-agent systems with jointly connected topologies ZHUANG Hao,YANG Hongyong School of Information and Electrical Engineering,Ludong University,Yantai 264025,China) Abstract:In this paper,we propose a containment control algorithm with finite-time convergence for a second-order networked system flocking with multiple leaders.By applying modern control theory,matrix theory,and algebraic graph theory,we theoretically analyzed our proposed control algorithm;by doing so,we identified the convergence conditions required for a second-order networked system to realize flocking within finite time when the communica- tion topology applies a dynamic joint connection.Through our containment control algorithm,the networked systems converge to object regions in finite time given the circumstances of static and jointly connected topologies.Finally, we verified the effectiveness of our proposed system via simulation examples. Keywords:multiple leaders;flocking;finite time;jointly-connected;containment control 多智能体系统协调控制是近几年迅速发展起来的 信息交流达到各个智能体特定状态的一致。包容控 复杂系统控制科学研究领域的热点问题，它在无线传 制是一种具有多领航者的类一致性问题，通过设计跟 感器网络、移动机器人编队控制、集群航天器深空探测 随者的控制协议使得跟随者最终收敛到领航者组成 等领域有广泛的应用，受到许多研究学者的关注。 的目标区域内（领航者围成的凸包）完成群体运 致性问题是分布式协同控制的一个重要研究 动4)。文献[4]研究了一阶系统的包容控制问题， 方向-)，多智能体系统通过系统中各智能体之间的 并证明了当网络拓扑连通时系统可以实现包容控制， 但并未讨论网络拓扑在联合联通条件下的包容控制 收稿日期：2016-05-16.网络出版日期：2017-01-11. 问题。文献[5]研究了有向网络中固定拓扑和切换拓 基金项目：国家自然科学基金项目(61273152)：国家自然科学基金项目 (61673200) 扑两种情况下一阶系统的包容控制问题，并给出了系 通信作者：杨洪勇.E-mail:yang@ycah.net 统收敛的充要条件，但未对二阶系统进行说明。文献

第 １２ 卷第 ２ 期 智 能 系 统 学 报 Ｖｏｌ．１２ №．２ ２０１７ 年 ４ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ａｐｒ． ２０１７ ＤＯＩ：１０．１１９９２ ／ ｔｉｓ．２０１６０５０１３ 网络出版地址：ｈｔｔｐ： ／ ／ ｗｗｗ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｅｔａｉｌ ／ ２３．１５３８．ｔｐ．２０１７０１１１．１７０５．０２０．ｈｔｍｌ 联合连通拓扑下的二阶多自主体系统 有限时间包容控制 庄昊，杨洪勇 （鲁东大学 信息与电气工程学院，山东 烟台 ２６４０２５） 摘 要：针对具有多领航者的二阶网络化系统群集运动问题，提出了一种有限时间收敛的包容控制算法。 在此基础 上，运用现代控制理论、代数图论和矩阵论等分析工具对所提出的控制算法进行理论分析，得到了当通信拓扑为动 态联合连通时，二阶网络化系统在有限时间内实现群集运动的收敛条件。 通过此包容控制算法，使得系统在静态拓 扑和联合连通条件下均在有限时间内收敛到目标区域内。 最后，应用系统仿真验证了所得结论的正确性。 关键词：多领航者；群集运动；有限时间；联合连通；包容控制 中图分类号： ＴＰ３９１ 文献标志码：Ａ 文章编号：１６７３－４７８５（２０１７）０２－０１８８－０８ 中文引用格式：庄昊，杨洪勇． 联合连通拓扑下的二阶多自主体系统有限时间包容控制［Ｊ］． 智能系统学报， ２０１７， １２（２）： １８８－１９５． 英文引用格式：ＺＨＵＡＮＧ Ｈａｏ，ＹＡＮＧ Ｈｏｎｇｙｏｎｇ． Ｆｉｎｉｔｅ⁃ｔｉｍｅ ｃｏｎｔａｉｎｍｅｎｔ ｃｏｎｔｒｏｌ ｏｆ ｓｅｃｏｎｄ⁃ｏｒｄｅｒ ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓｔｅｍｓ ｗｉｔｈ ｊｏｉｎｔｌｙ ｃｏｎｎｅｃｔｅｄ ｔｏｐｏｌｏｇｉｅｓ［Ｊ］． ＣＡＡＩ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｉｎｔｅｌｌｉｇｅｎｔ ｓｙｓｔｅｍｓ， ２０１７， １２（２）： １８８－１９５． Ｆｉｎｉｔｅ⁃ｔｉｍｅ ｃｏｎｔａｉｎｍｅｎｔ ｃｏｎｔｒｏｌ ｏｆ ｓｅｃｏｎｄ⁃ｏｒｄｅｒ ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓｔｅｍｓ ｗｉｔｈ ｊｏｉｎｔｌｙ ｃｏｎｎｅｃｔｅｄ ｔｏｐｏｌｏｇｉｅｓ ＺＨＵＡＮＧ Ｈａｏ， ＹＡＮＧ Ｈｏｎｇｙｏｎｇ （Ｓｃｈｏｏｌ ｏｆ Ｉｎｆｏｒｍａｔｉｏｎ ａｎｄ Ｅｌｅｃｔｒｉｃａｌ Ｅｎｇｉｎｅｅｒｉｎｇ， Ｌｕｄｏｎｇ Ｕｎｉｖｅｒｓｉｔｙ， Ｙａｎｔａｉ ２６４０２５， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｉｎ ｔｈｉｓ ｐａｐｅｒ， ｗｅ ｐｒｏｐｏｓｅ ａ ｃｏｎｔａｉｎｍｅｎｔ ｃｏｎｔｒｏｌ ａｌｇｏｒｉｔｈｍ ｗｉｔｈ ｆｉｎｉｔｅ⁃ｔｉｍｅ ｃｏｎｖｅｒｇｅｎｃｅ ｆｏｒ ａ ｓｅｃｏｎｄ⁃ｏｒｄｅｒ ｎｅｔｗｏｒｋｅｄ ｓｙｓｔｅｍ ｆｌｏｃｋｉｎｇ ｗｉｔｈ ｍｕｌｔｉｐｌｅ ｌｅａｄｅｒｓ． Ｂｙ ａｐｐｌｙｉｎｇ ｍｏｄｅｒｎ ｃｏｎｔｒｏｌ ｔｈｅｏｒｙ， ｍａｔｒｉｘ ｔｈｅｏｒｙ， ａｎｄ ａｌｇｅｂｒａｉｃ ｇｒａｐｈ ｔｈｅｏｒｙ， ｗｅ ｔｈｅｏｒｅｔｉｃａｌｌｙ ａｎａｌｙｚｅｄ ｏｕｒ ｐｒｏｐｏｓｅｄ ｃｏｎｔｒｏｌ ａｌｇｏｒｉｔｈｍ； ｂｙ ｄｏｉｎｇ ｓｏ， ｗｅ ｉｄｅｎｔｉｆｉｅｄ ｔｈｅ ｃｏｎｖｅｒｇｅｎｃｅ ｃｏｎｄｉｔｉｏｎｓ ｒｅｑｕｉｒｅｄ ｆｏｒ ａ ｓｅｃｏｎｄ⁃ｏｒｄｅｒ ｎｅｔｗｏｒｋｅｄ ｓｙｓｔｅｍ ｔｏ ｒｅａｌｉｚｅ ｆｌｏｃｋｉｎｇ ｗｉｔｈｉｎ ｆｉｎｉｔｅ ｔｉｍｅ ｗｈｅｎ ｔｈｅ ｃｏｍｍｕｎｉｃａ⁃ ｔｉｏｎ ｔｏｐｏｌｏｇｙ ａｐｐｌｉｅｓ ａ ｄｙｎａｍｉｃ ｊｏｉｎｔ ｃｏｎｎｅｃｔｉｏｎ． Ｔｈｒｏｕｇｈ ｏｕｒ ｃｏｎｔａｉｎｍｅｎｔ ｃｏｎｔｒｏｌ ａｌｇｏｒｉｔｈｍ， ｔｈｅ ｎｅｔｗｏｒｋｅｄ ｓｙｓｔｅｍｓ ｃｏｎｖｅｒｇｅ ｔｏ ｏｂｊｅｃｔ ｒｅｇｉｏｎｓ ｉｎ ｆｉｎｉｔｅ ｔｉｍｅ ｇｉｖｅｎ ｔｈｅ ｃｉｒｃｕｍｓｔａｎｃｅｓ ｏｆ ｓｔａｔｉｃ ａｎｄ ｊｏｉｎｔｌｙ ｃｏｎｎｅｃｔｅｄ ｔｏｐｏｌｏｇｉｅｓ． Ｆｉｎａｌｌｙ， ｗｅ ｖｅｒｉｆｉｅｄ ｔｈｅ ｅｆｆｅｃｔｉｖｅｎｅｓｓ ｏｆ ｏｕｒ ｐｒｏｐｏｓｅｄ ｓｙｓｔｅｍ ｖｉａ ｓｉｍｕｌａｔｉｏｎ ｅｘａｍｐｌｅｓ． Ｋｅｙｗｏｒｄｓ： ｍｕｌｔｉｐｌｅ ｌｅａｄｅｒｓ； ｆｌｏｃｋｉｎｇ； ｆｉｎｉｔｅ ｔｉｍｅ； ｊｏｉｎｔｌｙ⁃ｃｏｎｎｅｃｔｅｄ； ｃｏｎｔａｉｎｍｅｎｔ ｃｏｎｔｒｏｌ 收稿日期：２０１６－０５－１６． 网络出版日期：２０１７－０１－１１． 基金项目：国家自然科学基金项目（６１２７３１５２）；国家自然科学基金项目 （６１６７３２００）． 通信作者：杨洪勇． Ｅ⁃ｍａｉｌ： ｈｙｙａｎｇ＠ ｙｅａｈ．ｎｅｔ． 多智能体系统协调控制是近几年迅速发展起来的 复杂系统控制科学研究领域的热点问题，它在无线传 感器网络、移动机器人编队控制、集群航天器深空探测 等领域有广泛的应用，受到许多研究学者的关注。 一致性问题是分布式协同控制的一个重要研究 方向［１－３］ ，多智能体系统通过系统中各智能体之间的 信息交流达到各个智能体特定状态的一致。 包容控 制是一种具有多领航者的类一致性问题，通过设计跟 随者的控制协议使得跟随者最终收敛到领航者组成 的目标区域内（领航者围成的凸包） 完成群体运 动［４－９］ 。 文献［４］研究了一阶系统的包容控制问题， 并证明了当网络拓扑连通时系统可以实现包容控制， 但并未讨论网络拓扑在联合联通条件下的包容控制 问题。 文献［５］研究了有向网络中固定拓扑和切换拓 扑两种情况下一阶系统的包容控制问题，并给出了系 统收敛的充要条件，但未对二阶系统进行说明。 文献

第2期 庄吴，等：联合连通拓扑下的二阶多自主体系统有限时间包容控制 ·189. [6]对动态领航者的二阶系统进行研究，分别提出了 f(x),x(0)=x。∈R”。其中连续向量流f(x)= 连续渐近包容控制算法和离散渐近包容控制算法。 [f(x)(x)…f(x)]T与带有扩张r=(m, 文献[7]研究了随机切换拓扑下二阶系统的包容控制 2,…,「n),:>0的度k∈R是齐次的，如果对于任 问题，提出一种基于不可约马尔可夫链信息拓扑的包 意的E>0,x∈R”都有f(E”x1,E2x2,…,Exn)= 容控制算法。文献[8]研究了二阶系统的分布式包容 e+"f(x),i=1,2,…,n。 控制问题，并给出了系统收敛的充分必要条件。从以 上文献研究可知，虽然均能实现系统的包容控制要 引理1)设系统x=f(x),x(0)=x。∈ 求，但是实现时间是不确定的。 R”与带有扩张(r1,r2,…,Tn)的度k∈R是齐次 在工业应用中，仅实现各个智能体特定状态的 的，函数f(x)是连续的，且x=0是它的一个渐 渐近一致还不足以满足工业生产需要，还需要系统 近稳定平衡点，如果齐次度k0,否则，a=0。节点i的 的奇函数满足x:P(x:)>0(Hx:≠0)。假设 邻居集合定义为N,={行∈VI(i,j)∈E}。定义 sgn(x)"[sgn (x)a sgn (x2)a..sgn D=diag(d,d2,…,dn）∈R*a为图x,(t)的度矩 (xn)],sgn(x:)“=|x:sign(x),sigm(·）表示符 库，其中4=公i=12,…。权重图G的 号函数。并且&1，a2为常值，0<1<1，a2= Laplacian矩阵定义为：L=D-A∈Rmxm 21 定义11设集合X={x1,x2,…,xn}为实向 a,+1o 量空间VCR的子集，X的凸包定义为：CO(X)= 设跟随者之间通信拓扑图为G。,由于跟随者 x1x.sx.o.wo. 之间是双向交流信息，所以G为无向图。具有领航 者的多自主体系统的通信拓扑图为G,系统的 定义21s)设拓扑图G,G2,…,Gn具有相同的 Laplacian矩阵如下： 顶点集V,其并集记为G,-m,它的节点集是V,边集 是所有图G,G2,…,Gm的边的并集，它的第i个节点 L= (3) 0m×m 和第j个节点间的链接权重是图第i个节点和第j个 式中：Le为n阶方阵，是跟随者的Laplacian矩阵； 节点间所有的链接权重之和。如果它们的联合图 L为n×m阶矩阵。 G1-m是连通的，称G1,G2,…,Gm为联合连通。 假设1对任意一个跟随者i,至少存在一个领 定义3)考虑如下连续非线性系统：x= 航者j,使得从j到i存在一条通信路径

［６］对动态领航者的二阶系统进行研究，分别提出了 连续渐近包容控制算法和离散渐近包容控制算法。 文献［７］研究了随机切换拓扑下二阶系统的包容控制 问题，提出一种基于不可约马尔可夫链信息拓扑的包 容控制算法。 文献［８］研究了二阶系统的分布式包容 控制问题，并给出了系统收敛的充分必要条件。 从以 上文献研究可知，虽然均能实现系统的包容控制要 求，但是实现时间是不确定的。 在工业应用中，仅实现各个智能体特定状态的 渐近一致还不足以满足工业生产需要，还需要系统 在有限时间内达到收敛。 在航天器编队控制和机器 人编队对抗中，有限时间定理得到广泛应用，由于连 续有限时间控制的优点明显，有限时间控制问题受 到越来越多的关注。 文献［１０］ 对有限时间控制问 题进行了综述，介绍了有限时间稳定性的常用判据 和几类典型系统的有限时间控制。 文献［９］研究了 有限时间收敛和参数不确定性有向系统的姿态包容 控制问题。 文献［１１－１４］指出，连续有限时间控制 系统的验证方法主要包括：齐次性方法和有限时间 李雅普诺夫稳定性定理。 本文研究了静态拓扑和动态拓扑下的二阶多智 能体系统能在有限时间内实现包容控制的问题，本文 的创新点在于提出了动态联合连通条件下具有多领 航者的有限时间的包容控制算法，应用现代控制理论 及矩阵论等理论工具研究了算法的有限时间收敛，在 静态拓扑和动态拓扑下均能达到有限时间收敛。 １ 代数图论 设 Ｇ ＝ （Ｖ，Ｅ，Ａ） 是 ｎ 个节点的权重无向图， Ｖ ＝｛１，２，…，ｎ｝ 为一个顶点（或节点） 集合， Ｅ ⊆ Ｖ ×Ｖ 为一个边的集合， Ａ ＝ ［ａｉｊ］ ∈ Ｒ ｎ×ｎ 为权重邻 接矩阵。 对于 ∀ｉ∈Ｖ ， ａｉｉ ＝ ０；对于 ∀ｉ，ｊ∈Ｖ ， ｉ≠ ｊ ，若 （ｉ，ｊ） ∈ ω ，则 ａｉｊ ＞ ０，否则， ａｉｊ ＝ ０。 节点 ｉ 的 邻居集合定义为 Ｎｉ ＝ ｛ｊ ∈ Ｖ ｜ （ｉ，ｊ） ∈ Ｅ｝ 。 定义 Ｄ ＝ｄｉａｇ（ｄ１ ，ｄ２ ，…，ｄｎ ） ∈ Ｒ ｎ×ｎ 为图 ｘＬ（ｔ） 的度矩 阵，其中 ｄｉ ＝ ∑ ｊ∈Ｎｉ ａｉｊ ， ｉ ＝ １，２，…，ｎ 。 权重图 Ｇ 的 Ｌａｐｌａｃｉａｎ 矩阵定义为： Ｌ ＝ Ｄ － Ａ ∈ Ｒ ｎ×ｎ 。 定义 １ ［５］ 设集合 Ｘ ＝ ｛ｘ１ ，ｘ２ ，…，ｘｍ ｝ 为实向 量空间 Ｖ ⊆ Ｒ ｐ 的子集， Ｘ 的凸包定义为： ＣＯ（Ｘ） ＝ ｛∑ ｍ ｉ ＝ １ αｉ ｘｉ ｜ ｘｉ ∈ Ｘ，αｉ ≥ ０，∑ ｍ ｉ ＝ １ αｉ ＝ １｝ 。 定义 ２ ［１５］ 设拓扑图 Ｇ１ ，Ｇ２ ，…，Ｇｍ 具有相同的 顶点集 Ｖ ，其并集记为 Ｇ１－ｍ ，它的节点集是 Ｖ ，边集 是所有图 Ｇ１ ，Ｇ２ ，…，Ｇｍ 的边的并集，它的第 ｉ 个节点 和第 ｊ 个节点间的链接权重是图第 ｉ 个节点和第 ｊ 个 节点间所有的链接权重之和。 如果它们的联合图 Ｇ１－ｍ 是连通的，称 Ｇ１ ，Ｇ２ ，…，Ｇｍ 为联合连通。 定义 ３ ［１３］ 考虑如下连续非线性系统： ｘ · ＝ ｆ（ｘ） ， ｘ（０） ＝ ｘ０ ∈ Ｒ ｎ 。 其中连续向量流 ｆ（ｘ） ＝ ［ｆ １（ｘ） ｆ ２（ｘ） … ｆ ｎ（ｘ）］ Ｔ 与带有扩张 ｒ ＝ （ｒ１ ， ｒ２ ，…，ｒｎ ） ， ｒｉ ＞ ０ 的度 ｋ ∈ Ｒ 是齐次的，如果对于任 意的 ε ＞ ０， ｘ ∈ Ｒ ｎ 都有 ｆ ｉ（ε ｒ１ ｘ１ ，ε ｒ２ ｘ２ ，…，ε ｒｎ ｘｎ ） ＝ ε ｋ＋ｒ ｉ ｆ ｉ（ｘ） ， ｉ ＝ １，２，…，ｎ 。 引理 １ ［１４］ 设系统 ｘ · ＝ ｆ（ ｘ） ， ｘ（ ０） ＝ ｘ０ ∈ Ｒ ｎ 与带有扩张 （ ｒ１ ，ｒ２ ，…，ｒｎ ） 的度 ｋ ∈ Ｒ 是齐次 的，函数 ｆ（ ｘ） 是连续的，且 ｘ ＝ ０ 是它的一个渐 近稳定平衡点，如果齐次度 ｋ ＜ ０，则该系统就是 有限时间收敛的。 ２ 二阶多自主体系统的包容控制 假设二阶多自主体系统由 ｎ 个跟随者和 ｍ 个 领航者组成，其动力学模型描述为 ｘ · ｉ（ｔ） ＝ ｖｉ（ｔ）， ｖ ·{ ｉ（ｔ） ＝ ｕｉ（ｔ）， ｉ ＝ １，２，…，ｎ，ｎ ＋ １，…，ｎ ＋ ｍ （ １ ） 式中： ｘｉ（ｔ） ∈ Ｒ 表示第 ｉ 个智能体在 ｔ 时刻的位置， ｖｉ（ｔ） ∈ Ｒ 表示速度， ｕｉ（ｔ） ∈ Ｒ 表示控制输入。 跟 随者集合与领航者集合分别记为 Ｆ ＝ ｛１，２，…，ｎ｝ 和 Ｌ ＝ ｛ｎ ＋ １，ｎ ＋ ２，…，ｎ ＋ ｍ｝ ，本文考虑静态领航 者的情况，即 ｖｉ（ｔ） ＝ ０， ｉ ∈ Ｌ 。 本文的研究目标是设计一种控制器，使得系统 能在有限时间内实现包容控制。 考虑如下控制器： ｕｉ（ｔ） ＝ ｓｇｎ｛φ１ ［∑ ｊ∈Ｎｉ ａｉｊ（ｘｊ（ｔ） － ｘｉ（ｔ））］｝ α１ ＋ ｓｇｎ｛φ２ ［∑ ｊ∈Ｎｉ ａｉｊ（ｖｊ（ｔ） － ｖｉ（ｔ））］｝ α２ ，ｉ ∈ Ｆ（ ２ ） 式中： ａｉｊ（ｔ） 表示智能体 ｉ 与 ｊ 在 ｔ 时刻的连接权值， Ｎｉ 表 示 智 能 体 ｉ 的 邻 域， 假 设 φｌ（ｘ） ＝ ［φｌ（ｘ１ ） φｌ（ｘ２ ） … φｌ（ｘｎ ）］ ，且 φｌ 是一个连续 的奇 函 数 满 足 ｘｉφｌ（ｘｉ） ＞ ０（∀ｘｉ ≠ ０） 。 假 设 ｓｇｎ （ｘ） α ＝ ［ｓｇｎ （ｘ１ ） α ｓｇｎ （ｘ２ ） α … ｓｇｎ （ｘｎ ） α ］， ｓｇｎ （ｘｉ） α ＝ ｘｉ α ｓｉｇｎ（ｘｉ） ， ｓｉｇｎ（·） 表示符 号函数。 并且 α１ ， α２ 为常值， ０ ＜ α１ ＜ １， α２ ＝ ２α１ α１ ＋ １ 。 设跟随者之间通信拓扑图为 ＧＦ ，由于跟随者 之间是双向交流信息，所以 ＧＦ 为无向图。 具有领航 者的多自主体系统的通信拓扑图为 Ｇ ， 系统的 Ｌａｐｌａｃｉａｎ 矩阵如下： Ｌ ＝ ＬＦ ＬＦＬ ０ｍ×ｎ ０ｍ×ｍ é ë ê ê ù û ú ú （ ３ ） 式中： ＬＦ 为 ｎ 阶方阵，是跟随者的 Ｌａｐｌａｃｉａｎ 矩阵； ＬＦＬ 为 ｎ × ｍ 阶矩阵。 假设 １ 对任意一个跟随者 ｉ ，至少存在一个领 航者 ｊ ，使得从 ｊ 到 ｉ 存在一条通信路径。 第 ２ 期 庄昊，等： 联合连通拓扑下的二阶多自主体系统有限时间包容控制 ·１８９·

·190· 智能系统学报 第12卷 引理2[]若假设1成立且跟随者之间构成无 (∑ay[)-,()])] 向连通图，则Lp为正定阵，-LL为非负矩阵且 jeNt 每行元素和为1。 afw）-0] ( 令领航者的位置集合为x(t)= [xa+(t)…xntm(t)]T,领航者的速度集合为 T={1,2,…,N},由定义1和引理2，t位于领航者 A,0-] 围成的凸包内。下面给出包容控制的定义。 定理1令跟随者的位置集合为x(t)= ,(∑a[x()-x(t)]) [x(t)…x(t)],跟随者的速度集合为 r(t)=[,(t)…v(t)]T,控制器满足李雅普诺 sgn (Aa,0-1) 夫第二定理，并且若在控制器的作用下有x(t)一→ -LLx(t),(t)→0，表示跟随者位于领航者 围成的凸包内，则控制器可以实现包容控制。 p(∑a[x(t)-x.(t)]) 证明由系统动力学模型和控制器得： ve(t)=sgn([-Lx(t)-LELXL(t)]a+ 「a0-]》' sgn(2[-Lgv(t)-LFLVL(t)]a2 (4) （Aa0-o] 令跟踪方程： (x(t)=x(1)+LF LELX(t) (5) v(t)=v(t)+LF'LELVL(t) g,④-] 根据跟踪方程得： 「p(∑alx()-x(t)]) ve(t)=sgn(i[-Lxe(t)])a+ sgn(2[-Lv(t)]a2 (6) p(∑a[x()-x,()]） sgn jeNz 令 y=-Lx(t) (∑a[x()-x.()]) w=-Lpvp(t) (7) 所以方程(6)可表示为 wsgn [(y)]m 'r(t)=sgm[f(y）]a1+sgn[5(w)]a2,且y=0 得到： (8) V(t)=V(t)+V2(t)= 构造李雅普诺夫函数V(t)=V,(t)+V(t), -w'sgn [o2(w)]42= 式中： (w)sign[(w)] 0=200 -[w1 02…0n] |p2(w2）|2sign[p2(02)] V(t)= ( 2()sign[z(w) 式中：(0)=40-0 sg[p,(s)]ds。考 -（01lp2(01)2+…+|wn川p2(wn)2）≤0 注意到V(t)=0,当且仅当0=0，由 虑李雅普诺夫函数n。,沿着式(6)的导数： xP(x:)>0(Hx:≠0)和式(8)，得到y=0,由 V (t)=v(t)Lgv(t)= 引理2和式(7)得"(t)=0、x(t)=0,所以有 -w'sgn [(y)]"-w"sgn [:(w)] 且只有在平衡点时才有V(t)=0,根据李雅普诺 V()=(∑a,[()-()])× 夫第二定理，此多智能体系统在平衡点是渐近稳 jcN 定的。进一步根据式(5)得到v(t)→-L sgn(a[x(t)-x(]))"V(t)= L(t)、xr(t)→-LFLx(t),再由定理1 含600=豆6w 得出此多智能体系统能够实现包容控制。 由定义3和引理1推出，设扩张系数

引理 ２ ［９］ 若假设 １ 成立且跟随者之间构成无 向连通图，则 ＬＦ 为正定阵， － Ｌ －１ Ｆ ＬＦＬ 为非负矩阵且 每行元素和为 １。 令 领 航 者 的 位 置 集 合 为 ｘＬ（ｔ） ＝ ［ｘｎ＋１（ｔ） … ｘｎ＋ｍ（ｔ）］ Ｔ ，领 航 者 的 速 度 集 合 为 Γ ＝｛１，２，…，Ｎ｝ ，由定义 １ 和引理 ２， ｔ 位于领航者 围成的凸包内。 下面给出包容控制的定义。 定理 １ 令 跟 随 者 的 位 置 集 合 为 ｘＦ（ｔ） ＝ ［ｘ１（ｔ） … ｘｎ（ｔ）］ Ｔ ， 跟 随 者 的 速 度 集 合 为 ｖＦ（ｔ） ＝ ［ｖ１（ｔ） … ｖｎ（ｔ）］ Ｔ ，控制器满足李雅普诺 夫第二定理，并且若在控制器的作用下有 ｘＦ（ｔ） → － Ｌ －１ Ｆ ＬＦＬ ｘＬ（ｔ） ， ｖＦ（ｔ） → ０，表示跟随者位于领航者 围成的凸包内，则控制器可以实现包容控制。 证明 由系统动力学模型和控制器得： ｖ · Ｆ（ｔ） ＝ ｓｇｎ（ φ １ ［ － ＬＦ ｘＦ（ｔ） － ＬＦＬ ｘＬ（ｔ）］） α１ ＋ ｓｇｎ（ φ ２ ［ － ＬＦ ｖＦ（ｔ） － ＬＦＬ ｖＬ（ｔ）］） α２ （ ４ ） 令跟踪方程： ｘ － Ｆ（ｔ） ＝ ｘＦ（ｔ） ＋ Ｌ －１ Ｆ ＬＦＬ ｘＬ（ｔ） ｖ － Ｆ（ｔ） ＝ ｖＦ（ｔ） ＋ Ｌ －１ Ｆ ＬＦＬ ｖＬ（ｔ） { （ ５ ） 根据跟踪方程得： ｖ · Ｆ（ｔ） ＝ ｓｇｎ（ φ １ ［ － ＬＦ ｘ － Ｆ（ｔ）］） α１ ＋ ｓｇｎ（ φ ２ ［ － ＬＦ ｖ － Ｆ（ｔ）］） α２ （ ６ ） 令 ｙ ＝ － ＬＦ ｘ － Ｆ（ｔ） ｗ ＝ － ＬＦ ｖ － Ｆ（ｔ） （ ７ ） 所以方程（６）可表示为 ｖ · Ｆ（ｔ） ＝ ｓｇｎ［ φ １ （ｙ）］ α１ ＋ ｓｇｎ［ φ ２ （ｗ）］ α２ ，且 ｙ · ＝ ｗ （ ８ ） 构造李雅普诺夫函数 Ｖ（ｔ） ＝ Ｖ１（ｔ） ＋ Ｖ２（ｔ） ， 式中： Ｖ１（ｔ） ＝ １ ２ ｖ － Ｔ Ｆ（ｔ） ＬＦ ｖ － Ｆ（ｔ） Ｖ２（ｔ） ＝ ∑ ｎ ｉ ＝ １ Ｖ２ｉ（ｔ） 式中： Ｖ２ｉ（ｔ） ＝ ∫ （ ∑ ｊ∈Ｎｉ ａｉｊ ［ｘｊ （ｔ） －ｘｉ （ｔ）］） Ｔ ０ ｓｇｎ ［φ１（ｓ）］ α１ ｄｓ 。 考 虑李雅普诺夫函数 ｎσ ，沿着式（６）的导数： Ｖ · １（ｔ） ＝ ｖ － Ｔ Ｆ（ｔ） ＬＦ ｖ － · Ｆ（ｔ） ＝ － ｗ Ｔ ｓｇｎ ［φ１（ｙ）］ α１ － ｗ Ｔ ｓｇｎ ［φ２（ｗ）］ α２ Ｖ · ２ｉ（ｔ） ＝ （∑ ｊ∈Ｎｉ ａｉｊ［ｖｊ（ｔ） － ｖｉ（ｔ）］） Ｔ × ｓｇｎ（φ１（∑ ｊ∈Ｎｉ ａｉｊ［ｘｊ（ｔ） － ｘｉ（ｔ）］）） α１Ｖ · ２（ｔ） ＝ ∑ ｎ ｉ ＝ １ Ｖ · ２ｉ（ｔ）Ｖ · ２（ｔ） ＝ ∑ ｎ ｉ ＝ １ Ｖ · ２ｉ（ｔ） ＝ （∑ ｊ∈Ｎ１ ａ１ｊ［ｖｊ（ｔ） － ｖ１（ｔ）］） Ｔ （∑ ｊ∈Ｎ２ ａ２ｊ［ｖｊ（ｔ） － ｖ２（ｔ）］） Ｔ ︙ （∑ ｊ∈Ｎｎ ａｎｊ［ｖｊ（ｔ） － ｖｎ（ｔ）］） Ｔ é ë ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú α１ × ｓｇｎ φ１（∑ ｊ∈Ｎ１ ａ１ｊ［ｘｊ（ｔ） － ｘ１（ｔ）］） φ１（∑ ｊ∈Ｎ２ ａ２ｊ［ｘｊ（ｔ） － ｘ２（ｔ）］） ︙ φ１（∑ ｊ∈Ｎｎ ａｎｊ［ｘｊ（ｔ） － ｘｎ（ｔ）］） é ë ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú α１ ＝ （∑ ｊ∈Ｎ１ ａ１ｊ［ｖｊ（ｔ） － ｖ１（ｔ）］） Ｔ （∑ ｊ∈Ｎ２ ａ２ｊ［ｖｊ（ｔ） － ｖ２（ｔ）］） Ｔ ︙ （∑ ｊ∈Ｎｎ ａｎｊ［ｖｊ（ｔ） － ｖｎ（ｔ）］） Ｔ é ë ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú α１ × ｓｇｎ φ１（∑ ｊ∈Ｎ１ ａ１ｊ［ｘｊ（ｔ） － ｘ１（ｔ）］） φ１（∑ ｊ∈Ｎ２ ａ２ｊ［ｘｊ（ｔ） － ｘ２（ｔ）］） ︙ φ１（∑ ｊ∈Ｎｎ ａｎｊ［ｘｊ（ｔ） － ｘｎ（ｔ）］） é ë ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú α１ ＝ ｗ Ｔ ｓｇｎ ［φ１（ｙ）］ α１ 得到： Ｖ · （ｔ） ＝ Ｖ · １（ｔ） ＋ Ｖ · ２（ｔ） ＝ － ｗ Ｔ ｓｇｎ ［φ２（ｗ）］ α２ ＝ － ［ｗ１ ｗ２ … ｗｎ ］ φ２（ｗ１ ） α２ ｓｉｇｎ［φ２（ｗ１ ）］ φ２（ｗ２ ） α２ ｓｉｇｎ［φ２（ｗ２ ）］ ︙ φ２（ｗｎ ） α２ ｓｉｇｎ［φ２（ｗｎ ）］ é ë ê ê ê ê êê ù û ú ú ú ú úú ＝ － （ ｗ１ φ２（ｗ１ ） φ２ ＋ … ＋ ｗｎ φ２（ｗｎ ） φ２ ） ≤ ０ 注 意 到 Ｖ · （ ｔ） ＝ ０， 当 且 仅 当 ｗ ＝ ０， 由 ｘｉφｌ（ ｘｉ） ＞ ０（∀ｘｉ ≠ ０） 和式（ ８） ，得到 ｙ ＝ ０，由 引理 ２ 和式（ ７）得 ｖ － Ｆ（ ｔ） ＝ ０、 ｘ － Ｆ（ ｔ） ＝ ０，所以有 且只有在平衡点时才有 Ｖ · （ ｔ） ＝ ０，根据李雅普诺 夫第二定理，此多智能体系统在平衡点是渐近稳 定的。 进 一 步 根 据 式 （ ５ ） 得 到 ｖＦ（ ｔ） → － Ｌ － １ Ｆ ＬＦＬ ｖＬ（ ｔ） 、 ｘＦ（ ｔ） → － Ｌ － １ Ｆ ＬＦＬ ｘＬ（ ｔ） ， 再由定理 １ 得出此多智能体系统能够实现包容控制。 由定 义 ３ 和 引 理 １ 推 出， 设 扩 张 系 数 ·１９０· 智 能 系 统 学 报 第 １２ 卷

第2期 庄吴，等：联合连通拓扑下的二阶多自主体系统有限时间包容控制 ·191. (2,2,…,2,a1+1,a1+1,…a1+1),并且11=2， 领航者d。个，跟随者d。个，满足d。=d。+d.。 矩阵块L。为拓扑图G相对应的Laplacian矩阵。 r2=a1+1,k=a1-10。 在每个时间段[，w,41)内此多智能体系统可 假设每个时间段[(，‘+1)中存在一组非重叠的有限 以被分成n。个子系统，在每个时间段内的 子序列[4*1)，广=1,2，…，m,,且系统拓扑在 Laplacian矩阵为 [l,l41)内保持不变，其中1=4，，tm,+1=t+1, Lirue rw*1-tw≥T,T2>0。令o(t):[0,+o)→T, 。= (16) 0doxd0oxdo」 T={1,2,…,N}为一个分段切换常函数，N为总拓 扑数。系统在t时刻的信息拓扑图记为Go,相应 由系统动力学模型和控制器得，在时间段[， 的Laplacian矩阵记为Lw。其中，由n个跟随者 wt1)内： 构成的信息拓扑图记为Gr.o,相应的Laplacian矩 (t)=sgn(p[-LFex(t）-Loxi(t)])▣+ 阵记为Lpa(0o sgn(2[-Lre vro(t)-Lr vin(t)] 假设2由n个跟随者和m个领航者构成的网 (17) 络化系统拓扑在非重叠时间区间[t,t,+1),T=1, 令跟踪方程： 2,…内为联合连通的。 ((t)=x(t)+(Lr)Lxi(t) 假设3非重叠时间区间[tw,t+1)C[t, t+1),j=1,2,…,m,内，网络化系统存在一连通子 vre(t)=vre(t)+(LFe)LgLovin(t) 集。连通子集中任意一个跟随者i,至少与一个领 (18) 航者j之间存在一条路径。 根据跟踪方程得出： 假设系统通信拓扑图G。在时间段[t,t,+1)内 vio(t)=sgn([-Lee xro(t)])" 有。≥1个连通部分，且连通成分的子拓扑图记为 sgn(2[-Lre vre(t)])2 (19) G。,i=1,2,…,n。。图G内有d≥1个节点，其中 根据假设3、引理2、定理1得出，此二阶多智能

（２þ ，２ï ，ý…ï ，ü２ ｎ ，α１ ＋ １，α１ ＋ １，…α１ ＋ １ þ ï ï ï ï ý ï ï ï ï ü ｎ ） ，并且 ｒ１ ＝ ２， ｒ２ ＝ α１ ＋ １， ｋ ＝ α１ － １ ＜ ０。 假设原动力学方程可写为 ｆ １（ｘｉ，ｖｉ） ＝ ｖｉ ｆ ２（ｘｉ，ｖｉ） ＝ ｕｉ { （ ９ ） 则有 ｆ １（ε ｒ１ ｘｉ，ε ｒ２ ｖｉ） ＝ ε ｒ２ ｖｉ ＝ ε ｋ＋ｒ１ ｆ １（ｘｉ，ｖｉ） ｆ ２（ε ｒ１ ｘｉ，ε ｒ２ ｖｉ） ＝ ｓｇｎ（ φ １ ［∑ ｊ∈Ｎｉ ａｉｊ（ε ｒ１ ｘｊ － ε ｒ１ ｘｉ）］） α１ ＋ ｓｇｎ（ φ ２ ［∑ ｊ∈Ｎｉ ａｉｊ（ε ｒ２ ｖｊ － ε ｒ２ ｖｉ）］） α２ ＝ ε ｒ１α１ ｓｇｎ（ φ １ ［∑ ｊ∈Ｎｉ ａｉｊ（ｘｊ － ｘｉ）］） α１ ＋ ε ｒ２α２ ｓｇｎ（ φ ２ ［∑ ｊ∈Ｎｉ ａｉｊ（ｖｊ － ｖｉ）］） α２ 由已知得： ε ｒ１α１ ＝ ε ｒ２α２ ＝ ε ｋ＋ｒ２ ，所以上式可写为 ｆ ２（ε ｒ１ ｘｉ，ε ｒ２ ｖｉ） ＝ ε ｋ＋ｒ２ ｆ ２（ｘｉ，ｖｉ） 此 多 智 能 体 系 统 与 带 有 扩 张 （ ２þ ，２ï ，ý…ï ，ü２ ｎ ， α１ ＋ １，α１ ＋ １，…α１ ＋ １ þ ï ï ï ï ý ï ï ï ï ü ｎ ） 的度 ｋ ＝ α１ － １ ＜ ０ 是同 次的。 因此，由引理 １ 得到此系统可以达到有限时 间收敛。 ３ 联合连通下的控制算法分析 本节讨论多自主体系统在运动过程，出现通信 拓扑不连通的情况。 系统动力学模型和控制器不 变，动力学模型为式 （１） ，控制器为式 （２） 。 在联 合连通条件下分析此系统。 考虑一组无穷有序的有界连续时间段 ［ｔ ｒ， ｔ ｒ＋１ ） ， ｒ ＝ １，２，… ，且 ｔ １ ＝ ０， ｔ ｒ＋１ － ｔ ｒ ≤ Ｔ１ ， Ｔ１ ＞ ０。 假设每个时间段 ［ｔ ｒ，ｔ ｒ＋１ ） 中存在一组非重叠的有限 子序列 ［ｔ ｒ，ｊ，ｔ ｒ，ｊ＋１ ） ， ｊ ＝ １，２，…，ｍｒ ，且系统拓扑在 ［ｔ ｒ，ｊ，ｔ ｒ，ｊ＋１ ） 内保持不变，其中 ｔ ｒ，１ ＝ ｔ ｒ ， ｔ ｒ，ｍｒ ＋１ ＝ ｔ ｒ＋１ ， ｔ ｒ，ｊ＋１ － ｔ ｒ，ｊ ≥ Ｔ２ ， Ｔ２ ＞ ０。 令 σ（ｔ）：［０， ＋ ¥） → Γ ， Γ ＝ ｛１，２，…，Ｎ｝ 为一个分段切换常函数， Ｎ 为总拓 扑数。 系统在 ｔ 时刻的信息拓扑图记为 Ｇσ（ｔ） ，相应 的 Ｌａｐｌａｃｉａｎ 矩阵记为 Ｌσ（ｔ） 。 其中，由 ｎ 个跟随者 构成的信息拓扑图记为 ＧＦσ（ｔ） ，相应的 Ｌａｐｌａｃｉａｎ 矩 阵记为 ＬＦσ（ｔ） 。 假设 ２ 由 ｎ 个跟随者和 ｍ 个领航者构成的网 络化系统拓扑在非重叠时间区间 ［ｔ ｒ，ｔ ｒ＋１ ） ， ｒ ＝ １， ２，… 内为联合连通的。 假设 ３ 非重叠时间区间 ［ｔ ｒ，ｊ，ｔ ｒ，ｊ＋１ ） ⊂ ［ｔ ｒ， ｔ ｒ＋１ ） ， ｊ ＝ １，２，…，ｍｒ 内，网络化系统存在一连通子 集。 连通子集中任意一个跟随者 ｉ ，至少与一个领 航者 ｊ 之间存在一条路径。 假设系统通信拓扑图 Ｇσ 在时间段 ［ｔ ｒ，ｊ，ｔ ｒ，ｊ＋１ ） 内 有 ｎσ ≥ １ 个连通部分，且连通成分的子拓扑图记为 Ｇ ｉ σ ， ｉ ＝ １，２，…，ｎσ 。 图 Ｇ ｉ σ 内有 ｄ ｉ σ ≥１ 个节点，其中 领航者 ｄ ｉ Ｌσ 个，跟随者 ｄ ｉ Ｆσ 个，满足 ｄ ｉ σ ＝ ｄ ｉ Ｌσ ＋ ｄ ｉ Ｆσ 。 矩阵块 Ｌ ｉ σ 为拓扑图 Ｇ ｉ σ 相对应的 Ｌａｐｌａｃｉａｎ 矩阵。 根据Ｌσ 的定义，存在一个正交矩阵Ｅσ ∈Ｒ ｎ×ｎ ，使： Ｅ Ｔ σ Ｌσ Ｅσ ＝ ｄｉａｇ（Ｌ １ σ ，Ｌ ２ σ ，…，Ｌ ｎσ σ ） （ １０ ） ｘ Ｔ （ｔ） Ｅσ ＝ ［ｘ １Ｔ σ （ｔ） ｘ ２Ｔ σ （ｔ） … ｘ ｎσＴ σ （ｔ）］ （ １１ ） ｖ Ｔ （ｔ） Ｅσ ＝ ［ｖ １Ｔ σ （ｔ） ｖ ２Ｔ σ （ｔ） … ｖ ｎσＴ σ （ｔ）］ （ １２ ） 式中： ｘ ｉＴ σ （ｔ） ＝ ［ｘ ｉ σ１（ｔ） … ｘ ｉ σｄ ｉ Ｆσ （ｔ） ｘ ｉ σｄ ｉ Ｆσ ＋１（ｔ） … ｘ ｉ σｄ ｉ σ （ｔ）］ ｉ ＝ １，２，…，ｎσ （ １３ ） ｖ ｉＴ σ （ｔ） ＝ ［ｖ ｉ σ１（ｔ） … ｖ ｉ σｄ ｉ Ｆσ （ｔ） ｖ ｉ σｄ ｉ Ｆσ ＋１（ｔ） … ｖ ｉ σｄ ｉ σ （ｔ）］ ｉ ＝ １，２，…，ｎσ （ １４ ） 在动态切换拓扑下网络化系统的 Ｌａｐｌａｃｉａｎ 矩 阵为 Ｌσ ＝ ＬＦσ ＬＦＬσ ０ｍ×ｎ ０ｍ×ｍ é ë ê ê ù û ú ú （ １５ ） 令 ｘ（ｔ） ＝ ［ｘ Ｔ Ｆ（ｔ） ｘ Ｔ Ｌ（ｔ）］ Ｔ ， ｖ（ｔ） ＝ ［ｖ Ｔ Ｆ（ｔ） ｖ Ｔ Ｌ（ｔ）］ Ｔ 。 ｘＦ（ｔ） 表示跟随者的位置， ｘＬ（ｔ） 表示领航者的位 置， ｖＦ（ｔ） 表 示 跟 随 者 的 速 度， ｖＬ（ｔ） 表示领航者的速度。 其中： ｘＦ（ｔ） ＝ ［ｘ１（ｔ） ｘ２（ｔ） … ｘｎ（ｔ）］ Ｔ ｘＬ（ｔ） ＝ ［ｘｎ＋１（ｔ） ｘｎ＋２（ｔ） … ｘｎ＋ｍ（ｔ）］ Ｔ ｖＦ（ｔ） ＝ ［ｖ１（ｔ） ｖ２（ｔ） … ｖｎ（ｔ）］ Ｔ ｖＬ（ｔ） ＝ ［ｖｎ＋１（ｔ） ｖｎ＋２（ｔ） … ｖｎ＋ｍ（ｔ）］ Ｔ 在每个时间段 ［ｔ ｒ，ｊ，ｔ ｒ，ｊ＋１ ） 内此多智能体系统可 以被 分 成 ｎσ 个 子 系 统， 在 每 个 时 间 段 内 的 Ｌａｐｌａｃｉａｎ 矩阵为 Ｌ ｉ σ ＝ Ｌ ｉ Ｆσ ０ｄ ｉ Ｌσ ×ｄ ｉ Ｆσ é ë ê ê Ｌ ｉ ＦＬσ ０ｄ ｉ Ｌσ ×ｄ ｉ Ｌσ ù û ú ú （ １６ ） 由系统动力学模型和控制器得，在时间段 ［ｔ ｒ，ｊ， ｔ ｒ，ｊ＋１ ） 内： ｖ ·ｉ Ｆσ（ｔ） ＝ ｓｇｎ（φ１ ［ － Ｌ ｉ Ｆσ ｘ ｉ Ｆσ（ｔ） － Ｌ ｉ ＦＬσ ｘ ｉ Ｌσ（ｔ）］） α１ ＋ ｓｇｎ（φ２ ［ － Ｌ ｉ Ｆσ ｖ ｉ Ｆσ（ｔ） － Ｌ ｉ ＦＬσ ｖ ｉ Ｌσ（ｔ）］） α２ （ １７ ） 令跟踪方程： ｘ － ｉ Ｆσ（ｔ） ＝ ｘ ｉ Ｆσ（ｔ） ＋ （Ｌ ｉ Ｆσ ） －１ Ｌ ｉ ＦＬσ ｘ ｉ Ｌσ（ｔ） ｖ － ｉ Ｆσ（ｔ） ＝ ｖ ｉ Ｆσ（ｔ） ＋ （Ｌ ｉ Ｆσ ） －１ Ｌ ｉ ＦＬσ ｖ ｉ Ｌσ（ｔ） { （ １８ ） 根据跟踪方程得出： ｖ ·ｉ Ｆσ（ｔ） ＝ ｓｇｎ（φ１ ［ － Ｌ ｉ Ｆσ ｘ － ｉ Ｆσ（ｔ）］） α１ ＋ ｓｇｎ（φ２ ［ － Ｌ ｉ Ｆσ ｖ － ｉ Ｆσ（ｔ）］） α２ （ １９ ） 根据假设 ３、引理 ２、定理 １ 得出，此二阶多智能 第 ２ 期 庄昊，等： 联合连通拓扑下的二阶多自主体系统有限时间包容控制 ·１９１·

.192 智能系统学报 第12卷 体系统在联合连通条件下可以实现包容控制。 0 下面证明多智能体系统在联合连通条件下可以 实现有限时间收敛。令： 0 yi=-Lixe(t),wi=-Lrovre(t)20) 所以 vr(t)=sgn[(yi)a+sgn[(w)a2 且y=w (21) 构造李雅普诺夫函数V(t)=(t)+(t),其中： n0)=20L(0 图1跟随者与领航者静态拓扑图 r()=立()()= o Fig.1 The static topological graph of followers and leaders 令拓扑图每个边的权重均相等，假设为1。选 个a0-ao 取a1=0.8,a2=2a1/(a1+1),P(x)=3x, 式中：V(t)= sgm[p(s)]ds。 P,(x)=3x。目标区域的3个顶点位置为：专6= 上述李雅普诺夫函数沿着方程(19)的导数： [810],,=[108],专8=[1010]'，各跟随 (t)=(t)+(t)= 者的初始位置为：专，(0)=[20]T,专，(0)= -（|wIp2(wi)|2+…+w6|p2(wd)）≤0 [40]r,5(0)=[02]T,(0)=[04]r, 注意到V(t)=0当且仅当w=0,由x:P,(x:)> 专(0)=[31]”。各跟随者的初速度为：，(0)= 0(Hx,≠0)和式(21)，得到y=0,由引理2和式 [26],2(0)=[38]',(0)=[46], (20)得m(t)=0、x(t)=0,所以有且只有在平衡 ,(0)=[55]r,,(0)=[63]T。 基于图1的拓扑图以及上述初始条件，分别应 点时才有V(t)=0,根据李雅普诺夫第二定理，得到 联合连通条件下此多智能体系统在[1，，4，+)时间 用本文设计的控制器u,(t)=sgn(,(∑a,[x(t)- ie v 段内在平衡点是渐近稳定的。进一步根据式(18) 得到n(t)→(Lm)Lm(t)、xn(t)→ x()])+sg(92(∑a[()-()]),称 (L,）-1Lx(t),再由定理1得出此多智能体系 为控制器（1)；和一种传统控制策略u(t)= 统在联合连通条件下能够实现包容控制。 sgn(∑a,[x,()-x,()])+sgm(∑a,[y,()- 由于在每个时间段[1，，，+1)内此多智能体系 jeN 统被分为n。个子系统，由定义3和引理1分析知此 ,(t)]),称为控制器2：进行仿真实验。 多智能体系统与带有扩张（2,2，…，2 应用控制器1与控制器2的各个智能体的位 置、速度与时间的关系如图2~5。 1+1,a1+1,…,&1+1)的度k=a1-1<0是同 d 跟随者1跟随者2跟随者3 次的。因此，由引理1得到此多智能体系统可以达 到有限时间收敛。 4仿真验证 跟随者4跟随者5 4.1静态拓扑仿真 设系统中有5个跟随者，跟随者集合为F={1, 2,3,4,5},要将这5个跟随者控制到三角形区域内， 假设系统信息拓扑图如图1所示，取如下系统矩阵： 2-10001 101520 -12-100 s Le= 0 -13-10 图2控制器1跟随者位置横坐标与时间关系 0 0 -12 -1 Fig.2 The relationship between the abscissa of followers 00 0-12 position under the action of controllerl and time

体系统在联合连通条件下可以实现包容控制。 下面证明多智能体系统在联合连通条件下可以 实现有限时间收敛。 令： ｙ ｉ ＝ － Ｌ ｉ Ｆσ ｘ － ｉ Ｆσ（ｔ），ｗ ｉ ＝ － Ｌ ｉ Ｆσ ｖ － ｉ Ｆσ（ｔ） （ ２０ ） 所以 ｖ · ｉ Ｆσ（ｔ） ＝ ｓｇｎ［ φ １ （ｙ ｉ ）］ α１ ＋ ｓｇｎ［ φ ２ （ｗ ｉ ）］ α２ 且 ｙ · ｉ ＝ ｗ ｉ （ ２１ ） 构造李雅普诺夫函数 Ｖ ｉ （ｔ） ＝ Ｖ ｉ １（ｔ） ＋ Ｖ ｉ ２（ｔ） ，其中： Ｖ ｉ １（ｔ） ＝ １ ２ ｖ － ｉＴ Ｆσ（ｔ） Ｌ ｉ Ｆσ ｖ － ｉ Ｆσ（ｔ） Ｖ ｉ ２（ｔ） ＝ ∑ ｎ ｚ ＝ １ Ｖ ｉ ２ｚ（ｔ）Ｖ ｉ ２（ｔ） ＝ ∑ ｎ ｚ ＝ １ Ｖ ｉ ２ｚ（ｔ） 式中： Ｖ ｉ ２ｚ（ｔ） ＝ ∫ （∑ ｄ ｉ σ ｊ ＝ １ ａｚｊ ［ｘσｊ （ｔ） －ｘσｚ （ｔ）］） Ｔ ０ ｓｇｎ ［φ１（ｓ ｉ ）］ α１ ｄｓ ｉ 。 上述李雅普诺夫函数沿着方程（１９）的导数： Ｖ · ｉ （ｔ） ＝ Ｖ · ｉ １（ｔ） ＋ Ｖ · ｉ ２（ｔ） ＝ － （ ｗ ｉ １ φ２（ｗ ｉ １ ） φ２ ＋ … ＋ ｗ ｉ ｄ ｉ σ φ２（ｗ ｉ ｄ ｉ σ ） φ２ ） ≤ ０ 注意到 Ｖ · ｉ （ｔ） ＝ ０ 当且仅当 ｗ ｉ ＝ ０，由 ｘｉφｌ（ｘｉ） ＞ ０（∀ｘｉ ≠ ０） 和式（２１），得到 ｙ ｉ ＝ ０，由引理 ２ 和式 （２０）得 ｖ － ｉ Ｆσ（ｔ） ＝ ０、 ｘ － ｉ Ｆσ（ｔ） ＝ ０，所以有且只有在平衡 点时才有 Ｖ · ｉ （ｔ） ＝ ０，根据李雅普诺夫第二定理，得到 联合连通条件下此多智能体系统在 ［ｔ ｒ，ｊ，ｔ ｒ，ｊ＋１ ） 时间 段内在平衡点是渐近稳定的。 进一步根据式（１８） 得 到 ｖ ｉ Ｆσ（ｔ） → （Ｌ ｉ Ｆσ ） －１ Ｌ ｉ ＦＬσ ｖ ｉ Ｌσ（ｔ） 、 ｘ ｉ Ｆσ（ｔ） → （Ｌ ｉ Ｆσ ） －１ Ｌ ｉ ＦＬσ ｘ ｉ Ｌσ（ｔ） ，再由定理 １ 得出此多智能体系 统在联合连通条件下能够实现包容控制。 由于在每个时间段 ［ｔ ｒ，ｊ，ｔ ｒ，ｊ＋１ ） 内此多智能体系 统被分为 ｎσ 个子系统，由定义 ３ 和引理 １ 分析知此 多 智 能 体 系 统 与 带 有 扩 张 （ ２þ ，２ï ，ý…ï ，ü２ ｄ ｉ σ ， α１ ＋ １，α１ ＋ １，…，α１ ＋ １ þ ï ï ï ï ý ï ï ï ï ï ü ｄ ｉ σ ） 的度 ｋ ＝ α１ － １ ＜ ０ 是同 次的。 因此，由引理 １ 得到此多智能体系统可以达 到有限时间收敛。 ４ 仿真验证 ４．１ 静态拓扑仿真 设系统中有 ５ 个跟随者，跟随者集合为 Ｆ ＝ ｛１， ２，３，４，５｝ ，要将这 ５ 个跟随者控制到三角形区域内， 假设系统信息拓扑图如图 １ 所示，取如下系统矩阵： ＬＦ ＝ ２ － １ ０ ０ ０ － １ ２ － １ ０ ０ ０ － １ ３ － １ ０ ０ ０ － １ ２ － １ ０ ０ ０ － １ ２ é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú ＬＦＬ ＝ － １ ０ ０ ０ ０ ０ ０ － １ ０ ０ ０ ０ ０ ０ － １ é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú 图 １ 跟随者与领航者静态拓扑图 Ｆｉｇ．１ Ｔｈｅ ｓｔａｔｉｃ ｔｏｐｏｌｏｇｉｃａｌ ｇｒａｐｈ ｏｆ ｆｏｌｌｏｗｅｒｓ ａｎｄ ｌｅａｄｅｒｓ 令拓扑图每个边的权重均相等，假设为 １。 选 取 α１ ＝ ０．８， α２ ＝ ２α１ ／ （α１ ＋ １） ， φ１（ｘ） ＝ ３ｘ ， φ２（ｘ） ＝３ｘ 。 目标 区 域 的 ３ 个 顶 点 位 置 为： ξ６ ＝ ［８ １０］ Ｔ ， ξ７ ＝ ［１０ ８］ Ｔ ， ξ８ ＝ ［１０ １０］ Ｔ ，各跟随 者的 初 始 位 置 为： ξ１（０） ＝ ［２ ０］ Ｔ ， ξ２（０） ＝ ［４ ０］ Ｔ ， ξ３（０） ＝ ［０ ２］ Ｔ ， ξ４（０） ＝ ［０ ４］ Ｔ ， ξ５（０） ＝ ［３ １］ Ｔ 。 各跟随者的初速度为： ｖ１（０） ＝ ［２ ６］ Ｔ ， ｖ２（０） ＝ ［３ ８］ Ｔ ， ｖ３（０） ＝ ［４ ６］ Ｔ ， ｖ４（０） ＝ ［５ ５］ Ｔ ， ｖ５（０） ＝ ［６ ３］ Ｔ 。 基于图 １ 的拓扑图以及上述初始条件，分别应 用本文设计的控制器 ｕｉ（ｔ） ＝ ｓｇｎ（φ１（∑ ｊ∈Ｎｉ ａｉｊ［ｘｊ（ｔ） － ｘｉ（ｔ）］）） α１ ＋ ｓｇｎ（φ２（∑ ｊ∈Ｎｉ ａｉｊ［ｖｊ（ｔ） － ｖｉ（ｔ）］）） α２ ，称 为控 制 器 （ １ ）； 和 一 种 传 统 控 制 策 略 ｕｉ（ｔ） ＝ ｓｇｎ（∑ ｊ∈Ｎｉ ａｉｊ［ｘｊ（ｔ） － ｘｉ（ｔ）］） ＋ ｓｇｎ（∑ ｊ∈Ｎｉ ａｉｊ［ｖｊ（ｔ） － ｖｉ（ｔ）］） ，称为控制器 ２；进行仿真实验。 应用控制器 １ 与控制器 ２ 的各个智能体的位 置、速度与时间的关系如图 ２～５。 图 ２ 控制器 １ 跟随者位置横坐标与时间关系 Ｆｉｇ．２ Ｔｈｅ ｒｅｌａｔｉｏｎｓｈｉｐ ｂｅｔｗｅｅｎ ｔｈｅ ａｂｓｃｉｓｓａ ｏｆ ｆｏｌｌｏｗｅｒｓ’ ｐｏｓｉｔｉｏｎ ｕｎｄｅｒ ｔｈｅ ａｃｔｉｏｎ ｏｆ ｃｏｎｔｒｏｌｌｅｒ１ ａｎｄ ｔｉｍｅ ·１９２· 智 能 系 统 学 报 第 １２ 卷

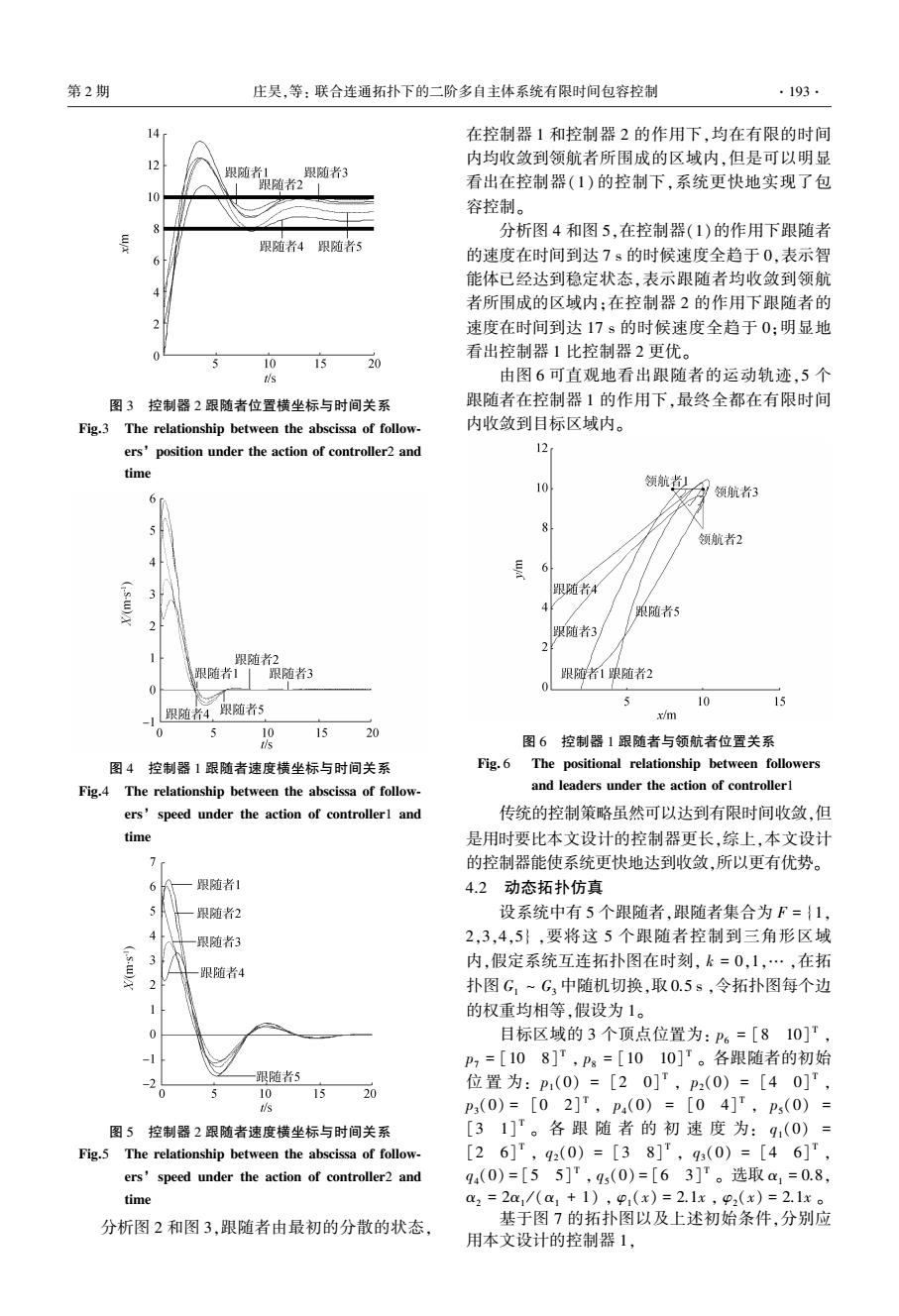
第2期 庄吴，等：联合连通拓扑下的二阶多自主体系统有限时间包容控制 .193, 14 在控制器1和控制器2的作用下，均在有限的时间 内均收敛到领航者所围成的区域内，但是可以明显 跟随者 跟随者3 跟随者2 看出在控制器(1)的控制下，系统更快地实现了包 10 容控制。 分析图4和图5，在控制器(1)的作用下跟随者 跟随者4跟随者5 的速度在时间到达7s的时候速度全趋于0，表示智 能体已经达到稳定状态，表示跟随者均收敛到领航 者所围成的区域内：在控制器2的作用下跟随者的 速度在时间到达17s的时候速度全趋于0：明显地 101520 看出控制器1比控制器2更优。 於 由图6可直观地看出跟随者的运动轨迹，5个 图3控制器2跟随者位置横坐标与时间关系 跟随者在控制器1的作用下，最终全都在有限时间 Fig.3 The relationship between the abscissa of follow- 内收敛到目标区域内。 ers'position under the action of controller2 and 12 time 10 领航者) 分领航者3 5 领航者2 6 跟随者4 4 踉随者5 跟随者3 3 跟随者2 跟随者1跟随者3 跟随者1跟随者2 跟随者4跟随者5 5 10 15 x/m 0 5 1520 图6控制器1跟随者与领航者位置关系 图4控制器1跟随者速度横坐标与时间关系 Fig.6 The positional relationship between followers Fig.4 The relationship between the abscissa of follow- and leaders under the action of controllerl ers'speed under the action of controllerl and 传统的控制策略虽然可以达到有限时间收敛，但 time 是用时要比本文设计的控制器更长，综上，本文设计 的控制器能使系统更快地达到收敛，所以更有优势。 跟随者1 4.2动态拓扑仿真 跟随者2 设系统中有5个跟随者，跟随者集合为F={1, 4 跟随者3 2,3,4,5},要将这5个跟随者控制到三角形区域 3 内，假定系统互连拓扑图在时刻，k=0,1,…,在拓 跟随者4 2 扑图G~G3中随机切换，取0.5s,令拓扑图每个边 的权重均相等，假设为1。 0 目标区域的3个顶点位置为：P6=[810]r, P,=[108]T,P=[1010]T。各跟随者的初始 -跟随者5 15 20 位置为：P(0)=[20]T,P2(0)=[40]T, 10 P(0)=[02]T,p4(0)=[04]T,P(0)= 图5控制器2跟随者速度横坐标与时间关系 [31]。各跟随者的初速度为：9(0)= Fig.5 The relationship between the abscissa of follow- [26]T,92(0)=[38],93(0)=[46]T, ers'speed under the action of controller2 and 9.(0)=[55]T,95(0)=[63]。选取a1=0.8, time a2=2a1/(a1+1),9(x)=2.1x,p2(x)=2.1x。 分析图2和图3，跟随者由最初的分散的状态， 基于图7的拓扑图以及上述初始条件，分别应 用本文设计的控制器1

图 ３ 控制器 ２ 跟随者位置横坐标与时间关系 Ｆｉｇ．３ Ｔｈｅ ｒｅｌａｔｉｏｎｓｈｉｐ ｂｅｔｗｅｅｎ ｔｈｅ ａｂｓｃｉｓｓａ ｏｆ ｆｏｌｌｏｗ⁃ ｅｒｓ’ ｐｏｓｉｔｉｏｎ ｕｎｄｅｒ ｔｈｅ ａｃｔｉｏｎ ｏｆ ｃｏｎｔｒｏｌｌｅｒ２ ａｎｄ ｔｉｍｅ 图 ４ 控制器 １ 跟随者速度横坐标与时间关系 Ｆｉｇ．４ Ｔｈｅ ｒｅｌａｔｉｏｎｓｈｉｐ ｂｅｔｗｅｅｎ ｔｈｅ ａｂｓｃｉｓｓａ ｏｆ ｆｏｌｌｏｗ⁃ ｅｒｓ’ ｓｐｅｅｄ ｕｎｄｅｒ ｔｈｅ ａｃｔｉｏｎ ｏｆ ｃｏｎｔｒｏｌｌｅｒ１ ａｎｄ ｔｉｍｅ 图 ５ 控制器 ２ 跟随者速度横坐标与时间关系 Ｆｉｇ．５ Ｔｈｅ ｒｅｌａｔｉｏｎｓｈｉｐ ｂｅｔｗｅｅｎ ｔｈｅ ａｂｓｃｉｓｓａ ｏｆ ｆｏｌｌｏｗ⁃ ｅｒｓ’ ｓｐｅｅｄ ｕｎｄｅｒ ｔｈｅ ａｃｔｉｏｎ ｏｆ ｃｏｎｔｒｏｌｌｅｒ２ ａｎｄ ｔｉｍｅ 分析图 ２ 和图 ３，跟随者由最初的分散的状态， 在控制器 １ 和控制器 ２ 的作用下，均在有限的时间 内均收敛到领航者所围成的区域内，但是可以明显 看出在控制器（１）的控制下，系统更快地实现了包 容控制。 分析图 ４ 和图 ５，在控制器（１）的作用下跟随者 的速度在时间到达 ７ ｓ 的时候速度全趋于 ０，表示智 能体已经达到稳定状态，表示跟随者均收敛到领航 者所围成的区域内；在控制器 ２ 的作用下跟随者的 速度在时间到达 １７ ｓ 的时候速度全趋于 ０；明显地 看出控制器 １ 比控制器 ２ 更优。 由图 ６ 可直观地看出跟随者的运动轨迹，５ 个 跟随者在控制器 １ 的作用下，最终全都在有限时间 内收敛到目标区域内。 图 ６ 控制器 １ 跟随者与领航者位置关系 Ｆｉｇ． ６ Ｔｈｅ ｐｏｓｉｔｉｏｎａｌ ｒｅｌａｔｉｏｎｓｈｉｐ ｂｅｔｗｅｅｎ ｆｏｌｌｏｗｅｒｓ ａｎｄ ｌｅａｄｅｒｓ ｕｎｄｅｒ ｔｈｅ ａｃｔｉｏｎ ｏｆ ｃｏｎｔｒｏｌｌｅｒ１ 传统的控制策略虽然可以达到有限时间收敛，但 是用时要比本文设计的控制器更长，综上，本文设计 的控制器能使系统更快地达到收敛，所以更有优势。 ４．２ 动态拓扑仿真 设系统中有 ５ 个跟随者，跟随者集合为 Ｆ ＝ ｛１， ２，３，４，５｝ ，要将这 ５ 个跟随者控制到三角形区域 内，假定系统互连拓扑图在时刻， ｋ ＝ ０，１，… ，在拓 扑图 Ｇ１ ～ Ｇ３ 中随机切换，取 ０．５ ｓ ，令拓扑图每个边 的权重均相等，假设为 １。 目标区域的 ３ 个顶点位置为： ｐ６ ＝ ［８ １０］ Ｔ ， ｐ７ ＝ ［１０ ８］ Ｔ ， ｐ８ ＝ ［１０ １０］ Ｔ 。 各跟随者的初始 位 置 为： ｐ１（０） ＝ ［２ ０］ Ｔ ， ｐ２（０） ＝ ［４ ０］ Ｔ ， ｐ３（０） ＝ ［０ ２］ Ｔ ， ｐ４（０） ＝ ［０ ４］ Ｔ ， ｐ５（０） ＝ ［３ １］ Ｔ 。 各 跟 随 者 的 初 速 度 为： ｑ１（０） ＝ ［２ ６］ Ｔ ， ｑ２（０） ＝ ［３ ８］ Ｔ ， ｑ３（０） ＝ ［４ ６］ Ｔ ， ｑ４（０） ＝ ［５ ５］ Ｔ ， ｑ５（０） ＝ ［６ ３］ Ｔ 。 选取 α１ ＝ ０．８， α２ ＝ ２α１ ／ （α１ ＋ １） ， φ１（ｘ） ＝ ２．１ｘ ， φ２（ｘ） ＝ ２．１ｘ 。 基于图 ７ 的拓扑图以及上述初始条件，分别应 用本文设计的控制器 １， 第 ２ 期 庄昊，等： 联合连通拓扑下的二阶多自主体系统有限时间包容控制 ·１９３·

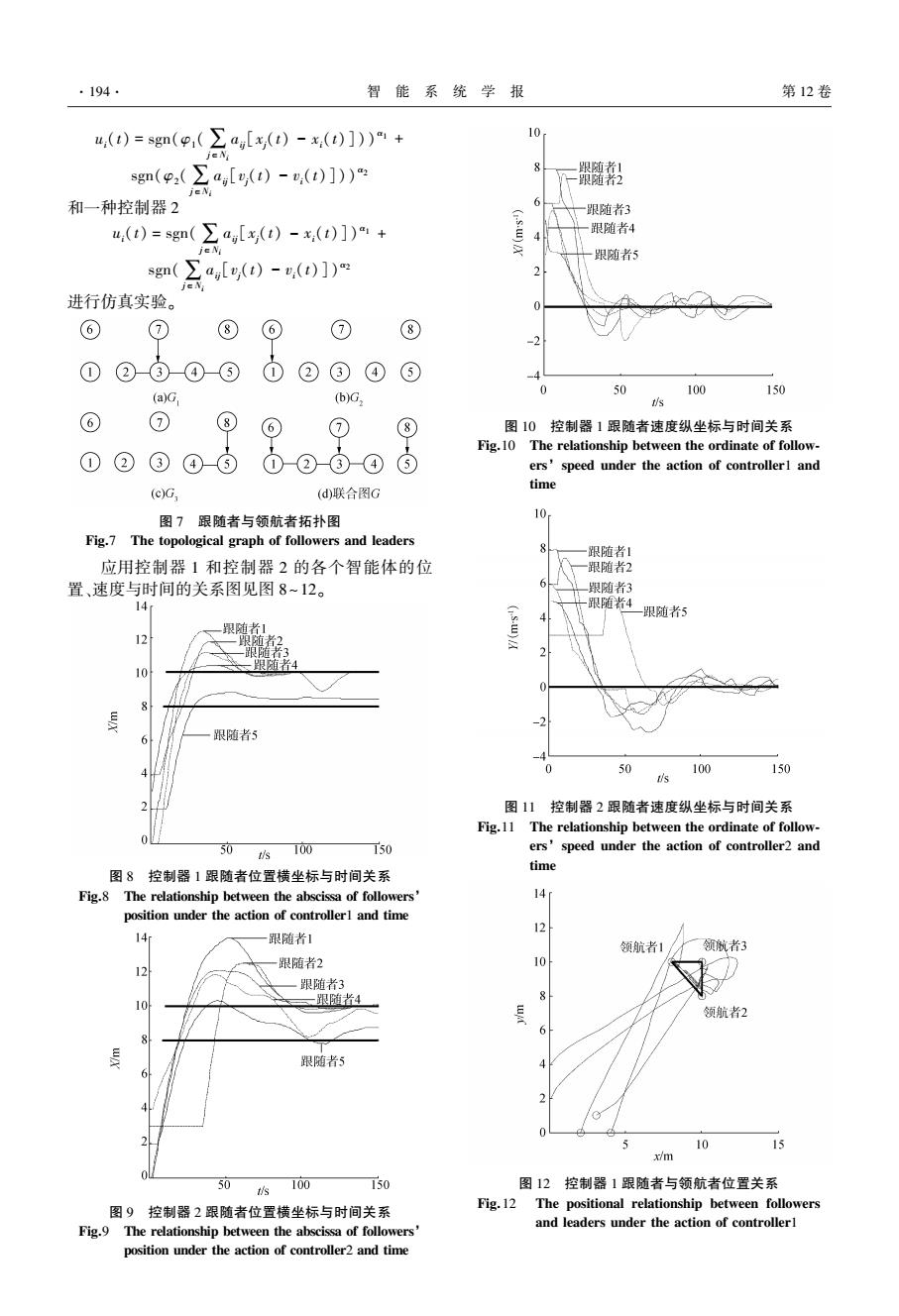
·194 智能系统学报 第12卷 u,()=sgm(p,(∑a[xy()-x,(t)])+ jeN sgn(2( ∑a,[,()-()]) jeNI 和一种控制器2 6 跟随者3 u.(t)=sgn(a[z(t)-x(t)])" 跟随者4 跟随者5 sg(∑a,[()-(t)]) jeN 进行仿真实验。 ⑥ ⑦ ⑧ 6 ⑦ ⑧ ① ②③④⑤ ① ② ③ ④ ⑤ 50 100 150 (a)G (b)G. s 6 ⑦ ⑧ 6 ⑦ ⑧ 图10控制器1跟随者速度纵坐标与时间关系 Fig.10 The relationship between the ordinate of follow- ① ② ③ ④⑤ ① ②-③④ ⑤ ers'speed under the action of controllerl and (c)G, (d)联合图G time 图7跟随者与领航者拓扑图 10 Fig.7 The topological graph of followers and leaders 跟随者1 应用控制器1和控制器2的各个智能体的位 跟随者2 置、速度与时间的关系图见图8~12。 跟随者3 14 -跟随者4 跟随者5 12 10 跟随者5 -41 0 50 100 150 s 图11控制器2跟随者速度纵坐标与时间关系 Fig.11 The relationship between the ordinate of follow- 50. 100 T50 ers'speed under the action of controller2 and time 图8控制器1跟随者位置横坐标与时间关系 Fig.8 The relationship between the abscissa of followers' 14r position under the action of controllerl and time 14 跟随者1 领航者1 领航者3 12 跟随者2 b 跟随者3 10 一跟随者4 8 领航者2 6 跟随者5 5 10 15 x/m 50 s100 150 图12。控制器1跟随者与领航者位置关系 图9控制器2跟随者位置横坐标与时间关系 Fig.12 The positional relationship between followers and leaders under the action of controllerl Fig.9 The relationship between the abscissa of followers position under the action of controller2 and time

ｕｉ（ｔ） ＝ ｓｇｎ（φ１（∑ ｊ∈Ｎｉ ａｉｊ［ｘｊ（ｔ） － ｘｉ（ｔ）］）） α１ ＋ ｓｇｎ（φ２（∑ ｊ∈Ｎｉ ａｉｊ［ｖｊ（ｔ） － ｖｉ（ｔ）］）） α２ 和一种控制器 ２ ｕｉ（ｔ） ＝ ｓｇｎ（∑ ｊ∈Ｎｉ ａｉｊ［ｘｊ（ｔ） － ｘｉ（ｔ）］） α１ ＋ ｓｇｎ（∑ ｊ∈Ｎｉ ａｉｊ［ｖｊ（ｔ） － ｖｉ（ｔ）］） α２ 进行仿真实验。 图 ７ 跟随者与领航者拓扑图 Ｆｉｇ．７ Ｔｈｅ ｔｏｐｏｌｏｇｉｃａｌ ｇｒａｐｈ ｏｆ ｆｏｌｌｏｗｅｒｓ ａｎｄ ｌｅａｄｅｒｓ 应用控制器 １ 和控制器 ２ 的各个智能体的位 置、速度与时间的关系图见图 ８～１２。 图 ８ 控制器 １ 跟随者位置横坐标与时间关系 Ｆｉｇ．８ Ｔｈｅ ｒｅｌａｔｉｏｎｓｈｉｐ ｂｅｔｗｅｅｎ ｔｈｅ ａｂｓｃｉｓｓａ ｏｆ ｆｏｌｌｏｗｅｒｓ’ ｐｏｓｉｔｉｏｎ ｕｎｄｅｒ ｔｈｅ ａｃｔｉｏｎ ｏｆ ｃｏｎｔｒｏｌｌｅｒ１ ａｎｄ ｔｉｍｅ 图 ９ 控制器 ２ 跟随者位置横坐标与时间关系 Ｆｉｇ．９ Ｔｈｅ ｒｅｌａｔｉｏｎｓｈｉｐ ｂｅｔｗｅｅｎ ｔｈｅ ａｂｓｃｉｓｓａ ｏｆ ｆｏｌｌｏｗｅｒｓ’ ｐｏｓｉｔｉｏｎ ｕｎｄｅｒ ｔｈｅ ａｃｔｉｏｎ ｏｆ ｃｏｎｔｒｏｌｌｅｒ２ ａｎｄ ｔｉｍｅ 图 １０ 控制器 １ 跟随者速度纵坐标与时间关系 Ｆｉｇ．１０ Ｔｈｅ ｒｅｌａｔｉｏｎｓｈｉｐ ｂｅｔｗｅｅｎ ｔｈｅ ｏｒｄｉｎａｔｅ ｏｆ ｆｏｌｌｏｗ⁃ ｅｒｓ’ ｓｐｅｅｄ ｕｎｄｅｒ ｔｈｅ ａｃｔｉｏｎ ｏｆ ｃｏｎｔｒｏｌｌｅｒ１ ａｎｄ ｔｉｍｅ 图 １１ 控制器 ２ 跟随者速度纵坐标与时间关系 Ｆｉｇ．１１ Ｔｈｅ ｒｅｌａｔｉｏｎｓｈｉｐ ｂｅｔｗｅｅｎ ｔｈｅ ｏｒｄｉｎａｔｅ ｏｆ ｆｏｌｌｏｗ⁃ ｅｒｓ’ ｓｐｅｅｄ ｕｎｄｅｒ ｔｈｅ ａｃｔｉｏｎ ｏｆ ｃｏｎｔｒｏｌｌｅｒ２ ａｎｄ ｔｉｍｅ 图 １２ 控制器 １ 跟随者与领航者位置关系 Ｆｉｇ． １２ Ｔｈｅ ｐｏｓｉｔｉｏｎａｌ ｒｅｌａｔｉｏｎｓｈｉｐ ｂｅｔｗｅｅｎ ｆｏｌｌｏｗｅｒｓ ａｎｄ ｌｅａｄｅｒｓ ｕｎｄｅｒ ｔｈｅ ａｃｔｉｏｎ ｏｆ ｃｏｎｔｒｏｌｌｅｒ１ ·１９４· 智 能 系 统 学 报 第 １２ 卷

第2期 庄吴，等：联合连通拓扑下的二阶多自主体系统有限时间包容控制 .195. 由此可知，传统的控制策略虽然可以达到有 of multi-agent systems with random switching interconnection 限时间收敛，但是用时要比本文设计的控制器更 topologies[J].Automatica,2012,48(5):879-885. 长，并且运动轨迹和速度曲线不如本文设计的控 [8]张安慧，陈健，孔宪仁，等.二阶系统包容控制算法及 制器的曲线平稳，综上，本文设计的控制器比传 其收敛速度分析[J].哈尔滨工业大学学报，2014,46 (9):1-8. 统策略更有优势。 ZHANG Anhui,CHEN Jian,KONG Xianren,et al.Con- 5结论 tainment control protocol and its convergence speed analysis for double-integrator dynamics systems[J].Journal of Har- 1)本文分别针对静态拓扑和动态拓扑的二 bin institute of technology,2014,46(9):1-8. 阶多自主体系统提出一般性的包容控制算法，并 [9]MENG Ziyang,REN Wei,YOU Zheng.Distributed finite- 运用现代控制理论及矩阵论等理论工具分析了 time attitude containment control for multiple rigid bodies 该算法的有限时间收敛问题，给出了二阶系统在 [J].Automatica,2010,46(12):2092-2099. 动态联合连通拓扑条件下的有限时间收敛条件， [10]丁世宏，李世华.有限时间控制问题综述[J].控制与 并给予仿真验证。 决策，2011,26(2)：161-169 2)本文研究的是连续条件下的有限时间收敛 DING Shihong,LI Shihua.A survey for finite-time control problems[J].Control and decision,2011,26(2):161- 问题，为了贴近实际应用，下一步将继续研究离散条 169. 件下的有限时间收敛问题。 [11]王付永，杨洪勇，韩辅君.多领航者网络化系统的动态 3)通过本文设计的包容控制算法，可以使网络 群集运动[J].电子学报，2016,44(7)：1751-1756. 化系统快速达到收敛，大大减少收敛时间，提高了系 WANG Fuyong,YANG Hongyong,HAN Fujun.Flocking 统收敛效率。 motion of dynamic networked systems with multiple leaders [J].Acta electronica sinica,2016,44(7):1751-1756. 参考文献： [12]XIAO Feng,WANG Long,CHEN Jie,et al.Finite-time 「1]杨洪勇，郭雷，张玉玲，等.复杂分数阶多自主体系统 formation control for multi-agent systems[].Automatica, 的运动一致性「J1.自动化学报，2014,40(3)：489- 2009,45(11):2605-2611. 496. [13]肖秋云.多智能体系统有限时间一致性若干问题研究 YANG Hongyong,GUO Lei,ZHANG Yuling,et al.Move- [D].无锡：江南大学，2015. ment consensus of complex fractional-order multi-agent sys- XIAO Qiuyun.Finite-time consensus problems of multi-a- tems[J].Acta automatica sinica,2014,40(3):489-496. gent systems[D].Wuxi:Jiangnan University,2015. [2]王祥科，李迅，郑志强.多智能体系统编队控制相关问 核对英文标题) 题研究综述[J].控制与决策，2013,28(11)：1601- [14]王付永，杨洪勇，翁灿.复杂多智能体系统的最大一致 1613. 性[J].计算机仿真，2015,32(6)：403-406， WANG Xiangke,LI Xun,ZHENG Zhiqiang.Survey of de- WANG Fuyong,YANG Hongyong,WENG Can.Maximum velopments on multi-agent formation control related problems consistence of complex multi-agent systems[J].Computer [J].Control and decision,2013,28(11)1601-1613. simulation,2015,32(6):403-406. [3]朱旭，月建国，屈耀红.高阶多智能体系统的一致性分 [15]LIN Peng,JIA Yingmin.Consensus of a class of second- 析[J刀.电子学报，2012,40(12)：2466-2471. order multi-agent systems with time-delay and jointly-con- ZHU Xu,YAN Jianguo,QU Yaohong.Consensus analysis nected topologies[J].IEEE transactions on automatic con- for high-order multi-agent systems[J].Acta electronica sini- tol,2010,55(3):778-784. ca,2012,40(12):2466-2471. 作者简介： [4]夏红.多智能体系统群一致性与编队控制研究[D].成 庄吴，男，1992年生，硕士研究生， 都：电子科技大学，2014. 主要研究方向为多智能体编队控制、通 XIA Hong.Research on group consensus and formation con- 信技术。 trol of multi-agent systems[D].Chengdu:University of E. lectronic Science and Technology of China,2014. [5]CAO Yongcan,REN Wei.Containment control with multiple stationary or dynamic leaders under a directed interaction graph[C]//Proceedings of the 48th IEEE Conference on 杨洪勇.男，1967年生，教授，主要 Decision and Control.Shanghai:IEEE,2009:3014-3019. 研究方向为网络应用技术、多智能体编 [6]LIU Huiyang,XIE Guangming,WANG Long.Necessary 队控制、复杂网络控制、非线性系统控 and sufficient conditions for containment control of net- 制。发表学术论文80余篇，曾获山东 worked multi-agent systems[J].Automatica,2012,48 省软科学优秀科研成果三等奖1项，烟 (7):1415-1422. 台市青年科技奖1项。 [7]LOU Youcheng,HONG Yiguang.Target containment control

由此可知，传统的控制策略虽然可以达到有 限时间收敛，但是用时要比本文设计的控制器更 长，并且运动轨迹和速度曲线不如本文设计的控 制器的曲线平稳，综上，本文设计的控制器比传 统策略更有优势。 ５ 结论 １）本文分别针对静态拓扑和动态拓扑的二 阶多自主体系统提出一般性的包容控制算法，并 运用现代控制理论及矩阵论等理论工具分析了 该算法的有限时间收敛问题，给出了二阶系统在 动态联合连通拓扑条件下的有限时间收敛条件， 并给予仿真验证。 ２）本文研究的是连续条件下的有限时间收敛 问题，为了贴近实际应用，下一步将继续研究离散条 件下的有限时间收敛问题。 ３）通过本文设计的包容控制算法，可以使网络 化系统快速达到收敛，大大减少收敛时间，提高了系 统收敛效率。 参考文献： ［１］杨洪勇， 郭雷， 张玉玲， 等． 复杂分数阶多自主体系统 的运动一致性［ Ｊ］． 自动化学报， ２０１４， ４０ （ ３）： ４８９ － ４９６． ＹＡＮＧ Ｈｏｎｇｙｏｎｇ， ＧＵＯ Ｌｅｉ， ＺＨＡＮＧ Ｙｕｌｉｎｇ， ｅｔ ａｌ． Ｍｏｖｅ⁃ ｍｅｎｔ ｃｏｎｓｅｎｓｕｓ ｏｆ ｃｏｍｐｌｅｘ ｆｒａｃｔｉｏｎａｌ⁃ｏｒｄｅｒ ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓ⁃ ｔｅｍｓ［Ｊ］． Ａｃｔａ ａｕｔｏｍａｔｉｃａ ｓｉｎｉｃａ， ２０１４， ４０（３）： ４８９－４９６． ［２］王祥科， 李迅， 郑志强． 多智能体系统编队控制相关问 题研究综述［ Ｊ］． 控制与决策， ２０１３， ２８ （ １１）： １６０１ － １６１３． ＷＡＮＧ Ｘｉａｎｇｋｅ， ＬＩ Ｘｕｎ， ＺＨＥＮＧ Ｚｈｉｑｉａｎｇ． Ｓｕｒｖｅｙ ｏｆ ｄｅ⁃ ｖｅｌｏｐｍｅｎｔｓ ｏｎ ｍｕｌｔｉ⁃ａｇｅｎｔ ｆｏｒｍａｔｉｏｎ ｃｏｎｔｒｏｌ ｒｅｌａｔｅｄ ｐｒｏｂｌｅｍｓ ［Ｊ］． Ｃｏｎｔｒｏｌ ａｎｄ ｄｅｃｉｓｉｏｎ， ２０１３， ２８（１１）： １６０１－１６１３． ［３］朱旭， 闫建国， 屈耀红． 高阶多智能体系统的一致性分 析［Ｊ］． 电子学报， ２０１２， ４０（１２）： ２４６６－２４７１． ＺＨＵ Ｘｕ， ＹＡＮ Ｊｉａｎｇｕｏ， ＱＵ Ｙａｏｈｏｎｇ． Ｃｏｎｓｅｎｓｕｓ ａｎａｌｙｓｉｓ ｆｏｒ ｈｉｇｈ⁃ｏｒｄｅｒ ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓｔｅｍｓ［Ｊ］． Ａｃｔａ ｅｌｅｃｔｒｏｎｉｃａ ｓｉｎｉ⁃ ｃａ， ２０１２， ４０（１２）： ２４６６－２４７１． ［４］夏红． 多智能体系统群一致性与编队控制研究［Ｄ］． 成 都：电子科技大学， ２０１４． ＸＩＡ Ｈｏｎｇ． Ｒｅｓｅａｒｃｈ ｏｎ ｇｒｏｕｐ ｃｏｎｓｅｎｓｕｓ ａｎｄ ｆｏｒｍａｔｉｏｎ ｃｏｎ⁃ ｔｒｏｌ ｏｆ ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓｔｅｍｓ［Ｄ］． Ｃｈｅｎｇｄｕ： Ｕｎｉｖｅｒｓｉｔｙ ｏｆ Ｅ⁃ ｌｅｃｔｒｏｎｉｃ Ｓｃｉｅｎｃｅ ａｎｄ Ｔｅｃｈｎｏｌｏｇｙ ｏｆ Ｃｈｉｎａ， ２０１４． ［５］ＣＡＯ Ｙｏｎｇｃａｎ， ＲＥＮ Ｗｅｉ． Ｃｏｎｔａｉｎｍｅｎｔ ｃｏｎｔｒｏｌ ｗｉｔｈ ｍｕｌｔｉｐｌｅ ｓｔａｔｉｏｎａｒｙ ｏｒ ｄｙｎａｍｉｃ ｌｅａｄｅｒｓ ｕｎｄｅｒ ａ ｄｉｒｅｃｔｅｄ ｉｎｔｅｒａｃｔｉｏｎ ｇｒａｐｈ［ Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ４８ｔｈ ＩＥＥＥ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｄｅｃｉｓｉｏｎ ａｎｄ Ｃｏｎｔｒｏｌ． Ｓｈａｎｇｈａｉ： ＩＥＥＥ， ２００９： ３０１４－３０１９． ［６］ ＬＩＵ Ｈｕｉｙａｎｇ， ＸＩＥ Ｇｕａｎｇｍｉｎｇ， ＷＡＮＧ Ｌｏｎｇ． Ｎｅｃｅｓｓａｒｙ ａｎｄ ｓｕｆｆｉｃｉｅｎｔ ｃｏｎｄｉｔｉｏｎｓ ｆｏｒ ｃｏｎｔａｉｎｍｅｎｔ ｃｏｎｔｒｏｌ ｏｆ ｎｅｔ⁃ ｗｏｒｋｅｄ ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓｔｅｍｓ ［ Ｊ ］． Ａｕｔｏｍａｔｉｃａ， ２０１２， ４８ （７）： １４１５－１４２２． ［７］ＬＯＵ Ｙｏｕｃｈｅｎｇ， ＨＯＮＧ Ｙｉｇｕａｎｇ． Ｔａｒｇｅｔ ｃｏｎｔａｉｎｍｅｎｔ ｃｏｎｔｒｏｌ ｏｆ ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓｔｅｍｓ ｗｉｔｈ ｒａｎｄｏｍ ｓｗｉｔｃｈｉｎｇ ｉｎｔｅｒｃｏｎｎｅｃｔｉｏｎ ｔｏｐｏｌｏｇｉｅｓ［Ｊ］． Ａｕｔｏｍａｔｉｃａ， ２０１２， ４８（５）： ８７９－８８５． ［８］张安慧， 陈健， 孔宪仁， 等． 二阶系统包容控制算法及 其收敛速度分析［ Ｊ］． 哈尔滨工业大学学报， ２０１４， ４６ （９）： １－８． ＺＨＡＮＧ Ａｎｈｕｉ， ＣＨＥＮ Ｊｉａｎ， ＫＯＮＧ Ｘｉａｎｒｅｎ， ｅｔ ａｌ． Ｃｏｎ⁃ ｔａｉｎｍｅｎｔ ｃｏｎｔｒｏｌ ｐｒｏｔｏｃｏｌ ａｎｄ ｉｔｓ ｃｏｎｖｅｒｇｅｎｃｅ ｓｐｅｅｄ ａｎａｌｙｓｉｓ ｆｏｒ ｄｏｕｂｌｅ⁃ｉｎｔｅｇｒａｔｏｒ ｄｙｎａｍｉｃｓ ｓｙｓｔｅｍｓ［ Ｊ］． Ｊｏｕｒｎａｌ ｏｆ Ｈａｒ⁃ ｂｉｎ ｉｎｓｔｉｔｕｔｅ ｏｆ ｔｅｃｈｎｏｌｏｇｙ， ２０１４， ４６（９）： １－８． ［９］ＭＥＮＧ Ｚｉｙａｎｇ， ＲＥＮ Ｗｅｉ， ＹＯＵ Ｚｈｅｎｇ． Ｄｉｓｔｒｉｂｕｔｅｄ ｆｉｎｉｔｅ⁃ ｔｉｍｅ ａｔｔｉｔｕｄｅ ｃｏｎｔａｉｎｍｅｎｔ ｃｏｎｔｒｏｌ ｆｏｒ ｍｕｌｔｉｐｌｅ ｒｉｇｉｄ ｂｏｄｉｅｓ ［Ｊ］． Ａｕｔｏｍａｔｉｃａ， ２０１０， ４６（１２）： ２０９２－２０９９． ［１０］丁世宏， 李世华． 有限时间控制问题综述［ Ｊ］． 控制与 决策， ２０１１， ２６（２）： １６１－１６９． ＤＩＮＧ Ｓｈｉｈｏｎｇ， ＬＩ Ｓｈｉｈｕａ． Ａ ｓｕｒｖｅｙ ｆｏｒ ｆｉｎｉｔｅ⁃ｔｉｍｅ ｃｏｎｔｒｏｌ ｐｒｏｂｌｅｍｓ［Ｊ］． Ｃｏｎｔｒｏｌ ａｎｄ ｄｅｃｉｓｉｏｎ， ２０１１， ２６（２）： １６１－ １６９． ［１１］王付永， 杨洪勇， 韩辅君． 多领航者网络化系统的动态 群集运动［Ｊ］． 电子学报， ２０１６， ４４（７）： １７５１－１７５６． ＷＡＮＧ Ｆｕｙｏｎｇ， ＹＡＮＧ Ｈｏｎｇｙｏｎｇ， ＨＡＮ Ｆｕｊｕｎ． Ｆｌｏｃｋｉｎｇ ｍｏｔｉｏｎ ｏｆ ｄｙｎａｍｉｃ ｎｅｔｗｏｒｋｅｄ ｓｙｓｔｅｍｓ ｗｉｔｈ ｍｕｌｔｉｐｌｅ ｌｅａｄｅｒｓ ［Ｊ］． Ａｃｔａ ｅｌｅｃｔｒｏｎｉｃａ ｓｉｎｉｃａ， ２０１６， ４４（７）： １７５１－１７５６． ［１２］ＸＩＡＯ Ｆｅｎｇ， ＷＡＮＧ Ｌｏｎｇ， ＣＨＥＮ Ｊｉｅ， ｅｔ ａｌ． Ｆｉｎｉｔｅ⁃ｔｉｍｅ ｆｏｒｍａｔｉｏｎ ｃｏｎｔｒｏｌ ｆｏｒ ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓｔｅｍｓ［ Ｊ］． Ａｕｔｏｍａｔｉｃａ， ２００９， ４５（１１）： ２６０５－２６１１． ［１３］肖秋云． 多智能体系统有限时间一致性若干问题研究 ［Ｄ］． 无锡： 江南大学， ２０１５． ＸＩＡＯ Ｑｉｕｙｕｎ． Ｆｉｎｉｔｅ⁃ｔｉｍｅ ｃｏｎｓｅｎｓｕｓ ｐｒｏｂｌｅｍｓ ｏｆ ｍｕｌｔｉ⁃ａ⁃ ｇｅｎｔ ｓｙｓｔｅｍｓ［Ｄ］． Ｗｕｘｉ： Ｊｉａｎｇｎａｎ Ｕｎｉｖｅｒｓｉｔｙ， ２０１５． （请 核对英文标题） ［１４］王付永， 杨洪勇， 翁灿． 复杂多智能体系统的最大一致 性［Ｊ］． 计算机仿真， ２０１５， ３２（６）： ４０３－４０６． ＷＡＮＧ Ｆｕｙｏｎｇ， ＹＡＮＧ Ｈｏｎｇｙｏｎｇ， ＷＥＮＧ Ｃａｎ． Ｍａｘｉｍｕｍ ｃｏｎｓｉｓｔｅｎｃｅ ｏｆ ｃｏｍｐｌｅｘ ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓｔｅｍｓ［ Ｊ］． Ｃｏｍｐｕｔｅｒ ｓｉｍｕｌａｔｉｏｎ， ２０１５， ３２（６）： ４０３－４０６． ［１５］ＬＩＮ Ｐｅｎｇ， ＪＩＡ Ｙｉｎｇｍｉｎ． Ｃｏｎｓｅｎｓｕｓ ｏｆ ａ ｃｌａｓｓ ｏｆ ｓｅｃｏｎｄ⁃ ｏｒｄｅｒ ｍｕｌｔｉ⁃ａｇｅｎｔ ｓｙｓｔｅｍｓ ｗｉｔｈ ｔｉｍｅ⁃ｄｅｌａｙ ａｎｄ ｊｏｉｎｔｌｙ⁃ｃｏｎ⁃ ｎｅｃｔｅｄ ｔｏｐｏｌｏｇｉｅｓ［Ｊ］． ＩＥＥＥ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ａｕｔｏｍａｔｉｃ ｃｏｎ⁃ ｔｒｏｌ， ２０１０， ５５（３）： ７７８－７８４． 作者简介： 庄昊，男，１９９２ 年生，硕士研究生， 主要研究方向为多智能体编队控制、通 信技术。 杨洪勇，男，１９６７ 年生，教授，主要 研究方向为网络应用技术、多智能体编 队控制、复杂网络控制、非线性系统控 制。 发表学术论文 ８０ 余篇，曾获山东 省软科学优秀科研成果三等奖 １ 项，烟 台市青年科技奖 １ 项。 第 ２ 期 庄昊，等： 联合连通拓扑下的二阶多自主体系统有限时间包容控制 ·１９５·