
第12卷第1期 智能系统学报 Vol.12 No.1 2017年2月 CAAI Transactions on Intelligent Systems Feb.2017 D0I:10.11992/tis.201604018 网络出版地址:http:/kns.cmki.net/kcms/detail/23.1538.TP.20170227.1801.012.html 一种协作型机器人运动性能分析与仿真 胡明伟2,王洪光,潘新安,田勇2,常勇 (1.中国科学院沈阳自动化研究所机器人学国家重点实验室,辽宁沈阳110016:2.中国科学院大学,北京100049) 摘要:随着制造模式的变革,协作型机器人在工业领域的应用日益广泛。本文介绍了协作型机器人的特性,并且 以KUKA LBR iiwa机器人为例,进行运动性能分析,旨在为研发此类机器人提供设计理论依据。利用Denavit-. Hartenberg法建立了该机器人运动学模型。基于蒙特卡洛法在MATLAB环境下对机器人灵活性和可操作性进行分 析,并对其在狭小空间内作业进行轨迹规划,仿真结果表明LBR iiwa机器人具有良好的灵活性、可操作性及避障 能力。 关键词:LBR iiwa:协作型机器人:灵活性:可操作性:狭小空间:轨迹规划 中图分类号:TP241文献标志码:A文章编号:1673-4785(2017)01-0075-07 中文引用格式:胡明伟,王洪光,潘新安,等.一种协作型机器人运动性能分析与仿真[J].智能系统学报,2017,12(1):75-81. 英文引用格式:HU Mingwei,Wang Hongguang,Pan Xin'an,etal.Analysis and simulation on kinematics performance of a collaborative robot[J].CAAI transactions on intelligent systems,2017,12(1):75-81. Analysis and simulation on kinematics performance of a collaborative robot HU Mingwei'2,WANG Hongguang',PAN Xin'an',TIAN Yong'2,CHANG Yong' (1.State Key Laboratory of Robotics,Shenyang Institute of Automation,Chinese Academy of Sciences,Shenyang 110016,China;2. University of Chinese Academy of Sciences,Beijing 110049,China) Abstract:With the revolution of manufacturing mode,the application of collaborative robot in industry is becoming increasingly widespread.This paper introduces the characteristics of collaborative robot and analyzes the kinematics performance of KUKA LBR iiwa which is the typical representative of collaborative robots.The aim of this work is to provide design theory basis for developing this kind of robot.The robot kinematic model is established by Denavit- Hartenberg method.Based on Monte-Carlo method,the flexibility and manipulability of robot are analyzed in MATLAB environment.The trajectory of robot working in narrow workspace is planned,simulation results show that LBR iiwa has good flexibility,manipulability and obstacle avoidance ability. Keywords:LBR iiwa;collaborative Robots;flexibility;manipulability;narrow workspace;trajectory planning 传统的工业机器人适应结构化生产环境、大批适应中小型企业的柔性制造场合。其工作环境由 量的制造模式,已经在汽车、电子电气、橡胶及塑料 封闭的结构化作业环境转变为与人共存的半结构 等行业得到了广泛的应用。近年来,随着市场需求 化作业环境。就性能要求而言,传统的制造模式要 向用户定制、多品种、中小批量生产的转变,对机器 求机器人具有较高的重复定位精度,当前的一些作 人的应用需求也发生了变化。就制造模式而言,机 业任务对机器人的绝对定位精度也提出了很高要 器人不仅要适应大型企业的刚性生产线要求,也要 求。显然,传统的工业机器人已不能适应上述生产 制造模式的变化,难以满足新的市场需求[-]。 收稿日期:2016-04-14.网络出版日期:2017-02-27. 基金项目:国家自然科学基金项目(51405482):辽宁省自然科学基金计划项 近年来,协作型机器人日益受到人们的重视, 目(2013020054):中国科学院重点部署项目(KGZD-EW-608-1): 已经有多家机器人制造商开发出这种可以与人协 辽宁省产业共性技术创新平台计划项目(2015106014) 通信作者:王洪光.E-mail:hgwang@sia.cn 同工作,更加安全且灵活的新型机器人,这种机器
第 12 卷第 1 期 智 能 系 统 学 报 Vol.12 №.1 2017 年 2 月 CAAI Transactions on Intelligent Systems Feb. 2017 DOI:10.11992 / tis.201604018 网络出版地址:http: / / kns.cnki.net / kcms/ detail / 23.1538.TP.20170227.1801.012.html 一种协作型机器人运动性能分析与仿真 胡明伟1,2 ,王洪光1 ,潘新安1 ,田勇1,2 ,常勇1 (1.中国科学院沈阳自动化研究所 机器人学国家重点实验室,辽宁 沈阳 110016; 2.中国科学院大学,北京 100049) 摘 要:随着制造模式的变革,协作型机器人在工业领域的应用日益广泛。 本文介绍了协作型机器人的特性,并且 以 KUKA LBR iiwa 机器人为例,进行运动性能分析,旨在为研发此类机器人提供设计理论依据。 利用 Denavit⁃ Hartenberg 法建立了该机器人运动学模型。 基于蒙特卡洛法在 MATLAB 环境下对机器人灵活性和可操作性进行分 析,并对其在狭小空间内作业进行轨迹规划,仿真结果表明 LBR iiwa 机器人具有良好的灵活性、可操作性及避障 能力。 关键词:LBR iiwa;协作型机器人;灵活性;可操作性;狭小空间;轨迹规划 中图分类号:TP241 文献标志码:A 文章编号:1673-4785(2017)01-0075-07 中文引用格式:胡明伟,王洪光,潘新安,等.一种协作型机器人运动性能分析与仿真 [J]. 智能系统学报, 2017, 12(1): 75-81. 英文引用格式:HU Mingwei, Wang Hongguang, Pan Xin’ an, et al. Analysis and simulation on kinematics performance of a collaborative robot[J]. CAAI transactions on intelligent systems, 2017, 12(1): 75-81. Analysis and simulation on kinematics performance of a collaborative robot HU Mingwei 1,2 , WANG Hongguang 1 , PAN Xin’an 1 ,TIAN Yong 1,2 ,CHANG Yong 1 (1. State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110016,China;2. University of Chinese Academy of Sciences, Beijing 110049, China) Abstract:With the revolution of manufacturing mode, the application of collaborative robot in industry is becoming increasingly widespread. This paper introduces the characteristics of collaborative robot and analyzes the kinematics performance of KUKA LBR iiwa which is the typical representative of collaborative robots. The aim of this work is to provide design theory basis for developing this kind of robot. The robot kinematic model is established by Denavit⁃ Hartenberg method. Based on Monte⁃Carlo method, the flexibility and manipulability of robot are analyzed in MATLAB environment. The trajectory of robot working in narrow workspace is planned, simulation results show that LBR iiwa has good flexibility, manipulability and obstacle avoidance ability. Keywords:LBR iiwa; collaborative Robots; flexibility; manipulability; narrow workspace; trajectory planning 收稿日期:2016-04-14. 网络出版日期:2017-02-27. 基金项目:国家自然科学基金项目(51405482);辽宁省自然科学基金计划项 目(2013020054);中国科学院重点部署项目(KGZD-EW-608-1); 辽宁省产业共性技术创新平台计划项目(2015106014). 通信作者:王洪光. E⁃mail:hgwang@ sia.cn . 传统的工业机器人适应结构化生产环境、大批 量的制造模式,已经在汽车、电子电气、橡胶及塑料 等行业得到了广泛的应用。 近年来,随着市场需求 向用户定制、多品种、中小批量生产的转变,对机器 人的应用需求也发生了变化。 就制造模式而言,机 器人不仅要适应大型企业的刚性生产线要求,也要 适应中小型企业的柔性制造场合。 其工作环境由 封闭的结构化作业环境转变为与人共存的半结构 化作业环境。 就性能要求而言,传统的制造模式要 求机器人具有较高的重复定位精度,当前的一些作 业任务对机器人的绝对定位精度也提出了很高要 求。 显然,传统的工业机器人已不能适应上述生产 制造模式的变化,难以满足新的市场需求[1-2] 。 近年来,协作型机器人日益受到人们的重视, 已经有多家机器人制造商开发出这种可以与人协 同工作,更加安全且灵活的新型机器人,这种机器

.76, 智能系统学报 第12卷 人已应用于精密装配、包装、打磨、检测及机床上下 划,分析结果表明该机器人具有良好的灵活性、可 料等生产制造领域。协作型机器人具有轻质、大负 操作性和避障能力,为研发七自由度协作型机器人 载自重比、灵活易用、安全性高、能够与人协同作业 提供了设计理论依据。 等特点。此项技术不仅有益于提高大型企业的生 产效率,也为中小型企业提高自动化作业水平提供 1机器人构型分析 了技术支撑。传统工业机器人与协作型机器人应 因协作型机器人与人共享工作空间,为保障操 用领域比较如表1所示。 作人员的安全,防止安全事故的发生,机器人就必 表1传统工业机器人与协作型机器人应用领域比较 须具有安全性,而实现安全性的基本保障就是机构 Table 1 Comparison of traditional robots and 设计刀。 collaborative robots in applications 根据自由度的不同,工业机器人可以分为非冗 传统工业机器人 协作型机器人 余自由度机器人和冗余自由度机器人。非冗余自 由度机器人的缺点是运动不灵活,无法躲避运动灵 制造模式 用户定制、多品种、 单一品种、大批量 中小批量 活性差的区域,不能躲避任务空间中的障得等劉。 如六自由度机器人由于不具有冗余自由度,因此在 工作环境 封闭、结构化 半结构化、与人协作 与人隔离 每个位姿仅有一组关节值(或有多组关节值,但考 焊接、物料搬运、 精密装配、检测、 虑到位姿运行的连续性,一般仅有一组是可行的), 应用领域 装配、喷涂等 产品包装、打磨等 因此机器人在指定位姿必须以特定的位形实现,无 避障能力。如图1所示,对于UR5机器人,其大臂 目前,协作型机器人已成为机器人领域的研究 和小臂一直形成一个竖直平面内的三角形,因此, 热点,并且已有部分厂商开发出了相应的产品,具 机器人肘部总是处在较高位置,妨碍机器人在高度 有代表性的有Universal Robots公司的UR3\51 方向上对障碍物的避障。 lo)、KUKA公司的LBRiiwa、Rethink Robotics公 司的Baxter和Sawyer、ABB公司的YuMi、沈阳新松 的柔性多关节机器人以及Smokie Robotics公司的 OUR等[。这些机器人都具有灵活易用、安全性 高、能与人协同作业等特点。 目前协作型机器人尚无统一的定义。KUKA公 此面总是垂 司将LBRiiwa机器人定义为可与人并肩作业的“智 直于水平面 能型工业助手”[a。Universal Robots公司对协作型 图1UR5机器人与障碍物干涉示意图 机器人的定义是一种易于安装和使用的能够与工 Fig.1 Demonstration of the UR5 manipulator interfere 人合作生产的轻型机器人[)。ABB公司则将协作 with obstacles 型机器人YMi定义为能够满足电子消费品行业对 冗余自由度机器人克服了非冗余自由度机器人的 柔性和灵活制造的需求,可应用于小件装配作业 缺点,对于任务空间中的点,关节空间可以有无穷多个 (尤其是3C产品)的能与人协同作业的机器人[。 解,或者说有无穷多个位形与之对应。另外,冗余自由 国际标准化组织(IS0)于2016年制定的IS0/TS 度构型具有良好的柔顺性,即机械臂在空间六个自由 15066标准对“协同操作”(collaborative operation)的 度方向都具有良好的运动能力,故其灵活性高、避障能 定义为:特殊设计的机器人系统与操作人员在协同 力强,但其缺点是运动学逆解较为复杂[少0 作业空间内进行的工作6。综上所述,协作型机 许多学者对七自由度机器人构型问题做了大 器人可描述为:一种能够与人协同作业,具有大负 量的研究[-),如Tsai等[劉对机器人位置和姿态构 载自重比、安全性高、灵活易用、用户友好等特点的 型进行了综合,提出了最佳位置构型和最佳姿态构 智能轻型工业机器人。 型:原培章等采用位置空间和奇异空间同时评价 本文介绍了协作型机器人的特性并以KUKA 七自由度机器人的机构选型并制作了机器人的选 开发的LBR iiwa协作型机器人为研究对象,对其构 型图谱。目前,七自由度机器人中有两种公认的最 型进行分析并利用Denavit-Hartenberg法建立了相 佳构型设计,如图2(b)、(©)所示。这两种构型都 应的运动学模型。在MATLAB环境下,利用 是在具有最优灵活工作空间的六自由度机器人构 Robotics Toolbox工具箱对机器人灵活性和可操作性 型(见图2(a))中添加了一个转动副。这两种构型 指标进行分析,给出了机器人条件数和可操作度在 都能产生自运动而不改变手部的位姿,从而完全消 工作空间内的分布图,分析了该机器人的灵活性和 除肩部和腕部出现的奇异情况,而且有利于避开障 可操作性,最后对其在狭小空间内作业进行轨迹规 碍物。而图2(b)所示构型在各方向上的灵活性基
人已应用于精密装配、包装、打磨、检测及机床上下 料等生产制造领域。 协作型机器人具有轻质、大负 载自重比、灵活易用、安全性高、能够与人协同作业 等特点。 此项技术不仅有益于提高大型企业的生 产效率,也为中小型企业提高自动化作业水平提供 了技术支撑。 传统工业机器人与协作型机器人应 用领域比较如表 1 所示。 表 1 传统工业机器人与协作型机器人应用领域比较 Table 1 Comparison of traditional robots and collaborative robots in applications 传统工业机器人 协作型机器人 制造模式 单一品种、大批量 用户定制、多品种、 中小批量 工作环境 封闭、结构化、 与人隔离 半结构化、与人协作 应用领域 焊接、物料搬运、 装配、喷涂等 精密装配、检测、 产品包装、打磨等 目前,协作型机器人已成为机器人领域的研究 热点,并且已有部分厂商开发出了相应的产品,具 有代表性的有 Universal Robots 公司的 UR3 \ 5 \ 10 [3] 、 KUKA 公司的 LBR iiwa、Rethink Robotics 公 司的 Baxter 和 Sawyer、ABB 公司的 YuMi、沈阳新松 的柔性多关节机器人以及 Smokie Robotics 公司的 OUR 等[4] 。 这些机器人都具有灵活易用、安全性 高、能与人协同作业等特点。 目前协作型机器人尚无统一的定义。 KUKA 公 司将 LBR iiwa 机器人定义为可与人并肩作业的“智 能型工业助手” [4] 。 Universal Robots 公司对协作型 机器人的定义是一种易于安装和使用的能够与工 人合作生产的轻型机器人[3] 。 ABB 公司则将协作 型机器人 YuMi 定义为能够满足电子消费品行业对 柔性和灵活制造的需求,可应用于小件装配作业 (尤其是 3C 产品)的能与人协同作业的机器人[4] 。 国际标准化组织( ISO) 于 2016 年制定的 ISO/ TS 15066 标准对“协同操作”(collaborative operation)的 定义为:特殊设计的机器人系统与操作人员在协同 作业空间内进行的工作[5-6] 。 综上所述,协作型机 器人可描述为:一种能够与人协同作业,具有大负 载自重比、安全性高、灵活易用、用户友好等特点的 智能轻型工业机器人。 本文介绍了协作型机器人的特性并以 KUKA 开发的 LBR iiwa 协作型机器人为研究对象,对其构 型进行分析并利用 Denavit⁃Hartenberg 法建立了相 应的 运 动 学 模 型。 在 MATLAB 环 境 下, 利 用 Robotics Toolbox 工具箱对机器人灵活性和可操作性 指标进行分析,给出了机器人条件数和可操作度在 工作空间内的分布图,分析了该机器人的灵活性和 可操作性,最后对其在狭小空间内作业进行轨迹规 划,分析结果表明该机器人具有良好的灵活性、可 操作性和避障能力,为研发七自由度协作型机器人 提供了设计理论依据。 1 机器人构型分析 因协作型机器人与人共享工作空间,为保障操 作人员的安全,防止安全事故的发生,机器人就必 须具有安全性,而实现安全性的基本保障就是机构 设计[7] 。 根据自由度的不同,工业机器人可以分为非冗 余自由度机器人和冗余自由度机器人。 非冗余自 由度机器人的缺点是运动不灵活,无法躲避运动灵 活性差的区域,不能躲避任务空间中的障碍等[8] 。 如六自由度机器人由于不具有冗余自由度,因此在 每个位姿仅有一组关节值(或有多组关节值,但考 虑到位姿运行的连续性,一般仅有一组是可行的), 因此机器人在指定位姿必须以特定的位形实现,无 避障能力。 如图 1 所示,对于 UR5 机器人,其大臂 和小臂一直形成一个竖直平面内的三角形,因此, 机器人肘部总是处在较高位置,妨碍机器人在高度 方向上对障碍物的避障。 图 1 UR5 机器人与障碍物干涉示意图 Fig.1 Demonstration of the UR5 manipulator interfere with obstacles 冗余自由度机器人克服了非冗余自由度机器人的 缺点,对于任务空间中的点,关节空间可以有无穷多个 解,或者说有无穷多个位形与之对应。 另外,冗余自由 度构型具有良好的柔顺性,即机械臂在空间六个自由 度方向都具有良好的运动能力,故其灵活性高、避障能 力强,但其缺点是运动学逆解较为复杂[9-10] 。 许多学者对七自由度机器人构型问题做了大 量的研究[9-11] ,如 Tsai 等[8] 对机器人位置和姿态构 型进行了综合,提出了最佳位置构型和最佳姿态构 型;原培章等[11]采用位置空间和奇异空间同时评价 七自由度机器人的机构选型并制作了机器人的选 型图谱。 目前,七自由度机器人中有两种公认的最 佳构型设计,如图 2( b)、( c) 所示。 这两种构型都 是在具有最优灵活工作空间的六自由度机器人构 型(见图 2(a))中添加了一个转动副。 这两种构型 都能产生自运动而不改变手部的位姿,从而完全消 除肩部和腕部出现的奇异情况,而且有利于避开障 碍物。 而图 2(b)所示构型在各方向上的灵活性基 ·76· 智 能 系 统 学 报 第 12 卷

第1期 胡明伟,等:一种协作型机器人运动性能分析与仿真 ·77 本相同,具有类似“各向同性”的特点,较多被采用。 导相应的运动学方程。 七自由度协作型机器人也大多采用此种构型,如 LBRiiwa、YuMi等。 最佳位置构型最准姿态构型 肩关节肘关节 腕关节 (a)六自由度最佳构型 图4 KUKA LBR iiwa构型 Fig.4 The configuration of KUKA LBR iiwa 表2 KUKA LBR iiwa机器人D-H参数 8 Table 2 D-H parameters of the KUKA LBR iiwa robot ia-i/mma-/(o)d,/mm 0,/()关节范围 (b)七自由度构型1 1 0 0 0 0 ±170° 2 0 90° 0 -90 ±120° 0 -90° 400 180 ±170° 4 0 -90° 0 0 ±120° 白 0 90° 400 0 ±170° 6 0 -90 0 0 ±120° 7 0 90 0 0 (c)七自由度构型2 ±175° 图2七自由度机器人构型图谱 运动学方程可以表示为 Fig.2 Atlas of 7-DOF robot manipulators 9T=TTT…T-T 这种构型具有和人的手臂相似的结构,如图3 式中: (a)[所示,可以将前3个关节看作一个球副的肩 ce -s0: 0 ai-1 关节,将后3个关节看作球副的腕关节,中间的关节 s0;co;-1 c0;ca;-1 -s:-1 sai-di 看作肘关节。这种构型的机器人可以绕连接肩腕 s0;sai-1 c0:s0a:-1 CO:-1 ca:-1di 两球副之间的直线做自运动,如图3(b)所示。利用 0 0 0 1 这种特性可以灵活地避开任务空间中的一些障碍 方程左端为末端位姿,可以表达为 物,而且可以完全消除手腕和肩部的奇异,所以采 n: Ox a p: 用此种构型的协作型机器人的灵活性和避障能力 T=[n o a p]= n 0,a,P 要优于六自由度机器人,非常适合于精密装配和狭 P 小工作空间作业任务。 0001 肩关节 3机器人运动性能分析 障碍 灵活性和可操作性是表征机器人运动性能的 肘关节 重要指标,灵活性能够反映机器人在工作空间位置 的灵巧性,而对可操作性的研究能够得到机器人的 奇异空间。 眼腕关节 本文分别使用雅克比矩阵的条件数和与其转 置之积的行列式作为灵活性和可操作性的度量指 (a)人体手臂结构 (b)拟人机械臂避障示意图 标。Salibury和Craig)]利用雅克比矩阵J(g)的条 图3拟人机械臂 件数即k=‖J川广‖作为评价机械臂灵活性的度 Fig.3 Humanoid robot arm 量指标。当k=1时,机械臂所具有的位形称为各向 2机器人运动学模型 同性,即灵活性最高。设计机器人机械结构时应尽 量使其最小条件数为1,这时灵活性最高,各奇异值 本文以七自由度协作型机器人KUKA LBR iiwa 相等。Yoshikawa将雅可比矩阵与其转置之积的行 为例,根据其构型和结构参数(如图4和表2),通过 列式w=0,σ2…σm定义为可操作性的度量指标,当机 Denavit-Hartenberg法[i)建立各杆件的坐标系并推 械臂处于奇异位形时,此时操作臂的可操作性为0,即
本相同,具有类似“各向同性”的特点,较多被采用。 七自由度协作型机器人也大多采用此种构型,如 LBR iiwa、YuMi 等。 (a) 六自由度最佳构型 (b)七自由度构型 1 (c)七自由度构型 2 图 2 七自由度机器人构型图谱 Fig.2 Atlas of 7⁃DOF robot manipulators 这种构型具有和人的手臂相似的结构,如图 3 (a) [12]所示,可以将前 3 个关节看作一个球副的肩 关节,将后 3 个关节看作球副的腕关节,中间的关节 看作肘关节。 这种构型的机器人可以绕连接肩腕 两球副之间的直线做自运动,如图 3(b)所示。 利用 这种特性可以灵活地避开任务空间中的一些障碍 物,而且可以完全消除手腕和肩部的奇异,所以采 用此种构型的协作型机器人的灵活性和避障能力 要优于六自由度机器人,非常适合于精密装配和狭 小工作空间作业任务。 (a)人体手臂结构 (b)拟人机械臂避障示意图 图 3 拟人机械臂 Fig.3 Humanoid robot arm 2 机器人运动学模型 本文以七自由度协作型机器人 KUKA LBR iiwa 为例,根据其构型和结构参数(如图 4 和表 2),通过 Denavit-Hartenberg 法[13]建立各杆件的坐标系并推 导相应的运动学方程。 图 4 KUKA LBR iiwa 构型 Fig.4 The configuration of KUKA LBR iiwa 表 2 KUKA LBR iiwa 机器人 D⁃H 参数 Table 2 D⁃H parameters of the KUKA LBR iiwa robot i ai-1 / mm αi-1 / (°) di / mm θi / (°) 关节范围 1 0 0 0 0 ±170° 2 0 90° 0 -90° ±120° 3 0 -90° 400 180° ±170° 4 0 -90° 0 0 ±120° 5 0 90° 400 0 ±170° 6 0 -90° 0 0 ±120° 7 0 90° 0 0 ±175° 运动学方程可以表示为 0 nT = 0 1T 1 2T 2 3T…n-2 n-1T n-1 n T 式中: i-1 i T = cθi - sθi 0 ai-1 sθi cαi-1 cθi cαi-1 - sαi-1 - sαi-1 di sθi sαi-1 cθi sαi-1 cαi-1 cαi-1 di 0 0 0 1 é ë ê ê ê ê ê ù û ú ú ú ú ú 方程左端为末端位姿,可以表达为 0 nT = [n o a p] = nx ox ax px ny oy ay py nz oz az pz 0 0 0 1 é ë ê ê ê ê ê ù û ú ú ú ú ú 3 机器人运动性能分析 灵活性和可操作性是表征机器人运动性能的 重要指标,灵活性能够反映机器人在工作空间位置 的灵巧性,而对可操作性的研究能够得到机器人的 奇异空间。 本文分别使用雅克比矩阵的条件数和与其转 置之积的行列式作为灵活性和可操作性的度量指 标。 Salibury 和 Craig [13]利用雅克比矩阵 J( q)的条 件数即 k =‖J‖‖J -1‖作为评价机械臂灵活性的度 量指标。 当 k = 1 时,机械臂所具有的位形称为各向 同性,即灵活性最高。 设计机器人机械结构时应尽 量使其最小条件数为 1,这时灵活性最高,各奇异值 相等。 Yoshikawa [14]将雅可比矩阵与其转置之积的行 列式 w=σ1σ2… σm 定义为可操作性的度量指标,当机 械臂处于奇异位形时,此时操作臂的可操作性为 0,即 第 1 期 胡明伟,等:一种协作型机器人运动性能分析与仿真 ·77·
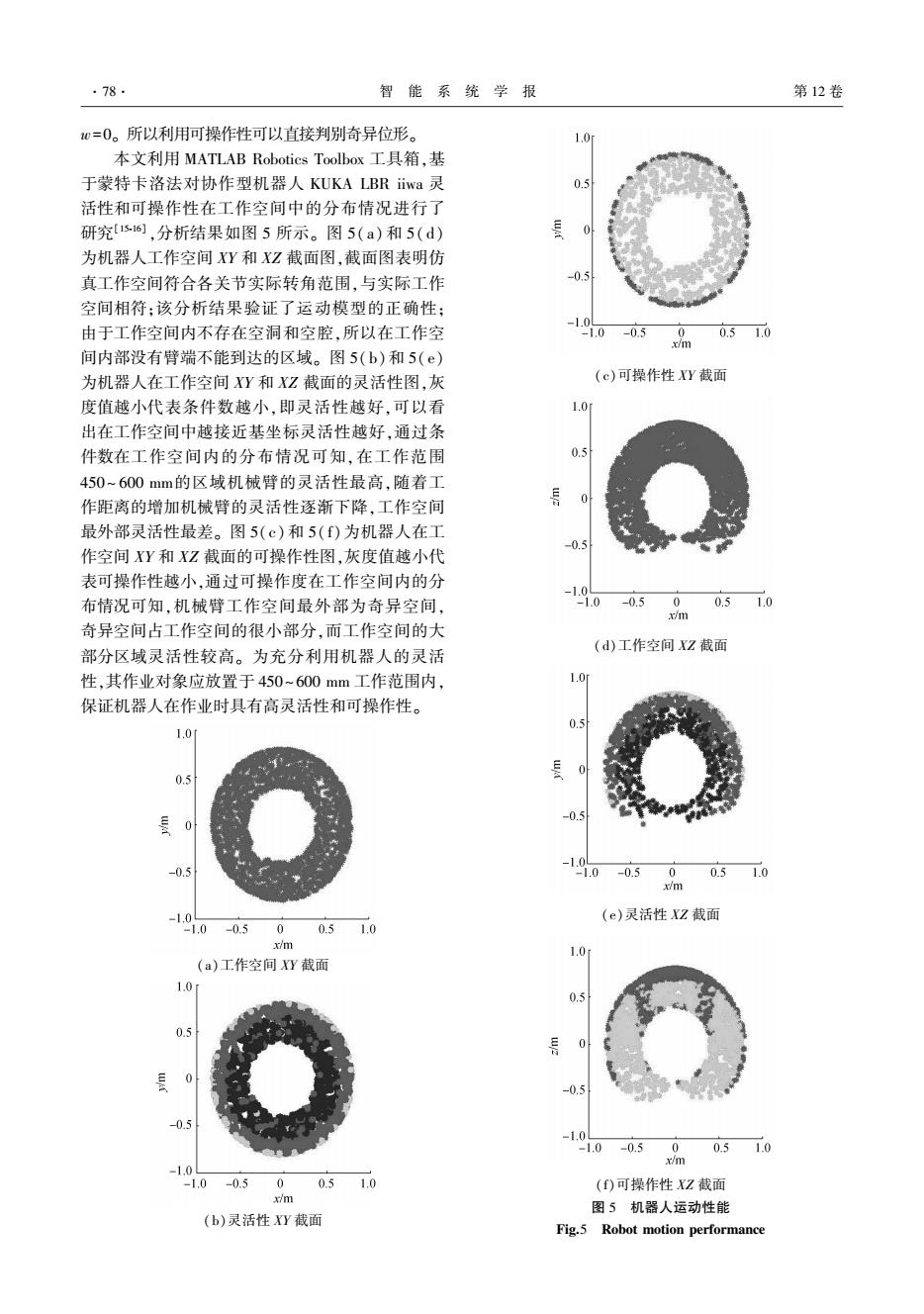
·78 智能系统学报 第12卷 0=0。所以利用可操作性可以直接判别奇异位形。 1.0 本文利用MATLAB Robotics Toolbox工具箱,基 于蒙特卡洛法对协作型机器人KUKA LBR iiwa灵 0.5 活性和可操作性在工作空间中的分布情况进行了 研究116),分析结果如图5所示。图5(a)和5(d) 为机器人工作空间XY和XZ截面图,截面图表明仿 真工作空间符合各关节实际转角范围,与实际工作 -0.5 空间相符:该分析结果验证了运动模型的正确性; 由于工作空间内不存在空洞和空腔,所以在工作空 -1.0 -0.5 0 0.51.0 x/m 间内部没有臂端不能到达的区域。图5(b)和5(e) 为机器人在工作空间XY和XZ截面的灵活性图,灰 (c)可操作性Y截面 度值越小代表条件数越小,即灵活性越好,可以看 1.0 出在工作空间中越接近基坐标灵活性越好,通过条 件数在工作空间内的分布情况可知,在工作范围 0.5 450~600mm的区域机械臂的灵活性最高,随着工 作距离的增加机械臂的灵活性逐渐下降,工作空间 最外部灵活性最差。图5(c)和5(f)为机器人在工 -0.5 作空间Y和XZ截面的可操作性图,灰度值越小代 表可操作性越小,通过可操作度在工作空间内的分 -.0 布情况可知,机械臂工作空间最外部为奇异空间, -1.0 -0.50 0.51.0 x/m 奇异空间占工作空间的很小部分,而工作空间的大 (d)工作空间XZ截面 部分区域灵活性较高。为充分利用机器人的灵活 性,其作业对象应放置于450~600mm工作范围内, 1.0 保证机器人在作业时具有高灵活性和可操作性。 0.5 1.0 05 0 -0.5 -1.0 -0.5 0 0.51.0 x/m -1.0 (e)灵活性XZ截面 .0 -0.5 0 0.51.0 x/m 1.0 (a)工作空间XY截面 1.0 0.5 0.5 -0.5 -0.5 -1.0 -1.0 -0.5 0 0.51.0 x/m -1.0 -1.0-0.500.510 ()可操作性XZ截面 x/m 图5机器人运动性能 (b)灵活性XY截面 Fig.5 Robot motion performance
w=0。 所以利用可操作性可以直接判别奇异位形。 本文利用 MATLAB Robotics Toolbox 工具箱,基 于蒙特卡洛法对协作型机器人 KUKA LBR iiwa 灵 活性和可操作性在工作空间中的分布情况进行了 研究[15⁃16] ,分析结果如图 5 所示。 图 5(a)和 5( d) 为机器人工作空间 XY 和 XZ 截面图,截面图表明仿 真工作空间符合各关节实际转角范围,与实际工作 空间相符;该分析结果验证了运动模型的正确性; 由于工作空间内不存在空洞和空腔,所以在工作空 间内部没有臂端不能到达的区域。 图 5(b)和 5(e) 为机器人在工作空间 XY 和 XZ 截面的灵活性图,灰 度值越小代表条件数越小,即灵活性越好,可以看 出在工作空间中越接近基坐标灵活性越好,通过条 件数在工作空间内的分布情况可知,在工作范围 450~ 600 mm的区域机械臂的灵活性最高,随着工 作距离的增加机械臂的灵活性逐渐下降,工作空间 最外部灵活性最差。 图 5(c)和 5( f)为机器人在工 作空间 XY 和 XZ 截面的可操作性图,灰度值越小代 表可操作性越小,通过可操作度在工作空间内的分 布情况可知,机械臂工作空间最外部为奇异空间, 奇异空间占工作空间的很小部分,而工作空间的大 部分区域灵活性较高。 为充分利用机器人的灵活 性,其作业对象应放置于 450~600 mm 工作范围内, 保证机器人在作业时具有高灵活性和可操作性。 (a)工作空间 XY 截面 (b)灵活性 XY 截面 (c)可操作性 XY 截面 (d)工作空间 XZ 截面 (e)灵活性 XZ 截面 (f)可操作性 XZ 截面 图 5 机器人运动性能 Fig.5 Robot motion performance ·78· 智 能 系 统 学 报 第 12 卷
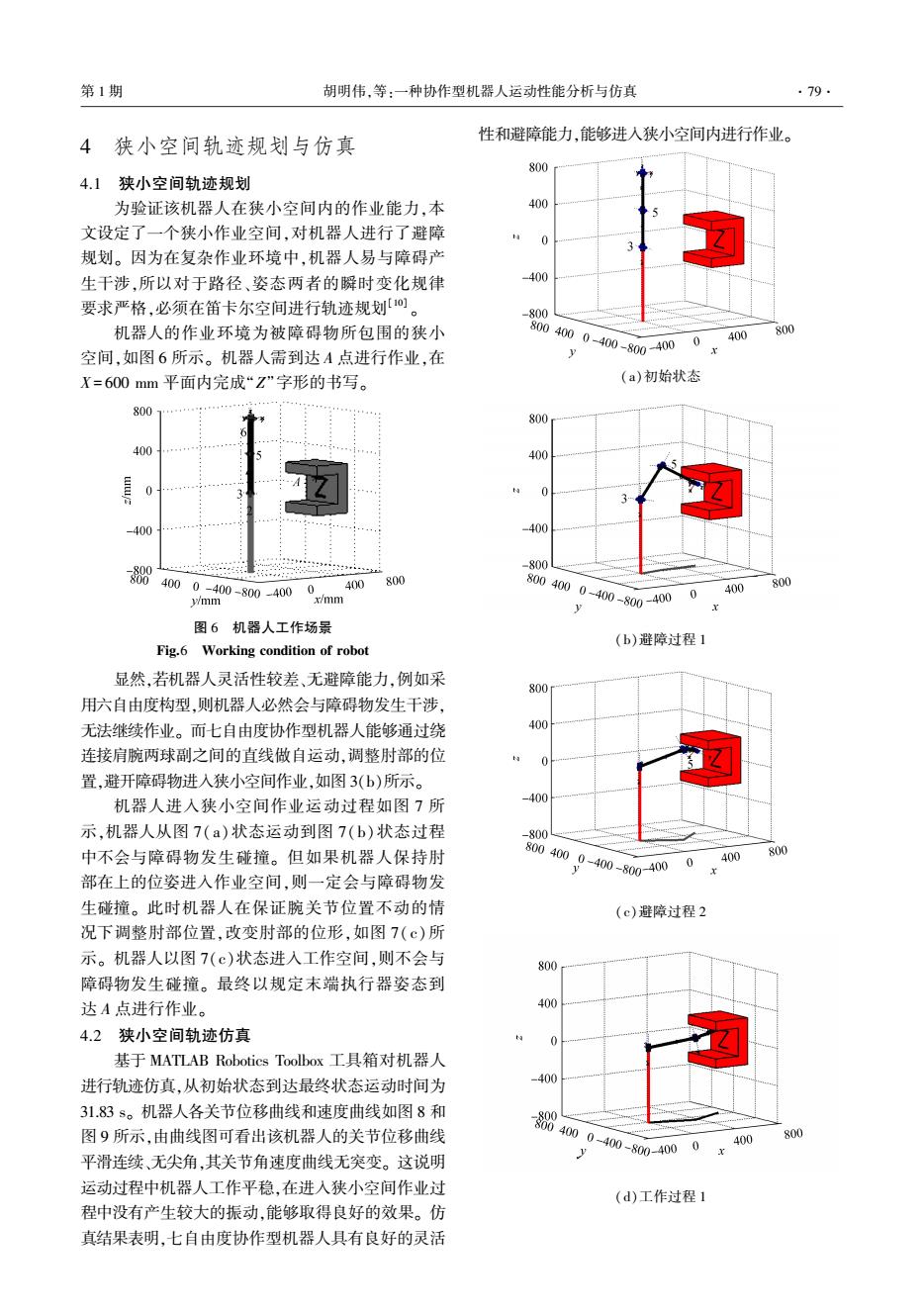
第1期 胡明伟,等:一种协作型机器人运动性能分析与仿真 ·79· 4 狭小空间轨迹规划与仿真 性和避障能力,能够进入狭小空间内进行作业。 800 4.1狭小空间轨迹规划 为验证该机器人在狭小空间内的作业能力,本 400 文设定了一个狭小作业空间,对机器人进行了避障 0 规划。因为在复杂作业环境中,机器人易与障碍产 生干涉,所以对于路径、姿态两者的瞬时变化规律 400 要求严格,必须在笛卡尔空间进行轨迹规划o。 -800 机器人的作业环境为被障碍物所包围的狭小 800400-400-800400 0 400 800 空间,如图6所示。机器人需到达A点进行作业,在 y X=600mm平面内完成“Z”字形的书写。 (a)初始状态 8001日 800 400 ” 400 0 0 -400 -400 -800 884000-400-800-40 0400 800 8004000-400-800-400 0 400 800 y/mm x/mm 图6机器人工作场景 (b)避障过程1 Fig.6 Working condition of robot 显然,若机器人灵活性较差、无避障能力,例如采 800 用六自由度构型,则机器人必然会与障碍物发生干涉, 无法继续作业。而七自由度协作型机器人能够通过绕 400 连接肩腕两球副之间的直线做自运动,调整肘部的位 置,避开障碍物进入狭小空间作业,如图3(b)所示。 机器人进入狭小空间作业运动过程如图7所 -400 示,机器人从图7(a)状态运动到图7(b)状态过程 -800 中不会与障碍物发生碰撞。但如果机器人保持肘 800400 0-400-800400 0 400 800 部在上的位姿进入作业空间,则一定会与障碍物发 生碰撞。此时机器人在保证腕关节位置不动的情 (c)避障过程2 况下调整肘部位置,改变肘部的位形,如图7(©)所 示。机器人以图7(c)状态进入工作空间,则不会与 800 障碍物发生碰撞。最终以规定末端执行器姿态到 达A点进行作业。 400 4.2狭小空间轨迹仿真 基于MATLAB Robotics Toolbox工具箱对机器人 进行轨迹仿真,从初始状态到达最终状态运动时间为 -400 31.83s。机器人各关节位移曲线和速度曲线如图8和 图9所示,由曲线图可看出该机器人的关节位移曲线 8004000-400-8004000x400 800 平滑连续、无尖角,其关节角速度曲线无突变。这说明 运动过程中机器人工作平稳,在进入狭小空间作业过 (d)工作过程1 程中没有产生较大的振动,能够取得良好的效果。仿 真结果表明,七自由度协作型机器人具有良好的灵活
4 狭小空间轨迹规划与仿真 4.1 狭小空间轨迹规划 为验证该机器人在狭小空间内的作业能力,本 文设定了一个狭小作业空间,对机器人进行了避障 规划。 因为在复杂作业环境中,机器人易与障碍产 生干涉,所以对于路径、姿态两者的瞬时变化规律 要求严格,必须在笛卡尔空间进行轨迹规划[10] 。 机器人的作业环境为被障碍物所包围的狭小 空间,如图 6 所示。 机器人需到达 A 点进行作业,在 X = 600 mm 平面内完成“Z”字形的书写。 图 6 机器人工作场景 Fig.6 Working condition of robot 显然,若机器人灵活性较差、无避障能力,例如采 用六自由度构型,则机器人必然会与障碍物发生干涉, 无法继续作业。 而七自由度协作型机器人能够通过绕 连接肩腕两球副之间的直线做自运动,调整肘部的位 置,避开障碍物进入狭小空间作业,如图 3(b)所示。 机器人进入狭小空间作业运动过程如图 7 所 示,机器人从图 7(a)状态运动到图 7(b)状态过程 中不会与障碍物发生碰撞。 但如果机器人保持肘 部在上的位姿进入作业空间,则一定会与障碍物发 生碰撞。 此时机器人在保证腕关节位置不动的情 况下调整肘部位置,改变肘部的位形,如图 7(c)所 示。 机器人以图 7(c)状态进入工作空间,则不会与 障碍物发生碰撞。 最终以规定末端执行器姿态到 达 A 点进行作业。 4.2 狭小空间轨迹仿真 基于 MATLAB Robotics Toolbox 工具箱对机器人 进行轨迹仿真,从初始状态到达最终状态运动时间为 31.83 s。 机器人各关节位移曲线和速度曲线如图 8 和 图 9 所示,由曲线图可看出该机器人的关节位移曲线 平滑连续、无尖角,其关节角速度曲线无突变。 这说明 运动过程中机器人工作平稳,在进入狭小空间作业过 程中没有产生较大的振动,能够取得良好的效果。 仿 真结果表明,七自由度协作型机器人具有良好的灵活 性和避障能力,能够进入狭小空间内进行作业。 (a)初始状态 (b)避障过程 1 (c)避障过程 2 (d)工作过程 1 第 1 期 胡明伟,等:一种协作型机器人运动性能分析与仿真 ·79·

.80 智能系统学报 第12卷 800 800 400 400 400 400 洲4o00-40-8004000。 A804000-400-800-4000 400 800 400 800 2 (i)最终状态 图7机器人轨迹规划 (e)工作过程2 Fig.7 Trajectory planning of robot 关节4 关节6 关节2 100 800 50 400 关节7 关节1 0 关节3 0 关节 -400 -100 0 5 10 15 202530 s -800 图8机器人关节位移曲线 800400,0-400-4000 400 800 Fig.8 Curves of robot joint displacement 30 (f)工作过程3 安-3005101520230 800 20 0 400 -50% 5 10 15 2530 0 30 -400 -48080400 40% 2530 9-400-800.400 400 800 0 (s-()/ 30 (g)工作过程4 4065 10 2530 (s()s 50 800 50 400 010 15 0 2530 50 0 -400 -40%510 15202530 880400-400-80400 800 0 400 女 -206 51015202530 (h)工作过程5 图9机器人关节速度曲线 Fig.9 Curves of robot joint velocity
(e)工作过程 2 (f)工作过程 3 (g)工作过程 4 (h)工作过程 5 (i)最终状态 图 7 机器人轨迹规划 Fig.7 Trajectory planning of robot 图 8 机器人关节位移曲线 Fig.8 Curves of robot joint displacement 图 9 机器人关节速度曲线 Fig.9 Curves of robot joint velocity ·80· 智 能 系 统 学 报 第 12 卷

第1期 胡明伟,等:一种协作型机器人运动性能分析与仿真 ·81 [10]赵占芳.机器人冗余特性和力控制研究[D].北京:北 5 结论 京航天航空大学研究生院,1991. 1)本文介绍了协作型机器人的特性,对其机构 ZHAO Zhanfang.Redundancy and force control of robot 构型进行了比较分析。 manipulators[D].Beijing:Graduate School of Beihang 2)利用Denavit-Hartenberg法建立了KUKA University,1991. [11]归形,原培章.7自由度机器人的图谱问题[J].机器 LBR iiwa机器人的运动学模型。在MATLAB环境 人,1991,13(4):27-30. 下对机器人运动性能进行分析,分析结果表明其具 GUI Tong,YUAN Peizhang.An atlas of 7-DOF robot 有良好的灵活性和可操作性。 manipulators[J].Robot,1991,13(4):27-30. 3)运用MATLAB Robotics Toolbox工具箱对 [12]HUO Xijian,LIU Yiwei,JIANG Li,et al.Design and KUKA LBR iiwa机器人进行狭小空间作业轨迹规 development of a 7-DOF humanoid arm[C]//Proceedings 划,验证机器人具有良好的灵活性和避障能力,能 of the 2012 IEEE International Conference on Robotics and 够进入狭小空间内进行作业。为研发七自由度协 Biomimetics.Guangzhou,China,2012:277-282. 作型机器人提供了理论依据。 [13]SALISBURY J K,CRAIG J J.Articulated hands:force control and kinematic issues[J].The international journal 参考文献: of robotics research,1982,1(1):4-17. [14]YOSHIKAWA T.Manipulability of robotic mechanisms [1]IFR Statistical Department.Global survey:human-robot []The international journal of robotics research,1985 teams capturing new sectors EB/OL].Germany:IFR, 4(2):3-9. (2014-12-02)[2015-10-18].htp:/www.if.org/news/ [15]蔡蒂,谢存禧,张铁,等.基于蒙特卡洛法的喷涂机器 ifr-press-release/global-survey-human-robot-teams- 人工作空间分析及仿真[J].机械设计与制造,2009 capturing-new-sectors-670/. (3):161-162. [2]HANSON K.Collaborative robots lend a helping hand[EB/ CAI Di,XIE Cunxi,ZHANG Tie,et al.Study on OL].USA:CTE Publications,(2015-01-01)[2015-10- workspace analysis and simulation of 6-DOF painting robot 18 ]https://www.ctemag.com/news-videos/articles/ based on Monte-Carlo method [J].Machinery design collaborative-robots-lend-helping-hand. manufacture,2009(3):161-162. [3]OSTERGAARD E.Lightweight robot for everybody[J].IEEE [16]CORKE P.Robotics,vision and control:fundamental robotics automation magazine,2012,19(4):17-18. algorithms in MATLAB M ]Berlin Heidelberg. [4]BARRETTE M B.Collaborative robot ebook EB/OL]. Germany:Springer,2011:135-160. Canada:Robotiq,(2015-04-09)[2015-10-18].http:/ 作者简介: robotiq.com/resource-c-enter/ebooks/. 胡明伟,男,1990年生,博士研究 [5]American National Standards Institute.ANSI/RIA R15.06- 生,主要研究方向为机械电子。 2012,Industrial robots and robot systems-safety requirements[S].American:ANSI,2012. [6]PILZ T.Guide to industry acceptance with the new "ISO TS 15066-collaborative robots"standard [C]//Proceedings of 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems.Hamburg,Germany:IEEE,2015. 王洪光.男,1965年,研究员,博士 [7]MATTHIAS B.New safety standards for collaborative 生导师,主要研究方向为机器人机构 robots,ABB YuMi dual-arm robot [C]//Proceedings of 学、特种机器人和机电一体化技术等。 2015 IEEE/RSJ International Conference on Intelligent 发表学术论文170余篇,授权发明和实 Robots and Systems.Hamburg,Germany:IEEE,2015. 用新型专利40余项。 [8]TSAI Y C,SONI A H.Workspace synthesis of 3R,4R,5R and 6R robots[J].Mechanism and machine theory,1985, 20(6):555-563. 潘新安,男,1982年,副研究员,博 [9]周东辉.冗余度机器人机构学研究[D].北京:北京航空 士,主要研究方向为机器人机构学等。 航天大学机器人研究所,1994. 发表学术论文10余篇,授权发明和实 ZHOU Donghui.On the mechanism study of redundant 用新型专利6项。 robots[D].Beijing:Graduate School of Beihang University,1994
5 结论 1)本文介绍了协作型机器人的特性,对其机构 构型进行了比较分析。 2) 利 用 Denavit⁃Hartenberg 法 建 立 了 KUKA LBR iiwa 机器人的运动学模型。 在 MATLAB 环境 下对机器人运动性能进行分析,分析结果表明其具 有良好的灵活性和可操作性。 3) 运用 MATLAB Robotics Toolbox 工 具 箱 对 KUKA LBR iiwa 机器人进行狭小空间作业轨迹规 划,验证机器人具有良好的灵活性和避障能力,能 够进入狭小空间内进行作业。 为研发七自由度协 作型机器人提供了理论依据。 参考文献: [1 ] IFR Statistical Department. Global survey: human⁃robot teams capturing new sectors [ EB/ OL]. Germany: IFR, (2014⁃12⁃02) [ 2015⁃10⁃18]. http: / / www. ifr. org / news/ ifr⁃press⁃release / global⁃survey⁃human⁃robot⁃teams⁃ capturing⁃new⁃sectors-670 / . [2]HANSON K.Collaborative robots lend a helping hand[EB/ OL].USA:CTE Publications,( 2015- 01- 01) [ 2015- 10 - 18 ]. https: / / www. ctemag. com/ news⁃videos/ articles/ collaborative⁃robots⁃lend⁃helping⁃hand. [3]OSTERGAARD E. Lightweight robot for everybody[J]. IEEE robotics & automation magazine, 2012, 19(4): 17-18. [4] BARRETTE M B. Collaborative robot ebook [ EB/ OL]. Canada:Robotiq,(2015-04-09) [2015-10-18].http: / / robotiq.com/ resource⁃c⁃enter/ ebooks/ . [5]American National Standards Institute. ANSI/ RIA R15.06- 2012, Industrial robots and robot systems⁃safety requirements[S]. American: ANSI, 2012. [6]PILZ T. Guide to industry acceptance with the new “ISO TS 15066⁃collaborative robots” standard [ C] / / Proceedings of 2015 IEEE/ RSJ International Conference on Intelligent Robots and Systems. Hamburg, Germany: IEEE, 2015. [ 7 ] MATTHIAS B. New safety standards for collaborative robots, ABB YuMi dual⁃arm robot [ C] / / Proceedings of 2015 IEEE/ RSJ International Conference on Intelligent Robots and Systems. Hamburg, Germany: IEEE, 2015. [8]TSAI Y C, SONI A H. Workspace synthesis of 3R, 4R, 5R and 6R robots[ J]. Mechanism and machine theory, 1985, 20(6): 555-563. [9]周东辉. 冗余度机器人机构学研究[D]. 北京: 北京航空 航天大学机器人研究所, 1994. ZHOU Donghui. On the mechanism study of redundant robots [ D ]. Beijing: Graduate School of Beihang University, 1994. [10]赵占芳. 机器人冗余特性和力控制研究[D]. 北京: 北 京航天航空大学研究生院, 1991. ZHAO Zhanfang. Redundancy and force control of robot manipulators [ D]. Beijing: Graduate School of Beihang University, 1991. [11]归彤, 原培章. 7 自由度机器人的图谱问题[ J]. 机器 人, 1991, 13(4): 27-30. GUI Tong, YUAN Peizhang. An atlas of 7⁃DOF robot manipulators[J]. Robot, 1991, 13(4): 27-30. [12] HUO Xijian, LIU Yiwei, JIANG Li, et al. Design and development of a 7⁃DOF humanoid arm[C] / / Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics. Guangzhou, China, 2012: 277-282. [13] SALISBURY J K, CRAIG J J. Articulated hands: force control and kinematic issues[J]. The international journal of robotics research, 1982, 1(1): 4-17. [ 14 ] YOSHIKAWA T. Manipulability of robotic mechanisms [J]. The international journal of robotics research, 1985, 4(2): 3-9. [15]蔡蒂, 谢存禧, 张铁, 等. 基于蒙特卡洛法的喷涂机器 人工作空间分析及仿真[ J]. 机械设计与制造, 2009 (3): 161-162. CAI Di, XIE Cunxi, ZHANG Tie, et al. Study on workspace analysis and simulation of 6⁃DOF painting robot based on Monte⁃Carlo method [ J]. Machinery design & manufacture, 2009(3): 161-162. [16 ] CORKE P. Robotics, vision and control: fundamental algorithms in MATLAB [ M ]. Berlin Heidelberg, Germany: Springer, 2011: 135-160. 作者简介: 胡明伟,男,1990 年生,博士研究 生,主要研究方向为机械电子。 王洪光,男,1965 年,研究员,博士 生导师,主要研究方向为机器人机构 学、特种机器人和机电一体化技术等。 发表学术论文 170 余篇,授权发明和实 用新型专利 40 余项。 潘新安,男,1982 年,副研究员,博 士,主要研究方向为机器人机构学等。 发表学术论文 10 余篇,授权发明和实 用新型专利 6 项。 第 1 期 胡明伟,等:一种协作型机器人运动性能分析与仿真 ·81·