【智能系统】A modified consensus algorithm for multi-UAV formations based on pigeon-inspired optimization with a slow diving strategy

第12卷第4期 智能系统学报 Vol.12 No.4 2017年8月 CAAI Transactions on Intelligent Systems Aug.2017 D0I:10.11992/is.201604006 网s络出版地址：http:/kns.cnki.net/kcms/detail/23.1538.TP.20170630.1420.004.html. A modified consensus algorithm for multi-UAV formations based on pigeon-inspired optimization with a slow diving strategy ZHANG Tianjie,DUAN Haibin (Science and Technology on Aircraft Control Laboratory,School of Automation Science and Electrical Engineering,Beihang University (BUAA),Beijing 100191,China) Abstract:This paper considers the formation control problem for a group of unmanned aerial vehicles (UAVs) employing consensus with different optimizers.A group of UAVs can never accomplish difficult tasks without formation because if disordered they do not work any better than a single vehicle,and a single vehicle is limited by its undeveloped intelligence and insufficient load.Among the many formation methods,consensus has attracted much attention because of its effectiveness and simplicity.However,at the beginning of convergence,overshoot and oscillation are universal because of the limitation of communication and a lack of forecasting,which are inborn shortcomings of consensus.It is natural to modify this method with lots of optimizers.In order to reduce overshoot and smooth trajectories,this paper first adopted particle swarm optimization (PSO),then pigeon-inspired optimization (PIO)to modify the consensus.PSO is a very popular optimizer,while PIO is a new method,both work but still retain disadvantages such as residual oscillation.As a result,it was necessary to modify PIO,and a pigeon-inspired optimization with a slow diving strategy (SD-PIO)is proposed.Convergence analysis was performed on the SD-PIO based on the Banach fixed-point theorem and conditions sufficient for stability were achieved. Finally,a series of comparative simulations were conducted to verify the feasibility and effectiveness of the proposed approach. Keywords:unmanned aerial vehicle (UAV);formation;consensus;pigeon-inspired optimization (PIO);Banach fixed-point theorem 中图分类号：TP18:TP273文献标志码：A文章编号：1673-4785(2017)04-0570-12 英文引用格式：ZHANG Tianjie,,DUAN Haibin.A modified consensus algorithm for multi-UAV formations based on pigeon-inspired optimization with a slow diving strategy[J].CAAI transactions on intelligent systems,2017,12(4):570-581. Formation control of unmanned aerial vehicles leader-follower approach artificial potential field (UAVs)can accomplish a task better than a single and sliding mode controlts]. UAV and has been studied using various methods. Among these approaches,consensus is an UAVs are widely adopted in various situationst-2]. effective and easy method for distributed controlt9. However,the requirements nowadays have already Using several simple consensus equations,UAVs can overtaken the current abilities of a single UAV.In fly along complex trajectories.Consensus originates order to satisfy the requirements,different plans for the from the natural behavior of animals such as fish and cooperation of many UAVs have been proposed by birds.A single bird or fish is small and weak,but a Chaumette3]and Raschet4,and the design of a population can hold a complicated formation.It is method for multi-UAV formation is importantts). consensus that plays an essential role in this Different methods have been proposed such as the phenomenon.Vicsek and Ren-]have achieved many results in this field.This paper adopts this 收稿日期：2017-04-11.网络出版日期：2017-06-30. method to design a controller for a multi-UAV 基金项目：Natural Science Foundation of China under Grant(61333004). 通信作者：ZHANG Tianjie..E-mail:11031148@buaa.edu.cn. formation

第 １２ 卷第 ４ 期 智 能 系 统 学 报 Ｖｏｌ．１２ №．４ ２０１７ 年 ８ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ａｕｇ． ２０１７ ＤＯＩ：１０．１１９９２ ／ ｔｉｓ．２０１６０４００６ 网络出版地址：ｈｔｔｐ： ／ ／ ｋｎｓ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｅｔａｉｌ ／ ２３．１５３８．ＴＰ．２０１７０６３０．１４２０．００４．ｈｔｍｌ． Ａ ｍｏｄｉｆｉｅｄ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ ｆｏｒ ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎｓ ｂａｓｅｄ ｏｎ ｐｉｇｅｏｎ⁃ｉｎｓｐｉｒｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ｗｉｔｈ ａ ｓｌｏｗ ｄｉｖｉｎｇ ｓｔｒａｔｅｇｙ ＺＨＡＮＧ Ｔｉａｎｊｉｅ， ＤＵＡＮ Ｈａｉｂｉｎ （Ｓｃｉｅｎｃｅ ａｎｄ Ｔｅｃｈｎｏｌｏｇｙ ｏｎ Ａｉｒｃｒａｆｔ Ｃｏｎｔｒｏｌ Ｌａｂｏｒａｔｏｒｙ， Ｓｃｈｏｏｌ ｏｆ Ａｕｔｏｍａｔｉｏｎ Ｓｃｉｅｎｃｅ ａｎｄ Ｅｌｅｃｔｒｉｃａｌ Ｅｎｇｉｎｅｅｒｉｎｇ，Ｂｅｉｈａｎｇ Ｕｎｉｖｅｒｓｉｔｙ （ＢＵＡＡ）， Ｂｅｉｊｉｎｇ １００１９１， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｔｈｉｓ ｐａｐｅｒ ｃｏｎｓｉｄｅｒｓ ｔｈｅ ｆｏｒｍａｔｉｏｎ ｃｏｎｔｒｏｌ ｐｒｏｂｌｅｍ ｆｏｒ ａ ｇｒｏｕｐ ｏｆ ｕｎｍａｎｎｅｄ ａｅｒｉａｌ ｖｅｈｉｃｌｅｓ （ＵＡＶｓ） ｅｍｐｌｏｙｉｎｇ ｃｏｎｓｅｎｓｕｓ ｗｉｔｈ ｄｉｆｆｅｒｅｎｔ ｏｐｔｉｍｉｚｅｒｓ． Ａ ｇｒｏｕｐ ｏｆ ＵＡＶｓ ｃａｎ ｎｅｖｅｒ ａｃｃｏｍｐｌｉｓｈ ｄｉｆｆｉｃｕｌｔ ｔａｓｋｓ ｗｉｔｈｏｕｔ ｆｏｒｍａｔｉｏｎ ｂｅｃａｕｓｅ ｉｆ ｄｉｓｏｒｄｅｒｅｄ ｔｈｅｙ ｄｏ ｎｏｔ ｗｏｒｋ ａｎｙ ｂｅｔｔｅｒ ｔｈａｎ ａ ｓｉｎｇｌｅ ｖｅｈｉｃｌｅ， ａｎｄ ａ ｓｉｎｇｌｅ ｖｅｈｉｃｌｅ ｉｓ ｌｉｍｉｔｅｄ ｂｙ ｉｔｓ ｕｎｄｅｖｅｌｏｐｅｄ ｉｎｔｅｌｌｉｇｅｎｃｅ ａｎｄ ｉｎｓｕｆｆｉｃｉｅｎｔ ｌｏａｄ． Ａｍｏｎｇ ｔｈｅ ｍａｎｙ ｆｏｒｍａｔｉｏｎ ｍｅｔｈｏｄｓ， ｃｏｎｓｅｎｓｕｓ ｈａｓ ａｔｔｒａｃｔｅｄ ｍｕｃｈ ａｔｔｅｎｔｉｏｎ ｂｅｃａｕｓｅ ｏｆ ｉｔｓ ｅｆｆｅｃｔｉｖｅｎｅｓｓ ａｎｄ ｓｉｍｐｌｉｃｉｔｙ． Ｈｏｗｅｖｅｒ， ａｔ ｔｈｅ ｂｅｇｉｎｎｉｎｇ ｏｆ ｃｏｎｖｅｒｇｅｎｃｅ， ｏｖｅｒｓｈｏｏｔ ａｎｄ ｏｓｃｉｌｌａｔｉｏｎ ａｒｅ ｕｎｉｖｅｒｓａｌ ｂｅｃａｕｓｅ ｏｆ ｔｈｅ ｌｉｍｉｔａｔｉｏｎ ｏｆ ｃｏｍｍｕｎｉｃａｔｉｏｎ ａｎｄ ａ ｌａｃｋ ｏｆ ｆｏｒｅｃａｓｔｉｎｇ， ｗｈｉｃｈ ａｒｅ ｉｎｂｏｒｎ ｓｈｏｒｔｃｏｍｉｎｇｓ ｏｆ ｃｏｎｓｅｎｓｕｓ． Ｉｔ ｉｓ ｎａｔｕｒａｌ ｔｏ ｍｏｄｉｆｙ ｔｈｉｓ ｍｅｔｈｏｄ ｗｉｔｈ ｌｏｔｓ ｏｆ ｏｐｔｉｍｉｚｅｒｓ． Ｉｎ ｏｒｄｅｒ ｔｏ ｒｅｄｕｃｅ ｏｖｅｒｓｈｏｏｔ ａｎｄ ｓｍｏｏｔｈ ｔｒａｊｅｃｔｏｒｉｅｓ， ｔｈｉｓ ｐａｐｅｒ ｆｉｒｓｔ ａｄｏｐｔｅｄ ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ （ ＰＳＯ）， ｔｈｅｎ ｐｉｇｅｏｎ⁃ｉｎｓｐｉｒｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ （ＰＩＯ） ｔｏ ｍｏｄｉｆｙ ｔｈｅ ｃｏｎｓｅｎｓｕｓ． ＰＳＯ ｉｓ ａ ｖｅｒｙ ｐｏｐｕｌａｒ ｏｐｔｉｍｉｚｅｒ， ｗｈｉｌｅ ＰＩＯ ｉｓ ａ ｎｅｗ ｍｅｔｈｏｄ， ｂｏｔｈ ｗｏｒｋ ｂｕｔ ｓｔｉｌｌ ｒｅｔａｉｎ ｄｉｓａｄｖａｎｔａｇｅｓ ｓｕｃｈ ａｓ ｒｅｓｉｄｕａｌ ｏｓｃｉｌｌａｔｉｏｎ． Ａｓ ａ ｒｅｓｕｌｔ， ｉｔ ｗａｓ ｎｅｃｅｓｓａｒｙ ｔｏ ｍｏｄｉｆｙ ＰＩＯ， ａｎｄ ａ ｐｉｇｅｏｎ⁃ｉｎｓｐｉｒｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ｗｉｔｈ ａ ｓｌｏｗ ｄｉｖｉｎｇ ｓｔｒａｔｅｇｙ （ＳＤ⁃ＰＩＯ） ｉｓ ｐｒｏｐｏｓｅｄ． Ｃｏｎｖｅｒｇｅｎｃｅ ａｎａｌｙｓｉｓ ｗａｓ ｐｅｒｆｏｒｍｅｄ ｏｎ ｔｈｅ ＳＤ⁃ＰＩＯ ｂａｓｅｄ ｏｎ ｔｈｅ Ｂａｎａｃｈ ｆｉｘｅｄ⁃ｐｏｉｎｔ ｔｈｅｏｒｅｍ ａｎｄ ｃｏｎｄｉｔｉｏｎｓ ｓｕｆｆｉｃｉｅｎｔ ｆｏｒ ｓｔａｂｉｌｉｔｙ ｗｅｒｅ ａｃｈｉｅｖｅｄ． Ｆｉｎａｌｌｙ， ａ ｓｅｒｉｅｓ ｏｆ ｃｏｍｐａｒａｔｉｖｅ ｓｉｍｕｌａｔｉｏｎｓ ｗｅｒｅ ｃｏｎｄｕｃｔｅｄ ｔｏ ｖｅｒｉｆｙ ｔｈｅ ｆｅａｓｉｂｉｌｉｔｙ ａｎｄ ｅｆｆｅｃｔｉｖｅｎｅｓｓ ｏｆ ｔｈｅ ｐｒｏｐｏｓｅｄ ａｐｐｒｏａｃｈ． Ｋｅｙｗｏｒｄｓ： ｕｎｍａｎｎｅｄ ａｅｒｉａｌ ｖｅｈｉｃｌｅ （ＵＡＶ）； ｆｏｒｍａｔｉｏｎ； ｃｏｎｓｅｎｓｕｓ； ｐｉｇｅｏｎ⁃ｉｎｓｐｉｒｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ （ＰＩＯ）； Ｂａｎａｃｈ ｆｉｘｅｄ⁃ｐｏｉｎｔ ｔｈｅｏｒｅｍ 收稿日期：２０１７－０４－１１． 网络出版日期：２０１７－０６－３０． 基金项目：Ｎａｔｕｒａｌ Ｓｃｉｅｎｃｅ Ｆｏｕｎｄａｔｉｏｎ ｏｆ Ｃｈｉｎａ ｕｎｄｅｒ Ｇｒａｎｔ （６１３３３００４）． 通信作者：ＺＨＡＮＧ Ｔｉａｎｊｉｅ． Ｅ⁃ｍａｉｌ：１１０３１１４８＠ ｂｕａａ．ｅｄｕ．ｃｎ． 中图分类号：ＴＰ１８；ＴＰ２７３ 文献标志码：Ａ 文章编号：１６７３－４７８５（２０１７）０４－０５７０－１２ 英文引用格式：ＺＨＡＮＧ Ｔｉａｎｊｉｅ， ＤＵＡＮ Ｈａｉｂｉｎ．Ａ ｍｏｄｉｆｉｅｄ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ ｆｏｒ ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎｓ ｂａｓｅｄ ｏｎ ｐｉｇｅｏｎ⁃ｉｎｓｐｉｒｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ｗｉｔｈ ａ ｓｌｏｗ ｄｉｖｉｎｇ ｓｔｒａｔｅｇｙ［Ｊ］． ＣＡＡＩ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｉｎｔｅｌｌｉｇｅｎｔ ｓｙｓｔｅｍｓ， ２０１７， １２（４）： ５７０－５８１． Ｆｏｒｍａｔｉｏｎ ｃｏｎｔｒｏｌ ｏｆ ｕｎｍａｎｎｅｄ ａｅｒｉａｌ ｖｅｈｉｃｌｅｓ （ＵＡＶｓ） ｃａｎ ａｃｃｏｍｐｌｉｓｈ ａ ｔａｓｋ ｂｅｔｔｅｒ ｔｈａｎ ａ ｓｉｎｇｌｅ ＵＡＶ ａｎｄ ｈａｓ ｂｅｅｎ ｓｔｕｄｉｅｄ ｕｓｉｎｇ ｖａｒｉｏｕｓ ｍｅｔｈｏｄｓ． ＵＡＶｓ ａｒｅ ｗｉｄｅｌｙ ａｄｏｐｔｅｄ ｉｎ ｖａｒｉｏｕｓ ｓｉｔｕａｔｉｏｎｓ ［１－２］ ． Ｈｏｗｅｖｅｒ， ｔｈｅ ｒｅｑｕｉｒｅｍｅｎｔｓ ｎｏｗａｄａｙｓ ｈａｖｅ ａｌｒｅａｄｙ ｏｖｅｒｔａｋｅｎ ｔｈｅ ｃｕｒｒｅｎｔ ａｂｉｌｉｔｉｅｓ ｏｆ ａ ｓｉｎｇｌｅ ＵＡＶ． Ｉｎ ｏｒｄｅｒ ｔｏ ｓａｔｉｓｆｙ ｔｈｅ ｒｅｑｕｉｒｅｍｅｎｔｓ， ｄｉｆｆｅｒｅｎｔ ｐｌａｎｓ ｆｏｒ ｔｈｅ ｃｏｏｐｅｒａｔｉｏｎ ｏｆ ｍａｎｙ ＵＡＶｓ ｈａｖｅ ｂｅｅｎ ｐｒｏｐｏｓｅｄ ｂｙ Ｃｈａｕｍｅｔｔｅ ［３］ ａｎｄ Ｒａｓｃｈｅ ［４］ ， ａｎｄ ｔｈｅ ｄｅｓｉｇｎ ｏｆ ａ ｍｅｔｈｏｄ ｆｏｒ ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎ ｉｓ ｉｍｐｏｒｔａｎｔ ［５］ ． Ｄｉｆｆｅｒｅｎｔ ｍｅｔｈｏｄｓ ｈａｖｅ ｂｅｅｎ ｐｒｏｐｏｓｅｄ ｓｕｃｈ ａｓ ｔｈｅ ｌｅａｄｅｒ⁃ｆｏｌｌｏｗｅｒ ａｐｐｒｏａｃｈ ［６］ ， ａｒｔｉｆｉｃｉａｌ ｐｏｔｅｎｔｉａｌ ｆｉｅｌｄ ［７］ ， ａｎｄ ｓｌｉｄｉｎｇ ｍｏｄｅ ｃｏｎｔｒｏｌ ［８］ ． Ａｍｏｎｇ ｔｈｅｓｅ ａｐｐｒｏａｃｈｅｓ， ｃｏｎｓｅｎｓｕｓ ｉｓ ａｎ ｅｆｆｅｃｔｉｖｅ ａｎｄ ｅａｓｙ ｍｅｔｈｏｄ ｆｏｒ ｄｉｓｔｒｉｂｕｔｅｄ ｃｏｎｔｒｏｌ ［９］ ． Ｕｓｉｎｇ ｓｅｖｅｒａｌ ｓｉｍｐｌｅ ｃｏｎｓｅｎｓｕｓ ｅｑｕａｔｉｏｎｓ， ＵＡＶｓ ｃａｎ ｆｌｙ ａｌｏｎｇ ｃｏｍｐｌｅｘ ｔｒａｊｅｃｔｏｒｉｅｓ． Ｃｏｎｓｅｎｓｕｓ ｏｒｉｇｉｎａｔｅｓ ｆｒｏｍ ｔｈｅ ｎａｔｕｒａｌ ｂｅｈａｖｉｏｒ ｏｆ ａｎｉｍａｌｓ ｓｕｃｈ ａｓ ｆｉｓｈ ａｎｄ ｂｉｒｄｓ． Ａ ｓｉｎｇｌｅ ｂｉｒｄ ｏｒ ｆｉｓｈ ｉｓ ｓｍａｌｌ ａｎｄ ｗｅａｋ， ｂｕｔ ａ ｐｏｐｕｌａｔｉｏｎ ｃａｎ ｈｏｌｄ ａ ｃｏｍｐｌｉｃａｔｅｄ ｆｏｒｍａｔｉｏｎ． Ｉｔ ｉｓ ｃｏｎｓｅｎｓｕｓ ｔｈａｔ ｐｌａｙｓ ａｎ ｅｓｓｅｎｔｉａｌ ｒｏｌｅ ｉｎ ｔｈｉｓ ｐｈｅｎｏｍｅｎｏｎ． Ｖｉｃｓｅｋ ［１０］ ａｎｄ Ｒｅｎ ［９，１１－１２］ ｈａｖｅ ａｃｈｉｅｖｅｄ ｍａｎｙ ｒｅｓｕｌｔｓ ｉｎ ｔｈｉｓ ｆｉｅｌｄ． Ｔｈｉｓ ｐａｐｅｒ ａｄｏｐｔｓ ｔｈｉｓ ｍｅｔｈｏｄ ｔｏ ｄｅｓｉｇｎ ａ ｃｏｎｔｒｏｌｌｅｒ ｆｏｒ ａ ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎ．

第4期 ZHANG Tianjie,et al.:A modified consensus algorithm for multi-UAV formations based on pigeon-inspired optimization with a slow diving strategy ·571- There are two main parts of the consensus proposed. algorithm[.First,the formation is treated as a The remainder of this paper is organized as virtual rigid body,every UAV has a desired position follows.In Section 2,details of the application of and this acts as a point on the body.Using consensus, consensus in a multi-UAV formation are given.The the UAVs'desired positions concentrate together and construction of SD-PIO and the convergence analysis is create the desired formation.However,a distance error considered in Section 3.In Section 4,the SD-PIO- always exists between the desired position and the real based consensus algorithm is proposed for a multi-UAV position for each UAV,and the second part of the formation,followed by numerical simulation and results algorithm deals with this problem by considering this analysis in Section 5.Finally,several conclusions error as a variable in consensus.By devising a useful concerning the use of optimal algorithms in consensus algorithm,the error closes to zero as time tends to theory are drawn. infinity.The real position for each UAV is the sum of the desired position and the error.In this way,UAVs 1 Controller design based on consensus with random initial locations always concentrate and fly 1.1 Multi-UAV formation controller design along their predesigned routes.These two parts of the It is supposed that each UAV possesses a moving algorithm added to the communication networks of the coordinate system with three axes (x,y,and z).The individual vehicles comprise the whole UAV shape of the UAV is ignored and a mass point model is system.However,consensus can only ensure that used instead.This is because the time delay of an all the variables are close to the given state and does aircraft control loop is much shorter than that of the not know whether the values of variables at each navigation and guidance loops.Therefore,when moment are optimal.It is a good idea to improve dealing with formation control,the UAV model can be consensus with optimal algorithms. simplified as a point,which means there is no need to Pigeon-inspired optimization (PIO)is a novel consider each UAV's attitude.Under this assumption, swarm intelligence optimizer proposed by Duan and all the UAV's x,y,and z axes are parallel. Qiao in 2014015).The method imitates pigeons' Consensus means that multiple UAVs reach an behavior when seeking a way back to their loft.It is agreement on a common state,e.g.,the UAV's believed that pigeons adopt different tools at different position.In detail,every UAV has its initial 3- stages when returning home.In the beginning,compass dimensional position (x,y,z)in an inertial and map factors are adopted,each pigeon's velocity coordinate system,namely the ground coordinate is updated by the linear combination of its neighbors' system.The velocity of the original UAV's moving including itself)best locations and its former velocity. coordinate system converges to the standard state of the When pigeons approach home,some smart ones with virtual leader UAVo by consensus.The UAVo's state good memories can recognize familiar landmarks which consists of a time-varying position and predesigned guide them,the others just need to follow these velocity.In this way,all the UAVs'coordinates leaders.The second part of PIO is designed to become one common moving coordinate system.After concentrate the average location of all the pigeons.It is adding the relative position of each UAV in the moving widely known that each optimizer fits one or several coordinate system,the desired time-varying position is problems,and PIO was first proposed for air robot path achieved for each UAV.When viewed as a mass of plannings],image processing,and orbit moving points,all these UAVs constitute a virtual formations(20].When it comes to the optimization of body. consensus mentioned above,disadvantages appear such The formation method consists of both single-and as the trajectory closes to the desired trace with double-integrator consensus algorithms.The latter aims oscillation to an unsatisfactory degree(This means to concentrate the UAVs with random initial positions that PIO needs to be modified and a pigeon-inspired and ensure that the desired positions of all the UAVs optimization with slow diving strategy (SD-PIO)is converge to points on the predesigned trajectory.The

Ｔｈｅｒｅ ａｒｅ ｔｗｏ ｍａｉｎ ｐａｒｔｓ ｏｆ ｔｈｅ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ ［１３－１４］ ． Ｆｉｒｓｔ， ｔｈｅ ｆｏｒｍａｔｉｏｎ ｉｓ ｔｒｅａｔｅｄ ａｓ ａ ｖｉｒｔｕａｌ ｒｉｇｉｄ ｂｏｄｙ， ｅｖｅｒｙ ＵＡＶ ｈａｓ ａ ｄｅｓｉｒｅｄ ｐｏｓｉｔｉｏｎ ａｎｄ ｔｈｉｓ ａｃｔｓ ａｓ ａ ｐｏｉｎｔ ｏｎ ｔｈｅ ｂｏｄｙ． Ｕｓｉｎｇ ｃｏｎｓｅｎｓｕｓ， ｔｈｅ ＵＡＶｓ’ ｄｅｓｉｒｅｄ ｐｏｓｉｔｉｏｎｓ ｃｏｎｃｅｎｔｒａｔｅ ｔｏｇｅｔｈｅｒ ａｎｄ ｃｒｅａｔｅ ｔｈｅ ｄｅｓｉｒｅｄ ｆｏｒｍａｔｉｏｎ． Ｈｏｗｅｖｅｒ， ａ ｄｉｓｔａｎｃｅ ｅｒｒｏｒ ａｌｗａｙｓ ｅｘｉｓｔｓ ｂｅｔｗｅｅｎ ｔｈｅ ｄｅｓｉｒｅｄ ｐｏｓｉｔｉｏｎ ａｎｄ ｔｈｅ ｒｅａｌ ｐｏｓｉｔｉｏｎ ｆｏｒ ｅａｃｈ ＵＡＶ， ａｎｄ ｔｈｅ ｓｅｃｏｎｄ ｐａｒｔ ｏｆ ｔｈｅ ａｌｇｏｒｉｔｈｍ ｄｅａｌｓ ｗｉｔｈ ｔｈｉｓ ｐｒｏｂｌｅｍ ｂｙ ｃｏｎｓｉｄｅｒｉｎｇ ｔｈｉｓ ｅｒｒｏｒ ａｓ ａ ｖａｒｉａｂｌｅ ｉｎ ｃｏｎｓｅｎｓｕｓ． Ｂｙ ｄｅｖｉｓｉｎｇ ａ ｕｓｅｆｕｌ ａｌｇｏｒｉｔｈｍ， ｔｈｅ ｅｒｒｏｒ ｃｌｏｓｅｓ ｔｏ ｚｅｒｏ ａｓ ｔｉｍｅ ｔｅｎｄｓ ｔｏ ｉｎｆｉｎｉｔｙ． Ｔｈｅ ｒｅａｌ ｐｏｓｉｔｉｏｎ ｆｏｒ ｅａｃｈ ＵＡＶ ｉｓ ｔｈｅ ｓｕｍ ｏｆ ｔｈｅ ｄｅｓｉｒｅｄ ｐｏｓｉｔｉｏｎ ａｎｄ ｔｈｅ ｅｒｒｏｒ． Ｉｎ ｔｈｉｓ ｗａｙ， ＵＡＶｓ ｗｉｔｈ ｒａｎｄｏｍ ｉｎｉｔｉａｌ ｌｏｃａｔｉｏｎｓ ａｌｗａｙｓ ｃｏｎｃｅｎｔｒａｔｅ ａｎｄ ｆｌｙ ａｌｏｎｇ ｔｈｅｉｒ ｐｒｅｄｅｓｉｇｎｅｄ ｒｏｕｔｅｓ． Ｔｈｅｓｅ ｔｗｏ ｐａｒｔｓ ｏｆ ｔｈｅ ａｌｇｏｒｉｔｈｍ ａｄｄｅｄ ｔｏ ｔｈｅ ｃｏｍｍｕｎｉｃａｔｉｏｎ ｎｅｔｗｏｒｋｓ ｏｆ ｔｈｅ ｉｎｄｉｖｉｄｕａｌ ｖｅｈｉｃｌｅｓ ｃｏｍｐｒｉｓｅ ｔｈｅ ｗｈｏｌｅ ＵＡＶ ｓｙｓｔｅｍ ［１３－１４］ ． Ｈｏｗｅｖｅｒ， ｃｏｎｓｅｎｓｕｓ ｃａｎ ｏｎｌｙ ｅｎｓｕｒｅ ｔｈａｔ ａｌｌ ｔｈｅ ｖａｒｉａｂｌｅｓ ａｒｅ ｃｌｏｓｅ ｔｏ ｔｈｅ ｇｉｖｅｎ ｓｔａｔｅ ａｎｄ ｄｏｅｓ ｎｏｔ ｋｎｏｗ ｗｈｅｔｈｅｒ ｔｈｅ ｖａｌｕｅｓ ｏｆ ｖａｒｉａｂｌｅｓ ａｔ ｅａｃｈ ｍｏｍｅｎｔ ａｒｅ ｏｐｔｉｍａｌ． Ｉｔ ｉｓ ａ ｇｏｏｄ ｉｄｅａ ｔｏ ｉｍｐｒｏｖｅ ｃｏｎｓｅｎｓｕｓ ｗｉｔｈ ｏｐｔｉｍａｌ ａｌｇｏｒｉｔｈｍｓ． Ｐｉｇｅｏｎ⁃ｉｎｓｐｉｒｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ （ ＰＩＯ） ｉｓ ａ ｎｏｖｅｌ ｓｗａｒｍ ｉｎｔｅｌｌｉｇｅｎｃｅ ｏｐｔｉｍｉｚｅｒ ｐｒｏｐｏｓｅｄ ｂｙ Ｄｕａｎ ａｎｄ Ｑｉａｏ ｉｎ ２０１４ ［１５］ ． Ｔｈｅ ｍｅｔｈｏｄ ｉｍｉｔａｔｅｓ ｐｉｇｅｏｎｓ􀆳 ｂｅｈａｖｉｏｒ ｗｈｅｎ ｓｅｅｋｉｎｇ ａ ｗａｙ ｂａｃｋ ｔｏ ｔｈｅｉｒ ｌｏｆｔ． Ｉｔ ｉｓ ｂｅｌｉｅｖｅｄ ｔｈａｔ ｐｉｇｅｏｎｓ ａｄｏｐｔ ｄｉｆｆｅｒｅｎｔ ｔｏｏｌｓ ａｔ ｄｉｆｆｅｒｅｎｔ ｓｔａｇｅｓ ｗｈｅｎ ｒｅｔｕｒｎｉｎｇ ｈｏｍｅ． Ｉｎ ｔｈｅ ｂｅｇｉｎｎｉｎｇ， ｃｏｍｐａｓｓ ａｎｄ ｍａｐ ｆａｃｔｏｒｓ ａｒｅ ａｄｏｐｔｅｄ ［１６］ ， ｅａｃｈ ｐｉｇｅｏｎ􀆳ｓ ｖｅｌｏｃｉｔｙ ｉｓ ｕｐｄａｔｅｄ ｂｙ ｔｈｅ ｌｉｎｅａｒ ｃｏｍｂｉｎａｔｉｏｎ ｏｆ ｉｔｓ ｎｅｉｇｈｂｏｒｓ’ （ ｉｎｃｌｕｄｉｎｇ ｉｔｓｅｌｆ） ｂｅｓｔ ｌｏｃａｔｉｏｎｓ ａｎｄ ｉｔｓ ｆｏｒｍｅｒ ｖｅｌｏｃｉｔｙ． Ｗｈｅｎ ｐｉｇｅｏｎｓ ａｐｐｒｏａｃｈ ｈｏｍｅ， ｓｏｍｅ ｓｍａｒｔ ｏｎｅｓ ｗｉｔｈ ｇｏｏｄ ｍｅｍｏｒｉｅｓ ｃａｎ ｒｅｃｏｇｎｉｚｅ ｆａｍｉｌｉａｒ ｌａｎｄｍａｒｋｓ ｗｈｉｃｈ ｇｕｉｄｅ ｔｈｅｍ ［１７］ ， ｔｈｅ ｏｔｈｅｒｓ ｊｕｓｔ ｎｅｅｄ ｔｏ ｆｏｌｌｏｗ ｔｈｅｓｅ ｌｅａｄｅｒｓ． Ｔｈｅ ｓｅｃｏｎｄ ｐａｒｔ ｏｆ ＰＩＯ ｉｓ ｄｅｓｉｇｎｅｄ ｔｏ ｃｏｎｃｅｎｔｒａｔｅ ｔｈｅ ａｖｅｒａｇｅ ｌｏｃａｔｉｏｎ ｏｆ ａｌｌ ｔｈｅ ｐｉｇｅｏｎｓ． Ｉｔ ｉｓ ｗｉｄｅｌｙ ｋｎｏｗｎ ｔｈａｔ ｅａｃｈ ｏｐｔｉｍｉｚｅｒ ｆｉｔｓ ｏｎｅ ｏｒ ｓｅｖｅｒａｌ ｐｒｏｂｌｅｍｓ， ａｎｄ ＰＩＯ ｗａｓ ｆｉｒｓｔ ｐｒｏｐｏｓｅｄ ｆｏｒ ａｉｒ ｒｏｂｏｔ ｐａｔｈ ｐｌａｎｎｉｎｇ ［１５，１８］ ， ｉｍａｇｅ ｐｒｏｃｅｓｓｉｎｇ ［１７，１９］ ， ａｎｄ ｏｒｂｉｔ ｆｏｒｍａｔｉｏｎｓ ［２０］ ． Ｗｈｅｎ ｉｔ ｃｏｍｅｓ ｔｏ ｔｈｅ ｏｐｔｉｍｉｚａｔｉｏｎ ｏｆ ｃｏｎｓｅｎｓｕｓ ｍｅｎｔｉｏｎｅｄ ａｂｏｖｅ， ｄｉｓａｄｖａｎｔａｇｅｓ ａｐｐｅａｒ ｓｕｃｈ ａｓ ｔｈｅ ｔｒａｊｅｃｔｏｒｙ ｃｌｏｓｅｓ ｔｏ ｔｈｅ ｄｅｓｉｒｅｄ ｔｒａｃｅ ｗｉｔｈ ｏｓｃｉｌｌａｔｉｏｎ ｔｏ ａｎ ｕｎｓａｔｉｓｆａｃｔｏｒｙ ｄｅｇｒｅｅ ［２１］ ． Ｔｈｉｓ ｍｅａｎｓ ｔｈａｔ ＰＩＯ ｎｅｅｄｓ ｔｏ ｂｅ ｍｏｄｉｆｉｅｄ ａｎｄ ａ ｐｉｇｅｏｎ⁃ｉｎｓｐｉｒｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ｗｉｔｈ ｓｌｏｗ ｄｉｖｉｎｇ ｓｔｒａｔｅｇｙ （ ＳＤ⁃ＰＩＯ） ｉｓ ｐｒｏｐｏｓｅｄ． Ｔｈｅ ｒｅｍａｉｎｄｅｒ ｏｆ ｔｈｉｓ ｐａｐｅｒ ｉｓ ｏｒｇａｎｉｚｅｄ ａｓ ｆｏｌｌｏｗｓ． Ｉｎ Ｓｅｃｔｉｏｎ ２， ｄｅｔａｉｌｓ ｏｆ ｔｈｅ ａｐｐｌｉｃａｔｉｏｎ ｏｆ ｃｏｎｓｅｎｓｕｓ ｉｎ ａ ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎ ａｒｅ ｇｉｖｅｎ． Ｔｈｅ ｃｏｎｓｔｒｕｃｔｉｏｎ ｏｆ ＳＤ⁃ＰＩＯ ａｎｄ ｔｈｅ ｃｏｎｖｅｒｇｅｎｃｅ ａｎａｌｙｓｉｓ ｉｓ ｃｏｎｓｉｄｅｒｅｄ ｉｎ Ｓｅｃｔｉｏｎ ３． Ｉｎ Ｓｅｃｔｉｏｎ ４， ｔｈｅ ＳＤ⁃ＰＩＯ⁃ ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ ｉｓ ｐｒｏｐｏｓｅｄ ｆｏｒ ａ ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎ， ｆｏｌｌｏｗｅｄ ｂｙ ｎｕｍｅｒｉｃａｌ ｓｉｍｕｌａｔｉｏｎ ａｎｄ ｒｅｓｕｌｔｓ ａｎａｌｙｓｉｓ ｉｎ Ｓｅｃｔｉｏｎ ５． Ｆｉｎａｌｌｙ， ｓｅｖｅｒａｌ ｃｏｎｃｌｕｓｉｏｎｓ ｃｏｎｃｅｒｎｉｎｇ ｔｈｅ ｕｓｅ ｏｆ ｏｐｔｉｍａｌ ａｌｇｏｒｉｔｈｍｓ ｉｎ ｃｏｎｓｅｎｓｕｓ ｔｈｅｏｒｙ ａｒｅ ｄｒａｗｎ． １ Ｃｏｎｔｒｏｌｌｅｒ ｄｅｓｉｇｎ ｂａｓｅｄ ｏｎ ｃｏｎｓｅｎｓｕｓ １．１ Ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎ ｃｏｎｔｒｏｌｌｅｒ ｄｅｓｉｇｎ Ｉｔ ｉｓ ｓｕｐｐｏｓｅｄ ｔｈａｔ ｅａｃｈ ＵＡＶ ｐｏｓｓｅｓｓｅｓ ａ ｍｏｖｉｎｇ ｃｏｏｒｄｉｎａｔｅ ｓｙｓｔｅｍ ｗｉｔｈ ｔｈｒｅｅ ａｘｅｓ （ ｘ， ｙ， ａｎｄ ｚ）． Ｔｈｅ ｓｈａｐｅ ｏｆ ｔｈｅ ＵＡＶ ｉｓ ｉｇｎｏｒｅｄ ａｎｄ ａ ｍａｓｓ ｐｏｉｎｔ ｍｏｄｅｌ ｉｓ ｕｓｅｄ ｉｎｓｔｅａｄ． Ｔｈｉｓ ｉｓ ｂｅｃａｕｓｅ ｔｈｅ ｔｉｍｅ ｄｅｌａｙ ｏｆ ａｎ ａｉｒｃｒａｆｔ ｃｏｎｔｒｏｌ ｌｏｏｐ ｉｓ ｍｕｃｈ ｓｈｏｒｔｅｒ ｔｈａｎ ｔｈａｔ ｏｆ ｔｈｅ ｎａｖｉｇａｔｉｏｎ ａｎｄ ｇｕｉｄａｎｃｅ ｌｏｏｐｓ． Ｔｈｅｒｅｆｏｒｅ， ｗｈｅｎ ｄｅａｌｉｎｇ ｗｉｔｈ ｆｏｒｍａｔｉｏｎ ｃｏｎｔｒｏｌ， ｔｈｅ ＵＡＶ ｍｏｄｅｌ ｃａｎ ｂｅ ｓｉｍｐｌｉｆｉｅｄ ａｓ ａ ｐｏｉｎｔ， ｗｈｉｃｈ ｍｅａｎｓ ｔｈｅｒｅ ｉｓ ｎｏ ｎｅｅｄ ｔｏ ｃｏｎｓｉｄｅｒ ｅａｃｈ ＵＡＶ’ｓ ａｔｔｉｔｕｄｅ． Ｕｎｄｅｒ ｔｈｉｓ ａｓｓｕｍｐｔｉｏｎ， ａｌｌ ｔｈｅ ＵＡＶ’ｓ ｘ， ｙ， ａｎｄ ｚ ａｘｅｓ ａｒｅ ｐａｒａｌｌｅｌ． Ｃｏｎｓｅｎｓｕｓ ｍｅａｎｓ ｔｈａｔ ｍｕｌｔｉｐｌｅ ＵＡＶｓ ｒｅａｃｈ ａｎ ａｇｒｅｅｍｅｎｔ ｏｎ ａ ｃｏｍｍｏｎ ｓｔａｔｅ， ｅ． ｇ．， ｔｈｅ ＵＡＶ’ ｓ ｐｏｓｉｔｉｏｎ． Ｉｎ ｄｅｔａｉｌ， ｅｖｅｒｙ ＵＡＶ ｈａｓ ｉｔｓ ｉｎｉｔｉａｌ ３⁃ ｄｉｍｅｎｓｉｏｎａｌ ｐｏｓｉｔｉｏｎ （ ｘ， ｙ， ｚ ） ｉｎ ａｎ ｉｎｅｒｔｉａｌ ｃｏｏｒｄｉｎａｔｅ ｓｙｓｔｅｍ， ｎａｍｅｌｙ ｔｈｅ ｇｒｏｕｎｄ ｃｏｏｒｄｉｎａｔｅ ｓｙｓｔｅｍ． Ｔｈｅ ｖｅｌｏｃｉｔｙ ｏｆ ｔｈｅ ｏｒｉｇｉｎａｌ ＵＡＶｉ ’ ｓ ｍｏｖｉｎｇ ｃｏｏｒｄｉｎａｔｅ ｓｙｓｔｅｍ ｃｏｎｖｅｒｇｅｓ ｔｏ ｔｈｅ ｓｔａｎｄａｒｄ ｓｔａｔｅ ｏｆ ｔｈｅ ｖｉｒｔｕａｌ ｌｅａｄｅｒ ＵＡＶ１０ ｂｙ ｃｏｎｓｅｎｓｕｓ． Ｔｈｅ ＵＡＶ１０ ’ ｓ ｓｔａｔｅ ｃｏｎｓｉｓｔｓ ｏｆ ａ ｔｉｍｅ⁃ｖａｒｙｉｎｇ ｐｏｓｉｔｉｏｎ ａｎｄ ｐｒｅｄｅｓｉｇｎｅｄ ｖｅｌｏｃｉｔｙ． Ｉｎ ｔｈｉｓ ｗａｙ， ａｌｌ ｔｈｅ ＵＡＶｓ ’ ｃｏｏｒｄｉｎａｔｅｓ ｂｅｃｏｍｅ ｏｎｅ ｃｏｍｍｏｎ ｍｏｖｉｎｇ ｃｏｏｒｄｉｎａｔｅ ｓｙｓｔｅｍ． Ａｆｔｅｒ ａｄｄｉｎｇ ｔｈｅ ｒｅｌａｔｉｖｅ ｐｏｓｉｔｉｏｎ ｏｆ ｅａｃｈ ＵＡＶ ｉｎ ｔｈｅ ｍｏｖｉｎｇ ｃｏｏｒｄｉｎａｔｅ ｓｙｓｔｅｍ， ｔｈｅ ｄｅｓｉｒｅｄ ｔｉｍｅ⁃ｖａｒｙｉｎｇ ｐｏｓｉｔｉｏｎ ｉｓ ａｃｈｉｅｖｅｄ ｆｏｒ ｅａｃｈ ＵＡＶ． Ｗｈｅｎ ｖｉｅｗｅｄ ａｓ ａ ｍａｓｓ ｏｆ ｍｏｖｉｎｇ ｐｏｉｎｔｓ， ａｌｌ ｔｈｅｓｅ ＵＡＶｓ ｃｏｎｓｔｉｔｕｔｅ ａ ｖｉｒｔｕａｌ ｂｏｄｙ． Ｔｈｅ ｆｏｒｍａｔｉｏｎ ｍｅｔｈｏｄ ｃｏｎｓｉｓｔｓ ｏｆ ｂｏｔｈ ｓｉｎｇｌｅ⁃ａｎｄ ｄｏｕｂｌｅ⁃ｉｎｔｅｇｒａｔｏｒ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍｓ． Ｔｈｅ ｌａｔｔｅｒ ａｉｍｓ ｔｏ ｃｏｎｃｅｎｔｒａｔｅ ｔｈｅ ＵＡＶｓ ｗｉｔｈ ｒａｎｄｏｍ ｉｎｉｔｉａｌ ｐｏｓｉｔｉｏｎｓ ａｎｄ ｅｎｓｕｒｅ ｔｈａｔ ｔｈｅ ｄｅｓｉｒｅｄ ｐｏｓｉｔｉｏｎｓ ｏｆ ａｌｌ ｔｈｅ ＵＡＶｓ ｃｏｎｖｅｒｇｅ ｔｏ ｐｏｉｎｔｓ ｏｎ ｔｈｅ ｐｒｅｄｅｓｉｇｎｅｄ ｔｒａｊｅｃｔｏｒｙ． Ｔｈｅ ·５７１· 第 ４ 期 ＺＨＡＮＧ Ｔｉａｎｊｉｅ， ｅｔ ａｌ．：Ａ ｍｏｄｉｆｉｅｄ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ ｆｏｒ ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎｓ ｂａｓｅｄ ｏｎ ｐｉｇｅｏｎ⁃ｉｎｓｐｉｒｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ｗｉｔｈ ａ ｓｌｏｗ ｄｉｖｉｎｇ ｓｔｒａｔｅｇｙ

.572. 智能系统学报 第12卷 former ensures the distance error between the desired that the directed communication topology graph must and the real position converges to 0[4).The real include a spanning tree position of each UAV can be easily acquired and the To attain the desired position for one single UAV UAV's trajectory is drawn. in the moving coordinate system,the error between the Consensus of moving desired and the real position should be treated as an coordinate system extra variable,this can be described by single- State variables of integrator dynamics for simplicity.The math model can Standard moving coordinate Communication be described as state network Errors added with relative er:=u (3) pesition in the formation and the consensus algorithm is in Ref [9]. Consensus of relative position in the moving UAV's u:=- (4) relative position coordinate system -∑ag(e,-er） in the system =rpi+er (5) JA JA JAV,-UAY Where7;is the real position of UAV:,UAV:in the moving coordinate system,er;is the distance error Fig.1 Frame of consensus controller in multi-UAV formation between the real and the desired position of UAVi,rP which is shown in Fig.2,is the desired position of For the formation problem in a multi-UAV UAV;in the moving coordinate system,i1,2,.., system,the UAVs'states should include both position 9.Equations (1~5)above can be transformed into a and velocity,and the control inputs are the collective matrix form, accelerations4.This model is always described by (L☒L)E+(b☒L)E=-K[(L⑧I)E+(b☒L)]- second-order differentiation equations,and as a result, a consensus algorithm for double-integrator dynamics is K[(L☒I3)E+(b☒13)E] required.The dynamic math model of the multi-UAV e=-(L☒I3)e system is given below, r=r+专=p+er+ (6) where Loxo is the Laplace matrix of the communication (1) topology graph,bRreflects which UAV can directly 5=[x] receive information from UAVo,is the desired where专：，i:h,∈R3 represent the position,.the velocity position and also the position of UAVo,which shows and the acceleration of UAV:,respectively and x,y, the desired path for all the UAVs,finally, are the3-dimensional positions,i∈{1,2，…，l0}.The represents the Kronecker product. consensus algorithm can be described as in Ref [14]. K,=diag(K1,K2,…,Kg）,K,=diag(Kl,K2, 三，咳-K--&G,-6]+ 1 …,Ky）,er=(erer…erg),f=(r7…fg)T,ris := the vector of the real position of each UAV,g is the 心-k-》-k-5】(2 vector of the position of the origin of each UAV's moving coordinate system. Where a;is element (i,j)in the adjacency matrix Equation (6)is the core of the multi-UAV 10 controller,and r provides the necessary positional A66∈R6x6,andk=∑ag,K.,K.isa3×3size information for all the UAVs for use in the next step. symmetric positive definite matrix,i1,2,..,9, After acquiring the target instructions,the UAVs fly in this work this is replaced by a Pascal matrix for toward their destinations. simplicity.The algorithm has been proven effective and 1.2 Multi-UAV formation task can make all the UAVs'both positions and velocities The desired formation shape is designed as converge to the state of the root.This is because the follows: graph satisfies the sufficient and necessary condition

ｆｏｒｍｅｒ ｅｎｓｕｒｅｓ ｔｈｅ ｄｉｓｔａｎｃｅ ｅｒｒｏｒ ｂｅｔｗｅｅｎ ｔｈｅ ｄｅｓｉｒｅｄ ａｎｄ ｔｈｅ ｒｅａｌ ｐｏｓｉｔｉｏｎ ｃｏｎｖｅｒｇｅｓ ｔｏ ０ ［１４］ ． Ｔｈｅ ｒｅａｌ ｐｏｓｉｔｉｏｎ ｏｆ ｅａｃｈ ＵＡＶ ｃａｎ ｂｅ ｅａｓｉｌｙ ａｃｑｕｉｒｅｄ ａｎｄ ｔｈｅ ＵＡＶ’ｓ ｔｒａｊｅｃｔｏｒｙ ｉｓ ｄｒａｗｎ． Ｆｉｇ．１ Ｆｒａｍｅ ｏｆ ｃｏｎｓｅｎｓｕｓ ｃｏｎｔｒｏｌｌｅｒ ｉｎ ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎ Ｆｏｒ ｔｈｅ ｆｏｒｍａｔｉｏｎ ｐｒｏｂｌｅｍ ｉｎ ａ ｍｕｌｔｉ⁃ＵＡＶ ｓｙｓｔｅｍ， ｔｈｅ ＵＡＶｓ’ ｓｔａｔｅｓ ｓｈｏｕｌｄ ｉｎｃｌｕｄｅ ｂｏｔｈ ｐｏｓｉｔｉｏｎ ａｎｄ ｖｅｌｏｃｉｔｙ， ａｎｄ ｔｈｅ ｃｏｎｔｒｏｌ ｉｎｐｕｔｓ ａｒｅ ｔｈｅ ａｃｃｅｌｅｒａｔｉｏｎｓ ［１４］ ． Ｔｈｉｓ ｍｏｄｅｌ ｉｓ ａｌｗａｙｓ ｄｅｓｃｒｉｂｅｄ ｂｙ ｓｅｃｏｎｄ⁃ｏｒｄｅｒ ｄｉｆｆｅｒｅｎｔｉａｔｉｏｎ ｅｑｕａｔｉｏｎｓ， ａｎｄ ａｓ ａ ｒｅｓｕｌｔ， ａ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ ｆｏｒ ｄｏｕｂｌｅ⁃ｉｎｔｅｇｒａｔｏｒ ｄｙｎａｍｉｃｓ ｉｓ ｒｅｑｕｉｒｅｄ． Ｔｈｅ ｄｙｎａｍｉｃ ｍａｔｈ ｍｏｄｅｌ ｏｆ ｔｈｅ ｍｕｌｔｉ⁃ＵＡＶ ｓｙｓｔｅｍ ｉｓ ｇｉｖｅｎ ｂｅｌｏｗ， ξ · ｉ ＝ ζｉ ζ · ｉ ＝ μｉ ξｉ ＝ ［ｘｉ ｙｉ ｚｉ］ Ｔ ì î í ï ïï ï ï （１） ｗｈｅｒｅ ξｉ，ζｉ，μｉ∈Ｒ ３ ｒｅｐｒｅｓｅｎｔ ｔｈｅ ｐｏｓｉｔｉｏｎ， ｔｈｅ ｖｅｌｏｃｉｔｙ ａｎｄ ｔｈｅ ａｃｃｅｌｅｒａｔｉｏｎ ｏｆ ＵＡＶｉ， ｒｅｓｐｅｃｔｉｖｅｌｙ ａｎｄ ｘｉ，ｙｉ，ｚｉ ａｒｅ ｔｈｅ ３⁃ｄｉｍｅｎｓｉｏｎａｌ ｐｏｓｉｔｉｏｎｓ， ｉ∈｛１，２，…，１０｝． Ｔｈｅ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ ｃａｎ ｂｅ ｄｅｓｃｒｉｂｅｄ ａｓ ｉｎ Ｒｅｆ ［１４］． μｉ ＝ １ ｋｉ ∑ ９ ｊ ＝ １ ａｉｊ［ζ · ｊ － Ｋｒｉ（ξｉ － ξｊ） － Ｋｖｉ（ζｉ － ζｊ）］ ＋ １ ｋｉ ａｉ１０ ［ζ · ｒ － Ｋｒｉ（ξｉ － ξ ｒ ） － Ｋｖｉ（ζｉ － ζ ｒ ）］ （２） Ｗｈｅｒｅ ａｉｊ ｉｓ ｅｌｅｍｅｎｔ （ ｉ， ｊ） ｉｎ ｔｈｅ ａｄｊａｃｅｎｃｙ ｍａｔｒｉｘ Ａ６×６ ∈Ｒ ６×６ ， ａｎｄ ｋｉ ＝ ∑ １０ ｊ ＝ １ ａｉｊ ， Ｋｒｉ，Ｋｖｉ ｉｓ ａ ３ × ３ｓｉｚｅ ｓｙｍｍｅｔｒｉｃ ｐｏｓｉｔｉｖｅ ｄｅｆｉｎｉｔｅ ｍａｔｒｉｘ， ｉ ∈ ｛１，２，…，９｝ ， ｉｎ ｔｈｉｓ ｗｏｒｋ ｔｈｉｓ ｉｓ ｒｅｐｌａｃｅｄ ｂｙ ａ Ｐａｓｃａｌ ｍａｔｒｉｘ ｆｏｒ ｓｉｍｐｌｉｃｉｔｙ． Ｔｈｅ ａｌｇｏｒｉｔｈｍ ｈａｓ ｂｅｅｎ ｐｒｏｖｅｎ ｅｆｆｅｃｔｉｖｅ ａｎｄ ｃａｎ ｍａｋｅ ａｌｌ ｔｈｅ ＵＡＶｓ’ ｂｏｔｈ ｐｏｓｉｔｉｏｎｓ ａｎｄ ｖｅｌｏｃｉｔｉｅｓ ｃｏｎｖｅｒｇｅ ｔｏ ｔｈｅ ｓｔａｔｅ ｏｆ ｔｈｅ ｒｏｏｔ． Ｔｈｉｓ ｉｓ ｂｅｃａｕｓｅ ｔｈｅ ｇｒａｐｈ ｓａｔｉｓｆｉｅｓ ｔｈｅ ｓｕｆｆｉｃｉｅｎｔ ａｎｄ ｎｅｃｅｓｓａｒｙ ｃｏｎｄｉｔｉｏｎ ｔｈａｔ ｔｈｅ ｄｉｒｅｃｔｅｄ ｃｏｍｍｕｎｉｃａｔｉｏｎ ｔｏｐｏｌｏｇｙ ｇｒａｐｈ ｍｕｓｔ ｉｎｃｌｕｄｅ ａ ｓｐａｎｎｉｎｇ ｔｒｅｅ ［１４］ ． Ｔｏ ａｔｔａｉｎ ｔｈｅ ｄｅｓｉｒｅｄ ｐｏｓｉｔｉｏｎ ｆｏｒ ｏｎｅ ｓｉｎｇｌｅ ＵＡＶ ｉｎ ｔｈｅ ｍｏｖｉｎｇ ｃｏｏｒｄｉｎａｔｅ ｓｙｓｔｅｍ， ｔｈｅ ｅｒｒｏｒ ｂｅｔｗｅｅｎ ｔｈｅ ｄｅｓｉｒｅｄ ａｎｄ ｔｈｅ ｒｅａｌ ｐｏｓｉｔｉｏｎ ｓｈｏｕｌｄ ｂｅ ｔｒｅａｔｅｄ ａｓ ａｎ ｅｘｔｒａ ｖａｒｉａｂｌｅ， ｔｈｉｓ ｃａｎ ｂｅ ｄｅｓｃｒｉｂｅｄ ｂｙ ｓｉｎｇｌｅ⁃ ｉｎｔｅｇｒａｔｏｒ ｄｙｎａｍｉｃｓ ｆｏｒ ｓｉｍｐｌｉｃｉｔｙ． Ｔｈｅ ｍａｔｈ ｍｏｄｅｌ ｃａｎ ｂｅ ｄｅｓｃｒｉｂｅｄ ａｓ ｅ · ｒｉ ＝ ｕｉ （３） ａｎｄ ｔｈｅ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ ｉｓ ｉｎ Ｒｅｆ ［９］． ｕｉ ＝ － ∑ ９ ｊ ＝ １ ａｉｊ（ｅｒｉ － ｅｒｊ） （４） ｒ ～ ｉ ＝ ｒｐｉ ＋ ｅｒｉ （５） Ｗｈｅｒｅ ｒ ～ ｉ ｉｓ ｔｈｅ ｒｅａｌ ｐｏｓｉｔｉｏｎ ｏｆ ＵＡＶｉ， ＵＡＶｉ ｉｎ ｔｈｅ ｍｏｖｉｎｇ ｃｏｏｒｄｉｎａｔｅ ｓｙｓｔｅｍ， ｅｒｉ ｉｓ ｔｈｅ ｄｉｓｔａｎｃｅ ｅｒｒｏｒ ｂｅｔｗｅｅｎ ｔｈｅ ｒｅａｌ ａｎｄ ｔｈｅ ｄｅｓｉｒｅｄ ｐｏｓｉｔｉｏｎ ｏｆ ＵＡＶｉ， ｒｐｉ ｗｈｉｃｈ ｉｓ ｓｈｏｗｎ ｉｎ Ｆｉｇ． ２， ｉｓ ｔｈｅ ｄｅｓｉｒｅｄ ｐｏｓｉｔｉｏｎ ｏｆ ＵＡＶｉ ｉｎ ｔｈｅ ｍｏｖｉｎｇ ｃｏｏｒｄｉｎａｔｅ ｓｙｓｔｅｍ， ｉ∈｛１，２，…， ９｝． Ｅｑｕａｔｉｏｎｓ （１～５） ａｂｏｖｅ ｃａｎ ｂｅ ｔｒａｎｓｆｏｒｍｅｄ ｉｎｔｏ ａ ｃｏｌｌｅｃｔｉｖｅ ｍａｔｒｉｘ ｆｏｒｍ， （Ｌ 􀱋Ｉ３）ξ ¨ ＋ （ｂ 􀱋Ｉ３）ξ ¨ ｒ ＝－ Ｋｒ［（Ｌ 􀱋Ｉ３）ξ ＋ （ｂ 􀱋Ｉ３）ξ ｒ ］－ Ｋｖ［（Ｌ 􀱋 Ｉ３ ）ξ · ＋ （ｂ 􀱋 Ｉ３ ）ξ ·ｒ ］ ｅ · ＝ － （Ｌ 􀱋 Ｉ３ ）ｅ ｒ ＝ ｒ ～ ＋ ξ ＝ ｒｐ ＋ ｅｒ ＋ ξ ì î í ï ï ï ï ï ï （６） ｗｈｅｒｅ Ｌ９×９ ｉｓ ｔｈｅ Ｌａｐｌａｃｅ ｍａｔｒｉｘ ｏｆ ｔｈｅ ｃｏｍｍｕｎｉｃａｔｉｏｎ ｔｏｐｏｌｏｇｙ ｇｒａｐｈ， ｂ ∈ Ｒ ９ ｒｅｆｌｅｃｔｓ ｗｈｉｃｈ ＵＡＶ ｃａｎ ｄｉｒｅｃｔｌｙ ｒｅｃｅｉｖｅ ｉｎｆｏｒｍａｔｉｏｎ ｆｒｏｍ ＵＡＶ１０ ， ξ ｒ ｉｓ ｔｈｅ ｄｅｓｉｒｅｄ ｐｏｓｉｔｉｏｎ ａｎｄ ａｌｓｏ ｔｈｅ ｐｏｓｉｔｉｏｎ ｏｆ ＵＡＶ１０ ， ｗｈｉｃｈ ｓｈｏｗｓ ｔｈｅ ｄｅｓｉｒｅｄ ｐａｔｈ ｆｏｒ ａｌｌ ｔｈｅ ＵＡＶｓ， ｆｉｎａｌｌｙ， 􀱋 ｒｅｐｒｅｓｅｎｔｓ ｔｈｅ Ｋｒｏｎｅｃｋｅｒ ｐｒｏｄｕｃｔ． Ｋｒ ＝ ｄｉａｇ（Ｋｒ１ ，Ｋｒ２ ，…，Ｋｒ９ ），Ｋｖ ＝ ｄｉａｇ （ Ｋｖ１ ，Ｋｖ２ ， …，Ｋｖ９ ），ｅｒ ＝ （ｅｒ Ｔ １ ｅｒ Ｔ ２… ｅｒ Ｔ ９ ） Ｔ ，ｒ ～ ＝ （ ｒ ～ Ｔ １ ｒ ～ Ｔ ２…ｒ ～ Ｔ ９ ） Ｔ ，ｒ ｉｓ ｔｈｅ ｖｅｃｔｏｒ ｏｆ ｔｈｅ ｒｅａｌ ｐｏｓｉｔｉｏｎ ｏｆ ｅａｃｈ ＵＡＶ， ξ ｉｓ ｔｈｅ ｖｅｃｔｏｒ ｏｆ ｔｈｅ ｐｏｓｉｔｉｏｎ ｏｆ ｔｈｅ ｏｒｉｇｉｎ ｏｆ ｅａｃｈ ＵＡＶ’ ｓ ｍｏｖｉｎｇ ｃｏｏｒｄｉｎａｔｅ ｓｙｓｔｅｍ． Ｅｑｕａｔｉｏｎ （ ６ ） ｉｓ ｔｈｅ ｃｏｒｅ ｏｆ ｔｈｅ ｍｕｌｔｉ⁃ＵＡＶ ｃｏｎｔｒｏｌｌｅｒ， ａｎｄ ｒ ｐｒｏｖｉｄｅｓ ｔｈｅ ｎｅｃｅｓｓａｒｙ ｐｏｓｉｔｉｏｎａｌ ｉｎｆｏｒｍａｔｉｏｎ ｆｏｒ ａｌｌ ｔｈｅ ＵＡＶｓ ｆｏｒ ｕｓｅ ｉｎ ｔｈｅ ｎｅｘｔ ｓｔｅｐ． Ａｆｔｅｒ ａｃｑｕｉｒｉｎｇ ｔｈｅ ｔａｒｇｅｔ ｉｎｓｔｒｕｃｔｉｏｎｓ， ｔｈｅ ＵＡＶｓ ｆｌｙ ｔｏｗａｒｄ ｔｈｅｉｒ ｄｅｓｔｉｎａｔｉｏｎｓ． １．２ Ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎ ｔａｓｋ Ｔｈｅ ｄｅｓｉｒｅｄ ｆｏｒｍａｔｉｏｎ ｓｈａｐｅ ｉｓ ｄｅｓｉｇｎｅｄ ａｓ ｆｏｌｌｏｗｓ： ·５７２· 智 能 系 统 学 报 第 １２ 卷

ZHANG Tianjie,et al.:A modified consensus algorithm for multi-UAV formations based on 第4期 pigeon-inspired optimization with a slow diving strategy .573. Table 1 Positions of 9 UAVs under the desired formation receive information from UAV,.There is also a virtual structure m leader named UAVio,which can emit an arrow to UAV number x another UAV so that the latter knows the predesigned UAV 0 12.60 10.00 trajectory. UAV2 -1.50 10.00 10.00 The communication topology among UAVs is UAV3 1.50 10.00 described as a directed graph in Fig.3.A graph with n 10.00 vertices can be denoted by G(V,E,A),V=(v1,2, UAVa -6.50 0 0 …,tn）is the set of vertices of graph G and:isa UAVs -8.00 -2.60 0 vertex.E=(e,e2,,e)is the edge set in which e UAV. -5.00 -2.60 0 means an edge.A=[a]demonstrates the adjacency UAV] 6.50 0 0 matrix of the graph G.If there is an edge from v:to, UAVs 5.00 -2.60 0 then a>0,otherwise ag=0.Usually,a=1 if a UAVo 8.00 -2.60 0 particular value is not given.The value of a is the weight of communication amount between vi and v;, which can influence the convergence speed between v UAV. 10 UAV. UAV. and v;.In the graph G(V,E,A),if there is a set of edges,(,2),(2,3）,…(v.-1,n),then there 0 is a path from v to v.If there is a vertex from which 10 many edges reach all the remaining vertices,then this UAV UAV 4UaV。 vertex is called a root and G(V,E,A)includes a direct ym o 10 spanning tree. -10 x/m Fig.2 Formation structure for UAVs There are nine UAVs flying at two different heights,they are divided into three groups,each group containing three UAVs.In every small group,the UAVs form a triangle and these are the same size,so the UAVs fly symmetrically.The side length of the triangle and the distance between different triangles is 6 much larger than the size of an UAV,so they can fly Fig.3 Communication topology for multiple UAVs safely without danger of collision.The desired heights For consensus,the adjacency matrix and the in Table I are relative values and the height of the Laplace matrix were acquired.The Laplace matrix L origin of the moving coordinate system is their reference [l]was the same size as the adjacency matrix.In the height,so when a UAV flies at zero or even a negative mati,h,=-ay,ifi≠j,otherise=立4，： height,it is still acceptable.The blue star in Fig.2 j=1j≠i According to the sufficient and necessary represents the center of the formation.x/m means condition of multi-UAV consensus,there is a directed distance along the x-axis in meters. spanning tree with its root UAVo,in the When designing the communication plan,the UAVs were numbered from I to 9.To clarify the plan, communication topology graph,and all the state variables converge to the state of the root as time tends some background knowledge on topology and graph to infinity theory is required. A graph with only vertices and arrows can be 2 Pigeon-inspired optimization with slow adopted to show the communication relationship among diving strategy all the UAVs.Each UAV acts as a vertex,and an 2.1 Basic pigeon-inspired optimization algorithm arrow from UAV to UAV2 means that UAV2 can Qiao [is]studied pigeon behavior when seeking

Ｔａｂｌｅ １ Ｐｏｓｉｔｉｏｎｓ ｏｆ ９ ＵＡＶｓ ｕｎｄｅｒ ｔｈｅ ｄｅｓｉｒｅｄ ｆｏｒｍａｔｉｏｎ ｓｔｒｕｃｔｕｒｅ ｍ ＵＡＶ ｎｕｍｂｅｒ ｘ ｙ ｚ ＵＡＶ１ ０ １２．６０ １０．００ ＵＡＶ２ －１．５０ １０．００ １０．００ ＵＡＶ３ １．５０ １０．００ １０．００ ＵＡＶ４ －６．５０ ０ ０ ＵＡＶ５ －８．００ －２．６０ ０ ＵＡＶ６ －５．００ －２．６０ ０ ＵＡＶ７ ６．５０ ０ ０ ＵＡＶ８ ５．００ －２．６０ ０ ＵＡＶ９ ８．００ －２．６０ ０ Ｆｉｇ．２ Ｆｏｒｍａｔｉｏｎ ｓｔｒｕｃｔｕｒｅ ｆｏｒ ＵＡＶｓ Ｔｈｅｒｅ ａｒｅ ｎｉｎｅ ＵＡＶｓ ｆｌｙｉｎｇ ａｔ ｔｗｏ ｄｉｆｆｅｒｅｎｔ ｈｅｉｇｈｔｓ， ｔｈｅｙ ａｒｅ ｄｉｖｉｄｅｄ ｉｎｔｏ ｔｈｒｅｅ ｇｒｏｕｐｓ， ｅａｃｈ ｇｒｏｕｐ ｃｏｎｔａｉｎｉｎｇ ｔｈｒｅｅ ＵＡＶｓ． Ｉｎ ｅｖｅｒｙ ｓｍａｌｌ ｇｒｏｕｐ， ｔｈｅ ＵＡＶｓ ｆｏｒｍ ａ ｔｒｉａｎｇｌｅ ａｎｄ ｔｈｅｓｅ ａｒｅ ｔｈｅ ｓａｍｅ ｓｉｚｅ， ｓｏ ｔｈｅ ＵＡＶｓ ｆｌｙ ｓｙｍｍｅｔｒｉｃａｌｌｙ． Ｔｈｅ ｓｉｄｅ ｌｅｎｇｔｈ ｏｆ ｔｈｅ ｔｒｉａｎｇｌｅ ａｎｄ ｔｈｅ ｄｉｓｔａｎｃｅ ｂｅｔｗｅｅｎ ｄｉｆｆｅｒｅｎｔ ｔｒｉａｎｇｌｅｓ ｉｓ ｍｕｃｈ ｌａｒｇｅｒ ｔｈａｎ ｔｈｅ ｓｉｚｅ ｏｆ ａｎ ＵＡＶ， ｓｏ ｔｈｅｙ ｃａｎ ｆｌｙ ｓａｆｅｌｙ ｗｉｔｈｏｕｔ ｄａｎｇｅｒ ｏｆ ｃｏｌｌｉｓｉｏｎ． Ｔｈｅ ｄｅｓｉｒｅｄ ｈｅｉｇｈｔｓ ｉｎ Ｔａｂｌｅ １ ａｒｅ ｒｅｌａｔｉｖｅ ｖａｌｕｅｓ ａｎｄ ｔｈｅ ｈｅｉｇｈｔ ｏｆ ｔｈｅ ｏｒｉｇｉｎ ｏｆ ｔｈｅ ｍｏｖｉｎｇ ｃｏｏｒｄｉｎａｔｅ ｓｙｓｔｅｍ ｉｓ ｔｈｅｉｒ ｒｅｆｅｒｅｎｃｅ ｈｅｉｇｈｔ， ｓｏ ｗｈｅｎ ａ ＵＡＶ ｆｌｉｅｓ ａｔ ｚｅｒｏ ｏｒ ｅｖｅｎ ａ ｎｅｇａｔｉｖｅ ｈｅｉｇｈｔ， ｉｔ ｉｓ ｓｔｉｌｌ ａｃｃｅｐｔａｂｌｅ． Ｔｈｅ ｂｌｕｅ ｓｔａｒ ｉｎ Ｆｉｇ． ２ ｒｅｐｒｅｓｅｎｔｓ ｔｈｅ ｃｅｎｔｅｒ ｏｆ ｔｈｅ ｆｏｒｍａｔｉｏｎ． ｘ ／ ｍ ｍｅａｎｓ ｄｉｓｔａｎｃｅ ａｌｏｎｇ ｔｈｅ ｘ⁃ａｘｉｓ ｉｎ ｍｅｔｅｒｓ． Ｗｈｅｎ ｄｅｓｉｇｎｉｎｇ ｔｈｅ ｃｏｍｍｕｎｉｃａｔｉｏｎ ｐｌａｎ， ｔｈｅ ＵＡＶｓ ｗｅｒｅ ｎｕｍｂｅｒｅｄ ｆｒｏｍ １ ｔｏ ９． Ｔｏ ｃｌａｒｉｆｙ ｔｈｅ ｐｌａｎ， ｓｏｍｅ ｂａｃｋｇｒｏｕｎｄ ｋｎｏｗｌｅｄｇｅ ｏｎ ｔｏｐｏｌｏｇｙ ａｎｄ ｇｒａｐｈ ｔｈｅｏｒｙ ｉｓ ｒｅｑｕｉｒｅｄ． Ａ ｇｒａｐｈ ｗｉｔｈ ｏｎｌｙ ｖｅｒｔｉｃｅｓ ａｎｄ ａｒｒｏｗｓ ｃａｎ ｂｅ ａｄｏｐｔｅｄ ｔｏ ｓｈｏｗ ｔｈｅ ｃｏｍｍｕｎｉｃａｔｉｏｎ ｒｅｌａｔｉｏｎｓｈｉｐ ａｍｏｎｇ ａｌｌ ｔｈｅ ＵＡＶｓ． Ｅａｃｈ ＵＡＶ ａｃｔｓ ａｓ ａ ｖｅｒｔｅｘ， ａｎｄ ａｎ ａｒｒｏｗ ｆｒｏｍ ＵＡＶ１ ｔｏ ＵＡＶ２ ｍｅａｎｓ ｔｈａｔ ＵＡＶ２ ｃａｎ ｒｅｃｅｉｖｅ ｉｎｆｏｒｍａｔｉｏｎ ｆｒｏｍ ＵＡＶ１ ． Ｔｈｅｒｅ ｉｓ ａｌｓｏ ａ ｖｉｒｔｕａｌ ｌｅａｄｅｒ ｎａｍｅｄ ＵＡＶ１０ ， ｗｈｉｃｈ ｃａｎ ｅｍｉｔ ａｎ ａｒｒｏｗ ｔｏ ａｎｏｔｈｅｒ ＵＡＶ ｓｏ ｔｈａｔ ｔｈｅ ｌａｔｔｅｒ ｋｎｏｗｓ ｔｈｅ ｐｒｅｄｅｓｉｇｎｅｄ ｔｒａｊｅｃｔｏｒｙ． Ｔｈｅ ｃｏｍｍｕｎｉｃａｔｉｏｎ ｔｏｐｏｌｏｇｙ ａｍｏｎｇ ＵＡＶｓ ｉｓ ｄｅｓｃｒｉｂｅｄ ａｓ ａ ｄｉｒｅｃｔｅｄ ｇｒａｐｈ ｉｎ Ｆｉｇ． ３． Ａ ｇｒａｐｈ ｗｉｔｈ ｎ ｖｅｒｔｉｃｅｓ ｃａｎ ｂｅ ｄｅｎｏｔｅｄ ｂｙ Ｇ（Ｖ，Ｅ，Ａ） ， Ｖ ＝ （ｖ１ ，ｖ２ ， …，ｖｎ ） ｉｓ ｔｈｅ ｓｅｔ ｏｆ ｖｅｒｔｉｃｅｓ ｏｆ ｇｒａｐｈ Ｇ ａｎｄ ｖｉ ｉｓ ａ ｖｅｒｔｅｘ． Ｅ ＝ （ｅ１ ，ｅ２ ，…，ｅｎ ） ｉｓ ｔｈｅ ｅｄｇｅ ｓｅｔ ｉｎ ｗｈｉｃｈ ｅｉ ｍｅａｎｓ ａｎ ｅｄｇｅ． Ａ ＝ ［ａｉｊ］ ｄｅｍｏｎｓｔｒａｔｅｓ ｔｈｅ ａｄｊａｃｅｎｃｙ ｍａｔｒｉｘ ｏｆ ｔｈｅ ｇｒａｐｈ Ｇ． Ｉｆ ｔｈｅｒｅ ｉｓ ａｎ ｅｄｇｅ ｆｒｏｍ ｖｉ ｔｏ ｖｊ ， ｔｈｅｎ ａｉｊ ＞ ０， ｏｔｈｅｒｗｉｓｅ ａｉｊ ＝ ０． Ｕｓｕａｌｌｙ， ａｉｊ ＝ １ ｉｆ ａ ｐａｒｔｉｃｕｌａｒ ｖａｌｕｅ ｉｓ ｎｏｔ ｇｉｖｅｎ． Ｔｈｅ ｖａｌｕｅ ｏｆ ａｉｊ ｉｓ ｔｈｅ ｗｅｉｇｈｔ ｏｆ ｃｏｍｍｕｎｉｃａｔｉｏｎ ａｍｏｕｎｔ ｂｅｔｗｅｅｎ ｖｉ ａｎｄ ｖｊ ， ｗｈｉｃｈ ｃａｎ ｉｎｆｌｕｅｎｃｅ ｔｈｅ ｃｏｎｖｅｒｇｅｎｃｅ ｓｐｅｅｄ ｂｅｔｗｅｅｎ ｖｉ ａｎｄ ｖｊ ． Ｉｎ ｔｈｅ ｇｒａｐｈ Ｇ（Ｖ，Ｅ，Ａ） ， ｉｆ ｔｈｅｒｅ ｉｓ ａ ｓｅｔ ｏｆ ｅｄｇｅｓ， （ｖ１ ，ｖ２ ） ， （ｖ２ ，ｖ３ ） ，… （ｖｎ－１ ，ｖｎ ） ， ｔｈｅｎ ｔｈｅｒｅ ｉｓ ａ ｐａｔｈ ｆｒｏｍ ｖ１ ｔｏ ｖｎ ． Ｉｆ ｔｈｅｒｅ ｉｓ ａ ｖｅｒｔｅｘ ｆｒｏｍ ｗｈｉｃｈ ｍａｎｙ ｅｄｇｅｓ ｒｅａｃｈ ａｌｌ ｔｈｅ ｒｅｍａｉｎｉｎｇ ｖｅｒｔｉｃｅｓ， ｔｈｅｎ ｔｈｉｓ ｖｅｒｔｅｘ ｉｓ ｃａｌｌｅｄ ａ ｒｏｏｔ ａｎｄ Ｇ（Ｖ，Ｅ，Ａ） ｉｎｃｌｕｄｅｓ ａ ｄｉｒｅｃｔ ｓｐａｎｎｉｎｇ ｔｒｅｅ． Ｆｉｇ．３ Ｃｏｍｍｕｎｉｃａｔｉｏｎ ｔｏｐｏｌｏｇｙ ｆｏｒ ｍｕｌｔｉｐｌｅ ＵＡＶｓ Ｆｏｒ ｃｏｎｓｅｎｓｕｓ， ｔｈｅ ａｄｊａｃｅｎｃｙ ｍａｔｒｉｘ ａｎｄ ｔｈｅ Ｌａｐｌａｃｅ ｍａｔｒｉｘ ｗｅｒｅ ａｃｑｕｉｒｅｄ． Ｔｈｅ Ｌａｐｌａｃｅ ｍａｔｒｉｘ Ｌ ＝ ［ｌ ｉｊ］ ｗａｓ ｔｈｅ ｓａｍｅ ｓｉｚｅ ａｓ ｔｈｅ ａｄｊａｃｅｎｃｙ ｍａｔｒｉｘ． Ｉｎ ｔｈｅ ｍａｔｒｉｘ， ｌ ｉｊ ＝ － ａｉｊ ， ｉｆ ｉ ≠ ｊ ， ｏｔｈｅｒｗｉｓｅ ｌ ｉｉ ＝ ∑ ｎ ｊ ＝ １，ｊ≠ｉ ａｉｊ ． Ａｃｃｏｒｄｉｎｇ ｔｏ ｔｈｅ ｓｕｆｆｉｃｉｅｎｔ ａｎｄ ｎｅｃｅｓｓａｒｙ ｃｏｎｄｉｔｉｏｎ ｏｆ ｍｕｌｔｉ⁃ＵＡＶ ｃｏｎｓｅｎｓｕｓ， ｔｈｅｒｅ ｉｓ ａ ｄｉｒｅｃｔｅｄ ｓｐａｎｎｉｎｇ ｔｒｅｅ ｗｉｔｈ ｉｔｓ ｒｏｏｔ ＵＡＶ１０ ， ｉｎ ｔｈｅ ｃｏｍｍｕｎｉｃａｔｉｏｎ ｔｏｐｏｌｏｇｙ ｇｒａｐｈ， ａｎｄ ａｌｌ ｔｈｅ ｓｔａｔｅ ｖａｒｉａｂｌｅｓ ｃｏｎｖｅｒｇｅ ｔｏ ｔｈｅ ｓｔａｔｅ ｏｆ ｔｈｅ ｒｏｏｔ ａｓ ｔｉｍｅ ｔｅｎｄｓ ｔｏ ｉｎｆｉｎｉｔｙ ［１１］ ． ２ Ｐｉｇｅｏｎ⁃ｉｎｓｐｉｒｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ｗｉｔｈ ｓｌｏｗ ｄｉｖｉｎｇ ｓｔｒａｔｅｇｙ ２．１ Ｂａｓｉｃ ｐｉｇｅｏｎ⁃ｉｎｓｐｉｒｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ Ｑｉａｏ ［１５］ ｓｔｕｄｉｅｄ ｐｉｇｅｏｎ ｂｅｈａｖｉｏｒ ｗｈｅｎ ｓｅｅｋｉｎｇ ·５７３· 第 ４ 期 ＺＨＡＮＧ Ｔｉａｎｊｉｅ， ｅｔ ａｌ．：Ａ ｍｏｄｉｆｉｅｄ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ ｆｏｒ ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎｓ ｂａｓｅｄ ｏｎ ｐｉｇｅｏｎ⁃ｉｎｓｐｉｒｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ｗｉｔｈ ａ ｓｌｏｗ ｄｉｖｉｎｇ ｓｔｒａｔｅｇｙ

.574. 智能系统学报 第12卷 their way home and proposed the two-stage algorithm. overshoot,but the result is not desirable,and the The first stage of PIO is the map and compass part.X= altitude of a UAV drops to the standard height with [XX…X…X]T is the vector of the pigeons' continual oscillation.To improve the performance of the positions,i is the number of virtual pigeons,and in algorithm,better methods are required. this paper the UAVs fly in 3-dimensional space,X=2.2 Improved method with slow diving strategy [x ]V=[VI V.V]T is the vector of the The problem in the former algorithm occurs mainly pigeons'velocities,V=[]is its element, in the altitude part,the height of the UAV decreases i∈{l,2,…,9}.Both X and V are randomly too fast and it dives sharply.To slow the process,the initialized when the program starts.The update update formula should be changed,not only to consider formulas are: the best local position but also the slowest diving (e:(t+1)=:(t)·exp(-Rt)+rand·(xe-x:) velocity.In the first part of PIO,the formula is not x:(t+1)=x,(t)+,(t+1) changed,but the method of acquiring the best local if t Tlabed (7) position is modified.The criterion is a linear In the formula above,the best local position combination of the distance error between the desired is selected from the distance between the desired and and the real positions and the diving speed.An UAV present positions.In order to find the best local that dives very slowly is imitated by the others.This is the so-called "slow diving strategy".The update position,all the distance errors are calculated and formula is: ranked,and only the position with the smallest e:(t+1)=v:(t)·exp(-Rt)+ distance is defined as the best local position.For the minimum optimization question,the fitness function is: r·[p·(xhea-x:)+(1-p）·] fitness(x (t))=x(t)-xmmdm(t)(8) x:(t+1)=x,(t)+,(t+1) After calculating the distance between the desired if t Tubd (10) and the present positions of all the pigeons,only half where serves as a regulatory factor in the range of(0, of the pigeons with lower fitness are selected for the 1);if approaches 0,the slowest pigeon will iteration.This ensures that the positions of these influence the team;if o approaches 1,best local pigeons converge to the desired position as fast as position will have much more of an effect.r(0,1)is possible. a random number. In the second part,the landmark operator is The second part of PIO should be modified in the employed.Its update formula is: following way:all the UAVs converge to the center of wu+1)=水四 the flock,which is calculated by a combination of the 2 UAV positions and the slowest diving speed.The ∑，()·fx,() update equation can be described as: xc(t+1)= ∑fx,(t) +1)=0 2 x,(t+1)=x,(t)+rand·(xc(t+1)-x:(t)) ∑x,()fx,()+10·x·f代x) ift≥Tlabel (9) xc(t+1)= ∑fx,(t)+10·xa·fx) Apparently,xic is the weighted average of all the x,(t+1)=x,(t)+rand·(xc(t+1)-x:(t)) nearby pigeons in pigeon i's communication distance. (11) It is supposed that the map and compass operator has ift≥Tlabel where x is the position of the UAV with the slowest already converged pigeons to the desired trajectory to a diving speed,this part represents the slowing diving great extent.As a result,the landmark operator only strategy. needs to speed up this process.The PIO algorithm has Fitness function Eq.(10)remains.Each UAV already been proven to be robust and reliable for an aircraft path planning problems However,for the has its own fitness value. optimization of consensus,PIO can improve the

ｔｈｅｉｒ ｗａｙ ｈｏｍｅ ａｎｄ ｐｒｏｐｏｓｅｄ ｔｈｅ ｔｗｏ⁃ｓｔａｇｅ ａｌｇｏｒｉｔｈｍ． Ｔｈｅ ｆｉｒｓｔ ｓｔａｇｅ ｏｆ ＰＩＯ ｉｓ ｔｈｅ ｍａｐ ａｎｄ ｃｏｍｐａｓｓ ｐａｒｔ． Ｘ ＝ ［Ｘ Ｔ １ Ｘ Ｔ ２ … Ｘ Ｔ ｉ … Ｘ Ｔ ｎ ］ Ｔ ｉｓ ｔｈｅ ｖｅｃｔｏｒ ｏｆ ｔｈｅ ｐｉｇｅｏｎｓ’ ｐｏｓｉｔｉｏｎｓ， ｉ ｉｓ ｔｈｅ ｎｕｍｂｅｒ ｏｆ ｖｉｒｔｕａｌ ｐｉｇｅｏｎｓ， ａｎｄ ｉｎ ｔｈｉｓ ｐａｐｅｒ ｔｈｅ ＵＡＶｓ ｆｌｙ ｉｎ ３⁃ｄｉｍｅｎｓｉｏｎａｌ ｓｐａｃｅ， Ｘｉ ＝ ［ｘｉ ｙｉ ｚｉ］ Ｔ ． Ｖ ＝ ［Ｖ Ｔ １ Ｖ Ｔ ２ … Ｖ Ｔ ｎ ］ Ｔ ｉｓ ｔｈｅ ｖｅｃｔｏｒ ｏｆ ｔｈｅ ｐｉｇｅｏｎｓ’ ｖｅｌｏｃｉｔｉｅｓ， Ｖｉ ＝ ［ｖｘ ｖｙ ｖｚ］ Ｔ ｉｓ ｉｔｓ ｅｌｅｍｅｎｔ， ｉ ∈｛１，２，…，９｝ ． Ｂｏｔｈ Ｘ ａｎｄ Ｖ ａｒｅ ｒａｎｄｏｍｌｙ ｉｎｉｔｉａｌｉｚｅｄ ｗｈｅｎ ｔｈｅ ｐｒｏｇｒａｍ ｓｔａｒｔｓ． Ｔｈｅ ｕｐｄａｔｅ ｆｏｒｍｕｌａｓ ａｒｅ： ｖｉ（ｔ ＋ １） ＝ ｖｉ（ｔ）·ｅｘｐ（ － Ｒｔ） ＋ ｒａｎｄ·（ｘｌｂｅｓｔ － ｘｉ） ｘｉ（ｔ ＋ １） ＝ ｘｉ（ｔ） ＋ ｖｉ（ｔ ＋ １） { ｉｆ ｔ ＜ Ｔｌａｂｅｌ （７） Ｉｎ ｔｈｅ ｆｏｒｍｕｌａ ａｂｏｖｅ， ｔｈｅ ｂｅｓｔ ｌｏｃａｌ ｐｏｓｉｔｉｏｎ ｘｌｂｅｓｔ ｉｓ ｓｅｌｅｃｔｅｄ ｆｒｏｍ ｔｈｅ ｄｉｓｔａｎｃｅ ｂｅｔｗｅｅｎ ｔｈｅ ｄｅｓｉｒｅｄ ａｎｄ ｐｒｅｓｅｎｔ ｐｏｓｉｔｉｏｎｓ． Ｉｎ ｏｒｄｅｒ ｔｏ ｆｉｎｄ ｔｈｅ ｂｅｓｔ ｌｏｃａｌ ｐｏｓｉｔｉｏｎ， ａｌｌ ｔｈｅ ｄｉｓｔａｎｃｅ ｅｒｒｏｒｓ ａｒｅ ｃａｌｃｕｌａｔｅｄ ａｎｄ ｒａｎｋｅｄ， ａｎｄ ｏｎｌｙ ｔｈｅ ｐｏｓｉｔｉｏｎ ｗｉｔｈ ｔｈｅ ｓｍａｌｌｅｓｔ ｄｉｓｔａｎｃｅ ｉｓ ｄｅｆｉｎｅｄ ａｓ ｔｈｅ ｂｅｓｔ ｌｏｃａｌ ｐｏｓｉｔｉｏｎ． Ｆｏｒ ｔｈｅ ｍｉｎｉｍｕｍ ｏｐｔｉｍｉｚａｔｉｏｎ ｑｕｅｓｔｉｏｎ， ｔｈｅ ｆｉｔｎｅｓｓ ｆｕｎｃｔｉｏｎ ｉｓ： ｆｉｔｎｅｓｓ（ｘｉ（ｔ）） ＝ ｘｉ（ｔ） － ｘｉｓｔａｎｄａｒｄ（ｔ） （８） Ａｆｔｅｒ ｃａｌｃｕｌａｔｉｎｇ ｔｈｅ ｄｉｓｔａｎｃｅ ｂｅｔｗｅｅｎ ｔｈｅ ｄｅｓｉｒｅｄ ａｎｄ ｔｈｅ ｐｒｅｓｅｎｔ ｐｏｓｉｔｉｏｎｓ ｏｆ ａｌｌ ｔｈｅ ｐｉｇｅｏｎｓ， ｏｎｌｙ ｈａｌｆ ｏｆ ｔｈｅ ｐｉｇｅｏｎｓ ｗｉｔｈ ｌｏｗｅｒ ｆｉｔｎｅｓｓ ａｒｅ ｓｅｌｅｃｔｅｄ ｆｏｒ ｔｈｅ ｉｔｅｒａｔｉｏｎ． Ｔｈｉｓ ｅｎｓｕｒｅｓ ｔｈａｔ ｔｈｅ ｐｏｓｉｔｉｏｎｓ ｏｆ ｔｈｅｓｅ ｐｉｇｅｏｎｓ ｃｏｎｖｅｒｇｅ ｔｏ ｔｈｅ ｄｅｓｉｒｅｄ ｐｏｓｉｔｉｏｎ ａｓ ｆａｓｔ ａｓ ｐｏｓｓｉｂｌｅ． Ｉｎ ｔｈｅ ｓｅｃｏｎｄ ｐａｒｔ， ｔｈｅ ｌａｎｄｍａｒｋ ｏｐｅｒａｔｏｒ ｉｓ ｅｍｐｌｏｙｅｄ． Ｉｔｓ ｕｐｄａｔｅ ｆｏｒｍｕｌａ ｉｓ： Ｎｐ（ｔ ＋ １） ＝ Ｎｐ（ｔ） ２ ｘｉＣ（ｔ ＋ １） ＝ ∑ｘｉ（ｔ）·ｆ（ｘｉ（ｔ）） ∑ｆ（ｘｉ（ｔ）） ｘｉ（ｔ ＋ １） ＝ ｘｉ（ｔ） ＋ ｒａｎｄ·（ｘｉＣ（ｔ ＋ １） － ｘｉ（ｔ）） ì î í ï ï ïï ï ï ïï ｉｆ ｔ ≥ Ｔｌａｂｅｌ （９） Ａｐｐａｒｅｎｔｌｙ， ｘｉＣ ｉｓ ｔｈｅ ｗｅｉｇｈｔｅｄ ａｖｅｒａｇｅ ｏｆ ａｌｌ ｔｈｅ ｎｅａｒｂｙ ｐｉｇｅｏｎｓ ｉｎ ｐｉｇｅｏｎ ｉ’ ｓ ｃｏｍｍｕｎｉｃａｔｉｏｎ ｄｉｓｔａｎｃｅ． Ｉｔ ｉｓ ｓｕｐｐｏｓｅｄ ｔｈａｔ ｔｈｅ ｍａｐ ａｎｄ ｃｏｍｐａｓｓ ｏｐｅｒａｔｏｒ ｈａｓ ａｌｒｅａｄｙ ｃｏｎｖｅｒｇｅｄ ｐｉｇｅｏｎｓ ｔｏ ｔｈｅ ｄｅｓｉｒｅｄ ｔｒａｊｅｃｔｏｒｙ ｔｏ ａ ｇｒｅａｔ ｅｘｔｅｎｔ． Ａｓ ａ ｒｅｓｕｌｔ， ｔｈｅ ｌａｎｄｍａｒｋ ｏｐｅｒａｔｏｒ ｏｎｌｙ ｎｅｅｄｓ ｔｏ ｓｐｅｅｄ ｕｐ ｔｈｉｓ ｐｒｏｃｅｓｓ． Ｔｈｅ ＰＩＯ ａｌｇｏｒｉｔｈｍ ｈａｓ ａｌｒｅａｄｙ ｂｅｅｎ ｐｒｏｖｅｎ ｔｏ ｂｅ ｒｏｂｕｓｔ ａｎｄ ｒｅｌｉａｂｌｅ ｆｏｒ ａｎ ａｉｒｃｒａｆｔ ｐａｔｈ ｐｌａｎｎｉｎｇ ｐｒｏｂｌｅｍ ［１５］ ． Ｈｏｗｅｖｅｒ， ｆｏｒ ｔｈｅ ｏｐｔｉｍｉｚａｔｉｏｎ ｏｆ ｃｏｎｓｅｎｓｕｓ， ＰＩＯ ｃａｎ ｉｍｐｒｏｖｅ ｔｈｅ ｏｖｅｒｓｈｏｏｔ， ｂｕｔ ｔｈｅ ｒｅｓｕｌｔ ｉｓ ｎｏｔ ｄｅｓｉｒａｂｌｅ， ａｎｄ ｔｈｅ ａｌｔｉｔｕｄｅ ｏｆ ａ ＵＡＶ ｄｒｏｐｓ ｔｏ ｔｈｅ ｓｔａｎｄａｒｄ ｈｅｉｇｈｔ ｗｉｔｈ ｃｏｎｔｉｎｕａｌ ｏｓｃｉｌｌａｔｉｏｎ． Ｔｏ ｉｍｐｒｏｖｅ ｔｈｅ ｐｅｒｆｏｒｍａｎｃｅ ｏｆ ｔｈｅ ａｌｇｏｒｉｔｈｍ， ｂｅｔｔｅｒ ｍｅｔｈｏｄｓ ａｒｅ ｒｅｑｕｉｒｅｄ． ２．２ Ｉｍｐｒｏｖｅｄ ｍｅｔｈｏｄ ｗｉｔｈ ｓｌｏｗ ｄｉｖｉｎｇ ｓｔｒａｔｅｇｙ Ｔｈｅ ｐｒｏｂｌｅｍ ｉｎ ｔｈｅ ｆｏｒｍｅｒ ａｌｇｏｒｉｔｈｍ ｏｃｃｕｒｓ ｍａｉｎｌｙ ｉｎ ｔｈｅ ａｌｔｉｔｕｄｅ ｐａｒｔ， ｔｈｅ ｈｅｉｇｈｔ ｏｆ ｔｈｅ ＵＡＶ ｄｅｃｒｅａｓｅｓ ｔｏｏ ｆａｓｔ ａｎｄ ｉｔ ｄｉｖｅｓ ｓｈａｒｐｌｙ． Ｔｏ ｓｌｏｗ ｔｈｅ ｐｒｏｃｅｓｓ， ｔｈｅ ｕｐｄａｔｅ ｆｏｒｍｕｌａ ｓｈｏｕｌｄ ｂｅ ｃｈａｎｇｅｄ， ｎｏｔ ｏｎｌｙ ｔｏ ｃｏｎｓｉｄｅｒ ｔｈｅ ｂｅｓｔ ｌｏｃａｌ ｐｏｓｉｔｉｏｎ ｂｕｔ ａｌｓｏ ｔｈｅ ｓｌｏｗｅｓｔ ｄｉｖｉｎｇ ｖｅｌｏｃｉｔｙ． Ｉｎ ｔｈｅ ｆｉｒｓｔ ｐａｒｔ ｏｆ ＰＩＯ， ｔｈｅ ｆｏｒｍｕｌａ ｉｓ ｎｏｔ ｃｈａｎｇｅｄ， ｂｕｔ ｔｈｅ ｍｅｔｈｏｄ ｏｆ ａｃｑｕｉｒｉｎｇ ｔｈｅ ｂｅｓｔ ｌｏｃａｌ ｐｏｓｉｔｉｏｎ ｉｓ ｍｏｄｉｆｉｅｄ． Ｔｈｅ ｃｒｉｔｅｒｉｏｎ ｉｓ ａ ｌｉｎｅａｒ ｃｏｍｂｉｎａｔｉｏｎ ｏｆ ｔｈｅ ｄｉｓｔａｎｃｅ ｅｒｒｏｒ ｂｅｔｗｅｅｎ ｔｈｅ ｄｅｓｉｒｅｄ ａｎｄ ｔｈｅ ｒｅａｌ ｐｏｓｉｔｉｏｎｓ ａｎｄ ｔｈｅ ｄｉｖｉｎｇ ｓｐｅｅｄ． Ａｎ ＵＡＶ ｔｈａｔ ｄｉｖｅｓ ｖｅｒｙ ｓｌｏｗｌｙ ｉｓ ｉｍｉｔａｔｅｄ ｂｙ ｔｈｅ ｏｔｈｅｒｓ． Ｔｈｉｓ ｉｓ ｔｈｅ ｓｏ⁃ｃａｌｌｅｄ “ ｓｌｏｗ ｄｉｖｉｎｇ ｓｔｒａｔｅｇｙ ”． Ｔｈｅ ｕｐｄａｔｅ ｆｏｒｍｕｌａ ｉｓ： ｖｉ（ｔ ＋ １） ＝ ｖｉ（ｔ）·ｅｘｐ（ － Ｒｔ） ＋ ｒ·［φ·（ｘｌｂｅｓｔ － ｘｉ） ＋ （１ － φ）·ｖｓｌｏｗ ］ ｘｉ（ｔ ＋ １） ＝ ｘｉ（ｔ） ＋ ｖｉ（ｔ ＋ １） ì î í ï ï ïï ｉｆ ｔ ＜ Ｔｌａｂｅｌ （１０） ｗｈｅｒｅ φ ｓｅｒｖｅｓ ａｓ ａ ｒｅｇｕｌａｔｏｒｙ ｆａｃｔｏｒ ｉｎ ｔｈｅ ｒａｎｇｅ ｏｆ （０， １） ； ｉｆ φ ａｐｐｒｏａｃｈｅｓ ０， ｔｈｅ ｓｌｏｗｅｓｔ ｐｉｇｅｏｎ ｗｉｌｌ ｉｎｆｌｕｅｎｃｅ ｔｈｅ ｔｅａｍ； ｉｆ φ ａｐｐｒｏａｃｈｅｓ １， ｂｅｓｔ ｌｏｃａｌ ｐｏｓｉｔｉｏｎ ｗｉｌｌ ｈａｖｅ ｍｕｃｈ ｍｏｒｅ ｏｆ ａｎ ｅｆｆｅｃｔ． ｒ ∈ （０，１） ｉｓ ａ ｒａｎｄｏｍ ｎｕｍｂｅｒ． Ｔｈｅ ｓｅｃｏｎｄ ｐａｒｔ ｏｆ ＰＩＯ ｓｈｏｕｌｄ ｂｅ ｍｏｄｉｆｉｅｄ ｉｎ ｔｈｅ ｆｏｌｌｏｗｉｎｇ ｗａｙ： ａｌｌ ｔｈｅ ＵＡＶｓ ｃｏｎｖｅｒｇｅ ｔｏ ｔｈｅ ｃｅｎｔｅｒ ｏｆ ｔｈｅ ｆｌｏｃｋ， ｗｈｉｃｈ ｉｓ ｃａｌｃｕｌａｔｅｄ ｂｙ ａ ｃｏｍｂｉｎａｔｉｏｎ ｏｆ ｔｈｅ ＵＡＶ ｐｏｓｉｔｉｏｎｓ ａｎｄ ｔｈｅ ｓｌｏｗｅｓｔ ｄｉｖｉｎｇ ｓｐｅｅｄ． Ｔｈｅ ｕｐｄａｔｅ ｅｑｕａｔｉｏｎ ｃａｎ ｂｅ ｄｅｓｃｒｉｂｅｄ ａｓ： Ｎｐ（ｔ ＋ １） ＝ Ｎｐ（ｔ） ２ ｘｉＣ（ｔ ＋ １） ＝ ∑ｘｉ（ｔ）·ｆ（ｘｉ（ｔ）） ＋ １０·ｘｓｌｏｗ·ｆ（ｘｓｌｏｗｓ） ∑ｆ（ｘｉ（ｔ）） ＋ １０·ｘｓｌｏｗ·ｆ（ｘｓｌｏｗ） ｘｉ（ｔ ＋ １） ＝ ｘｉ（ｔ） ＋ ｒａｎｄ·（ｘｉＣ（ｔ ＋ １） － ｘｉ（ｔ）） ì î í ï ï ïï ï ï ïï ｉｆ ｔ ≥ Ｔｌａｂｅｌ （１１） ｗｈｅｒｅ ｘｓｌｏｗ ｉｓ ｔｈｅ ｐｏｓｉｔｉｏｎ ｏｆ ｔｈｅ ＵＡＶ ｗｉｔｈ ｔｈｅ ｓｌｏｗｅｓｔ ｄｉｖｉｎｇ ｓｐｅｅｄ， ｔｈｉｓ ｐａｒｔ ｒｅｐｒｅｓｅｎｔｓ ｔｈｅ ｓｌｏｗｉｎｇ ｄｉｖｉｎｇ ｓｔｒａｔｅｇｙ． Ｆｉｔｎｅｓｓ ｆｕｎｃｔｉｏｎ Ｅｑ． （ １０） ｒｅｍａｉｎｓ． Ｅａｃｈ ＵＡＶ ｈａｓ ｉｔｓ ｏｗｎ ｆｉｔｎｅｓｓ ｖａｌｕｅ． ·５７４· 智 能 系 统 学 报 第 １２ 卷

第4期 ZHANG Tianjie,et al.:A modified consensus algorithm for multi-UAV formations based on pigeon-inspired optimization with a slow diving strategy ·575. 2.3 Convergence analysis of SD-PIO based on velocities,z(i)is theith element of z(t),i1,2,..., Banach fixed-point theorem 2n} In this section,convergence analysis of SD-PIO is z(i)∈u(z(t)=[xan(d)）…xa(t)h(t)…u(t)]' performed and a sufficient condition is proposed for the z()∈z),3K∈Na.st.u(2(t)=K&(). first part of SD-PIO SD-PIO-I).The main method d(T(a),T(a2)=max|T(a)-T(2)|= 1安12山 adopted to prove the stability of iteration is the Banach max Fz+Bu(z)-Fz2 Bu(z2)= 1名i名2m fixed-point theorem,as stated below: ‖Fz1+BK11-Fz2-BK22‖。(13) A map T from a normed space (V,d())into itself There is is a contraction if there exists入∈[0，l)such that for L=F(a-2)+B.[0…xa-x%0…6-%0…0] alx,y∈V,d(T(x),T(y))≤Ad(x,y) (14) In the first part of SD-PIO,each pigeon updates s.t.L=ll Fz +BK2-Fz2 BK222ll,thus the its speed and location according to Eq.(10),which largest element of Fz+BK21-Fz2 BK222 is can be transformed as selected and denoted as supposing it is thej thelement.F.and B..are the whole j th row of F and B, exp(-Rt) respectively.Ifjn,is the j th element of K121 -K2z2 and via-v2 is the (j n)th one, (12) otherwisex-xz is the (j-n)th element and v-v when it considers all the pigeons,(t 1)= is the j th one. Fz(t)+Bu(z(t)), |L=|F.(a-2)+B.[0…k4z0…k40…0]= where z(t)=[x(t)…xn(t),(t)…vn(t)]T, |F(a1-z2）+B.[0…k1…k2…0]4z≤ [1-9 exp(-Rt) ‖F(a1-2)+BK(a1-a2)‖。≤ lF+BK‖m‖a1-22‖。=lF+BKld(z1,a2） 1-ro exp(-Rt) (15) exp(-Rt) Whee4=maxl(i)-z(i)l,k,=xa-xsl/△， 1名i62 |k2=。-2sl/△，k,k2∈[-1,0)U(0,1], -rO exp(-Rt)」 「0 01 1-9 k K= ,,k2 lies in the j th column, 1- k2 B =r 1- Lo 0 The equation holds if and only ifx=v- 1-9 026=Az. u(z(t)=[xeai(t)…xuan(t)un(t）…tahn(t)] The Banach fixed-point theorem requires llF+ If iteration z(t+1)=Fz(t)+Bu(z(t))has a fixed- BKI∈[0,1) pointed',as a result,z'=Fz·+Bu(z）,then max1-or exp(-Rt)+rk o +rk2(1-), SD-PIO-I will converge to 2'and each pigeon will gr exp(-Rt)+rk rk2(1-p)<1 reach its final stable location as time tends to infinity. Denoting Z as a real number space R"and distance -仁120e1-o d(y)=yyeZ,Zhas been proven (16) as a complete metric space.There is a map T:Z-Z, Equation (16)is a sufficient condition for the T(z)=Fz+Bu(z),whereF∈R2xn,B∈R2nxn, convergence of SD-PIO-I,once it is satisfied,we have u(z)=K2x2n2,then Vz1,2∈Z,T(z1),T(a2）∈Z, d(T(x),T(y)≤IF+BKld(x,y),IF+BKIe∈ it can be proven that if d(T(x),T(y))sAd(x,y), [0,1),there exists a fixed-point z'satisfying z'= A [0,1),there exists a fixed-point which satisfies Fz·+Bu(z) the condition 2'=T(2)=Fz'Bu(z)and the x=v+x states of SD-PIO-I converge to z'.The following x=x+exp(-Ri)v'+r(imx)+(1-)vi] proves this conclusion. (17) Because the best local location and the slowest m°=0 Equation(17）→ .the states of SD-PIO-I speed are among all the pigeons'locations and

２． ３ Ｃｏｎｖｅｒｇｅｎｃｅ ａｎａｌｙｓｉｓ ｏｆ ＳＤ⁃ＰＩＯ ｂａｓｅｄ ｏｎ Ｂａｎａｃｈ ｆｉｘｅｄ⁃ｐｏｉｎｔ ｔｈｅｏｒｅｍ Ｉｎ ｔｈｉｓ ｓｅｃｔｉｏｎ， ｃｏｎｖｅｒｇｅｎｃｅ ａｎａｌｙｓｉｓ ｏｆ ＳＤ⁃ＰＩＯ ｉｓ ｐｅｒｆｏｒｍｅｄ ａｎｄ ａ ｓｕｆｆｉｃｉｅｎｔ ｃｏｎｄｉｔｉｏｎ ｉｓ ｐｒｏｐｏｓｅｄ ｆｏｒ ｔｈｅ ｆｉｒｓｔ ｐａｒｔ ｏｆ ＳＤ⁃ＰＩＯ （ ＳＤ⁃ＰＩＯ⁃Ｉ）． Ｔｈｅ ｍａｉｎ ｍｅｔｈｏｄ ａｄｏｐｔｅｄ ｔｏ ｐｒｏｖｅ ｔｈｅ ｓｔａｂｉｌｉｔｙ ｏｆ ｉｔｅｒａｔｉｏｎ ｉｓ ｔｈｅ Ｂａｎａｃｈ ｆｉｘｅｄ⁃ｐｏｉｎｔ ｔｈｅｏｒｅｍ， ａｓ ｓｔａｔｅｄ ｂｅｌｏｗ： Ａ ｍａｐ Ｔ ｆｒｏｍ ａ ｎｏｒｍｅｄ ｓｐａｃｅ （Ｖ，ｄ（）） ｉｎｔｏ ｉｔｓｅｌｆ ｉｓ ａ ｃｏｎｔｒａｃｔｉｏｎ ｉｆ ｔｈｅｒｅ ｅｘｉｓｔｓ λ ∈ ［０，１） ｓｕｃｈ ｔｈａｔ ｆｏｒ ａｌｌ ｘ，ｙ ∈ Ｖ，ｄ（Ｔ（ｘ），Ｔ（ｙ）） ≤ λｄ（ｘ，ｙ） ． Ｉｎ ｔｈｅ ｆｉｒｓｔ ｐａｒｔ ｏｆ ＳＤ⁃ＰＩＯ， ｅａｃｈ ｐｉｇｅｏｎ ｕｐｄａｔｅｓ ｉｔｓ ｓｐｅｅｄ ａｎｄ ｌｏｃａｔｉｏｎ ａｃｃｏｒｄｉｎｇ ｔｏ Ｅｑ． （１０）， ｗｈｉｃｈ ｃａｎ ｂｅ ｔｒａｎｓｆｏｒｍｅｄ ａｓ ｘｉ（ｔ ＋ １） ｖｉ（ｔ ＋ １） é ë ê ê ù û ú ú ＝ １ － ｒφ ｅｘｐ（ － Ｒｔ） － ｒφ ｅｘｐ（ － Ｒｔ） é ë ê ê ù û ú ú ｘｉ（ｔ） ｖｉ（ｔ） é ë ê ê ù û ú ú ＋ ｒ φ １ － φ φ １ － φ é ë ê ê ù û ú ú ｘｌｂｅｓｔ ｖｓｌｏｗ é ë ê ê ù û ú ú （１２） ｗｈｅｎ ｉｔ ｃｏｎｓｉｄｅｒｓ ａｌｌ ｔｈｅ ｐｉｇｅｏｎｓ， ｚ（ｔ ＋ １） ＝ Ｆｚ（ｔ） ＋ Ｂｕ（ｚ（ｔ）） ， ｗｈｅｒｅ ｚ（ｔ） ＝ ｘ１（ｔ） … ｘｎ（ｔ） ｖ１（ｔ） … ｖ [ ｎ（ｔ） ] Ｔ ， Ｆ ＝ １ － ｒφ ｅｘｐ（ － Ｒｔ） ⋱ ⋱ １ － ｒφ ｅｘｐ（ － Ｒｔ） － ｒφ ｅｘｐ（ － Ｒｔ） ⋱ ⋱ － ｒφ ｅｘｐ（ － Ｒｔ） é ë ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú Ｂ ＝ ｒ φ １ － φ ⋱ ⋱ φ １ － φ φ １ － φ ⋱ ⋱ φ １ － φ é ë ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ｕ（ｚ（ｔ））＝ ｘｌｂｅｓｔ１（ｔ） … ｘｌｂｅｓｔｎ（ｔ） ｖｓｌｏｗ１（ｔ） … ｖ [ ｓｌｏｗｎ（ｔ）] Ｔ ． Ｉｆ ｉｔｅｒａｔｉｏｎ ｚ（ｔ ＋ １） ＝ Ｆｚ（ｔ） ＋ Ｂｕ（ｚ（ｔ）） ｈａｓ ａ ｆｉｘｅｄ⁃ ｐｏｉｎｔｅｄ ｚ ∗ ， ａｓ ａ ｒｅｓｕｌｔ， ｚ ∗ ＝ Ｆｚ ∗ ＋ Ｂｕ（ｚ ∗ ） ， ｔｈｅｎ ＳＤ⁃ＰＩＯ⁃Ｉ ｗｉｌｌ ｃｏｎｖｅｒｇｅ ｔｏ ｚ ∗ ａｎｄ ｅａｃｈ ｐｉｇｅｏｎ ｗｉｌｌ ｒｅａｃｈ ｉｔｓ ｆｉｎａｌ ｓｔａｂｌｅ ｌｏｃａｔｉｏｎ ａｓ ｔｉｍｅ ｔｅｎｄｓ ｔｏ ｉｎｆｉｎｉｔｙ． Ｄｅｎｏｔｉｎｇ Ｚ ａｓ ａ ｒｅａｌ ｎｕｍｂｅｒ ｓｐａｃｅ Ｒ ｎ ａｎｄ ｄｉｓｔａｎｃｅ ｄ（ｘ，ｙ） ＝ ｍａｘ １≤ｉ≤２ｎ ｘｉ － ｙｉ ，ｘ，ｙ ∈ Ｚ，Ｚｈａｓ ｂｅｅｎ ｐｒｏｖｅｎ ａｓ ａ ｃｏｍｐｌｅｔｅ ｍｅｔｒｉｃ ｓｐａｃｅ． Ｔｈｅｒｅ ｉｓ ａ ｍａｐ Ｔ：Ｚ → Ｚ， Ｔ（ｚ） ＝ Ｆｚ ＋ Ｂｕ（ｚ） ，ｗｈｅｒｅ Ｆ ∈ Ｒ２ｎ×２ｎ ， Ｂ ∈ Ｒ２ｎ×２ｎ ， ｕ（ｚ） ＝ Ｋ２ｎ×２ｎ ｚ， ｔｈｅｎ ∀ｚ１ ，ｚ２ ∈Ｚ， Ｔ（ｚ１ ），Ｔ（ｚ２ ） ∈Ｚ， ｉｔ ｃａｎ ｂｅ ｐｒｏｖｅｎ ｔｈａｔ ｉｆ ｄ（Ｔ（ｘ），Ｔ（ｙ）） ≤ λｄ（ｘ，ｙ）， λ ∈［０，１）， ｔｈｅｒｅ ｅｘｉｓｔｓ ａ ｆｉｘｅｄ⁃ｐｏｉｎｔ ｗｈｉｃｈ ｓａｔｉｓｆｉｅｓ ｔｈｅ ｃｏｎｄｉｔｉｏｎ ｚ ∗ ＝ Ｔ（ｚ ∗ ） ＝ Ｆｚ ∗ ＋ Ｂｕ（ｚ ∗ ） ａｎｄ ｔｈｅ ｓｔａｔｅｓ ｏｆ ＳＤ⁃ＰＩＯ⁃Ｉ ｃｏｎｖｅｒｇｅ ｔｏ ｚ ∗ ． Ｔｈｅ ｆｏｌｌｏｗｉｎｇ ｐｒｏｖｅｓ ｔｈｉｓ ｃｏｎｃｌｕｓｉｏｎ． Ｂｅｃａｕｓｅ ｔｈｅ ｂｅｓｔ ｌｏｃａｌ ｌｏｃａｔｉｏｎ ａｎｄ ｔｈｅ ｓｌｏｗｅｓｔ ｓｐｅｅｄ ａｒｅ ａｍｏｎｇ ａｌｌ ｔｈｅ ｐｉｇｅｏｎｓ ’ ｌｏｃａｔｉｏｎｓ ａｎｄ ｖｅｌｏｃｉｔｉｅｓ， ｚ（ｉ） ｉｓ ｔｈｅｉｔｈ ｅｌｅｍｅｎｔ ｏｆ ｚ（ｔ）， ｉ ∈ ｛１，２，…， ２ｎ｝ ∀ｚ（ｉ）∈ｕ（ｚ（ｔ））＝ ｘｌｂｅｓｔ１（ｔ） … ｘｌｂｅｓｔｎ（ｔ） ｖｓｌｏｗ１（ｔ） … ｖ [ ｓｌｏｗｎ（ｔ）] Ｔ ｚ（ｉ） ∈ｚ（ｔ），∃Ｋ ∈Ｎ２ｎ×２ｎ，ｓ．ｔ． ｕ（ｚ（ｔ））＝ Ｋｚ（ｔ） ． ｄ（Ｔ（ｚ１ ），Ｔ（ｚ２ ）） ＝ ｍａｘ １≤ｉ≤２ｎ Ｔ（ｚ１ ） － Ｔ（ｚ２ ） ＝ ｍａｘ １≤ｉ≤２ｎ Ｆｚ１ ＋ Ｂｕ（ｚ１ ） － Ｆｚ２ － Ｂｕ（ｚ２ ） ＝ ‖Ｆｚ１ ＋ ＢＫ１ ｚ１ － Ｆｚ２ － ＢＫ２ ｚ２‖¥ （１３） Ｔｈｅｒｅ ｉｓ Ｌｊ ＝ Ｆ·ｊ （ｚ１ －ｚ２） ＋Ｂ·ｊ ［０ … ｘ１ａ － ｘ２ｂ ０ … ｖ１ａ － ｖ２ｂ ０ … ０］ Ｔ （１４） ｓ．ｔ． Ｌｊ ＝‖ Ｆｚ１ ＋ ＢＫ１ ｚ１ － Ｆｚ２ － ＢＫ２ ｚ２‖¥， ｔｈｕｓ ｔｈｅ ｌａｒｇｅｓｔ ｅｌｅｍｅｎｔ ｏｆ Ｆｚ１ ＋ ＢＫ１ ｚ１ － Ｆｚ２ － ＢＫ２ ｚ２ ｉｓ ｓｅｌｅｃｔｅｄ ａｎｄ ｄｅｎｏｔｅｄ ａｓ Ｌｊ ｓｕｐｐｏｓｉｎｇ ｉｔ ｉｓ ｔｈｅ ｊ ｔｈｅｌｅｍｅｎｔ． Ｆ·ｊ ａｎｄ Ｂ·ｊ ａｒｅ ｔｈｅ ｗｈｏｌｅ ｊ ｔｈ ｒｏｗ ｏｆ Ｆ ａｎｄ Ｂ， ｒｅｓｐｅｃｔｉｖｅｌｙ． Ｉｆ ｊ ≤ ｎ，ｘ１ａ － ｘ２ｂ ｉｓ ｔｈｅ ｊ ｔｈ ｅｌｅｍｅｎｔ ｏｆ Ｋ１ ｚ１ －Ｋ２ ｚ２ ａｎｄ ｖ１ａ － ｖ２ｂ ｉｓ ｔｈｅ （ｊ ＋ ｎ） ｔｈ ｏｎｅ， ｏｔｈｅｒｗｉｓｅ ｘ１ａ － ｘ２ｂ ｉｓ ｔｈｅ （ｊ － ｎ） ｔｈ ｅｌｅｍｅｎｔ ａｎｄ ｖ１ａ － ｖ２ｂ ｉｓ ｔｈｅ ｊ ｔｈ ｏｎｅ． Ｌｊ ＝ Ｆ·ｊ （ｚ１ － ｚ２）＋ Ｂ·ｊ ［０ … ｋ１Δｚ ０ … ｋ２Δｚ ０ … ０］ Ｔ ＝ Ｆ·ｊ （ｚ１ － ｚ２ ） ＋ Ｂ·ｊ ［０…ｋ１…ｋ２…０］ ＴΔｚ ≤ ‖Ｆ（ｚ１ － ｚ２ ） ＋ ＢＫ（ｚ１ － ｚ２ ）‖¥ ≤ ‖Ｆ ＋ ＢＫ‖¥‖ｚ１ － ｚ２‖¥ ＝ ‖Ｆ ＋ ＢＫ‖¥ｄ（ｚ１ ，ｚ２ ） （１５） Ｗｈｅｒｅ Δｚ ＝ ｍａｘ １≤ｉ≤２ｎ ｚ１（ｉ） － ｚ２（ｉ） ， ｋ１ ＝ ｘ１ａ － ｘ２ｂ ／ Δｚ， ｋ２ ＝ ｖ１ａ － ｖ２ｂ ／ Δｚ，ｋ１ ，ｋ２ ∈ ［ － １，０） ∪ （０，１］， Ｋ ＝ ０ ０ ⋱ ｋ１ ︙ ｋ２ ０ ０ é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú ，ｋ１ ，ｋ２ ｌｉｅｓ ｉｎ ｔｈｅ ｊ ｔｈ ｃｏｌｕｍｎ， Ｔｈｅ ｅｑｕａｔｉｏｎ ｈｏｌｄｓ ｉｆ ａｎｄ ｏｎｌｙ ｉｆ ｘ１ａ － ｘ２ｂ ＝ ｖ１ａ － ｖ２ｂ ＝ Δｚ ． Ｔｈｅ Ｂａｎａｃｈ ｆｉｘｅｄ⁃ｐｏｉｎｔ ｔｈｅｏｒｅｍ ｒｅｑｕｉｒｅｓ ‖Ｆ ＋ ＢＫ‖¥ ∈ ［０，１） ⇔ｍａｘ｛ １ － φｒ ＋ ｅｘｐ（ － Ｒｔ） ＋ ｒｋ１φ ＋ ｒｋ２（１ － φ） ， － φｒ ＋ ｅｘｐ（ － Ｒｔ） ＋ ｒｋ１φ ＋ ｒｋ２（１ － φ） ｝ ＜ １ ⇔ － １ ＜ － φｒ ＋ ｅｘｐ（ － Ｒｔ） ＋ ｒｋ１φ ＋ ｒｋ２（１ － φ）＜０ － １ ≤ ｋ１ ，ｋ２ ≤ １，ｋ１ ｋ２ ≠ ０ { （１６） Ｅｑｕａｔｉｏｎ （ １６） ｉｓ ａ ｓｕｆｆｉｃｉｅｎｔ ｃｏｎｄｉｔｉｏｎ ｆｏｒ ｔｈｅ ｃｏｎｖｅｒｇｅｎｃｅ ｏｆ ＳＤ⁃ＰＩＯ⁃Ｉ， ｏｎｃｅ ｉｔ ｉｓ ｓａｔｉｓｆｉｅｄ， ｗｅ ｈａｖｅ ｄ（Ｔ（ｘ），Ｔ（ｙ））≤‖Ｆ ＋ ＢＫ‖¥ｄ（ｘ，ｙ），‖Ｆ ＋ ＢＫ‖¥ ∈ ［０，１）， ｔｈｅｒｅ ｅｘｉｓｔｓ ａ ｆｉｘｅｄ⁃ｐｏｉｎｔ ｚ ∗ ｓａｔｉｓｆｙｉｎｇ ｚ ∗ ＝ Ｆｚ ∗ ＋Ｂｕ（ｚ ∗ ） ｘ ∗＝ ｖ ∗＋ ｘ ∗ ｘ ∗＝ ｘ ∗＋ ｅｘｐ（－ Ｒｔ）ｖ ∗＋ ｒ［φ（ｘ ∗ ｌｂｅｓｔ － ｘ ∗ ） ＋ （１ － φ）ｖ ∗ ｓｌｏｗ］ { （１７） Ｅｑｕａｔｉｏｎ （１７） ⇒ ｖ ∗ ＝ ０ ｘ ∗ ＝ ｘ ∗ ｌｂｅｓｔ { ， ｔｈｅ ｓｔａｔｅｓ ｏｆ ＳＤ⁃ＰＩＯ⁃Ｉ ·５７５· 第 ４ 期 ＺＨＡＮＧ Ｔｉａｎｊｉｅ， ｅｔ ａｌ．：Ａ ｍｏｄｉｆｉｅｄ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ ｆｏｒ ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎｓ ｂａｓｅｄ ｏｎ ｐｉｇｅｏｎ⁃ｉｎｓｐｉｒｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ｗｉｔｈ ａ ｓｌｏｗ ｄｉｖｉｎｇ ｓｔｒａｔｅｇｙ

,576 智能系统学报 第12卷 can only converge to a local optimal solution because where T is the moment when consensus replaces SD- each pigeon can only receive its neighbor's information instead of global information. PI0,±×arctan(R×(t-T)+0.5,the For the second part of SD-PIO,all the pigeons inverse trigonometric function,is utilized to modify the converge to the flock's center.Their trajectories can only output of the SD-PIO and consensus,it works as a contract and approach each other.In formation processes this part serves only as a transition,and as the traces do switch key to smoothly connect the two parts of the not diverge this second part satisfies the demands. trajectory.f((t),(t))is the output velocity of SD- Multi-UAV formations with a SD- PI0 from Eqs.(7）and(9）.The implementation PIO-based consensus algorithm procedure of the SD-PIO-based consensus algorithm is given as follows: The first three sections introduced consensus and 1)Input the number of UAVs in the formation SD-PIO,now this section uses them to optimize the trajectory of an UAV.When consensus is only applied task,give the expectation formation and consider the to the planned routes of all the UAVs,there is communication restriction. unavoidable overshoot because of the distributed control 2)Design a suitable communication network plan itself.Every UAV has its own limited topology and acquire its adjacency matrix and the communication relationship,which means it cannot Laplace matrix. always receive the desired trajectory.For example, 3)Randomly initialize the positions and velocities UAV can never acquire the planned trajectory of all the UAVs along with the parameters involved in directly,it relies on UAV,to pass on the information. If UAV3's initial altitude is much too high,it must the equations used in Eq.(18). dive to meet the desired trajectory.Because of inertia 4)Calculate the acceleration input,consensus, and a lack of forecasting,UAV,can only produce and the velocity input using Eq.(18) positive additions to its height when it goes below the 5)Update each UAV's position and velocity using desired trajectory and this is the reason for overshoot. Eq.(18) However,as for UAV,only when its leader UAV3 6)Draw the UAV's trajectory according to its flies below the proposed height does it begin to position in each iteration. recognize that it should fly a bit higher,then its velocity is changed by Eq.(7),followed by its The process is summarized in the following position.This process is much slower than a change in process flow chart: the desired route.As a result,the UAVs'trajectories Design the desired dive sharply and appear to overshoot,then they formation and give the converge to the desired trajectory.SD-PIO provides a communication topology gentle and slowly changing trajectory for each UAV at Acquire the adjacency matrix the start,then,as soon as the UAVs fly down and and the Laplace martix meet the desired trajectory,consensus starts to operate. Calculate the acceleration Initialize the positions and input by the second stage The formula of the combination of these two velocities of all the UAVs formula of SD-PIO,Eq.(18) algorithms can be described as: [x(t+1)=x(t)+T·((t+1)+,(t+1))》 Calculate the acceleration Update the velocity and input by the first stage v(t+1)=v(t)+T·a(t+1) position of each UAV formula of SD-PIO.Eq.(18) a(t+1)=-(L☒3)·x(t+1)+ Ift>Tlabel Update the velocity and N y·(L☒I3)·(t+1))· position of each UAV Y 三×arctan(R×(t-Ths)+0.5) Tlabel Draw the trajectories of UAVs 2(t+1)=f(x(t),v(t))· N ×arctan(R×(t-Te)+0.5) Fig.4 The process of the SD-PIO based consensus (18) algorithm for a multi-UAV formation

ｃａｎ ｏｎｌｙ ｃｏｎｖｅｒｇｅ ｔｏ ａ ｌｏｃａｌ ｏｐｔｉｍａｌ ｓｏｌｕｔｉｏｎ ｂｅｃａｕｓｅ ｅａｃｈ ｐｉｇｅｏｎ ｃａｎ ｏｎｌｙ ｒｅｃｅｉｖｅ ｉｔｓ ｎｅｉｇｈｂｏｒ’ｓ ｉｎｆｏｒｍａｔｉｏｎ ｉｎｓｔｅａｄ ｏｆ ｇｌｏｂａｌ ｉｎｆｏｒｍａｔｉｏｎ． Ｆｏｒ ｔｈｅ ｓｅｃｏｎｄ ｐａｒｔ ｏｆ ＳＤ⁃ＰＩＯ， ａｌｌ ｔｈｅ ｐｉｇｅｏｎｓ ｃｏｎｖｅｒｇｅ ｔｏ ｔｈｅ ｆｌｏｃｋ’ｓ ｃｅｎｔｅｒ． Ｔｈｅｉｒ ｔｒａｊｅｃｔｏｒｉｅｓ ｃａｎ ｏｎｌｙ ｃｏｎｔｒａｃｔ ａｎｄ ａｐｐｒｏａｃｈ ｅａｃｈ ｏｔｈｅｒ． Ｉｎ ｆｏｒｍａｔｉｏｎ ｐｒｏｃｅｓｓｅｓ ｔｈｉｓ ｐａｒｔ ｓｅｒｖｅｓ ｏｎｌｙ ａｓ ａ ｔｒａｎｓｉｔｉｏｎ， ａｎｄ ａｓ ｔｈｅ ｔｒａｃｅｓ ｄｏ ｎｏｔ ｄｉｖｅｒｇｅ ｔｈｉｓ ｓｅｃｏｎｄ ｐａｒｔ ｓａｔｉｓｆｉｅｓ ｔｈｅ ｄｅｍａｎｄｓ． ３ Ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎｓ ｗｉｔｈ ａ ＳＤ⁃ ＰＩＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ Ｔｈｅ ｆｉｒｓｔ ｔｈｒｅｅ ｓｅｃｔｉｏｎｓ ｉｎｔｒｏｄｕｃｅｄ ｃｏｎｓｅｎｓｕｓ ａｎｄ ＳＤ⁃ＰＩＯ， ｎｏｗ ｔｈｉｓ ｓｅｃｔｉｏｎ ｕｓｅｓ ｔｈｅｍ ｔｏ ｏｐｔｉｍｉｚｅ ｔｈｅ ｔｒａｊｅｃｔｏｒｙ ｏｆ ａｎ ＵＡＶ． Ｗｈｅｎ ｃｏｎｓｅｎｓｕｓ ｉｓ ｏｎｌｙ ａｐｐｌｉｅｄ ｔｏ ｔｈｅ ｐｌａｎｎｅｄ ｒｏｕｔｅｓ ｏｆ ａｌｌ ｔｈｅ ＵＡＶｓ， ｔｈｅｒｅ ｉｓ ｕｎａｖｏｉｄａｂｌｅ ｏｖｅｒｓｈｏｏｔ ｂｅｃａｕｓｅ ｏｆ ｔｈｅ ｄｉｓｔｒｉｂｕｔｅｄ ｃｏｎｔｒｏｌ ｐｌａｎ ｉｔｓｅｌｆ． Ｅｖｅｒｙ ＵＡＶ ｈａｓ ｉｔｓ ｏｗｎ ｌｉｍｉｔｅｄ ｃｏｍｍｕｎｉｃａｔｉｏｎ ｒｅｌａｔｉｏｎｓｈｉｐ， ｗｈｉｃｈ ｍｅａｎｓ ｉｔ ｃａｎｎｏｔ ａｌｗａｙｓ ｒｅｃｅｉｖｅ ｔｈｅ ｄｅｓｉｒｅｄ ｔｒａｊｅｃｔｏｒｙ． Ｆｏｒ ｅｘａｍｐｌｅ， ＵＡＶ１ ｃａｎ ｎｅｖｅｒ ａｃｑｕｉｒｅ ｔｈｅ ｐｌａｎｎｅｄ ｔｒａｊｅｃｔｏｒｙ ｄｉｒｅｃｔｌｙ， ｉｔ ｒｅｌｉｅｓ ｏｎ ＵＡＶ３ ｔｏ ｐａｓｓ ｏｎ ｔｈｅ ｉｎｆｏｒｍａｔｉｏｎ． Ｉｆ ＵＡＶ３ ’ ｓ ｉｎｉｔｉａｌ ａｌｔｉｔｕｄｅ ｉｓ ｍｕｃｈ ｔｏｏ ｈｉｇｈ， ｉｔ ｍｕｓｔ ｄｉｖｅ ｔｏ ｍｅｅｔ ｔｈｅ ｄｅｓｉｒｅｄ ｔｒａｊｅｃｔｏｒｙ． Ｂｅｃａｕｓｅ ｏｆ ｉｎｅｒｔｉａ ａｎｄ ａ ｌａｃｋ ｏｆ ｆｏｒｅｃａｓｔｉｎｇ， ＵＡＶ３ ｃａｎ ｏｎｌｙ ｐｒｏｄｕｃｅ ｐｏｓｉｔｉｖｅ ａｄｄｉｔｉｏｎｓ ｔｏ ｉｔｓ ｈｅｉｇｈｔ ｗｈｅｎ ｉｔ ｇｏｅｓ ｂｅｌｏｗ ｔｈｅ ｄｅｓｉｒｅｄ ｔｒａｊｅｃｔｏｒｙ ａｎｄ ｔｈｉｓ ｉｓ ｔｈｅ ｒｅａｓｏｎ ｆｏｒ ｏｖｅｒｓｈｏｏｔ． Ｈｏｗｅｖｅｒ， ａｓ ｆｏｒ ＵＡＶ１ ， ｏｎｌｙ ｗｈｅｎ ｉｔｓ ｌｅａｄｅｒ ＵＡＶ３ ｆｌｉｅｓ ｂｅｌｏｗ ｔｈｅ ｐｒｏｐｏｓｅｄ ｈｅｉｇｈｔ ｄｏｅｓ ｉｔ ｂｅｇｉｎ ｔｏ ｒｅｃｏｇｎｉｚｅ ｔｈａｔ ｉｔ ｓｈｏｕｌｄ ｆｌｙ ａ ｂｉｔ ｈｉｇｈｅｒ， ｔｈｅｎ ｉｔｓ ｖｅｌｏｃｉｔｙ ｉｓ ｃｈａｎｇｅｄ ｂｙ Ｅｑ． （ ７ ）， ｆｏｌｌｏｗｅｄ ｂｙ ｉｔｓ ｐｏｓｉｔｉｏｎ． Ｔｈｉｓ ｐｒｏｃｅｓｓ ｉｓ ｍｕｃｈ ｓｌｏｗｅｒ ｔｈａｎ ａ ｃｈａｎｇｅ ｉｎ ｔｈｅ ｄｅｓｉｒｅｄ ｒｏｕｔｅ． Ａｓ ａ ｒｅｓｕｌｔ， ｔｈｅ ＵＡＶｓ’ ｔｒａｊｅｃｔｏｒｉｅｓ ｄｉｖｅ ｓｈａｒｐｌｙ ａｎｄ ａｐｐｅａｒ ｔｏ ｏｖｅｒｓｈｏｏｔ， ｔｈｅｎ ｔｈｅｙ ｃｏｎｖｅｒｇｅ ｔｏ ｔｈｅ ｄｅｓｉｒｅｄ ｔｒａｊｅｃｔｏｒｙ． ＳＤ⁃ＰＩＯ ｐｒｏｖｉｄｅｓ ａ ｇｅｎｔｌｅ ａｎｄ ｓｌｏｗｌｙ ｃｈａｎｇｉｎｇ ｔｒａｊｅｃｔｏｒｙ ｆｏｒ ｅａｃｈ ＵＡＶ ａｔ ｔｈｅ ｓｔａｒｔ， ｔｈｅｎ， ａｓ ｓｏｏｎ ａｓ ｔｈｅ ＵＡＶｓ ｆｌｙ ｄｏｗｎ ａｎｄ ｍｅｅｔ ｔｈｅ ｄｅｓｉｒｅｄ ｔｒａｊｅｃｔｏｒｙ， ｃｏｎｓｅｎｓｕｓ ｓｔａｒｔｓ ｔｏ ｏｐｅｒａｔｅ． Ｔｈｅ ｆｏｒｍｕｌａ ｏｆ ｔｈｅ ｃｏｍｂｉｎａｔｉｏｎ ｏｆ ｔｈｅｓｅ ｔｗｏ ａｌｇｏｒｉｔｈｍｓ ｃａｎ ｂｅ ｄｅｓｃｒｉｂｅｄ ａｓ： ｘ（ｔ ＋ １） ＝ ｘ（ｔ） ＋ Ｔ·（ｖ（ｔ ＋ １） ＋ ｖ２（ｔ ＋ １）） ｖ（ｔ ＋ １） ＝ ｖ（ｔ） ＋ Ｔ·ａ（ｔ ＋ １） ａ（ｔ ＋ １） ＝ － （（Ｌ 􀱋 Ｉ３ ）·ｘ（ｔ ＋ １） ＋ γ·（Ｌ 􀱋 Ｉ３ ）·ｖ（ｔ ＋ １））· （ １ π × ａｒｃｔａｎ（Ｒ × （ｔ － Ｔｃｈｇ）） ＋ ０．５） ｖ２（ｔ ＋ １） ＝ ｆ（ｘ（ｔ），ｖ（ｔ））· （ － １ π × ａｒｃｔａｎ（Ｒ × （ｔ － Ｔｃｈｇ）） ＋ ０．５） ì î í ï ï ï ï ï ï ï ï ï ï ï ï （１８） ｗｈｅｒｅ Ｔｃｈｇ ｉｓ ｔｈｅ ｍｏｍｅｎｔ ｗｈｅｎ ｃｏｎｓｅｎｓｕｓ ｒｅｐｌａｃｅｓ ＳＤ⁃ ＰＩＯ， ± １ π × ａｒｃｔａｎ （Ｒ × （ｔ － Ｔｃｈｇ）） ＋ ０．５， ｔｈｅ ｉｎｖｅｒｓｅ ｔｒｉｇｏｎｏｍｅｔｒｉｃ ｆｕｎｃｔｉｏｎ， ｉｓ ｕｔｉｌｉｚｅｄ ｔｏ ｍｏｄｉｆｙ ｔｈｅ ｏｕｔｐｕｔ ｏｆ ｔｈｅ ＳＤ⁃ＰＩＯ ａｎｄ ｃｏｎｓｅｎｓｕｓ， ｉｔ ｗｏｒｋｓ ａｓ ａ ｓｗｉｔｃｈ ｋｅｙ ｔｏ ｓｍｏｏｔｈｌｙ ｃｏｎｎｅｃｔ ｔｈｅ ｔｗｏ ｐａｒｔｓ ｏｆ ｔｈｅ ｔｒａｊｅｃｔｏｒｙ． ｆ（ｘ（ｔ），ｖ（ｔ）） ｉｓ ｔｈｅ ｏｕｔｐｕｔ ｖｅｌｏｃｉｔｙ ｏｆ ＳＤ⁃ ＰＩＯ ｆｒｏｍ Ｅｑｓ． （ ７ ） ａｎｄ （ ９ ）． Ｔｈｅ ｉｍｐｌｅｍｅｎｔａｔｉｏｎ ｐｒｏｃｅｄｕｒｅ ｏｆ ｔｈｅ ＳＤ⁃ＰＩＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ ｉｓ ｇｉｖｅｎ ａｓ ｆｏｌｌｏｗｓ： １） Ｉｎｐｕｔ ｔｈｅ ｎｕｍｂｅｒ ｏｆ ＵＡＶｓ ｉｎ ｔｈｅ ｆｏｒｍａｔｉｏｎ ｔａｓｋ， ｇｉｖｅ ｔｈｅ ｅｘｐｅｃｔａｔｉｏｎ ｆｏｒｍａｔｉｏｎ ａｎｄ ｃｏｎｓｉｄｅｒ ｔｈｅ ｃｏｍｍｕｎｉｃａｔｉｏｎ ｒｅｓｔｒｉｃｔｉｏｎ． ２ ） Ｄｅｓｉｇｎ ａ ｓｕｉｔａｂｌｅ ｃｏｍｍｕｎｉｃａｔｉｏｎ ｎｅｔｗｏｒｋ ｔｏｐｏｌｏｇｙ ａｎｄ ａｃｑｕｉｒｅ ｉｔｓ ａｄｊａｃｅｎｃｙ ｍａｔｒｉｘ ａｎｄ ｔｈｅ Ｌａｐｌａｃｅ ｍａｔｒｉｘ． ３）Ｒａｎｄｏｍｌｙ ｉｎｉｔｉａｌｉｚｅ ｔｈｅ ｐｏｓｉｔｉｏｎｓ ａｎｄ ｖｅｌｏｃｉｔｉｅｓ ｏｆ ａｌｌ ｔｈｅ ＵＡＶｓ ａｌｏｎｇ ｗｉｔｈ ｔｈｅ ｐａｒａｍｅｔｅｒｓ ｉｎｖｏｌｖｅｄ ｉｎ ｔｈｅ ｅｑｕａｔｉｏｎｓ ｕｓｅｄ ｉｎ Ｅｑ． （１８）． ４） Ｃａｌｃｕｌａｔｅ ｔｈｅ ａｃｃｅｌｅｒａｔｉｏｎ ｉｎｐｕｔ， ｃｏｎｓｅｎｓｕｓ， ａｎｄ ｔｈｅ ｖｅｌｏｃｉｔｙ ｉｎｐｕｔ ｕｓｉｎｇ Ｅｑ． （１８） ５）Ｕｐｄａｔｅ ｅａｃｈ ＵＡＶ’ｓ ｐｏｓｉｔｉｏｎ ａｎｄ ｖｅｌｏｃｉｔｙ ｕｓｉｎｇ Ｅｑ． （１８） ６） Ｄｒａｗ ｔｈｅ ＵＡＶ’ ｓ ｔｒａｊｅｃｔｏｒｙ ａｃｃｏｒｄｉｎｇ ｔｏ ｉｔｓ ｐｏｓｉｔｉｏｎ ｉｎ ｅａｃｈ ｉｔｅｒａｔｉｏｎ． Ｔｈｅ ｐｒｏｃｅｓｓ ｉｓ ｓｕｍｍａｒｉｚｅｄ ｉｎ ｔｈｅ ｆｏｌｌｏｗｉｎｇ ｐｒｏｃｅｓｓ ｆｌｏｗ ｃｈａｒｔ： Ｆｉｇ． ４ Ｔｈｅ ｐｒｏｃｅｓｓ ｏｆ ｔｈｅ ＳＤ⁃ＰＩＯ ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ ｆｏｒ ａ ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎ ·５７６· 智 能 系 统 学 报 第 １２ 卷

ZHANG Tianjie,et al.:A modified consensus algorithm for multi-UAV formations based on 第4期 pigeon-inspired optimization with a slow diving strategy .577. 4 Simulation results and analysis from this perspective,however,it is important to clarify the fact that the trajectories do not cross and the To validate the SD-PIO-based consensus, UAVs do not crash in the sky. numerical simulations were conducted using MATLAB 2012a on a PC with an i5-480 m,2.67 GHz CPU and UAV Windows 10 operating system.SD-PIO was compared 40 with consensus itself and consensus with two other 号20 optimizations,particle swarm optimization (PSO)and UAV 6005004003002001000分m UAV PIO.The results prove the effectiveness of SD-PIO. m The main parameters in Egs.(7),(9),and Fig.5 Trajectories of 9 UAVs by consensus (18)are listed in Table 2 below.The time step for the simulation is T=0.05 s. To demonstrate the advantage of SD-PIO-based Table 2 Simulation parameters consensus,PSO-and PIO-based consensus algorithms were adopted to compare their performances with that R Tule/s Tae/s of the modified algorithm.In Fig.6,most trajectories 50 4 6 are apparently better than those in Fig.5,as the Nine UAVs were initialized with random positions trajectories are gentle at the beginning and turn without in a 3-dimensional environment as shown in Table 3. diving sharply.UAV3,UAVs,andUAV,serve as a set Table 3 Initial positions of 9 UAVs m of convincing simulations that support the conclusions UAV number above.In Figs.7 and 8,PIO and SD-PIO work and UAV, 20.804 30.971 30.477 further improve the performance.In Fig.7,the UAV2 12.685 37.633 31.252 overshoot almost disappears,but there is still UAV3 22.260 38.622 24.661 fluctuation in the trajectories from this perspective, UAVa 0.318 27.929 9.703 especially for UAV3,UAV,and UAVs.In Fig.8,the UAVs trajectories become much smoother and the overshoot 21.859 15.846 6.076 UAVo can be ignored compared with Figs.5 to 7.This is 16.942 13.999 6.644 reflected in the lowest parts of the trajectories of UAV7 19.293 20.723 17.662 UAV3,UAV,and UAVs. UAVs 24.806 23.061 9.317 UAVo 37.298 12.688 7.861 UAV These heights,the numbers on the z-axis,are 号20 UAV relative positions corresponding to the height of origin UAV of the common moving coordinate system in Fig.2. 0 UAV 60050040030020010006 Each UAV had the same initial position in the four x/m UAV 3/m simulations,i.e.,consensus,PSO-based consensus, Fig.6 Trajectories of 9 UAVs by PSO-based consensus PIO-based consensus,and SD-PIO-based consensus. As known from Sections 2 and 3,the performance of consensus cannot satisfy the requirements,which is 401 UAV UAV UAV clearly displayed in Fig.5.Because of communication UAV 20 -UAV restrictions and lack of forecasting,all the UAVs tend ≠9UAV。 UAVs to dive sharply and climb quickly.This causes great 6005040300200100六m0AV m UAV overload at the turning point,which may damage the UAV's structure and result in difficulties for flight Fig.7 Trajectories of 9 UAVs by PIO-based consensus control.Their routes seem to tie a knot when viewed

４ Ｓｉｍｕｌａｔｉｏｎ ｒｅｓｕｌｔｓ ａｎｄ ａｎａｌｙｓｉｓ Ｔｏ ｖａｌｉｄａｔｅ ｔｈｅ ＳＤ⁃ＰＩＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ， ｎｕｍｅｒｉｃａｌ ｓｉｍｕｌａｔｉｏｎｓ ｗｅｒｅ ｃｏｎｄｕｃｔｅｄ ｕｓｉｎｇ ＭＡＴＬＡＢ ２０１２ａ ｏｎ ａ ＰＣ ｗｉｔｈ ａｎ ｉ５⁃４８０ ｍ， ２．６７ ＧＨｚ ＣＰＵ ａｎｄ Ｗｉｎｄｏｗｓ １０ ｏｐｅｒａｔｉｎｇ ｓｙｓｔｅｍ． ＳＤ⁃ＰＩＯ ｗａｓ ｃｏｍｐａｒｅｄ ｗｉｔｈ ｃｏｎｓｅｎｓｕｓ ｉｔｓｅｌｆ ａｎｄ ｃｏｎｓｅｎｓｕｓ ｗｉｔｈ ｔｗｏ ｏｔｈｅｒ ｏｐｔｉｍｉｚａｔｉｏｎｓ， ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ （ＰＳＯ） ａｎｄ ＰＩＯ． Ｔｈｅ ｒｅｓｕｌｔｓ ｐｒｏｖｅ ｔｈｅ ｅｆｆｅｃｔｉｖｅｎｅｓｓ ｏｆ ＳＤ⁃ＰＩＯ． Ｔｈｅ ｍａｉｎ ｐａｒａｍｅｔｅｒｓ ｉｎ Ｅｑｓ． （ ７ ）， （ ９ ）， ａｎｄ （１８） ａｒｅ ｌｉｓｔｅｄ ｉｎ Ｔａｂｌｅ ２ ｂｅｌｏｗ． Ｔｈｅ ｔｉｍｅ ｓｔｅｐ ｆｏｒ ｔｈｅ ｓｉｍｕｌａｔｉｏｎ ｉｓ Ｔ ＝ ０．０５ ｓ． Ｔａｂｌｅ ２ Ｓｉｍｕｌａｔｉｏｎ ｐａｒａｍｅｔｅｒｓ γ Ｒ Ｔｌａｂｅｌ ／ ｓ Ｔｃｈｇ ／ ｓ ５ ５０ ４ ６ Ｎｉｎｅ ＵＡＶｓ ｗｅｒｅ ｉｎｉｔｉａｌｉｚｅｄ ｗｉｔｈ ｒａｎｄｏｍ ｐｏｓｉｔｉｏｎｓ ｉｎ ａ ３⁃ｄｉｍｅｎｓｉｏｎａｌ ｅｎｖｉｒｏｎｍｅｎｔ ａｓ ｓｈｏｗｎ ｉｎ Ｔａｂｌｅ ３． Ｔａｂｌｅ ３ Ｉｎｉｔｉａｌ ｐｏｓｉｔｉｏｎｓ ｏｆ ９ ＵＡＶｓ ｍ ＵＡＶ ｎｕｍｂｅｒ ｘ ｙ ｚ ＵＡＶ１ ２０．８０４ ３０．９７１ ３０．４７７ ＵＡＶ２ １２．６８５ ３７．６３３ ３１．２５２ ＵＡＶ３ ２２．２６０ ３８．６２２ ２４．６６１ ＵＡＶ４ ０．３１８ ２７．９２９ ９．７０３ ＵＡＶ５ ２１．８５９ １５．８４６ ６．０７６ ＵＡＶ６ １６．９４２ １３．９９９ ６．６４４ ＵＡＶ７ １９．２９３ ２０．７２３ １７．６６２ ＵＡＶ８ ２４．８０６ ２３．０６１ ９．３１７ ＵＡＶ９ ３７．２９８ １２．６８８ ７．８６１ Ｔｈｅｓｅ ｈｅｉｇｈｔｓ， ｔｈｅ ｎｕｍｂｅｒｓ ｏｎ ｔｈｅ ｚ⁃ａｘｉｓ， ａｒｅ ｒｅｌａｔｉｖｅ ｐｏｓｉｔｉｏｎｓ ｃｏｒｒｅｓｐｏｎｄｉｎｇ ｔｏ ｔｈｅ ｈｅｉｇｈｔ ｏｆ ｏｒｉｇｉｎ ｏｆ ｔｈｅ ｃｏｍｍｏｎ ｍｏｖｉｎｇ ｃｏｏｒｄｉｎａｔｅ ｓｙｓｔｅｍ ｉｎ Ｆｉｇ． ２． Ｅａｃｈ ＵＡＶ ｈａｄ ｔｈｅ ｓａｍｅ ｉｎｉｔｉａｌ ｐｏｓｉｔｉｏｎ ｉｎ ｔｈｅ ｆｏｕｒ ｓｉｍｕｌａｔｉｏｎｓ， ｉ． ｅ．， ｃｏｎｓｅｎｓｕｓ， ＰＳＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ， ＰＩＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ， ａｎｄ ＳＤ⁃ＰＩＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ． Ａｓ ｋｎｏｗｎ ｆｒｏｍ Ｓｅｃｔｉｏｎｓ ２ ａｎｄ ３， ｔｈｅ ｐｅｒｆｏｒｍａｎｃｅ ｏｆ ｃｏｎｓｅｎｓｕｓ ｃａｎｎｏｔ ｓａｔｉｓｆｙ ｔｈｅ ｒｅｑｕｉｒｅｍｅｎｔｓ， ｗｈｉｃｈ ｉｓ ｃｌｅａｒｌｙ ｄｉｓｐｌａｙｅｄ ｉｎ Ｆｉｇ． ５． Ｂｅｃａｕｓｅ ｏｆ ｃｏｍｍｕｎｉｃａｔｉｏｎ ｒｅｓｔｒｉｃｔｉｏｎｓ ａｎｄ ｌａｃｋ ｏｆ ｆｏｒｅｃａｓｔｉｎｇ， ａｌｌ ｔｈｅ ＵＡＶｓ ｔｅｎｄ ｔｏ ｄｉｖｅ ｓｈａｒｐｌｙ ａｎｄ ｃｌｉｍｂ ｑｕｉｃｋｌｙ． Ｔｈｉｓ ｃａｕｓｅｓ ｇｒｅａｔ ｏｖｅｒｌｏａｄ ａｔ ｔｈｅ ｔｕｒｎｉｎｇ ｐｏｉｎｔ， ｗｈｉｃｈ ｍａｙ ｄａｍａｇｅ ｔｈｅ ＵＡＶ’ ｓ ｓｔｒｕｃｔｕｒｅ ａｎｄ ｒｅｓｕｌｔ ｉｎ ｄｉｆｆｉｃｕｌｔｉｅｓ ｆｏｒ ｆｌｉｇｈｔ ｃｏｎｔｒｏｌ． Ｔｈｅｉｒ ｒｏｕｔｅｓ ｓｅｅｍ ｔｏ ｔｉｅ ａ ｋｎｏｔ ｗｈｅｎ ｖｉｅｗｅｄ ｆｒｏｍ ｔｈｉｓ ｐｅｒｓｐｅｃｔｉｖｅ， ｈｏｗｅｖｅｒ， ｉｔ ｉｓ ｉｍｐｏｒｔａｎｔ ｔｏ ｃｌａｒｉｆｙ ｔｈｅ ｆａｃｔ ｔｈａｔ ｔｈｅ ｔｒａｊｅｃｔｏｒｉｅｓ ｄｏ ｎｏｔ ｃｒｏｓｓ ａｎｄ ｔｈｅ ＵＡＶｓ ｄｏ ｎｏｔ ｃｒａｓｈ ｉｎ ｔｈｅ ｓｋｙ． Ｆｉｇ．５ Ｔｒａｊｅｃｔｏｒｉｅｓ ｏｆ ９ ＵＡＶｓ ｂｙ ｃｏｎｓｅｎｓｕｓ Ｔｏ ｄｅｍｏｎｓｔｒａｔｅ ｔｈｅ ａｄｖａｎｔａｇｅ ｏｆ ＳＤ⁃ＰＩＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ， ＰＳＯ⁃ ａｎｄ ＰＩＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍｓ ｗｅｒｅ ａｄｏｐｔｅｄ ｔｏ ｃｏｍｐａｒｅ ｔｈｅｉｒ ｐｅｒｆｏｒｍａｎｃｅｓ ｗｉｔｈ ｔｈａｔ ｏｆ ｔｈｅ ｍｏｄｉｆｉｅｄ ａｌｇｏｒｉｔｈｍ． Ｉｎ Ｆｉｇ． ６， ｍｏｓｔ ｔｒａｊｅｃｔｏｒｉｅｓ ａｒｅ ａｐｐａｒｅｎｔｌｙ ｂｅｔｔｅｒ ｔｈａｎ ｔｈｏｓｅ ｉｎ Ｆｉｇ． ５， ａｓ ｔｈｅ ｔｒａｊｅｃｔｏｒｉｅｓ ａｒｅ ｇｅｎｔｌｅ ａｔ ｔｈｅ ｂｅｇｉｎｎｉｎｇ ａｎｄ ｔｕｒｎ ｗｉｔｈｏｕｔ ｄｉｖｉｎｇ ｓｈａｒｐｌｙ． ＵＡＶ３ ，ＵＡＶ５ ， ａｎｄＵＡＶ９ ｓｅｒｖｅ ａｓ ａ ｓｅｔ ｏｆ ｃｏｎｖｉｎｃｉｎｇ ｓｉｍｕｌａｔｉｏｎｓ ｔｈａｔ ｓｕｐｐｏｒｔ ｔｈｅ ｃｏｎｃｌｕｓｉｏｎｓ ａｂｏｖｅ． Ｉｎ Ｆｉｇｓ． ７ ａｎｄ ８， ＰＩＯ ａｎｄ ＳＤ⁃ＰＩＯ ｗｏｒｋ ａｎｄ ｆｕｒｔｈｅｒ ｉｍｐｒｏｖｅ ｔｈｅ ｐｅｒｆｏｒｍａｎｃｅ． Ｉｎ Ｆｉｇ． ７， ｔｈｅ ｏｖｅｒｓｈｏｏｔ ａｌｍｏｓｔ ｄｉｓａｐｐｅａｒｓ， ｂｕｔ ｔｈｅｒｅ ｉｓ ｓｔｉｌｌ ｆｌｕｃｔｕａｔｉｏｎ ｉｎ ｔｈｅ ｔｒａｊｅｃｔｏｒｉｅｓ ｆｒｏｍ ｔｈｉｓ ｐｅｒｓｐｅｃｔｉｖｅ， ｅｓｐｅｃｉａｌｌｙ ｆｏｒ ＵＡＶ３ ，ＵＡＶ４ ， ａｎｄ ＵＡＶ５ ． Ｉｎ Ｆｉｇ． ８， ｔｈｅ ｔｒａｊｅｃｔｏｒｉｅｓ ｂｅｃｏｍｅ ｍｕｃｈ ｓｍｏｏｔｈｅｒ ａｎｄ ｔｈｅ ｏｖｅｒｓｈｏｏｔ ｃａｎ ｂｅ ｉｇｎｏｒｅｄ ｃｏｍｐａｒｅｄ ｗｉｔｈ Ｆｉｇｓ． ５ ｔｏ ７． Ｔｈｉｓ ｉｓ ｒｅｆｌｅｃｔｅｄ ｉｎ ｔｈｅ ｌｏｗｅｓｔ ｐａｒｔｓ ｏｆ ｔｈｅ ｔｒａｊｅｃｔｏｒｉｅｓ ｏｆ ＵＡＶ３ ，ＵＡＶ４ ， ａｎｄ ＵＡＶ５ ． Ｆｉｇ． ６ Ｔｒａｊｅｃｔｏｒｉｅｓ ｏｆ ９ ＵＡＶｓ ｂｙ ＰＳＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ Ｆｉｇ． ７ Ｔｒａｊｅｃｔｏｒｉｅｓ ｏｆ ９ ＵＡＶｓ ｂｙ ＰＩＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ ·５７７· 第 ４ 期 ＺＨＡＮＧ Ｔｉａｎｊｉｅ， ｅｔ ａｌ．：Ａ ｍｏｄｉｆｉｅｄ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ ｆｏｒ ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎｓ ｂａｓｅｄ ｏｎ ｐｉｇｅｏｎ⁃ｉｎｓｐｉｒｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ｗｉｔｈ ａ ｓｌｏｗ ｄｉｖｉｎｇ ｓｔｒａｔｅｇｙ

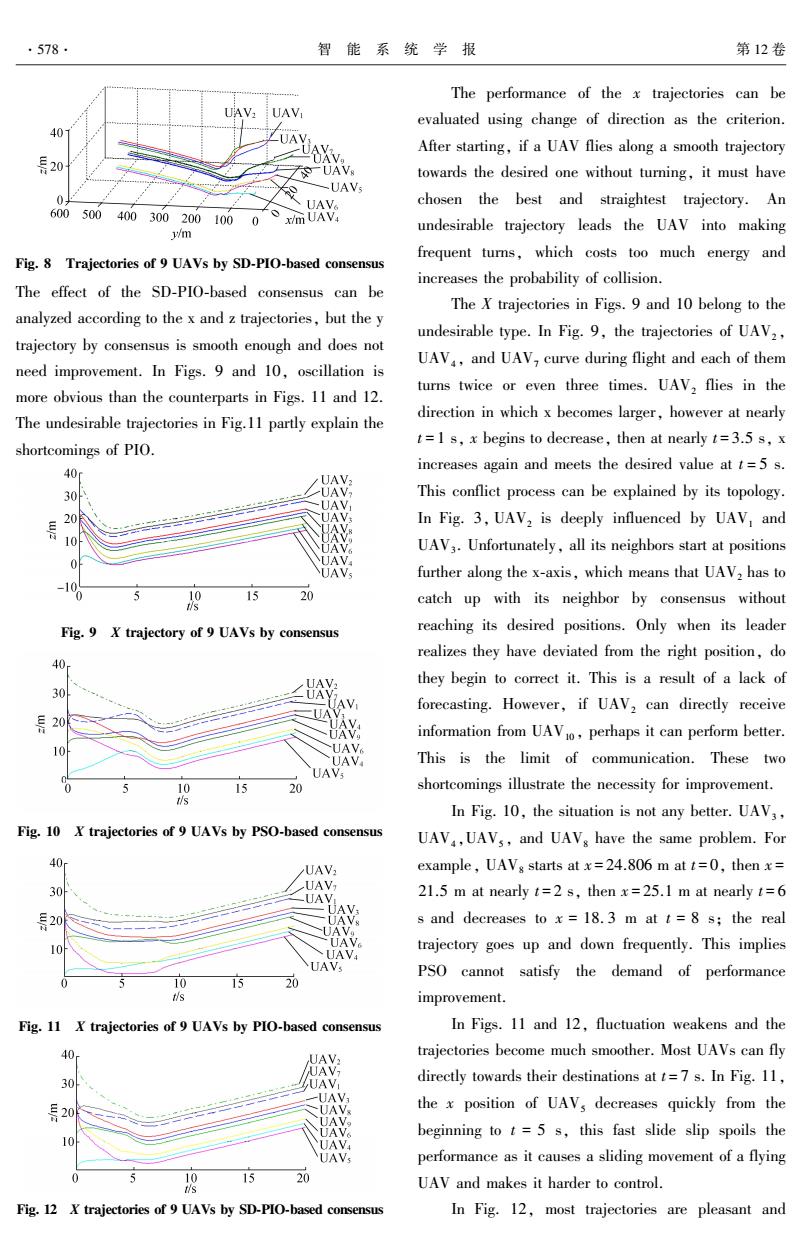
.578. 智能系统学报 第12卷 The performance of the x trajectories can be UAV: UAV evaluated using change of direction as the criterion. -UAV After starting,if a UAV flies along a smooth trajectory 号20 —UAVg towards the desired one without turning,it must have 0月 6005004003002001000⊙mUAV4 UAV chosen the best and straightest trajectory.An y/m undesirable trajectory leads the UAV into making frequent turns,which costs too much energy and Fig.8 Trajectories of 9 UAVs by SD-PIO-based consensus increases the probability of collision. The effect of the SD-PIO-based consensus can be The X trajectories in Figs.9 and 10 belong to the analyzed according to the x and z trajectories,but the y undesirable type.In Fig.9,the trajectories of UAV2, trajectory by consensus is smooth enough and does not UAV,and UAV,curve during flight and each of them need improvement.In Figs.9 and 10,oscillation is turns twice or even three times.UAV,flies in the more obvious than the counterparts in Figs.11 and 12. direction in which x becomes larger,however at nearly The undesirable trajectories in Fig.11 partly explain the t=1 s,x begins to decrease,then at nearly t=3.5 s,x shortcomings of PIO. increases again and meets the desired value at t=5 s. 40 30 This conflict process can be explained by its topology. 30 In Fig.3,UAV,is deeply influenced by UAV,and 10 UAV3.Unfortunately,all its neighbors start at positions further along the x-axis,which means that UAV2 has to -10 15 20 catch up with its neighbor by consensus without Fig.9 X trajectory of 9 UAVs by consensus reaching its desired positions.Only when its leader realizes they have deviated from the right position,do they begin to correct it.This is a result of a lack of 304 forecasting.However,if UAV2 can directly receive 票20 information from UAVo perhaps it can perform better. UAV UAV This is the limit of communication.These two UAV; 10 20 shortcomings illustrate the necessity for improvement. s In Fig.10,the situation is not any better.UAV3, Fig.10 X trajectories of 9 UAVs by PSO-based consensus UAV,UAVs,and UAVs have the same problem.For 40 UAV example,UAVs starts at x=24.806 m at t=0,then x= 30 UAV UAV 21.5 m at nearly t=2 s,then x=25.1 m at nearly t=6 UAV: UAV s and decreases to x =18.3 m at t=8 s;the real UAV UAV trajectory goes up and down frequently.This implies UAV UAV PSO cannot satisfy the demand of performance 1 20 t/s improvement. Fig.11 X trajectories of 9 UAVs by PlO-based consensus In Figs.11 and 12,fluctuation weakens and the 40 trajectories become much smoother.Most UAVs can fly UAV UAV 30 UAV directly towards their destinations at t=7 s.In Fig.11, UAV 层20 -UAV the x position of UAVs decreases quickly from the UAV beginning to t=5 s,this fast slide slip spoils the 10 UAV UAV performance as it causes a sliding movement of a flying 15 20 UAV and makes it harder to control. Fig.12 X trajectories of 9 UAVs by SD-PIO-based consensus In Fig.12,most trajectories are pleasant and

Ｆｉｇ． ８ Ｔｒａｊｅｃｔｏｒｉｅｓ ｏｆ ９ ＵＡＶｓ ｂｙ ＳＤ⁃ＰＩＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ Ｔｈｅ ｅｆｆｅｃｔ ｏｆ ｔｈｅ ＳＤ⁃ＰＩＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ ｃａｎ ｂｅ ａｎａｌｙｚｅｄ ａｃｃｏｒｄｉｎｇ ｔｏ ｔｈｅ ｘ ａｎｄ ｚ ｔｒａｊｅｃｔｏｒｉｅｓ， ｂｕｔ ｔｈｅ ｙ ｔｒａｊｅｃｔｏｒｙ ｂｙ ｃｏｎｓｅｎｓｕｓ ｉｓ ｓｍｏｏｔｈ ｅｎｏｕｇｈ ａｎｄ ｄｏｅｓ ｎｏｔ ｎｅｅｄ ｉｍｐｒｏｖｅｍｅｎｔ． Ｉｎ Ｆｉｇｓ． ９ ａｎｄ １０， ｏｓｃｉｌｌａｔｉｏｎ ｉｓ ｍｏｒｅ ｏｂｖｉｏｕｓ ｔｈａｎ ｔｈｅ ｃｏｕｎｔｅｒｐａｒｔｓ ｉｎ Ｆｉｇｓ． １１ ａｎｄ １２． Ｔｈｅ ｕｎｄｅｓｉｒａｂｌｅ ｔｒａｊｅｃｔｏｒｉｅｓ ｉｎ Ｆｉｇ．１１ ｐａｒｔｌｙ ｅｘｐｌａｉｎ ｔｈｅ ｓｈｏｒｔｃｏｍｉｎｇｓ ｏｆ ＰＩＯ． Ｆｉｇ． ９ Ｘ ｔｒａｊｅｃｔｏｒｙ ｏｆ ９ ＵＡＶｓ ｂｙ ｃｏｎｓｅｎｓｕｓ Ｆｉｇ． １０ Ｘ ｔｒａｊｅｃｔｏｒｉｅｓ ｏｆ ９ ＵＡＶｓ ｂｙ ＰＳＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ Ｆｉｇ． １１ Ｘ ｔｒａｊｅｃｔｏｒｉｅｓ ｏｆ ９ ＵＡＶｓ ｂｙ ＰＩＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ Ｆｉｇ． １２ Ｘ ｔｒａｊｅｃｔｏｒｉｅｓ ｏｆ ９ ＵＡＶｓ ｂｙ ＳＤ⁃ＰＩＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ Ｔｈｅ ｐｅｒｆｏｒｍａｎｃｅ ｏｆ ｔｈｅ ｘ ｔｒａｊｅｃｔｏｒｉｅｓ ｃａｎ ｂｅ ｅｖａｌｕａｔｅｄ ｕｓｉｎｇ ｃｈａｎｇｅ ｏｆ ｄｉｒｅｃｔｉｏｎ ａｓ ｔｈｅ ｃｒｉｔｅｒｉｏｎ． Ａｆｔｅｒ ｓｔａｒｔｉｎｇ， ｉｆ ａ ＵＡＶ ｆｌｉｅｓ ａｌｏｎｇ ａ ｓｍｏｏｔｈ ｔｒａｊｅｃｔｏｒｙ ｔｏｗａｒｄｓ ｔｈｅ ｄｅｓｉｒｅｄ ｏｎｅ ｗｉｔｈｏｕｔ ｔｕｒｎｉｎｇ， ｉｔ ｍｕｓｔ ｈａｖｅ ｃｈｏｓｅｎ ｔｈｅ ｂｅｓｔ ａｎｄ ｓｔｒａｉｇｈｔｅｓｔ ｔｒａｊｅｃｔｏｒｙ． Ａｎ ｕｎｄｅｓｉｒａｂｌｅ ｔｒａｊｅｃｔｏｒｙ ｌｅａｄｓ ｔｈｅ ＵＡＶ ｉｎｔｏ ｍａｋｉｎｇ ｆｒｅｑｕｅｎｔ ｔｕｒｎｓ， ｗｈｉｃｈ ｃｏｓｔｓ ｔｏｏ ｍｕｃｈ ｅｎｅｒｇｙ ａｎｄ ｉｎｃｒｅａｓｅｓ ｔｈｅ ｐｒｏｂａｂｉｌｉｔｙ ｏｆ ｃｏｌｌｉｓｉｏｎ． Ｔｈｅ Ｘ ｔｒａｊｅｃｔｏｒｉｅｓ ｉｎ Ｆｉｇｓ． ９ ａｎｄ １０ ｂｅｌｏｎｇ ｔｏ ｔｈｅ ｕｎｄｅｓｉｒａｂｌｅ ｔｙｐｅ． Ｉｎ Ｆｉｇ． ９， ｔｈｅ ｔｒａｊｅｃｔｏｒｉｅｓ ｏｆ ＵＡＶ２ ， ＵＡＶ４ ， ａｎｄ ＵＡＶ７ ｃｕｒｖｅ ｄｕｒｉｎｇ ｆｌｉｇｈｔ ａｎｄ ｅａｃｈ ｏｆ ｔｈｅｍ ｔｕｒｎｓ ｔｗｉｃｅ ｏｒ ｅｖｅｎ ｔｈｒｅｅ ｔｉｍｅｓ． ＵＡＶ２ ｆｌｉｅｓ ｉｎ ｔｈｅ ｄｉｒｅｃｔｉｏｎ ｉｎ ｗｈｉｃｈ ｘ ｂｅｃｏｍｅｓ ｌａｒｇｅｒ， ｈｏｗｅｖｅｒ ａｔ ｎｅａｒｌｙ ｔ ＝ １ ｓ， ｘ ｂｅｇｉｎｓ ｔｏ ｄｅｃｒｅａｓｅ， ｔｈｅｎ ａｔ ｎｅａｒｌｙ ｔ ＝ ３．５ ｓ， ｘ ｉｎｃｒｅａｓｅｓ ａｇａｉｎ ａｎｄ ｍｅｅｔｓ ｔｈｅ ｄｅｓｉｒｅｄ ｖａｌｕｅ ａｔ ｔ ＝ ５ ｓ． Ｔｈｉｓ ｃｏｎｆｌｉｃｔ ｐｒｏｃｅｓｓ ｃａｎ ｂｅ ｅｘｐｌａｉｎｅｄ ｂｙ ｉｔｓ ｔｏｐｏｌｏｇｙ． Ｉｎ Ｆｉｇ． ３， ＵＡＶ２ ｉｓ ｄｅｅｐｌｙ ｉｎｆｌｕｅｎｃｅｄ ｂｙ ＵＡＶ１ ａｎｄ ＵＡＶ３ ． Ｕｎｆｏｒｔｕｎａｔｅｌｙ， ａｌｌ ｉｔｓ ｎｅｉｇｈｂｏｒｓ ｓｔａｒｔ ａｔ ｐｏｓｉｔｉｏｎｓ ｆｕｒｔｈｅｒ ａｌｏｎｇ ｔｈｅ ｘ⁃ａｘｉｓ， ｗｈｉｃｈ ｍｅａｎｓ ｔｈａｔ ＵＡＶ２ ｈａｓ ｔｏ ｃａｔｃｈ ｕｐ ｗｉｔｈ ｉｔｓ ｎｅｉｇｈｂｏｒ ｂｙ ｃｏｎｓｅｎｓｕｓ ｗｉｔｈｏｕｔ ｒｅａｃｈｉｎｇ ｉｔｓ ｄｅｓｉｒｅｄ ｐｏｓｉｔｉｏｎｓ． Ｏｎｌｙ ｗｈｅｎ ｉｔｓ ｌｅａｄｅｒ ｒｅａｌｉｚｅｓ ｔｈｅｙ ｈａｖｅ ｄｅｖｉａｔｅｄ ｆｒｏｍ ｔｈｅ ｒｉｇｈｔ ｐｏｓｉｔｉｏｎ， ｄｏ ｔｈｅｙ ｂｅｇｉｎ ｔｏ ｃｏｒｒｅｃｔ ｉｔ． Ｔｈｉｓ ｉｓ ａ ｒｅｓｕｌｔ ｏｆ ａ ｌａｃｋ ｏｆ ｆｏｒｅｃａｓｔｉｎｇ． Ｈｏｗｅｖｅｒ， ｉｆ ＵＡＶ２ ｃａｎ ｄｉｒｅｃｔｌｙ ｒｅｃｅｉｖｅ ｉｎｆｏｒｍａｔｉｏｎ ｆｒｏｍ ＵＡＶ１０ ， ｐｅｒｈａｐｓ ｉｔ ｃａｎ ｐｅｒｆｏｒｍ ｂｅｔｔｅｒ． Ｔｈｉｓ ｉｓ ｔｈｅ ｌｉｍｉｔ ｏｆ ｃｏｍｍｕｎｉｃａｔｉｏｎ． Ｔｈｅｓｅ ｔｗｏ ｓｈｏｒｔｃｏｍｉｎｇｓ ｉｌｌｕｓｔｒａｔｅ ｔｈｅ ｎｅｃｅｓｓｉｔｙ ｆｏｒ ｉｍｐｒｏｖｅｍｅｎｔ． Ｉｎ Ｆｉｇ． １０， ｔｈｅ ｓｉｔｕａｔｉｏｎ ｉｓ ｎｏｔ ａｎｙ ｂｅｔｔｅｒ． ＵＡＶ３ ， ＵＡＶ４ ，ＵＡＶ５ ， ａｎｄ ＵＡＶ８ ｈａｖｅ ｔｈｅ ｓａｍｅ ｐｒｏｂｌｅｍ． Ｆｏｒ ｅｘａｍｐｌｅ， ＵＡＶ８ ｓｔａｒｔｓ ａｔ ｘ ＝ ２４．８０６ ｍ ａｔ ｔ ＝ ０， ｔｈｅｎ ｘ ＝ ２１．５ ｍ ａｔ ｎｅａｒｌｙ ｔ ＝ ２ ｓ， ｔｈｅｎ ｘ ＝ ２５．１ ｍ ａｔ ｎｅａｒｌｙ ｔ ＝ ６ ｓ ａｎｄ ｄｅｃｒｅａｓｅｓ ｔｏ ｘ ＝ １８． ３ ｍ ａｔ ｔ ＝ ８ ｓ； ｔｈｅ ｒｅａｌ ｔｒａｊｅｃｔｏｒｙ ｇｏｅｓ ｕｐ ａｎｄ ｄｏｗｎ ｆｒｅｑｕｅｎｔｌｙ． Ｔｈｉｓ ｉｍｐｌｉｅｓ ＰＳＯ ｃａｎｎｏｔ ｓａｔｉｓｆｙ ｔｈｅ ｄｅｍａｎｄ ｏｆ ｐｅｒｆｏｒｍａｎｃｅ ｉｍｐｒｏｖｅｍｅｎｔ． Ｉｎ Ｆｉｇｓ． １１ ａｎｄ １２， ｆｌｕｃｔｕａｔｉｏｎ ｗｅａｋｅｎｓ ａｎｄ ｔｈｅ ｔｒａｊｅｃｔｏｒｉｅｓ ｂｅｃｏｍｅ ｍｕｃｈ ｓｍｏｏｔｈｅｒ． Ｍｏｓｔ ＵＡＶｓ ｃａｎ ｆｌｙ ｄｉｒｅｃｔｌｙ ｔｏｗａｒｄｓ ｔｈｅｉｒ ｄｅｓｔｉｎａｔｉｏｎｓ ａｔ ｔ ＝ ７ ｓ． Ｉｎ Ｆｉｇ． １１， ｔｈｅ ｘ ｐｏｓｉｔｉｏｎ ｏｆ ＵＡＶ５ ｄｅｃｒｅａｓｅｓ ｑｕｉｃｋｌｙ ｆｒｏｍ ｔｈｅ ｂｅｇｉｎｎｉｎｇ ｔｏ ｔ ＝ ５ ｓ， ｔｈｉｓ ｆａｓｔ ｓｌｉｄｅ ｓｌｉｐ ｓｐｏｉｌｓ ｔｈｅ ｐｅｒｆｏｒｍａｎｃｅ ａｓ ｉｔ ｃａｕｓｅｓ ａ ｓｌｉｄｉｎｇ ｍｏｖｅｍｅｎｔ ｏｆ ａ ｆｌｙｉｎｇ ＵＡＶ ａｎｄ ｍａｋｅｓ ｉｔ ｈａｒｄｅｒ ｔｏ ｃｏｎｔｒｏｌ． Ｉｎ Ｆｉｇ． １２， ｍｏｓｔ ｔｒａｊｅｃｔｏｒｉｅｓ ａｒｅ ｐｌｅａｓａｎｔ ａｎｄ ·５７８· 智 能 系 统 学 报 第 １２ 卷

第4期 ZHANG Tianjie,et al.:A modified consensus algorithm for multi-UAV formations based on pigeon-inspired optimization with a slow diving strategy ·579 suitable as commands for multi-UAV formations. the designed trajectory. Performance of the z trajectories can be evaluated 40m UAV by the following criterion:diving slowly and never 30外 UAV;UAV: flying up and down.In Fig.13,all the trajectories 20 UAV quickly go down before t=4 s,this means that the 10UAV,UAV.UAV,UAV, UAVs dive sharply in the beginning,as shown in Fig. UAV o 1520 5.The aim of this work is to overcome this shortcoming. Fig.15 Z trajectories of 9 UAVs by PIO-based consensus The trajectories in Fig.14 clarify the advantage of 40 PSO-based consensus because the modified algorithm UAV can effectively reduce oscillation.UAV,and UAVs 20 AV? clarify UAVs this view as they both slowly decrease I0 AV.DAKV UAV their height following the desired trajectory instead of UAV 0 10 1520 diving down swiftly. 修 40- Fig.16 Z trajectories of 9 UAVs by SD-PIO-based consensus 30 UAV The SD-PIO-based consensus algorithm also -UAV 号20 follows the steps above,but the difference occurs in -UAV UAV the first 8 s as the UAVs descend more slowly and 10 smoothly.UAV,UAV2 and UAV3 can support this A UAV, 0 10 15 20 opinion,as they at the same respective height,but at ti t=5 s,UAV2 and UAV3 by SD-PIO are above 20 m Fig.13 Z trajectories of 9 UAVs by consensus while their counterparts are clearly lower.At t=7 s, 40 the height of UAV,by SD-PIO is 16.04 m and the outcome by PIO is only 15.47 m. 30 UAV From the fitness function Eg.(8),the closer the 2 -UAV:UAV UA UAV UAV;approaches its desired location,the smaller the AV 10 一UAV。UAV, fitness value.In Fig.17,as iteration Nc increases, UAV average fitness values decrease and finally approach 0 5 10 15 20 tis zero,and different optimizers possess different convergence rates.In Fig.17(a),PIO shows the Fig.14 Z trajectories of 9 UAVs by PSO-based consensus fastest speed in the beginning,SD-PIO is a bit slower However,reduplicative climb and dive still exist, and PSO shows the weakest performance of the three. which may induce oscillation.The dangerous However,after Ne 80,PIO becomes slow and is trajectories of UAV3 and UAVs at UAVst [0,10]s finally overtaken by SD-PIO at Ne 93.The poor efficiency of PIO is due to the inadequate local in Fig.14 reveal that they are not the desired ones that optimum. descend slowly at the beginning,then converge to the 12 desired trajectory.This is why there is great demand for -SDPIP 10 ·PIO another optimizer. oPSO In Fig.15,PIO is used to apply a gliding procedure.Before 4s,the map and compass operator takes effect and all the UAVs fly towards the best local position.In the time range,4 to 6 s,the landmark operator drives the UAVs nearby to the same height. When all of them fly to the standard height,the PIO 100 200300400 500 part stops working and consensus continues Nc concentrating the UAVs and guiding them to fly along (a)fitness value

ｓｕｉｔａｂｌｅ ａｓ ｃｏｍｍａｎｄｓ ｆｏｒ ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎｓ． Ｐｅｒｆｏｒｍａｎｃｅ ｏｆ ｔｈｅ ｚ ｔｒａｊｅｃｔｏｒｉｅｓ ｃａｎ ｂｅ ｅｖａｌｕａｔｅｄ ｂｙ ｔｈｅ ｆｏｌｌｏｗｉｎｇ ｃｒｉｔｅｒｉｏｎ： ｄｉｖｉｎｇ ｓｌｏｗｌｙ ａｎｄ ｎｅｖｅｒ ｆｌｙｉｎｇ ｕｐ ａｎｄ ｄｏｗｎ． Ｉｎ Ｆｉｇ． １３， ａｌｌ ｔｈｅ ｔｒａｊｅｃｔｏｒｉｅｓ ｑｕｉｃｋｌｙ ｇｏ ｄｏｗｎ ｂｅｆｏｒｅ ｔ ＝ ４ ｓ， ｔｈｉｓ ｍｅａｎｓ ｔｈａｔ ｔｈｅ ＵＡＶｓ ｄｉｖｅ ｓｈａｒｐｌｙ ｉｎ ｔｈｅ ｂｅｇｉｎｎｉｎｇ， ａｓ ｓｈｏｗｎ ｉｎ Ｆｉｇ． ５． Ｔｈｅ ａｉｍ ｏｆ ｔｈｉｓ ｗｏｒｋ ｉｓ ｔｏ ｏｖｅｒｃｏｍｅ ｔｈｉｓ ｓｈｏｒｔｃｏｍｉｎｇ． Ｔｈｅ ｔｒａｊｅｃｔｏｒｉｅｓ ｉｎ Ｆｉｇ． １４ ｃｌａｒｉｆｙ ｔｈｅ ａｄｖａｎｔａｇｅ ｏｆ ＰＳＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ ｂｅｃａｕｓｅ ｔｈｅ ｍｏｄｉｆｉｅｄ ａｌｇｏｒｉｔｈｍ ｃａｎ ｅｆｆｅｃｔｉｖｅｌｙ ｒｅｄｕｃｅ ｏｓｃｉｌｌａｔｉｏｎ． ＵＡＶ２ ａｎｄ ＵＡＶ８ ｃｌａｒｉｆｙ ＵＡＶ８ ｔｈｉｓ ｖｉｅｗ ａｓ ｔｈｅｙ ｂｏｔｈ ｓｌｏｗｌｙ ｄｅｃｒｅａｓｅ ｔｈｅｉｒ ｈｅｉｇｈｔ ｆｏｌｌｏｗｉｎｇ ｔｈｅ ｄｅｓｉｒｅｄ ｔｒａｊｅｃｔｏｒｙ ｉｎｓｔｅａｄ ｏｆ ｄｉｖｉｎｇ ｄｏｗｎ ｓｗｉｆｔｌｙ． Ｆｉｇ． １３ Ｚ ｔｒａｊｅｃｔｏｒｉｅｓ ｏｆ ９ ＵＡＶｓ ｂｙ ｃｏｎｓｅｎｓｕｓ Ｆｉｇ． １４ Ｚ ｔｒａｊｅｃｔｏｒｉｅｓ ｏｆ ９ ＵＡＶｓ ｂｙ ＰＳＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ Ｈｏｗｅｖｅｒ， ｒｅｄｕｐｌｉｃａｔｉｖｅ ｃｌｉｍｂ ａｎｄ ｄｉｖｅ ｓｔｉｌｌ ｅｘｉｓｔ， ｗｈｉｃｈ ｍａｙ ｉｎｄｕｃｅ ｏｓｃｉｌｌａｔｉｏｎ． Ｔｈｅ ｄａｎｇｅｒｏｕｓ ｔｒａｊｅｃｔｏｒｉｅｓ ｏｆ ＵＡＶ３ ａｎｄ ＵＡＶ５ ａｔ ＵＡＶ５ ｔ∈［０， １０］ ｓ ｉｎ Ｆｉｇ．１４ ｒｅｖｅａｌ ｔｈａｔ ｔｈｅｙ ａｒｅ ｎｏｔ ｔｈｅ ｄｅｓｉｒｅｄ ｏｎｅｓ ｔｈａｔ ｄｅｓｃｅｎｄ ｓｌｏｗｌｙ ａｔ ｔｈｅ ｂｅｇｉｎｎｉｎｇ， ｔｈｅｎ ｃｏｎｖｅｒｇｅ ｔｏ ｔｈｅ ｄｅｓｉｒｅｄ ｔｒａｊｅｃｔｏｒｙ． Ｔｈｉｓ ｉｓ ｗｈｙ ｔｈｅｒｅ ｉｓ ｇｒｅａｔ ｄｅｍａｎｄ ｆｏｒ ａｎｏｔｈｅｒ ｏｐｔｉｍｉｚｅｒ． Ｉｎ Ｆｉｇ． １５， ＰＩＯ ｉｓ ｕｓｅｄ ｔｏ ａｐｐｌｙ ａ ｇｌｉｄｉｎｇ ｐｒｏｃｅｄｕｒｅ． Ｂｅｆｏｒｅ ４ｓ， ｔｈｅ ｍａｐ ａｎｄ ｃｏｍｐａｓｓ ｏｐｅｒａｔｏｒ ｔａｋｅｓ ｅｆｆｅｃｔ ａｎｄ ａｌｌ ｔｈｅ ＵＡＶｓ ｆｌｙ ｔｏｗａｒｄｓ ｔｈｅ ｂｅｓｔ ｌｏｃａｌ ｐｏｓｉｔｉｏｎ． Ｉｎ ｔｈｅ ｔｉｍｅ ｒａｎｇｅ， ４ ｔｏ ６ ｓ， ｔｈｅ ｌａｎｄｍａｒｋ ｏｐｅｒａｔｏｒ ｄｒｉｖｅｓ ｔｈｅ ＵＡＶｓ ｎｅａｒｂｙ ｔｏ ｔｈｅ ｓａｍｅ ｈｅｉｇｈｔ． Ｗｈｅｎ ａｌｌ ｏｆ ｔｈｅｍ ｆｌｙ ｔｏ ｔｈｅ ｓｔａｎｄａｒｄ ｈｅｉｇｈｔ， ｔｈｅ ＰＩＯ ｐａｒｔ ｓｔｏｐｓ ｗｏｒｋｉｎｇ ａｎｄ ｃｏｎｓｅｎｓｕｓ ｃｏｎｔｉｎｕｅｓ ｃｏｎｃｅｎｔｒａｔｉｎｇ ｔｈｅ ＵＡＶｓ ａｎｄ ｇｕｉｄｉｎｇ ｔｈｅｍ ｔｏ ｆｌｙ ａｌｏｎｇ ｔｈｅ ｄｅｓｉｇｎｅｄ ｔｒａｊｅｃｔｏｒｙ． Ｆｉｇ． １５ Ｚ ｔｒａｊｅｃｔｏｒｉｅｓ ｏｆ ９ ＵＡＶｓ ｂｙ ＰＩＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ Ｆｉｇ． １６ Ｚ ｔｒａｊｅｃｔｏｒｉｅｓ ｏｆ ９ ＵＡＶｓ ｂｙ ＳＤ⁃ＰＩＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ Ｔｈｅ ＳＤ⁃ＰＩＯ⁃ｂａｓｅｄ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ ａｌｓｏ ｆｏｌｌｏｗｓ ｔｈｅ ｓｔｅｐｓ ａｂｏｖｅ， ｂｕｔ ｔｈｅ ｄｉｆｆｅｒｅｎｃｅ ｏｃｃｕｒｓ ｉｎ ｔｈｅ ｆｉｒｓｔ ８ ｓ ａｓ ｔｈｅ ＵＡＶｓ ｄｅｓｃｅｎｄ ｍｏｒｅ ｓｌｏｗｌｙ ａｎｄ ｓｍｏｏｔｈｌｙ． ＵＡＶ１ ， ＵＡＶ２ ａｎｄ ＵＡＶ３ ｃａｎ ｓｕｐｐｏｒｔ ｔｈｉｓ ｏｐｉｎｉｏｎ， ａｓ ｔｈｅｙ ａｔ ｔｈｅ ｓａｍｅ ｒｅｓｐｅｃｔｉｖｅ ｈｅｉｇｈｔ， ｂｕｔ ａｔ ｔ ＝ ５ ｓ，ＵＡＶ２ ａｎｄ ＵＡＶ３ ｂｙ ＳＤ⁃ＰＩＯ ａｒｅ ａｂｏｖｅ ２０ ｍ ｗｈｉｌｅ ｔｈｅｉｒ ｃｏｕｎｔｅｒｐａｒｔｓ ａｒｅ ｃｌｅａｒｌｙ ｌｏｗｅｒ． Ａｔ ｔ ＝ ７ ｓ， ｔｈｅ ｈｅｉｇｈｔ ｏｆ ＵＡＶ１ ｂｙ ＳＤ⁃ＰＩＯ ｉｓ １６． ０４ ｍ ａｎｄ ｔｈｅ ｏｕｔｃｏｍｅ ｂｙ ＰＩＯ ｉｓ ｏｎｌｙ １５．４７ ｍ． Ｆｒｏｍ ｔｈｅ ｆｉｔｎｅｓｓ ｆｕｎｃｔｉｏｎ Ｅｑ． （８）， ｔｈｅ ｃｌｏｓｅｒ ｔｈｅ ＵＡＶｉ ａｐｐｒｏａｃｈｅｓ ｉｔｓ ｄｅｓｉｒｅｄ ｌｏｃａｔｉｏｎ， ｔｈｅ ｓｍａｌｌｅｒ ｔｈｅ ｆｉｔｎｅｓｓ ｖａｌｕｅ． Ｉｎ Ｆｉｇ． １７， ａｓ ｉｔｅｒａｔｉｏｎ Ｎｃ ｉｎｃｒｅａｓｅｓ， ａｖｅｒａｇｅ ｆｉｔｎｅｓｓ ｖａｌｕｅｓ ｄｅｃｒｅａｓｅ ａｎｄ ｆｉｎａｌｌｙ ａｐｐｒｏａｃｈ ｚｅｒｏ， ａｎｄ ｄｉｆｆｅｒｅｎｔ ｏｐｔｉｍｉｚｅｒｓ ｐｏｓｓｅｓｓ ｄｉｆｆｅｒｅｎｔ ｃｏｎｖｅｒｇｅｎｃｅ ｒａｔｅｓ． Ｉｎ Ｆｉｇ． １７ （ ａ ）， ＰＩＯ ｓｈｏｗｓ ｔｈｅ ｆａｓｔｅｓｔ ｓｐｅｅｄ ｉｎ ｔｈｅ ｂｅｇｉｎｎｉｎｇ， ＳＤ⁃ＰＩＯ ｉｓ ａ ｂｉｔ ｓｌｏｗｅｒ ａｎｄ ＰＳＯ ｓｈｏｗｓ ｔｈｅ ｗｅａｋｅｓｔ ｐｅｒｆｏｒｍａｎｃｅ ｏｆ ｔｈｅ ｔｈｒｅｅ． Ｈｏｗｅｖｅｒ， ａｆｔｅｒ Ｎｃ ＝ ８０， ＰＩＯ ｂｅｃｏｍｅｓ ｓｌｏｗ ａｎｄ ｉｓ ｆｉｎａｌｌｙ ｏｖｅｒｔａｋｅｎ ｂｙ ＳＤ⁃ＰＩＯ ａｔ Ｎｃ ＝ ９３． Ｔｈｅ ｐｏｏｒ ｅｆｆｉｃｉｅｎｃｙ ｏｆ ＰＩＯ ｉｓ ｄｕｅ ｔｏ ｔｈｅ ｉｎａｄｅｑｕａｔｅ ｌｏｃａｌ ｏｐｔｉｍｕｍ． （ａ）Ｘ ｆｉｔｎｅｓｓ ｖａｌｕｅ ·５７９· 第 ４ 期 ＺＨＡＮＧ Ｔｉａｎｊｉｅ， ｅｔ ａｌ．：Ａ ｍｏｄｉｆｉｅｄ ｃｏｎｓｅｎｓｕｓ ａｌｇｏｒｉｔｈｍ ｆｏｒ ｍｕｌｔｉ⁃ＵＡＶ ｆｏｒｍａｔｉｏｎｓ ｂａｓｅｄ ｏｎ ｐｉｇｅｏｎ⁃ｉｎｓｐｉｒｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ｗｉｔｈ ａ ｓｌｏｗ ｄｉｖｉｎｇ ｓｔｒａｔｅｇｙ