
1956 03 基于字典学习和稀疏表示的全数据 02 01 驱动AVO反演方法 IDEA LEARNING CREATIVE INSPIRATION
基于字典学习和稀疏表示的全数据 驱动AVO反演方法

目录 CONTENT 1 地震反演基本原理 4 参数选择及鲁棒性分析 2 字典学习基本原理 5 实例应用及结果 3 传统反演方法与字典学习 6 总结和拓展
目录 CONTENT 1 地震反演基本原理 2 3 传统反演方法与字典学习 5 实例应用及结果 6 总结和拓展 4 参数选择及鲁棒性分析 字典学习基本原理

数理模型 1 图像SR 地震反演基本原理 褶积模型 THE BASIC PRINCIPLES OF SEISMIC INVERSION PROBLEM 反演类型 存在的问题及解 决思路
1 地震反演基本原理 THE BASIC PRINCIPLES OF SEISMIC INVERSION PROBLEM 数理模型 图像SR 褶积模型 反演类型 存在的问题及解 决思路

的 反演原理一 数理模型 已知A、X,求y → 正问题 y= Ax 已知A、y,求x → 反问题
反演原理 — 数理模型 y = Ax 已知A、x,求y 已知A、y,求x 正问题 反问题

反演原理一 数理模型 minJ(x)=llymx:1-Amxn×nx1陉 m=n,且A可逆 m<n m n 有唯一解 无穷解(最小范数解) 无解(最小二乘解) x=A-1y x=AT(AAT)-1y x=(ATA)-1ATy
𝒎𝒎𝒎𝒎𝒎𝒎 𝑱𝑱(𝒙𝒙) = 𝒚𝒚𝒎𝒎×𝟏𝟏 − 𝑨𝑨𝒎𝒎×𝒏𝒏 × 𝒙𝒙𝒏𝒏×𝟏𝟏 𝟐𝟐 𝟐𝟐 𝑚𝑚 = 𝑛𝑛,且𝐴𝐴可逆 𝑚𝑚 𝑛𝑛 有唯一解 无穷解(最小范数解) 无解(最小二乘解) 𝒙𝒙 = 𝑨𝑨−𝟏𝟏𝒚𝒚 𝒙𝒙 = 𝑨𝑨𝑻𝑻(𝑨𝑨𝑨𝑨𝑻𝑻)−𝟏𝟏𝒚𝒚 𝒙𝒙 = (𝑨𝑨𝑻𝑻𝑨𝑨)−𝟏𝟏𝑨𝑨𝑻𝑻𝒚𝒚 反演原理 — 数理模型

反演原理一图像SR Y:LR image X HR image → Y DHX +n H:blurring filter D:down-sampling operator n:additive noise
𝒀𝒀 = 𝑫𝑫𝑫𝑫𝑫𝑫 + 𝒏𝒏 Y : LR image X : HR image 𝑯𝑯 ∶ 𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏 𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓𝑓 𝑫𝑫 ∶ 𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 − 𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 𝒏𝒏 ∶ 𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎 𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛 反演原理 — 图像SR

反演原理一 褶积模型 S(t)= w(t)r(t)+n(t) 4 三 * 250 2 S- WR+N 50 0.3 1500 0.2 200 二 X 2500 200 -Q2 0.05 000 3000 50 100 150200 250 100150200250300 50 100150200250300 350 CMP CMP
𝒔𝒔(𝒕𝒕) = 𝒘𝒘(𝒕𝒕) ∗ 𝒓𝒓(𝒕𝒕) + 𝒏𝒏(𝒕𝒕) 0 50 100 150 200 250 300 Time(ms) -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 Amplitude 0 20 40 60 80 100 Time(ms) -0.2 0 0.2 0.4 0.6 0.8 1 Amplitude 0 0.05 0.1 0.15 0.2 0.25 0.3 Time(ms) -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 = * Amplitude 𝑺𝑺 = 𝑾𝑾𝑾𝑾 + 𝑵𝑵 (a) 50 100 150 200 250 300 350 CMP 1000 1500 2000 2500 3000 Time(ms) -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 (b) 50 100 150 200 250 300 50 100 150 200 250 300 0 0.2 0.4 0.6 0.8 1 (c) 50 100 150 200 250 300 350 CMP 1000 1500 2000 2500 3000 Time(ms) -0.05 0 0.05 0.1 = × 反演原理 — 褶积模型

反演原理一 反演类型 纵波速度 叠前反演 横波速度 (Zoeppritz方程 密度 地震反演 叠后反演 波阻抗
地震反演 叠后反演 波阻抗 纵波速度 横波速度 密度 叠前反演 (Zoeppritz方程) 反演原理 — 反演类型
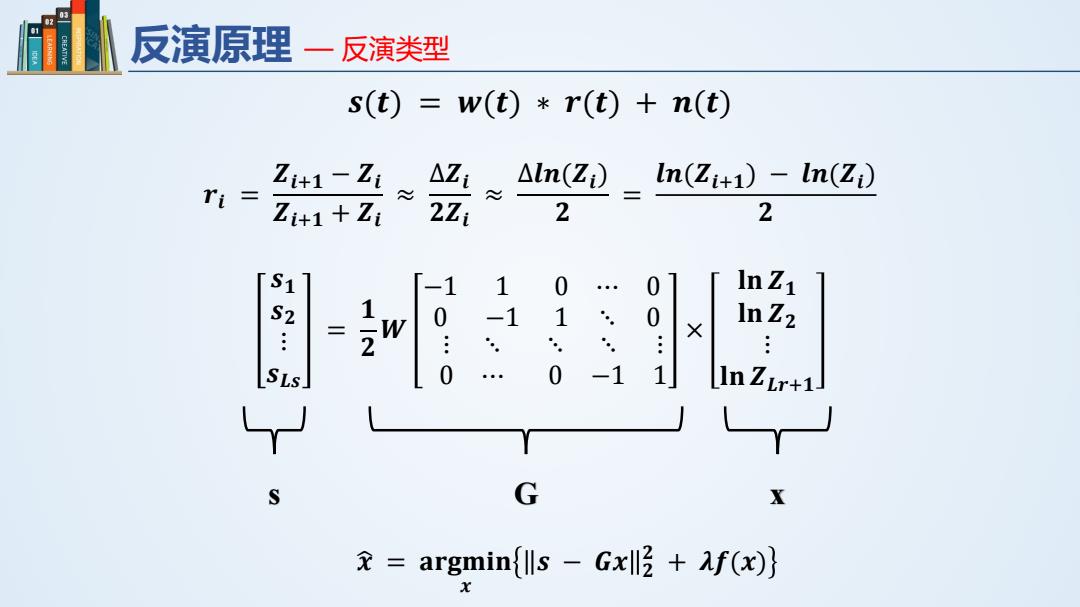
反演原理一 反演类型 s(t)=w(t)r(t)+n(t) Z41-Zi △Zi △ln(Zi) In(Zi+1)-In(Zi) Zi+1+Zi 2Zi 2 2 1 0 InZ1 70:0 -1 1 8 In Z2 SLs 0 二1 1 In ZLr+1- S G X =argminlls -Gxll af(x)}
𝒔𝒔(𝒕𝒕) = 𝒘𝒘(𝒕𝒕) ∗ 𝒓𝒓(𝒕𝒕) + 𝒏𝒏(𝒕𝒕) 𝒓𝒓𝒊𝒊 = 𝒁𝒁𝒊𝒊+𝟏𝟏 − 𝒁𝒁𝒊𝒊 𝒁𝒁𝒊𝒊+𝟏𝟏 + 𝒁𝒁𝒊𝒊 ≈ ∆𝒁𝒁𝒊𝒊 𝟐𝟐𝒁𝒁𝒊𝒊 ≈ ∆𝒍𝒍𝒍𝒍(𝒁𝒁𝒊𝒊) 𝟐𝟐 = 𝒍𝒍𝒍𝒍(𝒁𝒁𝒊𝒊+𝟏𝟏) − 𝒍𝒍𝒍𝒍(𝒁𝒁𝒊𝒊) 𝟐𝟐 𝒔𝒔𝟏𝟏 𝒔𝒔𝟐𝟐 ⋮ 𝒔𝒔𝑳𝑳𝑳𝑳 = 𝟏𝟏 𝟐𝟐 𝑾𝑾 −1 1 0 −1 0 ⋯ 0 1 ⋱ 0 ⋮ ⋱ 0 ⋯ ⋱ ⋱ ⋮ 0 −1 1 × 𝐥𝐥𝐥𝐥 𝒁𝒁𝟏𝟏 𝐥𝐥𝐥𝐥 𝒁𝒁𝟐𝟐 ⋮ 𝐥𝐥𝐥𝐥 𝒁𝒁𝑳𝑳𝑳𝑳+𝟏𝟏 s G x 𝒙𝒙 � = 𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚 𝒙𝒙 𝒔𝒔 − 𝑮𝑮𝑮𝑮 𝟐𝟐 𝟐𝟐 + 𝝀𝝀𝒇𝒇(𝒙𝒙) 反演原理 — 反演类型

反演原理一 反演存在的问题 由于地震数据频率的带限特征和噪声的存在,地震反演问题反演的适定性问 题受到很大挑战: >较小的观测数据误差或噪声便可带来反演结果非的较大误差(不稳定性) >同时,会存在多个能同样好地吻合该观测数据的解(不唯一性)。 因此,为了稳定求解过程和避免产生无效解,学者们提出了一系列基于先验 知识约束的正则化方法。这类方法通常用于促使反演结果表现出某些期望的 特性,比如:光滑性和块状性。 =argminls -Gxll+ 元=argmin{lls-Gxl陉+2L2xl陉} TV:block TK:smooth
𝒙𝒙 � = 𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚 𝒙𝒙 𝒔𝒔 − 𝑮𝑮𝑮𝑮 𝟐𝟐 𝟐𝟐 + 𝝀𝝀 𝑳𝑳𝟏𝟏𝒙𝒙 𝟏𝟏 TV : block 𝒙𝒙 � = 𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚 𝒙𝒙 𝒔𝒔 − 𝑮𝑮𝑮𝑮 𝟐𝟐 𝟐𝟐 + 𝝀𝝀 𝑳𝑳𝟐𝟐𝒙𝒙 𝟐𝟐 𝟐𝟐 TK : smooth 反演原理 — 反演存在的问题 由于地震数据频率的带限特征和噪声的存在,地震反演问题反演的适定性问 题受到很大挑战: 较小的观测数据误差或噪声便可带来反演结果非的较大误差(不稳定性); 同时,会存在多个能同样好地吻合该观测数据的解(不唯一性)。 因此,为了稳定求解过程和避免产生无效解,学者们提出了一系列基于先验 知识约束的正则化方法。这类方法通常用于促使反演结果表现出某些期望的 特性,比如:光滑性和块状性