
第四章晶向、晶面等概念 4.1原子坐标 4.2晶面及晶面指数 4.3晶向及晶向指数 4.4倒易点阵 4.5晶面间距、晶面夹角及晶带 4.6晶体的极射赤面投影表示 4.7晶体的定向方法
1 第四章 晶向、晶面等概念 4.1 原子坐标 4.2 晶面及晶面指数 4.3 晶向及晶向指数 4.4 倒易点阵 4.5 晶面间距、晶面夹角及晶带 4.6 晶体的极射赤面投影表示 4.7 晶体的定向方法

4.1原子坐标(三维) 晶体的结构具有周期性和对称性,描述晶体中微粒的相 对位置时,若使用普遍采用的三维直角坐标系直接描述每一 个粒子的坐标位置的话,十分不便。 这样需要结合晶体的点阵周期性,重新建立一套很方便 就可以描述晶体内部各粒子的位置的方法。 晶胞是基于“三原侧”选出的能够较好的反映晶体周期 性和对称性的最小单元,若描述了晶胞内的每一个粒子的坐 标位置,就知道了整个晶体内的粒子相对位置。 借助晶胞的三条棱向量建立一套坐标系,并借此描述晶 胞内部的每一个粒子的坐标位置(原子坐标)
2 4.1 原子坐标(三维) 晶体的结构具有周期性和对称性,描述晶体中微粒的相 对位置时,若使用普遍采用的三维直角坐标系直接描述每一 个粒子的坐标位置的话,十分不便。 这样需要结合晶体的点阵周期性,重新建立一套很方便 就可以描述晶体内部各粒子的位置的方法。 晶胞是基于“三原则”选出的能够较好的反映晶体周期 性和对称性的最小单元,若描述了晶胞内的每一个粒子的坐 标位置,就知道了整个晶体内的粒子相对位置。 借助晶胞的三条棱向量建立一套坐标系,并借此描述晶 胞内部的每一个粒子的坐标位置(原子坐标)
4.1原子坐标(三维) (1)取晶胞参数a、b、c的方向为 三维坐标系坐标轴的方向,满 足右手系; (2)以晶胞参数a、b、c的长度 为三个方向的长度单位1: X (3)一般将原点选在晶胞顶点上; (4)如此建立了O-XYZ的晶体坐标系;abc称作晶体坐标晶轴。 0sX<1 (5)当 0sy<1 时,取其原子坐标为:(xy) 0sz<1 (6)具有或b或向量平移关系的质点具有相同的原子坐标** 以上讨论均是在晶胞中讨论,晶体中的原子坐标如何?
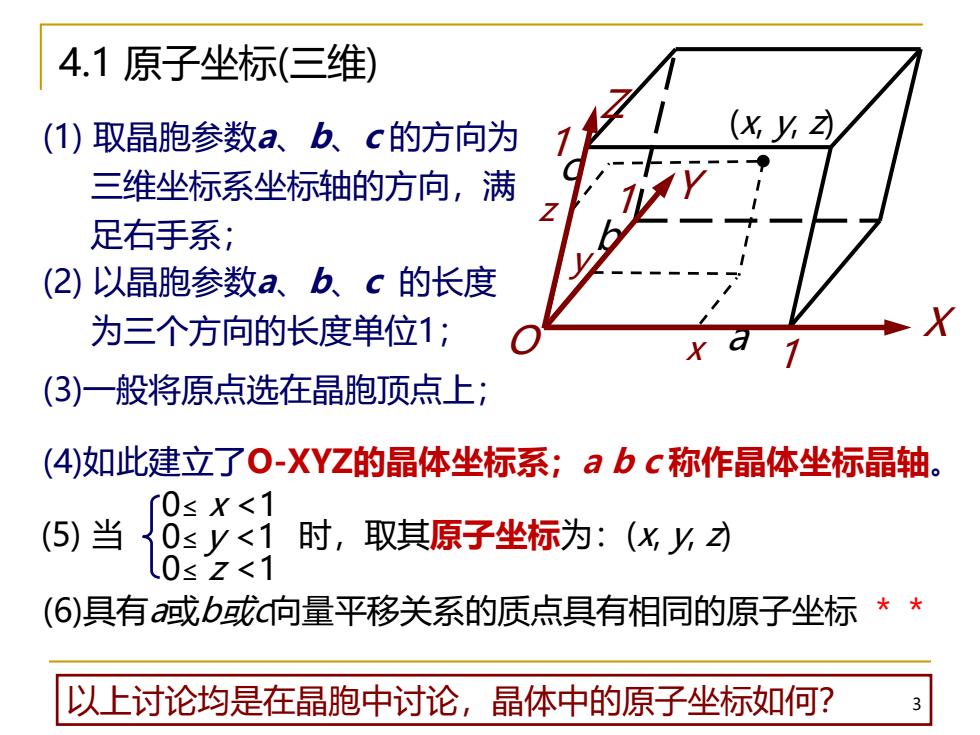
3 (3)一般将原点选在晶胞顶点上; 4.1 原子坐标(三维) a b c 1 1 1 x z y X Y Z O (x, y, z) (5) 当 0≤ y <1 时,取其原子坐标为:(x, y, z) 0≤ z <1 0≤ x <1 (6)具有a或b或c向量平移关系的质点具有相同的原子坐标 ** (1) 取晶胞参数a、b、c 的方向为 三维坐标系坐标轴的方向,满 足右手系; (2) 以晶胞参数a、b、c 的长度 为三个方向的长度单位1; (4)如此建立了O-XYZ的晶体坐标系;a b c 称作晶体坐标晶轴。 以上讨论均是在晶胞中讨论,晶体中的原子坐标如何?
4.1整个晶体中的原子坐标 (x,y 2 (x y 2 (x y 2) 一个晶胞中具有某个原子坐标的原子,整个晶体中与 之对称的原子也具有该原子坐标。 晶体中具有相同原子坐标的原子,满足晶胞棱向量a或 b或c向量平移的位置关系
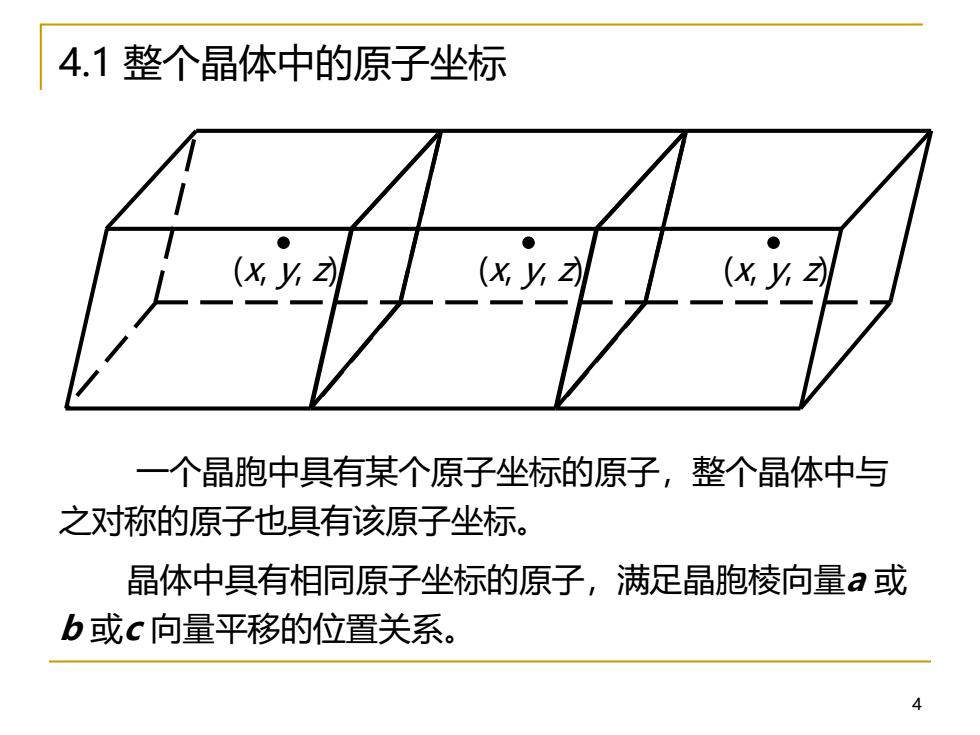
4 4.1 整个晶体中的原子坐标 (x, y, z) (x, y, z) (x, y, z) 一个晶胞中具有某个原子坐标的原子,整个晶体中与 之对称的原子也具有该原子坐标。 晶体中具有相同原子坐标的原子,满足晶胞棱向量a 或 b 或c 向量平移的位置关系
具有体心立方格子的晶胞 原子坐标Q.00)兮7之 (1/2.1/2.1/2) 5
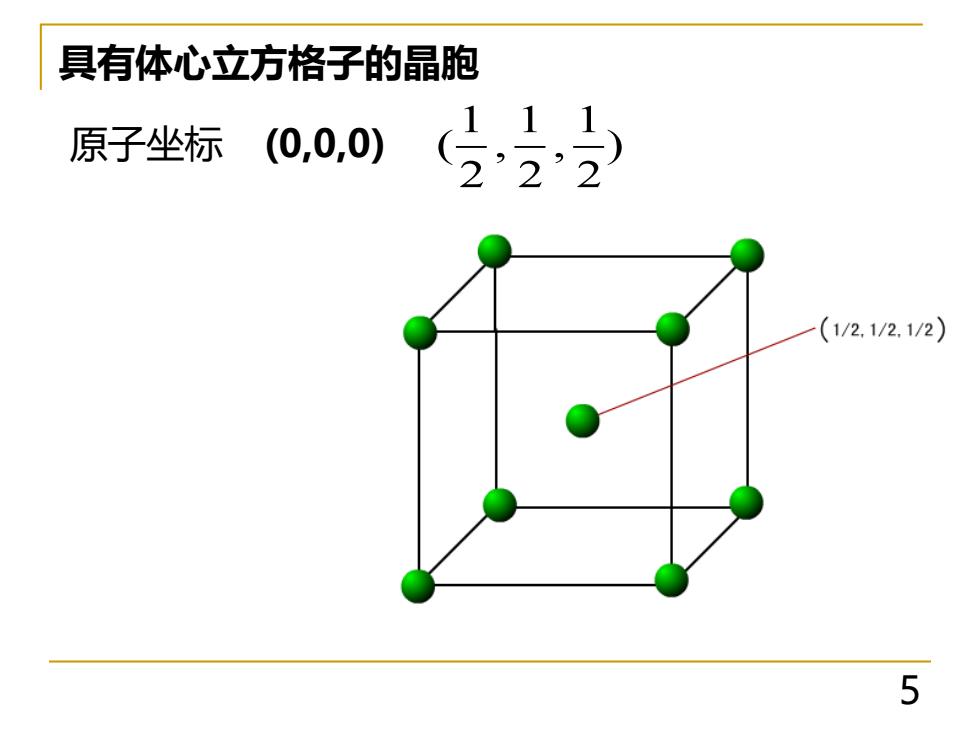
5 具有体心立方格子的晶胞 111 ( , , ) 222 原子坐标 (0,0,0)
具有面心立方格子的晶胞,原子坐标: 00,0)o,2·20.2)2·20) (1/2.1/2.0) 6
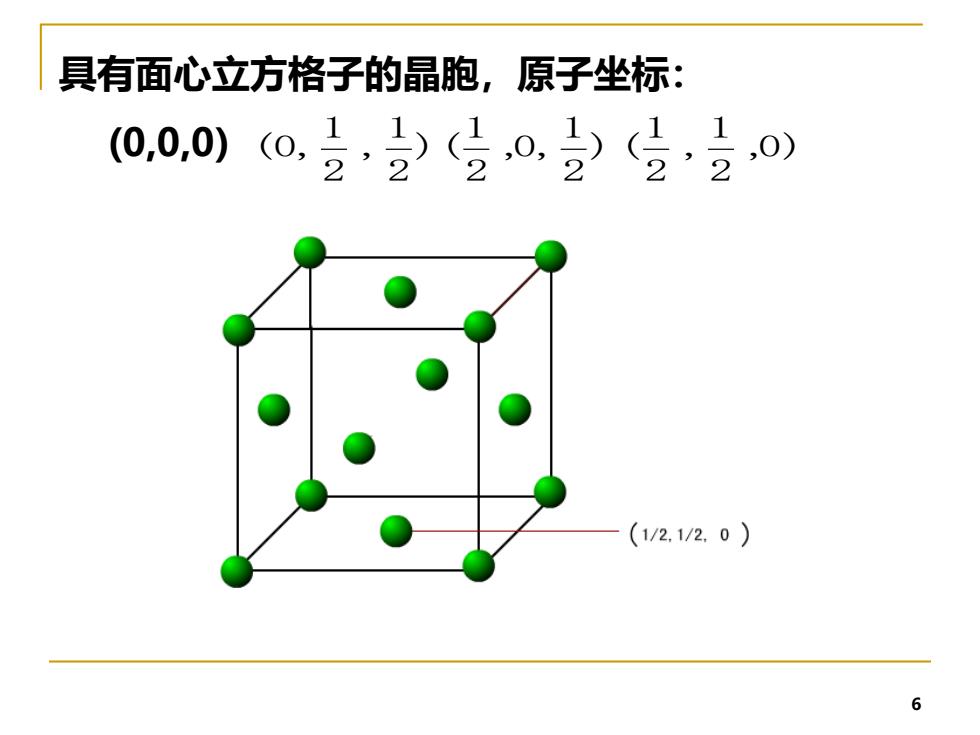
6 具有面心立方格子的晶胞,原子坐标: (0,0,0) ) 2 1 , 2 1 (0, ) 2 1 ,0, 2 1 ( ,0) 2 1 , 2 1 (
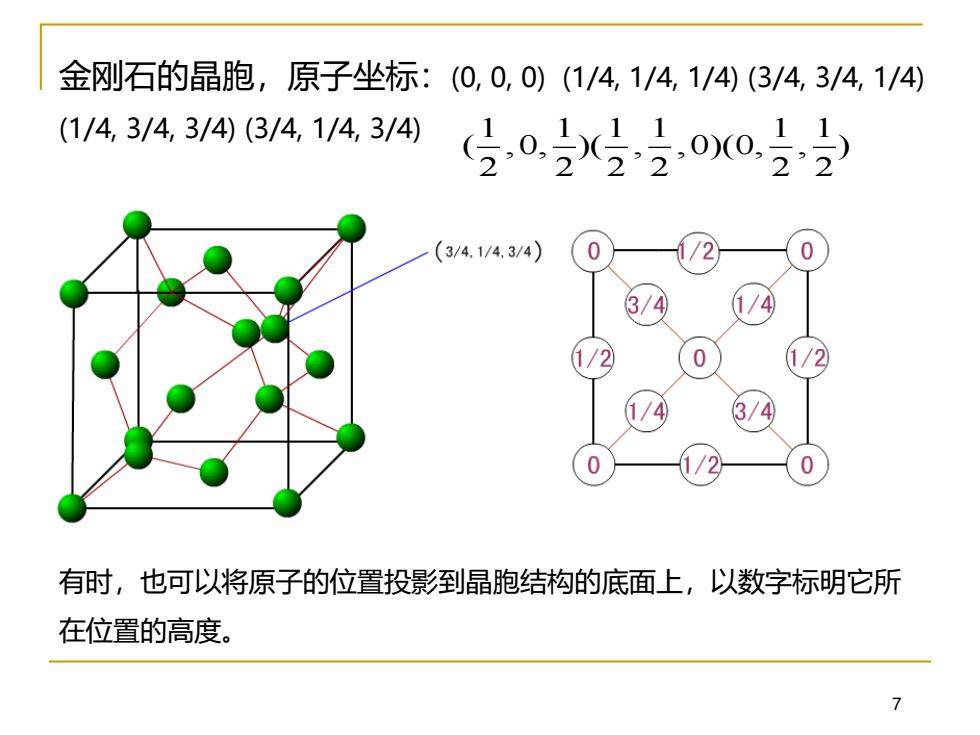
金刚石的晶胞,原子坐标:(0,0,0)(114,1/4,1/4)(3/4,3/4,1/4) (1/4,3/4,3/4)(3/4,1/4,3/4) 分3o022 (3/4.1/4.3/4) 0 3/4 4 1/2 0 1/2 4 4 有时,也可以将原子的位置投影到晶胞结构的底面上,以数字标明它所 在位置的高度
7 金刚石的晶胞,原子坐标:(0, 0, 0) (1/4, 1/4, 1/4) (3/4, 3/4, 1/4) (1/4, 3/4, 3/4) (3/4, 1/4, 3/4) 有时,也可以将原子的位置投影到晶胞结构的底面上,以数字标明它所 在位置的高度。 1 1 1 1 1 1 ( ,0, )( , ,0)(0, , ) 2 2 2 2 2 2
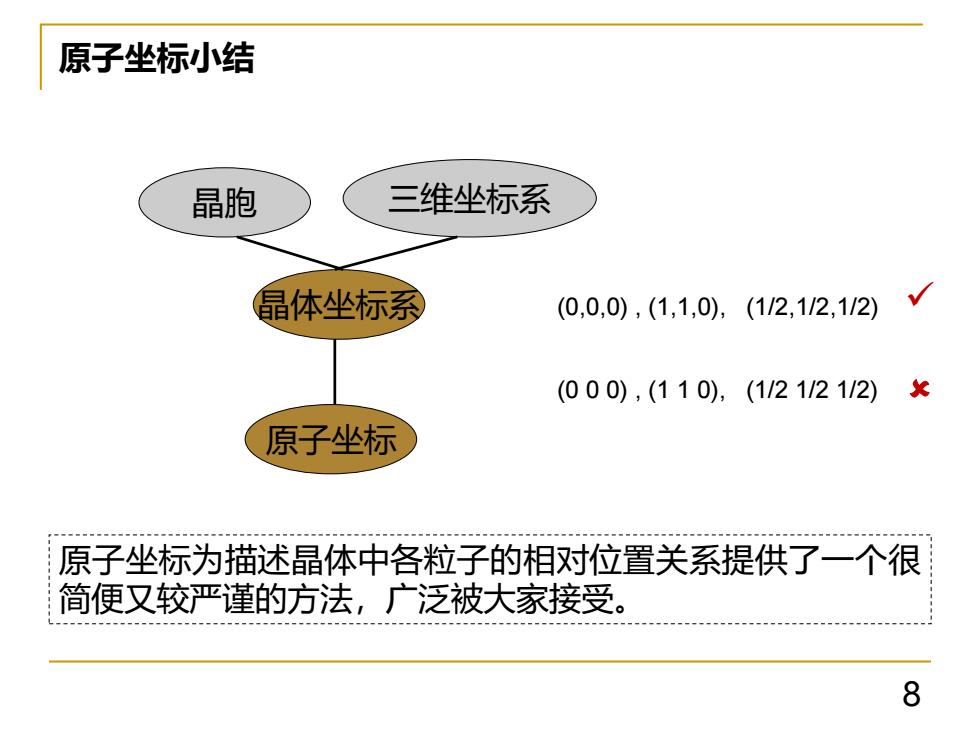
原子坐标小结 晶胞 三维坐标系 晶体坐标系 (0,0,0),(1,1,0),(112,112,112) (000),(110),(1/21/21/2) 原子坐标 原子坐标为描述晶体中各粒子的相对位置关系提供了一个很 简便又较严谨的方法,广泛被大家接受。 8
8 原子坐标小结 原子坐标为描述晶体中各粒子的相对位置关系提供了一个很 简便又较严谨的方法,广泛被大家接受。 晶胞 三维坐标系 晶体坐标系 原子坐标 (0,0,0) , (1,1,0), (1/2,1/2,1/2) (0 0 0) , (1 1 0), (1/2 1/2 1/2) ✓

4.2晶面及晶面指数 晶体中晶面:含有多于三个质点的平面 相邻两层平行晶面之间的距离,称晶面间距 晶面上单位面积上的质点个数称作晶面的面密度 不平行的晶面之间的夹角称作晶面夹角 在同一晶体的格子结构中,沿不同方向可以构成许多组 这样相互平行的晶面,不同晶面间彼此相差一定角度,并且 他们的晶面间距、面密度及质点种类、价键密度也不同,这 将导致这些晶面的物理、化学性质有所不同。 为区分晶体这些晶面,结晶学上人们用晶面指数来描述。 显然晶胞中包含了晶体中各种晶面
9 晶体中晶面: 含有多于三个质点的平面 相邻两层平行晶面之间的距离,称晶面间距 晶面上单位面积上的质点个数称作晶面的面密度 不平行的晶面之间的夹角称作晶面夹角 在同一晶体的格子结构中,沿不同方向可以构成许多组 这样相互平行的晶面,不同晶面间彼此相差一定角度,并且 他们的晶面间距、面密度及质点种类、价键密度也不同,这 将导致这些晶面的物理、化学性质有所不同。 为区分晶体这些晶面,结晶学上人们用晶面指数来描述。 显然晶胞中包含了晶体中各种晶面。 4.2 晶面及晶面指数

确定晶面指数的三个步骤(采用前述晶体坐标系): (1)该晶面与X,Y,Z轴相交的长度,5,t: (2)分别取其倒数1/仁,1/5,1/代,并对这 三个分数进行通分: (3)通分后三个分数的分子就是这个 晶面的晶面指数hk/。 这种晶面指数又称密勒指数。 例如图中晶面的晶面指数为: 2,2,3- 111.332 2'2'3666 →(332) 简单说晶面指数:”晶体坐标系下,截距倒数通分取分子” 10
10 s t r (1)该晶面与X, Y, Z轴相交的长度 r, s, t; (2)分别取其倒数1/r, 1/s, 1/t,并对这 三个分数进行通分; 1 1 1 3 3 2 2 2 3 332 2 2 3 6 6 6 ,→ → → , , ( ) (3)通分后三个分数的分子就是这个 晶面的晶面指数 h k l 。 例如图中晶面的晶面指数为: 确定晶面指数的三个步骤(采用前述晶体坐标系): X Y Z O 简单说晶面指数:”晶体坐标系下,截距倒数通分取分子” 这种晶面指数又称密勒指数