
第三章晶体的对称性理论 3.1对称性概念,对称动作和对称要素 3.2晶体的宏观对称性及32个点群 3.3晶体的微观对称性及230个空间群 1
1 第三章 晶体的对称性理论 3.1 对称性概念,对称动作和对称要素 3.2 晶体的宏观对称性及32个点群 3.3 晶体的微观对称性及230个空间群

什么是对称性? 自然界中的 对称性 建筑中的 对称性 生活中的 对称性 微观世界中 的对称性
什么是对称性? 自然界中的 对称性 建筑中的 对称性 生活中的 对称性 微观世界中 的对称性

什么是对称性? 生活当中许多物品具有一定的对称性; ◆晶体的外形和各种性质常具有一定的对称性; ◆选取单位的外形对称性(宏观对称性)应能充分反应空间 点阵的对称性.。 如何定义“对称”这一概念?
如何定义“对称”这一概念? 生活当中许多物品具有一定的对称性; ◆晶体的外形和各种性质常具有一定的对称性; ◆选取单位的外形对称性(宏观对称性)应能充分反应空间 点阵的对称性. 什么是对称性?

3.1对称性概念,对称动作和对称要素 3.1.1基本概念 1、等同图形:几何学上,将具有对称形象的物体的 各部分称为等同图形。 等同图形分为相等图形和不相等图形 2、相等图形:完全迭合的等同图形,或称全等图形。 例如:花瓣、雪花 3、不相等图形:互成镜像的等同而不相等图形。 例如:左右手 4、对称图形:由两个或两个以上的等同图形构成,并且很有 规律地重复着。对称图形中既包括相等图形又包括不相等图形
4 3.1 对称性概念,对称动作和对称要素 3.1.1 基本概念 1、等同图形:几何学上,将具有对称形象的物体的 各部分称为等同图形。 等同图形分为相等图形和不相等图形 2、相等图形:完全迭合的等同图形,或称全等图形。 例如:花瓣、雪花 3、不相等图形:互成镜像的等同而不相等图形。 例如:左右手 4、对称图形:由两个或两个以上的等同图形构成,并且很有 规律地重复着。对称图形中既包括相等图形又包括不相等图形

5、对称动作:将对称图形中某一部分中的任意点带到一个等 同部分中的相应点上去,使新图形与原图形重合的动作。 如:旋转、反映、倒反、平移. 6、对称要素:进行对称动作时,必须依据的几何元素,如点、 线、面等。 7、对称性:物体中各等同部分在空间排列的特殊规律性。 8、阶 次:对称图形中所包括的等同部分的数目,它代表 着对称程度的高低
5 5、对称动作:将对称图形中某一部分中的任意点带到一个等 同部分中的相应点上去,使新图形与原图形重合的动作。 如:旋转、反映、倒反、平移. 6、对称要素:进行对称动作时,必须依据的几何元素,如点、 线、面等。 7、对 称 性:物体中各等同部分在空间排列的特殊规律性。 8、阶 次:对称图形中所包括的等同部分的数目,它代表 着对称程度的高低
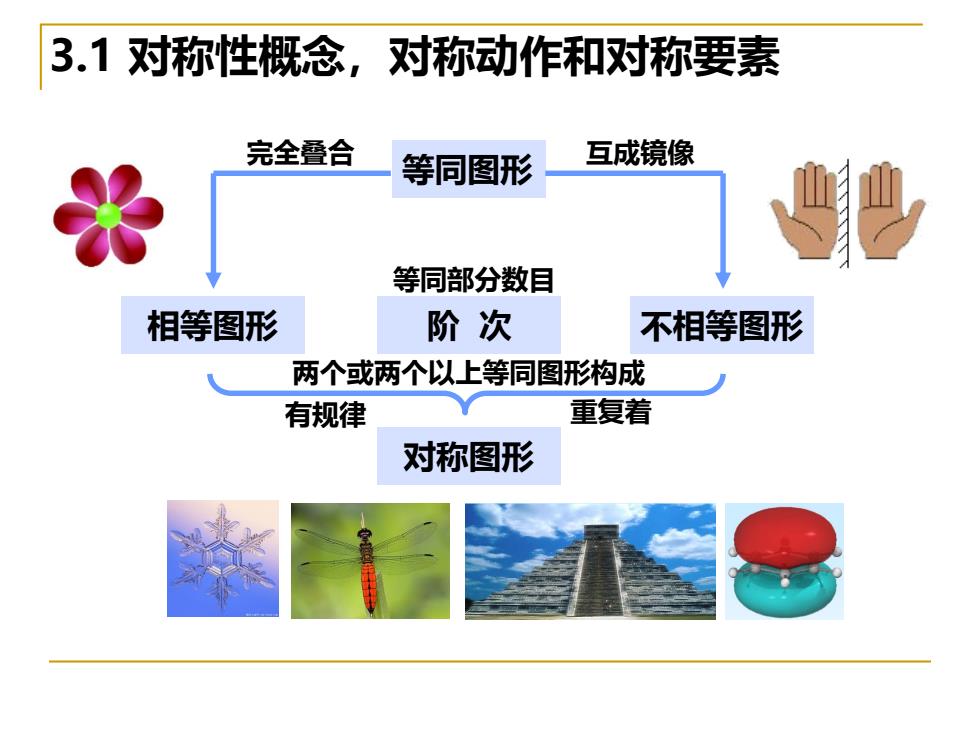
3.1对称性概念,对称动作和对称要素 完全叠合 等同图形 互成镜像 等同部分数目 相等图形 阶次 不相等图形 两个或两个以上等同图形构成 有规律 重复着 对称图形
3.1 对称性概念,对称动作和对称要素 等同图形 相等图形 不相等图形 对称图形 完全叠合 互成镜像 两个或两个以上等同图形构成 有规律 重复着 阶 次 等同部分数目
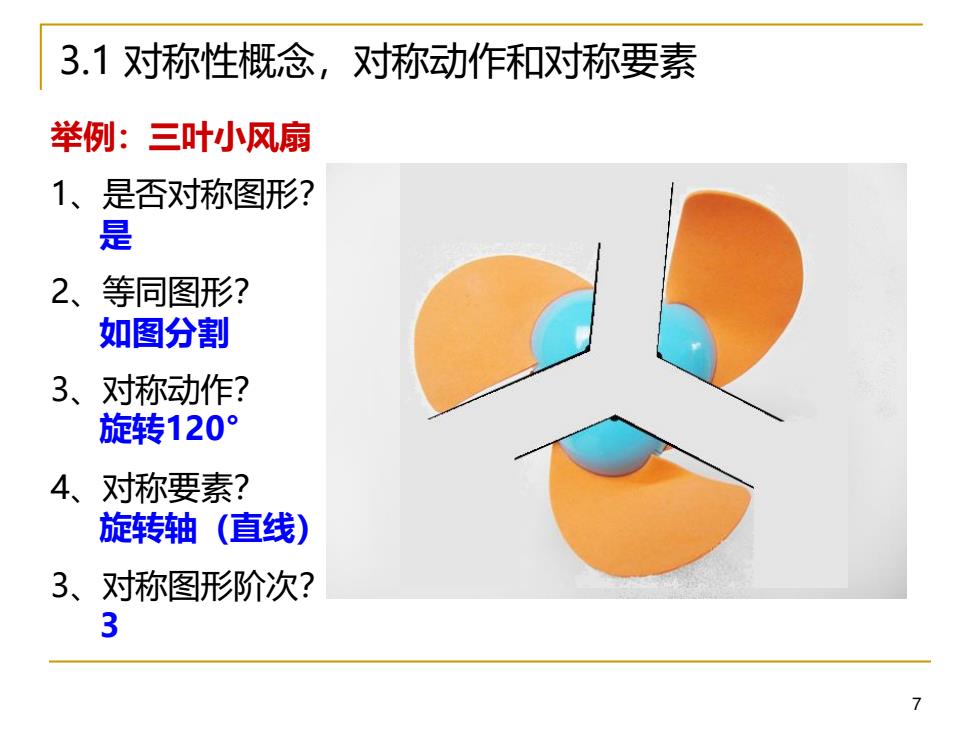
3.1对称性概念,对称动作和对称要素 举例:三叶小风扇 1、是否对称图形? 是 2、等同图形? 如图分割 3、对称动作? 旋转120° 4、对称要素? 旋转轴(直线) 3、对称图形阶次? 3
7 3.1 对称性概念,对称动作和对称要素 1、是否对称图形? 2、等同图形? 3、对称动作? 4、对称要素? 3、对称图形阶次? 是 如图分割 3 旋转120° 旋转轴(直线) 举例:三叶小风扇

3.1对称性慨念,对称动作和对称要素 举例:吉大唐敖庆楼 1、是否对称图形? 是 2、等同图形? 如图分割 3、对称图形阶次? 2 4、对称动作? 反映 5、对称要素? 反映面 8
8 3.1 对称性概念,对称动作和对称要素 举例:吉大唐敖庆楼 1、是否对称图形? 2、等同图形? 3、对称图形阶次? 4、对称动作? 5、对称要素? 是 如图分割 2 反映 反映面

于e
9

雪花 雪花 枝晶 分形
10