
第二章晶体构造理论
1 第二章 晶体构造理论

《结晶学》第二章 晶体构造理论 几何学的前辈们从最简单朴素出发,创造出许多十 分完美的概念:点、直线、平面、圆等等。人们借此 建立了各种各样解决实际问题的模型,十分方便。 §2.1点阵和平移群/格子 §2.2五种平面点阵形式 §2.3十四种空间点阵形式 §2.4晶体结构 §2.5晶体结构的描述方法
2 几何学的前辈们从最简单朴素出发,创造出许多十 分完美的概念:点、直线、平面、圆等等。人们借此 建立了各种各样解决实际问题的模型,十分方便。 晶体构造理论 《结晶学》第二章 §2.1 点阵和平移群/格子 §2.2 五种平面点阵形式 §2.3 十四种空间点阵形式 §2.4 晶体结构 §2.5 晶体结构的描述方法

2.1点阵和平移群 晶体的结构、形态、性质上的干差万别,取决 于构成晶体的微粒(原子、分子、离子及它们组成的 复杂的基团)的种类的不同,和取决这些微粒在空 间的排列方式的不同。 概念:晶体、结点、 点阵、结构基元、原 胞、晶胞
3 2.1 点阵和平移群 晶体的结构、形态、性质上的千差万别,取决 于构成晶体的微粒(原子、分子、离子及它们组成的 复杂的基团)的种类的不同,和取决于这些微粒在空 间的排列方式的不同。 概念:晶体、结点、 点阵、结构基元、原 胞、晶胞

2.1点阵和平移群 本节主要讨论的是晶体中微粒的排列方式问题, 因此可以抛开构成这些微粒的具体的物质内容(原子、 分子、离子及基团),把微粒抽象成几何学上的点。 称之为结点。这些结点在空间的规则排列的列阵就 称点阵。当把点阵上结点的位置安放上具体的物质 微粒(称结构基元),就构成了具体的晶体结构
4 2.1 点阵和平移群 本节主要讨论的是晶体中微粒的排列方式问题, 因此可以抛开构成这些微粒的具体的物质内容(原子、 分子、离子及基团),把微粒抽象成几何学上的点。 称之为结点。这些结点在空间的规则排列的列阵就 称点阵。当把点阵上结点的位置安放上具体的物质 微粒(称结构基元),就构成了具体的晶体结构
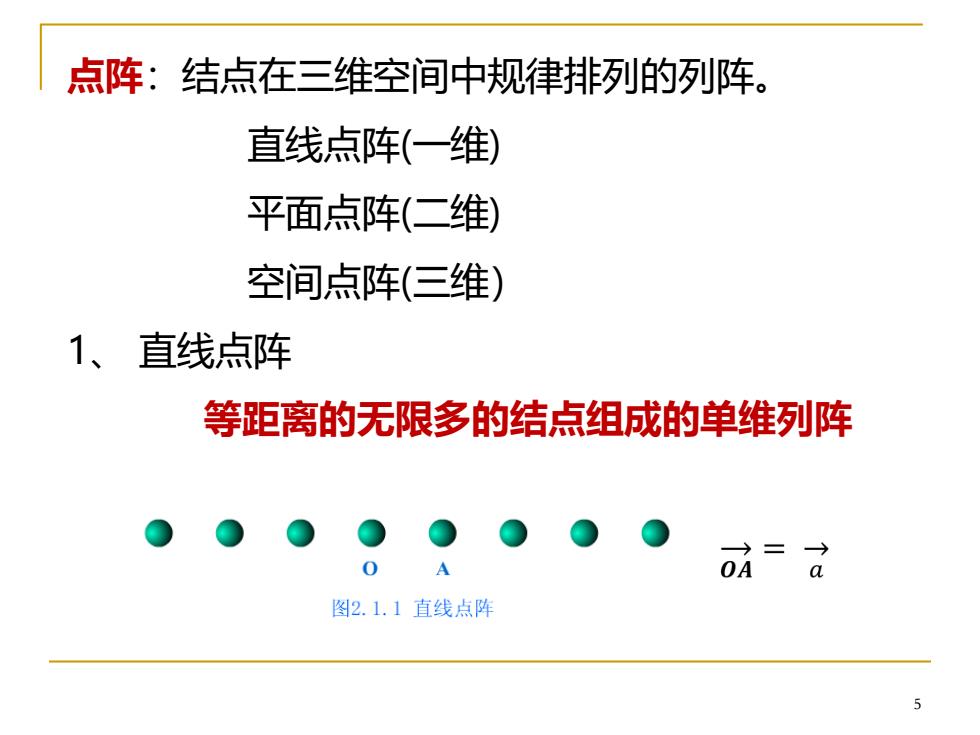
点阵:结点在三维空间中规律排列的列阵。 直线点阵(一维) 平面点阵(二维) 空间点阵(三维) 1、直线点阵 等距离的无限多的结点组成的单维列阵 =d OA 图2.1.1直线点阵 5
点阵:结点在三维空间中规律排列的列阵。 直线点阵(一维) 平面点阵(二维) 空间点阵(三维) 1、 直线点阵 等距离的无限多的结点组成的单维列阵 5

直线点阵可以由一组使点阵复原的素向量和复向量 来表示,称平移群。直线点阵的平移群可以写成: T=ma m的取值 (m=0,±1,±2,±3。.),它点阵的代 到多少? 点阵和平移群有如下的对应关系: (1)从点阵中某一点指向点阵中其它点的向量为平 移群所包括无遗。向量→表达式 (2)以点阵中任意点为起点时,平移群中的每一个向 量都指向点阵中的一个点。表达式→向量 6
6 直线点阵可以由一组使点阵复原的素向量和复向量 来表示,称平移群。直线点阵的平移群可以写成: (m=0,±1, ±2, ±3.),它是点阵的代数表达式。 点阵和平移群有如下的对应关系: (1) 从点阵中某一点指向点阵中其它点的向量为平 移群所包括无遗。向量→表达式 (2) 以点阵中任意点为起点时,平移群中的每一个向 量都指向点阵中的一个点。表达式→向量 m T = ma m的取值 到多少?
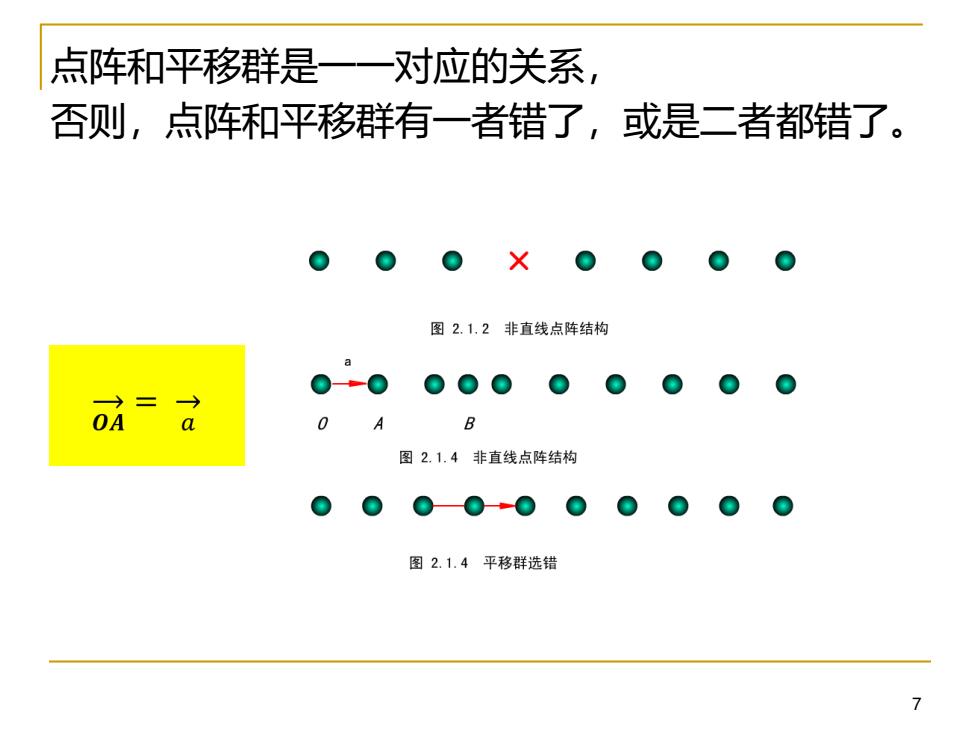
点阵和平移群是一一对应的关系, 否则,点阵和平移群有一者错了,或是二者都错了。 图2.1.2非直线点阵结构 OA a 0 A B 图2.1.4非直线点阵结构 0000 图2.1.4平移群选错
7 点阵和平移群是一一对应的关系, 否则,点阵和平移群有一者错了,或是二者都错了
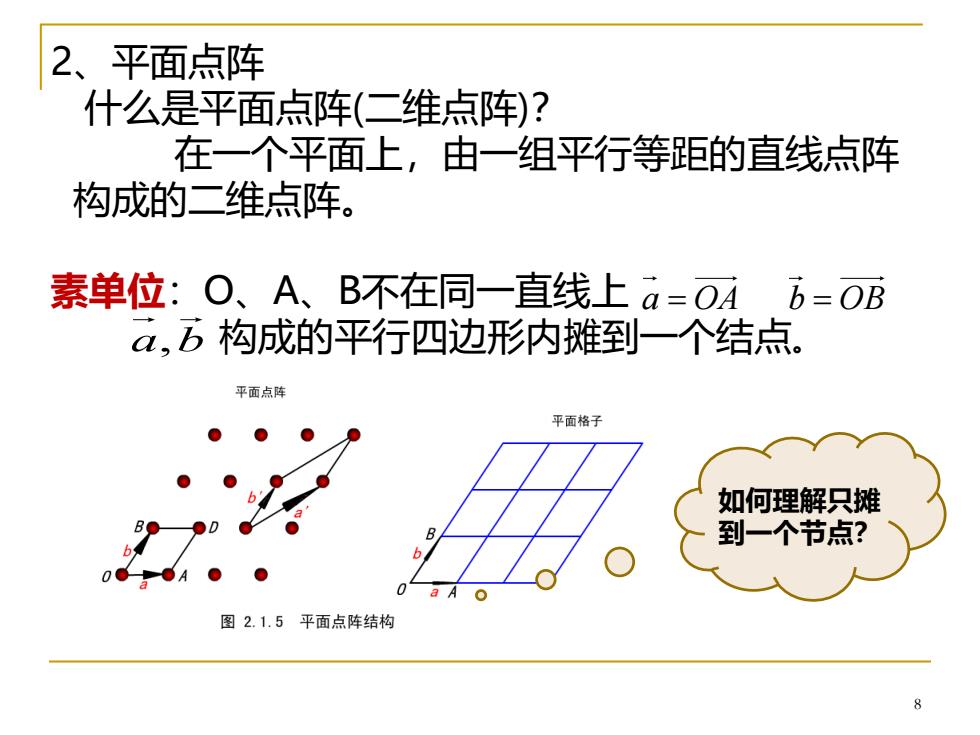
2、平面点阵 什么是平面点阵(二维点阵)? 在一个平面上,由一组平行等距的直线点阵 构成的二维点阵。 素单位:O、A、B不在同一直线上a=OA=OB a,五构成的平行四边形内摊到一个结点。 平面点阵 平面格子 如何理解只摊 到一个节点? 6 0 a A 图2.1.5平面点阵结构
8 2、平面点阵 什么是平面点阵(二维点阵)? 在一个平面上,由一组平行等距的直线点阵 构成的二维点阵。 素单位:O、A、B不在同一直线上 构成的平行四边形内摊到一个结点。 a OA = b OB = a b, 如何理解只摊 到一个节点?
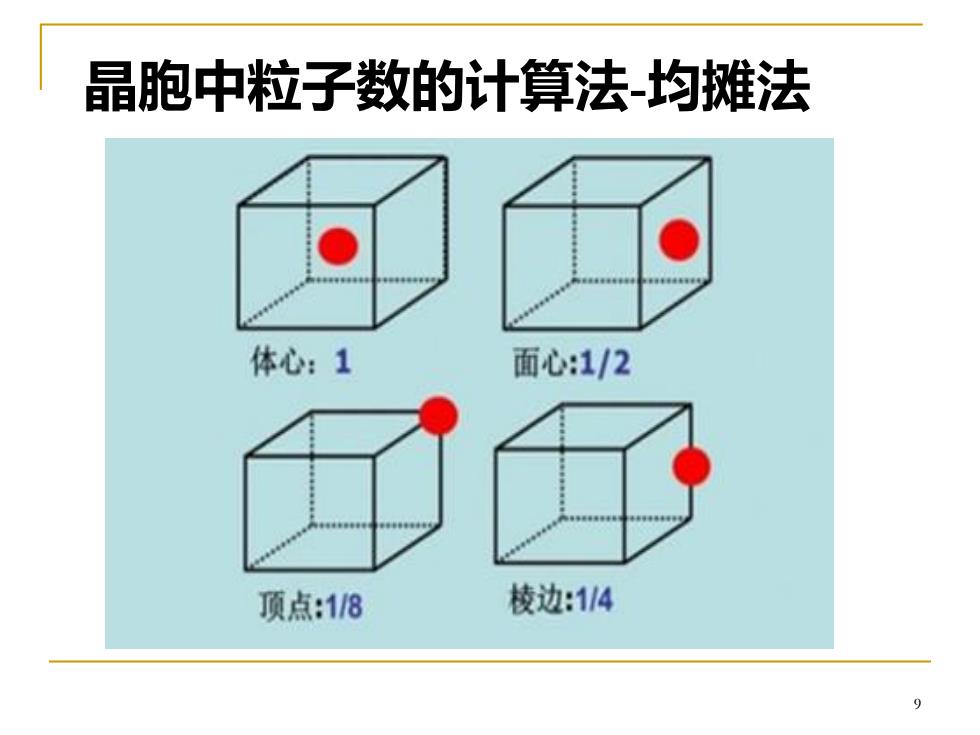
晶胞中粒子数的计算法-均摊法 体心:1 面心:1/2 顶点:1/8 棱边:1/4
晶胞中粒子数的计算法-均摊法 9
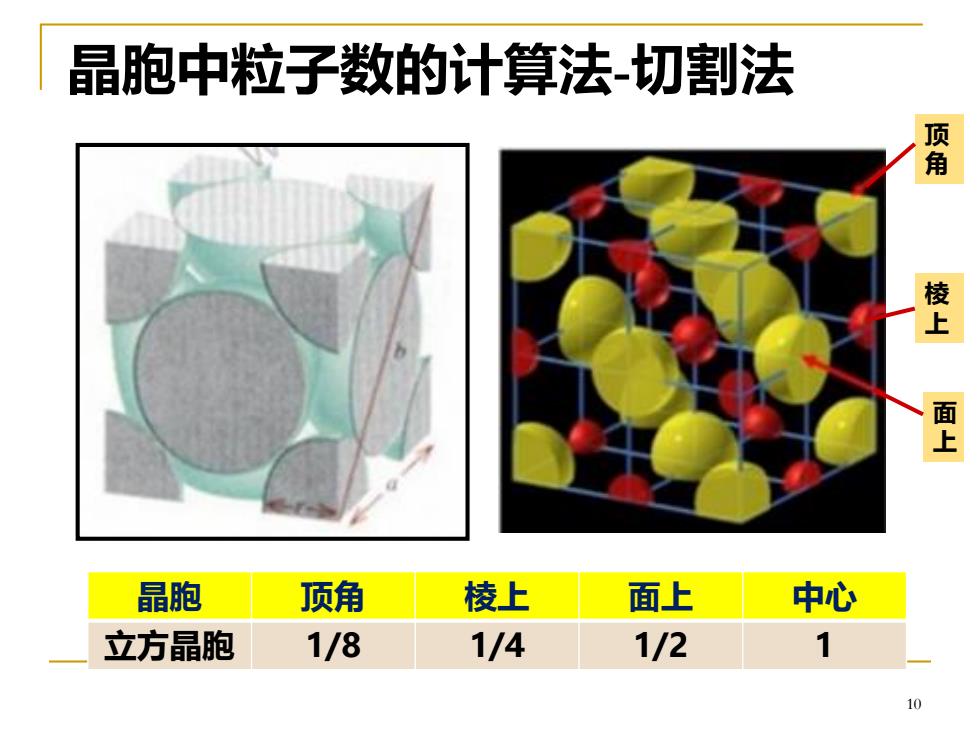
晶胞中粒子数的计算法切割法 檀 面 晶胞 顶角 棱上 面上 中心 立方晶胞 1/8 1/4 1/2 1
10 晶胞中粒子数的计算法-切割法 晶胞 顶角 棱上 面上 中心 立方晶胞 1/8 1/4 1/2 1 顶 角 棱 上 面 上