
第八章磁能 §8.1戴流线圈系统的磁能 §8.2戴流线圈在外磁场中的磁能 §8.3 磁场的能量和磁能密度 *§8.4非线性介质及磁滯损耗 *§8.5 利用磁能求磁力
第八章 磁能 §8.1 戴流线圈系统的磁能 §8.2 戴流线圈在外磁场中的磁能 §8.3 磁场的能量和磁能密度 *§8.4 非线性介质及磁滯损耗 *§8.5 利用磁能求磁力
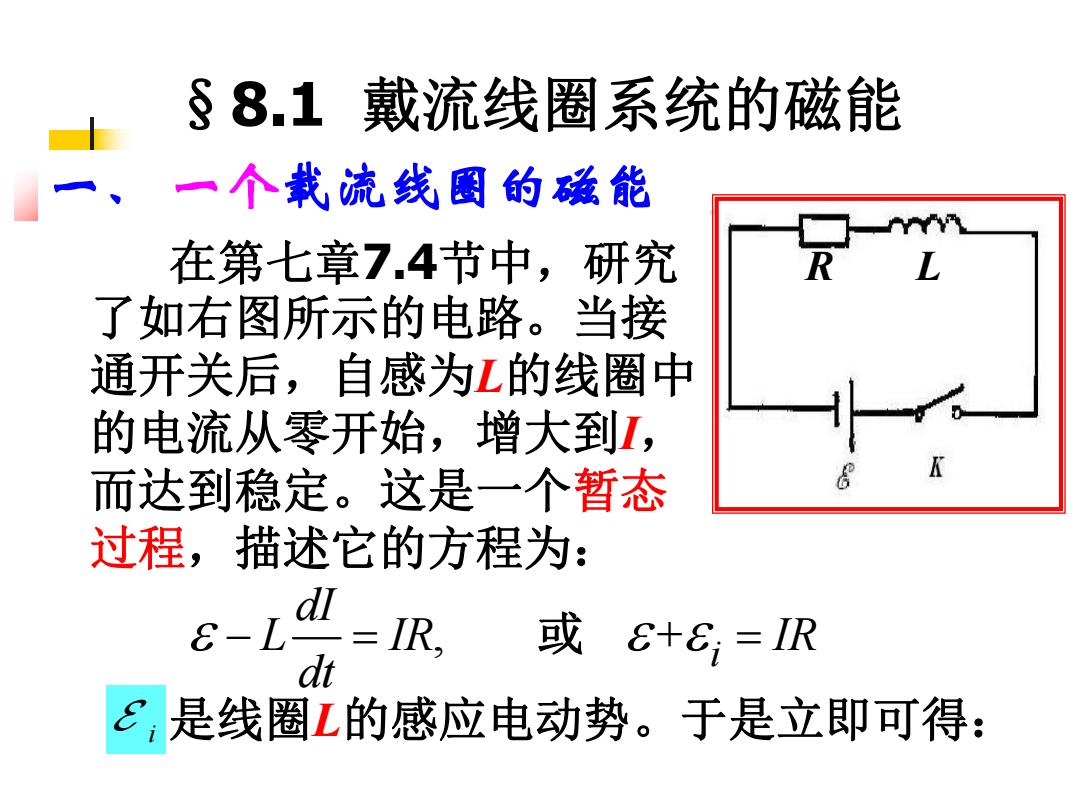
§8.1戴流线圈系统的磁能 一个载流线图的磁能 在第七章7.4节中,研究 R 了如右图所示的电路。当接 通开关后,自感为L的线圈中 的电流从零开始,增大到I, 而达到稳定。这是一个暂态 过程,描述它的方程为: dl -L=IR, 或&+E=IR dt ,是线圈L的感应电动势。于是立即可得:
§8.1 戴流线圈系统的磁能 一 、 一个载流线圈的磁能 在第七章7.4节中,研究 了如右图所示的电路。当接 通开关后,自感为L的线圈中 的电流从零开始,增大到I, 而达到稳定。这是一个暂态 过程,描述它的方程为: R L , + i dI L IR IR dt 或 i 是线圈L的感应电动势。于是立即可得:

Idt =i LIdI +I-Rdt (8.1.1) 或 8Idt =-8 Idt+I'Rdt (8.1.2) ■式(8.1.1)说明,电源在时间dt内作功并消耗能 量SIdi, 其中除一部分转变为电阻R的焦耳热I2Rdt 之外,另一部分用来反抗线圈的感应电动势作功,其 值为Lldl或-&,Idt。 ■我们知道,在开关接通以前线圈中的电流为零,其 磁场为零,作为零能态;开关接通后,电流逐渐增大, 线圈内磁场逐渐增强,这正是电源消耗一部分能量反 抗线圈的感应电动势作功的结果,该能量转变为线圈 的磁能(即磁场能)W
Idt LIdI I Rdt 2 或 2 i Id t Id t I R d t (8.1.1) (8.1.2) ■式(8.1.1)说明,电源在时间 内作功并消耗能 量 ,其中除一部分转变为电阻R的焦耳热 之外,另一部分用来反抗线圈的感应电动势作功,其 值为 或 。 ■我们知道,在开关接通以前线圈中的电流为零,其 磁场为零,作为零能态;开关接通后,电流逐渐增大, 线圈内磁场逐渐增强,这正是电源消耗一部分能量反 抗线圈的感应电动势作功的结果,该能量转变为线圈 的磁能(即磁场能) : dt Idt 2 I Rdt LIdI Wm i Idt
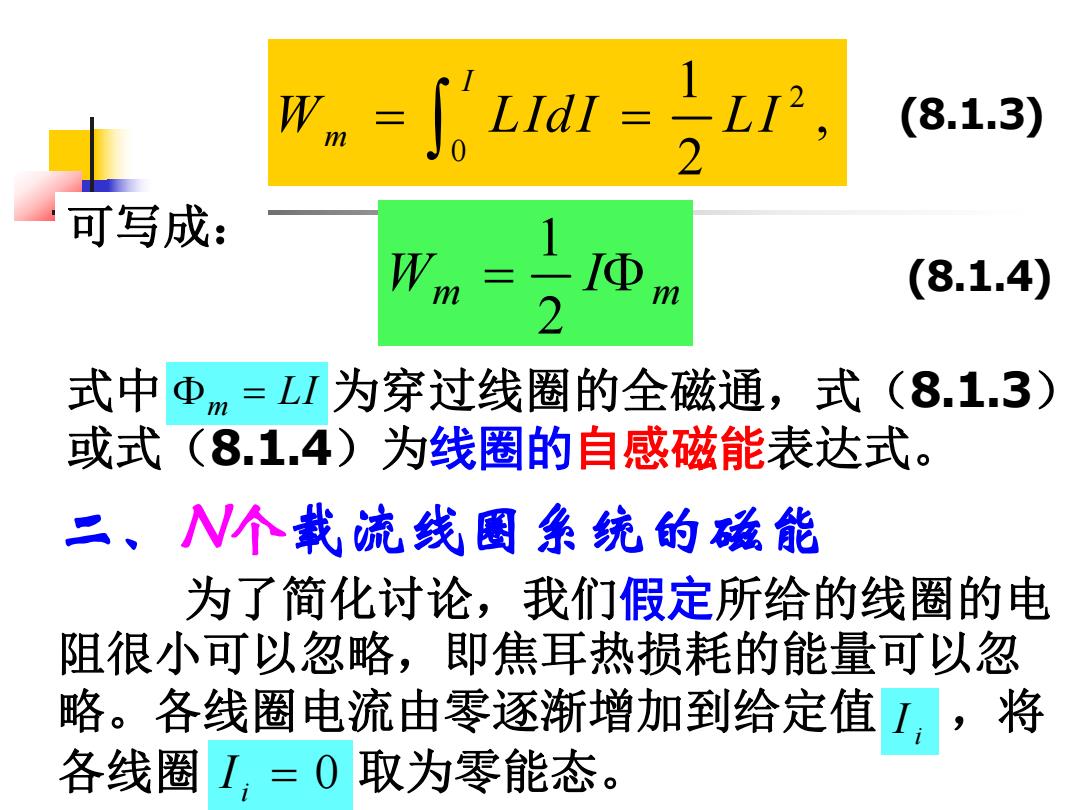
R。-ia=, (8.1.3) 可写成: m (8.1.4) 2 式中Φm=L1为穿过线圈的全磁通,式(8.1.3) 或式(8.1.4)为线圈的自感磁能表达式。 二、N个载流线图条统的強能 为了简化讨论,我们假定所给的线圈的电 阻很小可以忽略,即焦耳热损耗的能量可以忽 略。各线圈电流由零逐渐增加到给定值,,将 各线圈1,=0取为零能态
2 0 1 , 2 I Wm LIdI LI (8.1.3) 可写成: Wm Im 2 1 (8.1.4) 式中 为穿过线圈的全磁通,式(8.1.3) 或式(8.1.4)为线圈的自感磁能表达式。 m LI 二、N个载流线圈系统的磁能 为了简化讨论,我们假定所给的线圈的电 阻很小可以忽略,即焦耳热损耗的能量可以忽 略。各线圈电流由零逐渐增加到给定值 ,将 各线圈 取为零能态。 i I 0 i I

■ 在某一瞬间,在第个线圈中,感应电动势, 由下式确定: =-4-2w (8.1.5) dt k=1 dt k丰i L是第个线圈的自感, M H 是第k个线圈和第i 个线圈之间的互感。 ■因此,在第个线圈中, 电源反抗感应电动势£ 在t时间内所作的功是: W dj =-8 di ll dl,+ul dix (8.1.6) k=1 k≠i
■ 在某一瞬间,在第i个线圈中,感应电动势 由下式确定: i 1 N i k i i ki k k i dI dI L M dt dt (8.1.5) 是第i个线圈的自感, 是第k个线圈和第 i 个线圈之间的互感。 ■ 因此,在第i个线圈中,电源反抗感应电动势 在 dt 时间内所作的功是: L i M ki i N k i k i i i i i i ki i k dA I dt L I dI M I dI 1 (8.1.6)

■在N个线圈中,总的电源作功是: dAr=∑a4=∑L4,a,+∑M1,alg (8.1.7) i=1 i=1 i,k=1 k≠i ■由M:=Mk以及上式右边第二项互换求和指标 和k结果不变,得: i,k=1 4成2d i,k=1 i,k=1 i.k= k≠i k≠i i≠k i≠k 于是,可将式(8.1.7)写成: dA'= ∑Mkdu,Hk)+∑Ll,d山, 2 i,k=1 i=l i≠k
■在N 个线圈中,总的电源作功是: N i N k i i k i i i ki i k N i dA dAi L I dI M I dI 1 1 , 1 (8.1.7) ■由 以及上式右边第二项互换求和指标 i和k结果不变,得: ( ) 2 1 2 1 , 1 , 1 , 1 , 1 k N i k i k ik i N i k i k ik k i N k i i k ki i k N k i i k ki i k M I dI M I dI M I dI M d I I Mki Mik ■于是,可将式(8.1.7)写成: N i i i i N i k i k dA Mik d IiIk L I dI , 1 1 ( ) 2 1

将上式从始态(全部1,=0)至末态积分便得: 4+2, 23 i-1 i≠k 该功转换为系统的磁能 W 三拉1片 N (8.1.8) i,k=1 i≠k 于是,方程右边的第一项表示N个线圈系统的互 感磁能,第二项表示自感磁能
■将上式从始态(全部 I i 0 )至末态积分便得: N i i i N i k i k ik i k A M I I L I 1 2 , 1 2 1 2 1 ■该功转换为系统的磁能 Wm : N i i i N i k i k m ik i k W A M I I L I 1 2 , 1 2 1 2 1 (8.1.8) 于是,方程右边的第一项表示N个线圈系统的互 感磁能,第二项表示自感磁能

■进一步,记Mm=L,则式(8.1.8)可表为: W W m= (8.1.9) i,k=1 ■设Φa=MaI=MkIk,它表示第k个线圈的电流 的磁场通过第个线圈的磁通,且令: Φ,= ∑D:=∑MkIk (8.1.10) k=1 k=1 于是式(8.1.9)又可写成: 形m=2∑1, (8.1.11) 式(8.1.9)与式(8.1.11)只不过是式 (8.1.8)的另一种表述方式,便于记忆
■进一步,记 Mii Li ,则式(8.1.8)可表为: N i k m ik i k W M I I , 1 2 1 (8.1.9) ■设 ,它表示第k个线圈的电流 的磁场通过第i个线圈的磁通,且令: ki Mki k ik k I M I N k ik k N k i ki M I 1 1 (8.1.10) ■于是式(8.1.9)又可写成: N i m i i W I 1 2 1 (8.1.11) 式(8.1.9)与式(8.1.11)只不过是式 (8.1.8)的另一种表述方式,便于记忆

§ 8.2戴流线圈在外磁场中的磁能 对两个载流线圈的系统,我们应用式(8.1.9】 求得磁能的表达式如下: Wm =号L1+)L,4g+M21,1 (8.2.1) 上式右边第一、第二项分别是两个载流线圈的 自感磁能,第三项是两个载流线圈的互感磁能 当我们只对两个载流线圈的相互作用感兴趣时, 即只研究它们的互感磁能,也就是互能,把它 记为W12,,其表达式为: W12=M12I12=①1212 (8.2.2)
§8.2 戴流线圈在外磁场中的磁能 n 对两个载流线圈的系统,我们应用式(8.1.9) 求得磁能的表达式如下: 2 2 1 1 2 2 12 1 2 1 1 . 2 2 Wm L I L I M I I (8.2.1) 上式右边第一、第二项分别是两个载流线圈的 自感磁能,第三项是两个载流线圈的互感磁能。 ■ 当我们只对两个载流线圈的相互作用感兴趣时, 即只研究它们的互感磁能,也就是互能,把它 记为 W12 ,其表达式为: 12 12 1 2 12 2 W M I I I , (8.2.2)

式(8.2.2)可进一步写成: W2=12JB,(3)dS, (8.2.3) 我们可将该系统的互能看成为载流线圈2在外磁 场B,中所具有的磁能 对均匀外磁场中的载流线圈或非均匀外磁场中 的小载流线圈,式(8.2.3)右边的5)可从积 分号中提出,简记为B,以至: W2=B.(I2S2)=m·B. (8.2.4) 这是磁矩m在外磁场B中的磁能表达式,与第三章3.3 节例3.4中对应的电偶极子在外电场中的能量表达 式W。=-p·E相比差一负号,在§8.5中解释
式(8.2.2)可进一步写成: 2 12 2 1 2 ( ) , S W I d B r S (8.2.3) 我们可将该系统的互能看成为载流线圈2在外磁 场 中所具有的磁能。 ■对均匀外磁场中的载流线圈或非均匀外磁场中 的小载流线圈,式(8.2.3)右边的 可从积 分号中提出,简记为B,以至: B1 1 2 B(r) 12 2 2 W B(I S ) mB. (8.2.4) 这是磁矩m在外磁场B中的磁能表达式,与第三章3.3 节例3.4中对应的电偶极子p在外电场中的能量表达 式 We p E 相比差一负号,在§8.5中解释